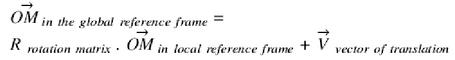DNA tri- and tetra-loops and RNA tetra-loops hairpins fold as elastic biopolymer chains in agreement with PDB coordinates

Abstract

The biopolymer chain elasticity (BCE) approach and the new molecular modelling methodology presented previously are used to predict the tri- dimensional backbones of DNA and RNA hairpin loops. The structures of eight remarkably stable DNA or RNA hairpin molecules closed by a mispair, recently determined in solution by NMR and deposited in the PDB, are shown to verify the predicted trajectories by an analysis automated for large numbers of PDB conformations. They encompass: one DNA tetraloop, -GTTA-; three DNA triloops, -AAA- or -GCA-; and four RNA tetraloops, -UUCG-. Folding generates no distortions and bond lengths and bond angles of main atoms of the sugar–phosphate backbone are well restored upon energy refinement. Three different methods (superpositions, distance of main chain atoms to the elastic line and RMSd) are used to show a very good agreement between the trajectories of sugar–phosphate backbones and between entire molecules of theoretical models and of PDB conformations. The geometry of end conditions imposed by the stem is sufficient to dictate the different characteristic DNA or RNA folding shapes. The reduced angular space, consisting of the new parameter, angle Ω, together with the χ angle offers a simple, coherent and quantitative description of hairpin loops.

INTRODUCTION

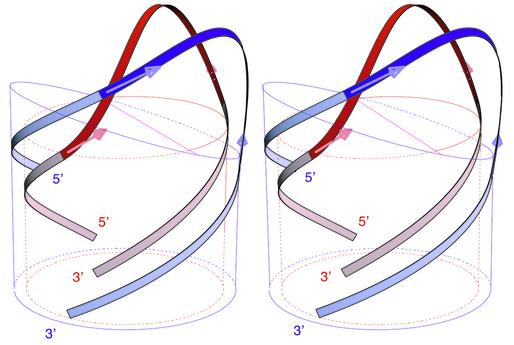
In the preceding article in this issue, we have postulated that the backbone of single-stranded DNA hairpin loops behaves as a continuous, inextensible and flexible thin rod. With this simple hypothesis, the tri-dimensional trajectory of this elastic line was derived from the theory of elasticity and we have shown how it can be used to predict the structures of the sugar–phosphate backbone of DNA hairpins. We have shown also how single-stranded trinucleotide B-DNA TTT could be folded into hairpin loops, G-TTT-C or C-TTT-G, where most torsion angles are preserved, to match four different sets of NMR data or five different molecular conformations (1–4). In this approach, called biopolymer chain elasticity (BCE), the trajectories of the two helical backbones of the hairpin stem define the geometry of the extremities of the hairpin loop. In the theory of elasticity of thin rods, the geometry of end conditions dictates the shape of the trajectories. Therefore the different shapes of DNA and RNA hairpin loops should be predicted or should result from the different geometries imposed by the stem structures. Double helical B-DNA and A-RNA differ in two respects. Firstly the planes of base pairs and of helical extremities are perpendicular to the helical axis in B-DNA whereas they are tilted in A-RNA. Secondly B-DNA helix has a smaller radius. As shown in Figure 1, when the backbones trajectories of the loops (in dark red or blue) are in perfect continuity with the backbones trajectories of the double helix (in light colour), we predict that the backbone of the DNA tetraloop must go over the surface of the DNA cylinder, whereas the trajectory of RNA backbone is circumscribed on or slightly outside the RNA cylinder as shown in Figure 1. In this article, we investigate whether the BCE methodology and its tri-dimensional predictions that were presented previously for DNA triloops (5) and build on previous ideas (6,7) can be applied not only to other hairpins of different structures, of different lengths, tri- and tetra-loops of DNA, but also to RNA tetraloops.

Figure 1.

Superimposed stereo views into the minor groove of the computed elastic rod curve for a DNA tetraloop hairpin, shown in red, and for an RNA tetraloop hairpin shown in blue. The radii of cylinders and circles are those of the sugar–phosphate backbones, DNA (red) and RNA (blue). The mean planes of base pairs are indicated by the top sections of the cylinders.

To this end, we have selected eight different molecules of which structures have been recently determined in solution by NMR and deposited in the Protein Data Bank (PDB) (8). They encompass: one DNA tetraloop, -GTTA-; three DNA triloops, -AAA-, -GCA-, -GCA-; and four RNA tetraloops, -UUCG-, as presented in Table 1. The DNA triloops and RNA tetraloops have been the subject of many determinations over the last decade and have given rise to well defined solution structures since early NMR studies (9,10). They have been used as test systems for theoretical studies (11–13). For brevity and convenience, the molecules are referred by their PDB identifications. These eight molecules have several features in common. They are all remarkably stable (7,14) and the loop is closed by a side-by-side sheared mispair (15,16) G·A (1ac7), A·A (1bjh), G·A (1xue, 1zhu), or by a head to side U·G mispair (17) (1aud, 1b36, 1c0o, 1hlx). Note that the DNA triloops studied here are structurally different from the TTT hairpins studied previously (5). In the latter, the first and last nucleoside of the loop were not stacked on the top base pair of the stem. They never formed a mispair. They were located in the minor groove, in the major groove or in the solvent and did not interact with each other.

Table 1. Molecular structures selected from the PDB, with PDB identification, number of structures in square brackets and tetraloop folding type (7,18), original authors, DNA or RNA sequences of PDB structures and of theoretical BCE models, and locations of the loop bases in the Major (M) groove, in the minor (m) groove, stacked in the central part of the helix (c) or in the solvent outside the structure (solv.).

PDB identification	Authors	DNA or RNA sequence solved experimentally & sequence used in theoretical models	Na	Nb	Nc	Nd
DNA
1ac7 [10] Type I	van Dongen et al. 1997 (15)	d(…ccta-GTTA-tagg…) & d(gcta-GTTA-tagc)	c/M	M	M / solv	c/m
1bjh [16]	Chou et al. 1996 (16)	d(gtac-AAA-gtac) & d(gcac-AAA-gtgc)	c/M	M	c	-
1xue [10]	Zhu et al. 1996 (30)	d(…gaat-GCA-atgg…) & d(gcat-GCA-atgc)	c/M	M	c	-
1zhu [10]	Zhu et al. 1995 (38)	d(caat-GCA-atg) & d(gcat-GCA-atgc)	c/M	M	c	-
RNA
1aud [31] Type II	Allain et al. 1997 (20)	r(…gucc-UUCG-ggac…) & r(gccc-UUCG-gggc)	c/M	m / solv	M	c
1b36 [10] Type II	Butcher et al. 1999 (21)	r(…gcgc-UUCG-gcgc…) & r(gcgc-UUCG-gcgc)	c/M	m / solv	M	c
1c0o [19] Type II	Colmenarejo and Tinoco 1999 (22)	r(…gguc-UUCG-gguc…) & r(gcuc-UUCG-gggc)	c/M	m / solv	M	c
1hlx [20] Type II	Allain and Varani 1995 (17)	r(…uaac-UUCG-guug…) & r(gcac-UUCG-gugc)	c/M	m / solv	M	c

Absence of fourth nucleotide in the loop is denoted (-). The loop bases are marked Na, Nb, Nc and Nd in the 5′ to 3′ direction.

Well defined DNA and RNA tetraloops come essentially in three different folds (7,18). Type-I loops are only observed for DNA. They adopt a conformation with the first three bases at the 5′-end of the loop forming a more or less continuous stack on the 3′-end of the stem (1ac7) (15). Type-II loops are found in both DNA (CTTG) (18) and RNA (1aud, 1b36, 1c0o, 1hlx). As indicated in Table 1, Nb is turned into or towards the minor groove and Nc lies over the closing base pair NaNd. A third fold, type-III, is only observed in RNA and is described by a continuous stacking of Nd, Nc and Nb on the 5′-end of the stem.

DNA hairpins can perform many important and diverse biological functions as recently established by numerous experiments and as briefly reviewed in the previous article in this issue. The DNA tetraloop -GTTA- (1ac7) is related to telomeric and centromeric structures (15). The DNA triloops -AAA- (1bjh) and -TTT- are important components of the adenoassociated virus 2 (4,5). The two DNA triloops -GCA- are encountered in human centromere repeats (1xue) and in centromeric GNA triplets (1zhu) and are important to account for the observed expansion of triplet repeats (5). RNA hairpins have been known to play essential structural and biological roles for several decades (14,19). In particular, the hairpin contained in 1aud is part of the polyadenylation inhibition element bound to the RNP domain of the human U1A protein (20). In 1b36, the -UUCG- tetraloop was added to stabilise the structure of one of the two domains essential for catalysis in a ribozyme molecule (21). Similarly in 1c0o, the stable -UUCG- loop was added to close an RNA metal hexammine binding site from the P5 helix of the catalytic core of the Tetrahymena group I intron ribozyme (22). In 1hlx, the tetraloop is the capping part of the P1 helix from group I self-splicing introns (17).

Advances in synthetic and spectroscopic techniques have recently extended the size and the accuracy of RNA molecular structures that can now be solved by NMR (20). The solution structures retained here for analysis were determined between 1995 and 1999, from large collections of NMR data. Due to their sizes, to the different complex protocols used, and to the rapid evolution of computer programs, the complete data may be only partly available and it may be difficult to analyse in an identical way to that of the original authors and as we have done in the previous article in this issue. For these reasons, the theoretical molecular structures built with the BCE approach were not compared with NMR-derived distances and to a single molecular structure as previously described (5), but directly to available PDB solution structures. Note that the eight corresponding PDB files contain many molecular conformations, in numbers from 10 up to 31 per coordinates file (Table 1), because solution structures were derived from NMR. Their total number is 126. Due to this large number, the computer program introduced previously, S-mol (5), was enhanced to deal with automatic comparisons. This is an important change that required specific modifications of the BCE methodology as explained in Materials and Methods and below.

In this article, our main focus is to search a general theoretical approach, which is capable of: (i) predicting a priori the tri-dimensional course of the sugar–phosphate chains, not only of DNA hairpin molecules structurally different from TTT hairpins, but also of RNA hairpins, (ii) generating models close to solution structures from these predictions and from large numbers of given PDB conformations, and (iii) characterising the importance of the sugar– phosphate chain and of its elastic properties in the folding process.

MATERIALS AND METHODS

Original molecular structures, PDBid

Original molecular conformations are from the PDB (8) and are referred by their PDBid: 1ac7, 1b36, 1xue, 1zhu, 1aud, 1bjh, 1c0o and 1hlx.

Initial stem and loop model building by molecular mechanics

All initial structures were generated from canonical B-DNA or A-RNA (23).

Theoretical molecular structures, BCE

A registered software Smol^©(5) was extended under UNIX and Linux environments using Mathematica (24), Geomview (25) and C languages to build and to compare BCE models with solution conformations of PDB files.

The complete DNA or RNA sequences of the theoretical molecular structures, given in Table 1, were simplified with the two following rules. The sequence of the loop and of the first two base pairs in the stem is identical to original PDB molecular structures. The length of stems is reduced to four base pairs and the remaining sequence of the stem is set to d(GC).d(GC) or r(GC).r(GC). Note that all PDB conformations proposed under a given PDB identification were used for building the theoretical structures. The length, L, of the capping rod was obtained as previously described (5) by fitting a helical line to the atoms of the main sugar–phosphate backbone (O5′, C5′, C4′, C3′, O3′, P) of a single-stranded helical A-RNA or B-DNA and by minimising the root-mean-square of the sum of squared distances to the helical line. For A-RNA radius of helical line was 9.35 Å and its pitch was 30.85 Å/turn. For B-DNA, values were respectively 8.35 Å and 33.74 Å/turn. Molecules were folded into hairpin loops using prescribed geometric boundary conditions.

Setting all PDB conformations in the laboratory reference frame

PDB conformations are moved onto BCE molecular models by a translation-rotation coordinate transformation.

Optimised molecular structures, ‘BCE3Ωopt’

Molecular structures provided in PDB files and summarised in Table 1 were used at the third step of theoretical molecular modelling to optimise the rotation angles about the elastic line, Ω, and the glycosidic torsion angles, χ, of each nucleoside in the loop independently from other nucleosides. This was performed by a least square fit on homologous atom positions to give optimised BCE models, BCE3Ωopt.

Final theoretical molecular structures, ‘BCE4finalm’

BCE molecular models were energy refined without restraints. Energy refinements were carried out with the program AMBER (5,26,27) without any restraints and with a large stopping root-mean-square energy gradient criterion 0.5 kcal/(mol.Å) to yield final molecular models, BCE4finalm.

RMSd analysis

RMSd are computed after superposing the two sets of matching atoms by a translation-rotation coordinate transformation.

RESULTS

The BCE approach enhanced to treat multiple PDB conformations

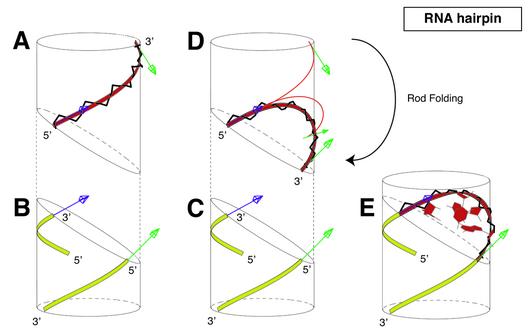
Folding a DNA or an RNA hairpin loop with the BCE approach can be described as a three-step procedure, completed by a short energy refinement step to restore backbone bond lengths and bond angles (5). A short and intuitive account of the procedure modified to treat multiple PDB conformations is given below and in Figure 2. (i) Single-stranded A-RNA or B-DNA are basically considered as a continuous and flexible thin rod in the following practical manner. These polymers are generated along helical lines, which are also viewed as elastic lines. The main atoms of the sugar–phosphate backbone (O5′, C5′, C4′, C3′, O3′, P) play a key role because they are attached to this line and because they are used to define the origins of local reference frames for all remaining atoms in the nucleotide. As a result, there are six different groups of atoms per nucleotide. The polymer may thus be viewed as a succession of individual solid blocks of atoms attached to the elastic line. Using this basic framework where all backbone atoms are made part of the elastic line as shown for A-RNA in Figure 2A, the biopolymer chain can be bent and twisted smoothly using elasticity theory of thin rods into a given loop with prescribed end conditions (Fig. 2B and C). This step yields a elastic curve, BCE1curve (Fig. 2D), which can be fitted onto the double helical stem (Fig. 2C). Note that the tri-dimensional trajectory of the elastic line is uniquely determined for end conditions of Figure 2B and C. (ii) Transportation of the biopolymer chain onto the elastic line step yields a molecular model, BCE2basicxyz (Fig. 2A, D and E). Crucial parameters are the length of the loop, tri- or tetra-loop, and the geometry of end conditions imposed by the A-RNA or B-DNA helices. (iii) A useful feature provided by this formalism is that each block of atoms, and consequently an entire nucleoside, can be rotated about the elastic line with an angle, Ω. Each nucleoside block can be rotated independently to match NMR-derived distances as in the previous article in this issue, or in order to match each one of the molecular conformations given in a PDB file as in this study. This step is defined here as an automated optimisation of angles, Ω, and of glycosidic torsion angles, χ, and yields optimised BCE molecular models, BCE3Ωopt. (iv) Individual molecular blocks are displaced by the folding procedure without internal deformation. However the chemical bonds and bond angles of the main atoms of the sugar–phosphate backbone (O5′, C5′, C4′, C3′, O3′, P) are modified by the BCE folding procedure. This is why each molecular structure is very shortly energy refined without restraints to restore backbone bond length and bond angles. This step yields the final theoretical molecular model, BCE4finalm.

Figure 2.

Schematic overview of the construction process of an RNA tetraloop hairpin molecular structure using the BCE approach proposed in the previous article in this issue (5). (A) A continuous and flexible thin rod, represented by a ribbon for better visibility, and shown in red is associated to a four nucleotides helical segment; (B and C) two helices of RNA are generated along helical lines, shown in yellow; (D) the flexible rod is bent smoothly into the capping elastic solution curve so that the tangents at its extremities, shown as blue and green arrows, match those of the two helices; helical segments and the capping rod are dissociated for clarity; (E) they are shown fully assembled; the complete molecular structure is the basic BCE molecular model and is computed after global deformation by keeping track of the translations and the rotations required to leave unchanged atoms in their nearest local reference frames along the helical segment.

In this article, we compare the large number of original molecular conformations supplied by a PDB file to their corresponding BCE4finalm molecular models. As summarised in Table 1, these molecules differ from one another in nature, DNA or RNA, in sequence, in length, and in protocol used to determine their solution structures. This may be a source of heterogeneity that is observed in the PDB files. To circumvent this difficulty each original molecular conformation in a PDB file is first translated in an absolute reference frame where all theoretical molecular models are folded. Deformations introduced in the sugar–phosphate backbone are examined at important steps of the folding. We are then in a position to compare each original model conformation of the PDB file to the model structure derived from our theoretical approach.

Multiplicity and heterogeneity of the PDB structures are overcome by setting each conformation in an absolute coordinate frame

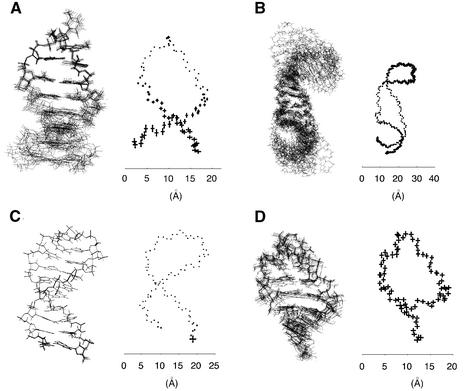
As all structures under study were derived from NMR data, their corresponding PDB files contain many proposed solution conformations (Table 1). A direct view of the first ten conformations of different PDB files demonstrates a wide heterogeneity as shown in Figure 3. For 1ac7 (Fig. 3A), the loop appears either very well determined or very rigid, whereas the stem appears either less well determined or more flexible. This view has the advantage of focusing on detailed features of the loop structures (15). The situation is reversed with 1b36 where the main focus is on the central region (Fig. 3B) (21). With the PDB file, 1xue (Fig. 3C), the molecule appears well determined or rigid at every atom positions, whereas with 1c0o, it appears homogeneously underdetermined or flexible (Fig. 3D). This heterogeneity in the PDB structures originates from the arbitrary choice of presentation of superposed molecules. It depends on the molecule and its properties (DNA or RNA, size and sequence, free or bound to a protein) and on the local nature of the two types of information derived from NMR data (torsion angle values from J-couplings and short distances <6 Å from NOE data).

Figure 3.

The first ten superimposed views (left) with the standard deviations of the main atoms of the sugar–phosphate backbone plotted at mean atom positions (right) of the n molecular conformations available in the PDB for the following PDB identifications and sequences: (A) n = 10, 1ac7, DNA tetraloop GTTA, (B) n = 10, 1b36, RNA tetraloop UUCG, (C) n = 10, 1xue, DNA triloop GCA, (D) n = 19, 1c0o, RNA tetraloop UUCG. The molecules are of different sizes, and the scale in Å is provided for comparison.

These observations introduce a supplementary difficulty to build the theoretical models at the three different stages of: (i) adjustment of helical thin rod onto the stem to set the elastic curve, BCE1curve, (ii) production of the basic model structure, BCE2basicxyz, (iii) optimisation of angles, Ω and χ of all nucleotides in the loop, BCE3Ωopt. For these matching operations and optimisations to make sense, both molecular models, PDB and theoretical conformations, must be set in the same reference frame coordinates. Since the PDB conformations under study are superposed in arbitrary reference frames, we may choose an absolute and unique reference frame to perform all building operations. It is chosen according to Cambridge conventions on nucleic acids (28). z is the axis of the double helical stem and the first stem base pair contiguous to the loop is used to set the origin, O, and the directions and orientations of axes, Ox and Oy. The loop of the theoretical model is then automatically built on top of this stem structure with the correct sequence, length and geometry (A-RNA or B-DNA) to yield the basic BCE model. At this point, the nucleotides in the loop have not been rotated, i.e. the loop has not been optimised. It is this unique BCE model that serves as a reference to set the coordinates of the n conformations of the PDB file. This is accomplished by superposing any given PDB conformation onto this BCE model. The matching subset is restricted to the sugar– phosphate backbone of the loop and to the first two base pairs of the stem to avoid giving too much weight to the loop or to the stem. Note at this step that the nucleosides in the loop cannot be used since they do not possess correct conformations. Starting from this unique BCE model, all theoretical models are then built by optimising Ω and χ angles of loop nucleosides to each of the n conformations in the PDB file as explained in Materials and Methods. Optimised BCE models are energy refined without restraints to yield final theoretical molecular models, BCE4finalm.

Analysis and detailed comparison of the 126 pairs of theoretical and PDB structures is a long task due to the number of molecules and to the complexity of each PDB conformation that reflect in part, the intrinsic properties of the sequence, original NMR data as well as modelling protocols used to derive the solution conformations. Presentation of these results is greatly simplified because they can be regrouped into three main homogeneous classes which exactly correspond to the three categories of molecules under study: the DNA tetraloop, DNA triloops and RNA tetraloops. Three representative molecules 1ac7, 1bjh and 1b36 of these categories are sufficient to illustrate all results (Figs 4–7).

Figure 4.

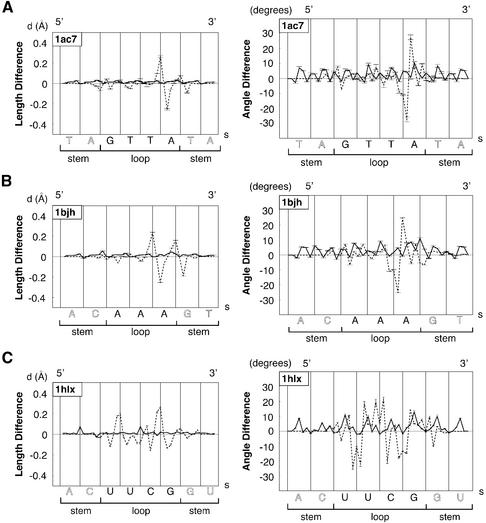
Typical plots of mean bond length differences in Å (left) and of mean bond angle differences in degrees (right) for the main chain atoms of the sugar–phosphate backbone (O5′, C5′, C4′, C3′, O3′, P) at two building steps along the loop sequence in the 5′→3′ direction as a function of arclength, s, in Å. Plots are representative of the three main classes of molecules, DNA tetraloop, DNA triloops and RNA tetraloops, and are computed with the following loop sequences and PDB identifications: (A) GTTA (1ac7); (B) AAA (1bjh); (C) UUCG (1b36). Dashed lines correspond to the third folding BCE step: differences of bond length or bond angle are between optimised, BCE theoretical structural models, BCE3Ωopt, and reference values from standard helical nucleic acids models (B-DNA or A-RNA before folding). Continuous lines correspond to the last building step: values are computed between energy refined theoretical molecular models, BCE4finalm, and reference values of standard helical nucleic acids. Error bars are calculated from the whole set of molecular conformations in the PDB file.

Figure 7.

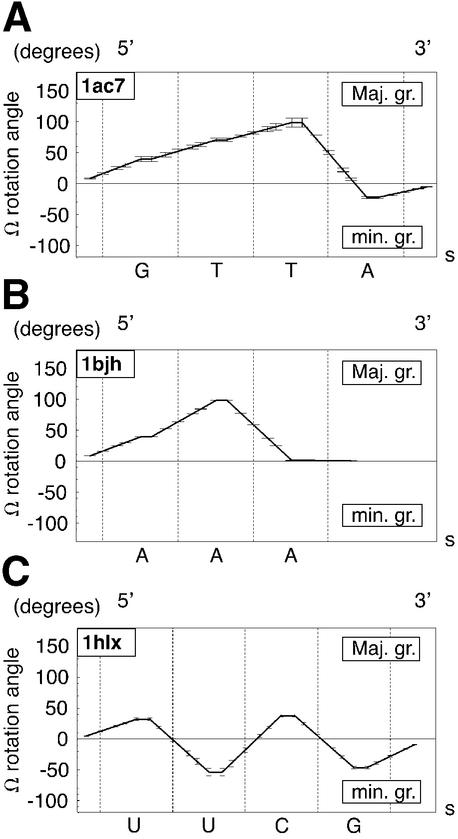
Representative plots of the nucleotide sub-blocks rotation angle, Ω, in degrees, about the elastic rod curve along the loop sequence in the 5′→3′ direction as a function of arclength, s, in Å, in the final theoretical models for the three main classes of molecules under study: DNA tetraloop, DNA triloops and RNA tetraloops: (A) GTTA (1ac7); (B) AAA (1bjh); (C) UUCG (1b36).

Quantitative deformation of the sugar–phosphate main chain

The basic BCE folding procedure described in Figure 2 generates no physical distortions of the initial molecular structure except for the bond lengths and bond angles of the main atoms of the sugar–phosphate backbone. As shown by the dashed lines of Figure 4 (right and left), deformations introduced are generally small: <0.1 Å for bond lengths and <10° for bond angles, except in the region of the sharp turn of B-DNA molecules and in different locations of UUCG RNA molecules. In these regions, deformations are, respectively, generally <0.25 Å and <25°. Note that both bond lengths and bond angles generally oscillate with positive and negative values and that, as expected, both types of plots are well correlated. As shown by the continuous lines of Figure 4, bond lengths and bond angles tend practically to normal values after a short energy refinement without restraints: small oscillations are on the order of thermal fluctuations of bond lengths and bond angles in double helical B-DNA or A-RNA.

Agreement of main chain atoms between theoretical and PDB structures

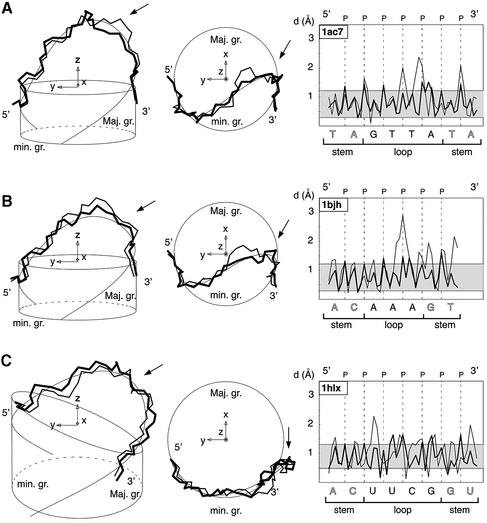
Three different methods are used here to compare and to show a very good agreement between the trajectories of the main atoms of the sugar–phosphate chains of theoretical models, BCE4finalm and of PDB conformations. Direct and visual comparisons are given in Figure 5 (left and centre) with the superpositions of theoretical and PDB structures and of the elastic line. A quantitative comparison is provided with the plot of distance (d) of main atoms of the sugar–phosphate chain to the elastic line as shown in Figure 5 (right). In these plots, d is <1.2 Å for the stem and for most of the loop except in the region of the sharp turn in DNA hairpins and in the UU region of RNA hairpins. Both sugar–phosphate chains oscillate practically in phase in the loop as in the stem region about the central elastic line. Another means of comparison is the computation of a global mean distance or RMSd for different subsets of atoms as summarised in the ‘backbone’ columns of Table 2. RMSd are in the range 0.67–1.56 Å for the main backbone atoms of the loop and 1.09–1.36 Å for the ‘stem+loop’. These values improve when the third nucleotide, Nc, is omitted from the matching set, respectively, 0.20–1.26 Å and 0.97–1.10 Å. This is expected for 1ac7 since Nc is the least well defined residue from NMR restraints (15). For 1bjh, 1xue and 1zhu, it suggests that Nc, which is in the sharp turn region, is less well resolved than the rest of the molecule. For 1aud, 1b36, 1c0o and 1hlx, it evaluates in part the cost of letting Nc in C3′ endo. Note that agreement is best for the DNA triloops and that representative molecules 1bjh and 1b36 of Figures 4–7 are characterised by the highest RMSd values, indicating that other PDB molecular conformations are better fitted by BCE models.

Figure 5.

Left and centre: superimposed views of the sugar–phosphate backbones of a molecular conformation available in the PDB, of its corresponding optimised theoretical molecular structure, highlighted in bold, calculated with the BCE approach and of its computed elastic rod curve shown as a thin line (left: view into the minor groove and centre: top view along the helical axis). Right: plot of the distance, d, in Å, of main atoms of the sugar–phosphate chain to the elastic line for the two molecular structures along the loop sequence in the 5′→3′ direction, as a function of arclength, s, in Å. These views and plots are representative of the three main classes of molecules: DNA tetraloop, DNA triloops and RNA tetraloops. Loop sequences and PDB identifications are respectively: (A) GTTA (1ac7); (B) AAA (1bjh); (C) UUCG (1b36). In the left and centre views, the molecular structures are centred in the same global reference frame; radii of the cylinders and circles are those of the sugar–phosphate backbones: (A–B) DNA or (C) RNA. In the right views, d is shown for the best molecular structure.

Table 2. Average and standard deviations in parentheses of RMSd in Å between the final theoretical molecular models, computed from a continuous and flexible thin rod model or ‘BCE’ model, versus published molecular conformations deposited in the PDB.

PDB identification	Main backbone atoms		Main backbone atoms without Nc		All atoms		All atoms without Nc
	Loop	Stem + loop	Loop	Stem + loop	Loop	Stem + loop	Loop	Stem + loop
DNA
1ac7	1.29 (0.07)	1.22 (0.13)	0.98 (0.06)	0.98 (0.15)	1.62 (0.10)	1.35 (0.10)	0.97 (0.09)	0.92 (0.11)
1bjh	0.91 (0.01)	1.19 (0.01)	0.37 (0.00)	0.99 (0.01)	1.57 (0.00)	1.38 (0.01)	1.27 (0.01)	1.24 (0.01)
1xue	0.67 (0.00)	1.22 (0.01)	0.20 (0.00)	1.07 (0.01)	1.27 (0.00)	1.34 (0.01)	0.97 (0.00)	1.22 (0.01)
1zhu	0.76 (0.13)	1.15 (0.03)	0.32 (0.05)	1.04 (0.05)	1.31 (0.05)	1.32 (0.02)	1.08 (0.03)	1.21 (0.03)
RNA
1aud	1.01 (0.11)	1.09 (0.23)	0.92 (0.12)	1.03 (0.21)	1.94 (0.24)	1.70 (0.19)	1.74 (0.29)	1.55 (0.18)
1b36	1.56 (0.12)	1.36 (0.10)	1.26 (0.13)	1.05 (0.11)	2.11 (0.10)	1.73 (0.09)	1.54 (0.12)	1.28 (0.10)
1c0o	1.36 (0.04)	1.24 (0.04)	1.10 (0.03)	0.97 (0.03)	1.92 (0.04)	1.64 (0.04)	1.43 (0.03)	1.26 (0.04)
1hlx	1.29 (0.07)	1.20 (0.07)	1.15 (0.05)	1.10 (0.08)	1.89 (0.08)	1.55 (0.08)	1.62 (0.11)	1.37 (0.11)

Different sets of atoms are taken into account in the RMSd computations with the following notations: ‘All atoms’ are all nucleotides atoms; ‘Main backbone atoms’ are: P, O5′, C5′, C4′, C3′, O3′; the ‘stem’ includes the first two base pairs below the loop. In columns ‘without Nc’, the third nucleotide, Nc, is not included in the computations.

Agreement between theoretical and PDB structures

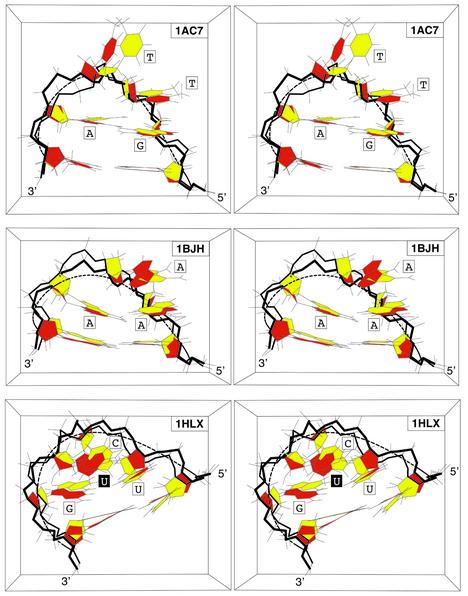
Agreement is very good for the DNA tetraloop, DNA triloops and for RNA tetraloops as shown by the direct and visual comparisons in Figure 6 with the superpositions of the theoretical molecular model and of its PDB conformation. Detailed RMSd for all atom subsets are summarised in the ‘All atoms’ columns of Table 2. They are in the range 1.27–2.11 Å for the loop and 1.32–1.73 Å for the ‘stem+loop’. As above these values are improved when the third nucleotide is omitted from the matching set, respectively: 0.97–1.74 Å and 0.92–1.55 Å. Agreements are very good when compared with estimated accuracy of NMR-derived solution structures, 1–1.5 Å (29).

Figure 6.

Superimposed stereo views into the major groove of hairpin molecular structures derived by the original authors, in yellow, and of the final molecular structures derived from the elastic curve approach, in red: (A) GTTA (1ac7); (B) AAA (1bjh); (C) UUCG (1b36). These views are representative of the three main classes of molecules under study: DNA tetraloop, DNA triloops and RNA tetraloops. The sugar–phosphate chain is highlighted in bold.

Ω Profiles as a function of sequence

Rotation angles, Ω, of blocks of atoms about the elastic line in the final theoretical models follow one of the three remarkable profiles shown in Figure 7 for the DNA tetraloop, DNA triloops and RNA tetraloops. Mean and standard deviation of Ω angle values are given for the nucleosides in Table 3. They are in good agreement with qualitative minor or major groove indications of Table 1. As discussed previously (7,18), the differences in Ω values between the DNA tetraloop and the RNA tetraloop, follow from the fact that in the DNA tetraloop the Nb and Nc nucleotides stack upon each other. In the chosen RNA tetraloop Nb folds into the minor groove, while Nc stacks upon the underlying base pair. Surprisingly, we observe that the DNA tetraloop profile and the DNA triloop profiles are very similar. As shown in Figure 7A and B, values of Ω at the 5′ and 3′ ends of the loops are close to zero, and are maximal in the range 89–99° (see also Table 3) for both classes of molecules. Therefore both types of Ω profiles are very close: the monotonous rise of Ω occurs over the first 3 nt for the DNA tetraloop, and over the first two for DNA triloops. Note RNA tetraloop profiles are different for reasons that may also result from the geometric predictions given in Figure 1.

Table 3. Average rotation angles, Ω_x, and standard deviation of the loop bases, N_x, of the final theoretical molecular models computed from the BCE curve with PDB conformation structures. Ω_a is the rotation angle of N_a, Ω_b of N_b, Ω_c of N_c and Ω_d of N_d.

PDB identification	Ωa	Ωb	Ωc	Ωd
DNA
1ac7	39.6 (3.9)	70.6 (2.9)	98.6 (7.4)	–22.6 (1.6)
1bjh	39.3 (0.2)	98.2 (0.1)	1.1 (0.1)	-
1xue	30.9 (0.0)	88.6 (0.0)	–0.5 (0.0)	-
1zhu	32.6 (0.3)	89.7 (2.2)	0.5 (0.6)	-
RNA
1aud	29.9 (33.1)	–92.7 (36.6)	41.1 (14.7)	–40.3 (7.5)
1b36	33.5 (3.8)	–57.4 (6.1)	43.2 (3.4)	–49.2 (4.3)
1c0o	32.4 (1.7)	–63.6 (3.2)	39.7 (1.2)	–44.1 (1.8)
1hlx	32.0 (1.9)	–53.7 (6.1)	37.7 (1.9)	–46.4 (2.3)

DISCUSSION

Quantitative deformations of the sugar–phosphate main chain

The BCE methodology permits global deformations of the macromolecule with small deformations of the sugar– phosphate chain. The helical line of B-DNA or A-RNA is chosen to pass in the middle of the main chain atoms. Therefore, curving of this elastic line upon folding of the macromolecular chain introduces alternatively compression of chemical bonds for atoms inside the regions of curvature and expansion for atoms outside. This observation explains in part the oscillatory character of the plots of Figure 4 and also why the bond lengths and bond angles are well restored upon a short energy refinement step. Finally, as shown here and in the different context of the preceding article in this issue, the short energy refinement step gives rise to practically no global deformations of the hairpin structure.

Complexity, multiplicity and heterogeneity of PDB structures: agreement between theoretical and PDB structures

Macromolecules such as DNA and RNA are intrinsically complex and deformable objects, and are therefore difficult to study and to compare with theoretical hairpin molecules. Setting all PDB hairpin coordinates in an absolute reference frame was necessary due to the use of arbitrary reference frames in PDB files. Owing to the flexibilities of the stem, loop and hinge region, we have chosen what seemed to be the best compromise where the weights are proportional to the sizes of the matching sets in stem and loop regions. This method has the advantage of unifying the building procedure of all theoretical structures.

In addition to all these sources of heterogeneity, some of the molecules under study possess outstanding features which may perturb the stem structures. In DNA molecule, 1xue, two unpaired guanines from opposite strands intercalate between sheared G·A base pairs below the first two stem base pairs (30). The 30 nt RNA molecule, 1aud, is part of an RNA–protein complex with 102 amino acids (20). The sequence of 1c0o contains G·U base pairs at the second and third base pairs in the stem, which binds a cobalt hexammine ion (22). Moreover, the numbers of NMR-derived constraints per nucleotide differ depending on the regions of the molecule: 40 for the tetraloop structure, 28 for the stem and an average of 35 for the entire molecule in 1hlx; this results in a higher precision for the loop (17).

All studies on UUCG loops report that the sugars of the two central nucleotides UC in the loop are in C2′ endo conformations whereas all other sugars in the loop or in the stem remain in C3′ endo (17,20–22,31,32). This feature was not taken into account in this preliminary study, and future extension of the folding computer program, S-mol, to DNA or RNA chains with variable puckers and with pucker-dependent chain length (7) should improve the regions of agreements between theoretical and PDB conformations.

These observations and the very good agreements between theoretical and PDB hairpin molecular structures show that the BCE approach and the building method yield robust molecular models. At the present stage of development, they should constitute good starting structures for extensive computational studies based on Metropolis Monte Carlo simulations (33–35) or on molecular dynamics studies (11–13,36,37), where detailed contributions to folding can be examined.

Trajectory of main chain atoms in DNA and RNA hairpins, Ω profiles as a function of sequence and number of nucleotides in the loops

DNA and RNA chains possess an intrinsic BCE that can account for the overall folding shape of these two chemically and geometrically different molecules. This property provides the theoretical grounds for a practical description of nucleotide locations in terms of Ω angles about the central elastic line. It is remarkable that this description appears to be simple transpositions for DNA triloops and the DNA tetraloop. This may be accounted for by the closure of these hairpins by mismatches as explained below.

Loops are closed by a ‘mispair’ that matches the geometry imposed by the BCE backbone

As remarked before (7,18), the stress induced in the CCCG tetraloop (18) may explain the conversion from Watson–Crick to Hoogsteen base pairing that is observed when pH is lowered. The formation of unusual base pairing for the closing base pair such as Hoogsteen C⁺G, or such as GA and UG is a stabilising factor, because the C1′-C1′ distance is shorter than in Watson–Crick base pair, which reduces the stress induced in the loop. The BCE approach should offer a quantitative description to model the loop stress.

The differences in Ω variation throughout the loop (Fig. 7) between DNA and RNA tetraloops are a direct consequence of the choice of loops. The positive Ω values seen in the Type-I, DNA tetraloop is a direct consequence of the continuous stacking. UUCG has a type-II fold: Nb lies then in the minor groove so that Ω is negative, Nc stacked on top closing base pair, so that Ω is positive. A type-II DNA tetraloop would show this same pattern in Ω variation. The BCE methodology gives a compact description of these folds. Another remarkable feature consistent with this analysis is that the loop nucleotides appear to literally fall into place upon Ω rotations, i.e. into the correct positions given in the PDB solution conformations. In particular, simple rotations of the first and of the last nucleotides about the elastic line are sufficient to form the required ‘mispairs’. This suggests that the G·A base pairing encountered in the DNA GCA or GTTA hairpins, the A·A pairing in the AAA hairpin, and the U·G base pairing in RNA UUCG hairpins should no longer be considered as ‘mismatches’ but rather as the best possible base pairings capable of fulfilling the geometric conditions imposed by the BCE hairpin fold. Up to now, these mispairs were regarded as major contributors to the stability because they augment stacking and the number of hydrogen bonding interactions. In contrast, these observations and those obtained previously (5) indicate that the sugar–phosphate backbones adopt a BCE conformation, whether a mismatch is formed or not (5), and that mispairs are an additional stabilising factor, if permitted by the BCE backbone. From this perspective, the most conceptually economical way to fold the DNA triloops is to regard them as hairpins with 3 nt in the loop and not as 1-nt loop. In the same way, loop -GTTA- should be regarded as a tetraloop and not as a hairpin with 2 nt in the loop, since the structure of the sugar–phosphate chain can be deduced from the geometry of the B-DNA stem and since the mispair G·A can be easily formed by two simple Ω rotations (Fig. 7) to add stabilising H bonding and stacking interactions. The same reasoning holds also for RNA UUCG loops. Although more molecules need to be studied in terms of this perspective, all these results appear remarkably coherent.

CONCLUSION

Bending a few nucleotides segment of a macromolecular chain as a thin rigid rod of elasticity theory is one of the simplest conceptual models to fold DNA or RNA macromolecules into hairpins. With this simple idea, we have shown that single-stranded B-DNA can be deformed into hairpin loops that match not only all published NMR data available for trinucleotide TTT loops (5), but also the PDB structures of tri- and tetra-loops of DNA. We have shown in addition that single-stranded A-RNA can be deformed with the same folding methodology into UUCG tetraloops. Note the shapes of DNA and RNA hairpins are different, but are well reproduced by the same methodology applied with the different end conditions imposed by B-DNA or A-RNA helical geometries. These results tend to demonstrate that elastic properties of the sugar–phosphate chains play a key role to understand the folding shapes of both DNA and RNA into hairpins. Up to now, several main types of interactions have been invoked to explain the remarkable stability of all hairpins under study: specific hydrogen bonding, stacking and hydrophobic interactions. The sugar–phosphate chains appear to fold along the smoothest lines of least deformation energy (given by elasticity theory) and most torsion angles remain close to their initial values (B-DNA or A-RNA). It suggests that, for these molecules, the elastic properties of sugar– phosphate chains are an important structural and energetic contribution to hairpin folding that may account for their extraordinary stability.

According to usual descriptions, hairpins are double helical base-paired stems capped by a loop sequence of unpaired or of mismatched nucleotides. In the proposed view, these strange mismatches (G·A in tetra- and tri-loops, A·A in triloop AAA, or U·G in UUCG) should rather be considered as very good base pairings that satisfy the geometric requirements imposed by the BCE fold. Note in contrast that Watson–Crick base pairs would not meet these requirements well.

The new parameter angles, Ω, offer a very coherent simplification of the descriptions of hairpin loops containing G·A, A·A or U·G base pairings. More studies are needed to check whether other hairpins can be reproduced with the BCE approach and described in terms of parameter angles, Ω. If so, they would provide the first quantitative measurements to classify and to understand the structures of DNA and RNA hairpin loops and possibly of many other important biological macromolecules.