Abstract
Background
Comparative analysis of sequenced genomes reveals numerous instances of apparent horizontal gene transfer (HGT), at least in prokaryotes, and indicates that lineage-specific gene loss might have been even more common in evolution. This complicates the notion of a species tree, which needs to be re-interpreted as a prevailing evolutionary trend, rather than the full depiction of evolution, and makes reconstruction of ancestral genomes a non-trivial task.
Results
We addressed the problem of constructing parsimonious scenarios for individual sets of orthologous genes given a species tree. The orthologous sets were taken from the database of Clusters of Orthologous Groups of proteins (COGs). We show that the phyletic patterns (patterns of presence-absence in completely sequenced genomes) of almost 90% of the COGs are inconsistent with the hypothetical species tree. Algorithms were developed to reconcile the phyletic patterns with the species tree by postulating gene loss, COG emergence and HGT (the latter two classes of events were collectively treated as gene gains). We prove that each of these algorithms produces a parsimonious evolutionary scenario, which can be represented as mapping of loss and gain events on the species tree. The distribution of the evolutionary events among the tree nodes substantially depends on the underlying assumptions of the reconciliation algorithm, e.g. whether or not independent gene gains (gain after loss after gain) are permitted. Biological considerations suggest that, on average, gene loss might be a more likely event than gene gain. Therefore different gain penalties were used and the resulting series of reconstructed gene sets for the last universal common ancestor (LUCA) of the extant life forms were analysed. The number of genes in the reconstructed LUCA gene sets grows as the gain penalty increases. However, qualitative examination of the LUCA versions reconstructed with different gain penalties indicates that, even with a gain penalty of 1 (equal weights assigned to a gain and a loss), the set of 572 genes assigned to LUCA might be nearly sufficient to sustain a functioning organism. Under this gain penalty value, the numbers of horizontal gene transfer and gene loss events are nearly identical. This result holds true for two alternative topologies of the species tree and even under random shuffling of the tree. Therefore, the results seem to be compatible with approximately equal likelihoods of HGT and gene loss in the evolution of prokaryotes.
Conclusions
The notion that gene loss and HGT are major aspects of prokaryotic evolution was supported by quantitative analysis of the mapping of the phyletic patterns of COGs onto a hypothetical species tree. Algorithms were developed for constructing parsimonious evolutionary scenarios, which include gene loss and gain events, for orthologous gene sets, given a species tree. This analysis shows, contrary to expectations, that the number of predicted HGT events that occurred during the evolution of prokaryotes might be approximately the same as the number of gene losses. The approach to the reconstruction of evolutionary scenarios employed here is conservative with regard to the detection of HGT because only patterns of gene presence-absence in sequenced genomes are taken into account. In reality, horizontal transfer might have contributed to the evolution of many other genes also, which makes it a dominant force in prokaryotic evolution.
Background
As soon as genome sequencing allowed phylogenetic analysis of large protein families, it became clear that different sets of orthologs often produce different tree topologies. The incongruence between tree topologies affects even the most fundamental splits in the history of life, such as the three-domain classification of life forms into bacteria, archaea and eukaryotes [1-4]. In particular, archaeal genes systematically show different phylogenetic affinities, with the components of translation, transcription and replication systems typically affiliating with eukaryotes, and metabolic enzymes and structural proteins displaying bacterial provenance [5,6]. Initially, the discrepancies between different trees have been attributed primarily to artifacts produced by tree-building methods. However, comparative genomics showed beyond reasonable doubt that lineage-specific gene loss and horizontal gene transfer (HGT) are major evolutionary phenomena, at least in the prokaryotic world [7-14]. The prominence of gene loss and HGT in the evolution of prokaryotes is apparent even without detailed phylogenetic tree analysis. Orthologous gene sets, such as those compiled in the database of Clusters of Orthologous Groups of proteins (COGs; http://www.ncbi.nlm.nih.gov/COG/), show a wide spread of phyletic patterns (i.e. patterns of presence-absence of genomes in COGs), with most COGs including only a few lineages, and many having an odd composition, e. g. two bacterial and one archaeal species [12,15,16]. The COG database has been manually curated, with a special emphasis on the correct representation of all analyzed genomes in each COG [15,16]. Therefore, it seems impossible to explain these patterns without invoking massive, lineage-specific gene loss and HGT, and recent quantitative analysis has suggested that these processes contributed to the evolution of a substantial majority of orthologous sets of prokaryotic proteins [17].
Thus, comparative genomics might potentially undermine the very idea of a universal species tree because, inasmuch as HGT is shown to make a substantial contribution to genome evolution, no tree can, in principle, fully reflect the course of evolution of species [7,9,11,18,19]. Attempts to salvage the concept of a species tree, at least in a "weak" form, have been undertaken using comparative analysis of large, in some cases, genome-wide, gene sets. The idea behind these "genome-tree" approaches is that, in spite of the wide spread of gene loss and HGT, genomes might carry a signal of vertical inheritance and the strength of this phylogenetic signal was likely to be, roughly, inversely proportional to the evolutionary distance between species. The methods employed for genome-tree construction included comparison of gene content of orthologous sets, local gene order, and mean similarity between orthologs, as well as more traditional phylogenetic analysis of large gene sets thought to be minimally subject to gene loss and HGT, e.g., genes for ribosomal proteins and other components of the translation machinery [20-29]. Taken together, these analyses suggest that, extensive gene loss and HGT notwithstanding, genome-wide sets of prokaryotic proteins still might carry a phylogenetic signal; moreover, some of the genome-tree approaches appear to have considerable resolution power and reveal potential new major clades among bacteria and archaea [30].
Thus, the species tree concept might survive the genomic challenge, although definitely not unscathed. The species tree can no longer be thought of as a complete depiction of the course of evolution, but only as a central trend in the evolution of organisms. Reconstruction of complete scenarios of genome evolution, including lineage-specific gene loss and HGT events, genomes remains an important goal. Obviously, such a scenario is the sum total of the evolutionary scenarios for individual genes or, more precisely, sets of orthologs (COGs). The reconstruction of the evolutionary scenario for an individual set of orthologous genes can be formulated as follows: given a species tree and a set of orthologs with a particular phyletic pattern (i.e. pattern of presence-absence of the species within the analyzed set of species; this set of species should be the same as in the tree), find the most parsimonious mapping of the set of orthologs on the tree. Such a mapping corresponds to the most parsimonious evolutionary scenario for the given set of orthologs, i.e. the scenario with the smallest possible number of events. A similar problem in phylogenetic analysis has been addressed by several groups who have developed algorithms for reconciling individual gene trees with species tree by constructing evolutionary scenarios with gene duplications and losses [31-36].
Under this approach, we rely on two assumptions that make the problem tractable but inevitably oversimplify it and could result in the produced scenarios being only rough approximations of the true complexity of the evolutionary history of life. First, we make conclusions on HGT solely on the basis of presence-absence patterns of genes, although many case studies have shown that, even for ubiquitous genes, phylogenetic trees are often in stark disagreement with the (hypothetical) species tree, signalling the occurrence of HGT [12,37]. Second, we ignore the issue of non-random gene order and the ensuing dependence between genes and treat genomes as "bags of genes". This is a simplification, but not an entirely unrealistic one, because there is minimal conservation of the long-range gene order in prokaryotes, and even operons, which tend to be conserved between close species, typically undergo rearrangements at greater evolutionary distances [38-41].
Recently, an attempt has been undertaken to reconstruct evolutionary scenarios and the gene sets of ancestors of certain prokaryotic taxa by mapping phyletic patterns of orthologous genes to a species tree [17]. Here, using the generalized parsimony principle, we develop more general and rigorous algorithms for such reconstruction, prove that these algorithms produce the most parsimonious evolutionary scenarios and investigate the properties of these scenarios in detail. We employ the COG database [15,16] as the collection of (probable) orthologous gene sets to be mapped on a species tree. To approximate the latter, we choose the emerging consensus of the genome trees [30], as well as the classic 16S rRNA tree [42], and we further investigate the effect of tree topology randomization on the resulting scenarios. We further concentrate on the reconstruction of the gene repertoire of the hypothetical Last Universal Common Ancestor (LUCA) of all extant life forms and examine the biological features of the LUCA gene sets reconstructed with different algorithm parameters. The unexpected outcome of this analysis is that HGT might have been as common in the evolution of prokaryotes as lineage-specific gene loss, particularly at the early stages. Given that, as indicated above, the analysis of gene presence-absence patterns underestimates HGT, it might be appropriate to speak of a dominance of HGT in prokaryotic evolution.
Results and Discussion
General definitions and concepts of evolutionary scenarios
When building evolutionary scenarios, we consider three elementary evolutionary events: i) gene loss, ii) emergence of a new gene (COG), and iii) acquisition of a gene (COG) via HGT. Emergence of a new COG is, typically, the result of an ancestral duplication, although de novo origin of a gene from a non-coding sequence also could contribute. Furthermore, given the limited size of the available collection of sequenced genomes, what appears to be emergence of a gene in an ancestral form could be the result of HGT from a lineage that is not represented in the current species tree. Therefore, since we cannot always distinguish between emergence of a COG and HGT, in the formal analysis that follows, we will collectively treat these events as gene gains as opposed to gene losses. An evolutionary scenario for a given COG is, then, any combination of elementary events that leads to the observed phyletic pattern, given the topology of the species tree. We will call the scenario for a given COG that includes the minimum number of events the (most) parsimonious scenario. In other words, the parsimonious scenario is one that is best consistent with the topology of the species tree. The parsimonious scenario is not necessarily unique, there may be multiple scenarios for a given COG with the same minimal number of events.
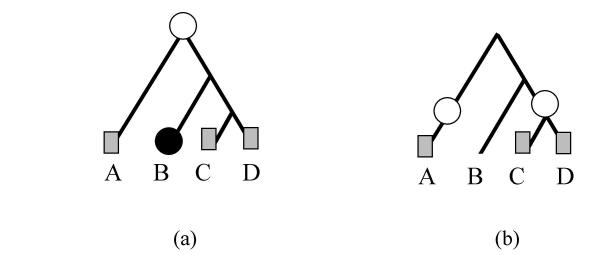
Consider, for instance, the possible evolutionary histories of genes (COGs) whose phyletic patterns are represented by I, II and III in Figure 1, given the evolutionary tree shown in the figure. Gene I is present in all extant species (A, B, C, and D) and thus can be inferred to have evolved in the common ancestor of all four species, the tree root, and to have been inherited by all of them. Gene II can be thought of as being present in the last common ancestor of species B, C, and D and inherited by all its descendants (Fig. 2a). However, another possible scenario for pattern II could be the gene's presence in the root, with a subsequent loss in species A (Fig. 2b). The scenario in 2a is the parsimonious one because it includes only one event as opposed to two events in the scenario 2b.
Figure 1.
Phyletic patterns of presence/absence of genes (1), (2) and (3) at an evolutionary tree with four current species A, B, C, and D being the tree leaves. The gene presence is shown with the patterned box.
Figure 2.
Two evolutionary scenarios leading to pattern II of Figure 1. The black circle represents gene loss and the white circle represents emergence of the COG.
Similarly, two scenarios can be considered to explain phyletic pattern III in Figure 1: (a) emergence in the root with a subsequent loss in B, and (b) emergence in either A or the last common ancestor of C and D with a subsequent HGT to the other branch (Fig. 3). Each of these scenarios includes two events, i.e. the two scenarios are equally parsimonious.
Figure 3.
Two evolutionary scenarios leading to pattern III of Figure 1. The designations are is Figs. 1 and 2.
There is an additional important issue to consider with regard to the scenarios in Figs. 2b and 3a. So far we discussed these scenarios under the assumption that the presence of a gene in the tree root counts as an event. However, this is not obvious and depends on whether or not we assume that the root, i.e. the last universal common ancestor (LUCA), represents the earliest life form. In the former case, all genes must be considered as emerging in the root and, accordingly, these gene emergence events should be counted when evolutionary scenarios are compared. In the latter case, genes present in the root can be treated as inherited from ancestors and, accordingly, should be excluded from the count because vertical inheritance is consistent with the species tree topology and requires no explanatory events. Although the species tree of all extant life forms is undoubtedly only a branch of the overall tree of life, the remaining branches being extinct, this is the only portion of that tree, which is within our "event horizon". Besides, the gene repertoire of LUCA necessarily must be the sum of inherited genes and those that have emerged in LUCA itself, and there is no obvious way to differentiate between these two categories of genes. For this reason, and because reconstruction of LUCA is a major goal of our efforts, we prefer to treat LUCA as the first life form in the "visible" part of the tree and to count emergence of a gene (COG) in LUCA as an event. However, mathematically, the alternative approach is more tractable because the tree root is treated identically to all other parental nodes in the tree. Therefore, we developed most of the formalisms described in the next section without counting emergence in the root as an event and subsequently introduce a correction to include these events. With the aforementioned alternative approach, the scenarios in Figs. 2a and 2b become equally parsimonious, whereas, among the scenarios in Figs. 3a and 3b, only the one in Fig. 3a is now parsimonious.
The two scenarios for pattern III are equally parsimonious only if all elementary events are considered equally likely. However, biological considerations suggest that gene loss might be, in general, a (much) more likely evolutionary event than gene gain or at least than HGT; this is amply illustrated by the massive gene loss in parasites compared to their free-living relatives, e.g. Buchnera sp. vs. Escherichia coli, Mycoplasma genitalium vs. Bacillus subtilis or Rickettsia sp. vs. Mesorhizobium loti [43-46]. Therefore, to construct realistic evolutionary scenarios, differential weighting of gains and losses may be required. This can be achieved by introducing a gain penalty for scoring evolutionary scenarios [17]. Then, a parsimonious scenario must minimize the total score, S = λ + gγ, where λ is the number of losses, γ is the number of gains and g is the gain penalty. This minimal score will be referred to as the inconsistency value for the given gene (COG) because it is equal to the minimal weighted number of events required to reconcile the evolutionary scenario for the given COG with the species tree. Here, we use these concepts to develop algorithms for deriving parsimonious evolutionary scenarios involving gene loss and gain events. We then apply these algorithms to the COG data set in order to assign gene loss/gain events to each node in the species tree and to reconstruct the gene repertoires of ancestral life forms.
Constructing a parsimonious evolutionary scenario
Parsimony analysis is one of the most commonly used and powerful phylogenetic approaches, which traditionally had been applied to binary characters and subsequently to molecular sequence data [47][48]. Typically, this methodology is used to identify the most parsimonious tree, i.e., the tree associated with the minimum number of events, among all possible tree topologies or among a subset of topologies selected on the basis of certain criteria. However, the parsimony approach also can be used for explicit reconstruction of ancestral character states and events associated with tree edges, given the topology. This approach is implemented, in particular, in the MacClade software package [49].
The problem addressed here is typical for parsimony analysis. Indeed, a two-state character can be associated with the phyletic pattern of any COG assuming that the states correspond to the presence and absence of a species in the COG. Then, a loss corresponds to the substitution of presence by absence, and a gain to the reverse substitution. Thus, parsimony algorithms developed by Fitch [50], Hartigan [51], Swofford and Maddison [52] and others for the minimum substitution problem, in principle, could be applied for building parsimonious evolutionary scenarios given a species tree and phyletic patterns of COGs. Character weighting, which is required to account for probable different likelihoods of gene gains and losses, has been implemented in so-called generalized parsimony approaches by Sankoff and coworkers [53,54] and considered in detail by Swofford and Maddison [47,55]. For the purpose of this work, however, we chose to devise an independent approach because the problem at hand had certain specific aspects that needed to be taken into account. In particular, the issue of different scoring systems corresponding to the cases when the presence of a gene in LUCA was counted or was not counted as an event had to be addressed and the number of parsimonious scenarios for each COG needed to be calculated. In addition, we proposed new approaches for resolving situations when several scenarios for the given COG were equally parsimonious.
For convenience and brevity of presentation, let us introduce the following conventions. Any ancestral node is considered to be uniquely labelled by the subset of the analysed species (tree leaves) in the subtree descending from this node; such a subset will be referred to as a tree cluster. For instance, in the tree in Figure 1, sets CD, BCD and ABCD are clusters, whereas sets AB and ABC are not. The cluster consisting of all the species under consideration corresponds to the root. Somewhat loosely, we will refer to the loss or gain of a gene at a tree cluster, meaning that the event is assumed to have occurred in the last common ancestor of the cluster, i.e. the node labelled by the cluster. Each extant species (tree leaf) also constitutes a cluster referred to as a singleton.
The problem of building a parsimonious evolutionary scenario, given a gene's phyletic pattern and a binary evolutionary tree, can be formalised in terms of iteratively processing the nodes of the tree in a bottom-up fashion. This is achieved by building a parsimonious scenario for a parent given parsimonious scenarios for its children. This requires maintaining, at each node of the tree, sets of loss and gain events under both the assumption that the gene has been inherited at the node and the assumption that it has not been inherited. It is necessary to distinguish these two cases because, clearly, it is only meaningful to consider the loss of a gene at a node if it was inherited at that node. Similarly, it is only meaningful to consider the gain of a gene if it was not inherited. Thus, a loss can occur only under the former assumption and a gain under the latter. We denote the assumption that the gene was inherited by Ai and the assumption that it was not inherited by An.
Let us now consider the parent-children triple shown in Figure 4. Each node in the triple is assigned with sets of loss and gain events under each of the above inheritance assumptions: [Gi, Li; Gn, Ln] for the parent and similar quadruples for the children (see Figure 4). The set Gi refers to gain events in the subtree descending from the parent under assumption Ai. The set Gi contains those nodes in the subtree descending from the parent, in which the gene has been gained under the inheritance assumption Ai. Conversely, the set Li contains those nodes, in which the gene has been lost under the assumption Ai. The sets Gn and Ln have similar meanings, but under the non-inheritance assumption An. Let us denote the total number of events by ei = | Gi | + | Li | under Ai, and by en = |Gn| + | Ln | under An. These will be referred to as the i-inconsistency and n-inconsistency of the given node, respectively. The corresponding sets for the child nodes are denoted by Gi1, Gi2 etc. as in Figure 4. An evolutionary scenario, at a given node, is thus defined by a pair of sets (G, L) representing the gains and losses in the subtree rooted at the node. We use (Gi, Li) and (Gn, Ln) to denote scenarios under assumptions Ai and An, respectively.
Figure 4.
Patterns of events in a parent-children triple according to a parsimonious scenario.
How can these sets in the parent be derived from those in the children? First, under assumption Ai, we will determine the sets Gi and Li given all the loss and gain sets at the children. There are two alternative scenarios: (i) the gene has been lost in the parent, or (ii) the gene has not been lost in the parent. In the first case, the lost gene could not have been inherited by the children and, thus, sets Ln1 and Ln2 are the relevant loss events and sets Gn1 and Gn2 are the relevant gain events. The sets for the parent are then determined by combining the corresponding sets for the children:
Gi = Gn1 ∪ Gn2, Li = Ln1 ∪ Ln2 ∪ {parent} (1)
The parent is added in the latter equation because of the assumed loss event. In the second case, the gene has been inherited and not lost; thus, the loss/gain event sets will be determined by the other sets of events in the children, viz. Li1, Li2, Gi1 and Gi2. The sets at the parent are given by:
Gi = Gi1 ∪ Gi2, Li = Li1 ∪ Li2 (2)
Of the two alternatives, the principle of parsimony suggests selecting the one with the smaller number of events. Under scenario (i), the total number of events is ei = en1 + en2 + 1 and, under scenario (ii), the total is ei = ei1 + ei2, according to (1) and (2), respectively. Parsimony suggests we select the scenario with the minimal total score:
ei = min (en1 + en2 + 1, ei1 + ei2) (3)
When en1 + en2 +1 = ei1 + ei2, either scenario may be selected. We may choose to remove this ambiguity by using an external criterion. For example, scenario (ii) may be preferred because this does not introduce an additional event in the parent.
Let us now determine the sets Gn and Ln under the assumption An. There are again two alternative scenarios: (i) the gene has been gained in the parent, or (ii) the gene has not been gained in the parent. In the first case, the gained gene should be inherited by the children and, thus, to determine Gn and Ln, sets Li1 and Li2 are the relevant loss events, and sets Gi1 and Gi2 are the relevant gain events. We now obtain:
Gn = Gi1 ∪ Gi2 ∪ {parent}, Ln = Li1 ∪ Li2 (4)
The parent is added in the former equation because of the assumed gain event.
Under scenario (ii), the gene has not been gained; thus, the loss and gain event sets will be determined by the other sets at the children, which yields:
Gn = Gn1 ∪ Gn2, Ln = Ln1 ∪ Ln2 (5)
Parsimony requires that the scenario with the smaller number of events is selected. The total number of events is en = ei1 + ei2 + 1 under scenario (i) and en = en1 + en2 under scenario (ii), according to (4) and (5), respectively. As discussed above, the likelihoods of gains and losses may not be equal; losses are generally considered to be more likely than gains. Therefore gains may be charged with a penalty, g, which corresponds to the generalized parsimony approach. Taking this into account, we redefine ei and en as
ei = g| Gi | + | Li | and en = g| Gn | + | Ln |,
(straight brackets denote the size of the respective set) and modify the recurrence under scenario (i) to en = ei1 + ei2 + g. Thus, the scenario to be selected is defined by:
en = min (ei1 + ei2 + g, en1 + en2) (6)
When ei1 + ei2 + g = en1 + en2, we may once again remove the ambiguity by selecting the scenario according to an external criterion. For instance, we may prefer scenario (ii) as it introduces no additional gain events at the parent.
The above discussion leads to the following iterative algorithm for building a parsimonious scenario given a gene's phyletic pattern and a species tree.
Algorithm PARS for building parsimonious scenarios
1. Assign each leaf of the tree with the four sets [Gi, Li; Gn, Ln] defined above. The four sets are empty except that Gn = {a} if gene a is present in the given leaf or Li = {a} if a is not present in the given leaf.
2. Among the assigned nodes, take any two siblings and assign their parent with the four sets according to rules (1) – (6) above; remove the siblings and repeat this step until the parent is the tree root.
3. If ei < en in the root, accept the scenario in which the gene was present in the root, the common ancestor for the given tree; the subsequent gain/loss history is determined according to the contents of sets Gi and Li in the root. If ei > en, accept the scenario in which the gene was not present in the root but was first gained in some node in Gn during evolution and then horizontally transferred to the other nodes in Gn. If ei = en, either scenario may be accepted, depending on considerations beyond the gene's phyletic pattern; this case will be described below.
Algorithm PARS takes a bottom-up approach, although it can be naturally reformulated as a recursive algorithm, which proceeds in a top-down fashion. For any node in the tree, an i-parsimonious scenario is any scenario (Gi, Li), for which ei is minimal under assumption Ai. Similarly, an n-parsimonious scenario (Gn, Ln) is defined under assumption An. A fully parsimonious scenario is an i-parsimonious or n-parsimonious scenario for which the inconsistency is min(ei, en).
Assertion 1
Scenarios (Gi, Li) and (Gn, Ln) generated by algorithm PARS are i-parsimonious and n-parsimonious, respectively.
Proof
Suppose that the tree has N nodes. We inductively assume that the algorithm generates parsimonious gain/loss sets for all subtrees with fewer than N nodes. Thus the gain/loss sets at the children of the root, viz. [Gi1, Li1; Gn1, Ln1] and [Gi2, Li2; Gn2, Ln2], are all parsimonious. We now show that it follows that the determination of gain/loss sets [Gi, Li; Gn, Ln] according to rules (1) – (6) leads to a pair of parsimonious scenarios for the parent. Indeed, let us assume that there exists a scenario  for the parent, in which the total numbers of events
for the parent, in which the total numbers of events  is less than that defined by (3) or (6). Suppose, for instance, that the gene is inherited in the scenario
is less than that defined by (3) or (6). Suppose, for instance, that the gene is inherited in the scenario  , thus
, thus  i < ei, where ei is defined by (3). If the gene was not lost in the parent, then scenario
i < ei, where ei is defined by (3). If the gene was not lost in the parent, then scenario  satisfies equations (2), which implies
satisfies equations (2), which implies  i =
i =  i1 +
i1 +  i2. However, by the inductive assumption ei1 ≤
i2. However, by the inductive assumption ei1 ≤  i1 and ei2 ≤
i1 and ei2 ≤  i2, which contradicts the proposition
i2, which contradicts the proposition  i < ei. The result follows in a similar fashion for the other three cases corresponding to equations (1), (4) and (5). It only remains to be stated that the assertion holds for N = 1 because, obviously, Step 1 of PARS introduces events parsimoniously. This completes the proof.
i < ei. The result follows in a similar fashion for the other three cases corresponding to equations (1), (4) and (5). It only remains to be stated that the assertion holds for N = 1 because, obviously, Step 1 of PARS introduces events parsimoniously. This completes the proof.
The following is a straightforward corollary of Assertion 1.
Assertion 2
At any node, i-inconsistency and n-inconsistency of a gene are related by the following inequalities:
en ≤ g + ei, ei ≤ 1 + en
Proof
Since an i-parsimonious scenario inherits the gene at the node, we may construct a non-inheritance scenario that includes a gain of the gene at the node together with all the subsequent events of the i-parsimonious scenario. This non-inheritance scenario has just one more gain than the i-parsimonious scenario. This justifies the first inequality because any n-parsimonious scenario cannot have a higher inconsistency score. Similarly, for any n-parsimonious scenario, there is an inheritance scenario, which includes the loss of the gene at the node together with all of the events in the n-parsimonious scenario, thus justifying the second inequality. This completes the proof.
When g = 1, Assertion 2 implies that the numbers of events in i-parsimonious and n-parsimonious scenarios differ by at most one, | ei - en | ≤ 1.
The recursive structure of algorithm PARS enables us to determine the number of parsimonious scenarios compatible with the phyletic pattern of a gene. To do this, we need two quantities assigned to each of the tree nodes, si and sn, the numbers of i-parsimonious and n-parsimonious scenarios, respectively.
Assertion 3
Given the numbers of parsimonious scenarios (si1, sn1) and (si2, sn2) at the children, the numbers for the parent are determined according to the following rule, depending on the relation between ei1 + ei2 and en1 + en2 in (3) and (6):

The validity of (7) and (8) is evident because each of the parsimonious scenarios in one child can be combined with each of the parsimonious scenarios in the other child. At the root, if ei < en the total number of parsimonious scenarios is si, whereas if ei > en it is sn. If ei = en the total is si + sn.
To narrow down the space of parsimonious scenarios, various strategies may be employed. One approach mentioned above suggests choosing those scenarios that, at each aggregation step where the values compared in (3) and (6) are equal, do not postulate new events, i.e. scenario (2) will be selected when the values compared in (3) are equal, and scenario (5) will be selected when the values compared in (6) are equal. We refer to the version of the PARS algorithm that utilises this strategy to choose between scenarios with the same inconsistency values as PARS-U.
In fact, there are clearly four different strategies of this type, depending on whether (1) or (2) is preferred in the case of identical inconsistency values in (3) and whether (4) or (5) is preferred in the case of identical inconsistency values in (6). We can associate evolutionary interpretations with each of these strategies. For instance, preferring (2) to (1) will tend to keep loss events as close to the leaves as possible. Indeed, not including a loss event at the parent means that, in this parsimonious scenario, the children accumulate more events than in a parsimonious scenario that includes the loss at the parent. This approach is analogous to the DELTRAN algorithm of the MacClade package. The opposite strategy will tend to push loss events higher up the tree, in an analogy to the ACCTRAN algorithm of MacClade [49]. Similarly, preferring (5) to (4) will tend to keep gain events as close to the leaves as possible. The opposite strategy will tend to push them higher up the tree. We can also combine these by applying different strategies at different parental nodes. However, there is no obvious justification for preferring any of these strategies. Accordingly, the selected strategy PARS-U will be used for illustrative purposes only, i.e. to demonstrate the multitude of parsimonious scenarios.
Another problem arises in step 3 of PARS when ei = en at the root because, in this case, there can be no loss in an i-parsimonious scenario nor gain in an n-parsimonious one. Thus, the strategies outlined above do not help us to resolve this case. A somewhat better justified external criterion, which is specific to the analysis of phyletic patterns, may be derived from the notion that, among scenarios with equal inconsistency values, the scenario with the minimal number of gains should be chosen (on the basis of the general belief that gene losses are likely to be more common than gene gains via HGT). This secondary criterion allows us to select a scenario from the set of parsimonious scenarios by locally minimizing the number of gains. The version of the PARS algorithm utilising this criterion for resolving indifference will be referred to as PARS-G.
Clearly, algorithm PARS-U always leads to unique scenarios under both Ai and An; this may or may not be the case with PARS-G. We suspect that PARS-G also always leads to a unique scenario and, indeed, for all 3166 COGs examined, PARS-G yielded a unique scenario; however, no proof of this conjecture has been found so far.
Example
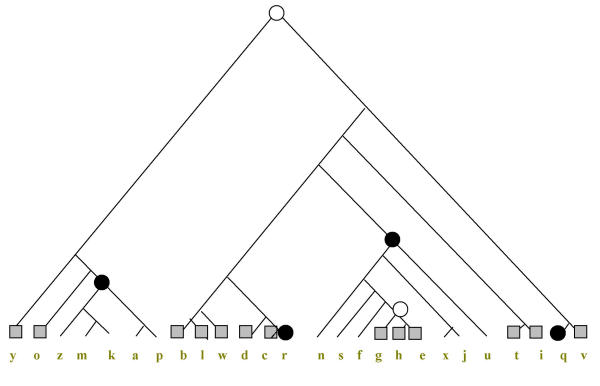
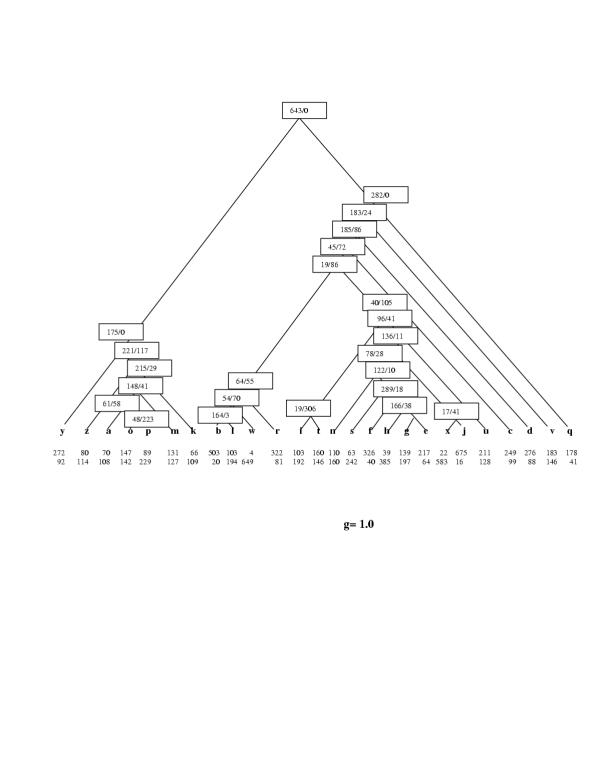
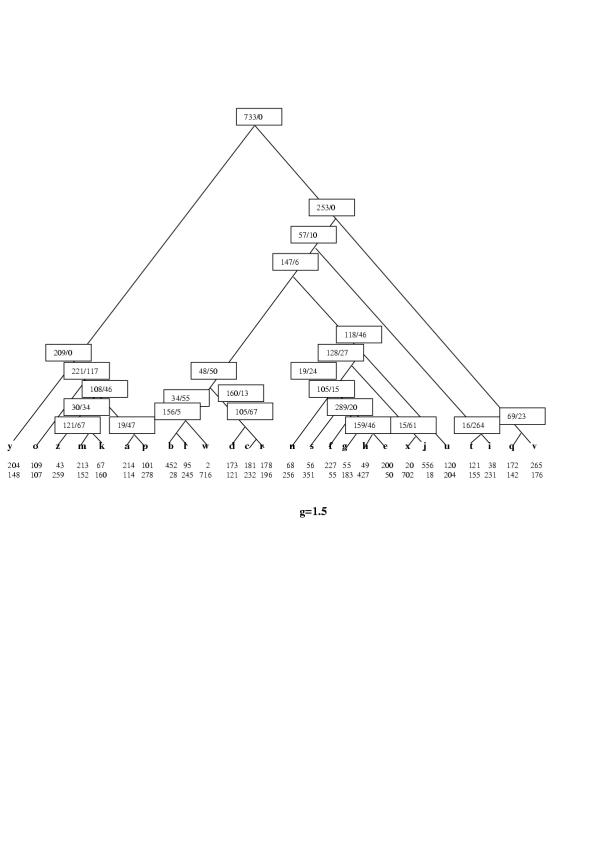
To illustrate the construction of parsimonious evolutionary scenarios with the PARS algorithm, let us map the phyletic pattern of COG0572 (uridine kinase), which is represented in 13 species, namely one eukaryote (Saccharomyces cerevisiae), one archaeon (Halobacterium sp) and 11 bacteria, onto two hypothetical species trees (Figures 5,6). The topology of the species tree in Figure 5 was derived from the concatenated tree of universal ribosomal proteins [24] and is close to the apparent consensus of various genome-tree approaches [30]. The topology of the tree in Figure 6 is from the classic 16S rRNA phylogeny [42]. Although the original genome trees are unrooted, a rooted tree was required for the purpose of this analysis; the root was forced between the bacterial and archaeal-eukaryotic branches in accord with the three-kingdom "standard model" of life's evolution [2-4,56]. All versions of the PARS algorithm were implemented using the MatLab program package http://www.mathworks.com/.
Figure 5.
The parsimonious scenario for COG0572 (Uridine kinase) under the genome-tree topology. The scenario is for g = 1. The designations are is Figs. 1 and 2. The following species name abbreviations are used here and throughout the rest of this work. Eukaryotes: y, Saccharomyces cerevisiae (yeast); archaea: a, Archaeoglobus fulgidus, k, Pyrococcus horikoshii, m, Methanococcus jannaschii or Methanothermobacter thermoautotrophicus, o, Halobacterium sp., p, Thermoplasma acidophilum, z, Aeropyrum pernix; bacteria: b, Bacillus subtilis, c, Synechocystis sp., d, Deinococcus radiodurans, e, Escherichia coli, f, Pseudomonas aeruginosa, g, Vibrio cholerae, h, Haemophiluc influenzae, i, Chlamydia trachomatis or Chlamydophila pneumoniae, j, Mesorhizobium loti, l, Lactococcus lactis or Streptococcus pyogenes, n, Neisseria meningitides, q, Aquifex aeolicus, r, Mycobacterium tuberculosis, s, Xylella fastidiosa, t, Treponema pallidum or Borrelia burgdorferi, u, Helicobacter pylori or Campylobacter jejuni, v, Thermotoga maritima, w, Mycoplasma genitalium or Mycoplasma pneumoniae, x, Rickettsia prowazekii. Pairs of related species designated by the same letter were treated in all analyses as a single entity, i.e. a COG was considered to be present in the respective leaf if it was represented in at least one of these species.
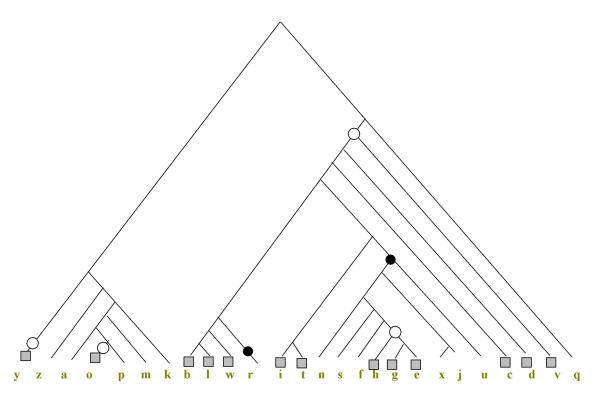
Figure 6.
The parsimonious scenario for COG0572 (Uridine kinase) under the rRNA tree topology. The scenario is for g = 1; the designations are as in Fig. 5
Let us consider one step of algorithm PARS applied to siblings blwdcr (an assemblage that unites low-GC Gram-positive bacteria with actinomycetes, cyanobacteria and Deinococcales and had been tentatively identified as a clade through genome-tree analysis) and nsfghexju (the classic Proteobacteria clade) in the tree of Figure 5. To this end, we need to determine gains and losses in both siblings under each of the alternative assumptions, Ai and An. Assuming that the COG had been inherited at the node blwdcr (Ai), there is only one loss in r (Mycobacterium tuberculosis) and no gains, i.e. one event in this cluster. Assuming that the COG had not been inherited at blwdcr (An), the minimum set of events includes a gain in the common ancestor of the cluster blwdcr, with the subsequent loss in r, a total of two events. Similarly, under the assumption Ai at nsfghexju, the optimal scenario is that the COG has been lost at this node and gained again at the ghe cluster, a total of two events. Under the assumption An at nsfghexju, the only event in this cluster is the gain at ghe (Vibrio cholerae, Haemophilus influenzae, and Escherichia coli). According to PARS, these scenarios are extended to the parent cluster blwdcrnsfghexju under both Ai and An. Let us consider first the assumption Ai, i.e. that the COG had been inherited in the parent. Then, if the COG had been lost at the parent and not inherited by the children, this would involve the gains at blwdcr and ghe and loss at r, a total of four evens. If the COG had not been lost and, accordingly, had been inherited by the children, this would involve losses in r and nsfghexju and a gain at ghe, three events altogether. Thus, the latter scenario should be chosen under the assumption Ai at the parent. Under the assumption An, i.e., the COG's absence in the parent, the COG was not inherited by the children either, thus leading to the aforementioned three events, the gains at blwdcr and ghe and the loss at r. If, in contrast, the COG had been gained in the parent and, accordingly, inherited by the children, this would involve losses at r and nsfghexju and the gain at ghe, a total of four events. Thus, the parsimonious pair of loss/gain sets at the parent is Gi = {ghe}, Li = {nsfghexju, r} and Gn = {blwdcr, ghe}, Ln = {r}. As we can see, the i-inconsistency and n-inconsistency for each cluster differ by at most one event, which conforms to Assertion 2. Continuing the aggregation toward the root of the tree, we arrive at the following parsimonious scenario: the COG was present in the tree root, i.e., in LUCA, and had been lost at r, q (Aquifex aeolicus), zmkap (a cluster that includes all archaeal species except for Halobacterium sp.), and nsfghexju, but then regained at the cluster ghe, a total of six events, including the gain at the root (Figure 5). Thus, although this COG has a scattered distribution and, in particular, is present in only one archaeal species, the parsimonious scenario for this tree topology indicates that it was most likely already present in LUCA, with its subsequent history defined primarily by losses.
The same analysis performed for the rRNA tree topology leads to a different parsimonious scenario, albeit with the same total number of events, six (Fig. 6). According to this scenario, the COG evolved in the common ancestor of the cluster blwritnsfhgexjucdv (the clade including all bacterial species other than A. aeolicus) and then had been lost in r and nsfhgexju (Proteobacteria) and regained, via HGT, in hge. Additionally, the COG had been horizontally transferred to y (yeast) and o (Halobacterium sp). Thus, in this case, the evolutionary scenario is dominated by HGT, with four HGT events against two losses. This example illustrates the critical dependence of the reconstructed parsimonious scenario on the tree topology, even for a case when the scenarios for alternative tree topologies consist of the same number of events.
A notable aspect of the reconstructed parsimonious history of this COG, under each of the alternative topologies, is that it was present in LUCA, then lost in a descendent (nsfghexju, the common ancestor of Proteobacteria) and subsequently regained in ghe (γ-proteobacteria). The question thus arises as to how many COGs have a history of re-appearance after a loss (see discussion below).
Independent gains
In this section, we consider a simplified view of the evolutionary scenarios by assuming that evolution of a COG may not involve a gain after a loss event, an assumption employed by Snel and coworkers [17]. In other words, gains are assumed to occur independently, in non-overlapping parts of the tree, and each may be succeeded by some losses but not regains. This independence hypothesis is equivalent to the well-known, but not necessarily realistic for all types of characters, assumption of the uniqueness of character changes during their evolution, which is employed, in particular, in the Dollo parsimony method [48,57].
For COG0572 and genome-tree topology in the example above, an independent gain scenario involves six gains along the tree: in singletons y, o, v and in clusters blwdcr, ghe, and ti, and only one loss, in r. This yields seven events altogether. Although, quantitatively, this does not differ much from the six events in the scenario in Figure 5, the qualitative difference is notable, including the absence of the COG from LUCA under the independence assumption.
The situation of independent gains can be dealt with by using recursive aggregation as in the PARS algorithm, but with the added restriction that no loss may occur in the parent when the set of gains in the children is not empty. In other words, if a gene has been lost at an interior node of the tree, then it must be absent from all descendants of this node. This leads to the following statement.
Assertion 4
Under the independence assumption, a loss may occur in a node if and only if the set of descendants of this node does not overlap with the set of extant species (leaves) that are present in the COG under consideration.
To formalize this statement, let us consider an evolutionary tree T with the set of leaves L. For a given COG, let us denote by C the set of leaves corresponding to the extant species that are present in the given COG. For a given node t ∈ T, let us denote by L(t) the set of leaves corresponding to extant organisms for which t represents their last common ancestor. Then the condition in Assertion 4 can be expressed as
L(t) ∩ C =  , (7)
, (7)
where  denotes the empty set.
denotes the empty set.
Proof
Suppose a gene has been lost at t but C and L(t) overlap, that is, some leaf j belongs to both L(t) and C. Then, the gene would have to have been gained either at j or carried down to j from an ancestor, which contradicts the independence assumption. Thus, condition (7) must hold. The converse implication is obvious.
Let us now consider the problem of building sets L of losses and G of gains for the parent, after they have been determined for the children under the independence assumption (see Figure 4). Consider first assumption Ai, that the COG was inherited by the parent. Then the situation depends on whether or not the COG overlaps the cluster of the parent's descendants, according to Assertion 4. If the parent t and COG C satisfy (7), then we have two alternative scenarios: (a) the gene has been lost in the parent, or (b) the gene has not been lost in the parent. In case (a), the lost gene cannot belong to any species among the parent's descendants, i.e.
Gi =  , Li = {parent} (1')
, Li = {parent} (1')
The parent is added in the latter equation because of the assumed loss event in (a). In case (b), the gene has been inherited and not lost; thus, the loss sets will be determined by the loss sets at the children:
Gi =  , Li = Li1 ∪ Li2 (2')
, Li = Li1 ∪ Li2 (2')
However, Li1 and Li2 are non-empty by virtue of (7), so (1') will always give a smaller inconsistency than (2'). When (7) does not hold, the gene could not have been lost in the parent, according to Assertion 4, thus only (2') is applicable.
Under the non-inheritance assumption An, combining loss and gain events in the parent under the independence condition does not differ from the same procedure for the general case. Thus, to adapt algorithm PARS for the independence condition, one must substitute rules (1') and (2') for rules (1), (2), and (3) to aggregate children's events under Ai, using (1') when (7) holds and (2') otherwise. The remaining rules, (4) through (6), remain the same. Algorithm PARS thus modified will be referred to as PARS-I.
Counting presence of a gene in LUCA as a gain
So far, we considered algorithm PARS without treating the tree root, which corresponds to LUCA, any differently from the internal nodes of the tree. In this section, we modify the approach by assuming that all genes present in LUCA must have emerged in the root and, accordingly, count as gains in evolutionary scenarios. This assumption does not lead to any changes in the initialisation step 1 or aggregation step 2 in algorithm PARS, but it does affect the final step 3, at which the two resulting parsimonious scenarios are compared, one under the inheritance assumption Ai and the other under the non-inheritance assumption An. If the presence in LUCA is not an event, the choice between these scenarios is made by comparing the numbers of events, ei and en, under the two assumptions. However, now, when the presence of the gene in LUCA is treated as a gain, its weight g has to be added to ei to obtain the total inconsistency of the i-parsimonious scenario. Therefore, at step 3 of algorithm PARS, ei + g and en have to be compared in order to choose the most parsimonious scenario.
However, this is not the only modification required. As stated in Assertion 2, ei + g ≥ en, that is, an i-parsimonious scenario for the entire tree can never be better than an n-parsimonious scenario (since the gene presence at LUCA is an event). In other words, the inconsistency of a COG is always equal to its n-inconsistency. This follows from the fact that each evolutionary scenario under Ai is equivalent to an evolutionary scenario under An, which involves a gain in the root together with the same events as in the scenario under Ai.
This last statement affects the formulas for computation of the numbers of parsimonious scenarios in Assertion 3. Since ei + g = en, the total number of parsimonious scenarios at the tree root is now always equal to sn, because, even when ei + g = en, the set of i-parsimonious scenarios is a subset of the set of n-parsimonious scenarios.
There are also modifications to the PARS-G and PARS-U versions of PARS under the assumption of this section; these apply when the i-inconsistency is equal to the n-inconsistency, i.e. ei = en. Using PARS-G, |Gi| and |Gn| were compared when the gene's presence at the root was not counted as an event. Under the assumptions of this section, the number of gains under Ai is |Gi| + 1, so when the i-inconsistency and the n-inconsistency are equal, i.e. ei + g = en, we have to compare |Gi| + 1 and |Gn|. Since the scenario under Ai leading to |Gi| + 1 gains can be interpreted as a scenario under An (with the gene gained at the root), the inequality |Gi| + 1 < |Gn| is not possible because of the minimality of |Gn|. Similarly, if |Gi| + 1 > |Gn|, then no gain in the root would occur under An. Thus, a gain may occur in the root with PARS-G if and only if |Gi| + 1 = |Gn|. This creates no new ambiguities in selecting between i- and n-parsimonious scenarios because, as noted above, each i-parsimonious scenario is also an n-parsimonious scenario.
With PARS-U, obviously, the selected n-parsimonious scenario in the root should always be preferred to the i-parsimonious scenario, since either it avoids a gain at the root or it is equivalent to the latter scenario.
The principle of parsimony implies some simple properties of parsimonious scenarios, some of which will be discussed below. The first observation concerns the pattern of gains and losses in the tree.
Assertion 5
Any gene gained (lost) in a parent node cannot be lost (gained) in either of its children in any parsimonious scenario.
Proof
Suppose that, in a scenario, a gene is gained at a node and lost at one of its children. Then, the inconsistency of this scenario can be reduced by removing the loss event at the child and moving the gain event to its sibling. The opposite case (loss at a node followed by a gain in its child) follows similarly, which proves the statement.
Another observation concerns the question of whether or not the presence of any particular gene can be forced into LUCA in a parsimonious scenario with a suitable gain penalty. The answer is no. Certain genes will always emerge in intermediate ancestors in parsimonious scenarios, whatever the gain penalty; we call these non-LUCA genes. The following gives a simple criterion for this.
Assertion 6
A gene is non-LUCA if and only if its phyletic pattern is completely contained in the set of descendants of only one of the children of LUCA.
Proof
Let us denote the children of LUCA by c1 and c2. Suppose a gene's phyletic profile is completely contained in the set of descendants of c1. Consider a scenario in which this gene is present in LUCA. The gene is inherited by c1 but must be lost in c2 or some of its descendants. Then the inconsistency of the scenario can be reduced by removing these loss events and moving the gain of the gene from LUCA to c1. Therefore the gene is non-LUCA.
Consider any non-LUCA gene. Then, in any parsimonious scenario, it must be gained either in, say, c1 or one of its descendants. The gene cannot also be gained in c2 or any of its descendants, since, if the gain penalty g is chosen to be equal to the number of nodes in the tree, the inconsistency of this scenario would be at least 2 g. However, the inconsistency of the scenario with a single gain at LUCA would be less than 2 g, which proves the statement.
Empirical Results and Discussion
Parsimonious scenarios of evolution and effect of algorithm parameters on reconstructed ancestral gene sets
Table 1 shows some of the summary statistics of parsimonious evolutionary scenarios reconstructed with the PARS algorithm when applied to the phyletic patterns of 3166 COGs available as of October 2001 and assuming the genome-tree topology (Figure 5). As indicated above, these and all other empirical results reported here were obtained under the assumption that the presence of a gene in LUCA constitutes a gain. The effects of variation of three parameters of PARS on the resulting parsimonious scenarios are presented: (1) whether a gain-after-loss is permitted or not, which are referred to as the general and independence cases, respectively, (2) choice among scenarios with equal inconsistency values by using either PARS-G or PARS-U, and (3) gain penalty (g values of 1, 2 or 3).
Table 1.
Number of events in parsimonious scenarios depending on PARS algorithm parameters
| Event | Number of genes (COGs)a | ||||||||||||
| g = 1 | g = 2 | g = 3 | |||||||||||
| General | independence | General | Independence | General | Independence | ||||||||
| G | U | G | U | G | U | G | U | G | U | G | U | ||
| I | Number of genes in LUCA | 572 | 315 | 506 | 305 | 956 | 788 | 926 | 750 | 1211 | 1049 | 1179 | 1029 |
| II | Total gain | 8661 | 11281 | 8892 | 11343 | 5812 | 6857 | 5853 | 6957 | 4461 | 5143 | 4476 | 5166 |
| III | Horizontal transfer (II-3166)b | 5495 | 8115 | 5726 | 8177 | 2646 | 3691 | 2687 | 3791 | 1295 | 1977 | 1310 | 2000 |
| IV | Total loss | 5121 | 2501 | 4909 | 2458 | 9944 | 7854 | 9953 | 7745 | 13695 | 11649 | 13736 | 11666 |
| V | Total events (II + IV) | 13782 | 13782 | 13801 | 13801 | 15756 | 14711 | 15806 | 14702 | 18156 | 16792 | 18212 | 16832 |
| VI | Inconsistency score [g(II + IV)] | 13782 | 13801 | 21568 | 21659 | 27078 | 27164 | ||||||
| VII | Average number of scenarios per COG | 2.10 | 1.74 | 1.36 | 1.27 | 1.23 | 1.18 | ||||||
| VIII | Single-scenario COGs | 1806 | 1944 | 2399 | 2518 | 2587 | 2666 | ||||||
| IX | Maximum number of scenarios | 39 | 18 | 8 | 7 | 8 | 6 | ||||||
aall data are for the genome-tree topology; G stands for PARS-G algorithm and U for PARS-U algorithm bThe number of horizontal transfers was derived from the total gain number by subtracting the total number of COGs, 3166, because any COG must have emerged in one of the ancestral forms.
The numbers in Table 1 show the expected dependence on the gain penalty: the predicted size of LUCA and the number of losses notably increased with the increase in the value of g. Obviously, the total inconsistency score also substantially increased at higher gain penalties, whereas the average number of scenarios per COG went down with the increase in the gain penalty. In other words, the loss-dominated scenarios produced at high gain penalties tend to be non-redundant or at least less redundant than HGT-enriched scenarios constructed with a low gain penalty. The effect of changing the gain penalty, the dependence of the results on the chosen species tree topology and possible implications for genome evolution and our ideas on the nature of LUCA are considered in greater detail in the next section.
The approach taken for choosing between equally parsimonious scenarios substantially affects the outcome (Table 1). Consider, for instance, the numbers for g = 1. With the same total inconsistency score, 13782, algorithm PARS-U yields twofold fewer losses than PARS-G and assigns only 315 COGs to LUCA in contrast to 572 COGs placed in LUCA by PARS-G. The 257 COGs assigned to LUCA by PARS-G but not PARS-U are distributed as gains among the other tree nodes by the latter algorithm.
Similar effects are produced by algorithm PARS-I, which works under the independence assumption. The independence assumption minimally affects the total inconsistency score of the parsimonious scenario: for g = 1, only 19 COGs had greater inconsistency scores under this assumption than without it and in each case the difference in the score was 1. However, when PARS-G was used to resolve ties between parsimonious scenarios, the number of genes assigned to LUCA substantially differed depending on whether or not the independence assumption was imposed, with 66 COGs (~12% of LUCA's gene repertoire) included in LUCA in the general case but not under the independence assumption. The example of COG0572 in Figure 5 illustrates how this could happen. Since algorithm PARS-G without the independence assumption seems to be the most general and the least arbitrary of the methods for parsimonious scenario construction, in the rest of this work, we consider only results produced by this method.
LUCA and the gain penalty: horizontal gene transfer might have been as common in the evolution of prokaryotes as gene loss
The gain penalty, which determines the relative contributions of lineage-specific gene loss and HGT, is undoubtedly the single most important parameter of the evolutionary scenarios considered here. In order to choose realistic scenarios, an independent estimate of g is needed but, to our knowledge, there is none at this time, beyond the intuitive notion that a loss is more likely than HGT, perhaps by a substantial margin. There seem to be two ways to determine the range of likely g values. First, by comparing the parsimonious scenarios obtained with different gain penalties, it might be possible to identify g values that result in scenarios with special properties, which could correspond to the "optimal" weighting of losses and HGT events. Secondly, a feedback approach can be employed. Since the g value affects the gene content of the reconstructed LUCA and other ancestral forms, one could examine these hypothetical ancestral gene sets from a biological perspective and attempt to select the minimal set containing the complete functional systems that are thought to be essential for a cell's functioning. Such an estimate is unlikely to be particularly precise because we do not have complete knowledge of the essential functional systems even for extant cells, let alone LUCA, whose phenotype and environmental conditions remain a mystery. However, since our goal is an approximate estimate of g, it seems likely that our understanding of cellular functional systems is sufficient to provide reasonable feedback.
Before turning to qualitative, biological assessment of different versions of LUCA, we examine the scenarios and ancestral gene sets reconstructed with different g values in greater detail. Table 2 shows the effect of changing the gain penalty from 0.1 (10 gains score the same as one loss) to 10 (10 losses score the same as one gain) for the genome-tree topology and the rRNA tree topology on the reconstructed gene sets of LUCA and the last common ancestors of archaea and bacteria, and on various characteristics of the parsimonious scenarios. The scenarios with g >> 1 conform to the intuitive notion of the prevalence of losses in evolution, whereas the scenarios with g < 1 imply that HGT is more likely than gene loss, which is often considered unrealistic. The data in Table 2 clearly show two expected monotonic trends, namely, the increase in the number of losses and decrease in the number of HGT events with the increase in g. The largest changes in the number of each type of events are seen between g values of 0.9 and 1.0. The transition between these g values is dramatic: for g = 0.9, there are almost four times as many HGT events as there are losses, whereas, for g = 1.0, the numbers of the two types of events are almost equal. However, the total number of events decreases monotonically when g approaches 1 from either side, with the global minimum observed for g = 0.9–1.9. This monotonicity, which implies that the total number of events for g = 1 is minimal, is a consequence of the parsimony principle and can be proved by straightforward algebraic manipulation (not shown).
Table 2.
Gene sets of ancestral forms and counts of various events in parsimonious scenarios depending on the gain penalty.
| Gain penalty (g) | Number of genes (COGs) | ||||||||||||||||
| .1 | .2 | .3 | .4 | .5 | .6 | .7 | .8 | .9 | 1 | 1.25 | 1.5 | 2 | 3 | 5 | 7 | 10 | |
| LUCA – genome tree | 84 | 98 | 109 | 132 | 212 | 214 | 266 | 285 | 310 | 572 | 623 | 733 | 956 | 1211 | 1525 | 1664 | 1725 |
| LUCA – rRNA tree | 84 | 112 | 151 | 195 | 271 | 240 | 304 | 293 | 319 | 643 | 645 | 682 | 894 | 1123 | 1407 | 1564 | 1668 |
| Archaeal Ancestor genome tree | 390 | 391 | 427 | 521 | 663 | 660 | 732 | 727 | 750 | 977 | 982 | 1046 | 1178 | 1295 | 1508 | 1619 | 1673 |
| Archaeal Ancestor rRNA tree | 390 | 431 | 511 | 599 | 709 | 672 | 740 | 729 | 755 | 922 | 922 | 958 | 1086 | 1209 | 1417 | 1544 | 1636 |
| Bacterial ancestor genome tree | 169 | 193 | 243 | 283 | 397 | 415 | 476 | 506 | 532 | 773 | 841 | 986 | 1259 | 1582 | 1879 | 2028 | 2091 |
| Bacterial ancestor rRNA tree | 169 | 267 | 355 | 525 | 613 | 585 | 653 | 646 | 672 | 925 | 928 | 961 | 1162 | 1380 | 1653 | 1807 | 1933 |
| HGT genome tree | 13241 | 13001 | 12315 | 11464 | 9462 | 9312 | 8733 | 8365 | 8315 | 5495 | 5136 | 4238 | 2646 | 1295 | 368 | 97 | 13 |
| HGT rRNA tree | 15145 | 14161 | 12949 | 11074 | 9133 | 9007 | 8416 | 8158 | 8146 | 5040 | 4961 | 4253 | 2654 | 1529 | 546 | 224 | 51 |
| Loss genome tree | 0 | 45 | 220 | 512 | 1506 | 1595 | 1989 | 2259 | 2301 | 5121 | 5562 | 6872 | 9944 | 13695 | 17535 | 19230 | 19947 |
| Loss rRNA tree | 0 | 172 | 478 | 1135 | 2100 | 2175 | 2567 | 2763 | 2773 | 5879 | 5977 | 6997 | 10137 | 13301 | 17489 | 19539 | 21050 |
| Total events genome tree | 16407 | 16212 | 15701 | 15142 | 14134 | 14073 | 13878 | 13790 | 13782 | 13782 | 13864 | 14276 | 15756 | 18156 | 21069 | 22493 | 23126 |
| Total events rRNA tree | 18311 | 17499 | 16593 | 15375 | 14399 | 14348 | 14149 | 14087 | 14085 | 14085 | 14104 | 14416 | 15957 | 17996 | 21201 | 22929 | 24267 |
| Single scenarios genome tree | 3166 | 3091 | 3163 | 3075 | 2496 | 3150 | 3166 | 3159 | 3166 | 1613 | 3150 | 2958 | 2246 | 2600 | 2907 | 3048 | 3122 |
| Single scenarios rRNA tree | 3166 | 3139 | 3164 | 3147 | 2494 | 3144 | 3166 | 3152 | 3166 | 1806 | 3108 | 2894 | 2399 | 2587 | 2982 | 3081 | 3154 |
Thus, g = 1 is a unique gain penalty value, which always entails the scenario with the smallest number of events. With the COG data set and the species tree topology, this minimum is highly stable, as indicated by the fact that the parsimonious scenario for g = 0.9 has the same number of events and all the scenarios for 0.7 ≤ g ≤ 1.25 have only slightly more.
Notably, for both small and large g values, the great majority of COGs (or even all as with g = 0.1, g = 0.7 and g = 0.9) have a unique parsimonious scenario, but for g = 1, there is a dramatic increase in redundancy. Apparently, many scenarios become equivalent when neither gains nor losses are given preference. Thus, g = 1 is a special case, under which the total number of events in the parsimonious scenarios is minimal and the redundancy of the parsimonious scenarios is maximal.
The trends noted above apply to both analysed tree topologies. However, the scenarios produced with the rRNA tree include a larger total number of events than those for the genome-tree topology at all gain penalties, with the sole exception of g = 3 (Table 2). In particular, at g = 1, the scenarios for the two alternative tree topologies differed by 303 events, which is a statistically significant difference (see below). The scenarios for the rRNA tree tend to include more losses and fewer gains (HGT events) than the scenarios for the genome-tree. However, the effect of the tree topology on the gains/loss ratio was less pronounced than the effect of changing the g value; thus, at g = 1, the numbers of gain and losses were close also for the rRNA tree topology (Table 2). The number of COGs assigned to LUCA under the rRNA topology was larger than that for the genome-tree topology at low g values (g ≤ 1.25), but for larger g values (g ≥ 1.5), the relationship was inverted. Interestingly, and in accord with the notion that g = 1 represents a special case, the difference was the greatest for this g value. Similar trends were seen for other ancestral forms (Table 2). The major difference between the topologies of the genome-tree and the rRNA tree is that the former has a more elaborate structure than the latter, with some additional major clades defined, e.g., the bacterial cluster that unites cyanobacteria, Deinococcales, and actinomycetes (compare the tree topologies in Figures 5 and 6). This probably explains why the parsimonious scenarios contain fewer events under the genome-tree topology: some of the phyletic patterns can be economically accounted for by HGT or gene loss at the ancestors of the major clades that are not present in the rRNA tree. The compatibility of many phyletic patterns with the topology of the genome tree, which leads to shorter scenarios than those produced with the less structured rRNA tree, might lend additional credence to the genome tree.
We further assessed the robustness of the obtained results by exploring the effect of randomizing the tree topology on the characteristics of the parsimonious scenarios. The clusters of archaea (ozmkap), bacteria (blwdcrnsfghexjutiqv), and four well-established bacterial lineages (blw, xj, nsfghexju and sfghe) were fixed; otherwise, the branches were shuffled to generate 50 randomized trees. The gain penalty weight was also uniformly randomized over the interval between 0.75 and 1.25. The results shown in Table 3 indicate that the total number of events in the parsimonious scenarios for the randomized trees exceeded that for the species tree adopted in this work (Figure 5) by three to four standard deviations. Since the rRNA tree retains the clusters that were fixed in the randomized trees, these experiments provided also for the statistical assessment of the difference between the parsimonious scenarios derived under the genome-tree and the rRNA topologies. In the case of g = 1, this difference was significant at the 1.5 σ level. The number of genes assigned to LUCA for random trees with larger weights also significantly deviated from the numbers in Table 2. Notably, however, the transition from the dramatic excess of HGT over gene loss for g < 1 to the approximately equal number of the two types of events for g = 1 persisted even in randomized trees.
Table 3.
Distribution of numbers of events in parsimonious scenarios for randomized trees.
| Gain penalty (g) | Numbers of events (mean/standard-deviation) | |||
| Total | Loss | HGT | LUCA | |
| g = 1 | 14446 / 180 | 5707 / 318 | 5543 / 223 | 650 / 42 |
| Random g values: 0.750 – 1.250 | 14489 / 199 | 4498 / 1604 | 6825 / 1582 | 476 / 176 |
| Random g values: 0.750–0.997 | 14479 / 227 | 2734 / 221 | 8578 / 185 | 289 / 30 |
| Random g values: 1.002–1.230 | 14497 / 181 | 5847 / 420 | 5484 / 318 | 620 / 71 |
Altogether, formal analysis of parsimonious evolutionary scenarios leads to the conclusion that g = 1 represents a special situation and might be the most appropriate value for the gain penalty. This points to the unexpected possibility that HGT had been as common as lineage-specific gene loss in prokaryotic evolution (Table 2). This runs against the notion of the prevalence of losses over HGT, which prompted us to examine in greater detail the gene sets assigned to LUCA for different g values.
The number of COGs assigned to LUCA increased monotonically with the increase in g, from 84 (g = 0.1), which is the set of ubiquitous COGs, to 1725 (g = 10), which is only two COGs short of the theoretical maximum of 1727 LUCA COGs (under the genome-tree topology, 1439 of the 3166 analysed COGs met the criterion of assertion 6 and could never be assigned to LUCA). Importantly, although the LUCA gene sets with different gain penalties were identified independently of each other, those derived at each successive g value always contained those obtained with lower g values; the same relation held for the two other ancestral forms included in Table 2. Table 4 shows the distribution of COGs assigned to LUCA under the genome-tree topology among broad functional categories depending on the gain penalty. The predictable general trend is for LUCA to become more functionally versatile and less dominated by highly conserved functions, such as translation and amino acid metabolism, with the increase in gain penalty that is accompanied by the growth in the total number of genes in LUCA.
Table 4.
Distribution of gene functions in LUCA depending on the gain penaltya
| Function | Number/percent of COGs assigned to LUCA | ||||
| g = 0.9 | g = 1.0 | g = 1.5 | g = 2.0 | g = 3.0 | |
| Translation | 64/20.6 | 97/17.0 | 102/13.9 | 109/11.4 | 113/9.3 |
| Transcription | 8/2.6 | 16/2.8 | 19/2.6 | 25/2.6 | 35/2.9 |
| Replication and repair | 14/4.5 | 31/5.4 | 37/5.0 | 55/5.8 | 71/5.9 |
| Cell division | 4/1.3 | 9/1.6 | 10/1.4 | 10/1.0 | 10/0.8 |
| Chaperones | 10/3.2 | 25/4.4 | 29/4.0 | 38/4.0 | 50/4.1 |
| Cell wall biogenesis | 5/1.6 | 10/1.7 | 17/2.3 | 25/2.6 | 31/2.6 |
| Secretion | 4/1.3 | 8/1.4 | 18/2.5 | 21/2.2 | 23/1.9 |
| Ion transport | 11/3.5 | 25/4.4 | 40/5.5 | 62/6.5 | 73/6.0 |
| Signal transduction | 2/0.6 | 10/1.7 | 12/1.6 | 15/1.6 | 19/1.6 |
| Sugar metabolism | 13/4.2 | 24/4.2 | 41/5.6 | 48/5.0 | 72/5.9 |
| Energy conversion | 19/6.1 | 46/8.0 | 67/9.1 | 99/10.4 | 127/10.1 |
| Amino acid metabolism | 61/19.7 | 88/15.4 | 95/13.0 | 121/12.7 | 145/12.0 |
| Nucleotide metabolism | 33/10.6 | 44/7.7 | 47/6.4 | 53/5.5 | 63/5.2 |
| Coenzyme metabolism | 24/7.7 | 47/8.2 | 65/8.9 | 80/8.4 | 94/7.8 |
| Lipid metabolism | 7/2.3 | 21/3.7 | 26/3.5 | 33/3.5 | 45/3.7 |
| Secondary metabolism | 6/1.9 | 6/1.0 | 9/1.2 | 12/1.3 | 15/1.2 |
| General functional prediction only | 24/7.7 | 53/9.3 | 78/10.6 | 112/11.7 | 152/12.6 |
| Function unknown | 1/0.3 | 12/2.1 | 21/2.9 | 38/4.0 | 78/6.4 |
aAll data are for the genome-tree topology
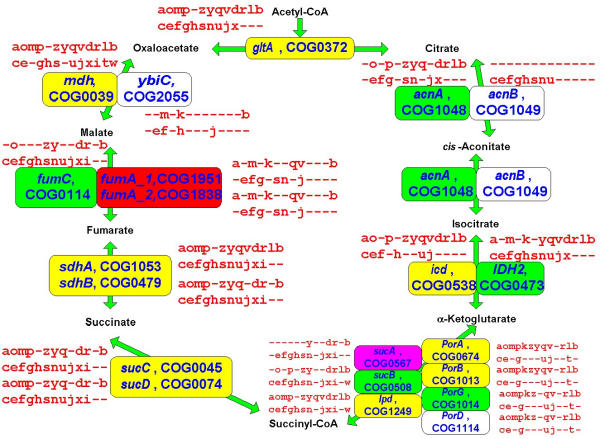
We further examined the LUCA gene sets obtained for different g values (hereinafter LUCA0.9, LUCA1.0 etc; these gene sets are available as Supplementary Material (See Additional file: 1) in a more qualitative manner, in order to determine which of them, if any, could, at least in principle, correspond to a viable organism. The main approach here is to reconstruct the major functional systems and pathways of the cell and to identify obvious "gaps" that make the hypothetical cell unsustainable. The substantial number of described cases of non-orthologous gene displacement, whereby the same essential function is performed by distantly related or unrelated proteins in different subsets of organisms [58,59], suggests that complete reconstruction of the LUCA gene set on the basis of extant phyletic patterns might not be realistic (or at least might require a very large number of genomes to be compared). Nevertheless, following the dynamics of "gap-filling" in the growing LUCA gene sets reconstructed with increasing gain penalties might point to a minimal reasonable LUCA. Moving along the growing LUCA gene sets (Table 2 and Additional file: 1), it was obvious that those produced with low g values were inadequate because they consist primarily of translation-associated genes. The first ancestral gene set that potentially could be a realistic candidate for a functioning cell was LUCA0.9. However, this version of LUCA still contains a considerable number of "gaps" in essential functional systems and pathways (Table 5). Most of these gaps are filled in LUCA1.0 and almost all of the rest disappear in LUCA1.5–3.0 (Table 5). In particular, LUCA1.0 has the complete translation system, with the sole exception of glycyl-tRNA synthetase (a well-known case of non-orthologous gene displacement), which appears in LUCA1.5; the set of basal RNA polymerases subunits, transcription termination factors and several helix-turn-helix transcription regulators; the complete set of the bacterial-type H+-ATPase subunits; and many (nearly) complete metabolic pathways (Figs. 7,8,9,10,11,12). Among the latter, only a few enzymes, which are particularly prone to non-orthologous displacement, do not appear in LUCA1.0, e.g. the essential glycolytic enzyme phosphoglyceromutase (Fig. 7). Notably, LUCA1.0 has a complete TCA cycle (Fig. 8), in spite of the fact that many modern bacteria and archaea have partial, non-cyclic variants of this pathway [60]. The pathways of purine and pyrimidine biosynthesis, as well as some of the amino acid biosynthesis pathways, are extremely conserved and tend to be represented in full even in LUCA0.9 (Fig. 7,8,9,10,11). In contrast, the fraction of unresolved cases of non-orthologous displacement is considerably larger in some of the coenzyme biosynthesis pathways (Fig. 12).
Table 5.
Essential genes missing in LUCA0.9 and their appearance in versions of LUCA with greater g-valuesa
| Gene name | COG no. | Minimal g-value | Function |
| TRANSLATION AND RIBOSOME BIOGENESIS | |||
| GatC | COG0721 | 1.0 | Asp-tRNAAsn/Glu-tRNAGln amidotransferase C subunit |
| LysU | COG1190 | 1.0 | Lysyl-tRNA synthetase |
| GRS1 | COG0423 | 1.5 | Glycyl-tRNA synthetase |
| CENTRAL METABOLIC PATHWAYS AND SUGAR METABOLISM | |||
| Glycolysis | |||
| PfkA | COG0205 | 1.0 | 6-phosphofructokinase |
| Fba | COG0191 | 1.0 | Fructose bisphosphate aldolase |
| GpsA | COG0240 | 1.0 | Glycerol 3-phosphate dehydrogenase |
| GpmA | COG0588 | 2 | Phosphoglycerate mutase, cofactor-dependent |
| TCA cycle | |||
| AcnA | COG1048 | 1.0 | Aconitase A |
| PorG | COG1014 | 1.0 | Pyruvate:ferredoxin oxidoreductase |
| AceF | COG0508 | 1.0 | Dihydrolipoamide acyltransferases |
| FumC | COG0114 | 1.0 | Fumarase |
| TtdA | COG1951 | 3.0 | Fumarate hydratase class I, N-terminal domain |
| FumA | COG1838 | 3.0 | Fumarate hydratase class I, C-terminal domain |
| Pentose phosphate shunt | |||
| Zwf | COG0364 | 1.0 | Glucose-6-phosphate 1-dehydrogenase |
| NagB | COG0363 | 1.0 | 6-phosphogluconolactonase/Glucosamine-6- |
| MipB | COG0176 | 1.0 | Transaldolase |
| Rpe | COG0036 | 1.0 | Pentose-5-phosphate-3-epimerase |
| RpiA | COG0120 | 1.0 | Ribose 5-phosphate isomerase |
| Gnd | COG0362 | 1.5 | 6-phosphogluconate dehydrogenase |
| NUCLEOTIDE METABOLISM | |||
| Adk | COG0563 | 1.0 | Adenylate kinase and related kinases |
| Cdd | COG0295 | 1.0 | Cytidine deaminase |
| - | COG0590 | 1.0 | Cytosine/adenosine deaminase |
| DeoC | COG0274 | 1.0 | Deoxyribose-phosphate aldolase |
| Gmk | COG0194 | 1.0 | Guanylate kinase |
| PurS | COG1828 | 1.0 | Phosphoribosylformylglycinamidine (FGAM) |
| THY1 (ThyX) | COG1351 | 1.0 | Predicted alternative thymidylate synthase |
| Pnp | COG0005 | 1.0 | Purine nucleoside phosphorylase |
| PyrH | COG0528 | 1.0 | Uridylate kinase |
| Cmk | COG1102 | >3 | Cytidylate kinase |
| Tdk | COG1435 | 1.5 | Thymidine kinase |
| AMINO ACID METABOLISM | |||
| AroG | COG0722 | 3.0 | 3-Deoxy-D-arabino-heptulosonate 7-phosphate (DAHP) synthase |
| AroA | COG2876 | 2.0 | 3-Deoxy-D-arabino-heptulosonate 7-phosphate (DAHP) synthase |
| AroD | COG0710 | 1.5 | 3-dehydroquinate dehydratase |
| AroQ | COG0757 | 1.5 | 3-dehydroquinate dehydratase II |
| AroK | COG0703 | 1.0 | Shikimate kinase |
| TyrB | COG1448 | 3.0 | Aspartate/aromatic aminotransferase |
| HIS2 | COG1387 | 1.0 | Histidinol phosphatase and related PHP family phosphatases |
aAll data are for the genome-tree topology. Only genes for enzymes of central metabolic pathways are included; genes appearing in LUCA at g >1.5 are indicated by shading
Figure 7.
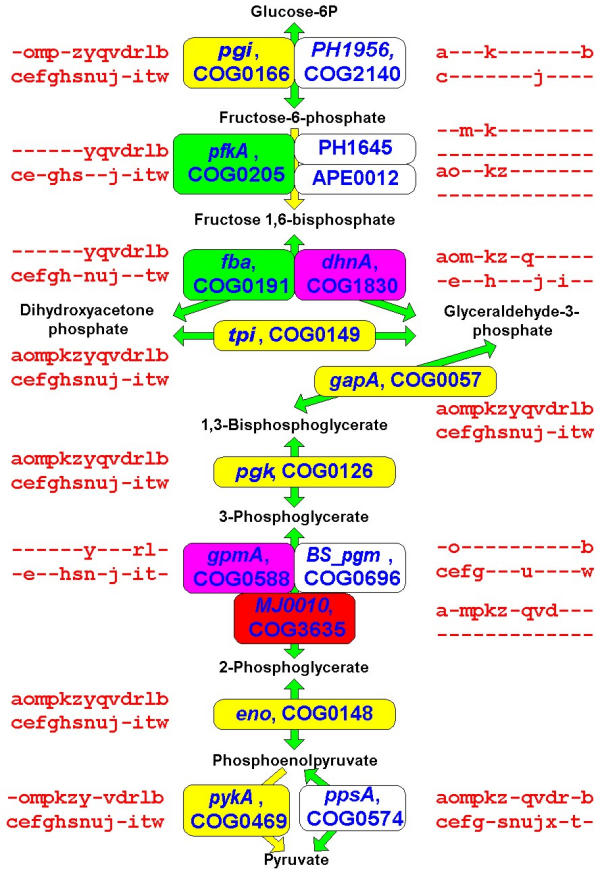
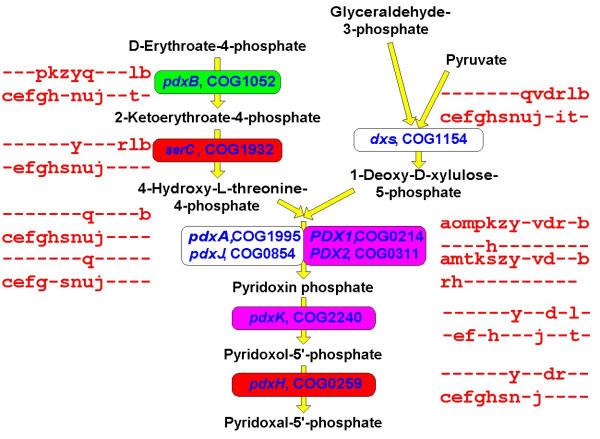
Representation of essential metabolic pathways in different versions of LUCA: glycolysis and gluconeogenesis. The enzyme names are accompanied by COG numbers and gene names (from E. coli unless indicated otherwise: PH, Pyrococcus horikoshii, BS, Bacillus subtilis). Phyletic patterns for all COGs are shown using the species abbreviations listed in the legend to Fig. 5. The COGs appearing in different reconstructed versions of LUCA are color-coded in this figure and Figures 7,8,9,10,11: LUCA0.9, yellow; LUCA1.0, green; LUCA1.5, blue; LUCA2.0 purple; LUCA3.0, red.
Figure 8.
Representation of essential metabolic pathways in different versions of LUCA: the TCA cycle. The designations are as in Fig. 6.
Figure 9.

Representation of essential metabolic pathways in different versions of LUCA: the purine biosynthesis. The designations are as in Fig. 6.
Figure 10.
Representation of essential metabolic pathways in different versions of LUCA: the pyrimidine biosynthesis. The designations are as in Fig. 6.
Figure 11.

Representation of essential metabolic pathways in different versions of LUCA: arginine biosynthesis. The designations are as in Fig. 6.
Figure 12.
Representation of essential metabolic pathways in different versions of LUCA: pyridoxal phosphate biosynthesis. The designations are as in Fig. 6.
A few genes that are normally considered to be essential for modern cells are missing in LUCA1.0 or, in several cases, in all reconstructed versions of LUCA, regardless of the gain penalty (Table 5). These genes could never make it to LUCA because they met the criterion of Assertion 6, i.e. are restricted in their phyletic distribution to one of the children of LUCA, either the bacterial or the archaeal-eukaryotic branch. The most conspicuous absences in LUCA are several essential components of the DNA replication machinery, including the replicative polymerase, helicase and initiation ATPase, whereas some other proteins involved in DNA replication, such as the sliding clamp or RNAse H, are present. Also notable is the absence of proteins involved in transcription initiation, such as bacterial sigma subunits. These lacunas in the reconstructed LUCA gene sets may be interpreted in two ways: i) the missing genes actually emerged at a post-LUCA stage of evolution, which suggests radical differences in some of the cellular functions between LUCA and modern cells, and ii) these are cases of ancient non-orthologous gene displacement, with the "memory" of the ancestral state obliterated. The first view is suggested by the parsimony principle and is compatible with the hypothesis that LUCA might have had an RNA-based genetic system that involved DNA intermediates [61]. However, it has to be emphasized that parsimony is valid (at best) as a statistical trend, i.e. for the majority of genes in a large ensemble. When individual functions are concerned, one cannot rule out that one of the extant forms, e.g. the bacterial one, originates from LUCA, but had been displaced at the base of the other major branch of life, or even that LUCA had a completely different gene for this function but this gene had been lost in the lineages leading to all extant species. Thus, while the first of the above views may be preferable as a general trend, in each particular case, discrimination between the two possibilities might not be feasible.
Conversely, LUCA1.0 (but apparently not LUCA0.9) has a considerable number of genes whose presence seems to result from limitations of the parsimony approach employed here. These are genes that are shared by multiple bacterial species and eukaryotes (represented in this analysis by yeast S. cerevisiae) and, in the latter, are known to function in the mitochondria. Examples include bacterial DNA polymerase I (PolA), which is orthologous to the eukaryotic mitochondrial replicative polymerase (Pol γ), and single-stranded DNA-binding protein (Ssb), also involved in eukaryotic mitochondrial DNA replication. Beyond reasonable doubt, these genes have been acquired by eukaryotes from the proto-mitochondrial endosymbiont. In and by itself, this does not preclude these genes from being part of the LUCA heritage; however, with this particular HGT event being a virtual certainty, a more sophisticated evolutionary reconstruction approach should have mapped their origin to the common ancestor of bacteria rather than to LUCA. The mitochondrial genes represent the most obvious case of genes erroneously included in LUCA due to HGT that went undetected by the employed algorithms; there might be other cases of cryptic HGT leading to inflation of LUCA.
Comparing LUCA1.0 obtained under the genome-tree topology to LUCA1.0 for the rRNA topology did not reveal many functions that were likely to be essential for cell function among the 117 COGs present in the latter but missing in the former (data not shown; see Additional file: 1). Possible exceptions are ribonuclease PH (COG0689) and ATP-dependent DNA ligase (COG1793). The reciprocal set of 46 COGs assigned to LUCA1.0 under the genome-tree topology but not under the rRNA tree topology contained a few more genes with apparent essential functions, e.g., the cell-division GTPase FtsZ (COG0206), peptidyl-prolyl cis-trans-isomerase (COG0652), fumarase, a TCA cycle enzyme (COG0114), and two enzymes that appear to be require for fatty acid biosynthesis (COG0183 and COG0318).
The differences in the gene sets assigned to LUCA under the genome-tree and the rRNA tree can be attributed to specific differences in the tree topologies. In particular, COGs shared by yeast, the majority of archaea and the hyperthermophilic bacterium A. aeolicus (q), which is thought to have acquired numerous archaeal genes via HGT [62], made it to LUCA1.0 under the rRNA tree topology but not the genome-tree topology. This is because, in the rRNA tree, A. aeolicus alone forms the earliest-branching bacterial clade, whereas, in the genome-tree, it clusters with the other hyperthermophilic bacterium, T. maritima, which lacks some of the genes shared by archaea and A. aeolicus (compare trees in Fig. 5 and Fig. 6). Several other COGs that are present in both hyperthermophilic bacteria and a subset of archaea are included in one version of LUCA, but not the other, because of the differences in the topology of the archaeal subtree, i.e., the basal position of Halobacterium sp (o). in the genome-tree but not the rRNA tree (Fig. 5,6). Interestingly, reverse gyrase, the enzyme, which is the genomic signature of hyperthermophiles [63] and is thought to be indispensable for DNA replication and transcription at extremely high temperatures [64], is part of the latter subset and belongs to LUCA1.0 under the rRNA tree topology but not under the genome-tree topology. Thus, the difference in the underlying species tree topologies, in some cases, could account for substantial differences in the interpretation of the reconstructed ancestral gene sets. In the present analysis, the rRNA tree topology but not the genome-tree topology seems to imply a hyperthermophilic LUCA; whether or not LUCA was a hyperthermophile, is the subject of an ongoing hot debate among origin of life researchers [65-69].
As outlined above, examination of the reconstructed LUCA gene sets suggests that LUCA1.0, with its 572 genes (under the genome-tree), might approximate a viable organism, at least numerically; to produce a more realistic reconstruction, at least a few genes that have not made the list because of non-orthologous gene displacement would have to be added, and perhaps a greater number of genes, including mitochondrial-bacterial ones, would need to be subtracted. The number of genes in this version of LUCA is somewhat greater than in the smallest genomes of modern bacteria, the mycoplasma (however, these are parasites that have lost most of the biosynthetic pathways), but almost three-fold less than in the smallest sequenced genome of a free-living organism, Thermoplasma acidophilum (1482 genes). Clearly, LUCA1.0 derived here is only a tentative pointer to the minimal reasonable size of the LUCA gene set and a more complex LUCA cannot be ruled out [69]. However, taken together with the support for g = 1 from the computational analysis described above, even this crude reconstruction suggests that, contrary to a widely held view, HGT might have been at least as common as lineage-specific gene loss in the evolution of prokaryotes.
Major trends in post-LUCA evolution suggested by the parsimonious scenarios
The most striking aspect of the parsimonious scenarios of genome evolution derived here is the prevalence of HGT and gene loss. According to the PARS algorithm, only a small minority of the COGs (315 of the 3166 analyzed COGs, ~10%; Table 6), namely those with the inconsistency value of 1, did not show evidence of such evolutionary events (in this case, the only event in the evolution of a COG is its "birth"). The evolution of the majority of the COGs was inferred to have involved one to 6 transfers and losses, and some COGs appear to have undergone as many as 10 such events (Table 6; these are the results for the genome-tree topology, but those for the rRNA tree topology were very similar; data not shown). The data in Table 6 indicate that these events are widely spread across (nearly) all categories of genes, which provides quantitative support for the general notion that lineage-specific gene loss and HGT have been major forces in the evolution of prokaryotes.
Table 6.
Distributions of COGs by the number of events in the most parsimonious scenario depending on the gain penaltya
| Number of events | Gain penalty (g) | ||||
| 0.9 | 1.0 | 1.5 | 2.0 | 3.0 | |
| 1 | 315 | 315 | 315 | 315 | 315 |
| 2 | 420 | 420 | 420 | 375 | 314 |
| 3 | 593 | 593 | 574 | 518 | 390 |
| 4 | 487 | 487 | 474 | 430 | 344 |
| 5 | 400 | 400 | 386 | 357 | 323 |
| 6 | 350 | 350 | 324 | 301 | 275 |
| 7 | 267 | 267 | 246 | 226 | 252 |
| 8 | 161 | 161 | 176 | 206 | 233 |
| 9 | 106 | 106 | 118 | 149 | 200 |
| 10 | 50 | 50 | 67 | 110 | 165 |
| 11 | 15 | 15 | 38 | 80 | 130 |
| 12 | 2 | 2 | 17 | 42 | 104 |
| 13 | 9 | 33 | 70 | ||
| 14 | 2 | 18 | 34 | ||
| 15 | 6 | 13 | |||
| 16 | 3 | ||||
| 17 | 1 | ||||
aAll data are for the genome-tree topology.
The distribution of gains and losses in the tree generally conforms to the intuitive notions in that numerous losses are associated with tree branches that include largely parasitic bacteria, whereas branches enriched in large genomes have many inferred gains (Fig. 13,14,15,16,17,18,19,20). Particularly striking are comparisons of closely related organisms with substantially different genome sizes, e.g. Rickettsia prowazekii (x), an intracellular parasite with a small genome, and Mesorhizobium loti (j), a symbiont with a large genome and elaborate physiology. The respective tree leaves show opposite evolutionary patterns, with the former dominated by losses, with only a few gains, and the latter by gains, with almost no losses. However, the clade that consists of free-living, hyperthermophilic bacteria (A. aeolicus and T. maritima, qv) has many associated gains, despite the small genome size. This is attributable to a major influx of archaeal genes via HGT [12,62,70].
Figure 13.
Gain and loss of COGs in internal nodes of the genome-tree according to PARS-G algorithm: g = 0.9. The boxes contain the number of gains (numerator) and losses (denominator) associated with each internal node; the gains (top) and losses (bottom) for each extant species are shown under the letter designating the species.
Figure 14.
Gain and loss of COGs in internal nodes of the rRNA tree according to PARS-G algorithm: g = 0.9. The designations are as in Fig. 13.
Figure 15.
Gain and loss of COGs in internal nodes of the genome-tree according to PARS-G algorithm: g = 1.0. The designations are as in Fig. 13.
Figure 16.
Gain and loss of COGs in internal nodes of the rRNA tree according to PARS-G algorithm: g = 1.0. The designations are as in Fig. 13.
Figure 17.
Gain and loss of COGs in internal nodes of the genome-tree according to PARS-G algorithm: g = 1.5. The designations are as in Fig. 13.
Figure 18.
Gain and loss of COGs in internal nodes of the rRNA tree according to PARS-G algorithm: g = 1.5. The designations are as in Fig. 13.
Figure 19.
Gain and loss of COGs in internal nodes of the genome tree according to PARS-G algorithm: g = 2.0. The designations are as in Fig. 13.
Figure 20.
Gain and loss of COGs in internal nodes of the rRNA tree according to PARS-G algorithm: g = 2.0. The designations are as in Fig. 13.
The common ancestors of bacteria and archaea-eukaryotes, which have no associated losses in accord with Assertion 5, are linked to massive gene gain. This is likely to reflect radical innovation at these evolutionary junctures, perhaps including even independent origin of DNA replication systems [61,71,72]. A general feature of the reconstructed scenarios, which is largely independent of the gain penalty value, is that the losses are largely associated with some of the leaves. This seems to reflect the relatively late, independent adaptation of many bacteria to the parasitic life style.
Changing the gain penalty affects the distribution of gains and losses among the vertices and leaves in a predictable way: scenarios for g = 0.9 are dominated by gains and have very few losses at internal nodes (Figs. 13,14), whereas the scenarios with increasing g values show progressive increase in the early losses, e.g. at the common ancestor of the archaea (Figs. 15,16,17,18,19,20).
The scenarios produced with the genome-tree topology and those for the rRNA tree topology were, in general very, similar with respect to the distribution of losses and gains (compare Figs. 13 and 14, 15 and 16, 17 and 18, 19 and 20). The reconstruction was substantially affected only for those few clades whose positions differed in the two trees, e.g., the spirochete-chlamydia clade (it), which branches off early in the genome-tree, but clusters with Proteobacteria in the rRNA tree. This resulted in a much greater amount of gene loss assigned to this clade under the rRNA tree topology compared to the genome-tree topology.
General discussion and conclusions
The analysis described here implements the most straightforward approach to the reconstruction of parsimonious scenarios by using phyletic patterns of orthologous gene sets (COGs) and a species tree as the only inputs. The general idea of this approach is the same as that of the recent work of Snel, Huynen and Bork [17]. However, Snel and co-workers employed a simple enumeration algorithm, which included the arbitrary condition of gain independence. We developed a rigorous method for reconstructing parsimonious evolutionary scenarios, investigated the effect of different criteria for choosing between scenarios with the same number of events and showed that the independence condition substantially affects the reconstructed ancestral gene sets. Furthermore, we used a different and larger collection of orthologous gene sets and compared the scenarios produced under two different species tree topologies, those of the consensus genome-tree and the rRNA tree.
This work yielded two central conclusions. First, we found that the evolutionary history of ~90% of the COGs included at least one but, typically, several events of gene loss and/or HGT. This puts concrete numbers to the general notion of a major role of these processes, at least in the evolution of prokaryotes [8-10,12,37,71,73], and supports and extends the (luckily named) "genomes in flux" concept of Snel and co-workers [17]. Second, however, this work suggests that the nature of this genomic flux is different from what had been typically envisaged before, in the work of Snel and co-workers [17] and in other studies as well [74,75]. Both the formal properties of the reconstructed parsimonious scenarios and the biologically oriented, informal analysis of the reconstructed LUCA gene sets suggested that, in the evolution of prokaryotes, HGT might have been as common as gene loss.
Moreover, the approach employed here clearly provides a conservative, low-bound estimate of the amount of HGT. In many cases, although the phyletic pattern of a COG does not offer any indication of HGT, phylogenetic tree analysis provides clear evidence. Perhaps the strongest case in point are translation system components, which are (nearly) ubiquitous and belong to the set of 315 genes whose evolution was here inferred to have included only one event, the original emergence (Table 6). For some of these genes, including aminoacyl-tRNA synthetases, translation factors and even ribosomal proteins, evidence of multiple HGT events has been obtained by phylogenetic analysis [26,76-82]. Undoubtedly, the history of many more COGs, which superficially, on the basis of examination of phyletic patterns alone, appear to have evolved vertically, had involved HGT [37]. Given these considerations and the fact that many of the gene losses are associated with the relatively recent evolution of parasites (Fig. 13,14,15,16,17,18,19,20), it seems likely that the early phase of the evolution of prokaryotes (which is the same as the evolution of life itself prior to the emergence of eukaryotes) had been dominated by HGT.
The conclusion on the probable high incidence of HGT is linked to the notion of a simple, as opposed to a complex, LUCA [69]. If LUCA was a (nearly) minimal free-living organism, subsequent evolution in each lineage should have generally proceeded in the direction of increasing complexity and, by necessity, would have been dominated by gene gain, via HGT and, to a lesser extent, "invention" of new genes. In contrast, the notion of a complex LUCA implies that LUCA already had the bulk of the prokaryotic gene repertoire and subsequent evolution was dominated by differential sampling of these genes, i.e., differential gene loss. The latter view of evolution is logically consistent and, at least at present, cannot be ruled out. However, it assigns the generation of most of the modern gene diversity (at least as far as prokaryotes are concerned) to the relatively short, pre-LUCA stage of life's evolution. Extensive evolution leading to the emergence of the majority of common protein folds definitely preceded LUCA [71,83]. However, saddling this, already "overloaded", early period with nearly all of the more subtle diversification and leaving mostly elimination for the rest of prokaryotic evolution does not seem to provide for a plausible picture of evolution.
In principle, reconstruction of evolutionary scenarios can provide feedback for comparative assessment of the plausibility of the species tree topologies. Here, we found the genome-tree topology consistently yielded scenarios with fewer events than the rRNA tree topology. The difference, although statistically significant, was, however, not overwhelming and probably should not be viewed as a strong argument for one species tree topology as opposed to another. It is nevertheless notable that using the genome-tree topology instead of the rRNA topology definitely did not lead to less parsimonious scenarios, which suggests that the new clades present in the genome-tree might not be altogether implausible.
This analysis is a preliminary, crude attempt on constructing evolutionary scenarios using comparative-genomic data. Further developments will include the use of phylogenetic tree topology for each orthologous gene set, in addition to the phyletic patterns, as input information for constructing more realistic evolutionary scenarios. It also has to be kept in mind that here we did not attempt to reconstruct the functional aspects of LUCA in full detail; our goal was merely a rough examination of the reconstructed gene sets, in order to assess their functional plausibility and the relative contributions of gene loss and HGT. With the rapid growth of the database of sequenced genomes, the information available for careful reconstruction of LUCA and other ancestral forms will progressively increase, and such reconstructions are expected to shed more light on the fundamental aspects of the evolutionary process.
Author Contributions
BGM and TIF developed the mathematical approaches and the algorithms and wrote the respective portions of the manuscript; BGM wrote the software and ran the calculations; MYG and EVK performed the biological analysis of the reconstructed gene sets; EVK incepted the study, contributed to the design of the approach, developed the biological implications, wrote the Background, Empirical results and General Discussion sections and edited the entire manuscript.
Supplementary Material
Additional file 1
Acknowledgments
Acknowledgements
The authors thank Igor Rogozin and Peter Gogarten for critical reading of the manuscript and numerous helpful suggestions.
Contributor Information
Boris G Mirkin, Email: mirkin@dcs.bbk.ac.uk.
Trevor I Fenner, Email: trevor@dcs.bbk.ac.uk.
Michael Y Galperin, Email: galperin@ncbi.nlm.nih.gov.
Eugene V Koonin, Email: koonin@ncbi.nlm.nih.gov.
References
- Woese CR. Bacterial evolution. Microbiol Rev. 1987;51:221–271. doi: 10.1128/mr.51.2.221-271.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gogarten JP, Kibak H, Dittrich P, Taiz L, Bowman EJ, Bowman BJ, Manolson MF, Poole RJ, Date T, Oshima T, et al. Evolution of the vacuolar H+-ATPase: implications for the origin of eukaryotes. Proc Natl Acad Sci U S A. 1989;86:6661–6665. doi: 10.1073/pnas.86.17.6661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iwabe N, Kuma K, Hasegawa M, Osawa S, Miyata T. Evolutionary relationship of archaebacteria, eubacteria, and eukaryotes inferred from phylogenetic trees of duplicated genes. Proc Natl Acad Sci U S A. 1989;86:9355–9359. doi: 10.1073/pnas.86.23.9355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woese CR, Kandler O, Wheelis ML. Towards a natural system of organisms: proposal for the domains Archaea, Bacteria, and Eucarya. Proc Natl Acad Sci U S A. 1990;87:4576–4579. doi: 10.1073/pnas.87.12.4576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golding GB, Gupta RS. Protein-based phylogenies support a chimeric origin for the eukaryotic genome. Mol Biol Evol. 1995;12:1–6. doi: 10.1093/oxfordjournals.molbev.a040178. [DOI] [PubMed] [Google Scholar]
- Gupta RS, Golding GB. The origin of the eukaryotic cell. Trends Biochem Sci. 1996;21:166–171. doi: 10.1016/0968-0004(96)20013-1. [DOI] [PubMed] [Google Scholar]
- Hilario E, Gogarten JP. Horizontal transfer of ATPase genes – the tree of life becomes a net of life. Biosystems. 1993;31:111–119. doi: 10.1016/0303-2647(93)90038-E. [DOI] [PubMed] [Google Scholar]
- Koonin EV, Mushegian AR, Galperin MY, Walker DR. Comparison of archaeal and bacterial genomes: computer analysis of protein sequences predicts novel functions and suggests a chimeric origin for the archaea. Mol Microbiol. 1997;25:619–637. doi: 10.1046/j.1365-2958.1997.4821861.x. [DOI] [PubMed] [Google Scholar]
- Doolittle WF. Phylogenetic classification and the universal tree. Science. 1999;284:2124–2129. doi: 10.1126/science.284.5423.2124. [DOI] [PubMed] [Google Scholar]
- Doolittle WF. Lateral genomics. Trends Cell Biol. 1999;9:M5–8. doi: 10.1016/S0962-8924(99)01664-5. [DOI] [PubMed] [Google Scholar]
- Gogarten JP, Olendzenski L. Orthologs, paralogs and genome comparisons. Curr Opin Genet Dev. 1999;9:630–636. doi: 10.1016/S0959-437X(99)00029-5. [DOI] [PubMed] [Google Scholar]
- Koonin EV, Makarova KS, Aravind L. Horizontal gene transfer in prokaryotes: quantification and classification. Annu Rev Microbiol. 2001;55:709–742. doi: 10.1146/annurev.micro.55.1.709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ragan MA. Detection of lateral gene transfer among microbial genomes. Curr Opin Genet Dev. 2001;11:620–626. doi: 10.1016/S0959-437X(00)00244-6. [DOI] [PubMed] [Google Scholar]
- Ragan MA. On surrogate methods for detecting lateral gene transfer. FEMS Microbiol Lett. 2001;201:187–191. doi: 10.1016/S0378-1097(01)00262-2. [DOI] [PubMed] [Google Scholar]
- Tatusov RL, Koonin EV, Lipman DJ. A genomic perspective on protein families. Science. 1997;278:631–637. doi: 10.1126/science.278.5338.631. [DOI] [PubMed] [Google Scholar]
- Tatusov RL, Natale DA, Garkavtsev IV, Tatusova TA, Shankavaram UT, Rao BS, Kiryutin B, Galperin MY, Fedorova ND, Koonin EV. The COG database: new developments in phylogenetic classification of proteins from complete genomes. Nucleic Acids Res. 2001;29:22–28. doi: 10.1093/nar/29.1.22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snel B, Bork P, Huynen MA. Genomes in flux: the evolution of archaeal and proteobacterial gene content. Genome Res. 2002;12:17–25. doi: 10.1101/gr.176501. [DOI] [PubMed] [Google Scholar]
- Pennisi E. Genome data shake tree of life. Science. 1998;280:672–674. doi: 10.1126/science.280.5364.672. [DOI] [PubMed] [Google Scholar]
- Pennisi E. Is it time to uproot the tree of life? Science. 1999;284:1305–1307. doi: 10.1126/science.284.5418.1305. [DOI] [PubMed] [Google Scholar]
- Snel B, Bork P, Huynen MA. Genome phylogeny based on gene content. Nat Genet. 1999;21:108–110. doi: 10.1038/5052. [DOI] [PubMed] [Google Scholar]
- Fitz-Gibbon ST, House CH. Whole genome-based phylogenetic analysis of free-living microorganisms. Nucleic Acids Res. 1999;27:4218–4222. doi: 10.1093/nar/27.21.4218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tekaia F, Lazcano A, Dujon B. The genomic tree as revealed from whole proteome comparisons. Genome Res. 1999;9:550–557. [PMC free article] [PubMed] [Google Scholar]
- Lin J, Gerstein M. Whole-genome trees based on the occurrence of folds and orthologs: implications for comparing genomes on different levels. Genome Res. 2000;10:808–818. doi: 10.1101/gr.10.6.808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolf YI, Rogozin IB, Grishin NV, Tatusov RL, Koonin EV. Genome trees constructed using five different approaches suggest new major bacterial clades. BMC Evol Biol. 2001;1:8. doi: 10.1186/1471-2148-1-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown JR, Douady CJ, Italia MJ, Marshall WE, Stanhope MJ. Universal trees based on large combined protein sequence data sets. Nat Genet. 2001;28:281–285. doi: 10.1038/90129. [DOI] [PubMed] [Google Scholar]
- Brochier C, Bapteste E, Moreira D, Philippe H. Eubacterial phylogeny based on translational apparatus proteins. Trends Genet. 2002;18:1–5. doi: 10.1016/S0168-9525(01)02522-7. [DOI] [PubMed] [Google Scholar]
- Matte-Tailliez O, Brochier C, Forterre P, Philippe H. Archaeal phylogeny based on ribosomal proteins. Mol Biol Evol. 2002;19:631–639. doi: 10.1093/oxfordjournals.molbev.a004122. [DOI] [PubMed] [Google Scholar]
- Clarke GD, Beiko RG, Ragan MA, Charlebois RL. Inferring genome trees by using a filter to eliminate phylogenetically discordant sequences and a distance matrix based on mean normalized BLASTP scores. J Bacteriol. 2002;184:2072–2080. doi: 10.1128/JB.184.8.2072-2080.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korbel JO, Snel B, Huynen MA, Bork P. SHOT: a web server for the construction of genome phylogenies. Trends in Genetics. 2002;18:158–162. doi: 10.1016/S0168-9525(01)02597-5. [DOI] [PubMed] [Google Scholar]
- Wolf Y, Rogozin I, Grishin N, Koonin E. Genome trees and the tree of life. Trends Genet. 2002;18:472–479. doi: 10.1016/S0168-9525(02)02744-0. [DOI] [PubMed] [Google Scholar]
- Page RDM. Maps between trees and cladistic analysis of historical associations among genes, organisms, and areas. Syst Biol. 1994;43:58–77. [Google Scholar]
- Mirkin B, Muchnik I, Smith TF. A biologically consistent model for comparing molecular phylogenies. J Comput Biol. 1995;2:493–507. doi: 10.1089/cmb.1995.2.493. [DOI] [PubMed] [Google Scholar]
- Zhang L. On a Mirkin-Muchnik-Smith conjecture for comparing molecular phylogenies. J Comput Biol. 1997;4:177–187. doi: 10.1089/cmb.1997.4.177. [DOI] [PubMed] [Google Scholar]
- Page RDM, Charleston AM. Reconciled trees and incongruent gene and species trees. In: Mirkin B, McMorris FR, Roberts SF, Rzhetsky A, editor. Mathematical Hierarchies in Biology. Vol. 37. Providence, RI: American Mathematical Society; 1997. [Google Scholar]
- Guigo R, Muchnik I, Smith TF. Reconstruction of ancient molecular phylogeny. Mol Phylogenet Evol. 1996;6:189–213. doi: 10.1006/mpev.1996.0071. [DOI] [PubMed] [Google Scholar]
- Eulenstein O, Mirkin B, Vingron M. Duplication-based measures of difference between gene and species trees. J Comput Biol. 1998;5:135–148. doi: 10.1089/cmb.1998.5.135. [DOI] [PubMed] [Google Scholar]
- Gogarten JP, Doolittle WF, Lawrence JG. Prokaryotic evolution in light of gene transfer. Mol Biol Evol. 2002;19:2226–2238. doi: 10.1093/oxfordjournals.molbev.a004046. [DOI] [PubMed] [Google Scholar]
- Mushegian AR, Koonin EV. Gene order is not conserved in bacterial evolution. Trends Genet. 1996;12:289–290. doi: 10.1016/0168-9525(96)20006-X. [DOI] [PubMed] [Google Scholar]
- Watanabe H, Mori H, Itoh T, Gojobori T. Genome plasticity as a paradigm of eubacteria evolution. J Mol Evol. 1997;44:S57–64. doi: 10.1007/pl00000052. [DOI] [PubMed] [Google Scholar]
- Dandekar T, Snel B, Huynen M, Bork P. Conservation of gene order: a fingerprint of proteins that physically interact. Trends Biochem Sci. 1998;23:324–328. doi: 10.1016/S0968-0004(98)01274-2. [DOI] [PubMed] [Google Scholar]
- Wolf YI, Rogozin IB, Kondrashov AS, Koonin EV. Genome alignment, evolution of prokaryotic genome organization and prediction of gene function using genomic context. Genome Res. 2001;11:356–372. doi: 10.1101/gr.GR-1619R. [DOI] [PubMed] [Google Scholar]
- Olsen GJ, Woese CR, Overbeek R. The winds of (evolutionary) change: breathing new life into microbiology. J Bacteriol. 1994;176:1–6. doi: 10.1128/jb.176.1.1-6.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moran NA, Mira A. The process of genome shrinkage in the obligate symbiont Buchnera aphidicola. Genome Biol. 2001;2:RESEARCH0054. doi: 10.1186/gb-2001-2-12-research0054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silva FJ, Latorre A, Moya A. Genome size reduction through multiple events of gene disintegration in Buchnera APS. Trends Genet. 2001;17:615–618. doi: 10.1016/S0168-9525(01)02483-0. [DOI] [PubMed] [Google Scholar]
- Himmelreich R, Plagens H, Hilbert H, Reiner B, Herrmann R. Comparative analysis of the genomes of the bacteria Mycoplasma pneumoniae and Mycoplasma genitalium. Nucleic Acids Res. 1997;25:701–712. doi: 10.1093/nar/25.4.701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogata H, Audic S, Renesto-Audiffren P, Fournier PE, Barbe V, Samson D, Roux V, Cossart P, Weissenbach J, Claverie JM, Raoult D. Mechanisms of evolution in Rickettsia conorii and R. prowazekii. Science. 2001;293:2093–2098. doi: 10.1126/science.1061471. [DOI] [PubMed] [Google Scholar]
- Swofford DL, Olsen GJ, Waddell PJ, Hillis DM. Phylogenetic Inference. In: Hillis DM, Moritz C, Mable BK, editor. Molecular Systematics. 2nd. Sunderland, MA: Sinauer Associates, Inc; 1996. [Google Scholar]
- Nei M, Kumar S. Molecular Evolution and Phylogenetics. Oxford: Oxford University Press; 2000. [Google Scholar]
- Maddison WP, Maddison DR. MacClade 30. Sunderland, MA: Sinauer Associates, Inc; 1992. [Google Scholar]
- Fitch WM. Towards defining the course of evolution: Minimum change for a specific tree topology. Syst Zool. 1971;20:406–416. [Google Scholar]
- Hartigan JA. Minimum evolution fits to a given tree. Biometrics. 1973;29:53–65. [Google Scholar]
- Swofford DL, Maddison WP. Reconstructing ancestral character states under Wagner parsimony. Math Biosci. 1987;87:199–299. doi: 10.1016/0025-5564(87)90074-5. [DOI] [Google Scholar]
- Sankoff D. Minimal mutation trees of sequences. SIAM J Appl Math. 1975;28:35–42. [Google Scholar]
- Sankoff D, Cedergeren RJ. Simultaneous comparison of three or more sequences related by a tree. In: Sankoff D, Kruskal JB, editor. Time Warps, String Edits, and Macromolecules: The Theory and Practice of Sequence Comparison. Reading, MA: Addison-Wesley; 1983. [Google Scholar]
- Swofford DL, Maddison WP. Parsimony, character-state reconstructions, and evolutionary inferences. In: Mayden RL, editor. Systematics, Historical Ecology, and North American Freshwater Fishes. Stanford: Stanford University Press; 1992. [Google Scholar]
- Brown JR, Doolittle WF. Archaea and the prokaryote-to-eukaryote transition. Microbiol Mol Biol Rev. 1997;61:456–502. doi: 10.1128/mmbr.61.4.456-502.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farris JS. Phylogenetic analysis under Dollo's Law. Syst Zool. 1977;26:77–88. [Google Scholar]
- Koonin EV, Mushegian AR, Bork P. Non-orthologous gene displacement. Trends Genet. 1996;12:334–336. doi: 10.1016/0168-9525(96)20010-1. [DOI] [PubMed] [Google Scholar]
- Koonin EV. How many genes can make a cell: the minimal-gene-set concept. Annu Rev Genomics Hum Genet. 2000;1:99–116. doi: 10.1146/annurev.genom.1.1.99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huynen MA, Dandekar T, Bork P. Variation and evolution of the citric-acid cycle: a genomic perspective. Trends Microbiol. 1999;7:281–291. doi: 10.1016/S0966-842X(99)01539-5. [DOI] [PubMed] [Google Scholar]
- Leipe DD, Aravind L, Koonin EV. Did DNA replication evolve twice independently? Nucleic Acids Res. 1999;27:3389–3401. doi: 10.1093/nar/27.17.3389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aravind L, Tatusov RL, Wolf YI, Walker DR, Koonin EV. Evidence for massive gene exchange between archaeal and bacterial hyperthermophiles. Trends Genet. 1998;14:442–444. doi: 10.1016/S0168-9525(98)01553-4. [DOI] [PubMed] [Google Scholar]
- Forterre P. A hot story from comparative genomics: reverse gyrase is the only hyperthermophile-specific protein. Trends Genet. 2002;18:236–237. doi: 10.1016/S0168-9525(02)02650-1. [DOI] [PubMed] [Google Scholar]
- Rodriguez AC, Stock D. Crystal structure of reverse gyrase: insights into the positive supercoiling of DNA. Embo J. 2002;21:418–426. doi: 10.1093/emboj/21.3.418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Di Giulio M. The universal ancestor was a thermophile or a hyperthermophile. Gene. 2001;281:11–17. doi: 10.1016/S0378-1119(01)00781-8. [DOI] [PubMed] [Google Scholar]
- Forterre P. Looking for the most "primitive" organism(s) on Earth today: the state of the art. Planet Space Sci. 1995;43:167–177. doi: 10.1016/0032-0633(94)00167-P. [DOI] [PubMed] [Google Scholar]
- DiRuggiero J, Brown JR, Bogert AP, Robb FT. DNA repair systems in archaea: mementos from the last universal common ancestor? J Mol Evol. 1999;49:474–484. doi: 10.1007/pl00006570. [DOI] [PubMed] [Google Scholar]
- Forterre P, Benachenhou-Lafha N, Labedan B. Universal tree of life. Nature. 1993;362:795. doi: 10.1038/362795b0. [DOI] [PubMed] [Google Scholar]
- Forterre P, Philippe H. The last universal common ancestor (LUCA), simple or complex? Biol Bull. 1999;196:373–375. doi: 10.2307/1542973. discussion 375–377. [DOI] [PubMed] [Google Scholar]
- Nelson KE, Clayton RA, Gill SR, Gwinn ML, Dodson RJ, Haft DH, Hickey EK, Peterson JD, Nelson WC, Ketchum KA, McDonald L, Utterback TR, Malek JA, Linher KD, Garrett MM, Stewart AM, Cotton MD, Pratt MS, Phillips CA, Richardson D, Heidelberg J, Sutton GG, Fleischmann RD, Eisen JA, Fraser CM, et al. Evidence for lateral gene transfer between Archaea and bacteria from genome sequence of Thermotoga maritima. Nature. 1999;399:323–329. doi: 10.1038/20601. [DOI] [PubMed] [Google Scholar]
- Koonin EV, Galperin MY. Sequence – Evolution-Function Computational Approaches in Comparative Genomics. New York: Kluwer Acad Publ; 2002. [PubMed] [Google Scholar]
- Forterre P. Genomics and early cellular evolution. The origin of the DNA world. C R Acad Sci III. 2001;324:1067–1076. doi: 10.1016/S0764-4469(01)01403-2. [DOI] [PubMed] [Google Scholar]
- Lawrence JG. Selfish operons and speciation by gene transfer. Trends Microbiol. 1997;5:355–359. doi: 10.1016/S0966-842X(97)01110-4. [DOI] [PubMed] [Google Scholar]
- Kurland CG. Something for everyone. Horizontal gene transfer in evolution. EMBO Rep. 2000;1:92–95. doi: 10.1093/embo-reports/kvd042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gupta RS, Griffiths E. Critical issues in bacterial phylogeny. Theor Popul Biol. 2002;61:423–434. doi: 10.1006/tpbi.2002.1589. [DOI] [PubMed] [Google Scholar]
- Doolittle RF, Handy J. Evolutionary anomalies among the aminoacyl-tRNA synthetases. Curr Opin Genet Dev. 1998;8:630–636. doi: 10.1016/S0959-437X(98)80030-0. [DOI] [PubMed] [Google Scholar]
- Wolf YI, Aravind L, Grishin NV, Koonin EV. Evolution of aminoacyl-tRNA synthetases – analysis of unique domain architectures and phylogenetic trees reveals a complex history of horizontal gene transfer events. Genome Res. 1999;9:689–710. [PubMed] [Google Scholar]
- Woese CR, Olsen GJ, Ibba M, Soll D. Aminoacyl-tRNA synthetases, the genetic code, and the evolutionary process. Microbiol Mol Biol Rev. 2000;64:202–236. doi: 10.1128/MMBR.64.1.202-236.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kyrpides NC, Woese CR. Universally conserved translation initiation factors. Proc Natl Acad Sci U S A. 1998;95:224–228. doi: 10.1073/pnas.95.1.224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leipe DD, Wolf YI, Koonin EV, Aravind L. Classification and evolution of P-loop GTPases and related ATPases. J Mol Biol. 2002;317:41–72. doi: 10.1006/jmbi.2001.5378. [DOI] [PubMed] [Google Scholar]
- Brochier C, Philippe H, Moreira D. The evolutionary history of ribosomal protein RpS14: horizontal gene transfer at the heart of the ribosome. Trends Genet. 2000;16:529–533. doi: 10.1016/S0168-9525(00)02142-9. [DOI] [PubMed] [Google Scholar]
- Makarova KS, Ponomarev VA, Koonin EV. Two C or not two C: recurrent disruption of Zn-ribbons, gene duplication, lineage-specific gene loss, and horizontal gene transfer in evolution of bacterial ribosomal proteins. Genome Biol. 2001;2:RESEARCH0033. doi: 10.1186/gb-2001-2-9-research0033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aravind L, Mazumder R, Vasudevan S, Koonin EV. Trends in protein evolution inferred from sequence and structure analysis. Curr Opin Struct Biol. 2002;12:392–399. doi: 10.1016/S0959-440X(02)00334-2. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Additional file 1