A Traditionally Administered Short Course Failed to Improve Medical Students’ Diagnostic Performance

Abstract

BACKGROUND

Quite often medical students or novice residents have difficulty in ruling out diseases even though they are quite unlikely and, due to this difficulty, such students and novice residents unnecessarily repeat laboratory or imaging tests.

OBJECTIVE

To explore whether or not a carefully designed short training course teaching Bayesian probabilistic thinking improves the diagnostic ability of medical students.

PARTICIPANTS AND METHODS

Ninety students at 2 medical schools were presented with clinical scenarios of coronary artery disease corresponding to high, low, and intermediate pretest probabilities. The students’ estimates of test characteristics of exercise stress test, and pretest and posttest probability for each scenario were evaluated before and after the short course.

RESULTS

The pretest probability estimates by the students, as well as their proficiency in applying Bayes's theorem, were improved in the high pretest probability scenario after the short course. However, estimates of pretest probability in the low pretest probability scenario, and their proficiency in applying Bayes's theorem in the intermediate and low pretest probability scenarios, showed essentially no improvement.

CONCLUSION

A carefully designed, but traditionally administered, short course could not improve the students’ abilities in estimating pretest probability in a low pretest probability setting, and subsequently students remained incompetent in ruling out disease. We need to develop educational methods that cultivate a well-balanced clinical sense to enable students to choose a suitable diagnostic strategy as needed in a clinical setting without being one-sided to the “rule-in conscious paradigm.”

A resident introduced a young female patient in an outpatient conference. She complained of general fatigue and a low-grade fever. Her physical examination was unremarkable. Because screening for antinuclear antibody was positive, an “autoantibody panel” was performed and some components of that panel were positive. The resident stated that he could not rule out “collagen vascular disease” and concluded by stating the need to carry out more thorough investigation. Quite often we encounter similar scenarios in which medical students or novice residents have difficulty ruling out certain diseases even though the likelihood of these diseases is quite low. In turn, because of this difficulty, the medical students or novice residents often repeat inadequate laboratory or imaging tests. They engage in endless diagnostic procedures and are often confused by false positive results, and ultimately end up administering unnecessary treatment.

In our previous study, we evaluated the diagnostic ability of medical students by utilizing the students’ estimations of pretest probability, sensitivity, and specificity. The methodology allowed us to determine which portion of the diagnostic thinking processes may be impaired or in need of remediation. The most remarkable findings in that study were as follows: the medical students could not rule out disease efficiently in low or intermediate pretest disease likelihood settings, and they were easily confused by test results contrary to their expectations. The former flaw was mainly due to poor estimations of pretest disease probability. The latter implies that medical students are not proficient in applying Bayes's theorem to real clinical situations.¹

The study presented here was designed for the follow-up of our previous work. To improve medical students’ diagnostic limitations, we planned to give a carefully designed short course on the diagnostic thinking process based upon Bayes's theorem. In this study, we evaluated 1) whether or not each element of the diagnostic thinking process improved after the short course, and 2) whether or not the course improved the overall diagnostic ability of medical students.

METHODS

We studied changes between pre- and postcourse estimates for the sensitivity/specificity of exercise stress test (EST), and pretest and posttest probability of hypothetical clinical scenarios in students who participated in a short course focusing on interpreting diagnostic test results.

Target Population

We asked medical students who had been subjects in our previous study to become subjects again in the current study. Participants were fifth-year medical students who joined the survey in the previous study and took a short course in clinical epidemiology after the survey. Nonparticipants were the students who did not attend the short course.

Timing of Pre-/Postcourse Survey

The precourse survey was performed before starting clinical clerkship (medical school B) or within 2 weeks after starting clerkship (medical school A) as a part of the previous study. Correct answers of the probability estimates were not revealed to the participants after the precourse survey. The postcourse survey was carried out at the end of the short course as a part of course evaluation.

The precourse survey and the short course were administered on different dates at medical school A. Elapsed time between the pre- and postcourse survey was less than 14 days for about 70% of students (mean 18.1 days). About half of the students submitted the postsurvey immediately after the short course and the other half did so within 1 week (mean 1.4 days). At medical school B, all activities were administered on the same day and all participants submitted the survey within the day (Table 1).

Table 1.

Demographic Information on Subjective Students

	Total	Medical School A	Medical School B
Number of students	90	31	59
Female percentage, %	24.4	6.5	33.9
Mean age, y ± SEM	23.9 ± 0.9	23.5 ± 0.2	23.9 ± 0.6
Mean elapsed time between pre- and postsurvey, days ± SEM	6.2 ± 2.0	18.1 ± 5.4	0
Range, days	0 to 98	0 to 98	0
Mean lapsed time between short course and postsurvey, days ± SEM	0.5 ± 0.1	1.4 ± 0.3	0
Range, days	0 to 7	0 to 7	0
Average response rate, %
Precourse	95.1	97.7	93.7
Postcourse	95.4	100.0	93.0
Confidence of understanding Bayesian way of thinking, percentage of a “yes” answer, %
Precourse	10.0	25.8	1.7
Postcourse	53.3	71.0	44.1

SEM, standard error of measurement.

No students had actual experience in clinical work at the time of the precourse survey. Some students in medical school A spent time in clinical clerkships between the pre- and postcourse survey (maximum about 3 months) but no students in medical school B did.

Short Course Curricula

One of the authors (YN) gave a short course in clinical epidemiology for both medical schools A and B. The short course focused on a hypothesis-deductive method for clinical diagnosis and the use of probabilistic perspective. The short course was administered as a half-day session in a rotation at the general medicine unit at medical school A and in introductory curricula for clinical clerkship at medical school B.

The purpose of the short course was not merely mastering Bayes's calculation but also developing the capacity of applying the concept of hypothesis-deductive diagnostic thinking to clinical situations. The contents of the short course are presented in Table 2. The course consisted of teaching a method of estimating pretest probability from symptoms and signs, Bayesian interpretation of test results, analysis of the diagnostic thinking process using real clinical cases, and lab exercises for calculating Bayes's theorem. We emphasized the distinctions between typical anginal chest pain, atypical anginal chest pain, and nonanginal chest pain according to Diamond's description.² We presented a change in disease probability for a typical angina case after getting negative EST results, and demonstrated that when pretest probability is very high, a disease cannot be ruled out despite a negative test result. We also presented an example of disease with an extremely low prevalence by screening for acute intermittent porphyria with porphobilinogen deaminase activity, because the pretest probability of porphyria is very low, such that a positive result on a screening test cannot increase disease probability.³ We emphasized the significance of pretest probability in interpreting test results in these confusing cases.

Table 2.

Topics Covered in the Short Course

A. Clinical diagnostic strategies
1.	Pattern recognition
2.	Algorithm method
3.	Exhaustive method
4.	Hypothesis-deductive method
B. How to diagnose disease with hypothesis-deductive method
1.	Generation of diagnostic hypothesis
2.	Probabilistic model and Bayesian approach
3.	Threshold and clinical actions
4.	Rule-in and rule-out
C. Performance of diagnostic test (test characteristics)
1.	Sensitivity and specificity
2.	Gold standard
3.	Cutoff (positivity criteria of diagnostic test)
4.	Positive predictive value and negative predictive value
5.	Disease prevalence
D. Case studies
Case 1.	A cardiac catheterization unit patient versus a general ward patient presented with elevated serum CPK level and diagnosis of acute myocardial infarction.
	Importance of pretest probability.
Case 2.	A 77-year-old female presenting typical anginal chest pain with negative ETT.
	Interpretation of negative test result with very high pretest probability.
Case 3.	Porphobilinogen deaminase and diagnosis of acute intermittent porphyria.
	Diagnosis of a disease with extremely low prevalence.

Data Collection

The details of hypothetical scenarios and questions were reported previously.¹ Briefly, the clinical scenarios consisted of typical anginal pain, atypical anginal pain, and nonanginal chest pain corresponding to pretest probabilities of coronary artery disease of 90%, 46%, and 5%, respectively. Students were encouraged not to calculate the posttest probability with Bayes's formula but to estimate the probabilities by intuition, because the purpose of this study was not to measure students’ capacity of Bayes's calculation but to measure the ability of practical application of Bayes's theorem.

Data Analysis

We used the following parameters to evaluate the students’ clinical diagnostic abilities: 1) intuitive estimates of sensitivity (Se_INT), specificity (Sp_INT), pretest probability (preProb_INT), and posttest probabilities (PPV_INT, NPV′_INT); 2) reference estimates of sensitivity (Se_REF), specificity (Sp_REF), pretest probability (preProb_REF), and posttest probabilities (PPV_REF, NPV′_REF); and 3) Bayesian estimates of posttest probability (PPV_BAY, NPV′_BAY). The detailed definitions of these parameters were also presented previously.¹

The difference between the intuitive and the reference estimates of sensitivity and specificity (Se_INT − Se_REF, Sp_INT− Sp_REF) reflects the accuracy of knowledge regarding the test characteristics. The difference between the intuitive and reference estimates of pretest probability (preProb_INT− preProb_REF) reflects the ability to estimate the pretest disease probability from the available clinical history. The difference between the intuitive and reference estimates of posttest probability (PPV_INT − PPV_REF, NPV′_INT − NPV′_REF) reflects overall diagnostic ability. The difference between the intuitive and Bayesian estimates of posttest probability (PPV_INT− PPV_BAY, NPV′_INT− NPV′_BAY) reflects the ability to estimate posttest probability from pretest probability and the test characteristics. Thus, smaller differences correspond to higher abilities.

We used Student's t test to test the hypothesis that there is no difference in the students’ estimate distributions between the 2 medical schools, between students who answered the postsurvey earlier and later, and between students who submitted the postsurvey immediately and later. The statistical significance of difference in the probability estimates was also checked by Student's t test. Summary measures of probability estimates were expressed as means ± the standard errors of the mean. Statistical analysis was performed using STATA statistical software (STATA Corporation, College Station, Tex).⁴

RESULTS

Ninety medical students took the short course and answered the survey questionnaire. Demographic information on the subject students from the 2 medical schools is presented in Table 1.

A significant difference in the means of the students’ estimates was observed for some questions between the 2 medical schools, between students who answered the postsurvey earlier (within 14 days, 81 students) and later (after 14 days, 9 students), and between students who submitted the postsurvey immediately (75 students) and later (15 students). However, these differences were not systematic and not associated with particular characteristics or case scenarios. Therefore, the results were aggregated and subgroup analyses were not performed.

Precourse confidence regarding understanding of the Bayesian probabilistic perspective of diagnostic thinking was substantially different between schools. Confidence in understanding this thought process showed a significant increase after the short course.

The difference between reference and intuitive estimates of sensitivity for EST (Se_INT− Se_REF) was rather large after the short course (precourse: 0.9±1.7% vs postcourse: 8.5±1.6, difference=8.1±2.0%; P < .01), and that between the reference and intuitive estimates of specificity (Sp_INT −Sp_REF) showed no change (precourse: −18.7±2.9 % vs postcourse: −16.4±2.7, difference=3.2±3.1%; P = .30).

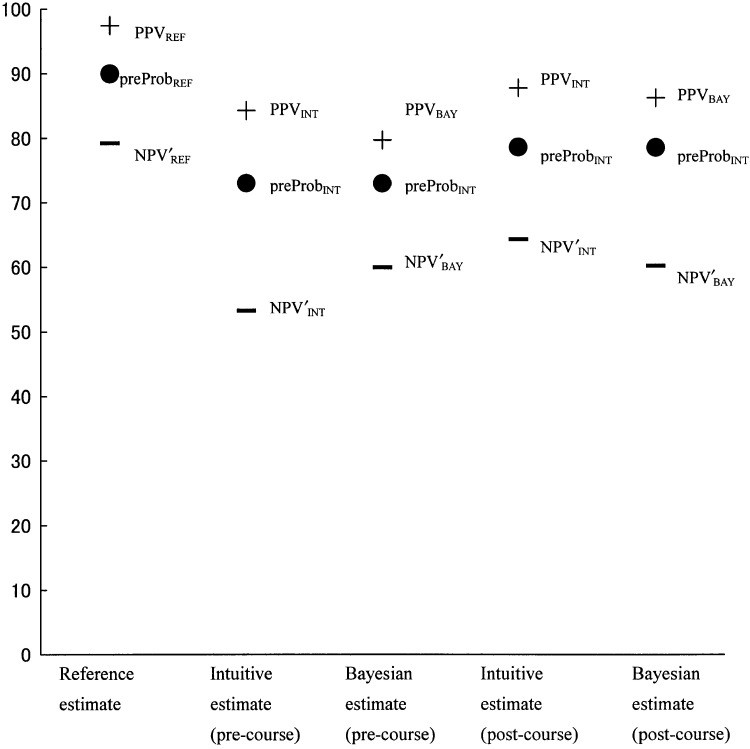
The relationship among reference, intuitive, and Bayesian estimates for each scenario before and after the short course are schematized in Figs. 1–3. For typical angina (case 1, Fig. 1), the intuitive estimate of pretest probability improved after the short course (precourse preProb_INT=73.1±1.5% vs postcourse preProb_INT=78.8 ± 1.4%, difference=6.7±1.7%; P < .01), as well as intuitive estimates of PPV (precourse PPV_INT=84.3±1.2% vs postcourse PPV_INT=87.9±1.3%, difference=3.9±1.5%; P < .01; precourse NPV′_INT=53.2±2.8% vs postcourse NPV′_INT= 64.4±2.3%, difference=13.0±3.0%; P < .01). The differences between intuitive estimates and Bayesian estimates of posttest probability were lower (i.e., improved) after the short course (precourse PPV_INT − PPV_BAY=−4.1 ± 1.9% vs postcourse PPV_INT − PPV_BAY=−1.5±1.5%; precourse NPV′_INT– NPV′_BAY=6.1±3.3% vs postcourse NPV′_INT –NPV′_BAY =−4.1±2.8%). Overestimation of the decline of NPV′ for typical anginal pain with positive EST observed in our previous study was partially corrected after the short course.

FIGURE 1.

Estimates and errors in case scenario 1 (typical anginal pain) before and after short course. The first column of each figure represents reference estimates of pretest probability (preProb_REF), PPV (PPV_REF), and NPV′ (NPV′_REF). NPV′ represents post-test probability given a negative result (i.e., 100%– NPV). The second column represents intuitive estimates of pretest probability (preProb_INT), PPV (PPV_INT), and NPV′ (NPV′_INT) before the short course. The third column represents intuitive estimates of pretest probability (preProb_INT) and Bayesian estimates of posttest probability (PPV_BAY/NPV′_BAY) before the short course. The fourth and fifth columns represent intuitive estimates after the short course. Markers •, +, and − represent pretest probability, positive predictive value (PPV), and negative predictive value (NPV′), respectively. The probability estimates are displayed as percentages. The distance between pretest probability and PPV/NPV′ (PPV − preProb or NPV′− preProb) represent the change of disease likelihood provided by the test results. The difference between the intuitive and reference estimates of pretest probability (preProb_INT− preProb_REF) is associated with the ability of estimating the pretest probability of a given disease from the available clinical history. The difference between the intuitive and reference estimates of posttest probability (PPV_INT− PPV_REF, NPV′_INT− NPV′_REF) are associated with the overall diagnostic ability. The difference between the intuitive and Bayesian estimates of posttest probability (PPV_INT− PPV_BAY, NPV′_INT− NPV′_BAY) are associated with the ability of estimating posttest probability from pretest probability and the test characteristics. The closer to 0 the error is, the higher the ability is.

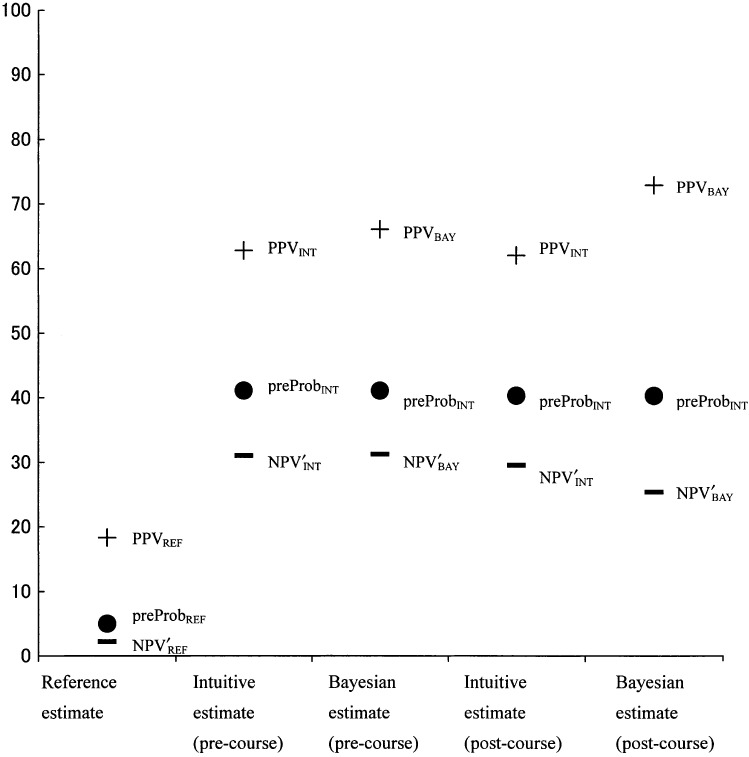
FIGURE 3.

Estimates and errors in case scenario 3 (nonanginal chest pain) before and after short course.

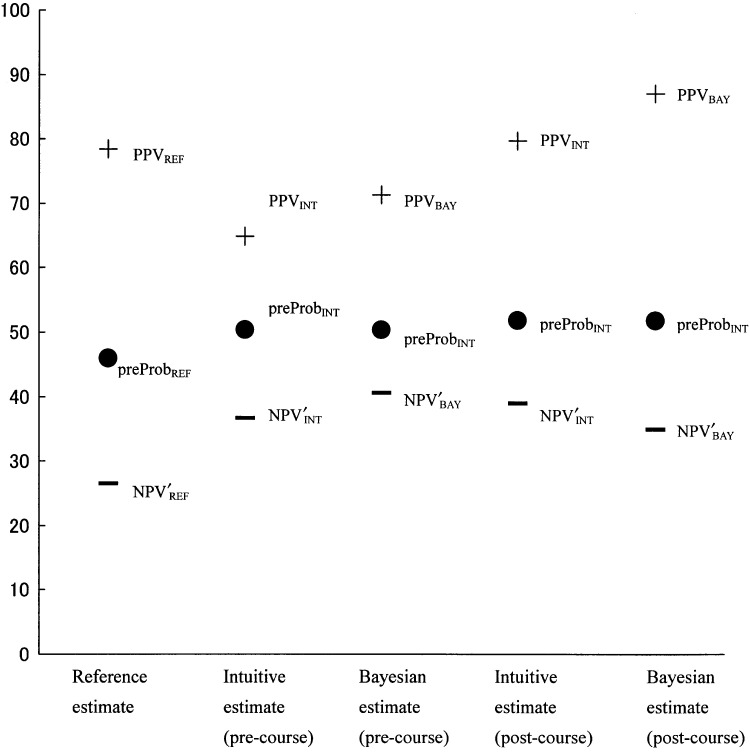
For atypical chest pain (case 2, Fig. 2), the intuitive estimates of pretest probability were appropriate before and after the short course (precourse preProb_INT=50.4±2.7% vs postcourse preProb_INT=51.9±2.6%, difference=2.8± 2.9%; P = .33). The intuitive estimates of posttest probability showed no significant improvement (precourse PPV_INT=64.9±2.7% vs postcourse PPV_INT=69.5±2.3%, difference=4.7±0.9%; P = .10; precourse NPV′_INT=36.7± 2.7% vs postcourse NPV′_INT=39.0±2.8%, difference=4.2± 1.6%; P = .15). The difference between intuitive estimates and Bayesian estimates of posttest probability did not improve after the short course (precourse PPV_INT – PPV_BAY=6.3± 2.5% vs postcourse PPV_INT – PPV_BAY=18.2±7.9%; precourse NPV′_INT– NPV′_BAY=4.2±2.9% vs postcourse NPV′_INT– NPV′_BAY=−4.0±2.7%). The underestimation of the NPV′ decrease in atypical chest pain with negative EST that was also seen in our previous study showed no improvement.

FIGURE 2.

Estimates and errors in case scenario 2 (atypical anginal pain) before and after short course.

Finally, for nonanginal chest pain (case 3, Fig. 3), the intuitive estimates of the pretest and posttest probabilities showed gross deviations toward overestimating from the reference estimates and showed no improvement after the short course (precourse preProb_INT=41.1±2.5% vs postcourse preProb_INT=40.3±2.6%, difference=1.1±2.7%; P = .67; precourse PPV_INT=62.8±2.4% vs postcourse PPV_INT=62.1±2.5%, difference=0.29±2.7%; P = .92; precourse NPV′_INT=31.0±2.5% vs postcourse NPV′_INT = 29.5±2.6%, difference=0.6±2.5%; P < .82). Students still could not rule out ischemic heart disease in a patient with nonanginal chest pain, regardless of the test results. Again, the difference between intuitive estimates and Bayesian estimates of posttest probability did not improve after the short course (precourse PPV_INT – PPV_BAY=3.3± 3.0% vs postcourse PPV_INT – PPV_BAY=10.9±2.5%; precourse NPV′_INT – NPV′_BAY=0.2±2.6% vs postcourse NPV′_INT – NPV′_BAY= −4.1±2.3%). Thus, student lack of competency in ruling out ischemic heart disease and lack of proficiency with Bayes's theorem remained uncorrected after the short course in this scenario (Table 3).

Table 3.

Summary of Change in Diagnostic Performance of Medical Students

	Total Diagnostic Performance	Performance of Estimating Pretest Probability	Performance of Application of Bayes's Theorem
High pretest probability scenario	Improved	Improved	Improved
Intermediate pretest probability scenario	No change	No change (appropriate before short course)	Worsened
Low pretest probability scenario	No change	No change (inappropriate before short course)	Worsened

DISCUSSION

In our previous study, we found medical students were unable to rule out disease in low or intermediate pretest disease likelihood settings. Their weakness in diagnostic thinking mainly originated from poor estimations of pretest disease probability and a lack of proficiency in applying Bayes's theorem to real clinical situations.¹

In this study, we examined whether or not a carefully prepared short course could improve students’ diagnostic abilities. The short course was designed to facilitate an accurate understanding of the Bayesian probabilistic perspective and its application to real clinical situations so as to avoid students’ dangerous pitfalls observed in the previous study. The pitfalls in their diagnostic thinking process included: 1) overestimating pretest probability for a patient with a low pretest probability, 2) overestimating posttest probability for a patient with a low pretest probability and positive test results as a consequence of overestimating the pretest probability, and 3) making an inadequately low estimate of posttest probability for a patient with typical symptoms when the test result was negative.

After participating in the short course, the pretest probability estimates by the students, as well as their proficiency in applying Bayes's theorem, were improved in high pretest probability case scenarios. Estimates of pretest probability in the low pretest probability case scenario, and the proficiency in applying Bayes's theorem in the low and intermediate pretest probability case scenario, showed no sign of improvement. Subsequently students remained lacking competence in ruling out disease (Table 3).

We inferred two mental attitudes of doctors that could explain these findings. One arises from a lack of probabilistic understanding of the world. Doctors assume that more information cannot hurt or can guarantee a more certain diagnosis. Therefore, they accept and promote an excessive use of diagnostic testing. Kassirer has suggested that the phenomenon was simply due to “our stubborn quest for diagnostic certainty.”⁵ It persists in spite of the fact that decision-analytic principles prove that one cannot reduce diagnostic uncertainty to zero. Performing multiple tests increases the number of positive tests, but many of them are false positives, yielding new uncertainty and misunderstanding.⁶

The other responsible attitude is doctors' fear of overlooking diseases. Doctors tend to regard positive test results as more important than negative test results. That is, they are more hostile toward false negative test results than toward false positive results because false negative results directly lead to overlooking diseases. As a consequence, doctors underappreciate the harm of false positive results, which is associated with overdiagnosis. As we mentioned in our previous study, physicians often fail to understand the importance of negative information.⁷ Teachers or textbooks often emphasize information related to abnormal findings, but not the significance of normal findings. Ruling out disease is also less emphasized than the importance of not overlooking a possible disease in traditional medical education.

The fear of overlooking diseases is universally observed in senior physicians, and we could call it a sort of “paradigm of rule-in conscious.” Lyman et al.⁸ reported the effect of test results on estimating disease likelihood. When hypothetical patients with breast lumps and the results of mammography were presented to physicians and nonphysicians, the subjects consistently overestimated the likelihood of breast cancer associated with a positive test result compared to the probabilities derived from Bayes's theorem based upon the subjects’ estimates of pretest probabilities and the tests characteristics. This finding contrasted with the result associated with negative test results. Gray et al.⁹ presented how doctors care about eliminating the possibility of disease even when the likelihood is very small. Many doctors cannot abandon the diagnostic hypothesis of pulmonary embolism after obtaining normal lung scan results, although normal lung scans actually rule out pulmonary embolism unless the pretest probability of pulmonary embolism is substantially high.¹⁰ The fear of overlooking diseases with serious and life-threatening outcomes such as breast cancer or pulmonary embolism seems to drive doctors to make light of negative results in these instances.

Thus, the harm of false negatives is straightforward and easy to understand, while the harm of false positives is indirect and easy to ignore. In reality, false positive test results may cause mischief in at least two ways: 1) by leading to more invasive follow-up testing and 2) by leading to inappropriate treatment of patients without disease. Both possibilities may increase the morbidity and cost of health care.¹¹ The harm of false positives should not be neglected.

The “rule-in conscious” strategy tries to minimize false negatives by accepting a certain level of false positives. This diagnostic approach is reasonable for the population of patients with high prevalence and high morbidity, because overlooking diseases often results in fatal outcomes. On the other hand, ruling out diseases is a more important task for physicians who work on the population of patients with lower disease prevalence. In this clinical setting, the “rule-in-conscious” strategy was not adequate because the abundance of false positives might inflict mischief on patients. In other words, we have to cultivate a well-balanced clinical sense to enable us to choose a suitable diagnostic strategy as needed in a clinical setting without being one sided according to the “rule-in conscious paradigm.”

There are some limitations to this study. The most important one is that failure to improve the students’ estimates of pretest probability and proficiency in applying Bayes's theorem might have resulted merely from a shortage of practice. Bayesian probabilistic perspective is not a native thinking pattern in human beings,¹² so that mastering it requires repetition and practice. Because the short course consisted of a 2-hour session of lectures and lab exercises, it is true that students did not have enough time to practice. However, because both estimates of pretest probability and proficiency in applying Bayes's theorem were improved in the high pretest probability scenario, it is reasonable to believe that rule-in ability was enforced by the short course according to their paradigm.

The fact that the subject students had little clinical experience is a limitation to this study. It may hamper the generalizability of the results of this study to medical learners in more advanced stages. However, one study reported that clinical “experience” did not have a clear role in probabilistic diagnostic performance.¹³ Even doctors with clinical experience without a clear aim might succumb to the same pitfall.

In conclusion, a carefully designed, but traditionally administered, short course could not improve the students’ ability to estimate pretest probability in low pretest probability settings. Accordingly, these students remained incompetent in ruling out disease. We need to develop educational methods that cultivate a well-balanced clinical sense to enable them to choose a suitable diagnostic strategy as needed in a clinical setting without being one-sided to the “rule-in conscious paradigm.”