From wavelets to adaptive approximations: time-frequency parametrization of EEG

Abstract

This paper presents a summary of time-frequency analysis of the electrical activity of the brain (EEG). It covers in details two major steps: introduction of wavelets and adaptive approximations. Presented studies include time-frequency solutions to several standard research and clinical problems, encountered in analysis of evoked potentials, sleep EEG, epileptic activities, ERD/ERS and pharmaco-EEG. Based upon these results we conclude that the matching pursuit algorithm provides a unified parametrization of EEG, applicable in a variety of experimental and clinical setups. This conclusion is followed by a brief discussion of the current state of the mathematical and algorithmical aspects of adaptive time-frequency approximations of signals.

EEG

The electroencephalogram (EEG), recorded from electrodes placed on the scalp, reflects the electrical activity of the brain.

First registered from human scalp in 1929 [1], until today EEG remains an important tool in neuroscience and clinical neurophysiology. For a long time it was the only objective parameter providing information on brain's function. Recently emerging dynamic imaging techniques like fMRI and PET offer a complementary information on brains functioning. Their drawbacks include significantly lower time resolution, high cost and invasiveness. Nevertheless, in spite of those drawbacks, they are often preferred for the straightforward interpretability. On the contrary, visual interpretation of EEG is a difficult, tedious and complicated task, requiring many years of experience. And even then it contains a significant subjective factor:

Every experienced electroencephalographer has his or her personal approach to EEG interpretation. (...) there is an element of science and element of art in a good EEG interpretation; it is the latter that defies standardization.

writes Prof. Ernst Niedermayer in the recent edition of a fundamental reference [2].

In spite of this discouraging opinion, application of various signal processing methods in this field is still very popular. First introduction of Fourier analysis to EEG is dated 1932 [3]. Since then spectral analysis has become a standard tool in this field. But until today, basically no other method gained a general acceptance – the few widely accepted and applied methods of EEG analysis still amount to [4]:

1. visual analysis of raw EEG traces,

2. Fourier estimation of spectral power in selected frequency bands,

3. description of evoked potentials, averaged in the time domain.

One of the reasons of this unsatisfactory situation is that among the variety of new methods, proposed each year for the analysis of EEG, very few have any direct relationship to the traditional, visual analysis. That means that their results usually cannot be directly related to the most valuable knowledge base of 70 years of experience, collected by means of the visual analysis of EEG. On the contrary, each new method needs to be evaluated from the scratch, in many laboratories and over many repeated studies, before it can be considered as a clinically usable parameter. And since there is a multitude of new methods being proposed, with few a priori hints for their possible performance, this process seems to be hardly convergent.

Wavelets: the first step towards time-frequency analysis

EEG as a signal is extremely complex and reveals both rhythmical and transient features. Therefore, when orthogonal wavelets triggered in eighties the time-frequency revolution in signal processing, analysis of EEG was one of the fields where hopes for a more "morphological" description of signal arose.

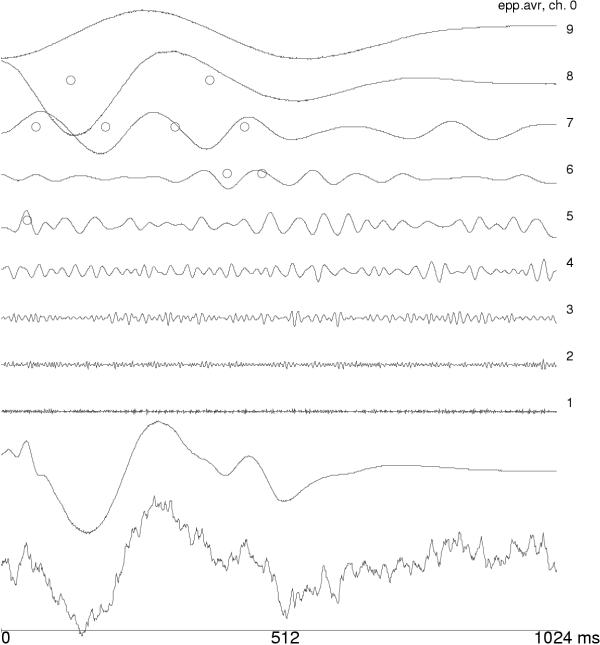
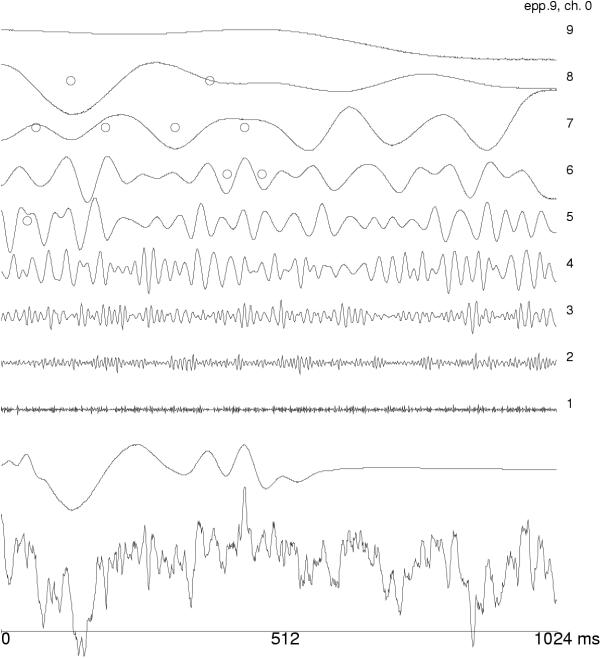
First successful applications of wavelets addressed the issue of evoked potentials (EP). Event-related potentials are small changes of EEG activity in response to an external (evoked) or internal stimulus. They are usually an order of magnitude weaker than the on-going EEG activity, so traditionally they were observed only in time averages of stimulus-synchronized repetitions. Owing to the property of the time synchronization, they can be studied in the space of orthogonal wavelet coefficients. Figures 2,3,4 present the first wavelet study of evoked potentials [5]. Randomly chosen epochs of on-going EEG were statistically compared – in the space of wavelet coefficients – to those synchronized by an auditory stimulus. As a result, only 9 out of 512 coefficients were found to discriminate between those conditions. They were enough to reproduce the basic morphology of the average EP. Figure 4 presents reconstruction of single evoked potentials using those coefficients.

Figure 2.

Average auditory evoked potential, it's decomposition in wavelet subbands and reconstruction from 9 wavelet coefficients, statistically differentiating EP from on-going EEG ([5]).

Figure 3.

Single AEP, reconstructed as in Figure 2

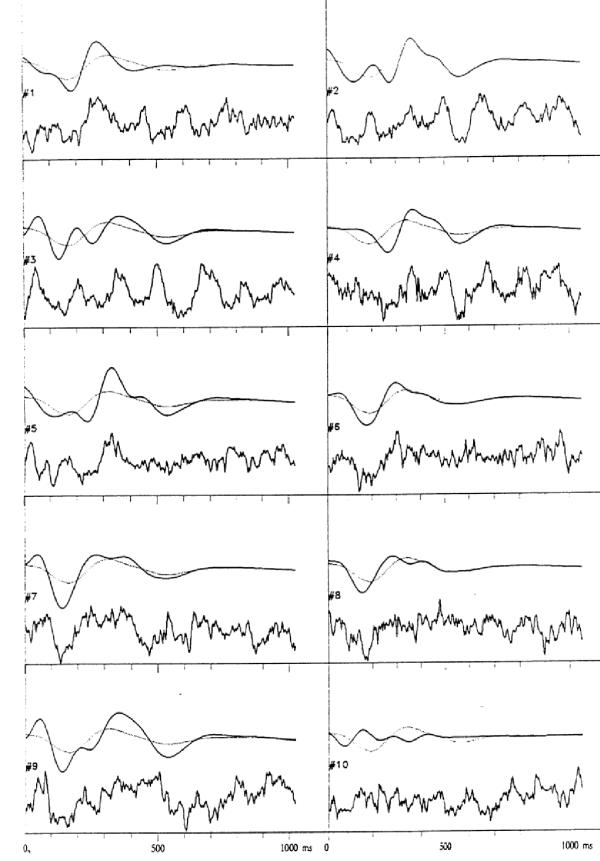
Figure 4.

In each of 10 subplots, from the bottom: a single AEP, it's reconstruction from wavelet coefficients as in fig. 2, and average of reconstructions (dotted line). From [5]

Figure 1.

70 years of progress in clinical EEG analysis: from visual analysis of EEG traces on paper (background picture) to visual analysis of EEG traces displayed on CRT (front). From [4].

Limitations of linear and quadratic time-frequency representations

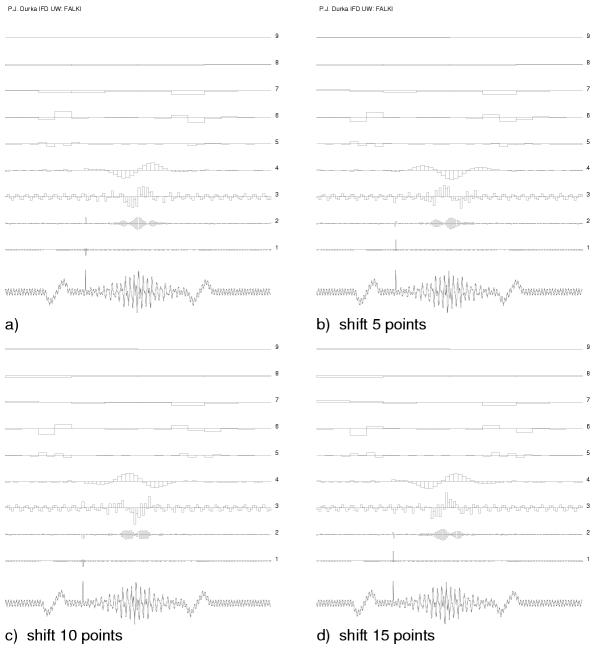
Further attempts to apply wavelets to the analysis of on-going EEG activity encountered a major drawback. Representation of the signal, obtained from orthogonal wavelet representation, is not time-shift invariant. This property is illustrated in Figure 5.

Figure 5.

Orthogonal wavelet representation is not time-shift invariant: wavelet decomposition of simulated signal shifted in time. Heights of rectangles at each level proportional to the value of wavelet coefficients at given scale.

This limitation is not present in the continuous wavelet transform, as well as several quadratic representations of signal's energy density in the time-frequency plane (c.f. [6] and Figure 8). However, in such case we loose the compact description offered by orthogonal wavelets – the representation is highly redundant. Another problem relates to the occurence of cross terms (Figure 6).

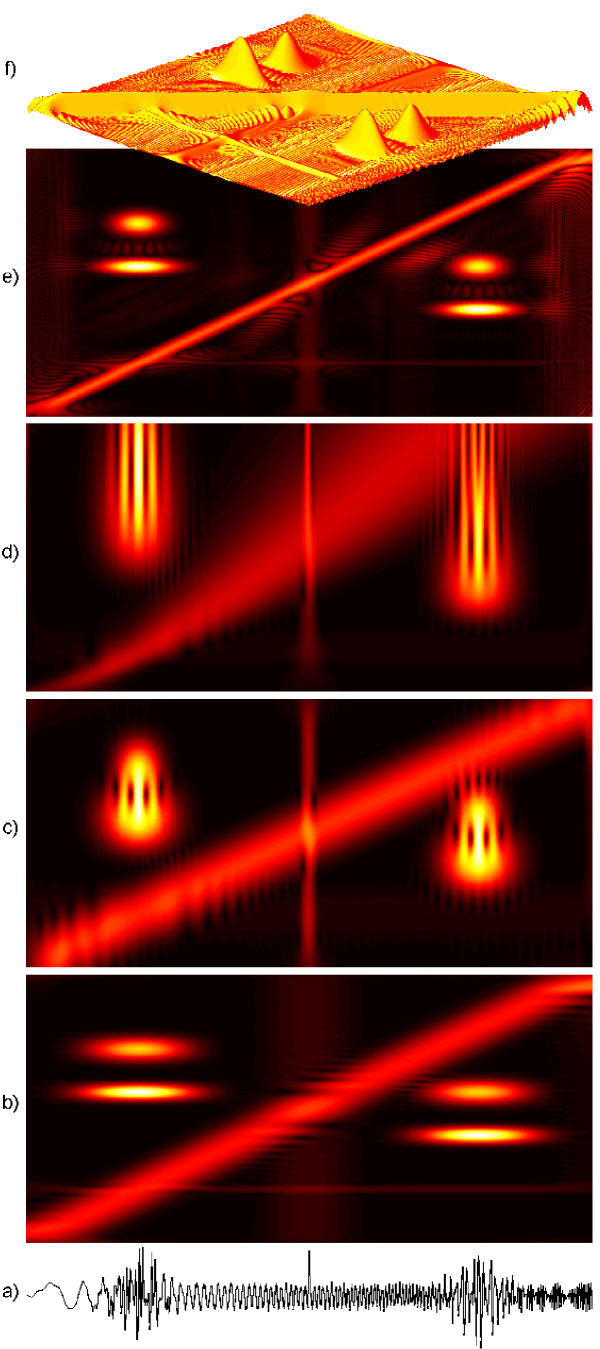
Figure 8.

Time-frequency distributions of energy of the simulated signal (here plotted as a) from Fig. 7. (b) and (c) present spectrograms (i.e. windowed or short-time Fourier transforms) calculated, respectively, for long (125 points) and short (21 points) windows. (d) is a scalogram (continuous wavelet transform), (e)-smoothed pseudo Wigner-Ville distribution, (f)-the same as (e) in 3 dimensions.

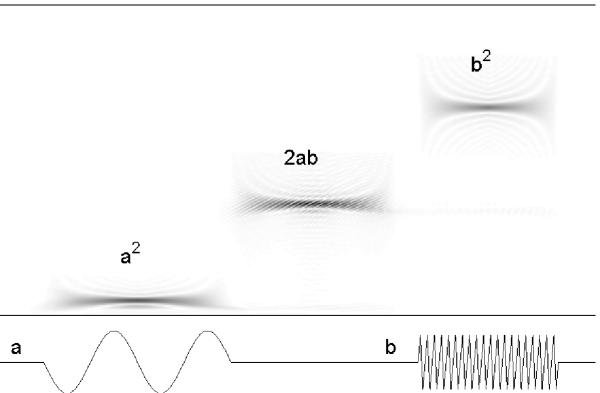
Figure 6.

Cross-terms in time-frequency representations of signal's energy: (a + b)² = a² + b² + 2ab. Wigner-De Ville transform (above) of a signal composed of two sine waves with compact and separated support (below). The structure appearing in the time coordinates where signal is flat (labelled "2ab") is a cross term.

Both these problems can be solved (or at least significantly reduced) by the solution proposed in the next section.

Adaptive approximations and matching pursuit

Given a set of functions (dictionary) D = {g₁,g₂...g_n} such that ||g_i|| = 1, we can define an optimal M-approximation as an expansion, minimizing the error ε of an approximation of signal f(t) by M waveforms:

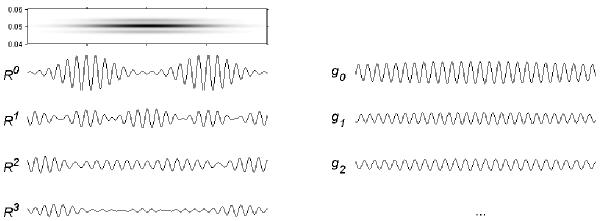
where {γ_i}_{i = 1..M} represents the indices of the chosen functions g_γi. Finding such an optimal approximation is an NP-hard problem. A suboptimal expansion can be found by means of an iterative procedure, such as the matching pursuit algorithm (MP) proposed by Mallat and Zhang [7].

In the first step of MP, the waveform g_γ0 which best matches the signal f(t) is chosen. In each of the consecutive steps, the waveform g_γn is matched to the signal Rⁿf, which is the residual left after subtracting results of previous iterations:

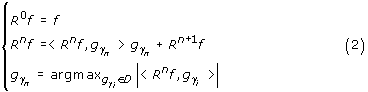
Orthogonality of Rⁿ⁺¹ f and g_γn in each step implies energy conservation:

For a complete dictionary the procedure converges to f:

From this equation we can derive a time-frequency distribution of the signal's energy, that is free of cross-terms, by adding Wigner distributions of selected functions:

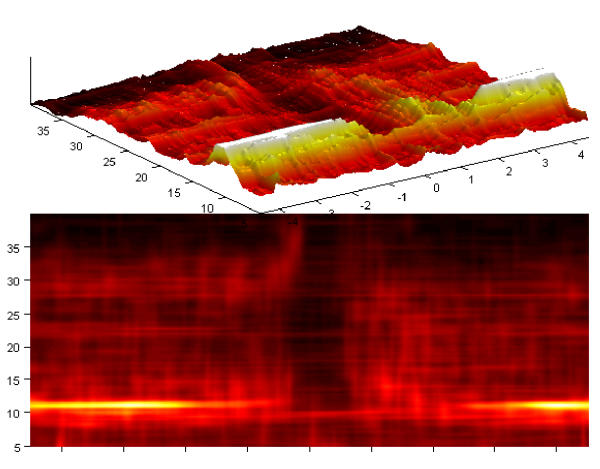
This magnitude is presented in Figure 7, calculated from MP decomposition of a simulated signal with known and simple content. We observe that most of the structures are represented compactly and with high resolution, except for the structure of changing frequency (linear chirp). It is represented by a series of structures of constant frequency, since in the applied Gabor dictionary (section 5) we have only constant frequency modulations. Section 7 presents an alternative approach to this issue.

Figure 7.

Time-frequency map of energy density of a 500-points simulated signal (e) composed of four sine-modulated Gaussians, i.e. Gabor functions (a-b), sine wave and one-point discontinuity (c) and sine wave with linear frequency modulation-chirp (d). Distribution (f) was obtained from a decomposition in a large (2 * 10⁶ waveforms) dictionary. Changing frequency of the chirp is represented as a series of functions, since in the Gabor dictionary (section 5) we have only constant frequency modulations, (g)-the same as (f), presented in 3 dimensions. Square root of energy proportional to the height of the surface or "temperature" on 2-dimensional plots. [22]

Figure 8 presents estimates of the time-frequency density of the same signal's energy, obtained from: spectrograms with different window widths, continuous wavelet transform and smoothed pseudo Wigner-Ville distribution. Only in the last case representation of the chirp looks better than on the plot obtained from MP decomposition, but we must take into account that in this case the parameters of the kernel of the distribution were optimized for this particular signal.

Except for the lack of cross terms and high resolution, adaptive time-frequency parametrizations exhibit one more basic and important advantage over the continuous time-frequency representations. Unlike the maps from Figure 8, for all the structures presented in Figure 7 we have a priori the exact values of their time and frequency centers, widths, amplitudes and phases. This property will be thoroughly explored in the following studies.

First application in EEG analysis: sleep spindles

The presence of sleep spindle should not be defined unless it is of at least 0.5 sec duration, i.e., one should be able to count 6 or 7 distinct waves within the half-second period. (...) The term should be used only to describe activity between 12 and 14 cps.

– says the definition from the basic reference [8] – "A manual of standardized terminology, techniques and scoring system for sleep stages in human subjects". It can be directly translated into the language of parameters of the structures fitted to the signal by the algorithm discussed in the previous section.

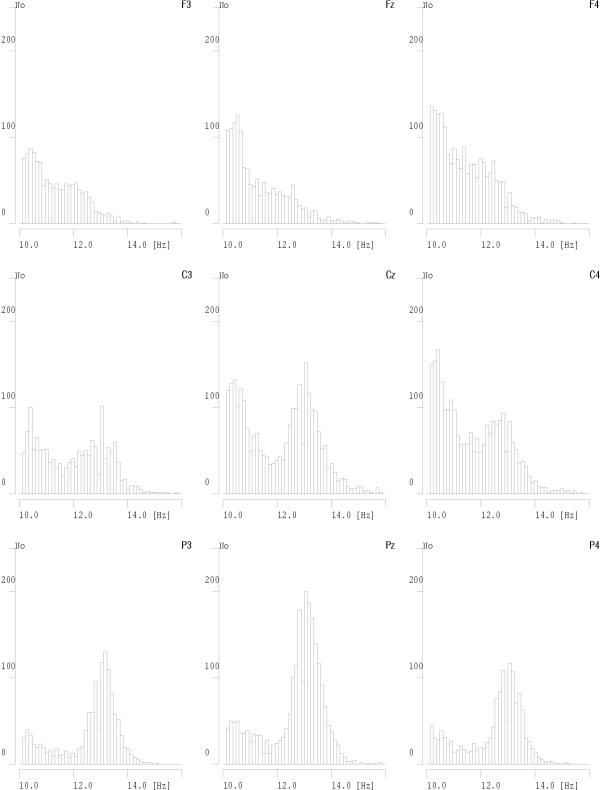
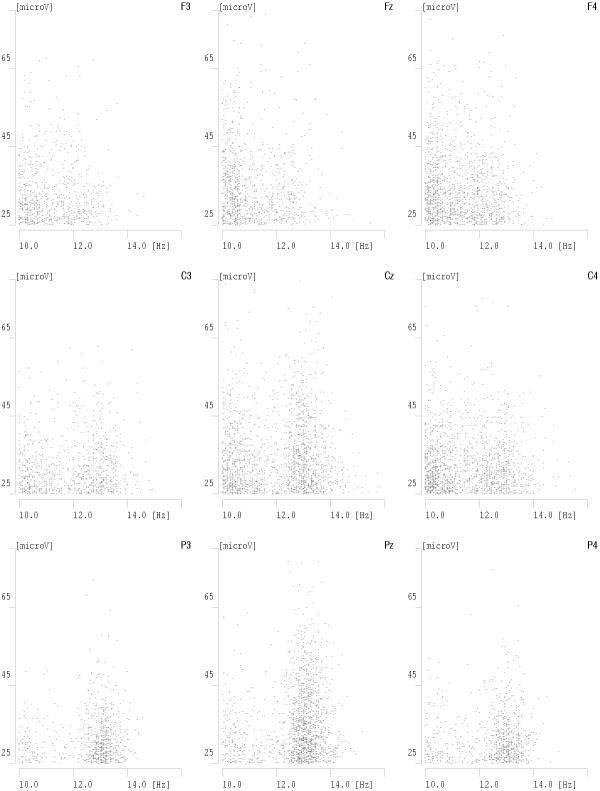
By choosing from the time-frequency atoms, fitted to EEG by the MP algorithm, those conforming to the above criteria, we obtain a detailed, automatic and high-resolution parametrization of the relevant structures, which correspond to sleep spindles [9,10]. Figures 10 and 11 present results of such a procedure carried out for several derivations of an overnight sleep EEG recording. This parametrization has proven to be consistent with visual detection, especially for the structures of higher amplitudes [11]. For lower amplitudes the algorithm detects also spindles elusive to a human expert.

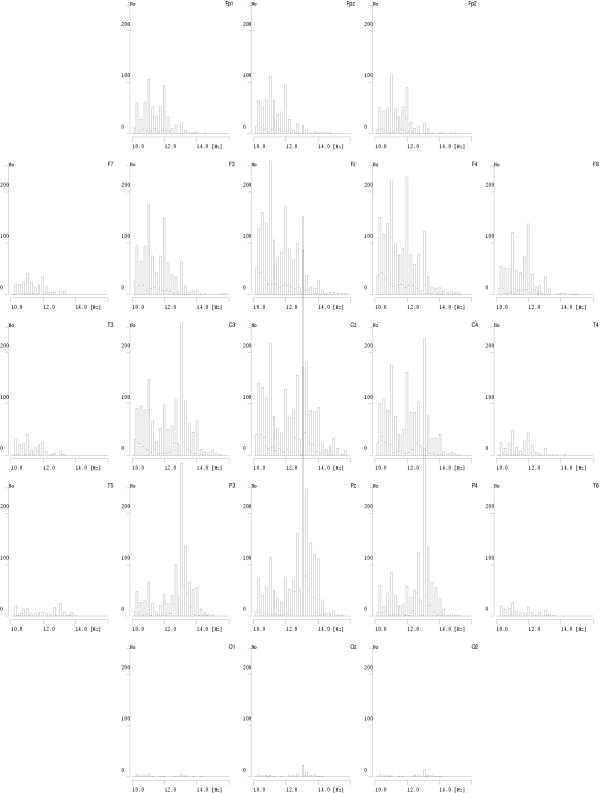
Figure 10.

Histograms of frequencies of sleep spindles detected in one overnight EEG recording. Plots are placed on page according to relative positions of corresponding derivations from the 10–20 system – front of head towards the top of page

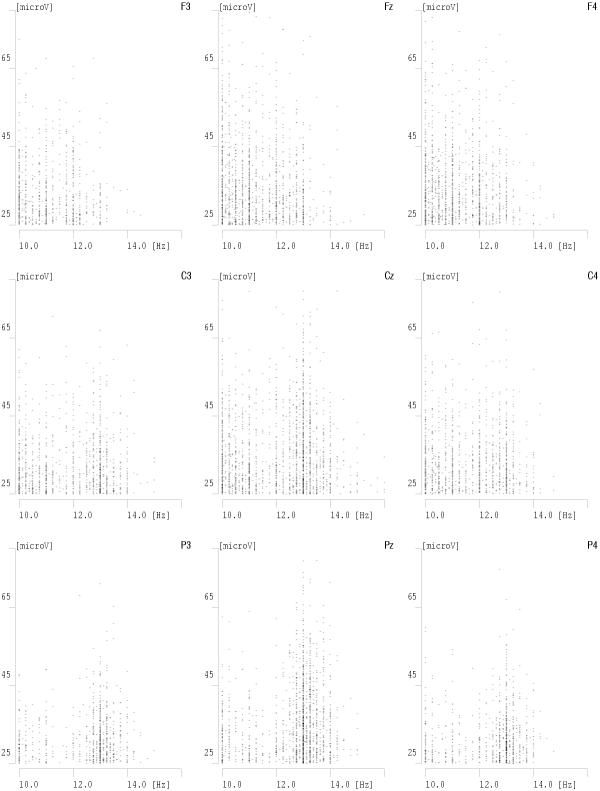
Figure 11.

Amplitudes of detected spindles (vertical) plotted versus their frequencies (horizontal) for the same data and derivations as Fig 10

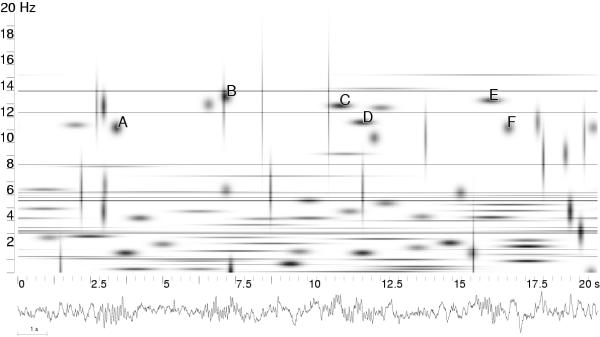
Figure 9.

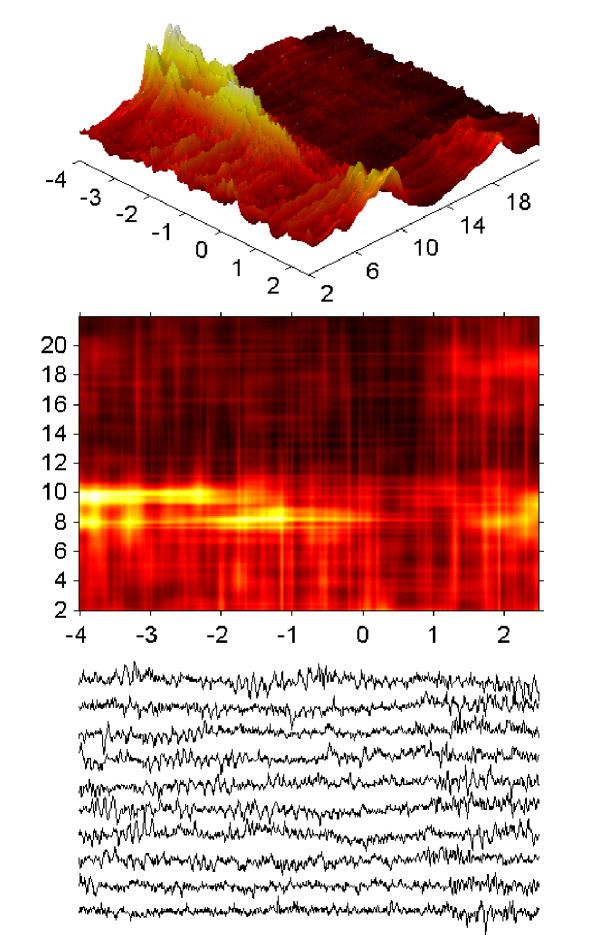
Time-frequency energy distribution (equation 5) of 20 seconds of sleep EEG; structures corresponding to sleep spindles are marked by letters A-F. Structures C and D, as well as E and F, were classified as one spindle, i.e. their centers fell within a time section marked by expert as one spindle's occurrence. [23]

Results presented in these figures conform also the previously observed effect of predominance of lower frequencies of sleep spindles in frontal derivations and higher frequencies in parietal derivations. We also notice that some frequencies on these plots are "prefereed", i.e. exhibit regular maxima in the histograms. But are they preferred by the brain or by the analysis algorithm? This question will be resolved in the next section.

Discrete Gabor dictionary

Gabor functions (sine-modulated Gaussian functions) provide optimal joint time-frequency localization. A real Gabor function can be expressed as:

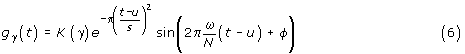
N is the size of the signal for which the dictionary is constructed, K(γ) is such that ||g_γ|| = 1. γ = {u,ω,s,φ } denotes parameters of the dictionary's functions (time-frequency atoms). These parameters generate a three-dimensional continuous space; this results in an infinite dictionary size. Therefore, in practical implementations, we use subsets of the possible dictionary's functions.

In the dictionary implemented originally by Mallat and Zhang in [7], parameters of these functions (time-frequency atoms) are chosen from dyadic sequences of integers. Their sampling is governed by an extra parameter – octave j (integer). Scale s, which corresponds to an atom's width in time, is derived from the dyadic sequence s = 2^j, 0 ≤ j ≤ L (signal size N = 2^L). Parameters u and ω, which correspond to position in time and frequency, are sampled for each octave j with interval s = 2^j, or, if oversampling by l is introduced, with interval 2^j-l.

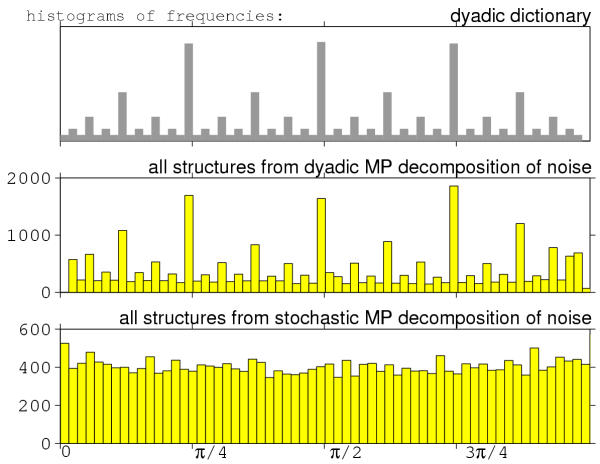
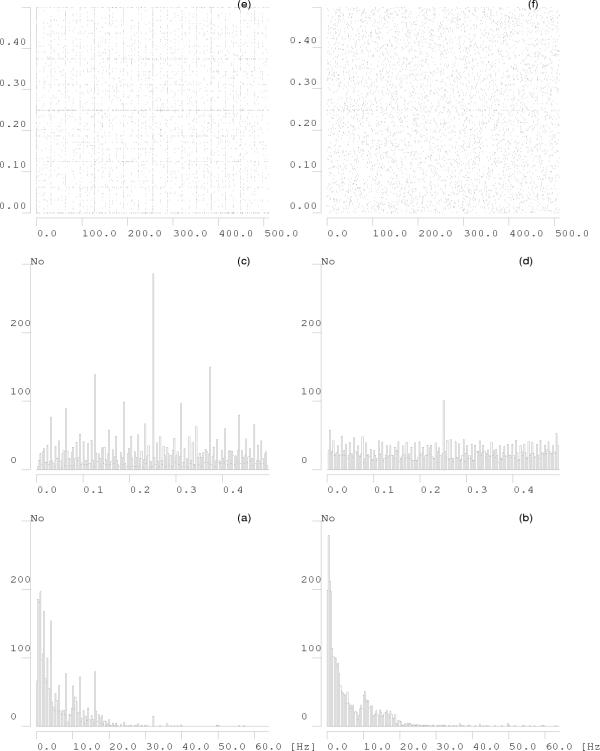
This specific wavelet-like structure of the dictionary is responsible for the fact that decomposition over such a dictionary "prefers" certain positions in frequency or time (Figures 12, 13). In those positions more atoms are available for decomposition due to the particular structure of the dictionary, i.e. scheme of subsampling the parameter space.

Figure 12.

200 realizations of 128-points white noise process were subjected to MP decomposition in dyadic (middle plot) and stochastic (bottom) dictionaries. The middle and lower plots present histograms of frequencies of all the structures fitted by MP. The upper plot is a histogram of frequencies of all the time-frequency atoms present in the dyadic dictionary used for the decomposition presented in the middle plot.

Figure 13.

Statistical properties of MP decomposition of 50 epochs of sleep EEG (a, b) and white noise (c-f) over dyadic (a, c, e) and stochastic (b, d, f) dictionaries. Histograms of frequency centers of atoms fitted by MP decomposition over dyadic dictionary to EEG (a) and noise (c) reveal additional structure, absent in corresponding decompositions performed over stochastic dictionaries b and d, respectively. Maximum in the middle of frequency range in panel d results from convention of assigning half of Nyquist frequency to Dirac's delta. In the top panel centers of atoms fitted to white noise are given in the time-frequency plane for dyadic (left, e) and stochastic (right, f) dictionaries

Stochastic dictionaries

In forming the dictionary used for MP decomposition, using any fixed scheme of subsampling the parameter space introduces statistical bias in the resulting parametrization. This bias becomes apparent only when statistics comes into play, like in parameterization of large amounts of data. Unbiased MP decompositions can be obtained by an analogue of Monte Carlo methods.

In [12] we proposed MP with stochastic dictionaries, where the parameters of a dictionary's atoms are randomized before each decomposition. A stochastic dictionary D is constructed for a given signal length N and chosen "resolutions"¹ in time, frequency and scale (Δt, Δω and Δs). The space of parameters t, ω and s is thereby divided into 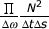bricks of size Δt by Δω by Δs each, where ω ∈ (0,π). In each of those bricks, one time-frequency atom is chosen by drawing its parameters from flat distributions within the given ranges of continuous parameters.

Figures 14 and 15 present results for the same data as Figures 10 and 11. These results, owing to the application of the above described stochastic dictionaries, are free from the statistical bias.

Figure 14.

Histograms of frequencies of sleep spindles detected in the same EEG recording as in Figure 10, decomposed in stochastic dictionaries

Figure 15.

Amplitudes of sleep spindles (vertical) plotted versus their frequencies (horizontal) detected in the same EEG recording as in Figure 11 (as well as 10 and 14), based upon MP decomposition with stochastic dictionaries

¹The resolution of the matching pursuit is hard to define in general, since the procedure is nonlinear and signal-dependent. It should be related to the distance between neighboring dictionary waveforms available for decomposition. In the described procedure, this distance does not exceed twice the value of the corresponding parameter (Δt, Δω or Δs).

Pharmaco EEG

This section presents an application of the proposed methodology to the standard clinical problem of testing influence of sleep inducing drugs on the sleep EEG.

The effects of zolpidem, midazolam and placebo, administered at bed time, were studied in 7 paid volunteers. From each of the 21 all-night recordings (3 nights for each subject) we extracted artifact-free epochs from derivation C3-A2 of the 10–20 system. For the analysis of slow wave activity (SWA) we used data from stages III and IV and for sleep spindles only data from sleep stage II.

Figures 16 and 18 present the classical approach to the analysis of these data, that is averaging the spectral integrals in the above mentioned ranges, for each of the analyzed recordings.

Figure 16.

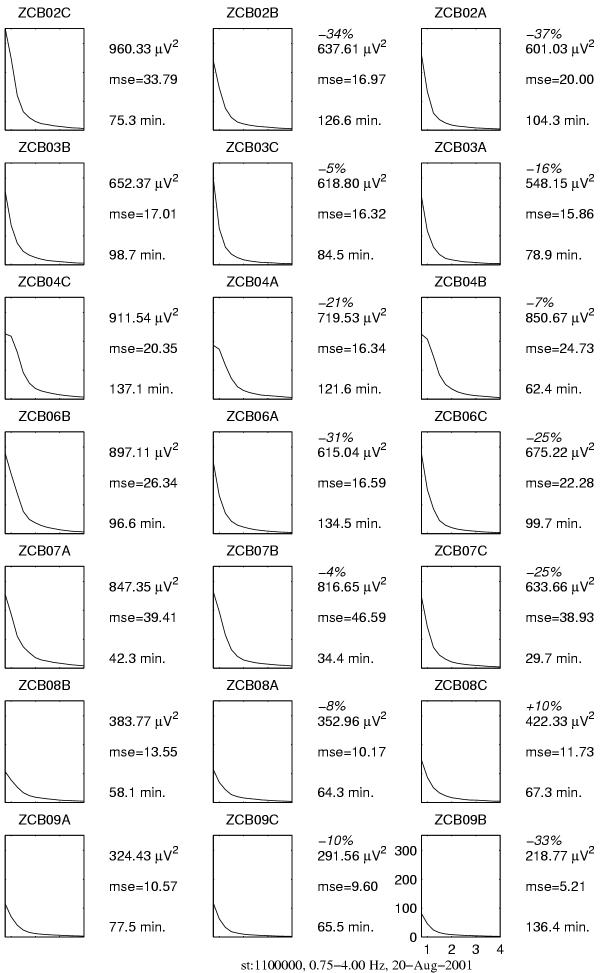
Spectral estimates of power in the frequency range of sleep spindles. Columns correspond to results for the night after administrating, from left to right: placebo, zolpidem, midazolam. Each row contains results for one subject. Plots present average (in stage II) spectrum between 12 and 14 Hz. Numbers on the right of each plot, from the top: % change of power related to the night after administrating placebo (absent in the first column), value of the total power between 12 and 14 Hz (μV²), it's mean square error (mse) and total time of stage II (in minutes) for given recording. We observe general trend of increase of power in this band, except for one case – the last subject, night after midazolam (bottom right)

Figure 18.

Spectral (FFT-based) estimates of power of slow wave activity (SWA) in the 0.75–4 Hz frequency range, plots and description organized as in Figure 16

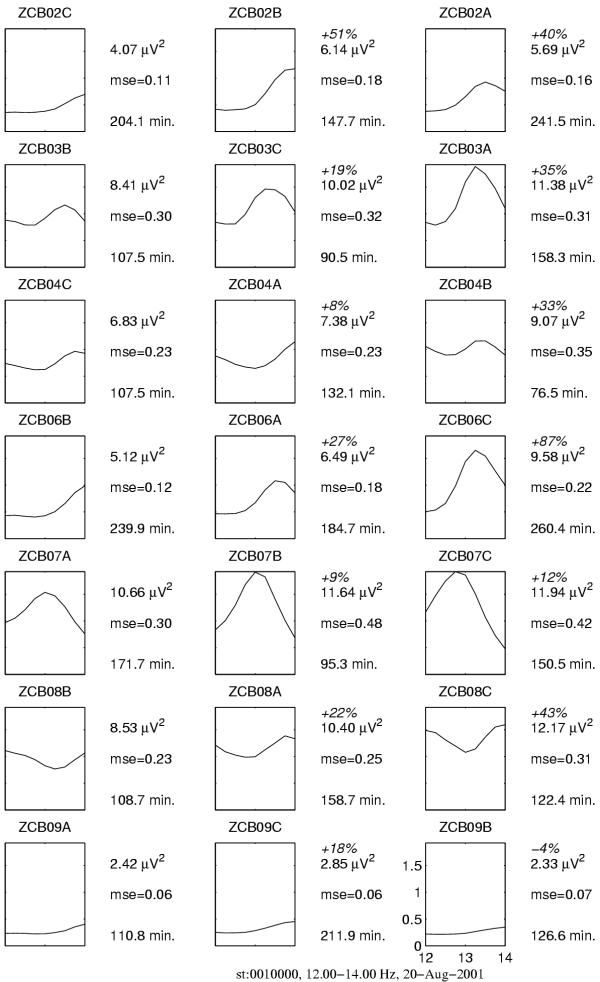
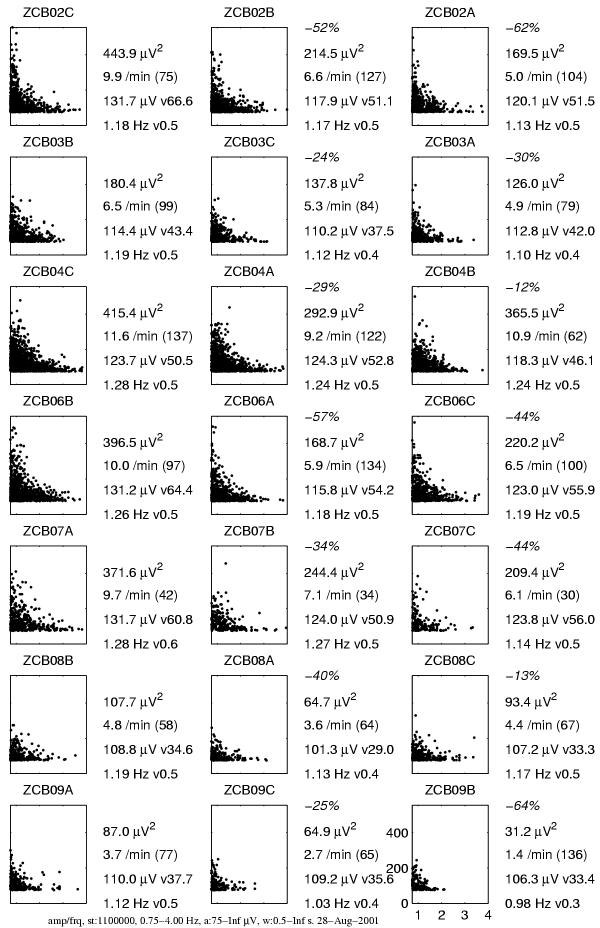
Figures 17 and 19 present each of the structures, classified as sleep spindles (Figure 17) or SWA (Figure 19) as a dot in the frequency-amplitude plane. These structures were selected using not only the frequency information, as in the "classical" approach, but also information on time duration and amplitude from Table 1. Total power carried by these structures, summed and normalized per time unit, is indicated on the right of each plot, together with the average number of occurrences per minute, average amplitude and frequency.

Figure 17.

Sleep spindles selected from the MP parametrization of the same recordings as in Figure 16 – plots organized accordingly – chosen as structures with frequency 12–14 Hz, amplitude above 15 μV and time duration 0.5–2.5 seconds. Each dot in the plots marks one spindle in the frequency (horizontal, Hz) versus amplitude (vertical, μV) coordinates. Numbers on the right of each plot give increase of total power relative to the night after placebo (absent in first column), power carried by selected structures, number of structures per minute (in parenthesis total time of qualified stages in min.), average amplitude and its variance, and average (weighted by amplitude) frequency with variance

Figure 19.

Slow wave activity (SWA) selected from the MP parametrization as structures of frequency 0.75–4 Hz, amplitude higher than 75 μV and duration above half a second. Plots and descriptions organized as in Figure 17

Table 1.

Criteria chosen for the automatic selection of EEG structures based upon the time-frequency parameters.

	frequency	duration	amplitude
SWA	0.75–4 Hz	0.5-∞s.	>75 μV
sleep spindles	12–14 Hz	0.5–2.5 s.	> 15 μV

We observe that selective MP-based estimates of power are more sensitive to the effect of influence of both drugs than the spectral integrals. This sensitivity becomes crucial in two of the analyzed cases:

1. In the recording of patient ZCB09, which revealed a very low spindling activity (last row in Figures 16 and 17), fluctuations in the background masked the power of sleep spindles to such an extent, that spectral integrals indicate a partially reverse trend, i.e. decrease of power of sleep spindles under the influence of midazolam. Selective estimates indicate the expected increase.

2. For patient ZCB08 (second row from the bottom) spectral integrals indicate increase of power of SWA (δ), while MP estimates reveal a decrease coherent with all the other cases.

Finally, as an example of an effect elusive to the classical methodology, these results indicate also a statistically significant decrease of the frequency of the slow wave activity. Further discussion and statistical evaluation of results can be found in [13].

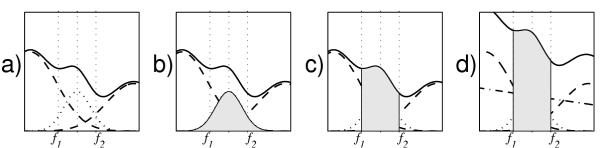
Figure 20 partially explains the increased sensitivity of the proposed approach as compared to the classical paradigm of band-limited spectral power integrals.

Figure 20.

Distinction between a spectral power integral from f₁ to f₂, and power actually carried by structures of frequencies centered between f₁ and f₂. Plot a) presents spectral power (versus frequency) of hypothetical structures with frequency centers lying inside (dotted) and outside (dashed line) the f₁-f₂ interval. Due to the uncertainty principle, their spectral contents overlap. Solid line presents their sum, i.e. total spectral power, as estimated e.g. by Fourier transform. In b) the actual power carried by structure of frequency originating between f₁ and f₂, as estimated in the proposed approach, is shaded. Plot c) highlights the power obtained from a spectral integral from f₁ to f₂. Finally in d) additional background (dotted-dashed line) is added. We observe that neighboring structures from outside the interval of interest may contribute significantly to the power estimated within the interval, and can even shift the actual position of the spectral peak related to the relevant structure (dotted line), while some of the power carried by the structure inside the interval of interest falls outside and does not contribute to the spectral integral

Representation of changing frequency

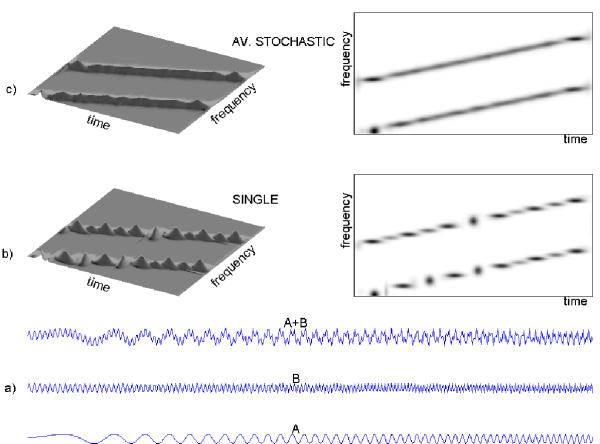
Another interesting property of the stochastic time-frequency dictionaries, discussed in section 5.1, relates to the representation of structures of changing frequency. Such structures are absent in the dictionaries usually applied for the decomposition, and therefore are represented as a series od fixed-frequency Gabor functions (Figure 22 (f) and Figure 21 (b)).

Figure 22.

Time-frequency maps of energy density of a 500-points simulated signal (e), the same as in Figure 7, composed of four sine-modulated Gaussians, i.e. Gabor functions (a-b), sine wave and one-point discontinuity (c) and sine wave with linear frequency modulation-chirp (d). Distribution (f) was obtained from a single decomposition in a large (2 * 10⁶ waveforms) dictionary: signal is described by only 30 functions, but changing frequency of the chirp is represented as a series of functions, since in the Gabor dictionary we have only constant frequency modulations. (g) presents average of 100 decompositions of the same signal in different realizations of smaller (5 * 10⁴ atoms) stochastic dictionaries. This smoothes the representation of the chirp, but underlying parametrization is no more compact, (h)-the same as (g), presented in 3 dimensions. Square root of energy proportional to the height of the surface or "temperature" on 2-dimensional plots. [22]

Figure 21.

Time-frequency energy density of a signal composed of two chirps presented in (a). In 3-dimensional plots on the left side energy is proportional to height, on flat pictures on the right – to the shades of gray. (b) presents results of a single decomposition over dictionary consisting of 500.000 atoms, and (c) – time-frequency representation averaged over 50 realizations of smaller dictionary (15.000 atoms)

However, by averaging several decompositions of the same signal in different realizations of smaller stochastic dictionaries, we obtain a more continuous representation like in Figures 22 (g) and Figure 21 (c). The representation is no more compact, but retains the general property of absence of cross terms.

Event-related desynchronization and synchronization

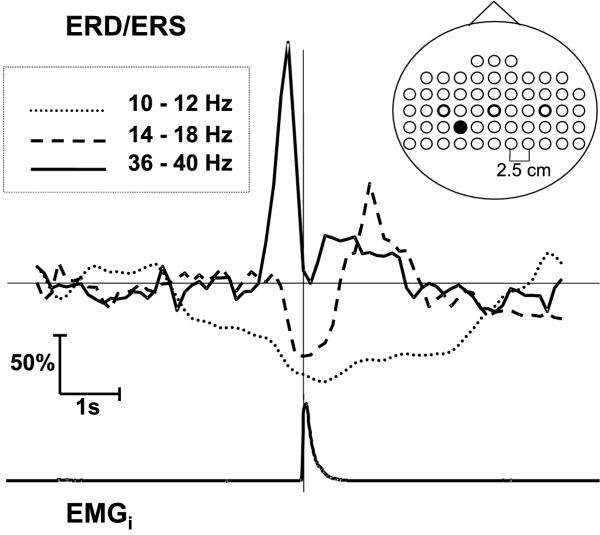
Advantages of the MP algorithm with stochastic dictionaries can be also combined with the stochastic element present inherently in the data, like e.g. in the case of analyzing repetitions of event-related potentials. This relates especially to the non-phase locked activity, i.e. such that would not be enhanced in the stimulus-synchronized time averages. Its detection requires a different analysis technique, allowing for averaging signal's energy irrelevant of the phase². Classically it was achieved by squaring the values of signals, band-pass filtered in a priori chosen frequency bands, before averaging ([14], Figure 23).

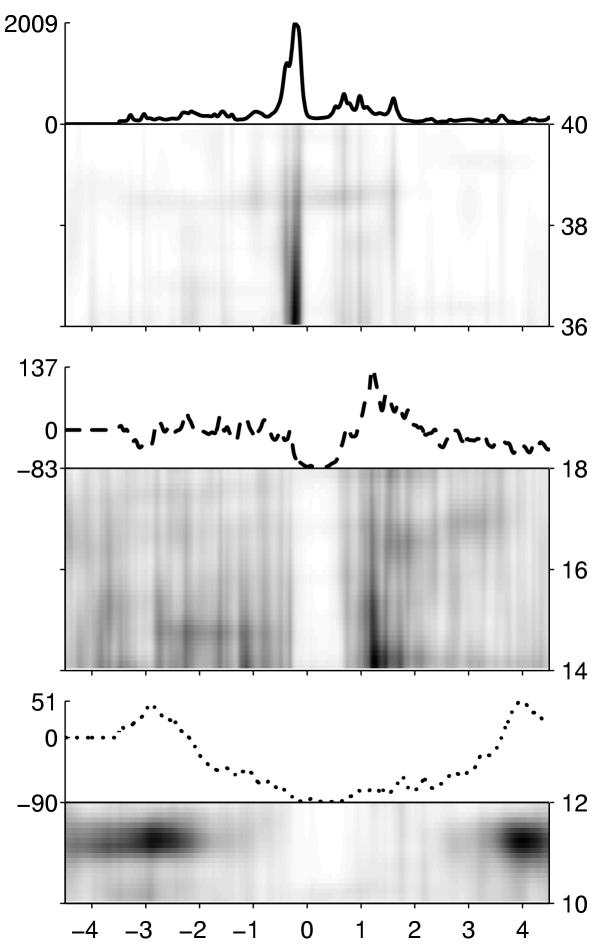
Figure 23.

Classical quantification of ERD/ERS in three bands: α 10–12 Hz, (β 14–18 Hz, γ 36–40 Hz. Insert indicates positions of electrodes used for recording. C3, Cz and C4 from the 10–20 system are marked by thicker circles. Results presented for electrode marked by filled circle [22].

This methodology has several drawbacks, including tha arbitrary choice of frequency bands and limited sensitivity (c.f. Figure 20). Averaging the time-frequency densities of energy, obtained from the MP decomposition, allows for an instantaneous evaluation of the complete picture of changes in the time-frequency plane, with high resolution. Figure 25 presents this picture for the same data as in Figure 23. Another study in Figure 26 reveals clearly splitting of the alpha band in the upper and lower frequencies, with different behaviour related to the finger movement. This phenomenon would be very difficult to find using the classical methodology.

Figure 25.

Complete time-frequency map (from 5 to 40 Hz), from which slices presented in Figure 23 were cut. Horizontal scale-seconds relative to the finger movement, vertical-frequency (Hz). Top-the same in 3 dimensions, but energy of the alpha band cut off in 50% of the height to show weaker high-frequency structures [22].

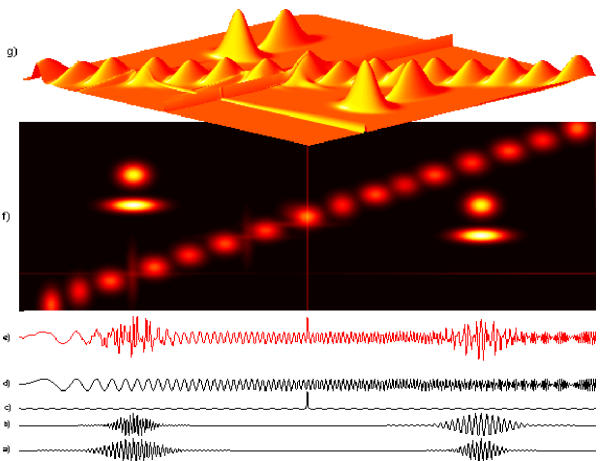
Figure 26.

Bottom: first 10 of 57 EEG trials (Hjorth source derivation) recorded during a voluntary finger movement (time 0). Middle plot – average of the time-frequency distributions of energy obtained from MP parametrization. Top: the same distribution in 3 dimensions. We clearly observe e.g. splitting of the alpha activity into two differently reacting subbbands, a phenomenon elusive to the classical approach.

Figure 24.

Average time-frequency maps of EEG energy density, obtained from the same data as in Figure 23. Horizontal axis-time in seconds relative to the finger movement. Vertical axes on the right of those maps indicate frequency in Hz. Energy proportional to shades of gray. Scale is arbitrary and different for each map. Curves above the maps, corresponding to figure 3, are frequency integrals of the maps below them. Vertical axes on their left sides indicate percent of change, relative to energy integrated between 3.5 and 4.5 seconds before the movement in given band. [22]

²If we want to analyze phasic synchronization in higher frequencies, like e.g. gamma band around 40 Hz, the accuracy of the triger's determination would have to be much better than e.g. 1 ms, which is rather beyond the accuracy of determining e.g. the moment of a finger movement. But non-phasic effects should be visible in the presented approach.

Epileptic seizures

Discussed advantages of time-frequency estimates of energy density, obtained from MP decomposition, allowed for identification of different dynamic states during evolution and propagation of epileptic seizures in [15].

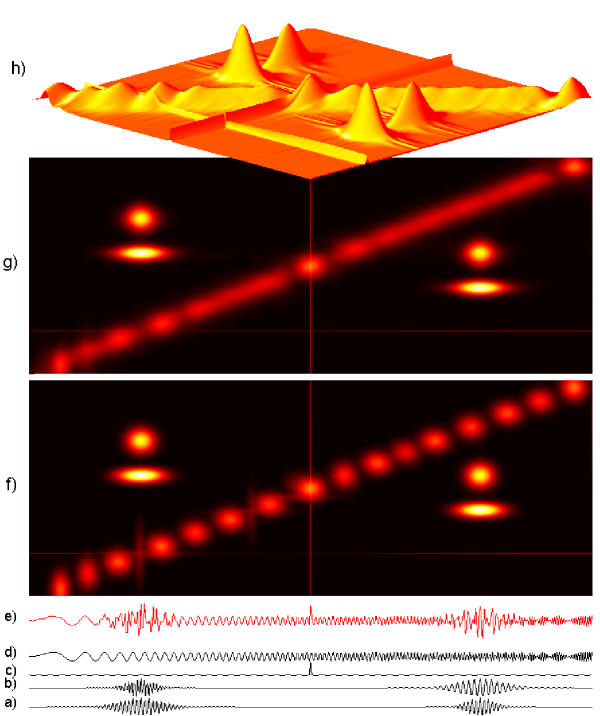
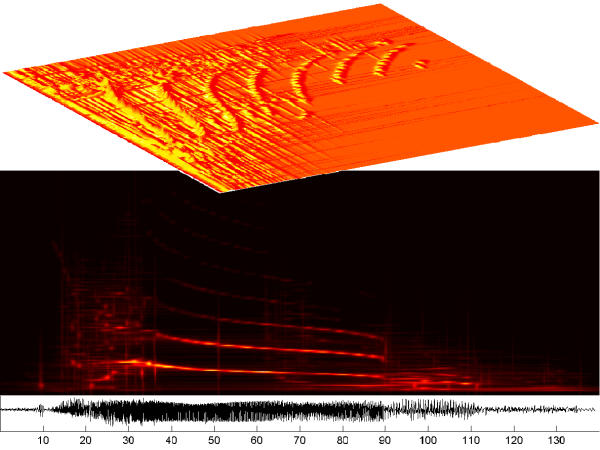
Figure 27 presents an example of time-frequency density of energy, calculated from the MP expansion of an intracranial recording of epileptic seizure. Sensitivity of the algorithm to the phase changes clearly distinguishes the initial less synchronized period of transitional rhytmic activity (starting near 15th second) from the organized rhytmic activity. In this period (starting about 30th second) all the harmonics, up to the Nyquist frequency, clearly follow the pattern of decreasing frequency. Such a clear representation of changing frequency was possible using the technique discussed in section 7.

Figure 27.

Bottom: intracranial recording of an epileptic seizure, horizontal axis in seconds, sampling 100 Hz. Middle time-frequency distribution of energy was obtained as average of 17 MP decompositions in different realizations of a stochastic dictionary (3 * 10⁶ atoms). Picture illustrates different dynamical states identified in [15]: near 15th second, the period of seizure initiation transforms into transitional rhythmic activity, then before 30th second the organized rhythmic activity with 8 visible harmonics becomes dominant, to dissolve into intermittent bursting activity near 90th second. Top-the same distribution in 3 dimensions. Data and interpretation courtesy of Prof. P. J. Franaszczuk and Prof. G. K. Bergey

Problems

As presented in figure 28, greedy MP algorithm in certain cases can fail to properly decompose signal containing even a simple combination of dictionary's functions. This counterexample was simulated especially for discussion of practical issues and as such may look scary, but on the other hand we never encountered such a failure in applications to real world signals. The trap in this case lies in the fact that both these structures have exactly the same phase, and it might be even dicussable if they should not be treated as one in the first approximation. If they were produced by two different biological generators, such a coincidence of phases would not be possible and they would be parametrized separately.

Figure 28.

A failure in feature extraction: MP decomposition of a signal consisting of two Gabor functions, both present in the dictionary used for decomposition. In the left column, from the top: slice of the time-frequency representation obtained from MP decomposition of the signal (R⁰) drawn below; R¹--R³ are first three residues. First three time-frequency atoms (g₀--g₂) fitted by MP are shown in the right column

Other, more theoretical examples of MP failures are given in [16] and [17]. Some of these cases can be properly solved by the orthogonalized matching pursuit [18], at a cost of increased computational requirements and a possibility of introducing numerical instabilities [19]. Another modification of the MP algorithm, discussed in [20], relies on a modification of the similarity function used in each step to choosed the "best fit". Other works [21] indicate that global optimalization of the l¹ norm of expansion's coefficients might be the best choice [17], but, in spite of recent advances in linear programming, computational complexity is still very high.

Other problems, awaiting better solutions, include: efficient and (at the same time) bias-free implementations, robust estimation of resolution, proper addressing of the tradeoff between resolution (increasing dictionary size) and computation cost, and extension of the algorithm to the multichannel case. Such research will improve effectivity and understanding of mathematical foundations of these higly nonlinear procedures. However, current implementations and knowledge of algorithm's properties are already sufficient for large scale applications in EEG research and clinical practice. They may serve as a basis for a unification of parametrization and description of EEG.

Implementations of MP with stochastic dictionaries is available from http://brain.fuw.edu.pl/mp.

Authors contributions

Parts of presented research, according to the quoted references, were coauthored by:

• Prof. Katarzyna J. Blinowska, head of the Laboratory of Medical Physics, Warsaw University, and my colleagues from the Lab: Józef Ginter Jr, Dobiesław Ircha, Jarosław Zygierewicz.

• Prof. Waldemar Szelenberger, Medical University of Warsaw

• Prof Ernest A. Bartnik, Inst. of Theoretical Physics, Warsaw University

• Prof. Piotr Franaszczuk, Johns Hopkins Medical University

• Prof. Gert Pfurtscheller and dr Christa Neuper, Graz Technical University