Optimizing Management and Financial Performance of the Teaching Ambulatory Care Clinic

Abstract

OBJECTIVE

To examine how to optimize teaching ambulatory care clinics performance with regard to access to care, access to teaching, and financial viability.

DESIGN

Optimization analysis using computer simulation.

METHODS

A discrete-event simulation model of the teaching ambulatory clinic setting was developed. This method captures flow time, waiting time, competition for resources, and the interdependency of events, providing insight into system dynamics. Sensitivity analyses were performed on staffing levels, room availability, patient characteristics such as “new” versus “established” status, and clinical complexity and pertinent probabilities.

MAIN RESULTS

In the base-case, 4 trainees:preceptor, patient flow time (registration to check out) was 148 minutes (SD 5), wait time was 20.6 minutes (SD 4.4), the wait for precepting was 6.2 minutes (SD 1.2), and average daily net clinic income was $1,413. Utilization rates were preceptors (59%), trainees (61%), medical assistants (64%), and room (68%). Flow time and the wait times remained relatively constant for strategies with trainee:preceptor ratios <4:1 but increased with number of trainees steadily thereafter. Maximum revenue occurred with 3 preceptors and 5 trainees per preceptor. The model was relatively insensitive to the proportion of patients presenting who were new, and relatively sensitive to average evaluation and management (E/M) level. Flow and wait times rose on average by 0.05 minutes and 0.01 minutes per percent new patient, respectively. For each increase in average E/M level, flow time increased 8.4 minutes, wait time 1.2 minutes, wait for precepting 0.8 minutes, and net income increased by $490.

CONCLUSION

Teaching ambulatory care clinics appear to operate optimally, minimizing flow time and waiting time while maximizing revenue, with trainee-to-preceptor ratios between 3 and 7 to 1.

There are over 700 million outpatient office visits each year. Over 67 million occur in hospital-based teaching ambulatory clinics.¹ Teaching ambulatory care clinics have several, often competing, goals: 1) to provide accessible and satisfactory health care to patients, 2) to train new physicians, and 3) to maintain financial viability.

In the early 1990s, the Office of the Inspector General ordered the Physicians at Teaching Hospitals (PATH) Audits to assess the quality of care patients receive at teaching hospitals. As a consequence of this audit, several new federal regulations for teaching hospitals were promulgated, i.e., CFR (Code of Federal Regulations) Title 42-Section 415.174(a), to ensure quality patient care. These regulations limit the number of residents that a precepting physician may supervise (up to 4 trainee physicians per preceptor) and limit the level at which these trainees may bill (up to evaluation and management [E/M] level 3). The E/M level is derived from a protocol developed in 1995 by the Health Care Financing Administration (now Centers for Medicare/Medicaid Services) in conjunction with the American Medical Association. The E/M level of the patients is based on the complexity of decision making and the length of time spent in the patient encounter. Reimbursement for federally funded insurance programs and many private ones are based on these E/M levels. These regulations were not based on clinical trials but rather developed through a consensus of expert opinion. It remains unclear if these specific staffing and billing limits are optimal for maintaining accessible and satisfactory care for patients. Also unclear is the effect of these limits on the time available for teaching and on the financial viability of these academic ambulatory medicine clinics. Conducting randomized controlled trials to explore the optimal trainee-to-preceptor mix is difficult, because such a trial could place patients at the kind of risk the regulations were enacted to prevent.

Simulation provides a good alternative to direct experimentation when direct experimentation is not feasible because of practical, ethical, or financial reasons.^2,3 Simulation, by definition, is any activity in which an actual or proposed system is replaced by a functioning model. These models may be physical, such as flight simulators or cardiopulmonary resuscitation mannequins, or abstract, such as mathematical constructions or computer models. All simulations are designed to approximate the cause and effect relationship of the system being studied. The purpose of simulations is to understand the nature of the “real” system and its behavior under varying conditions. Experiment is carried out through “what-if” experiments (in which the structure of the model is changed, e.g., residents have to share rooms or phlebotomy is located in a separate building), and sensitivity analyses (in which the parameters of the system are varied, e.g., the time needed to discuss and review a case with a trainee). Discrete-event simulation is a simulation method designed explicitly to capture process flow information and competition for resources, and has been used to help evaluate health care problems in outpatient practice for several years.^4–10

Computer simulation addresses real-world problems in several ways. First, simulation allows you to test every aspect of a proposed change before committing resources. Once systems have been installed, changing or correcting them can be very expensive. Second, it allows you to compress or expand time, speeding up or slowing down events so that you can explore them thoroughly. For instance, an entire clinical week may be examined within a few minutes, or hours can be spent examining and detailing all the events occurring from patient check-in to the time patients are shown into the exam room. This allows you trace and reconstruct the causes of events step by step, helping you diagnose problems and understand interactions within complex systems. Most real-world systems are too complex to consider all the interactions going on in a given instant. Third, it allows you to explore new policies, operating procedures, etc. without the expense or disruption of experimenting on the real system. Fourth, simulation allows you to identify system constraints, such as bottlenecks. Fifth, through its animation features, it may facilitate communication, help build consensus among stakeholders, allow participants to see how a proposed plan will actually function, and help specify requirements for the final real-world system. Finally, simulations can facilitate training, allowing team members to learn from their mistakes in a safe environment.

The disadvantages of simulations are that they typically require some degree of special training to build, their construction may be time-consuming, and like any tool, they may be used inappropriately. For example, simulation is often unnecessary when an analytic solution is possible, although this is infrequent in health care.

To examine the many possible configurations of residents and preceptors, we developed a model of the clinic processes, resource utilizations, and work flows. In this case, physician time and teaching time are resources that individual patients and residents compete for, respectively. Specific outcomes of interest are the number of patients that may be seen during a clinic day, how long patients spend in the clinic, how long patients spend waiting for care, the time spent waiting for discussion and review with preceptors, the amount of time preceptors are busy precepting. The specific amounts of time spent in the history and physical as well as in the discussion and review process between preceptor and resident for patients of varying complexity are reported in a separate paper (J.E. Stahl, MD, CM, MPH, G.S. Gazelle, MD, MPH, PhD, M. Beinfeld, MPH, unpublished data, May 2002).

METHODS

We performed an optimization analysis comparing current practice, i.e., a clinic with a 1:4 preceptor-to-trainee ratio to clinics with alternative staffing strategies.

Modeling Method

Discrete-event simulation, in addition to modeling process flow and competition for resources, also allows the system being modeled to undergo discrete and abrupt changes at variable times. These changes are not constrained to fixed-time intervals, as in state-transition Markov models, and are primarily generated by entity interactions and events. These interactions and events, e.g., competing for resources or entering the system, typically result in further changes to the system. The probability of events, the duration of processes, and the rate at which people may enter the system are typically derived from stochastic draws of either theoretical or empirically derived distributions. This methodology is designed to capture information relating to flow time, waiting time, competition for resources, and the interdependency of events, and thereby provides insight into system dynamics. The model was developed using SIMAN,¹¹ a general-purpose discrete-event simulation language, on the Arena software platform (Rockwell Software, Inc., West Allis, Wis).

Strategy Description

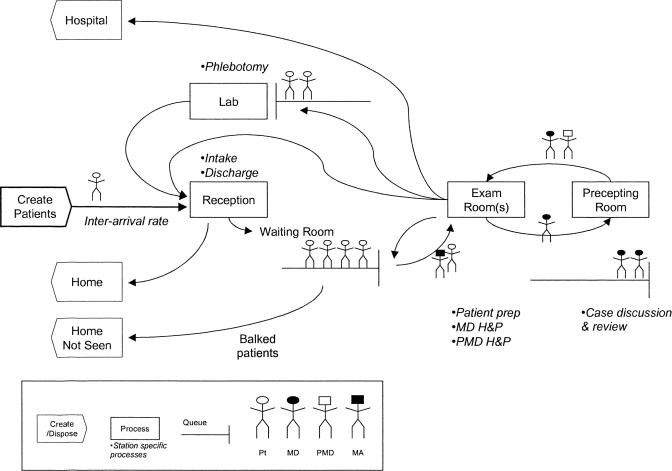
The model follows patients from registration through discharge and trainees from the history and physical with patients through the discussion and review with preceptors (Fig. 1). As patients enter the model, they are assigned several unique attributes, such as whether they are new or established patients, and their E/M level, a measure of patient clinical complexity. Once patients actually arrive at the clinic, they register with the receptionist. They then have a seat in the waiting room. If the time a given patient spends in the waiting room before being seen exceeds his/her tolerance for waiting, the patient leaves without being seen, i.e., he/she balks. If the patient has not left and an exam room becomes free, a medical assistant (MA) picks up the first available patient and escorts him/her to the exam room. Here the MA takes the patient's vital statistics. Once this is complete, the MA returns to the nurses' station to await the next free room and available patient. Once the patient is in the room and has had his/her vitals taken by the nurse, a trainee physician, if free, comes in, interviews the patient and conducts a physical exam. The duration of the history and physical is determined by a combination of the patient's new versus established status and his/her E/M level (Table 1). The trainee then leaves the exam room still occupied by the patient and proceeds to the precepting room. Once here, the trainee waits for the first available preceptor. Once the preceptor is free, the trainee presents the case for discussion and review. The duration of this process is determined by the patient's new versus established status and E/M level (Table 2). Depending on the trainee's year of training and the attributes of the patient, the precepting clinician may decide to accompany the trainee back to the exam room to perform a follow-up history and physical. Once these are complete, the patient is either sent to the phlebotomy lab for blood tests, sent home, or admitted to the hospital. Before returning home, either directly from the exam room or via the phlebotomy lab, the patient must check out with the receptionist.

FIGURE 1.

Ambulatory teaching clinic model. Pt, patient; MD, trainee physician; PMD, precepting physician; MA, medical assistant; H&P, history and physical; D&R, discussion and review.

Table 1.

Sample Mean Duration for History and Physicals for Different E/M Levels

E/M	Mean Minutes	SD
Established patients
Level 1	13.3	5.5
Level 3	19.8	6.8
Level 5	28.9	9.8
New patients
Level 1	15.2	9.3
Level 3	27.4	12.1
Level 5	42.4	15.8

E/M, evaluation and management.

Table 2.

Sample Mean Discussion and Review and Physicals for Different E/M Levels

E/M	Mean Minutes	SD
Established patients
Level 1	5.2	3.5
Level 3	7.7	4.2
Level 5	10.7	4.8
New patients
Level 1	4.4	3.5
Level 3	8.8	5.5
Level 5	13	6.9

E/M, evaluation and management.

Patient scheduling is manifested as the patient inter-arrival time, i.e., the time interval between a patient's arrival and the arrival of the next patient. In the model, the time interval was determined from a stochastic draw of an empirically derived distribution of arrival times. This distribution was derived from the actual recorded arrival times of scheduled patients seen in the University of Pittsburgh Medical Center's outpatient clinic each day, divided by the number of clinicians working on that day. The number of patients actually scheduled to arrive at a given time is directly proportional to the number of clinicians practicing at that time. The inter-arrival times fit the distribution, log normal (10.3 min, 29.5 min) per clinician. An 8-hour workday was modeled. Patients were allowed to register up to 30 minutes before the end of the clinic.

Our base-case assumed 1 preceptor to 4 trainees, 1 exam room for each trainee, 1 nurse for 2 exam rooms, and 1 phlebotomist for all active rooms. The base-case assumed that 16% of patients were new to the clinic¹² and that the E/M levels of the arriving patients were: E/M 1, 2%; E/M 2, 21%; E/M 3, 52%; E/M 4, 25%; and E/M 5, 2%. This distribution is derived from EpicCare, an electronic medical record system (Epic Systems Corporation, Madison, Wis). This distribution is very similar to that of the time estimates for patient visits captured in the National Hospital Ambulatory Medical Care Survey.² Finally, on the basis of the expert opinions of clinicians and scheduling staff, the base-case assumed that there would be a 20% patient no-show rate for the training clinic, that 20% of cases would require the preceptor to return to the exam room with the trainee, and that 70% of patients would require at least 1 blood test.

Model Assumptions

In developing the model, we made several necessary simplifying assumptions. First, we assumed that patient scheduling, i.e., patient inter-arrival times, could be adequately modeled as a stochastic draw from an empirically derived distribution of inter-arrival times. In real clinics, the system of processes that comprises patient scheduling is very complex, dynamic, and interdependent. For example, patients continually call for appointments up to several months in advance, drop into the clinic, and cancel their appointments. In addition, patients may arrive early, late, or not at all, with or without notifying the clinic of the arrival status. These individual behaviors and processes may be described as distributions of probabilities or times, which may or may not be independent of each other. This complex behavior holds true for an individual clinician's scheduled patients as well as the clinic as a whole. To model this level of detail would require a large complex dynamic model that continually updates itself as each of these events occurs. Fortunately, all these behaviors come together and are captured in the single distribution of inter-arrival times of patients at the registration desk.

In addition, because the inter-arrival times are drawn stochastically from this distribution, this method captures the underlying variability surrounding late and early arrivals as well as delayed session start times without the need to create a separate templated clinic schedule for each clinician. From the perspective of the clinic, patients arrive as if following a real-world scheduling system. A fixed deterministic arrival rate based on scheduled times would not capture this nor would a more random arrival rate, such as the rate that might occur in a walk-in clinic.

Second, we assumed that patients were seen on a first-come, first-served basis. This means that a patient sees the first available physician rather than the particular physician he/she might have been scheduled to see. Although not specifically done in this analysis, patients may be assigned to specific clinicians in this model through their attributes (entity-specific variables). This first-come, first-served assumption is important because it is the simplest queue-processing (scheduling) regime. This simplification allows us to concentrate on examining the effects of varying staffing while avoiding many of the confounding issues inherent in more-complex queue-processing regimes.

On the negative side, this patient-processing regime may remove some bottlenecks and smooth out some of the nonlinear behavior of the system that results from individual trainee physicians' performance characteristics, i.e., their ability to process patients. With standard patient-to-doctor scheduling, there is less capacity to adjust for these types of idiosyncratic delays.

Third, we assumed that the time spent in taking a history and performing the physical exam, as well as that spent in the discussion and review process, did not vary significantly across the trainees' year of postgraduate education. This assumption was in part due to limitations in our survey for acquiring this data; respondents in this survey were asked to group the performance of all trainees together, as opposed to by year of training. This was in part validated by data from other time motion studies^13–17 performed in training clinics, which did not demonstrate significantly different times for history and physical or precepting across post-graduate year of training. Finally, this being said, we felt that any additional differences in time spent in performing these tasks that resulted from level of trainee experience was substantially captured by varying the probability of the need for precepting and the probability of the preceptor needing to perform a follow-up history and physical.

Fourth, we assumed that the only laboratory tests that patients would receive on-site were blood draws. Plain x-rays were assumed to occur off-site and outside of clinic hours. Finally, we assumed, for our base-case analyses, 1 receptionist per preceptor and that the receptionist always had enough capacity to handle incoming patients. This was assumed so that the receptionist would not become a bottleneck under high-patient volumes when we were examining the relationship between trainee and preceptor.

DATA

Process Data

Estimates for the patient inter-arrival rates, average inter-arrival interval (min) = log normal (mean = 10.3, SD 29.5), and clinic flow times (mean 94 min, SD 77 min) were estimated using a 3 months extract of the University of Pittsburgh Medical Center outpatient clinic's EpicCare from 10/99 to 2/00. The only data obtained were the date, registration and discharge times, the number of physicians working in the clinic that day, and the final E/M level recorded at discharge. All unique patient identifiers were eliminated before use. The University of Pittsburgh Medical Center's Institutional Review Board (IRB) approval was obtained for this extract. Seven thousand two hundred and seventy-nine registration/discharges time pairs were recorded. The number of clinicians working averaged 8 (range 3 to 12) per day. Inter-arrival rates were calculated as the time between patient registrations. Because the clinic had a common registration desk, the inter-arrival rate was weighted by the number of clinicians working that day. More patients are scheduled when there are more clinicians available. For example, on average, the time between patient registrations for a clinic day with 1 clinician was twice as long as the average time between patient registrations for a day with 2 clinicians. These data were based on all patient registration during regular clinic hours during the above time period. Clinic flow time was calculated as the discharge time minus the registration time.

The process times for the trainees' patient history and physical and discussion and review of the case with the preceptor were derived through a national web-based survey of the Society of General Internal Medicine, a national society of academic general physicians (Tables 1 and Tables 2). In the survey, participants were presented with clinical scenarios derived from the Current Procedural Terminology (CPT) code books describing patients at various E/M levels. They were then asked what would be the minimum, median, average, and maximum times a trainee would need to perform a history and physical on a patient, and what would be the minimum, median, average, and maximum times a preceptor would need to discuss and review this patient with the trainee. This survey is not yet published. Approval for this survey was obtained from the IRB of Massachusetts General Hospital, the site at which it was based. Other process data, such as the times needed to register, take vitals, or draw blood were derived via time-motion studies and interviews with the relevant staff in a teaching ambulatory care clinic. Interviews took the form of asking the minimum, average, median, and maximum times needed to perform a given task. This is a standard method used in industrial engineering and yields a triangular timing distribution.

The model was validated by testing its performance, with regard to flow time and waiting time, against external data from teaching and nonteaching clinic settings. For example, if we adjust the history and physical times to those of fully trained clinicians,^18–22 our model yields estimates of flow time and waiting time very similar to independent estimates of waiting and flow time.^13,23 The data on time spent with the physician, from the National Ambulatory Medical Care Survey, was used to validate the E/M data, because time with the physician is a key component determining the E/M level.

Cost Data

Staffing costs were derived from the Bureau of Labor Statistics (http://www.bls.gov/oes/2000/oes_29He.htm) for general practitioners (internists and family practitioners), medical residents, staff nurses, phlebotomists, medical assistants, and receptionists. All costs were calculated in 2002 U.S. dollars. Revenue estimates were derived from the Health Care Administration's public use file's prospective payment fee schedule (http://www.hcfa.gov/stats/pufiles.htm) for outpatient office visit (CPT codes 99201–99205 [new patient visits] and 99211–99215 [established patient visits]). Revenue estimates were based on the facility-based reimbursement rates for the CPTs. Revenue was assumed to derive from the CPT-related reimbursement and 60% of the matched ambulatory payment classification (APC) group (http://www.hcfa.gov/regs/hopps/ChangeF4CY2002.htm) reimbursement. The remaining 40% of the APC reimbursement was assumed to cover all non-salary-related costs (National Archives and Records Administration Office of the Federal Register [http://www.access.gpo.gov/nara/090898/fr08se98p-34.txt]).

OUTCOMES

The outcomes of interest were teaching clinic process measures. Patient waiting time and flow time were considered measures of the accessibility and satisfactory delivery of health care.^24–26 The final quality of the care delivered can only be determined by examining the postclinic outcomes for these patients, which is beyond the scope of this paper. Furthermore, the PATH audits were designed specifically to address a billing and documentation issue, and were not intended to indicate or address quality of care or precepting, which is left up to the Residency Review Committee. Waiting time for trainees for teaching and the number of teaching encounters per trainee served as measures for achieving the goal of providing adequate access to teaching for trainees. Net income was the measure for the goal of financial viability. Staff utilization is defined as busy time divided by total scheduled time. This measure has implications for job satisfaction, productivity, and turnover.^27,28

SENSITIVITY ANALYSES

In our sensitivity analyses, we examined the effect of varying the number of trainees, preceptors, support staff, and rooms per trainee on the patient waiting time, flow time, trainee wait time, and net clinic revenue. Therefore, we conducted sensitivity analyses on all of these parameters as well as on the distribution of patient types (new versus established), and the distribution of E/M levels.

In our first analysis, we compared the staffing strategies of 1 preceptor to 2 to 8 trainees. We then increased the number of preceptors from 1 to 4. For each additional preceptor, we re-examined the ratio of trainees to preceptors from 2 to 8. Next, we re-examined these results varying the number of exam rooms (1 vs 2) available to the trainee physicians. Finally, we examined the effect of varying the number of available support staff, such as nurses and phlebotomists. We also varied the proportion of new patients from 0% to 100% and examined the effect if the mean E/M level of incoming patients was 1 to 5.

STATISTICS

This model was evaluated as a terminating system. The output from each simulation run was treated as an experimental sample. The independence of replications was achieved by using different random numbers for each replication. The minimum number of replications necessary to avoid initialization bias across all variables examined was used. Quantile-quantile plots were used to determine the normality of the sample sets. Strategy outcomes were compared using student's t test where appropriate.

RESULTS

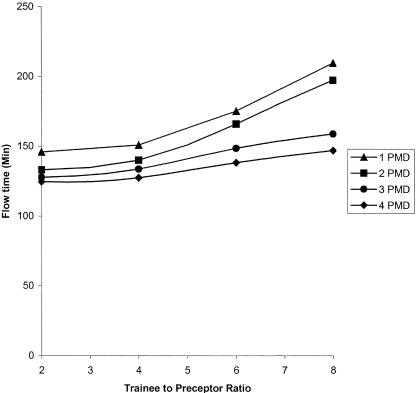
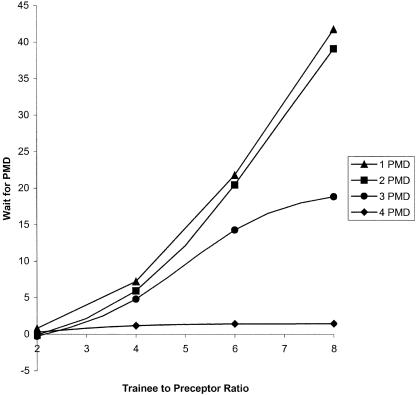
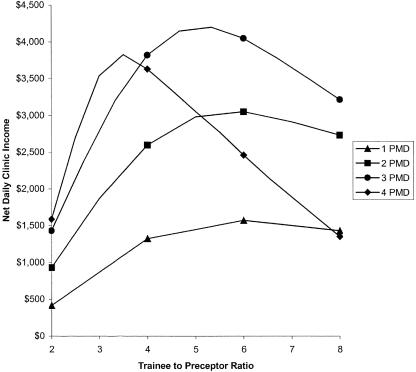
For the base-case analysis, the average flow time (registration to check out) and wait time (registration to room time) for patients were 148 minutes (SD 5) and 20.6 (SD 4.4), respectively. The average time spent waiting for the preceptor by trainees was 6.2 minutes (SD 1.2), and the average daily income for the clinic was $1,413. Staff utilization (which is defined as busy time divided by total scheduled time), was 59% for preceptors, 61% for trainees, and 64% for medical assistants. Average room utilization was 68%. Patient flow time and wait time remained relatively constant for trainee-to-preceptor ratios below 4:1 but increased steadily thereafter, regardless of the number of preceptors (Fig. 2). The waiting time for precepting rises steadily as the number of trainees rises for strategies with 1 or 2 preceptors. For strategies with 3 preceptors, waiting time peaks at 7.3 trainees per preceptor. For strategies with 4 preceptors, waiting time remains under 5 minutes (Fig. 3). For all strategies in which there are less than 5 trainees per preceptor, the wait time for discussion and review remains under 15 minutes. The maximum net clinic revenue occurs for trainee-to-preceptor ratios of 4 and 7, depending on the number of preceptors (Fig. 4). The maximum revenue for any strategy was with 3 preceptors and a trainee-to-preceptor ratio of 5:3.

FIGURE 2.

Patient flow time. PMD, preceptor.

Trainee wait fime for preceptor(PMD)

FIGURE 4.

Clinic net daily income. PMD, preceptor.

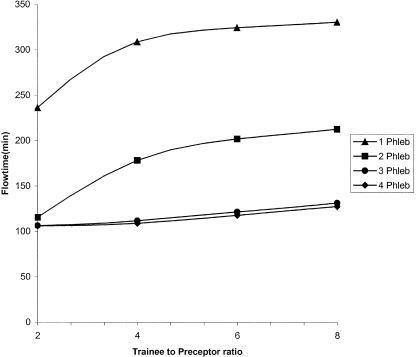
In our model, having more than 1 room available for trainees actually increases both flow time and waiting time for patients and waiting time for precepting for trainees while simultaneously increasing net daily revenue by approximately $280/day/additional preceptor. The delays are primarily due to the preceptors having trainees arrive faster than they can process them and consequently becoming system bottlenecks. The relative increase in net income as compared to the 1-room strategies is due to more patients being able to enter the system, i.e., getting into a room, before their wait time tolerance is reached. Finally, having insufficient support staff can also create bottlenecks. For example, as the ratio of phlebotomist to preceptors drops below 1:1, the flow time for patients rises substantially (see Fig. 5). Increasing the MA-to-room ratio from 1:2 to 1:1 did not significantly improve flow time or wait times and increased costs.

FIGURE 5.

Two-way sensitivity analysis of flow time with the number of preceptors being held constant at 3. Number of trainees versus number of phlebotomists. (Phleb)

The effect of varying the proportion of presenting patients who are “new” from 0 to 50%, showed only a modest effect on time and revenue. For example, for a strategies with 4 trainees to 1 preceptor, the average patient flow time and wait time remained relatively constant, rising on average 0.05 min/percent “new” patients and 0.01 min/percent “new” patients, respectively. Net daily income rose on average $27 (range $10.75 to $42.3) for each 1% increase in the proportion of new patients. The effect was larger when we varied the E/M level of patients. For example, if we constrained all presenting patients to 1 E/M level in strategies with 4 trainees to 1 preceptor, the average flow time increased by approximately 8.4 minutes per E/M level, wait time increased by an average 1.2 minutes per E/M level, and wait for precepting increased by 0.8 minutes per E/M level. Net income starts off at approximately $486/day, if all patients are level 1, and increases by $490 per E/M level thereafter.

DISCUSSION

This study had 3 main aims: first, to gain insight into the processes of care and teaching in ambulatory medicine teaching clinics and to understand, given their constraints, how best to achieve the goals of improving the accessibility and satisfactory delivery of care, and improving the accessibility of teaching to physician trainees while maintaining the financial viability of these clinics; second, to test the validity of the 4 trainees per preceptor limit; and third, to develop a tool with which to analyze ambulatory care clinic processes and to help design future clinics.

Our analysis shows the maximum net daily income for the clinic for all strategies occurs with a strategy using 3 preceptors and a trainee-to-preceptor ratio of approximately 5:1. This ratio ranges between 3:1 and 7:1, depending on the number of preceptors in the strategy. Strategies using trainee-to-preceptor ratios within this range also keep the patient flow time and waiting time and wait for teaching at a minimum. These results help confirm the intuition leading to the PATH regulation. Reflexively, this also helps validate our model. Our analysis also appears to show that training clinics can be net revenue generators.

If one assumes that process measures such as waiting time for precepting can be linked to educational outcomes, then this simulation model can help assess the different education values of a variety of clinic strategies. We must say at the outset that the authors are not aware at this time of any studies directly linking clinic performance parameters, such as waiting time for precepting, to educational outcomes, such as test scores. Therefore, any conclusions must be tentative. It should be noted, however, that many theoretical models of learning²⁹ emphasize that prompt practice, early review, and interaction with teachers and classmates help integrate new experiences and improve the retention of lessons. It is therefore reasonable to hypothesize that reducing the time spent waiting between history and physical and discussion and review during clinic might improve the quality of trainee learning. This in turn may be tested through clinical trial. For example, one might test whether the average time spent waiting for precepting correlates with higher trainee test scores or higher compliance with preventative care measures such as ordering mammograms.

We might also use these models to design and test clinic structures to maximize patient satisfaction. There already exists substantial evidence that patient waiting time is a significant factor in patient satisfaction.^30–35 Once such hypotheses are either confirmed or disproved, the results can be incorporated into the model. One of the strengths of simulation is its ability to point to gaps in our knowledge and point us toward avenues of potentially fruitful investigation.

To keep the model simple, we did not explicitly examine the effects of assigning specific clinicians or preceptors to specific patients or trainees in this analysis. This may be done easily, though, by assigning these constraints to the relevant patients or trainees as attributes (entity-specific variables) as they arrive in the model. It might be noted, however, that contrary to what might be expected, constraining trainees to specific teachers may not necessarily help the operational characteristics of the clinic. For example, consider the common scenario in which the preceptor is responsible for more than 1 trainee. Now consider the following situation. Preceptor A (matched to trainee A) is waiting for her trainee to finish the history and physical and present his patient, i.e., she is idle. Preceptor B is currently precepting trainee B1 when trainee B2 shows up after having finished with her patient. Should preceptor A precept the waiting trainee B2 or let her wait for preceptor B? Remember, while trainee B2 waits, her patient remains in the exam room awaiting disposition and the room remains unavailable for a new patient to be brought in. While not necessarily creating a system bottleneck, stratifying trainees in this fashion limits the precepting resources available to the trainee. This is consistent with our own preliminary analyses in this area.

In interdependent systems, in which an individual's freedom of action depends closely on the actions of others, system productivity (throughput) can be limited by both resource and policy constraints. For example, insufficient resources, such as too few preceptors or nurses, can rapidly become system bottlenecks. Consider the situation in which a trainee finishes with a patient and sends them on their way. Unless an unoccupied MA is available (resource) to bring the next patient back, the exam room will remain empty and idle until the MA finishes with his/her current task. This resource constraint might be avoided if the trainee is allowed to bring the patient back, a policy constraint. In either case, clinic productivity, the ability to move a patient from registration to discharge, is constrained.

Utilization, in contrast to throughput, is a measure of how often an individual resource is being used. For example, room utilization is a measure of the time a room is being used divided by the total time it is scheduled to be available. In our model, exam rooms averaged 68% utilization. This means that exam rooms stood unused for approximately 6 out of every 20 minutes. This idle time was a direct consequence of the interdependency of the various clinic resources and the variability involved in completing their tasks. Because of this interdependency, any delay swiftly migrates through the system. Two of the most important factors driving delays are insufficient resources, as mentioned in the above examples, and the variability in how these resources process tasks. Flow time and waiting time are directly proportional to the square of the standard deviation of the process time that a resource requires to perform a task.² In our model, there is significant variability surrounding the time an MA needs to prepare a patient. According to the survey of support staff used to develop this model, this process takes between 2 and 10 minutes, with a median of 5 minutes. If there were no variability, idle time would be less and utilization higher. But what is a desirable level of utilization for a specific resource?

Optimizing a system's performance, clinic or otherwise, does not necessarily mean maximizing the utilization of all its component resources. A system's performance is almost always limited by its slowest component. This becomes a bottleneck if the demand exceeds a resource's ability to process its designated task. A bottleneck resource is almost always the resource in the system with the highest utilization. Having resources upstream produce more than the bottleneck resource can handle only costs the system in money, inventory, or wear and tear. Therefore, individual resource utilization is only a rough marker of overall system performance, but a good marker for system breakdown. It should be noted that support staff often have the highest utilization rates in a clinic. This is significant in that it is these staff who are often the first cut when cost-cutting measures are instituted. Fewer support staff results in ever higher utilization and often more frequent burnout. Clinics then pay the cost of searching for and hiring new staff, reduced initial productivity of new staff learning their jobs, and perhaps prolonged reduced productivity for “burned out” staff.

The results of this model have to be adjusted to each clinical setting. Most hospitals have limited space for outpatient clinics and cannot afford to devote more than a few rooms to it. In addition, the process measures used, particularly those for accessibility and quality, are only one aspect of the quality of care delivered. Ultimately, patient clinical outcomes must be part of any quality assessment.

Finally, as health care becomes more competitive and resources more constrained, computer simulation provides an effective tool with which to test hypotheses and trade-offs regarding staffing, scheduling, and process flow in current clinic settings, as well as to plan clinics in the future. This is particularly necessary in environments such as the teaching outpatient clinic, which have complex roles to play. In future analyses, this clinic model will be expanded to address issues such as the effect of electronic medical records on the process flow in clinics, scheduling for individual physicians and patient preference for specific clinicians, combination strategies of walk-in and pre-arranged clinic slots, and more.