Quantitative Evaluation of the Diagnostic Thinking Process in Medical Students

Abstract

OBJECTIVE

To explore the diagnostic thinking process of medical students.

SUBJECTS AND METHODS

Two hundred twenty-four medical students were presented with 3 clinical scenarios corresponding to high, low, and intermediate pre-test probability of coronary artery disease. Estimates of test characteristics of the exercise stress test, and pre-test and post-test probability for each scenario were elicited from the students (intuitive estimates) and from the literature (reference estimates). Post-test probabilities were calculated using Bayes' theorem based upon the intuitive estimates (Bayesian estimates of post-test probability) and upon the reference estimates (reference estimates of post-test probability). The differences between the reference estimates and the intuitive estimates, and between Bayesian estimates and the intuitive estimates were used for assessing knowledge of test characteristics, and ability of estimating pre-test and post-test probability of disease.

RESULTS

Medical students could not rule out disease in low or intermediate pre-test probability settings, mainly because of poor pre-test estimates of disease probability. They were also easily confused by test results that differed from their anticipated results, probably because of their inaptitude in applying Bayes' theorem to real clinical situations. These diagnostic thinking patterns account for medical students or novice physicians repeating unnecessary examinations.

CONCLUSIONS

Medical students' diagnostic ability may be enhanced by the following educational strategies: 1) emphasizing the importance of ruling out disease in clinical practice, 2) training in the estimation of pre-test disease probability based upon history and physical examination, and 3) incorporation of the Bayesian probabilistic thinking and its application to real clinical situations.

Evaluating the thought process of clinical diagnosis is difficult because of the methodological difficulty in studying complex cognitive skills including clinical reasoning and judgment. Sackett et al. described 4 types of diagnostic thinking styles—pattern recognition, multiple-branching method, method of exhaustion, and hypothetico-deductive method—based upon results in cognitive psychology theory. He emphasized the usefulness of the hypothetico-deductive method for clinical diagnosis in the primary care setting.¹ This method is based on Bayes' theorem and naturally lends itself to integration in quantitative decision analysis.² The diagnostic behavior of seasoned physicians seems to fit the hypothetico-deductive method. Experienced physicians usually focus their attention quite narrowly to provide only a few specific diagnostic hypotheses. They then evaluate new clinical data in the light of these hypotheses, adjust for the likelihood of each hypothesis, reject some as implausible, and introduce a new hypothesis. This process of sequential revision is interrupted when the likelihood of one diagnosis becomes high enough to warrant action (i.e., a special test or an urgent therapy) or low enough to abandon further consideration of the disease.

Little is known, however, regarding how to evaluate a physician's diagnostic thinking process and how to improve a novice physician's diagnostic expertise efficiently. Quite often we encounter cases in which medical students or novice residents have difficulty in differentiating diagnosis and repeat inadequate laboratory or imaging tests. Accordingly, we planned this study to clarify the following: 1) how closely medical students follow the hypothetico-deductive method in diagnostic thinking process; and 2) the nature of the problems they face in their diagnostic process. We analyzed their diagnostic abilities in terms of 3 elements of the hypothetico-deductive method, knowledge of test characteristics (sensitivity and specificity), ability to estimate pre-test disease probability from clinical history, and ability to estimate post-test probability from pre-test probability and test characteristics.

METHODS

Target Population and Data Collection

We surveyed fifth-year medical students between September 1999 and May 2000 at 3 medical schools in Japan. The total number of years in medical school in Japan is universally 6. The curricula generally consist of 1 to 2 years of liberal arts education, 1 to 2 years of basic medical science courses, and 2 to 3 years of clinical science courses and clinical rotations. The curricula of the these medial schools are similar and include 2 or 3 sessions of primer courses on clinical epidemiology that cover basic principles of epidemiology, design of clinical trials, and the concepts of frequency, risk, and probability. The curricula also include an introduction to Bayes' theorem and the use of the probabilistic perspective in clinical diagnosis.

Subject students were surveyed before starting clinical rotation (medical school B and C) or within 2 weeks after starting rotation (medical school A), so that the medical students had no actual experience of clinical work at the time of this study. The students had completed at least 1 session of Bayes' theorem.

We presented hypothetical scenarios of chest pain patients to the students and asked them to answer questions. Each student was asked to provide answers independently to the best of his or her ability, based on the scenarios along with their own knowledge and experience. Clinical scenarios of typical anginal pain, atypical anginal pain, and non-anginal chest pain were provided. The corresponding pre-test probabilities of coronary artery disease were calculated as 90%, 46%, and 5%, respectively, from the data of Diamond et al. (Table 1).^3,4

Table 1.

Hypothetical Clinical Scenarios

Case scenario 1 (typical anginal pain, reference estimate of pre-test probability is 90%)

A 55-year-old man presented to your office with 4-week history of substernal, pressure-like chest pain. The chest pain is induced by exertion such as climbing stairs and relieved by a 3- to 5-minute rest. It sometimes radiates to the throat, left shoulder, down the arm.

Case scenario 2 (atypical anginal pain, reference estimate of pre-test probability is 46%)

A 45-year-old man without past medical history and coronary risk factors presented with 3-week history of stabbing chest pain in the retrosternal area. The patient reported that the pain was usually stabbing-like but sometimes pressure-like and developed during both rest and exercise. On physical examination, there is vague tenderness on costochondral joints.

Case scenario 3 (non-anginal chest pain, reference estimate of pre-test probability is 5%)

A 30-year-old man without a significant medical problem and coronary risk factors presented with 6-week history of squeezing pain in the lower retrosternal area to upper abdomen. The pain develops after meals, especially when he is lying down after late dinner.

The questionnaire consisted of 3 sections: 1) test characteristics questions, 2) pre-test and post-test probability questions, and 3) decision questions (Table 2). The test characteristics questions were asked before presenting the clinical scenarios. Then, the pre-test and post-test probability questions were posed for each scenario, followed by the decision questions regarding typical anginal chest pain with a negative exercise stress test (EST) result (Case scenario 1), or atypical chest pain with a positive EST result (Case scenario 3). Students were expected to provide a dichotomized answer for closed-ended questions and to provide a single numerical value for open-ended questions.

Table 2.

Questionnaire

1) Test characteristics questions

1. Do you understand clearly about the idea of sensitivity, specificity, or pre-test and post-test probability? Yes or No?

2. What is the sensitivity of the exercise stress test (EST)? Or what proportion of those patients with significant coronary artery disease (CAD) will show more than 1 mm of horizontal or downward ST-segment depression with EST? Significant CAD is defined as the presence of at least 75% of luminal narrowing of 1 or more major coronary vessels.

3. What is the specificity of EST? Or what proportion of those patients without significant CAD will not show more than 1 mm of horizontal or downward ST-segment depression with EST?

2) Pre-test and post-test probability questions

1. What is the probability that this patient has significant CAD?

2. What is the probability that this patient has significant CAD if EST shows more than 1 mm of horizontal or downward ST-segment depression?

3. What is the probability that this patient has a significant CAD if EST is negative?

3) Decision questions

1. For case scenario 1 (typical anginal pain) Should this patient be treated with beta-antagonists or nitrates when the EST is negative? Yes or No?

2. For case scenario 2 (atypical anginal pain) Should this patient be treated with beta-antagonists or nitrates when the EST is positive? Yes or No?

Data Analysis

We defined 3 parameters (3 probability estimates) to evaluate the students' clinical diagnostic ability (Appendix A). 1) Intuitive estimates were defined as sensitivity, specificity, and pre-test probability estimates provided by the students (Se_INT, Sp_INT, preProb_INT). Intuitive estimates of post-test probabilities were separately defined as positive predictive value (PPV) estimates provided by the students for positive EST result (PPV_INT) or negative predictive value (NPV) estimates provided by the students for negative EST result (NPV_INT). 2) Reference estimates of sensitivity, specificity, and pre-test probability (Se_REF, Sp_REF, preProb_REF) were obtained from Diamond et al.^3,4 Reference estimates of the post-test probabilities were calculated by substituting the reference estimates of sensitivity, specificity, and pre-test probability into Bayes' formula (PPV_REF, NPV_REF). 3) Bayesian estimates were defined as the post-test probability estimates calculated based on each student's intuitive estimates of sensitivity, specificity, and pre-test probability, by using Bayes' formula (PPV_BAY, NPV_BAY).

The difference between the intuitive and the reference estimate of sensitivity and specificity (Se_INT− Se_REF, Sp_INT− Sp_REF) reflects the accuracy of knowledge on test characteristics. The difference between the intuitive and reference estimate of pre-test probability (preProb_INT− preProb_REF) reflects the ability to estimate the pre-test probability of the disease from the available clinical history. The difference between the intuitive and reference estimates of post-test probability (PPV_INT− PPV_REF, NPV_INT− NPV_REF) reflects overall diagnostic ability. The difference between the intuitive and Bayesian estimates of post-test probability (PPV_INT− PPV_BAY, NPV_INT− NPV_BAY) reflects the ability to estimate post-test probability from pre-test probability and the test characteristics. Thus, the smaller the differences are, the higher ability the student has.

To calculate the contribution of post-test probability to the students' decision to start therapy, we used logistic-regression analysis.⁵ The dichotomized answer to the question whether to start medical therapy for angina pectoris (i.e., starting or not starting a medical therapy) was regressed to post-test probability estimated by students (PPV_INT or NPV_INT). In this model, a positive β coefficient means that there is a positive association between post-test probability and the action of starting a therapy.

To test the hypothesis that there is no difference in students' estimates distribution among 3 medical schools, we used the Kruskal-Wallis test. Summary measures of probability estimates were expressed as means ± SEM. Statistical significance of difference in probability estimates was checked by Student's t test. Statistical analysis was performed using STATA statistical software (Intercooled Stata for Windows95/98/NT, edition 6.0; Stata Corp., College Station, Tex).

RESULTS

Two hundred twenty-four medical students answered the questionnaire. Demographic information on the subject students in 3 medical schools is presented in Table 3. The characteristics of the students in 3 medical schools were similar, but confidence in their understanding of Bayesian diagnostic thinking was substantially different among schools. Although a significant difference in means of students' estimates among schools was observed for some questions, the difference was not systematic and not associated with a particular school. Therefore, the results for all 3 schools were aggregated.

Table 3.

Demographic Information of Subject Students

		Medical School
	Total	A	B	C
Number of students	224	92	71	61
Female, %	22.8	7.6	33.8	32.8
Mean age ± SEM	23.5 ± 2.8	23.8 ± 2.0	23.9 ± 4.2	22.6 ± 0.8
Average response rate, %	97.2	98.0	95.8	99.2
Confidence in understanding of Bayesian thinking, % yes	14.3	22.8	5.6	11.5

The difference between reference and intuitive estimates of sensitivity for EST (Se_INT− Se_REF) was −2.8%± 1.5% (P < .05), and that between reference and intuitive estimates of specificity (Sp_INT− Sp_REF) was −21.1%± 2.0% (P < .01). Thus, the associated error in estimating specificity was larger than that in estimating sensitivity.

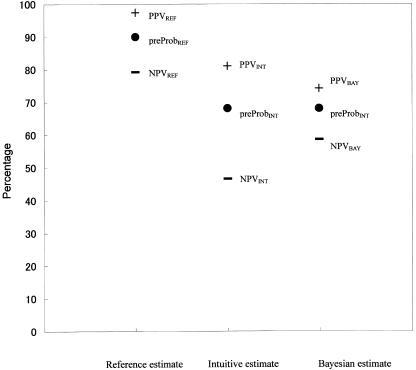
The relationships among reference, intuitive, and Bayesian estimates for each scenario are schematized in the Figures.

For typical angina (Case 1, Fig. 1), the intuitive estimate of pre-test probability was much lower than the reference estimate (preProb_INT = 68.1%± 1.3% vs preProb_REF = 90%, difference = −21.9%± 1.3% [P < .01]), and subsequently intuitive estimates of post-test probability were underestimated (PPV_INT = 81.1%± 1.2% vs PPV_REF = 97.5%, difference = −16.4%± 1.2% [P < .01]; NPV_INT = 46.6%± 1.8% vs NPV_REF = 79.2%, difference = −32.6.6%± 1.8% [P < .01]). The intuitive estimates of post-test probability were more exaggerated than Bayesian estimates (PPV_INT = 81.1%± 1.2% vs PPV_BAY = 74.2%± 1.7%, difference = −6.8%± 1.3% [P < .01]; NPV_INT = 46.6%± 1.8% vs NPV_BAY = 58.6%± 1.6%, difference = −11.9%± 2.1% [P < .01]); consequently, the usefulness of EST was overestimated. This overestimation of the EST effect was more conspicuous when the test result was negative, resulting in underestimated NPV_INT. In the setting of typical angina with a positive EST result, the associated error between the intuitive estimate and the reference estimate was relatively small. This finding indicates that students can rule in the diagnosis when a patient presents typical symptoms of effort angina in conjunction with positive test results.

Figure 1.

Estimates and errors in Case Scenario 1 (typical anginal pain). The first column represents reference estimates of pre-test probability, PPV, and NPV. The second column represents intuitive estimates of pre-test probability, PPV, and NPV. The third column represents intuitive estimate of pre-test probability and Bayesian estimates of post-test probability. Makers •, +, – represent pre-test probability, positive predictive value (PPV), and negative predictive value (NPV), respectively. The estimate of probabilities is displayed as a percentage. The difference between pre-test probability and PPV/NPV (PPV − preProb or NPV − preProb) represents a change of disease likelihood provided by test result. The difference between the intuitive and reference estimates of pre-test probability (preProb_INT− preProb_REF) is associated with the ability to estimate the pre-test probability of the disease from the available clinical history. The difference between the intuitive and reference estimates of post-test probability (PPV_INT− PPV_REF, NPV_INT− NPV_REF) is associated with overall diagnostic ability. The difference between the intuitive and Bayesian estimates of post-test probability (PPV_INT− PPV_BAY, NPV_INT− NPV_BAY) is associated with the ability to estimate post-test probability from pre-test probability and the test characteristics. The closer to 0 the error is, the higher the ability is.

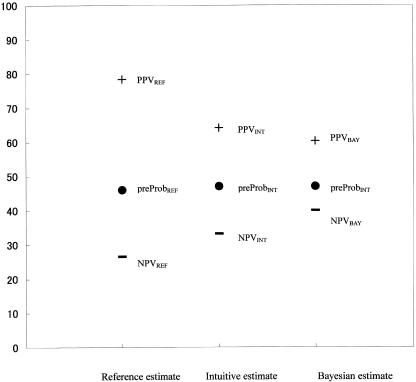
For atypical chest pain (Case 2, Fig. 2), the intuitive estimate of pre-test probability was almost appropriate (preProb_INT = 47.1%± 1.6% vs preProb_REF = 46%, difference = 1.1%± 1.6% [P = .51]). However, the intuitive estimates of post-test probability were more conservative than the reference estimates (PPV_INT = 64.2%± 1.6% vs PPV_REF = 78.4%, difference = −14.2%± 1.6% [P < .01]; NPV_INT = 33.2%± 1.7% vs NPV_REF = 26.5%, difference = 6.7%± 1.7% [P < .01]). The intuitive estimates of PPV were appropriate (PPV_INT = 64.2%± 1.6% vs PPV_BAY = 60.3%± 2.0%, difference = 2.0%± 1.7% [P = .23]), but those of NPV were exaggerated compared to Bayesian estimates (NPV_INT = 33.2%± 1.7% vs NPV_BAY = 40.0%± 1.9%, difference = 7.0%± 1.9% [P < .01]). It was inferred that the students' difficulty lay in applying Bayes' theorem to the clinical situation in this setting.

Figure 2.

Estimates and errors in Case Scenario 2 (atypical anginal pain). See also the legend for Figure 1.

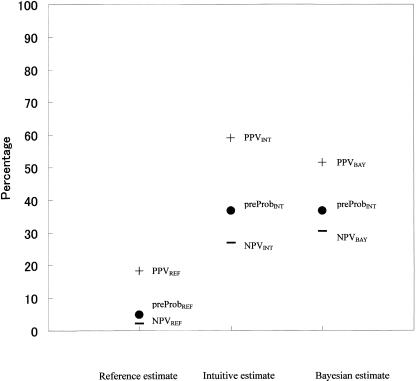
Finally, for non-anginal chest pain (Case 3, Fig. 3), the intuitive estimates of the pre-test probability and post-test probability showed gross deviations toward overestimating from the reference estimates (preProb_INT = 36.7%± 1.5% vs preProb_REF = 5%, difference = 31.7%± 1.5% [P < .01]; PPV_INT = 59.0%± 1.5% vs PPV_REF = 18.3%, difference = 40.7%± 1.5% [P < .01]; NPV_INT = 26.8%± 1.5% vs NPV_REF = 2.2%, difference = 24.6%± 1.5% [P < .01]). This finding suggests that students cannot effectively rule out ischemic heart disease when a patient presents with non-anginal chest pain regardless of the test results. The intuitive estimates of post-test probability were more exaggerated than the Bayesian estimates (PPV_INT = 59.0%± 1.5% vs PPV_BAY = 51.5%± 1.9%, difference = −7.4%± 1.6% [P < .01]; NPV_INT = 26.8%± 1.5% vs NPV_BAY = 30.5%± 1.7%, difference = 3.8%± 1.8% [P < .05]); and the usefulness of EST was overestimated. The overestimation was larger when the EST was positive (PPV_BAY− preProb_INT). This observation indicates that students were easily confused by test results that differed from their anticipated results.

Figure 3.

Estimates and errors in Case Scenario 3 (non-anginal chest pain). See also the legend for Figure 1.

For decision questions, 117 students (52.2%) answered that the patient with typical anginal pain should be treated in spite of a negative EST result, 101 students (45.1%) provided the opposite answer, and 6 students (2.7%) did not respond. One hundred forty-four students (64.3%) recommended no therapeutic action for the patient with atypical chest pain and a positive EST, 69 students (30.8%) answered the opposite, and 11 students (4.9%) provided no answer. The β-coefficient of the logistic regression model was 0.02 (P < .01) for decision question 1 and 0.05 (P < .01) for decision question 2. Thus, in both situations, the association between the post-test probability and the decision to start therapy is positive, which means that the higher the post-test probability a student estimates, the more likely he/she is to consider starting therapy.

DISCUSSION

The formal diagnostic thinking process in clinical epidemiology is divided into 3 stages: 1) hypothesis generation of possible diagnoses; 2) estimation of pre-test probability; and 3) interpretation of test results, i.e., revision of pre-test probability by test results to obtain post-test probability. When the post-test probability of a diagnostic hypothesis exceeds the action threshold for a specific treatment, a physician starts the treatment (rule in). When negative test results decrease the post-test probability low enough to refute the hypothesis, the physician stops further examination or therapeutic action (rule out) and starts to assess the next diagnostic hypothesis.⁶

In an earlier study, Lyman and Balducci⁷ assessed the effect of test results on the estimation of disease likelihood using hypothetical scenarios involving a common clinical situation. Hypothetical patients with a breast lump were presented to physicians and nonphysicians, and estimates of the pre-test and post-test probability of breast cancer and mammography sensitivity and specificity were elicited. The subjects consistently overestimated the disease likelihood associated with a positive test result compared to the probabilities derived from Bayes' theorem based on the subjects' estimates of pre-test probabilities and the test characteristics, in contrast to that associated with negative test results.

The most remarkable findings in our study were as follows: medical students could not rule out disease efficiently in low or intermediate pre-test disease likelihood settings; and they were easily confused by test results that differed from those anticipated. The former flaw was mainly due to poor estimations of pre-test probability of the disease. Students failed to lower the pre-test probability on the basis of the information derived from the clinical scenario. The latter flaw indicates that medical students are not proficient in applying Bayes' theorem to real clinical situations. These diagnostic thinking patterns account for medical students or novice physicians sometimes repeating inadequate or unnecessary examinations.

Some explanations can be given for students' inaccuracy in estimating pre-test probabilities of disease on the basis of clinical information. First, psychological research has found that in a variety scientific problem-solving situations, people have a preference for confirming strategies over disconfirming strategies, although logically, disconfirmation is more conclusive and potentially efficient.^8,9Confirming strategy refers to the search for or the use of evidence to prove a hypothesis, whereas disconfirming strategy refers to the search for or the use of evidence to rule out or reduce the probability of a given hypothesis. The confirming strategy approach supports a “rule in” rather than a “rule out” thinking process. It has also been found that the number of hypotheses that are generated affects the use of confirmation or disconfirmation strategies. When subjects were instructed to consider a single hypothesis, they showed a preference for a “confirming” strategy, but when instructed to consider several hypotheses, they tended to use a “disconfirming” strategy.¹⁰ Because students were presented a single diagnostic hypothesis (i.e., coronary artery disease) and requested to estimate the probability of the hypothesis, they might have preferred gathering information for confirming or ruling in to disconfirming or ruling out the diagnostic hypothesis.

Second, it has been pointed out that physicians often fail to understand the importance of negative information.¹¹ This tendency may be related to the traditional medical education, i.e., focusing on acquiring basic science/medical knowledge in the framework of a biomedical model. In fact, teachers or textbooks often emphasize information on abnormal findings, not the significance of normal findings. Ruling out disease is also less emphasized than the importance of not overlooking a possible disease.

The most important criticism of this study is the assumption of students' Bayesian probabilistic thinking process. Although we modeled the students' diagnostic thinking process according to the Bayesian perspective, the Bayesian thinking process is not a native thinking process but is acquired only by education, and students may not think consistently in the Bayesian perspective.¹² To verify whether the students' diagnostic thinking process was independent from the Bayesian perspective, we analyzed the association between the post-test probability estimated by the student and his/her decision to take a therapeutic action. The result (i.e., the higher the post-test probability, the more likely the student was to initiate therapy) suggests that medical students, at least in part, think in accordance with the Bayesian perspective.

The fact that subject students had little clinical experience is another limitation of this study. It might hamper generalization of the results of this study to medical learners in more advanced stages.

One of the most important tasks in primary care is ruling out the possibilities of serious diseases on the basis of history and physical examination. In this study, medical students could not rule out disease in low or intermediate pre-test probability settings, mainly because of poor pre-test estimates of disease probability. They were also easily confused by test results that were not in agreement with those anticipated, probably because of their inaptitude in applying Bayes' theorem to real clinical situations. It is clear that the students' diagnostic thinking process presented here cannot deal optimally with these needs.

In conclusion, medical students' diagnostic abilities are likely to be enhanced by: 1) emphasizing the importance of ruling out disease in clinical practice; 2) training to estimate pre-test probability of disease on the basis of history and physical examination; and 3) incorporating the Bayesian probabilistic perspective and the application of the theory to real clinical situations.

APPENDIX A

Definitions of Parameters Used in the Article

1. Intuitive estimates

SeINT, SpINT: Intuitive estimate of sensitivity and specificity, sensitivity, specificity, estimates provided by the students

preProbINT: Intuitive estimate of pre-test probability, pre-test probability estimates provided by the students

PPVINT: Intuitive estimate of positive predictive value, post-test probability estimates provided by the students for positive EST result

NPVINT: Intuitive estimate of negative predictive value, post-test probability estimates provided by the students for negative EST result

2. Reference estimates

SeREF, SpREF, preProbREF: sensitivity, specificity, and pretest probability obtained from literature

PPVREF, NPVREF: PPV and NPV calculated by substituting reference estimates of sensitivity, specificity, and pretest probability into Bayes' formula

3. Bayesian estimates of PPV and NPV

PPVBAY, NPVBAY: PPV and NPV calculated based on each student's intuitive estimates of sensitivity, specificity, and pretest probability and Bayes' theorem