Skip to main content
PMC home page
Nucleic Acids Research logoLink to Nucleic Acids Research
. 2003 Mar 1;31(5):1497–1501. doi: 10.1093/nar/gkg231

Comparing the fine specificity of DNA binding by NF-κB p50 and p52 using principal coordinates analysis

Anastasia Nijnik 1, Richard Mott 1, Dominic P Kwiatkowski 1,2, Irina A Udalova 1,a
PMCID: PMC149824  PMID: 12595558

Abstract

Principal coordinates analysis has been proposed as an efficient way of predicting the binding affinity of a transcription factor to different DNA motifs, as it can model complex interactions that are difficult to represent with standard position-weight matrices. Here we evaluate its ability to distinguish the DNA binding properties of two closely related proteins, the homodimeric forms of NF-κB p50 and p52. When tested experimentally against 50 different variants of the generalised NF-κB motif GGRRNNYYCC, the binding specificities of p50 and p52 were similar but not identical (correlation ρ = 0.86). These experimental data can be modelled accurately with six principal coordinates that are similar for p50 and p52, plus one principal coordinate that is significantly stronger for p52 than for p50, relating to the inner positions of the binding site. These findings are compatible with crystallographic data showing that p52 has greater ability than p50 to form water molecule-mediated hydrogen bonds with inner nucleotide positions of the binding site.

INTRODUCTION

Polymorphisms within transcription factor binding sites are not uncommon, and in some cases cause quantitative variation in gene expression and hence subtly affect phenotypes of medical importance such as disease susceptibility. However, in general, it is not known how each of these polymorphisms affects the binding of the transcription factor in question. Such an analysis requires both quantitative binding data together with an accurate statistical model to predict the effect of polymorphisms. Information of this sort might greatly assist our efforts to identify, out of the millions of non-coding polymorphisms that exist throughout the human genome, those that are most likely to have a functional impact on gene regulation.

The traditional way of predicting whether any given DNA sequence will bind a given transcription factor is to use a statistical model based on a position-weight matrix, in which each position within the binding site is assumed to act independently (1–3). Interactions between base pair positions are ignored. Although in many cases profiles provide a good approximation of the nature of the protein–DNA interactions (4), they do not generally provide a perfect fit for the data. There is now a need to develop models that can test if interactions are present, and if necessary to improve prediction accuracy. Two such methods have been published recently, one used a hidden Markov model approach (5), another, a principal coordinates model (6).

The principal coordinates approach has several attractions. First, only a relatively small subset of potential binding sites needs to be assayed in order to generate accurate predictions for the remainder. Second, the number of parameters estimated is small, which in general makes a more stable predictor. The model is constructed for a given set of DNA sequences by using a projection into a high-dimension Euclidean space. Each sequence is represented as a point in that space, and the Euclidean distance between two points is a close approximation to the differences in base pairs between the corresponding sequences. The binding affinity of the transcription factor to different DNA sequences is modelled as a function of these spatial coordinates, and statistical analysis is then performed to identify the principal coordinates (i.e. those axes of the Euclidean space) that are the major predictors of binding affinity. When a principal coordinates model is developed for a given transcription factor, it allows for quantitative prediction of its affinity to any given DNA sequence in the consensus space, and automatically incorporates the effects of interactions between base pair positions in the binding site.

An important test of the principal coordinates model is whether it is able to distinguish the DNA binding specificity of different proteins belonging to the same family of transcription factors. To address this question, we here compare the binding patterns of the homodimeric forms of p50 and p52, which are structurally similar members of the NF-κB family. Crystallographic data suggest that the critical structural difference between p50 and p52 lies largely in one amino acid, Tyr285 in loop de of the C-terminal region of p52 Rel homology domain (RHD), which can form water-mediated interactions with the central residues of the DNA binding site (7–9). The equivalent Phe310 residue in p50 cannot form such interactions. Small differences in the DNA binding properties of p50 and p52 could be of some functional importance at the cellular level, as two homodimers are downstream of separate signal transduction cascades (10–12), and may activate different subsets of genes. The goal of this study was to determine whether the principal coordinates model is able to detect a minor difference in the DNA binding properties of homodimeric p50 and p52 and, if so, how this relates to the existing structural data.

MATERIALS AND METHODS

DNA constructs

p50 expression construct was previously described (13). The protein sequence corresponding to amino acids 1–332 of human p52 were recovered by RT–PCR using the appropriate primers and total cDNA derived from Mono Mac 6 cells. cDNA was cloned into BamHI/XhoI sites of the pET32a(–) bacterial expression vector (Novagen). All constructs were verified by DNA sequencing.

Protein expression and purification

BL21 cells were grown at 37°C to an OD600 of 0.4, induced with 0.1 mM isopropyl-1-thio-β-d-galactopyranoside (IPTG) (Sigma) and shaken at 30°C overnight. Cells were harvested by centrifugation at 5000 g at 4°C for 20 min, lysed and nickel-affinity purification was performed according to Protein Mini-Prep Under Native Conditions protocol (Novagen) with 125 mM imidazole elution buffer. Concen tration and purity of recombinant proteins was assessed on 10% SDS–PAGE gel against a full-range rainbow marker (Amersham Pharmacia Biotech, Little Chalfont, UK) using Coomassie SimplyBlue stain (Invitrogen).

Binding assays

Standardised oligonucleotide probes (e.g. F, 5′-agctGG GGTTCCCC-3′; R, 5′-agctGGGGAACCCC-3′) were radiolabelled with [α-32P]dCTP (Amersham Pharmacia Biotech). Labelled probe (0.2–0.5 ng) (1–5 × 104 c.p.m.) was used in the binding reaction that contained 12 mM HEPES, pH 7.8, 80–100 mM KCl, 1 mM EDTA, 1 mM EGTA, 12% glycerol, 0.2 µg of BSA, 0.5 µg of poly(dI–dC) (Amersham Pharmacia Biotech) and 10–50 ng of recombinant protein. The reaction was analysed by non-denaturing 5% PAGE at 4°C. Gels were quantified using Cyclone PhosphorImager and OptiQuant software (Packard Co.).

Principal coordinates model

The principal coordinates model is described in detail in Udalova et al. (6). In brief, the model predicts the binding affinities of all 256 sequences matching the generalised NF-κB consensus GGRRNNYYCC from observations on a subset of 50 sequences, chosen so the remainder are not more than one nucleotide difference away from at least one of the 50. Metric scaling was used to map the DNA sequences as points in a Euclidean space, such that the distance between the points representing any pair of sequences approximated to their sequence dissimilarity. The axes in the space are termed principal coordinates. We found that a 10-dimensional subspace explained almost 90% of the sequence variance between the sites, with 10 additional principal coordinates cumulatively accounting for the remaining 10% of the variance. The four first principal coordinates explain 50% of the variance.

As in Udalova et al. (6), the logarithm of binding affinity yi is modelled by least-squares linear regression on the m largest principal coordinates containing most of the variance between the sequences:

log yi = µi + Σk ≤ m xikbk + ei.1

The term µi is a factor that models the experimental gel effect. It is represented in the regression design matrix by eight columns corresponding to the eight gels, constrained such that only the element in the column corresponding to that observation’s gel is non-zero. b is a vector of coefficients, and ei is the residual error. The columns (principal coordinates) of the matrix xik are orthogonal, so the least-squares estimates of the bk are uncorrelated.

The significant coefficients identify principal coordinates that influence binding affinity, while non-significant coefficients indicate where the consensus can vary without affecting binding. To investigate the differences between p50p50 and p52p52, we augmented equation 1 by including a term proportional to log p50p50:

(log p52p52)i = (log p50p50)i + µi + Σk ≤ m xikbk + ei.2

The estimates of the coefficients bk now indicate which principal coordinates differ between the two dimers.

The predicted affinity of each sequence was expressed relative to the affinity of sequence GGGGTTCCCC (also used as an experimental control on each gel) and ranked as percentiles, from 0 (weakest) to 1 (strongest). Cross-validation was used to verify the accuracy of the model.

RESULTS

Variation in NF-κB p52p52 and p50p50 binding affinity

In this study, the original NF-κB consensus GGGRNYYYCC (9) was further generalised by introducing variation (G/A) at position 3 and N at position 6, resulting in a fully palindromic representation of the binding site. This generalised consensus generates 256 variant motifs (e.g. GGAAAATTCC, GGG AAATTCC, etc.), 50 of which were analysed by EMSA for binding affinity to the recombinant p50p50 and p52p52 homodimers. The selection of 50 experimental sequences was such that each of the putative 256 NF-κB binding sites differs by no more than one nucleotide change from one of the experimental sequences (or its reverse complement) (see Materials and Methods). All measurements were repeated twice. As a standard, the control oligonucleotide GGGGTTC CCC was ran on each gel (Table S1, Supplementary Material).

The selected sequences covered a very wide range of p52p52 and p50p50 affinities (Fig. 1). EMSA measurements were reproducible and we observed >500-fold difference in binding among the sites for both dimers.

Figure 1.

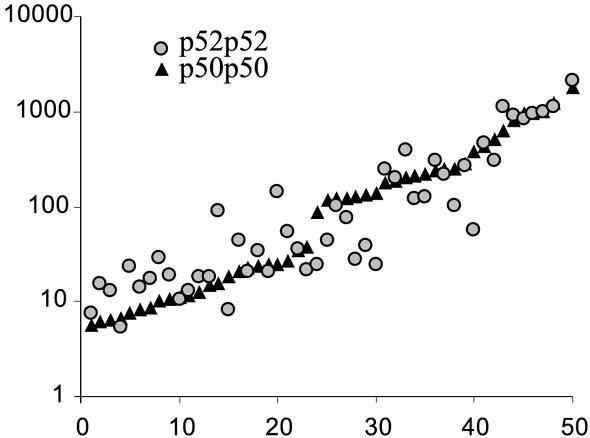
Figure 1

Open in a new tab

p50p50 and p52p52 binding affinities for 50 variants of GGRRNNYYCC motif. The data for both p50p50 and p52p52 homodimers are the geometric means of two independent measurements. The sequences are sorted along the x-axis by their binding affinity to p50p50. p50p50 binding data are from Udalova et al. (6).

Principal coordinate models for predicting binding affinities of p52 and p50 homodimers

The principal coordinate model described in Udalova et al. (6) was fitted to the p50 and p52 homodimer binding data. The 10 largest principal coordinates explained 88% of the variance of the GGRRNNYYCC sequence space. The model was fitted to the logarithms of data for p52p52 binding, consisting of the duplicated observations for each assayed sequence, with extra terms included to account for between-gel effects. Seven principal coordinates out of 10 in the regression had significant coefficients (P-value < 0.05), explaining 87% of total binding variance. In comparison, only six out of 10 coefficients, PC3 excluded, were significant for p50p50 binding (Table 1). The significant coefficients identify principal coordinates that influence binding affinity, while non-significant coefficients indicate where the consensus can vary without affecting binding.

Table 1. Comparison of principal coordinate models for quantitative prediction of DNA binding specificity of p50 and p52 homodimers.

Coordinate p50p50     p52p52    
  bp50p50 SE P-value bp52p52 SE P-value
1 1.5729 0.1496 <1.0E–05 0.8849 0.1692 <1.0E–05
2 –1.8132 0.1721 <1.0E–05 –1.5876 0.1957 <1.0E–05
3     NS 0.7820 0.2478 2.0E–03
4 –0.8899 0.2072 <1.0E–05 –0.7592 0.2443 3.0E–03
5     NS     NS
6 2.0165 0.2679 <1.0E–05 2.4773 0.3277 <1.0E–05
7     NS     NS
8 1.2460 0.3125 1.0E–04 1.1590 0.3708 2.5E–03
9     NS     NS
10 –1.3437 0.3865 8.0E–03 –1.6558 0.4349 3.0E–04
Open in a new tab

Logarithms of p50p50 and p52p52 binding data were fitted to a model comprising the orthogonal principal coordinates of the metric scaling projection of 50 oligonucleotides together with terms for inter-gel effects (data not shown): regression coefficients b, standard errors (SE) and P-values. p50p50 data are from Udalova et al. (6). NS, non-significant coefficient.

In addition, we generated p52p52 binding affinity predictions for all 256 variants of the GGRRNNYYCC consensus sequence (Table S2, Supplementary Material). Predictions for p50 homodimer are described elsewhere (6).

Differences between p52p52 and p50p50

When experimental data were statistically analysed, we found a highly significant correlation between the affinities of two homodimers (ρ = 0.86, P < 0.01) (Fig. 1). But we also noticed sequences that showed stronger binding preferences for one of the homodimers (e.g. GGAACGTCCC bound approximately five times better to p52p52, and GGGGGCTCCC approximately six times better to p50p50).

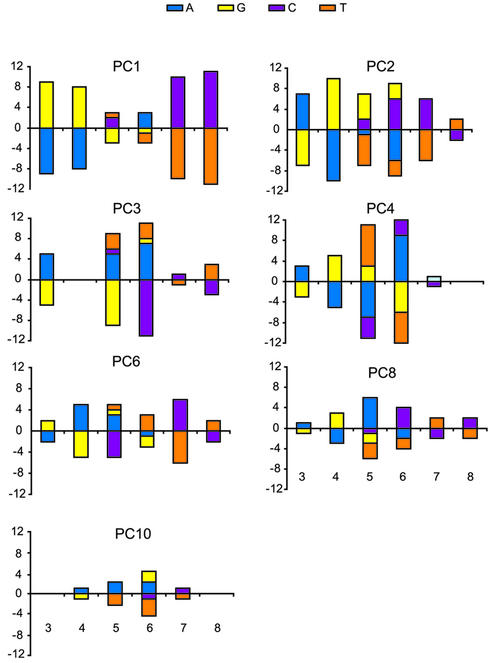
Next we analysed the regression coefficients in Table 1. Despite the fact that the regression coefficients for p52 and p50 homodimers were broadly similar in sign and magnitude, there were systematic differences in binding affinity between the two dimers. Principal coordinate PC3 was only significant for p52p52. Moreover, when we regressed p52p52 on p50p50 binding data as well as on the principal coordinates and terms modelling inter-gel effects, to remove common features, PC3 (P < 0.005) and PC6 (P < 0.0013) were the only principal coordinates that remained significant (Table 2). This analysis was more sensitive that the comparison of the two independent regressions because more variance (93 versus 87%) was explained in the latter model, thus the difference between the dimers for PC6 became detectable. Both coordinates PC3 and PC6 mainly involve variation at the inner core positions 5 and 6, although PC6 also extends over the positions 4–7 (Fig. 2).

Table 2. Principal coordinates model regression coefficients.

Coordinate p52p52/p50p50    
  bp52p52/p50p50 SE P-value
1 –0.0213 0.1806         0.9065
2 –0.3836 0.2242 0.0912
3 0.5604 0.1935 0.0050
4 –0.0680 0.2111 0.7481
5 0.3239 0.2174 0.1404
6 1.0636 0.3191 0.0013
7 0.1757 0.2518 0.4875
8 0.3551 0.3067 0.2506
9 0.2235 0.3237 0.4919
10 –0.5498 0.3684 0.1399
Open in a new tab

p52p52 binding data were regressed on p50p50 binding data and principal coordinates and terms modelling the inter-gel effects: regression coefficients b, standard errors (SE) and P-values.

Figure 2.

Figure 2

Open in a new tab

Sequence characteristics of seven major principal coordinates significant for p52 homodimer. PC3 is significant for p52p52 complex only. PC6 contributes to both p50p50 and p52p52 binding, but significantly more to p52p52. For each principal coordinate, sequences were sorted along the coordinate and the mean base frequencies were computed for the top and bottom quartiles at each variable position of the NF-κB site. For example, for position 4 in PC3, top quartile sequences had eight As, two Gs and no Cs or Ts, whereas bottom quartile sequences had one A, one G, 11 Cs and no Ts. The result of subtracting sequence composition from the top and bottom quartiles (A = 7, G = 1, C = –11, T = 0) is plotted. The sequence characteristics of coordinates PC1–PC4 were identical to those reported in Udalova et al. (6).

DISCUSSION

This study demonstrates the sensitivity of the principal coordinates method to subtle differences in binding specificity of homologous transcription factors. Although the binding affinities of p50p50 and p52p52 are highly correlated (ρ = 0.86, P < 0.01), differences in binding affinity of p50p50 and p52p52 to natural enhancer sequences have been reported (14). When the principal coordinates models for p50p50 and p52p52 were compared (Table 1), the regression coefficients of the logarithm of binding affinity on PC3 was found to be significant for p52p52 but not for p50p50. As PC3 is mainly determined by the inner core positions 5 and 6 of the binding site (Fig. 2), this identifies a systematic difference in the pattern of binding of p50p50 and p52p52 to DNA. Interestingly, principal coordinate PC6, which defines a certain combination of the positions 4, 5, 6 and 7, was significant for both homodimers but had more impact on the p52p52 binding.

Comparison of principal coordinates models for p50p50 and p52p52 suggests that inner positions of the binding site determine the difference in DNA binding specificity of the two factors. This is in agreement with predictions made from crystallographic structures of these proteins bound to DNA (7) and with systematic structure-based modelling of protein– DNA interactions using the same subset of DNA sequence variants as in this study (M.Totrov, personal communication). The structures show that a large water cavity is located between the major groove at the centre of the binding site and the dimer interface formed by the C-terminal regions of RHD of the two NF-κB subunits. In the p52p52–DNA complex, water molecules establish a network of hydrogen bonds between loops bc and de of the protein and the inner positions of the binding site. The hydroxyl group of Tyr285 in loop de plays a central role in the maintenance of this network. The equivalent residue in p50p50 is Phe310, which cannot form a water-mediated hydrogen-bonding network. Hence, p50p50 does not form sequence-specific interactions with the inner positions of the binding site.

A number of studies suggest that water-mediated hydrogen bonds can contribute to specificity of protein–DNA interactions. Examples of the role of water in sequence-specific binding include tryptophan repressor (15,16), papilloma E2 protein (17) and Antennapedia homeodomain transcription factor (18). Moreover, variations in water-mediated interactions are suggested to be the cause of the differences in DNA binding specificity within the homeodomain transcription factor family (19). The results of our study are consistent with the crystallographic studies of NF-κB p50 and p52 homodimers, suggesting that NF-κB binding specificities may derive from the specificity of water-mediated hydrogen bonds.

In this study, the training set for the principal coordinates model included 50 sequences, which covered the consensus space of the GGRRNNYYCC motif. Hence, the model only predicts the effect of sequence variation within this motif. However, nucleotides outside this motif may also contribute to the binding affinity (7,9,20). For the principal coordinates method to predict the effect of variations outside the GGRRNNYYCC motif, the number of sequence variants tested experimentally will have to increase to cover the new sequence space.

Such subtle differences in DNA binding properties of the two proteins are likely to result in different subsets of the NF-κB gene being regulated. This is of particular biological relevance, as p50 and p52 have specific biological functions. p52, but not p50, is activated in development of B-cell tolerance to LPS, in rheumatoid synoviocytes and in some forms of cancer (21–24). p52 knockout mice phenotypically are more similar to LTβR–/–, NIK–/– and Bcl3–/– animals than to p50 knockouts (25–29). Moreover, whereas whether the processing of p50 is constitutive or inducible remains in question (30–32), the clear evidence for regulated p52 processing has emerged. LTβ receptor signalling activates NIK, which in turn activates IKKα, leading to p100 phosporylation, ubiquitination and processing by proteasome (10,11).

In summary, we show that the principal coordinates method can differentiate the binding specificities of two highly homologous transcription factors, NF-κB p50 and p52. Consistent with crystallographic data, the model highlighted the importance of the inner core positions for the p52p52 binding. Since the principal coordinates model can be generated for any DNA binding protein, it establishes a new tool for dissecting subtle differences in binding specificities of the transcription factors, with a variable degree of homology in protein structures.

SUPPLEMENTARY MATERIAL

Supplementary Material is available at NAR Online.

[Supplementary Material]
nar_31_5_1497_v2_index.html (873B, html)

REFERENCES

  • 1.Stormo G.D. (2000) DNA binding sites: representation and discovery. Bioinformatics, 16, 16–23. [DOI] [PubMed] [Google Scholar]
  • 2.Benos P.V., Lapedes,A.S. and Stormo,G.D. (2002) Is there a code for protein–DNA recognition? Probab(ilistical)ly. Bioessays, 24, 466–475. [DOI] [PubMed] [Google Scholar]
  • 3.Quandt K., Frech,K., Karas,H., Wingender,E. and Werner,T. (1995) MatInd and MatInspector: new fast and versatile tools for detection of consensus matches in nucleotide sequence data. Nucleic Acids Res., 23, 4878–4884. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Benos P.V., Bulyk,M.L. and Stormo,G.D. (2002) Additivity in protein–DNA interactions: how good an approximation is it? Nucleic Acids Res., 30, 4442–4451. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Bulyk M.L., Johnson,P.L. and Church,G.M. (2002) Nucleotides of transcription factor binding sites exert interdependent effects on the binding affinities of transcription factors. Nucleic Acids Res., 30, 1255–1261. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Udalova I.A., Mott,R., Field,D. and Kwiatkowski,D. (2002) Quantitative prediction of NF-kappa B DNA–protein interactions. Proc. Natl Acad. Sci. USA, 99, 8167–8172. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Cramer P., Larson,C.J., Verdine,G.L. and Muller,C.W. (1997) Structure of the human NF-kappaB p52 homodimer–DNA complex at 2.1 Å resolution. EMBO J., 16, 7078–7090. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Ghosh G., van Duyne,G., Ghosh,S. and Sigler,P.B. (1995) Structure of NF-kappa B p50 homodimer bound to a kappa B site. Nature, 373, 303–310. [DOI] [PubMed] [Google Scholar]
  • 9.Chen F.E. and Ghosh,G. (1999) Regulation of DNA binding by Rel/NF-kappaB transcription factors: structural views. Oncogene, 18, 6845–6852. [DOI] [PubMed] [Google Scholar]
  • 10.Xiao G., Harhaj,E.W. and Sun,S.C. (2001) NF-kappaB-inducing kinase regulates the processing of NF-kappaB2 p100. Mol. Cell, 7, 401–409. [DOI] [PubMed] [Google Scholar]
  • 11.Senftleben U., Cao,Y., Xiao,G., Greten,F.R., Krahn,G., Bonizzi,G., Chen,Y., Hu,Y., Fong,A., Sun,S.C. et al. (2001) Activation by IKKalpha of a second, evolutionary conserved, NF-kappa B signaling pathway. Science, 293, 1495–1499. [DOI] [PubMed] [Google Scholar]
  • 12.Karin M. (1999) How NF-kappaB is activated: the role of the IkappaB kinase (IKK) complex. Oncogene, 18, 6867–6874. [DOI] [PubMed] [Google Scholar]
  • 13.Udalova I.A., Knight,J.C., Vidal,V., Nedospasov,S.A. and Kwiatkowski,D. (1998) Complex NF-kappaB interactions at the distal tumor necrosis factor promoter region in human monocytes. J. Biol. Chem., 273, 21178–21186. [DOI] [PubMed] [Google Scholar]
  • 14.Perkins N.D., Schmid,R.M., Duckett,C.S., Leung,K., Rice,N.R. and Nabel,G.J. (1992) Distinct combinations of NF-kappa B subunits determine the specificity of transcriptional activation. Proc. Natl Acad. Sci. USA, 89, 1529–1533. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Otwinowski Z., Schevitz,R.W., Zhang,R.G., Lawson,C.L., Joachimiak,A., Marmorstein,R.Q., Luisi,B.F. and Sigler,P.B. (1988) Crystal structure of trp repressor/operator complex at atomic resolution. Nature, 335, 321–329. [DOI] [PubMed] [Google Scholar]
  • 16.Joachimiak A., Haran,T.E. and Sigler,P.B. (1994) Mutagenesis supports water mediated recognition in the trp repressor-operator system. EMBO J., 13, 367–372. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Janin J. (1999) Wet and dry interfaces: the role of solvent in protein–protein and protein–DNA recognition. Struct. Fold Des., 7, 277–279. [DOI] [PubMed] [Google Scholar]
  • 18.Billeter M., Qian,Y.Q., Otting,G., Muller,M., Gehring,W. and Wuthrich,K. (1993) Determination of the nuclear magnetic resonance solution structure of an Antennapedia homeodomain–DNA complex. J. Mol. Biol., 234, 1084–1093. [DOI] [PubMed] [Google Scholar]
  • 19.Wilson D.S., Sheng,G., Jun,S. and Desplan,C. (1996) Conservation and diversification in homeodomain–DNA interactions: a comparative genetic analysis. Proc. Natl Acad. Sci. USA, 93, 6886–6891. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Chen Y.Q., Ghosh,S. and Ghosh,G. (1998) A novel DNA recognition mode by the NF-kappa B p65 homodimer. Nature Struct. Biol., 5, 67–73. [DOI] [PubMed] [Google Scholar]
  • 21.Wedel A., Frankenberger,M., Sulski,G., Petersmann,I., Kuprash,D., Nedospasov,S. and Ziegler-Heitbrock,H.W. (1999) Role of p52 (NF-kappaB2) in LPS tolerance in a human B cell line. Biol. Chem., 380, 1193–1199. [DOI] [PubMed] [Google Scholar]
  • 22.Nakazawa M., Ishii,H., Nakamura,H., Yoshino,S.I., Fukamizu,A., Nishioka,K. and Nakajima,T. (2001) NFkappaB2 (p52) promoter activation via Notch signaling pathway in rheumatoid synoviocytes. Int. J. Mol. Med., 7, 31–35. [DOI] [PubMed] [Google Scholar]
  • 23.Ammon C., Mondal,K., Andreesen,R. and Krause,S.W. (2000) Differential expression of the transcription factor NF-kappaB during human mononuclear phagocyte differentiation to macrophages and dendritic cells. Biochem. Biophys. Res. Commun., 268, 99–105. [DOI] [PubMed] [Google Scholar]
  • 24.Cogswell P.C., Guttridge,D.C., Funkhouser,W.K. and Baldwin,A.S.,Jr (2000) Selective activation of NF-kappa B subunits in human breast cancer: potential roles for NF-kappa B2/p52 and for Bcl-3. Oncogene, 19, 1123–1131. [DOI] [PubMed] [Google Scholar]
  • 25.Poljak L., Carlson,L., Cunningham,K., Kosco-Vilbois,M.H. and Siebenlist,U. (1999) Distinct activities of p52/NF-kappa B required for proper secondary lymphoid organ microarchitecture: functions enhanced by Bcl-3. J. Immunol., 163, 6581–6588. [PubMed] [Google Scholar]
  • 26.Yamada T., Mitani,T., Yorita,K., Uchida,D., Matsushima,A., Iwamasa,K., Fujita,S. and Matsumoto,M. (2000) Abnormal immune function of hemopoietic cells from alymphoplasia (aly) mice, a natural strain with mutant NF-kappa B-inducing kinase. J. Immunol., 165, 804–812. [DOI] [PubMed] [Google Scholar]
  • 27.De Togni P., Goellner,J., Ruddle,N.H., Streeter,P.R., Fick,A., Mariathasan,S., Smith,S.C., Carlson,R., Shornick,L.P., Strauss-Schoenberger,J. et al. (1994) Abnormal development of peripheral lymphoid organs in mice deficient in lymphotoxin. Science, 264, 703–707. [DOI] [PubMed] [Google Scholar]
  • 28.Schwarz E.M., Krimpenfort,P., Berns,A. and Verma,I.M. (1997) Immunological defects in mice with a targeted disruption in Bcl-3. Genes Dev., 11, 187–197. [DOI] [PubMed] [Google Scholar]
  • 29.Snapper C.M., Zelazowski,P., Rosas,F.R., Kehry,M.R., Tian,M., Baltimore,D. and Sha,W.C. (1996) B cells from p50/NF-kappa B knockout mice have selective defects in proliferation, differentiation, germ-line CH transcription and Ig class switching. J. Immunol., 156, 183–191. [PubMed] [Google Scholar]
  • 30.Ciechanover A., Gonen,H., Bercovich,B., Cohen,S., Fajerman,I., Israel,A., Mercurio,F., Kahana,C., Schwartz,A.L., Iwai,K. et al. (2001) Mechanisms of ubiquitin-mediated, limited processing of the NF-kappaB1 precursor protein p105. Biochimie, 83, 341–349. [DOI] [PubMed] [Google Scholar]
  • 31.Belich M.P., Salmeron,A., Johnston,L.H. and Ley,S.C. (1999) TPL-2 kinase regulates the proteolysis of the NF-kappaB-inhibitory protein NF-kappaB1 p105. Nature, 397, 363–368. [DOI] [PubMed] [Google Scholar]
  • 32.Dumitru C.D., Ceci,J.D., Tsatsanis,C., Kontoyiannis,D., Stamatakis,K., Lin,J.H., Patriotis,C., Jenkins,N.A., Copeland,N.G., Kollias,G. et al. (2000) TNF-alpha induction by LPS is regulated posttranscriptionally via a Tpl2/ERK-dependent pathway. Cell, 103, 1071–1083. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplementary Material]
nar_31_5_1497_v2_index.html (873B, html)
nar_31_5_1497_v2_1.pdf (34.9KB, pdf)

Articles from Nucleic Acids Research are provided here courtesy of Oxford University Press

RESOURCES