Despite the enormous diversity and complexity of ecological systems, when data for many individuals of many different species are analyzed, there are emergent regularities in the statistical distributions of numerical abundance, spatial dispersion, trophic relations, and species richness, and in bivariate and multivariate relationships among these variables (e.g., refs. 1–3). These empirical macroecological patterns have been known for many decades, but now ecology is beginning to understand the mechanistic processes that produce them. This conceptual unification is being facilitated by two breakthroughs. First, intensive, technology-assisted empirical studies are generating vast quantities of new and better data. Second, theoretical advances are characterizing the interrelationships among ecological phenomena and explaining them in terms of first principles of physics, chemistry, and biology. There is much still to be done, but recent progress is encouraging.
The paper on food webs in this issue of PNAS (4) offers an excellent example of what can be done by using new data to inspire theoretical exploration. Food webs are representations of trophic relationships, network diagrams in which each node represents a species and each line linking two nodes represents one species feeding on another. Food webs are known to exhibit emergent empirical patterns in number of trophic levels (successive nodes in a food chain from green plant producer through herbivore and carnivore to decomposer), number of links per species, and ratios of predators to prey (5–7). Food webs potentially provide the basis for conceptual unification between two major areas of ecological research: (i) biodiversity theory, which endeavors to explain the number of species that coexist within an ecosystem in terms of the interactions of these species with each other and with their nonliving environment; and (ii) metabolic theory, which endeavors to explain the structure and dynamics of ecosystems in terms of the flux, transformation, and storage of energy and materials. To date, however, theoretical progress has been hampered by lack of adequate data. Most food webs that document all of the species provide only qualitative data on who eats whom, whereas most trophic studies that quantify energy and material fluxes lump many species into “trophic levels” or “functional groups.”
The present paper shows how much progress can be made when there are sufficiently detailed high-quality data to provide grist for food web theory. The superb long-term database on the biota of Tuesday Lake, WI, quantifies the trophic relations of all 66 pelagic species from unicellular algae (phytoplankton) through small invertebrates (zooplankton) to fish (8). Data on the abundance, body size, and trophic links of each species allow quite precise estimation of the fluxes and stocks of energy and materials through the ecological community. Such precision is afforded largely by two bodies of theory: (i) physical principles, most notably the laws of thermodynamics and of mass, energy, and stoichiometric balance, that place powerful constraints on the flows and transformations; and (ii) biological principles of allometry that relate the metabolic rates of organisms to body size, allowing the magnitudes of flux, transformation, and storage in each species to be estimated quite accurately from abundance and body mass.
An important question concerns the relationship between abundance and body size.
Cohen et al. (4) use metabolic theory and data from Tuesday Lake to characterize important features of the structure and dynamics of this ecosystem. Much of their emphasis is on “trivariate patterns,” which are summarized in their figure 2 (4). These patterns have the advantage of displaying all of the data, with each species plotted as a separate point and trophic position (phytoplankton, zooplankton, or fish) indicated with a symbol. They focus largely on interrelationships among four variables: (i) trophic level, which they scale in a nonstandard way and refer to as trophic height; (ii) abundance or population density, N; (iii) average body mass, M; and (iv) biomass abundance (B), which is simply M × N. We find these graphs somewhat difficult to interpret, in part because the scales of the axes of figure 2 (4) are not given, and in part because no regression lines or theoretically predicted values for the scalings are plotted. Nevertheless, the patterns are clear. With increasing trophic level, from phytoplankton to zooplankton to fish, body size increases, abundance decreases, and biomass abundance remains relatively invariant. These results, together with the relationships between abundance, body size, and biomass abundance between predators and their prey (figure 4 in ref. 4) are consistent with patterns found by other research groups, most notably by R. H. Peters, H. Cyr, and J. A. Downing (9–11) in comparative studies applying allometric approaches to lake ecosystems. A longstanding problem, to quantify trophic relations of each species, has recently been addressed powerfully by using stable isotopes to characterize trophic level and to relate it to body size in aquatic ecosystems (12, 13).
An important theoretical question concerns the relation between abundance and body size within and across trophic levels, which is addressed in figure 3 (4), plotting body mass as a function of abundance. We quibble with the designation of the axes, in part because allometric convention would plot body mass on the x axis, and in part because body size is indeed the primary independent variable, as many other studies and the authors' multiple regression analysis shows. The negative scaling is clear, and the value of the slope or scaling exponent (−1.21, and therefore close to −3/4 if body mass had been plotted on the x axis) suggests that the Tuesday Lake data (figure 3 in ref. 4) are consistent with energetic invariance (14–16). Because metabolic rate or rate of energy use per species, E, scales as M3/4, if abundance or population density scales as M−3/4, then the rate of energy use per species per unit area scales as M0. This means that each species tends to use energy at an approximately equal rate.
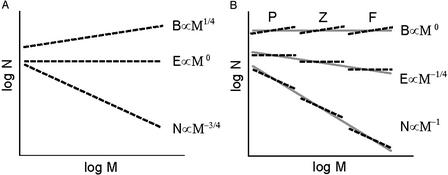
The situation is complicated, however, because energy invariance theoretically applies to the situation when all species use a common source of energy. The species in Tuesday Lake represent three trophic levels, so collectively they use three different sources of energy: sunlight for phytoplankton, phytoplankton for zooplankton, and zooplankton for fish. Due to the second law of thermodynamics, there is a low efficiency of energy transfer, usually thought to be no more than ≈10%, between each successive trophic level. Because the largest organisms are at the highest trophic levels, metabolic scaling theory would predict a steeper scaling than the observed M−3/4. If we assume that between trophic levels the efficiency of energy transfer is 10% and that the average difference in body mass is four orders of magnitude (104), we can predict the scalings for abundance, biomass abundance, and rate of energy use: N ∝ M−1, B ∝ M−1/4, and E ∝ M0 (Fig. 1). This seems to be the pattern commonly observed in pelagic marine ecosystems (17–19). So Tuesday Lake is one of many cases where macroecological data should be reconciled with metabolic scaling theory.
Figure 1.
Relationships of abundance (N), biomass abundance (B), and rate of energy use (E) as functions of body mass (M) predicted by metabolic scaling theory for multiple species within a trophic level (either phytoplankton, zooplankton, or fish) (A) and across three trophic levels [phytoplankton (P), zooplankton (Z), and planktivorous fish (F)] (B). Predicted scalings across trophic levels assume that, between each trophic level, the efficiency of energy transfer is 10% and the difference in average body size increases by four orders of magnitude.
Cohen et al. (4) readily admit that their study is just a first step in relating food web structure and dynamics to the body size, abundance, and other characteristics of the component species. One issue is potential biases in or misinterpretations of the data, perhaps due to artifacts of sampling or seasonal fluctuations. Other challenges are conceptual. To the authors' list of “major tasks” that remain, we would add some items and change the emphasis somewhat. The authors' treatment of the trophic organization of Tuesday Lake treats the fluxes and storage of energy and materials only indirectly, through the currencies of body size, abundance, and trophic relations. The recent development of metabolic scaling theory (20) offers the potential for additional conceptual unification that would explicitly incorporate the flows and standing stocks. Because energy metabolism is such a fundamental biological process, the fluxes of other materials and the vast majority of other biological rates and times vary closely and directly with metabolic rate. The scaling of metabolic rate with body size and temperature appears to be nearly universal across taxa and functional groups of organisms and across geographic regions and kinds of ecosystems (21). These scalings lead directly to predictions that should encourage further interplay between theoretical models and empirical data. One example, mentioned above, is the possible energy invariance across species and trophic levels.
Here is another example. Cohen et al.'s (4) treatment of food webs is still fairly static or structural. Incorporating a more explicit metabolic framework should allow building and testing more dynamic models that predict turnover times within and rates of flow between species or trophic levels. Cohen et al. (4) suggest that dynamics could be introduced by incorporating a Leslie matrix, which would give fertility and longevity coefficients for each species. We agree in principle, but suggest that such detail and precision, which would be difficult to obtain empirically, is not necessary. The life history and demographic characteristics of species are so well correlated with body size that they can be estimated simply and robustly from allometric theory (20).
As ecologists seek conceptual synthesis to understand the mechanistic processes that underlie the increasingly well-characterized empirical patterns, they are developing theories that depict the seemingly infinite variety of nature as variations on a small number of universal themes. They are finding unexpected new interrelationships among seemingly distinct patterns and processes and are explaining these unifying themes and relationships in terms of first principles. This study, applying food web and allometric theory to the detailed data on the body sizes, abundances, and trophic relations of the species inhabiting Tuesday Lake, reveals both the exciting progress that is being made and the substantial challenges that still remain.
Footnotes
See companion article on page 1781.
References
- 1.Williams C B. Patterns in the Balance of Nature and Related Problems in Quantitative Ecology. New York: Academic; 1964. [Google Scholar]
- 2.Brown J H. Macroecology. Chicago: Univ. Chicago Press; 1995. [Google Scholar]
- 3.Gaston K J, Blackburn T M. Pattern and Process in Macroecology. Oxford: Blackwell Science; 2000. [Google Scholar]
- 4.Cohen J E, Jonsson T, Carpenter S R. Proc Natl Acad Sci USA. 2003;100:1781–1786. doi: 10.1073/pnas.232715699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cohen J E, Briand F, Newman C M. Community Food Webs: Data and Theory. Berlin: Springer; 1990. [Google Scholar]
- 6.Martinez N D. Am Nat. 1992;139:1208–1218. [Google Scholar]
- 7.Dunne J A, Williams R J, Martinez N D. Proc Natl Acad Sci USA. 2002;99:12917–12922. doi: 10.1073/pnas.192407699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Jonsson, T., Cohen, J. E. & Carpenter, S. R. (2003) Adv. Ecol. Res., in press.
- 9.Peters R H. Ecological Implications of Body Size. Cambridge, U.K.: Cambridge Univ. Press; 1983. [Google Scholar]
- 10.Cyr H, Downing J A, Peters R H. Oikos. 1997;79:333–346. [Google Scholar]
- 11.Cyr H, Peters R H, Downing J A. Oikos. 1997;80:139–149. [Google Scholar]
- 12.France R, Chandler M, Peters R. Mar Ecol Prog Ser. 1998;174:301–306. [Google Scholar]
- 13.Jennings S, Warr K J, Mackinson S. Mar Ecol Prog Ser. 2002;240:11–20. [Google Scholar]
- 14.Damuth J. Nature. 1981;290:699–700. [Google Scholar]
- 15.Enquist B J, Brown J H, West G B. Nature. 1998;395:163–165. [Google Scholar]
- 16.Li W K W. Nature. 2002;419:154–157. doi: 10.1038/nature00994. [DOI] [PubMed] [Google Scholar]
- 17.Sheldon R W, Prakash A, Sutcliffe W H., Jr Limnol Oceanog. 1972;17:327–340. [Google Scholar]
- 18.Kerr S R, Dickie L M. Biomass Spectrum. New York: Columbia Univ. Press; 2001. [Google Scholar]
- 19.Rinaldo A, Maritan A, Cavender-Bares K K, Chisholm S W. Proc R Soc London Ser B. 2002;269:2051–2059. doi: 10.1098/rspb.2002.2102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Brown, J. H., Gillooly, J. F., West, G. B. & Savage, V. M. in Macroecology: Concepts and Consequences, eds. Blackburn, T. M. & Gaston, K. J. (Blackwell, Oxford), in press.
- 21.Gillooly J F, Brown J H, West G B, Savage V M, Charnov E L. Science. 2001;293:2248–2251. doi: 10.1126/science.1061967. [DOI] [PubMed] [Google Scholar]