Cells lying on a bed of microneedles: An approach to isolate mechanical force

Abstract

We describe an approach to manipulate and measure mechanical interactions between cells and their underlying substrates by using microfabricated arrays of elastomeric, microneedle-like posts. By controlling the geometry of the posts, we varied the compliance of the substrate while holding other surface properties constant. Cells attached to, spread across, and deflected multiple posts. The deflections of the posts occurred independently of neighboring posts and, therefore, directly reported the subcellular distribution of traction forces. We report two classes of force-supporting adhesions that exhibit distinct force–size relationships. Force increased with size of adhesions for adhesions larger than 1 μm², whereas no such correlation existed for smaller adhesions. By controlling cell adhesion on these micromechanical sensors, we showed that cell morphology regulates the magnitude of traction force generated by cells. Cells that were prevented from spreading and flattening against the substrate did not contract in response to stimulation by serum or lysophosphatidic acid, whereas spread cells did. Contractility in the unspread cells was rescued by expression of constitutively active RhoA. Together, these findings demonstrate a coordination of biochemical and mechanical signals to regulate cell adhesion and mechanics, and they introduce the use of arrays of mechanically isolated sensors to manipulate and measure the mechanical interactions of cells.

Mechanical force plays a critical role in the interactions of cells with their surrounding extracellular matrix (ECM). Cell adhesion involves binding and clustering of integrins to ECM ligands (1, 2), active spreading of the cells across the substrate (3, 4), and contraction of the actomyosin cytoskeleton, generating mechanical traction forces at the sites of adhesion (5–7). Although the processes of binding, spreading, and contraction are each well described, little is known about how they are temporally and spatially coordinated, in part because cells use these processes as an integrated mechanochemical sensory system to probe for chemical and mechanical cues within the ECM (8–10). While many tools exist to manipulate the biochemical adhesiveness of experimental substrates, relatively few approaches have been developed to engineer substrate mechanics to study the mechanical forces of cell adhesion. As a result, although mechanical interactions between cells and their substrates clearly direct how cells organize and function in their environment (11–13), our understanding of the biology of traction forces, cell adhesion, and substrate mechanics remains incomplete.

Cells probe the mechanical compliance of the ECM in part by locally deforming it with nanonewton-scale traction forces (14). To study these minute forces, investigators have relied on soft materials such as lightly crosslinked hydrogels or silicone elastomers, where the crosslinking chemistry is used to control mechanical compliance (5–7, 15–19). Attached to appropriately compliant substrates, cells generate deformations that can be tracked by the displacement of beads or microfabricated markers embedded in the substrate; the deformations are then deconvolved to calculate the forces that created them (19, 20). Although important advances have been progressively made in tracking deformations and calculating forces (19, 21, 22), several fundamental limitations remain. Because deformations propagate on these continuous substrates, the calculation of forces is computationally intensive. In addition, the displacements of discrete markers do not fully describe the deformation of the continuous surfaces because of error in the measurement of displacements of individual markers and uncertainty of deformations in the space between markers (20, 23); as a result, the inverse problem of finding a unique solution of forces can be achieved only by placing constraints on the deformation field, the nature of the cellular forces, and/or the location of adhesions (24). Furthermore, manipulating the compliance of the materials by altering bulk chemistry may inadvertently affect surface hydration, chemistry, and adhesiveness (25), making it difficult to isolate the effects of substrate mechanics on cell adhesion and behavior. These limitations are inherent to flat, continuous substrates. One study used a device containing a horizontally mounted cantilever that would deflect along one axis as individual cells migrated across it (26). This method circumvented the computational and materials problem, but could be used only to measure force projected along one axis and generated at one location.

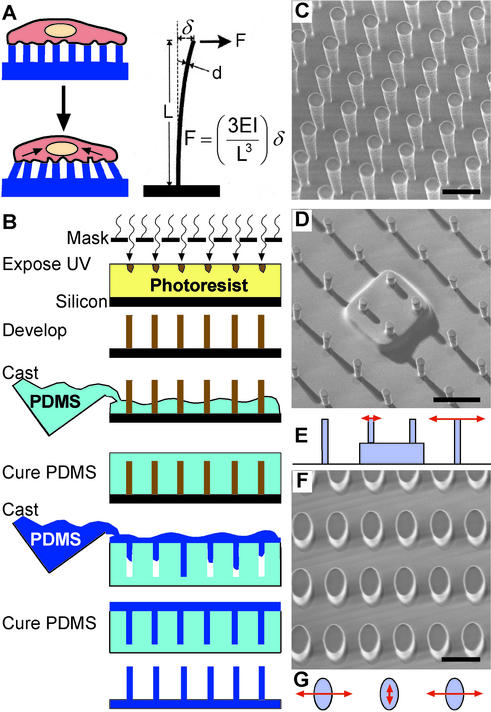
To address these limitations in the design of soft substrates, we present a strategy to independently manipulate mechanical compliance and surface chemistry, to control the spatial presentation of these properties across a surface with micrometer resolution, and to measure traction forces generated by cells at multiple locations. Arrays of closely spaced vertical microneedles (posts) of silicone elastomer were designed to encourage cells to attach and spread across multiple posts, and to bend the posts like vertical cantilevers as the cells probe the surface (Fig. 1A). For small deflections, the posts behave like simple springs such that the deflection is directly proportional to the force applied by the attached cell. This behavior is described for beams composed of linearly elastic material under pure bending by Eq. 1,

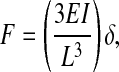1

where F, E, I, L, and δ are the bending force, Young's modulus, moment of inertia, length, and resulting deflection of the post, respectively (27). Thus, changing post geometry will vary post stiffness without altering bulk mechanical properties or surface chemistry of the material used to fabricate the substrate. We call these substrates microfabricated post-array-detectors (mPADs), and describe their development to investigate the mechanical interactions between cells and substrates.

Figure 1.

Fabrication of arrays of posts. (A) With the appropriate surface density of vertical posts positioned on a substrate, a cell should spread across multiple posts as depicted. Under the proper geometric constraints of post height and width, cells exerting traction forces would deflect the elastomeric posts. (B) Schematic drawing of the method used to fabricate posts. (C–G) Scanning electron micrographs of fabricated arrays (C, D, and F) and schematic drawings indicating the compliance of posts (E and G). (C) A uniform array of posts. (D and E) An array of posts whose tips all lie in one plane, but the bases of certain posts are raised with respect to surrounding posts to generate spatially controlled step-increases in substrate stiffness. (F and G) An array of posts with oval cross sections to introduce anisotropic stiffness. Lengths of arrows in E and G indicate the relative magnitude of the deflection with the application of a constant force in the direction of the arrow. (Scale bars indicate 10 μm.)

Materials and Methods

Fabrication and Preparation of mPADs.

mPADs were fabricated by replica-molding (Fig. 1B). To make a template containing an array of holes, prepolymer of poly(dimethylsiloxane) (PDMS; Sylgard 184, Dow-Corning) was poured over an array of SU-8 (Microchem, Newton, MA) posts made on silicon wafers by standard photolithography (28), cured at 65°C overnight, peeled off, oxidized in an air plasma for 1 min [≈200 millitorr (27 Pa); Plasma Prep II, SPI Supplies, West Chester, PA], and silanized with (tridecafluoro-1,1,2,2-tetrahydrooctyl)-1-trichlorosilane (United Chemical Technologies, Bristol, PA) vapor overnight under vacuum to aid subsequent release of PDMS from the template. To make mPADs, prepolymer of PDMS was poured over the template, degassed under vacuum, cured at 110°C for 20 h, and peeled off the template. The substrates were then either immersed for 1 h in 50 μg/ml human fibronectin (BD Biosciences) or printed with ECM protein. For microcontact printing, stamps of PDMS were made as described (29), immersed for 1 h in 50 μg/ml fibronectin or collagen IV (Alexa-488-conjugated; Molecular Probes), washed, blown dry under nitrogen, placed in conformal contact with a surface-oxidized mPADs (7 min in UV ozone cleaner; Jelight, Irvine, CA), and peeled. The substrate was then immersed in 0.1% Pluronic F127 (BASF, Mount Olive, NJ) in PBS for 1 h and washed.

Calibration of mPADs.

Spring constants of pulled glass micropipettes (mTip; World Precision Instruments, Sarasota, FL) were obtained as described previously (30). Briefly, deflection of the tip of a micropipette was measured under the weight of small crystals of p-nitrophenol (Sigma). The mass of the crystal was determined by dissolving it in bicarbonate buffer and diluting until the absorbance of the solution at 400 nm was within the range of a linear absorbance curve generated from solutions containing known concentrations of p-nitrophenol. Calibrated glass micropipettes were then mounted onto a piezoelectric manipulator fitted on a microscope stage. Viewed under a ×100 objective, the tip of the pipette was maneuvered into contact with the top of an individual post. The entire glass pipette was then repeatedly moved various set distances by the piezomanipulator and the deflection of the post in response (1–4 μm) was recorded. The ratio of the deflection of the pipette tip to the deflection of the post equals the ratio of the spring constant of the post to the calibrated spring constant of the pipette.

Measurement of Traction Forces.

The tips of posts were fluorescently stained for fibronectin and visualized with a ×100 objective under confocal microscopy (fixed samples) or were coated with fluorescently labeled collagen IV (Molecular Probes) and visualized with a ×60 objective under fluorescence microscopy (live studies). Bright-field images were used to locate posts not fluorescently labeled. The tips of posts in a field of view, both attached and not attached to cells, were manually assigned coordinates. A regularly spaced grid of coordinates representing the ideal undeflected positions of the posts was formed, minimizing the difference between the assigned coordinates of posts not attached to cells and the ideal grid. Once minimized, the standard deviation of these differences was 0.2 μm for the posts used in this study. To calculate the force on each post, the distance between real and ideal position of the post was multiplied by the spring constant of the post (measured to be 32 nN/μm for the 3-μm-diameter, 11-μm-tall posts used in Figs. 3 and 4). The resolution of force was limited by the deviation of unattached posts from the ideal grid (0.2 μm); thus, we were able to resolve forces greater than 12 nN. The spatial resolution, defined by the periodicity of the post array, was 9 μm.

Figure 3.

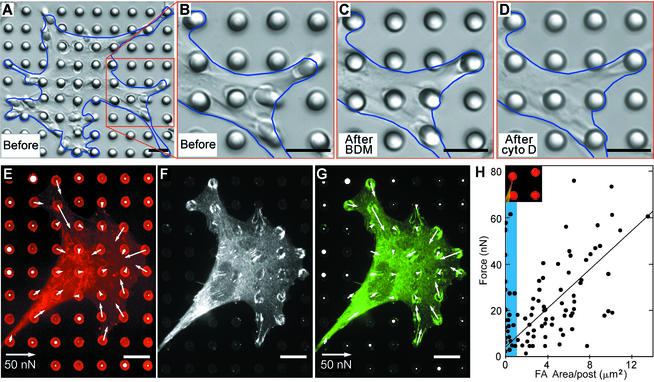
Measurement of contractile forces in cells. (A–D) Differential interference contrast micrographs of a smooth muscle cell (outlined in blue) cultured for 2 h on an array of posts in 10% serum (A and B), 20 min after 20 mM 2,3-butanedione monoxime (BDM) was added to the culture to inhibit myosin contractility (C), and after 2 μg/ml cytochalasin D (cyto D) was added to the same culture for an additional 10 min to disrupt the actin cytoskeleton (D). In each case, longer treatments did not result in additional loss of contractility. (E–G) Confocal images of immunofluorescence staining of a smooth muscle cell on posts. Position of fibronectin (E, red) on the tips of the posts was used to calculate force exerted by cells (white arrows). The force map was spatially correlated to immunofluorescence localization of the focal adhesion protein vinculin (F, white; G, green). A similar correlation in the orientation and the quantity of focal adhesion with the traction forces was observed in all cells examined (n > 10). The lengths of arrows indicate the magnitude of the calculated force (top right arrow indicates 50 nN); white circles on undeflected posts depict the background error in the force measurement, where the diameter of the circle (same length scale as the arrows) indicates the magnitude of calculated force on each post not attached to a cell. (Scale bars indicate 10 μm.) (H) Plot of the force generated on each post as a function of total area of focal adhesion staining per post. Each point represents the force and area of vinculin staining associated with each post; focal adhesions from five cells were analyzed. The shaded region (blue) indicates the adhesions smaller than 1 μm². (Inset) Image of a typical small adhesion (<1 μm²) formed by a cell (green) generating substantial force on a post (red).

Figure 4.

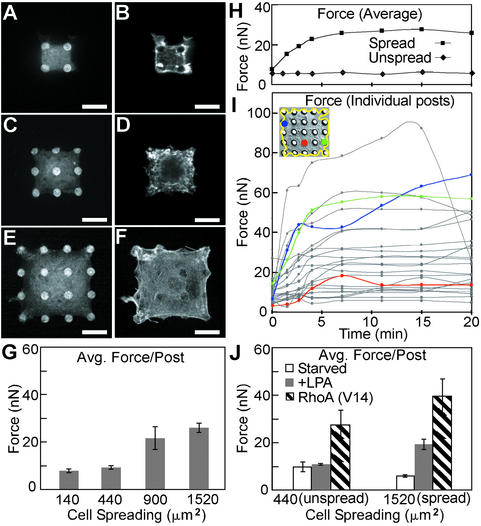
Role of cell spreading in regulating contractile forces. (A–F) Confocal micrographs of smooth muscle cells attached onto different-sized sets of fibronectin-coated posts. Cells attached to 2 × 2 (A and B), 3 × 3 (C and D), or 4 × 4 (E and F) sets of posts were costained for fibronectin (A, C, and E) and filamentous actin (B, D, and F). (Scale bars indicate 10 μm.) (G) Plot of average force generated per post for cells spread to different degrees (140, 440, 900, or 1,520 μm²) on arrays of posts (2 × 2, 3 × 3, 4 × 4, or 5 × 5, respectively) for 20 h in standard culture media. (H) Plot of average force generated per post over time for a cell cultured on either a 5 × 5 (“spread”) or 3 × 3 (“unspread”) set of posts. Cells were serum-starved for 12 h on the posts and were exposed to LPA (10 μg/ml) at time 0. (I) Plot of force exerted on each of the 25 posts over time for the spread cell plotted in H and shown as the Inset. The forces exerted on the posts colored in the Inset are indicated by line plots of the same color. (J) Plot of average force exerted per post for cells cultured on 5 × 5 (spread) or 3 × 3 (unspread) posts and were serum-starved, exposed to LPA for 12 min, or transfected with constitutively active RhoA. A total of 18 cells in G and 25 cells in J were analyzed across three independent experiments; error bars indicate standard error of the mean.

Cell Culture and Reagents.

Bovine pulmonary artery smooth muscle cells (BPASMCs; gift from D. Ingber, Harvard University) and NIH/3T3 mouse fibroblasts (ATCC CRL-1658) were cultured in Dulbecco's modified Eagle's medium (DMEM) containing 2 mM glutamine, 100 units/ml penicillin, and 100 mg/ml streptomycin with 10% calf serum (Life Technologies). Bovine pulmonary artery endothelial cells (BPAECs; VEC Technologies, Rensselaer, NY), were cultured in DMEM with 5% calf serum. BPASMCs were used in all studies; 3T3s and BPAECs were used to confirm results in Figs. 2 and 3 A–D. Lysophosphatidic acid (LPA; Sigma), 2,3-butanedione monoxime (Sigma), and cytochalasin D (Calbiochem) were used as described. The expression construct for pEGFP-RhoA-G14V was mutagenized from pEGFP-WT-RhoA (gift from M. Phillips, New York University). Transfection was carried out by using Lipofectamine (Life Technologies) for 24 h, and transfected cells were enriched by flow cytometry (FACStar, Becton Dickinson); sorted cells were seeded onto mPADs and fixed after 10 h.

Figure 2.

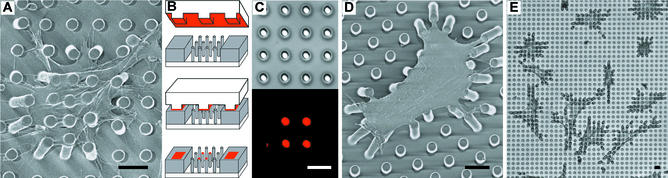
Cell culture on arrays of posts. (A) Scanning electron micrograph of a representative smooth muscle cell attached to an array of posts that was uniformly coated with fibronectin. Cells attached at multiple points along the posts as well as the base of the substrates. (B) Schematic of microcontact printing of protein (red), precoated on a PDMS stamp, onto the tips of the posts (gray). (C) Differential interference contrast (Upper) and immunofluorescence (Lower) micrographs of the same region of posts where a 2 × 2 array of posts has been printed with fibronectin. (D and E) Scanning electron micrograph (D) and phase-contrast micrograph (E) of representative smooth muscle cells attached to posts where only the tips of the posts have been printed with fibronectin by using a flat PDMS stamp. Cells deflected posts maximally during the 1- to 2-h period after plating, were fully spread after 2 h, and were fixed and critical point dried 4 h after plating. (Scale bars indicate 10 μm.)

Immunofluorescence Microscopy and Image Analysis.

Cells were fixed with 4% paraformaldehyde in PBS, rinsed with 10 mM glycine in 0.1% BSA in PBS, permeabilized with 0.1% Triton X-100 in PBS, incubated with antibody against vinculin (Sigma) or fibronectin (ICN, Costa Mesa, CA), and detected with fluorophore-conjugated isotype-specific anti-IgG antibodies (Molecular Probes). Filamentous actin was visualized by incubating samples with fluorophore-conjugated phalloidin (Molecular Probes). Images of focal adhesions were collected by using a ×60 objective on a confocal microscope (UltraView, Perkin–Elmer) with a 2-sec exposure time followed by contrast-enhancement applied equally to all images. Areas of focal adhesions were segmented and measured by using image analysis software (iplab, Scanalytics, Billerica, MA).

Results and Discussion

To fabricate mPADs with stiffnesses relevant for mammalian cells, we micromolded PDMS into arrays of posts from templates generated by photolithography (Fig. 1 B and C). Substrates with posts of different dimensions (2 to 10 μm in diameter and from 3 to 50 μm in height) were made such that the range of stiffnesses of the posts (1,600 to 2.7 nN/μm) would encompass the stiffnesses detectable by cells (16). Substrates were made by using PDMS with a Young's modulus of 2.5 MPa; a flat surface of this material would have an effective stiffness of ≈10,000 nN/μm. The stiffness of the posts calculated with Eq. 1 was similar to experimental measurements obtained by using calibrated glass needles to deflect the posts.

We explored engineering substrates with mechanical properties that are difficult to generate with planar substrates. By varying the heights and therefore the stiffnesses of specific posts within an array, we defined spatial changes in local substrate stiffness (Fig. 1D). Because the stiffness of posts varies as the inverse cube of their height, decreasing the height by half caused a local change in stiffness by 8-fold (Fig. 1E). By using geometric anisotropy we generated mechanical anisotropy in the substrate, creating oval posts that required 8 times more force to deflect along the long axis than along the short axis (Fig. 1 F and G). Thus, geometric parameters, which are easily defined by our fabrication processes, can be used to engineer well-defined mechanical terrains for cellular studies.

To examine the adhesion of cells on the mPADs, we uniformly adsorbed fibronectin and seeded cells onto a substrate containing posts of 3-μm diameter, 11-μm height, and 6-μm spacing. Cells attached, spread across multiple posts, and deflected underlying posts (Fig. 2A). However, cells spread down the length of the posts, and therefore were exposed to a range of local compliances. The deflection of the posts therefore does not quantitatively reflect the applied traction force. To restrict cell adhesion to the tips of the posts, and thereby precisely define the surface mechanics, we used microcontact printing to deliver fibronectin from a stamp onto the tips of the posts (Fig. 2B), and adsorbed Pluronics F127 onto the remaining unstamped regions of the array to block nonspecific protein adsorption and cell adhesion (31, 32). Using this method, we can print fibronectin onto specific posts within the array to spatially pattern the adhesiveness of the surface toward cells (Fig. 2C). On substrates where the tips of all of the posts were printed with fibronectin by using a flat stamp, cells attached, spread, and migrated selectively across the tips of the posts, bending the posts centripetally toward the interior of the cell (Fig. 2D). The general morphology of the cells on posts was similar to that of cells cultured on planar substrates (Fig. 2E).

To determine whether actively generated contractile forces caused the deflection of posts, we disrupted components of the actin–myosin cytoskeleton. Inhibition of myosin-generated contractility with 2,3-butanedione monoxime decreased post deflection over several minutes (Fig. 3 A–C), and contractility further decreased upon disruption of the actin cytoskeleton with cytochalasin D (Fig. 3D). Occasional small deflections remaining after cytoskeletal disruption were immediately lost when cells were detached from the substrate.

When adhered strictly to the top surface of mPADs, cells locally exert forces on the tips of each post. Because the posts deflect independently of each other, localizing the origin of forces exerted by the cell is straightforward. To quantify subcellular distribution of exerted forces, we tracked the position of the tips of multiple posts simultaneously by using immunofluorescence microscopy (Fig. 3E), and we calculated the magnitude and direction of deflections of posts relative to their undeflected, ideal position; corresponding force vectors were then obtained by multiplying deflections with the measured spring constant of the posts. Consistent with our expectations, the force vectors measured for a cell summed to zero, and posts not attached to cells showed negligible deflections. Importantly, the distribution of forces was directly obtained without introducing computational assumptions. Independent of force measurements, we stained and imaged focal adhesions in the same cells (Fig. 3F) and compared the focal adhesion quantity with the magnitude of force at each post (Fig. 3G). In individual cells, there appeared to be a correlation between the subcellular distribution of focal adhesions and local traction forces. To examine this correlation quantitatively, we plotted the area of focal adhesion staining per post against the forces generated at each post for five cells (Fig. 3H). Defining focal adhesions as adhesions larger than 1 μm², we show that focal adhesion size correlates with stresses experienced at these adhesions, agreeing with previous observations (19). Interestingly, adhesions smaller than 1 μm² appear to be able to generate large forces that do not correlate to adhesion size (Fig. 3H, blue shading) and may correspond to the previously defined focal complexes (33).

To further illustrate how mPADs can be used to investigate other aspects of cellular mechanics, we examined whether changes in cell morphology could modulate the magnitude of contractile forces. Taking advantage of our ability to modify the adhesiveness of each individual post, we printed fibronectin onto sets of neighboring posts surrounded by nonadhesive posts, such that the size of the set (2 × 2 to 5 × 5 array of posts) controlled the extent of cell spreading (140 to 1,520 μm²) (Fig. 4 A–F). Cells were incubated overnight on the substrates and contractile forces were measured. Because traction forces are discretized by the posts, we can easily and quantitatively compare forces between cell populations. Progressively increasing cell spreading caused a serum-dependent increase in stress fiber formation and cytoskeletal tension (Fig. 4G). To study the effects of cell morphology on the initial activation of cell contractility, cells were attached on different-sized sets of posts, serum-starved overnight, and stimulated with LPA, a phospholipid in serum that stimulates actin–myosin contraction (34). In the absence of serum, cell contractility was low in both “unspread” (440-μm²) and “spread” (1,520-μm²) cells. Within 12 min after exposure to LPA, spread cells formed stress fibers and increased their contractility to levels similar to those in serum-cultured cells, whereas unspread cells did not respond (Fig. 4H). A comparison of the traction forces measured by the 25 posts for the LPA-stimulated spread cell reveals differences from post to post, not only in magnitude but also in the temporal and spatial dynamics of activation after stimulation (Fig. 4I). To test whether unspread cells were capable of contraction, cells were transfected with constitutively active RhoA, a small G protein that mediates LPA-induced contractility (34), and placed on arrays of posts. The transfected unspread cells formed distinct stress fibers and recovered the ability to generate contractile force (Fig. 4J), suggesting that cell morphology regulates the biochemical activation of contractility.

Previous studies have used continuous surfaces made of compliant materials to study traction forces generated by cells. These approaches have become progressively more sophisticated by the introduction of microfabricated markers and computational algorithms to calculate traction forces based on observed deformations (24). However, fundamental limitations remain in this approach, and have been previously described (20, 23). To address these concerns, we used arrays of deformable posts as an approach to control and study the mechanical interactions between cells and surfaces. The geometry of isolated elements, rather than the bulk stiffness of continuous substrates, was used to engineer compliances relevant to cells without altering surface chemistry. Because each post deflects independently of its neighbors, deflection of each post unambiguously and quantitatively reports the location, direction, and magnitude of the cell-generated force without the need for a priori assumptions.

Using this system, we demonstrated that a positive correlation exists between the size of focal adhesions and the force generated at those adhesions. In addition, we observed in the same cells a subset of smaller adhesions (<1 μm² in area) that exerted significant traction forces in which the magnitude of the exerted forces did not correlate with adhesion size. Previously, Beningo et al. (35) reported that adhesion size inversely correlated with traction force, whereas others suggested that adhesion size directly correlated with force (6, 19, 36). Here, our findings suggest the existence of two classes of force-supporting adhesions that exhibit distinct force–size relationships. Importantly, we show that both classes of adhesions can coexist within the same cell.

Prior studies have demonstrated that cell morphology is an important mechanical regulator of many processes that occur on a time scale of hours to days, including cell proliferation, differentiation, and apoptosis (37). In contrast, the immediate effects of cell morphology on cellular events are less well known. Here, we found that cell shape can direct soluble signals into distinct contractile responses within minutes. Because contractile force can in turn alter cell adhesion and integrin signaling in an inside-out manner (6, 7), these findings may provide the first indication of the early signaling events that transduce cell shape into a regulatory response.

The demonstration of cellular processes that link cell morphology, traction force, and focal adhesions highlights the interplay between mechanical and biochemical control systems that cells use to navigate in their physical microenvironment, and illustrates the challenges in characterizing the mechanics of cells. Compliance, topology, and surface chemistry of the substrate each have been shown to alter cell adhesion and cytoskeletal organization (16, 38, 39). Thus, the properties of the substrate used to measure traction forces may affect the contractile behavior being studied. This fundamental connection between substrate properties and cell mechanics underscores the importance of providing chemically and mechanically well-defined measurement systems in which the properties of the interface can be easily manipulated. mPADs represent one approach that provides such control.

Here, we used photolithography and molding of silicone elastomers to engineer surfaces with a wide range of useful mechanical properties, and we combined these processes with microcontact printing to demonstrate the control of cell adhesion and spreading in this system. Manufacturing based on replica-molding allows rapid fabrication of identical substrates, and is compatible with the integration of microfluidics and other actuator devices (40). The resolution of mPADs can be further improved by using available technologies to increase the density of posts in the array and the precision in measuring deflections. Because post geometry determines substrate mechanics, the choice of bulk material used to fabricate a compliant substrate is no longer constrained to a few soft materials, and could include materials as rigid as polystyrene, silicon, or glass. We believe that mPAD provides a viable strategy to independently control substrate mechanics and surface chemistry to study the mechanisms by which cells probe the mechanical and biochemical aspects of their adhesive environment.

Abbreviations

ECM

extracellular matrix

mPADs

microfabricated post-array-detectors

PDMS

poly(dimethylsiloxane)

LPA

lysophosphatidic acid