Ecological community description using the food web, species abundance, and body size

Abstract

Measuring the numerical abundance and average body size of individuals of each species in an ecological community's food web reveals new patterns and illuminates old ones. This approach is illustrated using data from the pelagic community of a small lake: Tuesday Lake, Michigan, United States. Body mass varies almost 12 orders of magnitude. Numerical abundance varies almost 10 orders of magnitude. Biomass abundance (average body mass times numerical abundance) varies only 5 orders of magnitude. A new food web graph, which plots species and trophic links in the plane spanned by body mass and numerical abundance, illustrates the nearly inverse relationship between body mass and numerical abundance, as well as the pattern of energy flow in the community. Species with small average body mass occur low in the food web of Tuesday Lake and are numerically abundant. Larger-bodied species occur higher in the food web and are numerically rarer. Average body size explains more of the variation in numerical abundance than does trophic height. The trivariate description of an ecological community by using the food web, average body sizes, and numerical abundance includes many well studied bivariate and univariate relationships based on subsets of these three variables. We are not aware of any single community for which all of these relationships have been analyzed simultaneously. Our approach demonstrates the connectedness of ecological patterns traditionally treated as independent. Moreover, knowing the food web gives new insight into the disputed form of the allometric relationship between body mass and abundance.

Ecological communities are not purely randomly constituted (1). For example, predators are often larger and rarer than their prey (2, 3), if parasites and herbivorous insects on trees are ignored. To illuminate the structure of an ecological community in finer detail and more comprehensively, we combine its food web, body sizes, and species abundances. A food web (4) is a directed graph or flow diagram. Each node is labeled by a species' name and each arrow (link or directed edge) from one node to another indicates a flow of nutrients from a resource (prey) species to a consumer (predator) species. How trophic relations among the species are related to patterns such as rank-abundance relations, body size distributions, abundance-body size allometry, and biomass spectra has been little studied. Augmenting a traditional food web with information on the average body mass M and numerical abundance N of each species makes it possible to study trivariate patterns that involve the food web, M and N; bivariate patterns that involve any pair of these; and univariate patterns that involve any one (Table 1). The approach is illustrated and tested using data on Tuesday Lake from 1984 (Fig. 1).

Table 1.

Ecological community descriptions that combine the food web, body size, and abundance

Food web	Body size	Abundance	Distributions and relationships
Yes			Food web statistics, distributions of trophic links and chain lengths, trophic generality and vulnerability
	Yes		Distribution and rank of body size
		Yes	Distribution and rank of numerical and biomass abundance
Yes	Yes		Predator–prey body size allometry, body size vs. trophic height, trophic generality and vulnerability
	Yes	Yes	Abundance–body size allometry and spectrum, species diversity in relation to body size and abundance
Yes		Yes	Predator–prey abundance allometry, abundance vs. trophic height, generality, and vulnerability
Yes	Yes	Yes	All trophic variables in relation to body size and abundance

Figure 1.

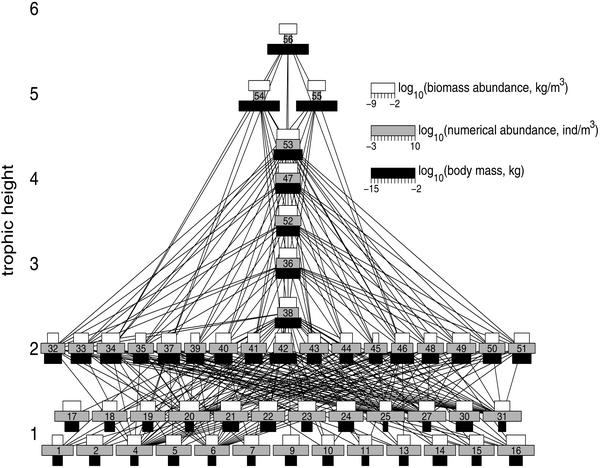
The food web of Tuesday Lake in 1984. The width of the black, gray, and white horizontal bars shows the log₁₀ body mass (kg), log₁₀ numerical abundance (individuals per m³), and log₁₀ biomass abundance (kg/m³), respectively, of each biological species. Species numbers are identified in ref. 5. The vertical positions of the species show trophic height. Basal species have a trophic height of 1, but to allow for wider, nonoverlapping bars the vertical positions of the basal species have been adjusted around 1. The horizontal position is arbitrary. Isolated species are omitted. Species with a trophic height of 1 are phytoplankton, those with trophic height >4.5 are fish, and those with intermediate trophic heights are zooplankton.

This brief report focuses on the trivariate relationships (last line of Table 1). Jonsson et al. (5) report trivariate, bivariate, and univariate patterns, evaluate a major experimental manipulation (6, 7) of Tuesday Lake in 1985, review related work, and give complete data for 1984 and 1986.

In the next section, we develop some energetic theory to guide description. The following section presents definitions and the data on Tuesday Lake from 1984. Then the trivariate patterns derived from these data are described. Some major findings regarding bivariate and univariate patterns are summarized. The concluding section reviews the insights gained by our trivariate approach.

Theory

Body Mass Rank and the Distributions of Body Mass, Abundance, and Trophic Height.

Cohen (8) hypothesized that the average body mass M of a species in a community could be related to its rank in M, where the biggest species has rank i = 1, the next biggest has rank i = 2, and so on. If M is allometrically related to rank i in M by log M_i = a − b log i, where a and b are known constants, then the distribution of M in a community can be predicted from the number of species S. If N is allometrically related to M by log N_i = c − d log M_i (9–11), then log N_i = (c − da) + (db)log i, i.e., N is allometrically related to M-rank i. Then biomass abundance B = MN is also allometrically related to M-rank because log B_i = log M_i + log N_i = c + a(1 − d) + b(d − 1)log i. If larger species on average are found higher up in a food web than smaller species, the trophic height H (defined below) of species could be related to M-rank. If the simple models presented here hold, then the expected M, N, and H of all species in a community could be calculated using only S and a few regression coefficients.

Linking the Food Web to the Relationship Between Body Size and Numerical Abundance.

The following theory pertains to all consumers in a community. Assume that N_j, the numerical abundance of consumer population j, is proportional to the total amount of resources available to the consumer population per unit time (i.e., resource supply rate, ρ_j) divided by the resource use per consumer individual per unit time, and that the resource use per individual per unit time is proportional to the metabolic rate R_j of individuals. For lack of detailed data, we ignore variations in body mass within a species. Then R_j ∝ M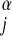, where α < 1 and α is claimed to be ¾ (12, 13) or 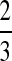(14, 15), and N_j ∝ ρ_j/R_j ∝ ρ_jM_j^−α or N_j/ρ_j ∝ M 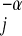(16). This argument predicts that, over all consumer species i, the slope of N_j/ρ_j vs. M_j will be closer to −α on log–log scales than the slope of N_j vs. M_j.

The following theory pertains to a single consumer species c (with numerical abundance N_c and average body mass M_c) that is the sole consumer of a particular resource species r with productivity ρ_r, which is modeled allometrically as ρ_r ∝ N_rM. If N_c ∝ ρ_rM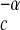, as derived above, then

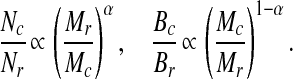The larger M_c is relative to M_r, the smaller the ratio of predator N to prey N is predicted to be, but the larger the ratio of predator B to prey B is predicted to be. Treating the log abundance ratio (log N_c/N_r or log B_c/B_r) as the dependent variable (ordinate) and the log body mass ratio (log M_r/M_c or log M_c/M_r, respectively) as the independent variable (abscissa), the slope of the former relationship is predicted to be greater than that of the latter, because α > 1 − α. B_c may be smaller than B_r (at least in terrestrial systems), but B_c may also be greater than B_r if the consumer's biomass turnover is sufficiently slower than that of its resource. Because turnover rates in general are allometrically related to M, B_c can exceed B_r if the predator's M is sufficiently larger than the prey's M.

In a single food chain, if the ratio of predator M to prey M remains constant, the ratio of predator B to prey B is predicted not to change systematically along the food chain. In cross-linked food chains, the picture could be more complicated (see below).

Data and Limitations

Tuesday Lake is a small, mildly acidic lake in Michigan, United States (89° 32′ W, 46° 13′ N). The fish populations are not exploited and the drainage basin is not developed. The data (see ref. 5 for details) consist of a list of species, and for each species, its predator species and its prey species (for the body sizes and life stages present in the lake in 1984), its average body mass M (kg fresh weight per individual), and its numerical abundance N (individuals per m³ in the epilimnion where the trophic interactions take place). The biomass abundance B (kg/m³) is M × N. The data represent seasonal averages during summer stratification. Most numerical variables, reported as mean values, were estimated by continuing sampling until the standard error of the mean was <10%.

Limitations of the data could affect the relationships analyzed. First, the community boundaries exclude the littoral zone and Sphagnum bog that surround Tuesday Lake. Nutrient flux from the littoral zone to the fishes in Tuesday Lake is nontrivial (17). However, the littoral zone is small and sparsely vegetated. Macrophytes are nearly absent. Benthic invertebrates are associated with the bog edge. Our analyses focus on the pelagic linkages and do not address feeding by fishes in benthic and bog-edge habitats. The other animals that we consider feed only pelagically. Linkages between the pelagic and littoral or benthic zones may be more important in other temperate lakes (18). Second, the pelagic community is incompletely described. Microbes and parasites are missing. Other species may have been missed despite extensive sampling. Third, although a community changes in time, the data are static averages over time and space. Uncertainty remains over how well the estimates of M and N reflect the mean values of temporally variable quantities. Preliminary simulations suggest that variation within an order of magnitude at the species level will have small effects at the level of the community (5). Fourth, not all of the data analyzed were independently obtained because relative sizes of consumers and potential prey were used in some cases to infer trophic relations. However, relationships involving M and N are unaffected by inferences about the food web. Fifth, the volume where a species feeds may not be identical to the volume where the species lives. However, N and B of zooplankton would be affected by less than one order of magnitude (a factor of 6) if the volume where zooplankton live were used instead of the volume where they feed. Most major patterns reported here would be little altered. Sixth, the data in this study describe just one ecosystem. Improved data from other ecosystems will establish to what extent the new trivariate and bivariate patterns observed in Tuesday Lake hold elsewhere.

Definitions

The trophic position of a species in a food chain is one plus the number of species below it. (In a recursive definition, species A is said to be below species B in a food chain if species A is eaten by species B or if species A is below any species that is below species B.) An autotrophic species with no species below it is defined to have trophic position 1. In a food web with omnivory, cannibalism, or loops, a species may have different trophic positions, depending on which food chain is specified. The trophic height (H) of a species is the average trophic position in all food chains it belongs to. Cannibalism and loops are ignored, but not omnivory, in computing trophic heights to assure that they are all finite.

Here only the unlumped web of Tuesday Lake using biological species is described. The trophic vulnerability (V) and the trophic generality (G) of a species are the number of consumers and the number of prey, respectively, that species has (19).

For each consumer species j that eats a nonempty set of resource species R_j, the available resource biomass β_j and the available resource productivity Π_j are defined in terms of N, M, and the vulnerability V_i of its resource species i in R_j as

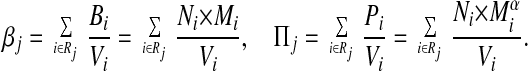The denominator V_i reflects the assumption that each consumer species of resource species i consumes an equal share of the biomass or productivity, respectively, of i. (Future work will improve this crude assumption.) Both β_j and Π_j depend on trivariate information: the food web (which specifies the resource species of each consumer, and the consumer species of each of those resource species), M, and N.

All logarithms in this paper are calculated with base 10. All figures plot all species recorded in Tuesday Lake except six isolated phytoplankton species not eaten by any herbivores in Tuesday Lake.

Results: Trivariate Patterns in the Pelagic Community of Tuesday Lake

In Tuesday Lake, small, numerically abundant species occur at low H, whereas larger, less abundant species occur at higher H (Figs. 1 and 2A), as observed (2, 3). Compared with N, B has a much more variable relation with M or H (Figs. 1 and 2B).

Figure 2.

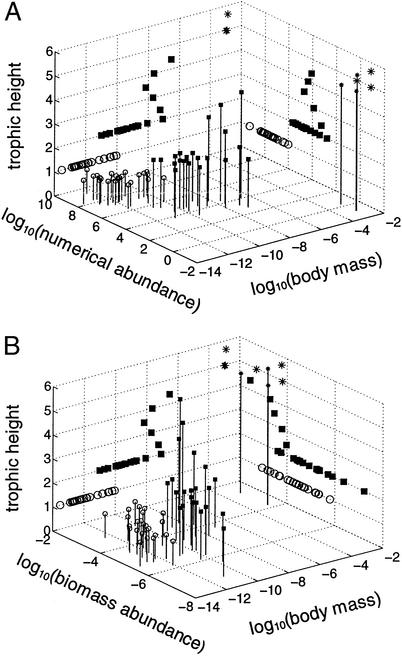
Body mass (kg), trophic height, and abundance of the species in Tuesday Lake in 1984. Numerical abundance (individuals per m³) is shown in A and biomass abundance (kg/m³) in B. Circles represent phytoplankton, squares represent zooplankton, and stars represent fish. Small markers on stems show the position of each species in the three-dimensional space. Larger markers on the walls and the base of the stems on the floor of the box show the bivariate distribution of the species in two-dimensional space.

In the space with axes given by N, M, and H, phytoplankton, zooplankton, and fish form three distinct clusters that lie roughly on a diagonal between the lower left corner and the upper right corner in Fig. 2A. A multiple linear regression of H (dependent variable) on log N and log M (independent variables) indicates that almost all of the variation that can be explained (r² = 0.84) by M and N jointly can be attributed to M alone (r² = 0.83) rather than to N alone (r² = 0.76). The regression equation is H = 0.3421 log M − 0.1040 log N + 5.8697. The first coefficient in this regression equation indicates that an increase in mean H by 1 is associated with an increase in M by a factor of >800 (because 1/0.3421 = 2.9231 and 10^2.9231 = 837.8), if all else is constant. In fact, not all else is constant. In Tuesday Lake, an increase in M is usually closely associated with a decrease in N. Among the phytoplankton, M and N are negatively correlated, although all phytoplankton have H of 1. For 17 species of zooplankton with H = 2, M and N are significantly negatively correlated (r₈₄ = −0.53, P < 0.05).

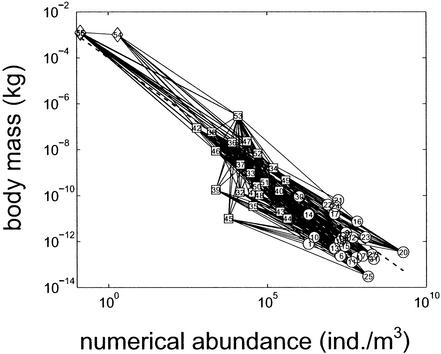
A graph inspired by diagrams in refs. 20 and 21 shows the food web of Tuesday Lake in the plane with abscissa log N and with ordinate log M (Fig. 3). Animal ecologists generally put log M on the abscissa, whereas plant ecologists generally put log M on the ordinate (22). Because food webs are conventionally represented with food flowing in an upward direction, we prefer the choice of axes customary among plant ecologists so that food usually flows upward from smaller-bodied, more abundant prey to larger-bodied, rarer predators. This food web diagram carries more information on the pattern of energy flow within a community than a traditional food web graph. For all 56 species, the linear regressions are log M = −4.3510 − 1.0178 log N and log N = −2.6863 − 0.8271 log M, with 95% confidence intervals (−1.14, −0.90) around the slope −1.0178 and (−0.92, −0.73) around the slope −0.8271 (cf. refs. 23 and 24).

Figure 3.

Tuesday Lake food web in 1984, plotted in the plane with abscissa measured by numerical abundance (individuals per m³) and ordinate measured by body mass (kg) (log scales on both axes). Species are identified in ref. 5. Circles represent phytoplankton, squares represent zooplankton, and diamonds represent fish. Edges or links show feeding relations. Biomass abundance B equals 10⁻⁴ kg/m³ along the dashed line.

The slope of a link between two species in this diagram indicates the biomass ratio between a consumer species and one of its resource species. A slope of −1 means that consumer B equals resource B. A slope more (or less) negative than −1 indicates that the consumer has greater (or smaller) B, respectively, than the resource, assuming that the consumer is above and to the left of the resource in this plane, as is usually the case. The mean slope of all links that join individual pairs of consumers and resources is −1.1585. Consumer B on average is slightly greater than B of their individual resource species.

Most species fall near a diagonal with slope −1 at B = 10⁻⁴ kg/m³. If a littoral subsidy greatly affected fishes' M or N, then fishes would be outliers in plots such as Fig. 3, contrary to observation. From the bottom to the top of the food web, while M increases almost 12 orders of magnitude as N decreases almost 10 orders of magnitude, B increases roughly 2 orders of magnitude (as expected, 12 − 10 = 2). Over all species, B varies only 5 orders of magnitude. In many aquatic and pelagic communities the distribution of biomass is approximately uniform in equal intervals of log body mass (e.g., refs. 25–27; later work discussed in ref. 5).

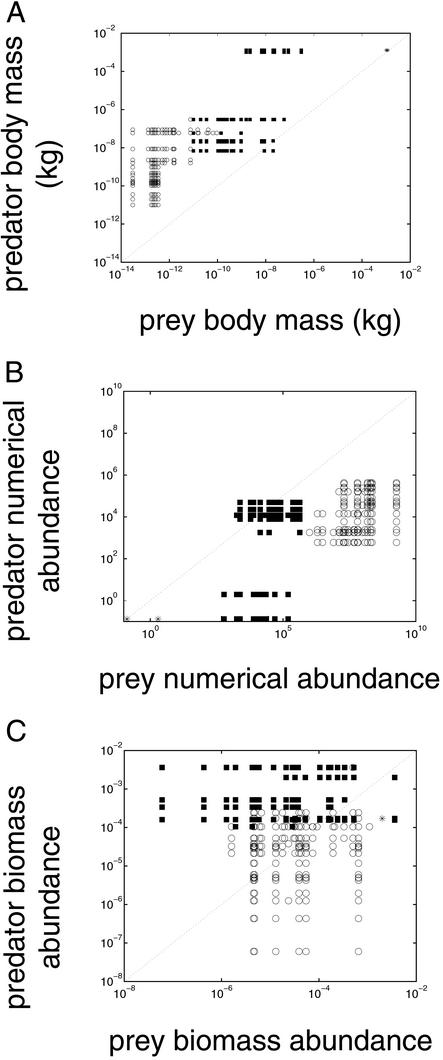
In most links, predator M is greater than the prey M (Fig. 4A) and predator N is less than prey N (Fig. 4B). Fig. 4A plots all of the species in a single community. By contrast, figure 7.5 of Peters (ref. 28, based on ref. 29), which Fig. 4A superficially resembles, plots terrestrial predators and their prey from a composite of different communities. Predator B may or may not exceed prey B (Fig. 4C). In 1984, 61% of links have prey B smaller than predator B.

Figure 4.

(A) Prey and predator average body mass M (kg), (B) numerical abundance N (individuals per m³), and (C) biomass abundance (kg/m³) in Tuesday Lake in 1984. One marker represents each link in the unlumped food web. Cannibalistic links are excluded. Dotted line shows prey M, N, or B equal to predator M, N, or B. Open circles represent links where the prey is phytoplankton. Solid squares represent links where the prey is zooplankton. Asterisks represent links where the prey is fish.

The food web makes it possible to refine the superficially bivariate relationship between N and M. In Tuesday Lake, across all consumer species, the slope of log N as a function of log M is −0.67. (This way of computing the slope implicitly exchanges the axes in Fig. 3.) Being greater (less negative) than −1, this slope shows that consumer biomass abundance increases from the bottom to the top of the food web.

The food web helps explain why. Bigger-bodied consumer species may have greater biomass in part because they have more available resource biomass β_j as a result of having larger generality G_j or having resource species with larger B_i, or both. In Tuesday Lake, consumer generality G_j increases with M_j (P < 0.05 across all consumer species). Accordingly, on log–log scales, β_j increases significantly with M_j across all consumer species j (P < 0.001), as well as for zooplankton separately (P < 0.05).

The theory above predicts, and the data confirm, that over all links there is a positive correlation between the slope of the link and the trophic generality of the consumer (P < 0.001), treating log N as the dependent variable (ordinate) and log M as the independent variable (abscissa). In the same coordinates, over all links there is also a negative correlation between the slope of the link and the trophic vulnerability of the prey species (P < 0.005). A consumer species' N in Tuesday Lake is greater than expected if the consumer has more species of prey and less than expected if the consumer shares its prey with other consumer species.

However, the resource supply rate need not be proportional to the standing stock of prey biomass. Smaller organisms typically have higher energetic and biomass turnover rates than larger organisms. In line with the theory above, the slope −0.70 of log(N_j/Π_j) vs. log M_j over all consumers is closer to −¾ than is the slope −0.67 of log N_j vs. log M_j. By contrast, dividing the consumer N by the total productivity of all prey species in the diet of a consumer, without dividing each prey species' productivity by its vulnerability, hardly changes the regression slope or the goodness of fit of the regression of log N as a function of log M.

The slope −0.91 of log(N_j/β_j) vs. log M_j is closer to −1 than the slope −0.67 of log N_j vs. log M_j. This finding in Tuesday Lake parallels that for carnivores from many different communities (16). Both findings indicate that the conversion efficiency of prey to predator biomass is roughly similar over a wide range of predator body sizes. The regression of log (N_j/β_j) vs. log M_j has r² = 0.86, whereas the regression of log N_j vs. log M_j has r² = 0.79. The B_i of each prey species must be divided by the prey's vulnerability, crudely assuming equal resource use by each of the consumer species. A slope equal to (greater than) −1 for the relationship between consumer log (N_j/β_j) (dependent variable) and consumer log M_j (independent variable) would mean that one unit of available resource biomass supports a constant (increasing) amount of consumer biomass as the consumer's M_j increases.

There is a statistically significant negative correlation between prey B and predator B (Fig. 4C). Predators that eat zooplankton in most cases have larger B than their prey. No clear trend for the B of predators that eat phytoplankton (circles in Fig. 4C) can be seen.

There is a significant negative correlation between H and N (projection on right rear wall in Fig. 2A) across all species. For the zooplankton, the relationship is nonsignificant. The relationship between H and B (Fig. 2B) across all species and for zooplankton is significantly positive.

As predicted above, in Tuesday Lake (i) the ratio between predator log N and prey log N is positively correlated to the prey–predator M ratio (P < 0.001) and (ii) the ratio between predator log B and prey log B is positively correlated to the predator–prey M ratio (P < 0.05). The change along a single link in N and B can be inferred on average from the ratio of consumer M to prey M for that link. Furthermore, log(B_j/β_j) for consumer j changes only slightly with increasing log M_j.

Summary of Other Results on Tuesday Lake

This section summarizes and extends additional findings of Jonsson et al. (5).

Bivariate Relationships.

The pelagic community of Tuesday Lake shows a pyramid of numbers (decreasing numbers of individuals with increasing H) but not a pyramid of biomass. The B–M spectrum (histogram of total biomass in logarithmically equal intervals of body size) is roughly flat, as it is at larger spatial scales (25, 26). Prey M is positively correlated to predator M. Prey N and predator N are positively correlated but not prey B and predator B. There is a positive correlation between M and H, and a negative correlation between M and N. The slope of the linear regression of log N on log M is not significantly different from −¾ across all species. The slope within the phytoplankton and zooplankton, each group considered separately, is much less steep than −¾. The slope of the linear regression of log N on log M is similar to that at larger, regional scales, but different from that suggested for local scales.

The theory developed above predicts well the slope of the allometric relationship between B_i and rank i in body mass and explains why B_i falls with increasing i, as we show now. The coefficients in the remainder of this paragraph include the isolated phytoplankton species, because the food web is not involved in these relationships. In the notation used (above) the negative slope of log M_i as a function of log i is b₁₉₈₄ = 6.1552, b₁₉₈₆ = 5.4398 (ref. 5, their figure 9). The negative slope of log N_i as a function of log M_i is d₁₉₈₄ = 0.8271, d₁₉₈₆ = 0.7397 (ref. 5, their table 6). The predicted slope of log B vs. log i is b(d − 1). The predicted [b(d − 1)]₁₉₈₄ = −1.0642, whereas the actual is −1.0762. The predicted [b(d − 1)]₁₉₈₆ = −1.4160, whereas the actual is −1.4506 (actual slopes are from ref. 5, their figure 12).

Univariate Relationships.

Tuesday Lake has decreasing numbers of species with increasing H. The number of links between species in nearby trophic levels, defined by H, is higher than would be expected if links were distributed randomly among the species. Food chains are shorter than would be expected if links were distributed randomly. Species of low H tend to have more predators and fewer prey than species of high H. The distribution of N is approximately broken-stick within phytoplankton and zooplankton. The distribution of B is approximately log-normal across all species. The distribution of log M is right skewed. The slope of the right tail of the M distribution is much less steep than has been suggested for regional scales and not log-uniform as found at local scales for restricted taxonomic groups.

Effect of Food Web Perturbation.

In 1985, three species of planktivorous fishes were removed and one species of piscivorous fish was introduced. Comparisons of the data from 1984 and 1986 show that the manipulation produced at most minor differences between 1984 and 1986 in the trivariate, bivariate, and univariate relationships analyzed. The food webs, the rank–abundance relationships, and abundance–M relationships are similar in shape. In both years, the distribution of log M is right skewed and the biomass spectrum across all species flat, and consumers are with few exceptions larger and less numerically abundant than their prey. Species composition changed, as did N, B, and relative abundance among species categories.

Conclusions

This analysis of the food web, species abundance, and body size in the pelagic community of Tuesday Lake illustrates an integrated approach (Table 1) using a new data structure for the description of ecological communities. Different fields of ecology have focused on different sets of the bivariate relationships in Table 1. For example, the B–M spectrum has mainly been studied by limnologists or marine scientists (27), whereas rank–abundance and predator–prey M relationships are studied mainly in terrestrial ecology. In the famous tale of the blind men and the elephant, the blind men cannot agree because they are experiencing different parts of the strange animal. The diverse patterns analyzed here are like the trunk, ears, legs, and tail of the elephant: they all follow from the food web, M, and N of the species in the community (8). A clear vision of these three features, and their connectedness, gives a more comprehensive picture of the ecological elephant.

Many previously reported patterns are confirmed. In addition, we identified some relationships rarely, if ever, analyzed for an entire community before: trophic generality and vulnerability with respect to H (reported in 5); M and N within a food web; abundance–M allometry; predator–prey abundance allometry; and relationships between H and M and between H and N. The food web gave insight into the disputed form of the allometric relationship between M and N: dividing consumers' N by the available resource productivity improves the linear relationship to M on log–log scales. Many of the relations were very robust to a major perturbation of Tuesday Lake. If this robustness applies generally, communities may have consistent, predictable properties.

Major tasks remain: (i) to test the generality of the present findings by analyzing comparable or better data on other communities, including temporal and spatial variation and heterotrophic microorganisms and parasites; (ii) to explain consistent patterns with persuasive quantitative theory; and (iii) to extend and apply the data structure introduced here. For example, if dates and places of observation were added to data associated with each node of a food web, a dynamic, spatially explicit description would become possible. If each node also had an associated Leslie matrix, in which fertility coefficients depended on the abundance of species consumed by the nodal species, and in which the survival coefficients depended on the abundance of the species that consume the nodal species, then dynamic modeling of age- or stage-structured populations (30) could be integrated with dynamic food web modeling, bringing together population biology and community ecology. If chemical compositions of each species (21) were added to the vector of attributes, and if all coefficients of the Leslie matrix also took explicit account of abiotic environmental variables (such as chemical concentrations of nutrients and toxins), then population biology and community ecology could integrate with biogeochemistry. Food webs with flow measurements of energy and nutrients for each link would permit better understanding of how trophic structure affects the relationship between M and N.

Abbreviations

B

biomass abundance

H

trophic height

M

body mass

N

numerical abundance

R

metabolic rate