Using temporal context to improve biosurveillance

Abstract

Current efforts to detect covert bioterrorist attacks from increases in hospital visit rates are plagued by the unpredictable nature of these rates. Although many current systems evaluate hospital visit data 1 day at a time, we investigate evaluating multiple days at once to lessen the effects of this unpredictability and to improve both the timeliness and sensitivity of detection. To test this approach, we introduce simulated disease outbreaks of varying shapes, magnitudes, and durations into 10 years of historical daily visit data from a major tertiary-care metropolitan teaching hospital. We then investigate the effectiveness of using multiday temporal filters for detecting these simulated outbreaks within the noisy environment of the historical visit data. Our results show that compared with the standard 1-day approach, the multiday detection approach significantly increases detection sensitivity and decreases latency while maintaining a high specificity. We conclude that current biosurveillance systems should incorporate a wider temporal context to improve their effectiveness. Furthermore, for increased robustness and performance, hybrid systems should be developed to capitalize on the complementary strengths of different types of temporal filters.

With the very real threat of bioterrorism, the critical need for timely detection of an outbreak has accelerated the time frame for major enhancements to the public health infrastructure. One of the earliest developments produced by these efforts has been the syndromic surveillance system (1).§ The Centers for Disease Control and Prevention define public health surveillance as “the ongoing systematic collection, analysis, and interpretation of health data essential to the planning, implementation, and evaluation of public health practice, closely integrated with the timely dissemination of these data to those who need to know” (2).

In syndromic surveillance, healthcare utilization patterns are monitored in real time for the first signs of a covert germ warfare attack, which may appear as clusters of infected victims seeking health care. For example, patients with early-stage anthrax infection may develop influenza-like symptoms and might visit primary care physicians or emergency departments for treatment (3, 4). By detecting a surge in visits of patients with flu-like symptoms, a public health authority could get an early warning of a covert anthrax attack (5, 6), perhaps within the first 2 days, enabling prompt identification, containment, treatment, and prophylaxis.

Many current detection approaches, reviewed in refs. 7 and 8 and references therein, attempt to detect outbreaks by comparing a single day's actual visit rates with a model-generated forecast for that day. A suspicious increase in the actual visit rate over the forecast is a potential sign of an emerging outbreak.

The primary challenge to interpreting the output of these surveillance systems is the signal noise, or unpredictability, that prevents accurate modeling of the data and leads to errors in the model's predictions. These errors appear as noise that may cause false positives and false negatives. False positives occur when noise spikes in the model's predictions are detected as possible outbreaks, lowering the system's overall specificity. False negatives occur when noise in the model's predictions masks the effects of actual outbreaks, lowering overall sensitivity.

Most importantly, the effects of noise limit the early-detection capabilities of standard syndromic surveillance systems. Bioterrorist agents, such as anthrax, can spread very quickly through a population (9). With only narrow time windows available for effective public health response, knowing early is often as important as knowing at all. Until currently experimental rapid screening technologies become widely available (10), it is essential to extract the earliest possible detection capabilities from existing syndromic surveillance systems.

To address these pressing needs, we set out to develop a syndromic-based detection approach that uses an expanded temporal window: Multiple days are examined together to produce a more comprehensive picture of the recent healthcare utilization. With this approach, we hope to improve specificity by reducing the system's vulnerability to noise spikes. We also hope to improve sensitivity by aggregating signal strength over a period, thereby enabling detection of a weak signal spread over a number of days. Finally, we hope to improve timeliness of detection over existing methods.

To achieve these aims, we systematically investigated a variety of approaches to temporally enhanced detection. Box and Luceno (11) describe cuscore statistics as various functions that look for specific types of signals within noisy data streams. Similarly, we constructed various filters, or sets of weights, that evaluate surveillance data using a sliding detection window. We tested these filters with historical visit data infused with simulated outbreaks that vary in size, shape, and duration. The general methods set forth here can be applied to the monitoring of other surveillance data, such as sales of over-the-counter medications (12).

Methods

We analyzed all visits to the emergency department at Children's Hospital Boston, a major metropolitan pediatric tertiary-care hospital, between June 1, 1992 and January 1, 2002 (3,505 days totaling >500,000 visits). Daily forecasts of visit rates were generated from a historical model of healthcare utilization. The forecasts represent the expected visit rates and serve as a basis for comparison with actual rates.

Modeling.

The focus of the present article is to improve the detection stage of a surveillance system by mitigating the effects of modeling noise. The enhanced detection approach described herein is independent of any one particular approach to modeling and is expected to yield benefits when coupled with other types of models as well. The modeling methodology used here is described in brief, and in further detail in ref. 13.

A trimmed-mean seasonal model was calculated to capture both the yearly and weekly trends in daily utilization rates. The model was generated by separating the original signal into its component parts, as follows: The average daily volume was calculated and subtracted from the signal. The average of the remaining signal was then calculated for each individual day of the week. This average weekly signal was then subtracted away, and the average of the remaining signal was calculated for each individual day of the year. In calculating the yearly signal, a trimmed mean was used to remove noise by ignoring the top and bottom 25% of values for each day. This average yearly signal was then subtracted away to yield the residual error signal.

The residual error signal from the trimmed-mean seasonal model was then fit with an Auto-Regressive Moving Average (1, 2) time-series model (14) by using the sas release v. 8.2 software package Time Series Forecasting System (SAS Institute, Cary, NC) (15). The Auto-Regressive Moving Average model captures autocorrelations in the signal and helps adjust the forecasts to local trends. Following standard time series modeling practice, different low-order Auto-Regressive Moving Average models were iteratively tested and the Auto-Regressive Moving Average (1, 2) model was found to have the best fit. The sas toolkit was then used to automatically fit the parameters for the model.

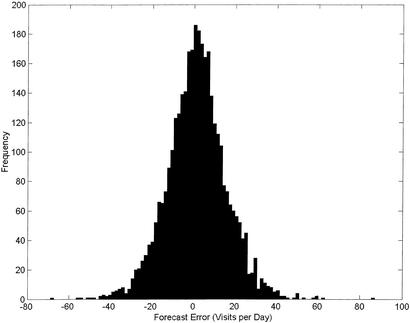
The average daily volume of the historical data was 136.9 visits per day with a standard deviation of 22.4 visits. The distribution of the forecast errors from the model described above is shown in Fig. 1. The standard deviation of the model-generated forecast error was 14.25 visits per day, with a mean absolute percentage error of 8.11%. The mean absolute percentage error was not found to vary significantly with the seasons.

Figure 1.

The distribution of forecast errors (in visits per day) from a historical model of emergency department visit rates. These errors inhibit reliable detection of outbreaks. Specifically, minor outbreaks that cause only small increases in visit rates can be totally masked by these forecast errors.

Simulated Outbreaks.

The historical dataset used here was devoid of any known outbreaks. Because there is a paucity of data available on actual germ warfare attacks (12), we introduced a set of simulated outbreaks into the historical visit data by adding a certain number of simulated visits on specified days. Any experimental study with simulated outbreak data necessarily relies on assumptions about the nature of the outbreaks. To enable a systematic study to be performed, we parameterized the simulated outbreak models, varying the size, shape, and duration of the outbreaks.

Each complete 3,505-day simulation used outbreaks of only one size, shape, and duration. Three different shapes of outbreaks were tested: a fixed number of additional visits over a period, a linearly increasing number of visits, and an exponentially increasing number of visits. Many different sizes of outbreaks were also tested, ranging from 5 to 45 visits per day.

Three durations of 3, 7, and 14 days were tested. Although real outbreaks may last well beyond these durations, we focused on the first few days because useful detection systems should be able to spot outbreaks within that time frame.

The detection filters had a time window of at most 7 days. We therefore spaced all outbreaks 15 days apart, more than double this time window. This spacing ensured that all of the effects of any previous outbreak could be reset from the detection system's memory before the onset of the next outbreak. Furthermore, because the only significant periodicities present in the data were 7-day (weekly) and 365.25-day (yearly), the 15-day spacing of outbreaks yielded a good unbiased sample of days for infusing outbreaks. There were 233 simulated 7-day outbreaks in total in the data.

Detection Filters.

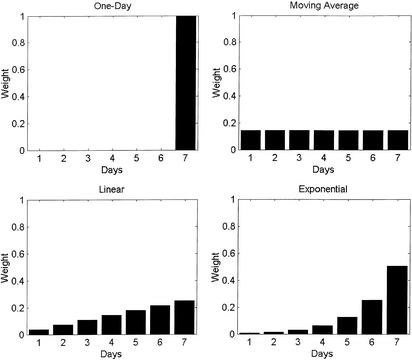
We set out to systematically study the effects of using a wider temporal context for detection. To this end, we investigated the performance of four different classes of detection filters (shown in Fig. 2), each attributing a different set of weights to the various days in a sliding 7-day detection window. Choosing these four representative examples of filter classes enables a systematic study to be done: (i) a standard 1-day detector representing the currently most widely used approach; (ii) a flat, moving average filter that weights all days in the time window equally; (iii) a linearly increasing filter with a slope of 1; and (iv) an exponentially increasing filter with each day given twice as much weight as the day before. The weights for each filter were normalized, so that the sum of the weights for all 7 days was 1.0.

Figure 2.

The shapes of four multiday temporal filters used for detecting disease outbreaks with a 7-day detection time window. The value for each day represents the relative weight attributed to that day by the detection filter.

Attempted outbreak detection was performed as follows. For each filter, a weighted sum was calculated over the 7-day sliding detection window: The forecast errors on each day were multiplied by the filter weights of the corresponding days of the sliding detection window. These products were then summed to form the overall detection score for each filter. If this score exceeded a predefined threshold, an alarm was triggered.

Calibration of Thresholds.

There are many possible ways to select alarm thresholds. To allow for comparison across different filters and outbreak types, we chose to set a fixed false-alarm rate (equivalent to 1 − specificity). This is an important and appropriate parameter to use as a benchmark, as surveillance systems that generate too many false alarms risk losing credibility. We tuned the threshold for each detection system to allow an average of 1 false alarm per month (12 per year, or 3.3%, probably a manageable level for intended users of surveillance systems) over the full 3,505 days of no-outbreak conditions. This false alarm rate can be adjusted to the needs of different systems.

Results

Simulations.

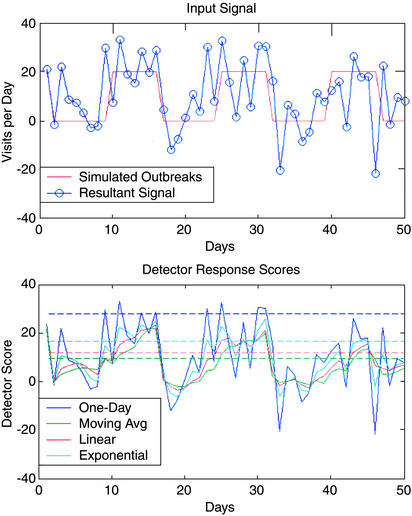
Fig. 3 shows the results of adding a series of simulated outbreaks of magnitude 20 visits per day and duration 7 days to the historical visit data. The top plot shows the input exceedance signal (blue): the actual number of visits minus the expected number of visits based on the model. The masking effects of noise can be seen clearly in the top plot; despite the addition of the simulated 20 extra visits (red), the resultant exceedance signal on some days still remains negative. This masking occurs when a large preexisting forecast error masks the additional visits of a simulated outbreak.

Figure 3.

Simulation results. (Upper) Stimulus: When adding simulated outbreaks (7-day, flat, size 20) to the noisy historical visit data, some outbreaks (red) are masked by the noise, appearing broken up in the resultant input exceedance signal (blue; actual visits minus expected visits plus outbreaks). (Lower) Response: The responses of the different temporal filters to the stimulus above. The dashed lines are the alarm thresholds for the various filters. Some filters react quickly to increased visit rates, whereas others react more slowly.

The bottom plot of Fig. 3 shows the responses of the different filters to the simulated outbreaks in the presence of the real noise signal. Some filters respond more quickly and dramatically than others to changes in the signal. These response characteristics have both benefits and drawbacks, as detailed below.

Specificity and Sensitivity.

The standard quantitative metrics of sensitivity and specificity were used to measure detection system performance. Of the 233 simulated outbreaks of size 20 visits per day, the four filters successfully detected 218 (1-day), 232 (moving-average), 230 (linear), and 228 (exponential).

In this article, we do not report sensitivities and specificities based on whole outbreaks, i.e., whether or not a particular outbreak was detected at any point during its progress. Instead, we view each day of an outbreak as an individual observation. Sensitivity is defined as the number of days with true alarms divided by the number of days with outbreaks. Specificity is defined as the number of days with true negatives divided by the number of nonoutbreak days. This more detailed approach toward measuring performance rewards earlier detection of outbreaks. It also allows careful study of the detection properties of the various filters, as described below.

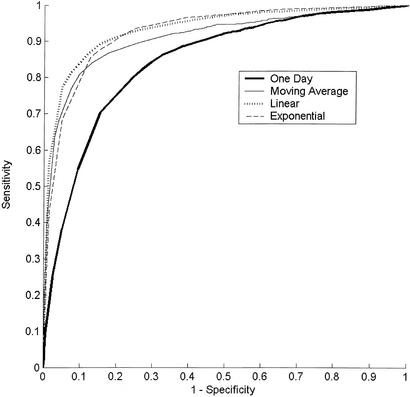
The sensitivities and specificities for the various filters are shown in Table 1 with 95% confidence intervals. To get a better sense of the tradeoff between sensitivity and specificity, Receiver Operator Characteristic (ROC) curves were calculated, plotting sensitivity vs. 1 − specifcity (Fig. 4). The area under the ROC curve serves as an aggregate measure of overall detection quality. The areas for the various filters are reported in Table 2 with 95% confidence intervals. Bivariate correlated χ² test statistics were calculated to test the statistical significance of the difference between the areas for the 1-day filter and each of the other filters. Confidence intervals and test statistics were calculated by using the rockit toolset (16).

Table 1.

Detection performance of filters given simulated outbreaks 7 days long and 20 visits per day, with 95% confidence intervals shown

Filter type	Sensitivity	Specificity
1-day	0.30 (0.28, 0.32)	0.97 (0.96, 0.98)
Moving avg.	0.65 (0.64, 0.68)	0.97 (0.96, 0.97)
Linear	0.71 (0.69, 0.73)	0.97 (0.96, 0.97)
Exponential	0.61 (0.60, 0.64)	0.97 (0.96, 0.98)

Figure 4.

ROC curve shows the tradeoff between sensitivity and specificity for all four filters, given outbreaks of size 20 visits per day.

Table 2.

Area under the ROC curve for all filters, with 95% confidence intervals for outbreak size 20

Filter type	Area	χ2 Test
1-day	0.85 (0.83, 0.86)	—
Moving avg.	0.91 (0.90, 0.92)	P < 0.0001
Linear	0.94 (0.93, 0.94)	P < 0.0001
Exponential	0.93 (0.92, 0.94)	P < 0.0001

Outbreak Size.

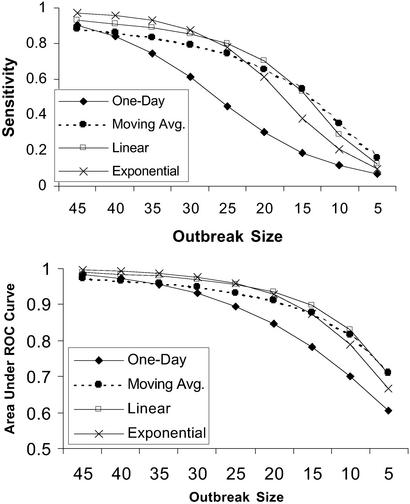
We varied the size of the simulated outbreaks to study the effects of outbreak size on detection performance. The top plot of Fig. 5 shows the sensitivities of the four filters as a function of outbreak size, all maintaining a fixed 0.97 benchmark specificity.

Figure 5.

Sensitivities using the benchmark specificity of 0.97 (Upper) and areas under the ROC curve (Lower) of the four filters, shown for a range of outbreak sizes.

Varying the signal size yielded the following results: As signal strength weakened with respect to noise, the sensitivity decreased for all of the filters. As signal strength rose, detection sensitivity improved for all filters, and the relative differences in sensitivities between the filters were less pronounced as the filters became saturated at their maximum sensitivities.

Another perspective on the effects of outbreak size is shown in the bottom plot of Fig. 5. The areas under the ROC curves are shown for all of the filters as a function of outbreak size.

Timeliness of Detection.

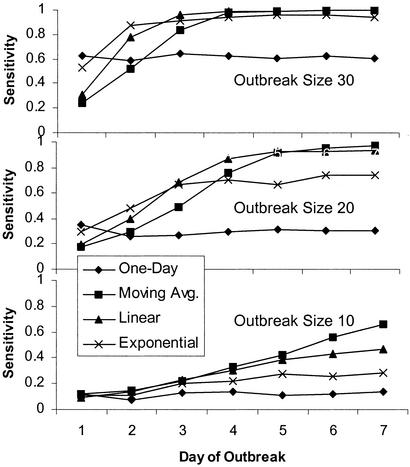
Fig. 6 shows the sensitivities of all four filters measured throughout the course of a flat, 7-day long, outbreak, maintaining the benchmark specificity of 0.97. Results are shown for outbreak sizes of 10, 20, and 30 visits per day.

Figure 6.

Timeliness of detection: Sensitivities of all four filters during different stages of the outbreaks, using the benchmark specificity of 0.97. Comparisons are shown for different outbreak sizes 30 (Top), 20 (Middle), and 10 (Bottom).

Outbreak Duration.

Shorter outbreak durations decreased the sensitivity of the temporally enhanced filters, as there were fewer days of temporal context available to help detect the signal in the presence of noise. Longer outbreak durations increased the sensitivities of all temporally enhanced filters. As expected, varying outbreak duration had no effect on the performance of the 1-day filter.

Outbreak Shape.

The shape of the outbreaks directly affected the shape of the filter's responses. For the purposes of the comparisons being investigated here, however, the relative advantages of the different filters applied similarly across different outbreak shapes.

Discussion

The results show that employing multiple temporal filters can enhance detection performance. These results build on the work of Williamson and Hudson (17), who suggest using multiple filters for detection, as well as Box and Luceno (11), whose cuscore statistics are used to detect specific signals in noisy series data.

It is not the goal of this article to describe a process for selecting a single filter that is best suited for a particular surveillance task. Instead, we characterize the performance of different filter types under varying conditions. We recommend that a detection system employ multiple filters simultaneously to provide a broader perspective on the data.

Sensitivity and Specificity.

As Table 1 shows, compared with the 1-day filter, each of the temporally enhanced filters yielded over twice the sensitivity while maintaining the same high benchmark specificity, resulting in much better overall detection performance.

Table 2 shows that the areas under the ROC curves of the temporally enhanced filters are greater than that of the 1-day filter. The χ² statistics have a P value of <0.0001, indicating that this difference in areas is statistically significant. The ROC analysis shows that the sensitivity advantages of the temporally enhanced filters apply broadly over a range of specificity levels and not just at the specificity level reported in Table 1.

Outbreak Size.

As shown in the top of Fig. 5, the temporally enhanced filters consistently outperform the 1-day filter. Note that each of the temporally enhanced filters in turn yields the best sensitivity for a different range of outbreak sizes. The moving average filter is best at smoothing out noise and picking up weak signals over many days and thus offers the greatest sensitivity in the noisiest environment: the smallest outbreaks. The exponential filter performs the least smoothing and is thus best at detecting the strongest signals: the largest outbreaks. The linear filter is a compromise between the two and delivers the best performance in the intermediate outbreak sizes.

Similarly, the bottom plot of Fig. 5 shows that all temporally enhanced filters outperform the 1-day filter in terms of area under the ROC curve. Again, each temporally enhanced filter delivers the largest area under the ROC curve at a different range of outbreak sizes.

Timeliness of Detection.

In developing surveillance systems, it is crucial to minimize the amount of time before an outbreak is detected. Fig. 6 shows the sensitivities measured throughout the course of a 7-day-long outbreak, maintaining the benchmark specificity of 0.97. Comparisons are shown for three outbreak sizes.

Even in cases where Fig. 5 indicates that one filter offers superior overall sensitivity for a particular outbreak size, Fig. 6 shows that all of the filters can offer superior sensitivity during specific stages of an outbreak. For example, for outbreak size 20, although Fig. 5 reveals that the linear filter offers superior overall sensitivity, the middle plot in Fig. 6 reveals that each of the four filters offers superior sensitivity for a particular stage of the outbreak. Based on all of the data above, the strengths and benefits of each filter will now be discussed in turn.

The 1-day filter inherently has no temporal context and achieves no smoothing. It thus performs best at the start of an outbreak when other filter's contexts still include nonoutbreak conditions. It is also the most vulnerable to noise of all of the filters compared here.

The moving average filter, although starting off with relatively poor sensitivity at the beginning of an outbreak, gradually improves over time. This slow build-up results from the fact that the 7 most recent days are all weighted equally, and so it takes continuous signal strength over an extended period to raise the detection score. Its broad temporal context means that this filter consistently reaches the highest sensitivity of any filter on the seventh day of an outbreak. The moving average filter is also the most robust to noise and thus offers the greatest advantage in the presence of weak signals.

The sensitivity of the linear filter is in most cases better than that of the moving average filter during the early and middle stages of an outbreak. This can be explained by the extra weight attributed to the more recent days, meaning that it takes less time to build up the detection score to the point when an alarm is triggered.

Of all of the temporally enhanced filters, the exponential filter has the heaviest emphasis on the recent days, giving it good sensitivity in the early stages of an outbreak. However, this also means that less weight is attributed to the wider temporal context, decreasing the system's capability to spot weak signals over many days, and limiting the ultimate sensitivity the system can reach.

The results suggest that temporally enhanced filters can help achieve earlier detection of outbreaks, enabling effective and timely public health interventions such as containment and prophylaxis. Even for larger outbreaks of size 30, where the 1-day filter offers the best sensitivity advantage on the 1st day of an outbreak, the exponential filter has 16% greater overall sensitivity over the first 2 days than the 1-day filter. (The overall sensitivities for the first 2 days are 0.61 and 0.70 for the 1-day and exponential filters, respectively). The difference in sensitivities is even greater for moderate outbreaks of size 20, where the exponential filter beats the 1-day filter by 27%. (The overall sensitivities for the first 2 days are 0.30 and 0.39 for the 1-day and exponential filters, respectively.)

This improved early detection capability allows more outbreaks to be detected within the first 2 days and is thus crucial for enabling an effective and timely response by public health authorities. Furthermore, if an outbreak is not caught within the first 2 days, the temporally enhanced filters offer even greater sensitivity advantages during the middle and later stages of an outbreak (in some cases many times greater than the 1-day filter; see Fig. 6), enabling more outbreaks to be detected overall.

We note also that the general approach of enhancing detection with different filters using expanded temporal context may have benefits in fields other than biosurveillance, specifically where the particular benefits of the various filters studied here are desirable.

Conclusions

The results from this systematic study indicate that using temporally enhanced filters can result in significantly improved sensitivity and early detection capabilities while maintaining a high specificity. These benefits are achieved primarily by combating noise through filtering (increased specificity) and by exploiting all of the information available in the full temporal context (increased sensitivity). These findings are both explained theoretically and supported experimentally by using historical visit data and simulated outbreaks.

Furthermore, each filter type has its own merits and drawbacks, with, for example, certain filters trading off timeliness of detection for maximum sensitivity. Based on these results, we recommend the development of an integrated multialarm framework, incorporating the use of multiple filters operating in parallel.

The results reported here can be put to use today in confronting the growing bioterrorist threat.