Abstract
Current theories of environmental cognition typically differentiate between an online, transient, and dynamic system of spatial representation and an offline and enduring system of memory representation. Here we present additional evidence for such two-system theories in the context of the disorientation paradigm introduced by Wang and Spelke (2000). Several experiments replicate the finding that disorientation results in a decrease in the precision of people’s estimates of relative directions. In contrast to the typical interpretation of this effect as indicating the primacy of a transient spatial system, our results are generally more consistent with an interpretation of it as indicating a switch from a relatively precise online representation to a relatively coarse enduring one. Further experiments examine the relative precision of transient and enduring representations, and show that switching between them does not require disorientation, but can also be produced by self-rotations as small as 135°.
Keywords: Spatial representation, spatial memory, egocentric updating, spatial updating, cognitive maps
Transient and enduring spatial representations under disorientation and self-rotation
Knowing the locations of objects in one’s environment is a fundamental competence that is critical for survival. Because of this, understanding how humans (and other animals) interpret, monitor, and internally represent spatial information about their environment has been one of the major driving issues in the contemporary study of spatial cognition. In the past 15 years, several investigators have proposed theories of environmental behavior that posit a two-system or two-process account of spatial cognition (Amorim, Glasauer, Corpinot, & Berthoz, 1997; Arbib, 1999; Creem & Proffitt, 1998; Easton & Sholl, 1995; Gallistel, 1990; Hartley & Burgess, 2005; Huttenlocher, Hedges, & Duncan, 1991; McNamara, 2003; Mou, McNamara, Valiquette, & Rump, 2004; Wang, 2000; Wang & Spelke, 2000). Although these accounts differ in many of their details, in general, they all contrast an online transient system that is chiefly supported by perceptual processes and that codes spatial information with relatively high precision, with an offline enduring system that is supported primarily by long-term memory and whose codes are relatively coarse and/or biased (for a review, see Allen & Haun, 2004; for details about the possible neural underpinnings of these systems, see Burgess, Jeffery, & O’Keefe, 1999; Colby & Olson, 2003). Despite the appeal of these theories, and the general consensus about the need for two-system approaches to spatial cognition, the variety of plausible models in the literature attests to the fact that most of the details (and, indeed, many of the fundamental tenets) of these theories have not been firmly established empirically.
One potential way to distinguish different two-system theories empirically is to note that they can differ dramatically in the degree to which they emphasize the importance of an offline, enduring system of spatial representation. Some models, such as those proposed by Gallistel (1990) and Mou et al. (2004) place primary emphasis on the organization of enduring memory representations of space. Gallistel, for example, frequently employs the metaphor of a “cognitive map,” (Tolman, 1948) which suggests that mental representations of space, like physical, cartographic maps, code information in an enduring form that is global and abstract enough to serve multiple functions. Similarly, Mou et al. emphasize the reference frames in which long-term representations of space are coded, and regard an online transient system as enabling little more than successful locomotion through one’s environment. On the other hand, the model proposed by Wang and Spelke (2000) concentrates primarily on the importance of transient and dynamic spatial codes that are monitored and updated in real time. In their model, enduring spatial representations are neither comprehensive nor abstract, but merely code for the geometry of one’s immediate environment, and are used only when reorienting oneself to this environment.
In the present paper we examine the circumstances under which enduring spatial representations tend to be used instead of transient and dynamic ones. Our approach will be to demonstrate an empirical phenomenon we call the disorientation effect that has, to date, been used as evidence for the existence and primacy of a transient and dynamic system of spatial representation (Wang & Spelke, 2000). In four experiments, we provide evidence for an alternative interpretation of this effect that enables us to examine the properties of both enduring and transient spatial representations, as well as the conditions under which one type of representation tends to be employed over the other. Our evidence will provide additional support for recent theories that posit the existence of two systems of spatial representation, and will further suggest that people rely quite readily on enduring, but relatively coarse, mental representations of their environment. To enable these endeavors, we must first describe the disorientation effect and consider some of the conclusions that can follow from it.
Wang and Spelke’s disorientation effect
Wang and Spelke (2000) noted that one way to establish that people rely on transient, dynamic representations of their environment is to examine what happens to people’s knowledge of the relative directions (i.e., the bearing differences) among locations in their environment after they have been disoriented. According to their logic, if pointing to unseen objects is exclusively driven by an enduring cognitive map, then disorientation should have no effect on people’s knowledge of the relative directions to targets. This is because, when using a cognitive map, people will rely on the same, unchanged, mental representation of their environment both before and after disorientation. On the other hand, if one’s knowledge consists of transient perceptual codes that relate oneself to the environment, then estimates of relative directions can be affected by disorientation. This is because, as one rotates, one must update multiple self-to-object spatial relationships individually, on a target-by-target basis. As one becomes disoriented, knowledge of the directions to targets is thus not lost at once, but is rather lost target-by-target. Similarly, when disoriented individuals are required to estimate directions, these directions are not computed at once from a global representation, but are rather computed individually, without regard to the metric properties of their overall configuration. This differential variability in recomputing self-to-object relationships after disorientation decreases the precision of people’s knowledge of relative directions.
In an elegant series of experiments, Wang & Spelke (2000) demonstrated that measures of participants’ error in estimating the relative directions to targets increased as a result of disorientation – a phenomenon we call the disorientation effect. Participants in their experiments learned the locations of several objects in a lab room, and then entered a small chamber, located in the center of the lab, where they sat on a rotating stool. While in the chamber, participants pointed several times to each object, both before and after a disorientation procedure. The variability of participants’ errors (defined on the basis of an initial round of pointing estimates made before disorientation) increased by a large (Cohen’s d ≈ 1.08) and statistically significant amount after disorientation. Wang and Spelke interpreted this effect as evidence for dynamic representations of space that were intact and precise before disorientation, but were “impaired” (p. 243) and “degraded” (p. 236) after disorientation. Based on this interpretation, Wang and Spelke concluded that their experiments cast doubt on the existence of enduring, comprehensive cognitive maps (see also Wang & Spelke, 2002) and suggested that transient egocentric codes constitute the “primary representations” (p. 244) used in human navigation.
Throughout this paper, we will pursue an alternative interpretation of the disorientation effect – one that is relatively accepting of the existence of rich, enduring mental representations of the environment. Rather than treating the effect of disorientation as an impairment of one’s transient egocentric knowledge, we explore the idea that, instead, disorientation results in a replacement of one’s transient knowledge with a more enduring, but less precise, long-term memory representation. By this account, both a transient and an enduring spatial representation is formed during learning, and the act of disorientation causes people to switch their reliance from one representation to the other. The disorientation effect is thus not interpreted as evidence of dynamic transient representations per se, but rather as evidence for both transient and enduring spatial representations. One observation that is consistent with this account is that, even after disorientation, participants’ knowledge of relative directions in Wang and Spelke’s experiments did not completely disappear. In fact, relative to chance performance (which is associated with an error of approximately 101°), participants’ mean error of approximately 20° was quite small. Although Wang and Spelke recognized that rich enduring spatial representations provided one way to describe the spatial knowledge that people retain after disorientation, their data were also consistent with the idea that people represented little more than a (non-spatial) ordered list of directions.
In the present paper, we examine the idea that the disorientation effect is the result of a switch between two types of representation, both of which code spatial information, but which differ in their permanence and fidelity. Our experiments will provide tentative support for this “switch” interpretation. Experiment 1 provides evidence that is consistent with our contention that both enduring and transient spatial representations mediate performance in Wang and Spelke’s (2000) paradigm. Experiment 2 then illustrates the idea that enduring spatial representations may be typically less precise than transient spatial representations. Having gained some empirical support for the assumptions underlying the switch hypothesis, Experiment 3 will examine another situation besides disorientation that can result in a switch in reliance between an online transient spatial representation and a more enduring memory of the environment. Finally, Experiment 4 will illustrate that the change from a transient to an enduring representation is better described as a discrete “switch” than as a gradual transformation.
Experiment 1
Most accounts of environmental cognition that put forward two separable systems of spatial representation or processing have provided evidence for these two systems by observing task dissociations. For example, Creem & Proffit (1998) demonstrated that people exhibit different patterns of accuracy between their verbal and motoric estimates of geographical slant. The differences between these types of estimates across time as well as their relative accuracy led Creem and Proffitt to conclude that two separable (though interactive) systems mediated performance – a perceptual-motor system that controlled motoric estimates in the short term, and an explicit cognitive system that controlled verbal estimates and delayed motoric estimates. Despite the appeal and clarity of these claims, it is possible for the evidence obtained by such task dissociations to be consistent with a single underlying system (Ashby & Ell, 2002; Dunn & Kirsner, 1988; Haun, Allen, & Wedell, 2005).
Relatively compelling evidence for two psychological systems can also be garnered by exhibiting a double dissociation, in which two tasks that putatively tap different systems interact with an independent variable to have opposite effects on the same dependent variable (Ashby & Ell, 2002; Baddeley, 2003; Ellis & Young, 1988). Such a disordinal interaction is often interpreted as evidence for two mental systems: one that enables relatively good performance on one task, and another that enables relatively good performance on the other task. We used Experiment 1 to exhibit a double dissociation in Wang and Spelke’s (2000) disorientation experiment as a means of providing support for our contention that two systems – both a transient and an enduring one – mediate performance in this paradigm.
To exhibit a double dissociation in Wang and Spelke’s (2000) disorientation paradigm, we asked participants in Experiment 1 to perform two different pointing tasks that putatively required either a transient egocentric spatial representation, or a more enduring and comprehensive memory of the environment. The pointing task that tapped the transient system (called “Egocentric pointing”) was identical to the task used by Wang and Spelke – participants pointed from their current location to a target in their local environment. By contrast, the pointing task that putatively required a more enduring memory system involved judgments of relative directions (JRDs), in which participants imagined being at a given position (that always differed from their actual position) and in a given orientation (that typically differed from their actual orientation) in their environment before judging the direction to a target. For example, a JRD trial might ask: “Imagine that you are at the TV, facing the door. Point to the fabric.” Judgments of relative direction are commonly used to assess memory of the object-to-object relationships in an environment (Mou et al., 2004; Shelton & McNamara, 2001) and are facilitated when one uses an enduring abstract representation (Mou et al., 2004). We thus expected performance on JRDs to be at least partially mediated by a system or process that employs relatively enduring and comprehensive spatial memories.
If, as Wang and Spelke (2000) suggest, performance in their experiment is controlled exclusively by transient and dynamic spatial codes, then one would predict that the effect of disorientation on JRDs would be similar to that of its effect on egocentric pointing. Without knowledge of one’s current orientation, direction estimates of all types would be computed individually, would be differentially error-prone, and would thus tend to have greater variable error than estimates made when oriented.
However, positing two systems of spatial representation enables one to predict that disorientation, while improving performance with egocentric pointing, will actually facilitate JRDs. This is because JRDs in the eyes-closed phase, when participants are still oriented to their environment, require participants to ignore information from their online transient system about their actual orientation. In such a case, the orientation information provided by the online transient system will interfere with the ability to imagine an alternative orientation in the JRD task. On the other hand, when one is disoriented, there is no online transient information about one’s current orientation, and this interferes relatively little with the processes required for making a JRD. There is a good deal of support for this interpretation of how one’s current awareness of his or her orientation affects performance on JRDs. Empirically, the difficulty of imagining alternative orientations generally corresponds to the disparity between one’s real and imagined heading (Presson & Montello 1994; Rieser, 1989; Waller, Montello, Richardson, & Hegarty, 2002; but see Mou et al., 2004). Moreover, imagining alternative orientations is facilitated when one has no awareness of one’s actual orientation (May, 1996; Waller et al., 2002). Theoretical accounts of these effects suggest that they can be largely explained in terms of interference between an online perceptual system and a higher-level cognitive system (May, 2004; Presson and Montello, 1994).
We thus anticipated that disorientation would result in improved performance on JRDs. On the other hand, based on the findings of Wang and Spelke, we anticipated that disorientation would result in impaired performance on egocentric pointing. These opposing effects of disorientation would then constitute a double dissociation, providing evidence for two systems of spatial representation. Dunn and Kirsner (1988) noted that such a double dissociation can provide particularly compelling evidence for two mental systems when it can additionally be shown that the two tasks (e.g., egocentric pointing and JRDs) can be positively associated with each other. We examined a likely positive association between tasks by correlating each participants’ performance on egocentric pointing with their performance on JRDs, anticipating a positive relationship. The resultant combination of a double dissociation and a positive association between tasks would constitute Dunn and Kirsner’s (1988) “reversed association,” and would thus provide compelling evidence for two systems of spatial representation that underlie performance in this paradigm.
Method
Participants
36 students (18 male, 18 female) participated in the experiment in return for credit in their Introductory psychology course.
Materials
Participants learned the locations of six objects (a shelf, a bolt of fabric, a table, a chair, a TV, and the chamber door) located in an 8.66 m x 8.40 m laboratory room (see Figure 1). These objects were laid out in the same configuration as illustrated in Figure 1 of Wang and Spelke (2000). Testing occurred within a 1.9 m x 1.9 m x 2.0 m high wood-framed chamber placed in the center of the laboratory. Three walls of the chamber and its ceiling were covered with opaque white fabric, and the fourth wall was covered with opaque red fabric (matching the chamber used by Wang and Spelke). During testing, participants sat on a 0.48 m high silently rotating stool and grasped a gun-shaped pointing device (ACT Labs PC USB Light Gun) in their hand. An Intersense InertiaCube was affixed to the pointer, providing online (72 Hz) measurements of the pointer’s direction (yaw) to within 1° of RMS accuracy. When participants pulled the trigger of the pointer, its current orientation was written to a data file for later analysis. During the blindfolded phases of the experiment, participants wore a “Mindfold” by Mindfold, Inc. (Tucson, AZ) – a commercial blindfold that comfortably surrounds the user’s eyes with foam and opaque black plastic. Four speakers were placed on the floor immediately outside the chamber, one at each corner. These speakers announced the target objects during testing, and at all other times, played a continual stream of white noise (76 dB-SPL, A-weighted). A script in the Python programming language controlled the presentation of the auditory stimuli and the recording of participants’ responses.
Figure 1.
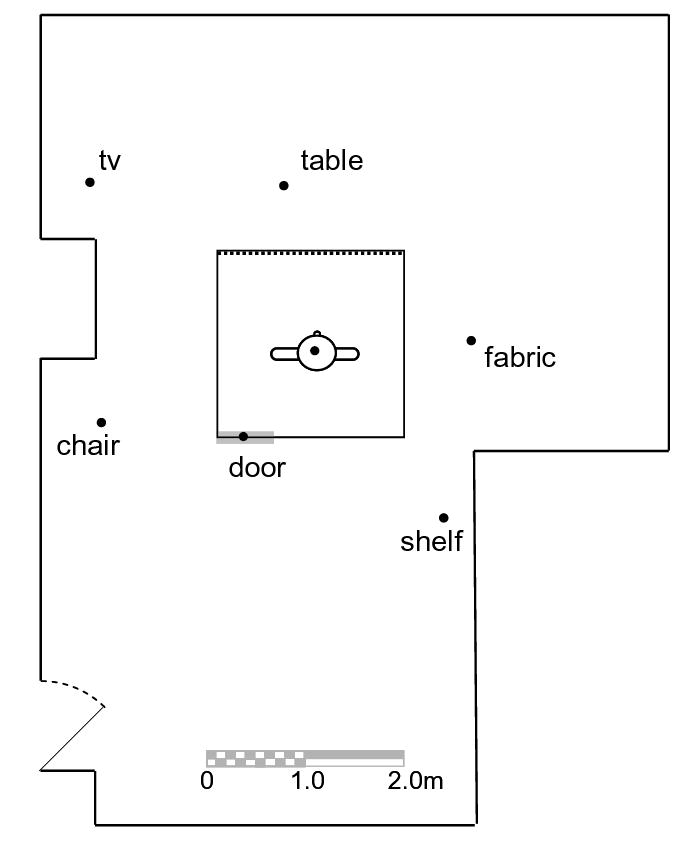
Plan view of the laboratory and object locations used in Experiments 1 and 2.
Procedure
In general, the procedures for Experiment 1 matched very closely those originally used in Experiment 2 of Wang and Spelke (2000). Participants were met in the laboratory, and introduced to the experiment and their tasks. In particular, during the introduction to the experiment, the experimenter instructed participants on the difference between the two types of pointing tasks, and administered several informal practice trials with JRDs based on a small array of objects on the lab floor. Next, the experimenter walked the participant past each of the six target objects, pointed to each, and named it. Participants were then told to continue studying where the objects were, and to notify the experimenter when they considered themselves ready to be tested. In general, participants spent between one and two minutes learning the placements of the objects.
When participants indicated that they were ready for testing, they were escorted into the chamber and asked to sit on the stool. To confirm that participants had adequately learned the layout, the experimenter asked the participant to point (with their hand) to each object. Had a participant made a mistake at this task, he or she would have been asked to exit the chamber and continue studying the layout; however, no participant erred during this initial test.1
The experimenter then handed the pointing device to the participant and instructed him or her that all subsequent targets would be announced by the computer, and that all subsequent pointing estimates would be made with the pointing device. The experimenter instructed the participant to point with whichever arm was most comfortable for each trial, and to point with their arm fully extended. Participants were told to take as much time as they needed on each trial to be as accurate as possible.
Each participant was then tested in three different phases, each of which consisted of a block of 12 egocentric pointing trials (two replications of each of the six targets) followed by a block of 12 JRDs (two replications of six randomly chosen inter-object angles). The order of questions was randomized separately for each participant, each phase (eyes-open, eyes-closed, and disoriented) and each task type (egocentric pointing and JRD) with the constraint that no two replicates were asked consecutively.
For each egocentric pointing estimate, the computer announced the target (e.g., “Point to the fabric.”), and the participant estimated its direction by pointing and then clicking the trigger button of the pointer. Each JRD trial began with an auditory message of the form “Imagine you are at the X, facing the Y”. Participants were instructed that when they could imagine themselves at the appropriate location, they should aim the pointing device directly in front of them (to simulate pointing to Y) and then click the trigger button of the pointer. On this click, a second auditory message of the form “Point to Z” announced the target. Participants then estimated the relative direction to the target by pointing the device and clicking a second time. The pointer’s orientation (yaw) for both clicks was recorded and used to compute a signed bearing difference that represented the estimated inter-object angle. In order to reduce the possibility of participants recognizing the same inter-object angle and simply repeating a previous response, replications of each JRD switched the order of the target and the imagined orienting object2. Thus, for example, if on one JRD trial, the participant was asked to point to the TV as if she was at the door, facing the shelf, then the “replication” of this JRD asked the participant to point to the shelf as if she was at the door facing the TV. Note that both replicates involve estimating the same inter-object angle.
Each phase of the experiment began when the participant pulled the trigger of the pointing device. This briefly caused the computer to stop playing white noise over the speakers and to announce the first target. For egocentric pointing trials during the first phase (eyes-open) of the experiment, participants were asked to face a random wall or corner of the chamber and to point to each target as it was announced. For JRDs during the eyes-open phase, the participant was told to move around the testing chamber and to assume physically the orientations (and to approximate the locations) that he or she was asked to imagine. For example, if an item asked a participant to imagine being at the table, facing the door (see Figure 1) the participant could move so that her back was against the wall of the chamber nearest the table, and thus make the JRD while physically facing the door. We encouraged participants to do this because, in general, the eyes-open phase serves as a baseline for assessing participants’ knowledge of the layout. Allowing participants to move during this phase enabled us to measure this knowledge while minimizing the possible interference from their online awareness of their physical orientation. All estimates in all other phases of the experiment were made while the participant was stationary and seated on the stool.
After pointing in the eyes-open condition, participants were asked to don their blindfolds and were then asked to turn themselves slowly to their left or right (counterbalanced) to a new orientation that was approximately 40° away from their previous facing direction. The second phase of pointing estimates (eyes-closed) then ensued, consisting again of a block of egocentric estimates and a block of JRDs. Next, participants were asked to turn slowly and continuously in their stool for one minute. They were told to spin quickly enough to become disoriented, but not enough to make them sick or dizzy. Participants were told (correctly) that, while they were spinning, the experimenter would walk around them, and that they could thus not use her voice as an orientation cue. After spinning in place for one minute, participants were given 30 seconds to sit quietly and to recover from any adverse effects of the spinning. As in previous phases, participants then made a block of egocentric estimates followed by a block of JRDs. Unlike the procedures used by Wang and Spelke (2000), we instructed participants at the beginning of the disoriented phase to imagine facing a randomly chosen object that was different from the nearest object they faced in the eyes open phase. To encourage participants to make consistent estimates relative to this facing direction, every fourth pointing command (beginning with the first) was preceded with the phrase “Given that you’re facing the X. . .” This procedure reduces the possibility that participants respond in the disoriented phase by imagining themselves in the same orientation as in a previous phase and by merely repeating motor movements across phases. Previous experiments (Waller & Hodgson, 2005) had indicated that, in comparison to the procedures used by Wang and Spelke, these additional procedures significantly reduce the variability with which participants point to individual targets (i.e., “pointing error,” described below).
When participants had completed all three phases, they were escorted out of the chamber and asked several follow-up questions. The experimenter asked the participant whether he or she could see through the blindfold, whether he or she had any awareness of his or her orientation after spinning, and whether he or she had enough time to recover from any dizziness that resulted from spinning.
Design, analysis, and dependent measures
Most of our statistical analyses rely on the construction and examination of 95% confidence intervals. The half-width of these intervals is appended to our parameter estimates. Null hypothesis significance tests generally involve planned comparisons in the context of the ANOVA. The experiment represents a fully within-subjects 2 (Task: Egocentric pointing vs. JRD) x 2 (Phase: Eyes-closed vs. Disoriented) design. For all ANOVAs conducted in this paper, gender was initially included as a factor, but failed to exhibit any significant effect or interaction. As a result, the analyses we report do not include gender as a factor. It is instructive to note, however, that for Experiment 1, the lack of a task by gender interaction demonstrates one variable (gender) across which the two tasks are likely to be positively associated (i.e., across genders, good/bad performance in the egocentric pointing task was associated with good/bad performance in the JRD task). This positive association constitutes one of Dunn and Kirsner’s (1988) conditions for exhibiting the existence of two mental systems by means of a reversed association.
We adopt the labels suggested by Cohen (1988) to describe the magnitudes of our effects. Post hoc power for null effects was computed using G*Power (Faul & Erdfelder, 1992) and was based on standard deviations of the difference scores between conditions (instead of the mean standard deviation between conditions) and on unbiased estimates of the population correlations of performance between within-subject conditions. Because effect sizes for the disorientation effect have not been well-established, we conducted these power analyses by holding power constant at .80, and then calculating the effect size in raw scale units (degrees) required to achieve this power.
We conducted our analyses separately on the three measures of directional error used by Wang and Spelke (2000). Each measure was calculated for each participant in the eyes-closed, and disoriented phases of the experiment based on the exact procedures used by Wang and Spelke (R. F. Wang, personal communication, July 29, 2003). Wang and Spelke called their first measure heading error (more commonly known as constant error – see Schmidt, 1982; Schultz & Roy, 1973) to examine whether participants were disoriented as a result of having spun in place. For each phase, heading error was calculated as the mean difference between pointing responses to the same target in that phase and the eyes-open phase. This measure is uniformly distributed3 when participants are disoriented and unimodally distributed around zero when they are oriented. It is important to note that our interpretation of the “disorientation effect” as a switch between two spatial representations does not regard disorientation as a necessary prerequisite. (Indeed, we will demonstrate in Experiments 3 and 4 that other procedures besides disorientation can result in a decrease in the precision of one’s knowledge of relative directions.) Thus, an analysis of heading error is not required by our interpretation of the disorientation effect. However, because previous investigations of the disorientation effect (Brou & Doane, 2003; Holmes & Sholl, 2005; Wang & Spelke, 2000) have examined heading error, we briefly include comparable analyses.
Second, to measure participants’ knowledge of relative directions, Wang and Spelke calculated a variable they called configuration error, which was defined for the eyes-closed and disoriented phases as the standard deviation of the signed bearing differences between pointing responses in that phase and the eyes-open phase. Because, for egocentric pointing estimates, this variable does not measure what many would regard as “configurational” knowledge (i.e., knowledge of object-to-object relations), we prefer to call it variable error instead of configuration error. In general, variable error will be low only when, relative to the eyes-open phase, direction estimates in a subsequent phase have shifted by approximately the same amount. On the other hand, variable error can be relatively large if either: (a) there is variability between targets in the errors of their direction estimates, or (b) there is variability among multiple pointing estimatess to an individual target. Because only the former source of variance represents a valid measure of people’s knowledge of relative directions, it is necessary to account for the latter “within-target” variation. Wang and Spelke did this by calculating a third variable, called pointing error, which was defined for each phase as the mean standard deviation of pointing responses to the same target, averaged over the six targets. Based on standard statistical assumptions, Wang and Spelke determined that the predicted change in variable error due to changes in pointing error equals the obtained change in pointing error divided by the square root of the number of times to which an individual target is pointed in each phase. In all experiments reported in this paper, the number of replicates per phase for each target is two.
Results
Heading error
Heading error was calculated on the basis of participants’ egocentric pointing responses. Heading error was unimodally distributed in the eyes-closed phase (r = .96, p < .005) and uniformly distributed in the disoriented phase (r = .24; p = .12).
Pointing error
For each phase of the experiment, pointing error was calculated for JRDs in the same way as it was calculated for egocentric pointing – as a mean standard deviation of estimates of the same inter-object angle, averaged over the six queried inter-object angles3. The bottom portions of the bars in Figure 2 illustrate that, in general, changes in pointing error as a result of disorientation were small (d = 0.15 for egocentric pointing and d = 0.30 for JRDs). For egocentric responses, pointing error rose 1.26° ± 2.80, from 10.79° ± 2.14 in the eyes-closed phase, to 12.05° ± 2.21 in the disoriented phase. For JRDs, pointing error fell 4.80° ± 5.33, from 39.19° ± 6.02 in the eyes-closed phase, to 34.39° ± 5.17 in the disoriented phase.
Figure 2.
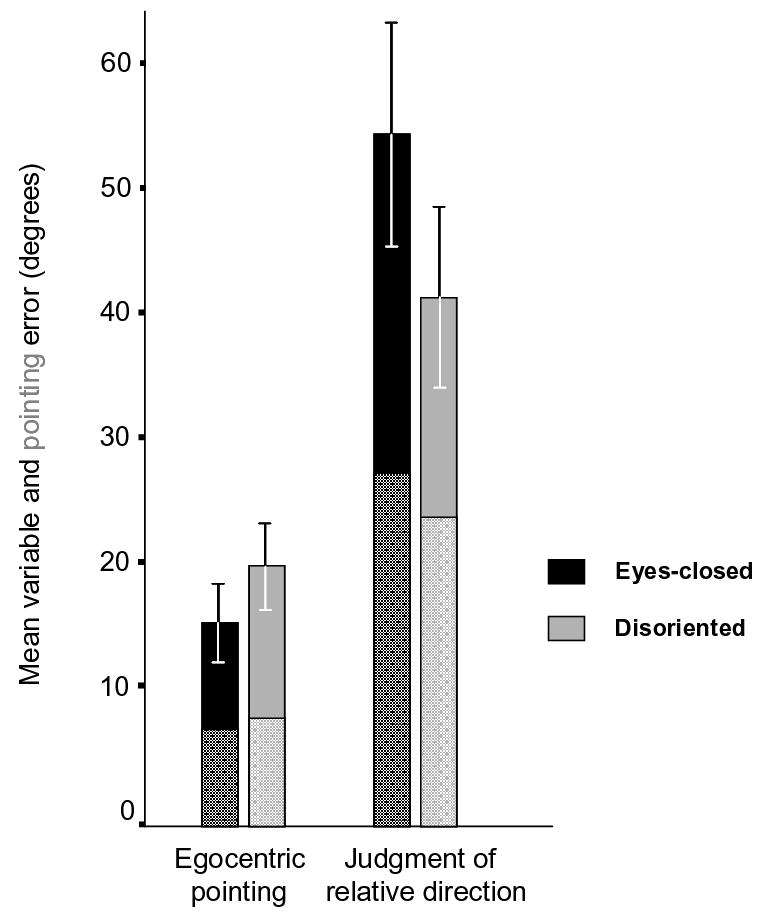
Mean variable error (defined in the text) for egocentric pointing and judgments of relative direction (JRDs) in the eyes-closed and disoriented phases of Experiment 1. The portion of variable error that can be accounted for by pointing error (defined in the text) is shown in the bottom region of each bar. Error bars represent 95% confidence intervals that include between-subject variation.
Variable error
In order to analyze (and portray) the same dependent variable for both egocentric pointing and JRDs, we calculated variable error for JRDs in the same was as we calculated variable error for egocentric pointing – as the standard deviation of the (signed) differences between estimates of bearing differences in the eyes closed (or disoriented) and eyes opened phases.4 Figure 2 illustrates that, in general, changes in variable error as a result of disorientation were moderate for both egocentric pointing (d = 0.45) and JRDs (d = 0.55). As predicted, these effects were in the opposite direction. For egocentric pointing, variable error rose 4.16° ± 3.15, from 15.96° ± 3.13 in the eyes-closed phase, to 20.12° ± 3.46 in the disoriented phase. Note that the confidence interval for the increase in variable error does not contain the 0.89° increase that would be predicted from participants’ increase in egocentric pointing error, indicating that the increase in variable error cannot be fully accounted for by increases in pointing error. For JRDs, variable error dropped 12.84° ± 7.87, from 54.40° ± 8.76 in the eyes-closed phase, to 41.57° ± 7.11 in the disoriented phase. Note that the confidence interval for this difference does not contain the 3.40° decrease that would be predicted from participants decrease in JRD pointing error.
The difference between the change in variable error for egocentric pointing and the change in variable error for JRDs was examined by testing the interaction effect in a 2 (task: Egocentric vs. JRD) x 2 (phase: eyes-closed or disoriented) ANOVA. This interaction was significant (F(1,35) = 13.81, MSE = 188.37, p = .001). As is evident from Figure 2, the main effect of task was also significant (F(1,35) = 73.69, MSE = 438.02, p < .001).
To assess the possibility of interference for JRDs made while oriented, we conducted an additional analysis on the JRDs in the eyes-closed phase to examine how the disparity between participants’ actual and imagined heading was related to their error in estimating bearing differences. For each participant and each trial in the eyes-closed phase, we computed an actual/imagined disparity as the absolute difference between the actual heading (indicated by their first trigger button press in the JRD trial) and the heading they were asked to imagine (indicated by the first trigger button press for the same JRD in the eyes-open phase). Similarly, for each trial, we computed error as the absolute difference between the participant’s indicated bearing difference (yaw at the first trigger button press minus the yaw at the second trigger button press) in the eyes-closed phase and their indicated bearing difference in the eyes-open phase. For each participant, we then correlated their actual/imagined disparity with their error across trials. These correlations averaged .19 ± .12.
Finally, we confirmed that performance on egocentric pointing was not negatively associated with performance on JRDs by calculating the correlation between variable error on the two tasks (each collapsed over the eyes-closed and disoriented phases). Our estimate of this correlation was small, but non-negative (r(34) = .16, p = .349).
Discussion
Variable error for egocentric pointing increased significantly as a result of disorientation, replicating the effect found by Wang and Spelke (2000). The effect of disorientation on variable egocentric error was much smaller in the present experiment than that obtained by Wang and Spelke; however, as they point out, any significant increase in variable egocentric error would not be predicted by theories positing that behavior is controlled exclusively by an enduring cognitive map of one’s environment. Our replication of Wang and Spelke’s disorientation effect thus implicates the existence of a transient online system of spatial representation that was presumably intact before disorientation.
Importantly, however, variable error for estimates of inter-object angles decreased as a result of disorientation – a result that would not be predicted by the hypothesis that behavior is controlled exclusively by a transient online spatial representational system. This double dissociation, in conjunction with the positive association between tasks that was demonstrated across subjects (and genders), constitutes a reversed association (Dunn and Kirsner, 1988), and is highly consistent with the hypothesis that pointing behavior in this experiment was based both on a transient online representation and on an enduring memory representation. This explanation fits well with contemporary theories of spatial cognition that posit the existence of two representational systems, and provides a basis of support for our interpretation of the disorientation effect as a switch between two types of representation. Further support for our interpretation that the decrease in variable error with JRDs as a result of disorientation was due to a lack of interference from the transient representation system comes from the observation that participants’ error on JRDs in the eyes-closed phase was, on average, significantly correlated with the disparity between their actual and imagined orientation. This suggests that, during the eyes-closed phase, participants’ awareness of their actual orientation interfered with their ability to perform JRDs.
Of course, any behavioral study that exhibits a double dissociation or a reversed association (including the present experiment) must be somewhat circumspect about the nature and constitution of the two systems for which it provides evidence. We have conceptualized Experiment 1 as providing additional support for existing theories of spatial cognition that posit two separable (though interacting) representational systems; however, the present data do not preclude the possibility of a single representational system on which multiple psychological processes operate. Thus, for example, it is possible to conceptualize the JRD task, not as involving an enduring memory system, but rather as involving a transformation of the representations used by a transient system. Such an explanation, however, would still need to rely on two “systems” to explain the present results, as long as one broadens the concept of different mental systems to include different sets of cognitive processes.
While the interaction effect of task and phase in Experiment 1 provides evidence that is consistent with two systems of spatial representation, another clear (though theoretically less interesting) effect involved the main effect of task. Figure 2 shows that variable error for JRDs was more than twice as high as it was for egocentric pointing (though both were well below the 101° that would be predicted by chance). Because JRDs had been posited to rely more heavily on an enduring spatial memory system than were egocentric pointing estimates, this finding is consistent with the hypothesis that enduring spatial representations are generally less precise than online egocentric representations of one’s immediate environment. This idea was explored more carefully in Experiment 2.
Experiment 2
One aspect of our interpretation of the disorientation effect as a switch between mental representations is the idea that the offline enduring memory system generally codes spatial information with less precision than that of the online transient system. This idea is consistent with several existing two-system theories of spatial cognition (Amorim et al., 1997; Creem & Proffitt, 1998; Huttenlocher et al., 1991) each of which contrasts a transient perceptual system that is relatively accurate and precise with an explicit cognitive system that is relatively error-prone.
Although Experiment 1 was consistent with the notion that enduring spatial representations are less precise than transient online representations, it cannot rule out at least two alternative explanations of the difference in precision between egocentric pointing and JRDs. First, it is possible that enduring spatial representations are equally (or perhaps more) precise as transient representations, but that our task requiring JRDs was simply more difficult than that requiring an egocentric response – perhaps because JRDs involve conflicts between actual and imagined headings. In Experiment 2, we address this issue by measuring both types of representations with the same egocentric pointing task. Second, it is possible that enduring spatial representations can be as precise as representations in the egocentric updating system, but that they require time or thorough familiarity to become precise. Indeed, it is rather easy to argue that the represented environment in Experiment 1 (a recently-learned, immediate, small-scale space) is not the type of environment that is normally considered as being represented in an enduring cognitive map. Instead, cognitive maps are typically conceptualized as long-term memory structures that enable the retrieval of spatial relations in large (Downs & Stea, 1973; Golledge, 1999; Trowbridge, 1913), well-learned (Shemyakin, 1966; Siegel & White, 1975), or remote environments.
In Experiment 2, we examined the relative precision of enduring and transient spatial representations in a situation in which we expected participants to have an enduring spatial memory that was as accurate and precise as possible. Participants were asked to point egocentrically to objects, before and after disorientation as if they were sitting in the middle of a highly familiar environment: their bedroom. If one grants that pointing in this condition is at all times governed by an enduring memory (i.e., it is rather implausible that participants in our lab were continuing to track their changing spatial relationships with the objects in their bedroom – see, for example, Wang & Brockmole, 2003a, 2003b), then we would expect no effect of disorientation on variable error in this condition. We can also use performance in this condition to examine the precision of an enduring spatial representation when it is likely to be as accurate and precise as possible. Based on prior theories that posit relatively lower precision in enduring than in transient systems (Amorim et al., 1997; Creem & Proffitt, 1998; Huttenlocher et al., 1991), we anticipated that an enduring memory – even when representing a structured, highly familiar, and overlearned environment – would be less precise than a transient representation of one’s immediate environment. Accordingly, we predicted that variable error in the Bedroom condition both before and after rotation would be greater than that in the eyes-closed phase of a Replication condition in which, as in Experiment 1, participants pointed egocentrically to objects in their immediate, recently-learned environment.
Method
Participants
54 students (27 male, 27 female) participated in the experiment in return for credit in their Introductory psychology course. Data from six participants were lost because of faulty tracking equipment. Analyses were conducted on the 48 (24 male, 24 female) participants with complete data.
Procedure
The procedures for Experiment 2 were identical to those of the egocentric pointing condition of Experiment 1.
The primary differences between Experiment 2 and Experiment 1 involved: (a) the addition of a new condition called the Bedroom condition, and (b) the elimination of JRDs . Before participating in the Bedroom condition, each participant was given a list of ten common items that could appear in a person’s bedroom. They were asked to check from this list all of the items that were in their own bedroom. The experimenter then entered the list of the participant’s bedroom objects into the computer and escorted the participant into the chamber for testing.
In each testing phase of the Bedroom condition, participants were asked to point to objects in their bedroom as if they were located at the center of their bedroom. In the initial pointing phase before the eyes-open phase, the computer controlled the verbal commands for the participant to point to all of the indicated bedroom objects on his or her list. The computer measured the indicated directions to each object and subsequently determined the subset of six indicated directions that had the maximal angular dispersal. The six targets associated with these indicated directions were then used for the eyes-open, eyes-closed and disoriented phases of the experiment. These phases of the Bedroom condition proceeded similarly as those in the Replication condition with the exception that at the beginning of the disoriented phase, participants were not asked to imagine facing a particular object, nor were they reminded to keep their answers consistent to their imagined heading. The order of conditions (Replication and Bedroom) was counterbalanced across participants.
Results
Heading error
Heading error for both the Replication and Bedroom conditions was unimodally distributed in the eyes-closed phase (Replication: r = .94, p < .005; Bedroom: r = .92, p < .005). Heading error was uniformly distributed in the disoriented phase of the Replication condition (r = .20, p = .16). Although heading error in the disoriented phase of the Bedroom condition was widely dispersed (r = .35), it was deemed by the Rayleigh test as being unimodally distributed (p < .005) around a mean of 6.28° ± 31.62. Because every participant subsequently reported being disoriented in this phase, and because previous experiments have shown that the procedures we followed are successful at producing disorientation, we assumed that participants in the disoriented phase of the Bedroom condition were disoriented. The necessity of this assumption is examined in Experiments 3 and 4.
Pointing error
The bottom portions of the bars in Figure 3 illustrate that, in general, changes in pointing error were small (d = 0.23 in the Replication and d = 0.04 in the Bedroom) as a result of disorientation. In the Replication condition, pointing error rose 2.37° ± 3.02, from 13.05° ± 2.81 in the eyes-closed phase, to 15.42° ± 2.83 in the disoriented phase. In the Bedroom condition, pointing error fell 0.46° ± 3.44, from 18.07° ± 4.58 in the eyes-closed phase, to 17.61° ± 3.90 in the disoriented phase.
Figure 3.
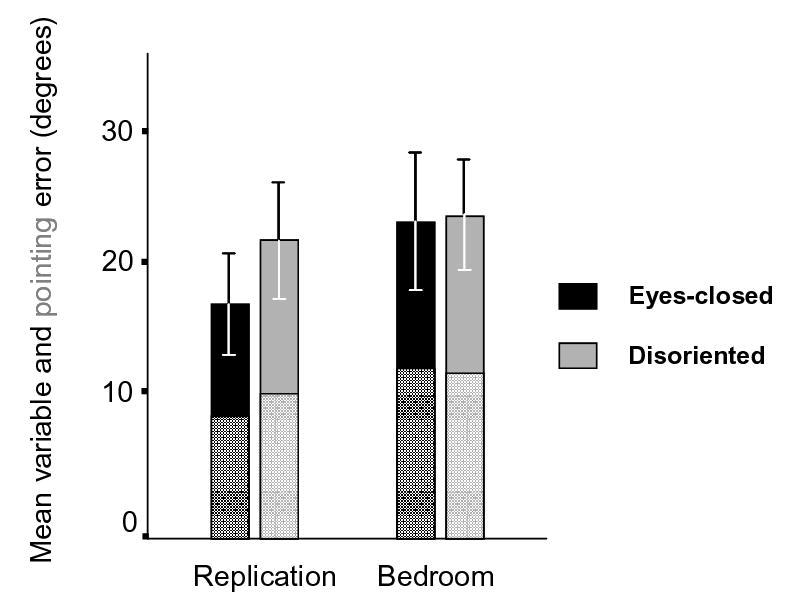
Mean variable error (defined in the text) for each environment in the eyes-closed and disoriented phases of Experiment 2. The portion of variable error that can be accounted for by pointing error (defined in the text) is shown in the bottom region of each bar. Error bars represent 95% confidence intervals that include between-subject variation.
Variable error
Figure 3 illustrates that, in general, changes in variable error as a result of disorientation were moderate (d = 0.50) in the Replication condition, but small (d = 0.03) in the Bedroom condition. In the Replication condition, variable error rose 4.73° ± 2.72, from 17.62° ± 3.84 in the eyes-closed phase, to 22.35° ± 4.36 in the disoriented phase. Note that the confidence interval for the increase in variable error does not contain the 1.68° increase that would be predicted from participants’ increase in pointing error, indicating that the increase in variable error cannot be fully accounted for by increases in pointing error. In the Bedroom condition, variable error rose 0.41° ± 4.54, from 23.70° ± 5.17 in the eyes-closed phase, to 24.11° ± 4.17 in the disoriented phase. Note that the confidence interval for the increase in variable error contains zero, as well as the 0.33° decrease that would be predicted from participants’ increase in pointing error.
Planned contrasts revealed that variable error in the Bedroom condition (collapsed over both eyes-closed and disoriented phases) was significantly different from variable error in the eyes-closed phase of the Replication condition (t(47) = 2.21, p = .032), but not significantly different from the disoriented phase of the Replication condition (t(47) = 0.54, p = .593). The power to detect this latter difference is discussed in the following section.
Discussion
In addition to again replicating Wang and Spelke’s (2000) disorientation effect, Experiment 2 provides support for two additional conclusions. First, the lack of a disorientation effect in the Bedroom condition suggests that the same spatial representation was likely used in both phases of this condition. It is probably non-controversial to consider this representation as an enduring spatial memory of a remote, familiar environment.
Second, and more importantly, if one grants that performance in the Bedroom condition relied on an enduring spatial representation, it is interesting that the performance based on this representation was significantly less precise than when participants pointed to recently-learned objects in their immediate environment. How could this be? Our participants presumably had had daily experience with their bedroom, and had seen it many times from a wide variety of perspectives. Moreover, objects in one’s bedroom are typically arranged purposefully, and this arrangement often adheres to a functional schema that would presumably aid in recall. Despite all of these factors that would have tended to enhance the accuracy of one’s representation of their bedroom, participants’ memory of their bedroom was less precise than was their memory of a briefly-viewed and randomly-placed set of objects in their immediate environment (prior to being disorientated). This result thus illustrates and strengthens the claim that enduring spatial representations are generally less precise than the transient egocentric representations that are implicated by the disorientation effect.
Despite the clarity of these conclusions, one methodological factor may enable an alternative interpretation of its results. In Experiment 2, participants in the Replication condition were asked to face a predetermined wall or corner of the testing chamber in the eyes open phase, and also to face another predetermined object in disoriented phase. However, they were not asked to assume an imagined orientation in any phase of the Bedroom condition. It is thus possible that, during all phases of the Bedroom condition of Experiment 2, participants imagined themselves facing in the same direction in their bedroom. Several studies have demonstrated that memory for room-sized spaces is stored with a single, “preferred” orientation (Shelton & McNamara, 2001; Roskos-Ewoldsen, McNamara, Shelton, & Carr, 1998; Waller et al., 2002), and thus it seems possible – perhaps likely – that, in the absence of instructions, participants would perform their pointing task by adopting this preferred orientation. If so, then, similar performance across phases of the experiment could have been the result of merely repeating the motor movements from an earlier phase.
In order to eliminate the possibility that participants were relying on a single, fixed imagined heading in the Bedroom condition, we conducted another experiment (n = 24) that was identical to Experiment 2 except that participants were instructed to imagine facing a different random bedroom object in the eyes open and disoriented phases of the Bedroom condition. The results of this experiment were nearly identical to those of Experiment 2. In the Replication condition, variable error rose 5.14° ± 2.72, from 12.21° ± 2.68 in the eyes-closed phase, to 17.34° ± 3.53 in the disoriented phase. This increase was greater than the 0.54° expected increase based on changes in pointing error. In the Bedroom condition, however, variable error rose only 1.58° ± 7.91, from 18.25° ± 6.34 in the eyes-closed phase, to 19.83° ± 5.17 in the disoriented phase. Planned contrasts revealed that variable error in the Bedroom condition (collapsed over both eyes-closed and disoriented phases) was significantly different from variable error in the eyes-closed phase of the Replication condition (t(23) = 2.99, p = .007.), but not significantly different from the disoriented phase of the Replication condition (t(23) = 0.75, p = .459). Because the results of this follow-up experiment were not qualitatively different from those of Experiment 2, the data from the two experiments were combined to estimate their power to uncover their null effects. Based on the combined data set, the change in variable error (before and after disorientation) in the Bedroom condition was still small (d = 0.05) and was estimated at 0.80° ± 3.90. For a paired-samples t-test to achieve a power of .80, the difference in variable error between phases would have needed to have been larger than 3.71° (corresponding to a Cohen’s d of 0.29). Similarly, the difference between variable error in the Bedroom condition (collapsed over the eyes-closed and disoriented phases) and the disoriented Replication condition was also small (d = 0.09) and was estimated at 1.60° ± 4.10. For a t-test to achieve a power of .80, the difference between these conditions would have needed to have been larger than 5.02° (corresponding to a Cohen’s d of 0.29).
Collectively, Experiments 1 and 2 are highly consistent with our interpretation of the disorientation effect as signifying a switch in reliance – from a transient and relatively precise spatial representation before disorientation, to an enduring and relatively coarse representation after disorientation. When one interprets the rise in variable error after disorientation as indicating such a switch, it seems entirely plausible that other situations besides disorientation may be able to produce this switch. We examined one such situation in Experiments 3 and 4.
Experiment 3
Although the previous experiments support the notion that disorientation is sufficient to cause a switch from a transient to an enduring representation, it is not clear that disorientation is necessary. In Experiment 3, we begin to examine other circumstances that might lead a person to switch their reliance from an online transient spatial representation to a more enduring memory representation.
Most theorists conceptualize transient spatial representations as relying predominantly on tightly-coupled dynamic information available from visual and idiothetic sensory modalities (see, for example, Rieser, Pick, Ashmead, & Garing, 1995). Accordingly, situations in which online sensory information is reduced, unavailable, or disrupted from its typical pattern of covariation could potentially cause a switch in reliance to an enduring memory representation. In the previous experiments, participants’ knowledge of relative directions was relatively precise in the eyes-open and eyes-closed phases of the experiment. Thus, the lack of concomitant visual information during the approximate 40° rotation between these two phases was apparently insufficient for participants to switch their reliance to a more enduring form of spatial memory.5 However, it is possible that performing a larger rotation would yield such a switch. We examined this possibility in Experiment 3 by asking participants to point to a set of objects while blindfolded, both before (in an eyes-closed phase) and after (in a rotated phase) rotating. Unlike the previous experiments, however, participants only spun approximately 135° between these phases. Although this rotation was more than the 40° between the eyes-open and eyes-closed phases of previous experiments, it was considerably less than the one minute of spinning between the eyes-closed and disoriented phases, and was not anticipated to induce disorientation.
Three different possible outcomes of this experiment correspond to different conclusions about the relationship between transient and enduring spatial representations. First, variable pointing error may not increase as a result of a self-rotation of 135°. We would interpret this result as signifying that people continue to rely on a relatively precise online transient representation of their environment through a 135° turn. Second, variable error may increase significantly, but not increase as much as it did in Experiments 1 and 2. We would interpret this result as evidence that transient spatial representations break down gradually as a result of rotation, and that the phenomenon of disorientation may not be an “all or nothing” event. Finally, it is possible that a rotation of 135° will result in an increase in variable error that is comparable to the increase resulting from disorientation that we observed in Experiments 1 and 2. This outcome would illustrate that disorientation is not necessary for the “disorientation effect,” and would be most consistent with our interpretation of the disorientation effect as a discrete switch between two types of spatial representation that differ in their precision.
Experiment 3 was conducted (but not reported) in a separate line of experiments that examined spatial updating of environments of varying complexity (Hodgson & Waller, in press). As such, its procedures differed slightly from those of Experiments 1 and 2. Most notably, participants in Experiment 3 were not tested within an enclosed chamber that was nested in the learned environment. The removal of the testing chamber meant that targets would have been visible during an “eyes-open” phase of the experiment. Because performance in such a phase would have relied on participants’ perception – not memory – of object directions, and because the perception of directions is generally considered to be veridical, we eliminated the eyes-open phase of the experiment and defined participants’ pointing errors relative to the true (instead of the indicated) directions to the targets. As a precaution, we examined the data from the 108 participants in Experiments 1 and 2 (including the data reported in the Discussion section of Experiment 2) to determine whether defining errors on the basis of the true (instead of the indicated) target directions might affect our results. In the eyes-closed conditions, for egocentric pointing to objects in one’s immediate environment, variable error computed on the basis of the true target direction averaged 15.79° ± 1.73. This was only 0.08° ± 1.59 different from the 15.86° ± 2.07 average we obtained when variable error was computed on the basis of the directions that participants had indicated in the eyes-open phase. Given this minimal difference between the two methods of computing errors, it was clear that Experiment 3 enabled us to address the issue of whether procedures other than disorientation can result in a significant increase in variable pointing error.
Method
Participants
27 students (12 female, 15 male) participated in return for credit in their introductory psychology course.
Materials
Participants learned a layout of six objects6 drawn from one of four different thematically-related sets of objects (kitchen objects, office objects, stuffed animals, or sports equipment). For each participant, the locations of these targets were randomly selected from a set of 15 predetermined positions that surrounded the participant in the lab room. The distances and directions between the participant and these possible positions were varied to create irregular stimulus arrays.
During the experiment, participants were seated on the rotating stool in the center of the layout. During testing, they wore a V8 virtual headset (HMD) that obstructed any vision of the layout, and displayed either an all-black screen or text instructions (i.e., “Point to the Cup”). Responses were made and recorded with the same gun-shaped pointing device and inertial tracker used in the previous experiments. Headphones mounted on the HMD played white noise that masked ambient noise during testing.
Procedure
After being briefly introduced to the experiment, participants were seated on the stool in the center of the lab room, where they were instructed that their task was to learn the locations of the six objects and to point to them while blindfolded before and after a small rotation. Participants were allowed to study the configuration of targets until they indicated that they were ready for testing (generally around one to two minutes). They were then given several practice trials with their eyes open in order to gain familiarity with using the pointing device. After this practice, they donned the HMD and were tested in both an eyes-closed and a rotated phase. Between these phases, participants were asked to rotate slowly either to the right or left (approximately counterbalanced across participants). After a rotation of approximately 135º, the experimenter instructed the participant to stop.
On each testing trial, text instructions (e.g., “Point to the Glue”) were displayed in the HMD, and remained until the participant indicated his or her pointing response by pulling the trigger on the pointing device. A two second delay then preceded the next trial. As with previous experiments, each target was tested twice per phase, once in two randomized blocks. Target order was randomized separately for each block, phase, and participant, with the constraint that no target was tested on two consecutive trials.
Results
Occasionally, participants pointed in the eyes-closed phase with uncharacteristically high error to an individual target (e.g., prior to rotating, one participant had a mean absolute error of 14º for 11 of the 12 trials, and an error of 104º error on the 12th). Because these outliers likely represented a failure of encoding, and not a failure of retrieval from either a transient or enduring spatial representation, we eliminated them from the data set. Thus, if a participant failed to point within 45º (half of chance) of the true location of a target on either trial before rotating, all trials that tested that particular object (both before and after rotation) were omitted for that participant. This criterion resulted in the omission of 16 trials, representing 2.4% of the data.
Heading error
Heading error was unimodally distributed both before (r = .99, p < .001) and after (r = .89, p < .001) the 135º rotation. Additionally, mean heading errors were very close to zero (4.92º ± 3.64 before rotation; 11.01º ± 10.42 after rotation), indicating that participants were oriented in both phases of the experiment.
Pointing error
The bottom portions of the bars in Figure 4 illustrate that pointing error did not change appreciably (d = 0.03) as a result of rotation. Pointing errors were 8.58º ± 2.22 and 8.77º ± 1.60 before and after the rotation, respectively, yielding a slight increase of 0.19º ± 2.45.
Figure 4.
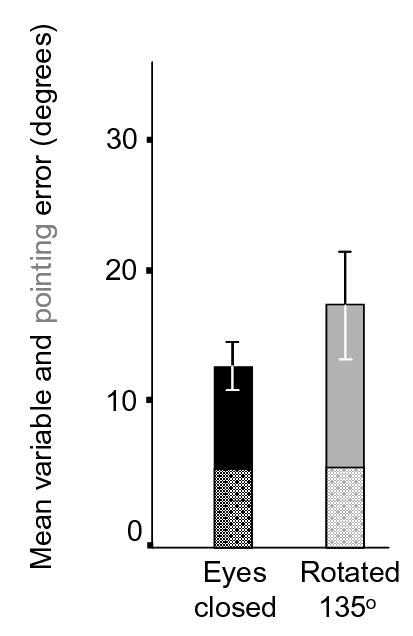
Mean variable error (defined in the text) for before and after rotation in Experiment 3. The portion of variable error that can be accounted for by pointing error (defined in the text) is shown in the bottom region of each bar. Error bars represent 95% confidence intervals that include between-subject variation.
Variable error
Variable error in Experiment 3 is illustrated in Figure 4. Because there was no eyes-open phase in this experiment, we calculated variable error for the eyes-closed and rotated phases based on the true – not the previously indicated – directions to the targets. By this measure, variable error increased moderately (d = 0.48) as a result of the 135º rotation. Variable error rose 4.72º ± 3.92, from 13.89º ± 1.85 in the eyes-closed phase to 18.61º ± 4.16 in the Rotated phase. Note that the 95% confidence interval for the increase in variable error does not contain the 0.13º increase that would be predicted from the change in pointing error, indicating that the rise in variable error cannot be accounted for by a rise in pointing error.
Discussion
Participants in Experiment 3 exhibited a rise in variable error comparable to that of participants in Experiments 1 and 2. However, unlike in prior experiments, it is very doubtful that participants in Experiment 3 showed this increase because they were disoriented. Heading error was unimodally distributed around zero before and after rotation, indicating that participants were generally oriented to their environment. These results thus illustrate that the act of disorientation is not necessary to exhibit the “disorientation effect.”
It is especially notable that the increase in variable error in participants’ pointing responses in this experiment (4.72°) was comparable to that in previous experiments in which participants were likely to have been completely disoriented (mean increase [weighted by sample size] in Experiments 1 and 2 = 4.63°). The equivalent magnitudes of this effect across these experiments cast further doubt on the idea that performance in this paradigm is controlled exclusively by online transient spatial representations. For example, although it may be possible to interpret the increase in variable error in Experiment 3 as merely an increase in difficulty with egocentric pointing as one rotates (as opposed to interpreting it as a switch to a different mental representation) it would not be clear under this interpretation why the further rotation and subsequent disorientation in Experiments 1 and 2 did not serve to increase this difficulty even further.
Although the increase in variable error as a result of self rotation was comparable to the significant increase in previous experiments, it is not clear from these experiments how this increase comes about. On one hand, it is possible that the precision of a transient representation degrades gradually as one turns (Wang & Spelke, 2000), and that by the time participants had rotated 135° their representations had already reached their maximum amount of degradation. According to this account, one would expect to find a gradual increase in variable error as participants approached the 135° rotation. Alternatively, it is possible that the increase in variable error resulting from a 135° rotation was not due to a gradual accumulation of error, but rather to a one-time switch to a qualitatively different mental representation. We examined the different predictions of these two accounts in Experiment 4.
Experiment 4
Experiment 3 suggested that participants readily adopt an enduring and relatively coarse spatial representation of their environment as a result of self-rotation. In Experiment 4, we examined more precisely how and when this change in representation might occur. Participants learned four separate layouts and pointed to targets in each one before and after either a 0°, 45°, 90°, or 135° self-rotation. If the effect of rotation and disorientation in our previous experiments is due to a gradual degradation of a transient representation, then we would expect a monotonic accrual of variable error over the four rotations. On the other hand, if the effect of rotation (and disorientation) is better described as a one-time switch between different representations, we would expect little or no effect of rotation until participants reach their “switch point”. These alternative predictions were tested with planned contrasts that represented linear and step-wise effects of rotation.
Method
Participants
48 students (24 male, 24 female) participated in the experiment in return for credit in their introductory psychology course.
Materials & Procedure
The materials and procedures for Experiment 4 were identical to those of Experiment 3 with the following exceptions. First, instead of learning a single layout of six targets, participants learned four layouts, one from each of four different thematically-related set of objects. Across these layouts, we manipulated the amount that the participant rotated (0º, 45º, 90º, or 135º) between the eyes-closed and rotated phases. Across participants, all possible orders of rotation magnitude were used an equal number of times.
Second, in order to exert more precise experimental control over the magnitude of participants’ turns, we programmed the computer to measure the participants’ rotation in each condition and to provide visual cues that signaled when they should stop turning. When a participant finished pointing to all targets in the eyes-closed phase, she was instructed to hold the pointing device directly in front of her and to depress the pointer’s button to begin the rotation. At this point, a green arrow was displayed in the HMD to indicate the direction of the turn (left or right). The participant then rotated in the indicated direction until seeing a red post centered in the display. Upon reaching this endpoint, she again depressed the button to indicate that she was finished turning. The arrow and post were rendered as fixed objects in an otherwise empty (black) virtual environment, and the view of this environment was updated with yaw readings from the inertial tracker mounted to the pointing device. Thus, participants had rudimentary visual flow available as they moved through a precisely-measured rotation. Participants were given practice with this rotation procedure before starting the experiment, and were informed that in one of the four layouts they would not have to rotate (0º condition).
Finally, we added a between-participant manipulation to disambiguate the role of time (time spent rotating) with that of distance (magnitude of rotation). Half of the participants (counterbalanced across gender) were asked to rotate slowly, while the other half were instructed to make a brisk turn.
Results
In general, instructions to rotate quickly or slowly were effective, but had no appreciable effect on our dependent measures. Participants’ rotation speed was calculated as the quotient of each turning angle and the time difference in trigger presses at the beginning and end of rotation. Participants who were instructed to turn quickly rotated on average at 13.67° ± 1.62 per second, which was significantly faster than the 10.79° ± 1.41 per second speed of those who were instructed to turn slowly (t(46) = 2.36, p = .023). Rotation time (slow versus fast) was entered as a factor in our analyses of pointing error and variable error, but neither exhibited a main effect nor interacted with the effect of rotation. The following results thus collapsed over this factor.
Heading error
For all four rotations, heading error was unimodally distributed both before and after rotation. Before rotation, mean vector lengths for the 0°, 45°, 90°, and 135° conditions were .98, .98, .98, and .99, respectively (all p’s < .001). After rotation, these mean vector lengths were .97, .94, .94, and .91 (all p’s < .001). 95% confidence intervals for the mean vectors in all conditions both before and after rotation included zero, indicating that participants were oriented in all portions of the experiment.
Pointing Error
In the 0° rotation condition, pointing error decreased 0.16° ± 1.77 between phases, from 8.67° ± 1.35 to 8.51° ± 1.53. In the other three conditions, pointing error increased after rotation. In the 45° condition, pointing error rose 2.03° ± 2.89, from 9.32° ± 2.51 to 11.35° ± 2.61. In the 90° condition, it rose 2.16° ± 1.80, from 7.74° ± 1.37 to 9.91° ± 1.74. In the 135° condition, it rose 3.29° ± 2.27, from 7.63° ± 1.35 to 10.91° ± 1.98.
Variable error
In the 0°, 45°, and 90° conditions, variable error did not increase beyond what would be predicted by changes in pointing error. More specifically, in the the 0° rotation condition, variable error decreased 0.53° ± 2.76 between phases, from 14.44° ± 2.29 to 13.92° ± 2.09. In the 45° condition, variable error increased 0.99° ± 4.18, from 16.01° ± 4.62 to 17.00° ± 2.34. In the 90° condition, variable error increased 1.28° ± 2.48, from 14.99° ± 2.58 to 16.27° ± 2.91. Note that, in each of these conditions, the confidence interval for the change in variable error contains both zero degrees, as well as the predicted 0.11°, 1.44°, and 1.53° change that would be predicted based on changes in pointing error in the 0°, 45°, and 90° conditions, respectively.
In contrast to these null effects, variable error increased 6.02° ± 3.39 after a 135° rotation, from 12.82° ± 2.02 to 18.84° ± 3.69°. Note that the 95% confidence interval for the increase in variable error does not contain the 2.33º increase that would be predicted from the change in pointing error, indicating that the rise in variable error cannot be accounted for by a rise in pointing error. The effects of rotation on variable error are depicted in Figure 5, which presents the mean increase in adjusted variable error across the four rotation conditions. Adjusted variable error was computed for each participant as the participant’s increase in variable error minus the increase in variable error that would be predicted by a change in pointing error. We tested several planned contrasts to examine linear and step-wise effects of rotation on changes in adjusted variable error. As is clear from Figure 5, the contrast testing for a step function at 135° (-1, -1, -1, 3) provided the best description of the effect of rotation, accounting for over 99% of the sums of squares of its main effect.
Figure 5.
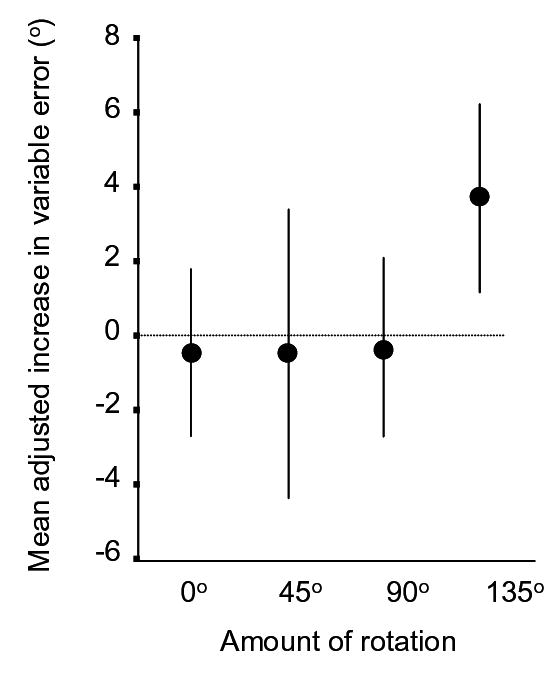
Mean increase in variable error (adjusted by the predicted increase based on pointing error) across rotations in Experiment 4. Error bars represent 95% confidence intervals that include between-subject variation.
Discussion
Experiment 4 replicated our finding from Experiment 3 that a rotation of 135° does not generally disorient people, yet is sufficient to result in a significant increase in variable pointing error. However, the present experiment makes clear that this increase does not occur before 90°. For turns of 0, 45, and 90 degrees, participants exhibited no significant increase in variable error. We interpret this lack of an effect as signifying that the same spatial representation was used to guide performance both before and after turns up to 90°. In accord with our previous interpretations (as well as those of Wang and Spelke, 2000), we suggest that this is a transient and dynamic online representation of one’s immediate environment.
On the other hand, for the larger rotation of 135°, variable error increased significantly as a result of rotation. As in previous experiments, we interpret this effect as signifying a switch in reliance, from an online transient representation to another, more enduring, spatial representation. This “switch” interpretation gains further support by noting the pattern of error differences over rotations in Figure 5. Instead of a gradual accumulation of error, sufficient rotation instead resulted in a sudden increase in variable error that is similar in magnitude to that of previous experiments, particularly those in which participants were completely disoriented. This pattern would not be expected if a transient representation slowly degraded as a result of sufficient rotation and/or disorientation. In general, then, these data support our interpretation of the effect of rotation/disorientation involving a one-time switch in reliance between two types of spatial representation.
The findings from Experiments 3 and 4 that disorientation is not necessary for an increase in variable error offers a possibility why other investigators have recently been unable to replicate the disorientation effect. Recently, Holmes and Sholl (2005) conducted five experiments that attempted to replicate Wang and Spelke’s disorientation effect in a recently-learned room-sized environment. In none of these experiments did participants’ knowledge of relative directions decrease significantly as a result of disorientation. However, if participants in Holmes and Sholl’s experiments had rotated sufficiently between the eyes-open and eyes-closed phases, it is possible that they had already begun to rely on an enduring and relatively coarse spatial representation in the eyes-closed phase of their experiments. Subsequent disorientation would thus not be expected to cause a switch in representations. The relatively high variable errors in both the eyes-closed and disoriented phases of Holmes and Sholl’s experiments help to corroborate this possibility. For example, the average variable error (weighted by sample size) in the eyes-closed phases of Holmes and Sholl’s Experiments 3 – 7 was 27.35°, which is yet larger than the 20.49° average variable error in the disoriented phases of our Experiments 1 and 2. It should be noted that this explanation of Holmes and Sholl’s failure to replicate comports well with their own theoretical explanation involving a “relaxation” of direction codes as a result of movement.
General Discussion
Our experiments generally provide strong additional support for Wang and Spelke’s (2000) finding that disorientation results in decreased precision at indicating the relative egocentric directions to locations in one’s environment. However, collectively, these experiments also serve to constrain the size and generality of the effect, as well as giving credence to an alternative interpretation of it that involves a ready reliance on enduring spatial representations. With respect to the magnitude of the disorientation effect, it is instructive to note that the increase in variable error in the present experiments ranged from 4.2° to 6.0°, which, although statistically significant, was markedly smaller than the 7° to 18° differences depicted by Wang and Spelke. Despite its smaller-than-anticipated magnitude, the reliable existence of the disorientation effect poses a challenge to theories of spatial knowledge that describe behavior as being controlled exclusively by an enduring cognitive map. Our demonstration of this effect thus offers additional evidence for a psychological system or process that is based on transient, dynamic egocentric codes.
Critically, however, these experiments also provide support for a second psychological system or process that is based on enduring and relatively imprecise spatial representations. Evidence consistent with the existence of two systems was provided by Experiment 1, in which we demonstrated that, in addition to decreasing the precision of estimates of egocentric directions, disorientation also results in increased precision for indications of the inter-target angles among objects in one’s environment. One of the more parsimonious explanations of this interaction is that two systems of spatial representation – a transient one and an enduring one – mediate performance in this paradigm. This interpretation fits well with contemporary theories of spatial cognition that posit two systems of spatial representation (Arbib, 1999; Amorim et al., 1997; Creem & Proffitt, 1998; Easton & Sholl, 1995; Gallistel, 1990; Hartley & Burgess, 2005; Huttenlocher et al., 1991; McNamara, 2003; Mou et al., 2004; Wang, 2000; Wang & Spelke, 2000).
If one grants that both transient and enduring spatial representations can influence performance in these experiments, then a natural avenue of inquiry is to determine the situations in which one type of representation is used over the other. We have suggested that the disorientation effect itself can be used to examine this issue, because it represents a switch from a relatively precise online transient representation to a relatively coarse enduring representation. Experiment 2 supported this interpretation of the disorientation effect by demonstrating that transient and enduring representations likely code spatial information with different levels of precision. Experiment 4 further bolstered our switch interpretation by suggesting that transient representations are not gradually degraded as one rotates, but are rather replaced wholesale by a relatively coarse spatial representation. Finally, Experiments 3 and 4 illustrated the readiness with which people switch to an enduring spatial representation and thus challenge theories of spatial cognition that regard transient dynamic codes as constituting the primary basis of spatial representation.
One issue raised by this investigation involves the nature of the imprecision in one’s spatial knowledge that is introduced by employing an enduring representation. What accounts for the additional variability in people’s knowledge of relative directions after disorientation? We found that the existing literature on the schematization of human spatial memory helps to inform this question. For example, several investigators have noted that estimates of the angles in one’s environment made from memory tend to be biased toward right angles (Byrne, 1979; Chase & Chi, 1981; Moar & Bower, 1983; Waller, Beall, & Loomis, 2004; see also Tversky, 1981). We examined this tendency in our experiments, exploring the hypothesis that rotation and disorientation caused our participants to “normalize” their estimates of the bearing differences between adjacent targets. To do this, we combined the data from the Replication conditions of Experiments 1 and 2 (including the supplementary experiment reported in the Discussion section of Experiment 2) as well as the data from Experiment 3, and the data from the 135° condition of Experiment 4. For each participant and each phase of the experiment, we computed an “orthogonality” score as the mean absolute difference between direction estimates for adjacent targets and the closer of 0°, 90°, or 180°. As expected, the change in mean orthogonality between the eyes-open (or, for Experiments 3 and 4, the actual directions) and the eyes-closed phases of the experiment condition was small (M = 0.62°, d = 0.12) and nonsignficant (t(155) = 1.48, p = .142). By contrast, the change in mean orthogonality between the eyes-open (or actual directions) and the disoriented (or rotated) phase was larger (M = 1.53°, d =0.28) and significant (t(155) = 3.46, p = .001). This finding indicates that some of the decreased precision in participants’ spatial knowledge after disorientation can be accounted for by a well-documented normalization bias that affects human memory for angles.
Elaborating two systems: a framework for understanding human spatial representation
In this closing section, we summarize what we believe these experiments tell us about how people represent the locations of objects in their environment. By our account, as a person interacts with an environment, two systems of spatial representation simultaneously work to code spatial information about the environment. A transient, egocentric representation system can dominate performance, but only when one is fully-oriented to his or her environment and one’s task demands interaction with the immediate environment. This system works to track the changing spatial relations between oneself and the objects in his or her environment. This online system is dynamic; its codes are transient, but relatively precise and accurate; and it works in real-time to enable immediate interaction with the environment. Typically, this system relies on tightly-coupled dynamic information available from visual and idiothetic modalities. However, the system can remain intact for short periods of time based solely on non-visual modalities such as vestibular, proprioceptive, and efferent information (Beritoff, 1965; Jürgens, Boß, & Becker, 1999; Loomis et al., 1993; Potegal, 1982) and may, in some circumstances, be able to operate solely on the basis of visual information (Riecke, van Veen, & Bülthoff, 2002). Thus, for example, in our Experiments 1 and 2, when participants entered the chamber in our lab after learning the locations of the targets, although they no longer had immediate visual access to their targets, the transient egocentric system was still able to use the nonvisual information (and perhaps optic flow) from their body movement to track the directions to the targets. As participants were blindfolded and rotated slightly before the eyes-closed phase, there was no visual information available to maintain their orientation; yet the transient egocentric system was still likely able to control performance, as evidenced by the relatively low variable error in the eyes-closed phase of these experiments.
When online information from the environment becomes unavailable for a relatively long period or is unreliable (e.g., after disorientation or sufficient self-motion), one’s performance switches its reliance from the transient egocentric system to an enduring representational system. The spatial representations in this system are based in long-term memory and are relatively stable over time, but are generally less precise than the representations in the transient egocentric system. The enduring representational system generally works remotely and offline, enabling one to judge the spatial relations of environments that are not immediately available to the senses. When sensory information about one’s immediate environment is restored or becomes relevant to one’s task, it is possible to switch reliance back to the transient egocentric system.
An important issue raised by this account involves better understanding how and when the transient egocentric system and the enduring representational system interact with each other. In Experiments 3 and 4, the interaction between these systems appeared mostly as a seamless hand-off of control from one system to the other. On the other hand, the results of Experiment 1 were consistent with the idea that the transient egocentric system can interfere with judgments that are based on enduring representations. In particular, in Experiment 1, the ability to judge relative directions from imagined perspectives (a task that presumably taps an enduring representational system) was impaired when people were oriented to their environment (and thus presumably had access to online information from the transient egocentric system). Recent work investigating the source of this impairment has implicated the conflict between high-level cognitive spatial representations and the egocentrically-referenced perceptual representations that are required for producing an action-based response (Avraamides, Klatzky, Loomis, & Golledge, 2004; May, 2004). In general, this literature has shown that action-based responses (such as the manual pointing used in the present experiments) are relatively more likely to lead to interference effects than are, for example, verbal responses (de Vega & Rodrigo, 2001; Wang, 2005; Wraga, 2003). In the present context, this literature suggests that the use of a manual pointing response in Experiment 1 may have been necessary in order to exhibit evidence for two systems of spatial representation. If this is true, then it would follow that the online transient spatial representations implicated by Wang and Spelke’s disorientation paradigm are intimately tied to the observer’s actions.
It is worth noting that, in addition to implicating two different types of spatial representation, the present results are also highly consistent with recent work positing two different types of spatial processing. A rich area of research in spatial cognition has investigated how people in motion account for (i.e., update) the changing relations between themselves and the objects in their environment. From our perspective, much of the literature on spatial updating has focused on examining situations in which people are likely to use transient, dynamic spatial representations (Avraamides et al., 2004; Farrell & Thomson, 1999, Klatzky, Loomis, Beall, Chance, & Golledge, 1998; Rieser, 1989). This literature has suggested that spatial updating is performed automatically (Farrell & Robertson, 1998; Farrell & Thomson, 1998; May & Klatzky, 2000) and in real-time (Farrell & Thomson, 1999; Lindberg & Gärling, 1981). However, our participants’ ready reliance on coarse enduring spatial representations suggests that people can forego the simultaneous online updating of multiple spatial relations in favor of an offline reconstructive process that works on enduring spatial memories. The present results thus offer support to recent theories of updating that posit the existence of two forms of spatial updating – an “online” form of updating that works in real time on dynamic spatial representations, and an “offline” form that works on enduring representations as a post-hoc reconstructive process (Amorim et al., 1997; Hodgson & Waller, in press; Loomis, Klatzky, Golledge, & Philbeck, 1999).
The two-system account of spatial representation described here is highly consonant with the model recently proposed by Mou et al. (2004; see also McNamara, 2003), and shares other similarities with theories proposed by Sholl and colleagues (Easton & Sholl, 1995; Holmes & Sholl, 2005). Each of these theories proposes a two-system account of spatial representation in which an egocentric system tracks relationships in one’s immediate environment, and an enduring memory system enables retrieval of spatial relations offline.
On the other hand, our theoretical account differs from these previous theories in several of its details. For example, Mou et al. (2004) describe their transient egocentric system as allowing people “to avoid obstacles, walk through doorways, stay on the sidewalk, and so on, but it does not prevent the observer from getting lost” (p. 154). However, for us, this system enables more than locomotion and obstacle avoidance. Locomotion and obstacle avoidance were not elements of participants’ task in our experiments, yet their knowledge of unseen locations was well-explained by an online egocentric system. Thus, in addition to the functions of maneuvering ascribed to the transient egocentric system by Mou et al., we regard one of its primary functions as keeping one oriented to specific objects in one’s immediate environment (i.e., not lost). Another difference between our framework and that proposed by Mou et al. concerns the degree of interactivity that is allowed between the two system. For example, unlike Mou et al.’s conceptualization, in which spatial relations coded in an enduring memory system (which they call the environmental subsystem) are relatively unaffected by physical movements in one’s immediate environment, our framework permits online movements registered by the egocentric updating system to interfere with the cognitive mapping system.
Similarly, several aspects of the present theory can be distinguished from Sholl’s theoretical framework (Easton & Sholl, 1995; Holmes & Sholl, 2005; Sholl, 2001). For example, whereas Holmes and Sholl (2005) interpret the disorientation effect as a “decline in the precision of the underlying metric codes” (p. 1086) we regard it as evidence for a switch between the codes contained in two separable systems.
A more notable difference between our work and Sholl’s is that we do not currently posit part of the enduring representational system as necessarily coding object-to-object relations in an allocentric frame of reference. We believe that the present data do not inform the question of which reference systems are used to represent object locations. In particular, our investigations (nor any investigations that have used Wang and Spelke’s [2000] disorientation paradigm) do not address whether enduring representations are coded with respect to an egocentric or nonegocentric reference system. Although spatial knowledge that is coded in a nonegocentric reference system is unlikely to be impaired by disorientation, it does not follow that an absence of the disorientation effect implies a nonegocentrically-coded representation. Indeed, in most of our experiments, participants were explicitly tested on their knowledge of self-to-object relationships. It seems most natural to consider these relationships as being directly coded in memory with respect to an egocentric reference system. Because the JRD task that we used in Experiment 1 involves estimating spatial relationships that are invariant over one’s movement through the environment, it is often assumed that this task involves retrieval of nonegocentric information (Mou et al., 2004). However, it is possible that egocentric (e.g., view-based or vector-based) representations are retrieved and transformed only as one’s task demands estimates of object-to-object relationships. Thus, while the present experiments inform us about the relative reliance on transient and enduring spatial representations, additional evidence – likely from other paradigms – will be required to draw conclusions about many of the properties of these representations.
Footnotes
One participant in Experiment 2 required a brief period of re-learning after this initial test.
Results and conclusions did not change qualitatively when JRDs were not collapsed over replicates, but were, rather, treated as 12 independent estimates in each phase.
Because indicated directions and signed bearing differences are circular variables (i.e., the highest possible value – 360° – is adjacent to the lowest, 0°) properties of their distributions were analyzed with circular statistics (see, for example, Batschelet, 1981). In particular, the uniformity of the distribution of heading error was tested with the Rayleigh test, which tests the significance of the length of the mean vector, r. In general, r is a measure of angular dispersion that ranges from zero to one and is relatively large when observations are relatively concentrated.
Although it is relatively common to analyze the variability of errors in direction estimates, it is generally uncommon to analyze the variability of errors in estimates of inter-object angles. Traditionally, such errors are analyzed by examining changes in mean absolute error. In this experiment, across all participants, absolute error (computed using the eyes-open phase as a baseline) was largely determined by variability – not bias. Both within and across participants, mean bias in JRDs was not significantly different from zero (for the eyes-closed condition t(35) = 1.12, p = .270; for the disoriented condition, t(35) = 0.85, p = .401). Thus, our measure of variable error that was calculated over bearing differences correlated extremely highly with the more traditional measure of mean absolute error (for the eyes-closed condition, r(34) = .98, p < .001; for the disoriented condition, r(34) = .98, p < .001). As a consequence, our results and conclusions would not change if we had measured mean absolute error for JRDs instead of variable error.
In Experiments 1 and 2, the rise in variable error (defined on the basis of the actual target directions) rose significantly between the eyes-open and eyes-closed phases; however, nearly all of this increase was explained by increases in pointing error.
Participants were also tested with sets of 4, 8, and 10 targets. The pattern of results for each set size was the same. Here, we focus on the set with six targets to facilitate comparison with prior experiments.
David Waller, and Eric Hodgson, Department of Psychology, Miami University, Oxford, Ohio. This research was partially supported by NIMH grant MH068245 to David Waller. We thank Amanda Campbell, Megan Crawford, and Morgan Gardai for assistance with conducting the experiments. We also thank John Dunn, Yvonne Lippa, Wayne Shebilske, Jeanne Sholl, and Frances Wang for helpful comments on previous drafts. Correspondence should be addressed to David Waller, Department of Psychology, Miami University, Oxford, OH 45056. Email: wallerda@muohio.edu
References
- Allen, G. L., & Haun, D. B. M. (2004). Proximity and precision in spatial memory. In G. L. Allen (Ed.), Human Spatial Memory: Remembering Where (pp. 41–63). Mahwah, NJ: Erlbaum.
- Amorim M, Glasauer S, Corpinot K, Berthoz A. Updating an object’s orientation and location during nonvisual navigation: A comparison between two processing modes. Perception & Psychophysics. 1997;59:404–418. doi: 10.3758/bf03211907. [DOI] [PubMed] [Google Scholar]
- Arbib, M. A. (1999). Parietal cortex and hippocampus: from visual affordances to the world graph. In N. Burgess, K. J. Jeffery, & J. O’Keefe (Eds.), The Hippocampal and Parietal Foundations of Spatial Cognition, (pp. 416–442). Oxford: Oxford University Press.
- Ashby, F. G., & Ell, S. W. (2002). Single versus multiple systems of learning and memory. In J. Wixted & H. Pashler (Eds.), Stevens’ Handbook of Experimental Psychology: Vol. 4 Methodology in Experimental Psychology (3rd ed., pp. 655–691). New York: Wiley.
- Avraamides MN, Klatzky RL, Loomis JM, Golledge RG. Use of cognitive versus perceptual heading during imagined locomotion depends on the response mode. Psychological Science. 2004;15:403–408. doi: 10.1111/j.0956-7976.2004.00692.x. [DOI] [PubMed] [Google Scholar]
- Baddeley A. Double dissociations: Not magic, but still useful. Cortex. 2003;39:129–131. doi: 10.1016/s0010-9452(08)70082-0. [DOI] [PubMed] [Google Scholar]
- Batschelet, E. (1981). Circular Statistics in Biology London: Academic Press.
- Beritoff, J. S. (1965). Neural Mechanisms of Higher Vertebrate Behavior Boston: Little, Brown.
- Brou RJ, Doane SM. Individual differences in object localization in virtual environments. Spatial Cognition & Computation. 2003;3:291–314. [Google Scholar]
- Burgess, N., Jeffery, K. J., & O’Keefe, J. (Eds.) (1999). The hippocampal and parietal foundations of spatial cognition. Oxford: Oxford University Press.
- Byrne RW. Memory for urban geography. Quarterly Journal of Experimental Psychology. 1979;31:147–154. [Google Scholar]
- Chase, W. G., & Chi, M. T. H. (1981). Cognitive skill: Implications for spatial skill in large-scale environments. In J. H. Harvey (Ed.), Cognition, Social Behavior, and the Environment (pp. 111–135). Hillsdale, NJ: Erlbaum.
- Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences (2ndEd.) Hillsdale, NJ: Erlbaum.
- Colby, C. L., & Olson, C. R. (2003). Spatial Cognition. In L. R. Squire, F. E. Bloom, S. K., McConnell, J. L. Roberts, N. C. Spitzer, & M. J. Zigmond (Eds.), Fundamental neuroscience (pp. 1229–1247). New York: Academic Press.
- Creem SH, Proffitt DR. Two memories for geographical slant: Separation and interdependence of action and awareness. Psychonomic Bulletin & Review. 1998;5:22–36. doi: 10.3758/bf03209455. [DOI] [PubMed] [Google Scholar]
- de Vega M, Rodrigo MJ. Updating spatial layouts mediated by pointing and labeling under physical and imaginary rotation. European Journal of Cognitive Psychology. 2001;13:369–393. [Google Scholar]
- Downs, R. M., & Stea, D. (1973). Image and Environment Chicago: Aldine.
- Dunn JC, Kirsner K. Discovering functionally independent mental processes: The principle of reversed association. Psychological Review. 1988;95:91–101. doi: 10.1037/0033-295x.95.1.91. [DOI] [PubMed] [Google Scholar]
- Easton RD, Sholl MJ. Object-array structure, frames of reference, and retrieval of spatial knowledge. Journal of Experimental Psychology: Learning, Memory, & Cognition. 1995;21:483–500. doi: 10.1037//0278-7393.21.2.483. [DOI] [PubMed] [Google Scholar]
- Ellis, A. W., & Young, A. W. (1988). Human Cognitive Neuropsychology. Hillsdale, NJ: Erlbaum.
- Farrell MJ, Robertson IH. Mental rotation and automatic updating of body-centered spatial relationships. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1998;24:227–233. [Google Scholar]
- Farrell MJ, Thomson JA. Automatic spatial updating during locomotion without vision. Quarterly Journal of Experimental Psychology A: Human Experimental Psychology. 1998;51A:637–654. doi: 10.1080/713755776. [DOI] [PubMed] [Google Scholar]
- Farrell MJ, Thomson JA. On-line updating of spatial information during locomotion without vision. Journal of Motor Behavior. 1999;31:39–53. doi: 10.1080/00222899909601890. [DOI] [PubMed] [Google Scholar]
- Faul, F., & Erdfelder, E. (1992). GPOWER: A priori, post-hoc, and compromise power analysis for MS-DOS [Computer Program]. Bonn, FRG: Bonn University, Department of Psychology.
- Gallistel, C. R. (1990). The Organization of Learning Cambridge, MA: MIT Press.
- Golledge, R. G. (1999). Human wayfinding and cognitive maps. In R. G. Golledge (Ed.), Wayfinding Behavior: Cognitive Mapping and Other Spatial Processes, (pp. 5–45). Baltimore: Johns Hopkins University Press.
- Hartley T, Burgess N. Complementary memory systems: competition, cooperation, and compensation. Trends in Neuroscience. 2005;28:169–170. doi: 10.1016/j.tins.2005.02.004. [DOI] [PubMed] [Google Scholar]
- Haun DBM, Allen GL, Wedell DH. Bias in spatial memory: A categorical endorsement. Acta Psychologica. 2005;118:149–170. doi: 10.1016/j.actpsy.2004.10.011. [DOI] [PubMed] [Google Scholar]
- Hodgson, E., & Waller, D. (in press). Lack of set size effects in spatial updating: Evidence for offline updating. Journal of Experimental Psychology: Learning, Memory, & Cognition. [DOI] [PubMed]
- Holmes MC, Sholl MJ. Allocentric coding of object-to-object relations in over-learned and novel environments. Journal of Experimental Psychology: Learning, Memory, & Cognition. 2005;31:1069–1087. doi: 10.1037/0278-7393.31.5.1069. [DOI] [PubMed] [Google Scholar]
- Huttenlocher J, Hedges LV, Duncan S. Categories and particulars: Prototype effects in estimating spatial location. Psychological Review. 1991;98:352–376. doi: 10.1037/0033-295x.98.3.352. [DOI] [PubMed] [Google Scholar]
- Jürgens R, Boß T, Becker W. Estimation of self-turning in the dark: Comparison between active and passive rotation. Experimental Brain Research. 1999;128:491–504. doi: 10.1007/s002210050872. [DOI] [PubMed] [Google Scholar]
- Klatzky RL, Loomis JM, Beall AC, Chance SS, Golledge RG. Updating an egocentric spatial representation during real, imagined, and virtual locomotion. Psychological Science. 1998;9:293–298. [Google Scholar]
- Lindberg E, Gärling T. Acquisition of locational information about reference points during blindfolded and sighted locomotion: Effects of a concurrent task and locomotion paths. Scandinavian Journal of Psychology. 1981;22:101–108. doi: 10.1111/j.1467-9450.1981.tb00384.x. [DOI] [PubMed] [Google Scholar]
- Loomis JM, Klatzky RL, Golledge RG, Cincinelli JG, Pellegrino JW, Fry PA. Nonvisual navigation by blind and sighted: Assessment of path integration ability. Journal of Experimental Psychology: General. 1993;122:73–91. doi: 10.1037//0096-3445.122.1.73. [DOI] [PubMed] [Google Scholar]
- Loomis, J. M., Klatzky, R. L., Golledge, R. G., & Philbeck, J. W. (1999). Human navigation by path integration. In R. G. Golledge (Ed.), Wayfinding behavior: Cognitive mapping and other spatial processes (pp. 125–151). Baltimore: Johns Hopkins Press.
- May M. Cognitive and embodied modes of spatial imagery. Psychologische Beitrage. 1996;38:418–434. [Google Scholar]
- May M. Imaginal perspective switches in remembered environments: Transformation versus interference accounts. Cognitive Psychology. 2004;48:163–206. doi: 10.1016/s0010-0285(03)00127-0. [DOI] [PubMed] [Google Scholar]
- May M, Klatzky RL. Path integration while ignoring irrelevant movement. Journal of Experimental Psychology: Learning, Memory, & Cognition. 2000;26:169–186. doi: 10.1037//0278-7393.26.1.169. [DOI] [PubMed] [Google Scholar]
- McNamara, T. P. (2003). How are the locations of objects in the environment represented in memory? In C. Freksa, W. Brauer, C. Habel, & K. Wender (Eds.), Spatial cognition III: Routes and navigation, human memory and learning, spatial representation and spatial reasoning (pp. 174–191). Berlin: Springer-Verlag.
- Moar I, Bower GH. Inconsistency in spatial knowledge. Memory & Cognition. 1983;11:107–113. doi: 10.3758/bf03213464. [DOI] [PubMed] [Google Scholar]
- Mou W, McNamara TP, Valiquette CM, Rump B. Allocentric and egocentric updating of spatial memories. Journal of Experimental Psychology: Learning, Memory, & Cognition. 2004;30:142–157. doi: 10.1037/0278-7393.30.1.142. [DOI] [PubMed] [Google Scholar]
- Potegal, M. (1982). Vestibular and neostriatal contributions to spatial orientation. In M. Potegal (Ed.), Spatial Abilities: Development and Physiological Foundations (pp. 361–387). New York: Academic Press.
- Presson CC, Montello DR. Updating after rotational and translational body movements: Coordinate structure of perspective space. Perception. 1994;23:1447–1455. doi: 10.1068/p231447. [DOI] [PubMed] [Google Scholar]
- Riecke BE, van Veen HAHC, Bülthoff HH. Visual homing is possible without landmarks: A path integration study in virtual reality. Presence: Teleoperators & Virtual Environments. 2002;11:443–473. [Google Scholar]
- Rieser JJ. Access to knowledge of spatial structure at novel points of observation. Journal of Experimental Psychology: Learning, Memory, & Cognition. 1989;15:1157–1165. doi: 10.1037//0278-7393.15.6.1157. [DOI] [PubMed] [Google Scholar]
- Rieser JJ, Pick HL, Ashmead DH, Garing AE. Calibration of human locomotion and models of perceptual-motor organization. Journal of Experimental Psychology: Human Perception and Performance. 1995;21:480–497. doi: 10.1037//0096-1523.21.3.480. [DOI] [PubMed] [Google Scholar]
- Roskos-Ewoldsen B, McNamara TP, Shelton AL, Carr W. Mental representations of large and small spatial layouts are orientation dependent. Journal of Experimental Psychology: Learning, Memory, & Cognition. 1998;24:215–226. doi: 10.1037//0278-7393.24.1.215. [DOI] [PubMed] [Google Scholar]
- Schmidt, R. A. (1982). Motor Control and Learning Champaign, IL: Human Kinetics.
- Schultz RW, Roy EA. Absolute error: The devil in disguise. Journal of Motor Behavior. 1973;5:141–153. doi: 10.1080/00222895.1973.10734959. [DOI] [PubMed] [Google Scholar]
- Shelton AL, McNamara TP. Systems of spatial reference in human memory. Cognitive Psychology. 2001;43:274–310. doi: 10.1006/cogp.2001.0758. [DOI] [PubMed] [Google Scholar]
- Shemyakin, F. N. (1966). Orientation in space. In G. G. Anan’yev et al. (Eds.) Psychological Science in the USSR. Vol 1, Part 1 (pp. 186–255). Washington, DC: US Office of Technical Reports.
- Sholl, M. J. (2001). The role of a self-reference system in spatial navigation. In D. R. Montello (Ed.) Spatial Information Theory: Foundations of Geographic Information Science (International Conference, COSIT 2001 Proceedings) (pp. 217–232). Berlin: Springer-Verlag.
- Siegel, A. W., & White, S. H. (1975). The development of spatial representations of large-scale environments. In H. Reese (Ed.), Advances in Child Development and Behavior, Vol. 10 (pp. 10–55). New York: Academic Press. [DOI] [PubMed]
- Tolman EC. Cognitive maps in rats and men. Psychological Review. 1948;55:189–208. doi: 10.1037/h0061626. [DOI] [PubMed] [Google Scholar]
- Trowbridge CC. On fundamental methods of orientation and ‘imaginary maps’. Science. 1913;38:888–897. doi: 10.1126/science.38.990.888. [DOI] [PubMed] [Google Scholar]
- Tversky B. Distortion in memory for maps. Cognitive Psychology. 1981;13:407–433. [Google Scholar]
- Waller D, Beall AC, Loomis J. Using virtual environments to asses directional knowledge. Journal of Environmental Psychology. 2004;24:105–116. [Google Scholar]
- Waller, D., & Hodgson, E. (2005). Two systems of human spatial memory: Egocentric updating and cognitive mapping. Unpublished manuscript.
- Waller D, Montello DR, Richardson AE, Hegarty M. Orientation specificity and spatial updating of memories for layouts. Journal of Experimental Psychology: Learning, Memory, & Cognition. 2002;28:1051–1063. doi: 10.1037//0278-7393.28.6.1051. [DOI] [PubMed] [Google Scholar]
- Wang RF. Representing a stable environment by egocentric updating and invariant representations. Spatial Cognition & Computation. 2000;1:431–445. [Google Scholar]
- Wang RF. Beyond imagination: Perspective change problems revisited. Psicologica. 2005;26:25–38. [Google Scholar]
- Wang RF, Brockmole JR. Human navigation in nested environments. Journal of Experimental Psychology: Learning, Memory, & Cognition. 2003a;29:398–404. doi: 10.1037/0278-7393.29.3.398. [DOI] [PubMed] [Google Scholar]
- Wang RF, Brockmole JR. Simultaneous spatial updating in nested environments. Psychonomic Bulletin & Review. 2003b;10:981–986. doi: 10.3758/bf03196562. [DOI] [PubMed] [Google Scholar]
- Wang RF, Spelke ES. Updating egocentric representations in human navigation. Cognition. 2000;77:215–250. doi: 10.1016/s0010-0277(00)00105-0. [DOI] [PubMed] [Google Scholar]
- Wang RF, Spelke ES. Human spatial representation: Insights from animals. Trends in Cognitive Science. 2002;6:376–382. doi: 10.1016/s1364-6613(02)01961-7. [DOI] [PubMed] [Google Scholar]
- Wraga MJ. Thinking outside the body: An advantage for spatial updating during imagined versus physical self-rotation. Journal of Experimental Psychology: Learning, Memory, & Cognition. 2003;29:993–1005. doi: 10.1037/0278-7393.29.5.993. [DOI] [PubMed] [Google Scholar]


