Packing, tiling, and covering with tetrahedra

Abstract

It is well known that three-dimensional Euclidean space cannot be tiled by regular tetrahedra. But how well can we do? In this work, we give several constructions that may answer the various senses of this question. In so doing, we provide some solutions to packing, tiling, and covering problems of tetrahedra. Our results suggest that the regular tetrahedron may not be able to pack as densely as the sphere, which would contradict a conjecture of Ulam. The regular tetrahedron might even be the convex body having the smallest possible packing density.

The problem of how densely given solid objects can pack in space has been a source of fascination since the dawn of civilization. Dense packing of convex objects is intimately related to the arrangement of molecules in condensed states of matter (1) and to the best way to transmit encoded messages over a noisy channel (2). Three-dimensional Euclidean space ℜ³ (3-space) already provides many challenging open problems. It was only recently that Kepler’s conjecture, which postulated that the densest packings of congruent spheres in 3-space have packing density (fraction of space covered by the spheres) Δ = π/$\sqrt{\mathrm{18}}$ = 74.048 … %, realized by variants of the face-centered cubic (FCC) lattice packing, was proved (3). Much less is known about the packing characteristics of other congruent convex objects that do not tile 3-space. For example, an ellipsoid is simply obtained by an affine (linear) transformation of a sphere, and yet the densest packing of ellipsoids is an open problem. The rotational degrees of freedom of an ellipsoid (absent in a sphere) enables such packings to achieve densities greater than π/$\sqrt{\mathrm{18}}$, the densest sphere packing density (4–6). There is a family of periodic arrangements of nearly spherically shaped ellipsoids that surpass the density of the optimal sphere packing and that has a maximal density of Δ = 0.7707 … % (6), which is the highest known density for any ellipsoid packing.

The evidence below suggests that the regular tetrahedron is a counterexample to Ulam’s conjecture (Martin Gardner, private communication; see also ref. 7), which states that the optimal density for packing congruent spheres is smaller than that for any other convex body. Indeed, it suggests that perhaps the regular tetrahedron achieves this minimum. However, our interest in tetrahedra in this work goes beyond their packing characteristics. Tetrahedra have interesting connections to sphere packings, certain tilings of space (including foams), liquids, and glasses, and complex alloy structures. It is well known that the maximum number of spheres in 3-space that can be locally packed such that each sphere contacts the others is four. The polyhedron that results by taking the sphere centers as vertices is the regular tetrahedron, but such a tetrahedron cannot tile space because its dihedral angle [cos⁻¹(1/3) ≈ 70.53°] is not a submultiple of 360°. Interestingly, the ratio of the volume of the portion of this tetrahedron covered by the spheres to the volume of the tetrahedron leads to the Rogers upper bound of 77.96 … % on the sphere packing density (8).

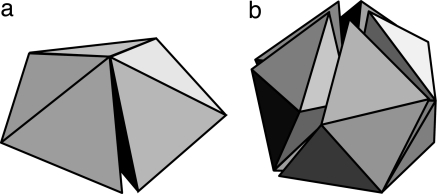
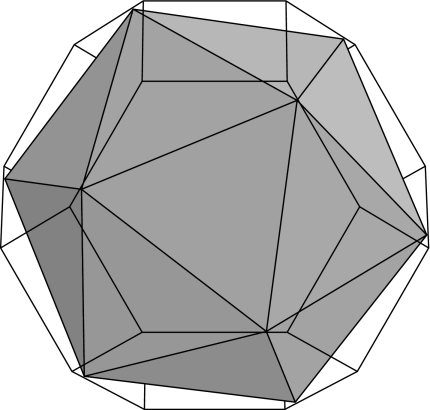
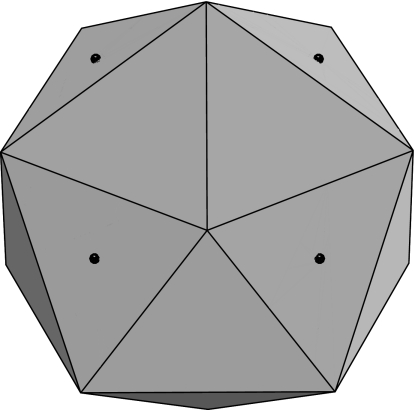
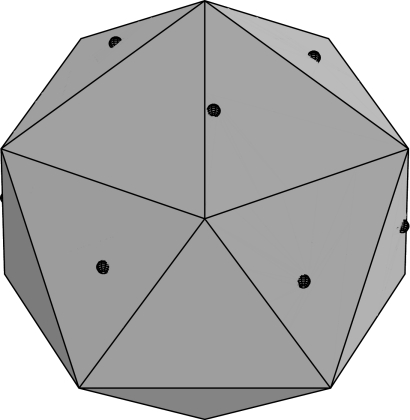
It was Frank and Kasper (9, 10) who proposed that the underlying “polytetrahedral” network of sphere packings can serve to explain the crystalline structure of complex alloys, particularly those of transition metals. These arrangements are now known as “Frank–Kasper” phases. If 5 regular tetrahedra are packed around a common edge, there remains a small gap of 7.36°, and if 20 regular tetrahedra are packed around a common vertex, the gaps amount to a solid angle of 1.54 steradians (see Fig. 1). By closing these gaps by a slight deformation, we get a regular icosahedron, which corresponds to a 12-coordinated sphere whose vertices correspond to the vertices of the icosahedron. A 12-fold coordination is an important case of the Frank–Kasper phases; others include 14-, 15-, and 16-fold coordinations (13 is not possible), corresponding to triangular-faced tetrahedra constructed from tetrahedra sharing a single vertex. The Frank–Kasper phases thus consist of various tilings of space by “almost-regular” tetrahedra with atoms at their vertices. It also has been shown that the structure of atomic liquids and glasses has significant polytetrahedral character (11). The dual Voronoi regions of the vertices of the Frank–Kasper structures (obtained by joining the centers of every pair of tetrahedra in face contact) together fill space and consist of polyhedra with 12, 14, 15, and 16 faces. It is well known that periodic structures with atoms at the vertices of these dual tilings occur in clathrate hydrates (12). This type of polyhedral tiling inspired Weaire and Phelan (13) in their discovery of a minimal area foam with a smaller average surface area per cell (“bubble”) than Kelvin’s best solution (14).

Fig. 1.

Certain arrangements of tetrahedra. (a) Five regular tetrahedra about a shared edge. The angle of the gap is 7.36°. (b) Twenty regular tetrahedra about a shared vertex. The gaps amount to 1.54 steradians.

The fact that congruent regular tetrahedra cannot be used to tile 3-space gives rise to several mathematical questions.

1. What are the “closest-to-regular” tetrahedra that will tile 3-space?

2. What is the least covering density for congruent regular tetrahedra in 3-space?

3. What is the greatest packing density for such tetrahedra?

Of course question (i), which we discuss first, is itself several different problems, according to how we interpret closest-to-regular. We will show that our answers to these questions will introduce us to many of the polyhedral tilings of space discussed immediately above. The best solution we offer for question (iii) leads to the possibility that the regular tetrahedron contradicts Ulam’s conjecture and might itself have the least packing density of any convex body.

Scottish, Irish, and Welsh Configurations

In 1887, Lord Kelvin conjectured that a certain system of equal-volume bubbles, which we shall call the “Scottish bubbles,” was optimal in the sense that it minimized the mean surface per bubble (14). This conjecture was disproved by the “Irish bubbles” found by Weaire and Phelan in 1994 (13). We define both systems in this work, along with a third system, the “Welsh bubbles.” Many of the other configurations we need are related to these three bubble-systems and so are also appropriately described as Scottish, Irish, and Welsh.

For example, the Scottish, Irish, and Welsh

• “Nuclei” are the centers of the bubbles;

• “Vocells” are the cells of the Voronoi tessellation that they determine;

• “Irregulars” are the dual (Delaunay) tessellations by irregular tetrahedra;

• “Nodes” are the vertices of the Vocells, which are equally the circumcenters of these tetrahedra.

Some terms used here will be defined below.

Definitions: Marked Points

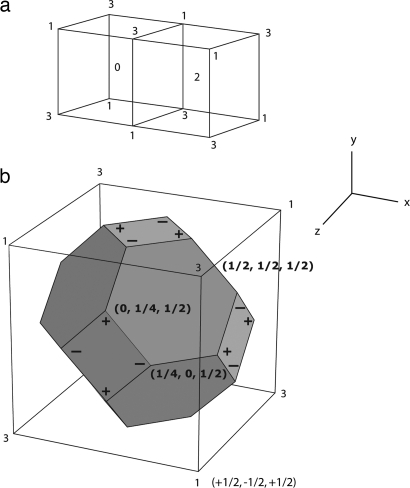
We now introduce some notation and distinguish certain points as “marked.” Some of these are the points of the body-centered cubic (BCC) lattice, namely those points (x, y, z) for which x, y, z are either all integers or all halves of odd integers. We mark these nodes with the numbers 0, 1, 2, and 3 (modulo 4), by the rule

Geometrically, the points of one of the two cubic sublattices are marked alternately 0 and 2; those of the other are alternately 1 and 3. Fig. 2a shows these marks for two adjacent cells. The Voronoi cells of this lattice are truncated octahedra, whose vertices are the points (x, y, z) for which one of the coordinates (n) is an integer, one (h) an integer +1/2, and one (q) an integer ±1/4. We mark these alternately + and −, by the rule that the combinations

Fig. 2.

Description of our notation. (a) Two adjacent cells of a cubic lattice and colorings of the two cubic sublattices of the BCC lattice as described in the text. (b) The Voronoi cell of a BCC lattice and the notation described in the text. The center of the cube is the origin of the coordinate system.

whereas

Fig. 2b depicts the Voronoi cell inside one of the cubes with these marks.

There are good reasons why this marking notation provides extremely succinct descriptions of our packings, tilings, and coverings by tetrahedra, as well as many other interesting configurations. It is taken from ref. 15, where it is shown that it can describe any object that has at least the order 3 symmetries of the cubic lattice.

A “tiling” or “tessellation” is a partition of Euclidean space ℜ^d into closed regions whose interiors are disjoint regions. Consider any discrete set of points (our nuclei) (position vectors) X = {r₁, r₂, … } in ℜ^d. Associated with each point r_i ∈ X is its “Voronoi cell,” Vor(r_i), which is defined to be the region of space nearer to the point at r_i than to any other point r_j in the set, i.e.

The Voronoi cells are convex polyhedra whose interiors are disjoint but share common faces, and therefore the union of all of the polyhedra is the whole of ℜ^d. This subdivision of space is the Voronoi tessellation.

Its vertices (our nodes) are the points whose distance from the nuclei is a local maximum. Attached to each such node is a “Delaunay cell,” which can be defined as the convex hull of the nuclei nearest to it, and these Delaunay cells also tile space. Geometrically, the Voronoi and Delaunay tessellations are dual to each other. In our three cases, the Delaunay cells are tetrahedra: our Scottish, Irish, and Welsh irregulars.

Scottish Bubbles and Irregulars.

In 1887, Lord Kelvin asked which tiling of 3-space by unit-volume bubbles minimized the average surface area per bubble and proposed that the answer was the “Scottish bubbles,” which are obtained by relaxing our “Scottish Vocells,” the Voronoi cells whose nuclei are our points marked 0, 1, 2, 3. The “Scottish nodes” are therefore the remaining marked points + or −.

The “Scottish irregulars” are the dual tiling of tetrahedra (centered at + or −), whose vertices are 0, 1, 2, 3, with edges joining each to its 14 closest neighbors. These tetrahedra are a putative solution to our question (i) if we take closest-to-regular to mean “with the ratio (longest edge)/(shortest edge) as near to 1 as possible.” For the Scottish irregulars, this ratio is 2/$\sqrt{3}$ = 1.15 … . Each tetrahedron is fixed by eight symmetries of the tessellation.

The relation to Kelvin’s problem explains our use of “Scottish” for these objects.^§

Irish Bubbles and Irregulars.

To everybody‘s surprise, Weaire and Phelan (13) found in 1994 that Kelvin’s Scottish bubbles were not in fact the optimal answer to his problem. We start by defining the Irish nuclei to be the points marked 0, 1, 2, 3, + that determine the Irish Vocells, which are then relaxed subject to the requirement that their volumes become equal. The surface area per bubble is 99.7% of the Scottish ones.

The Vocells or bubbles are of two shapes: dodecahedra that are topologically regular but not metrically so and “dodecadihedra,” which have 12 (“dodeca”) pentagonal faces and two (“di”) hexagonal ones. The Irish irregulars are the dual (Delaunay) tessellation of the tetrahedra with vertices at 0, 1, 2, 3, +. The most symmetric (“high”) tetrahedra are fixed by eight symmetries of this tessellation; the least symmetric (“low”) only by two, and the remaining (“medial”) ones by three (although abstractly these tetrahedra have six symmetries).

It is known that no more than four bubbles of an arbitrary system can meet at a point and that when four bubbles do meet, the local configuration is dual to a regular tetrahedron. This fact makes it natural to give close-to-regular a second meaning, namely “being dual to a good system of bubbles.” If in particular, we interpret closest-to-regular to mean “dual to the bubble-tiling with minimal surface-area per bubble,” then the Irish bubbles are likely to be the best answer.

Welsh Configurations.

A third interpretation of closest-to-regular has been proposed by Joseph Gerver (private communication), who asked the following question: What is the shortest possible interval that contains all of the dihedral angles of a system of tetrahedra that tile space? He observed that because presumably some edges must be surrounded by at most five tetrahedra and others by at least six, this interval must contain [60°, 72°]. The interval [60°, 74.2°] for the Welsh irregulars we are about to define is so close to this lower bound that they are virtually certain to be the answer. We use this name despite the fact that every 17th Welsh irregular is actually a regular tetrahedron.

They are related to what we call the “primitive Welsh” tessellation of space into truncated tetrahedra (centered at nodes 0 and 1) and ordinary tetrahedra (centered at 2 and 3). The vertices of that tessellation are the midpoints 23 of the shortest line-segments joining nodes of types 2 and 3. Their geometry is related to that of a diamond crystal, whose carbon atoms are situated at the nodes 2 and 3, so that 23 are the midpoints of the valence bonds.

The Welsh nuclei are these points 23 together with the nodes 0, 1 that are the centers of the truncated tetrahedra. The resulting Welsh Vocells are again of two shapes; three of four of them are topological dodecahedra, whereas the remaining one is a dodecatetrahedron with 12 pentagonal faces and 4 hexagonal ones. Relaxing them, we find the Welsh bubbles, which have greater surface-area per bubble than either the Scottish or Irish ones.

The Welsh irregulars that form the dual tessellation are of three types: the high ones that are actually the regular tetrahedra of the primitive Welsh tessellation and whose four vertices have type 23; together with the medial ones (fixed by six symmetries) that abut them, which have one vertex of type 0 or 1 and three of type 23; and finally the low ones (fixed by only two symmetries), whose four vertices have types 0, 1, 23, 23.

Summary.

The three bubble systems are obtained by relaxing the cells of the three Voronoi tessellations, which are the Scottish (truncated octahedra), Irish (nonregular dodecahedra and dodecadihedra) and Welsh (nonregular dodecahedra and dodecatetrahedra) systems. The centers of these bubbles are the vertices of the corresponding irregulars.

In Tables 1–3, we give, for sample tetrahedra from each of the three tessellations, the coordinates of each vertex and the node that is its circumcenter. Recall that the vertices are the nuclei of the Vocells, and the nodes are their vertices.

Table 1.

A typical Scottish tetrahedron

Points	Scottish: 8 symmetries
	Coordinates	Type
Vertices	(0, 0, 0)	0
	(−1/2, 1/2, 1/2)	1
	(0, 0, 1)	2
	(1/2, 1/2, 1/2)	3
Node	(0, 1/4, 1/2)	+

Vocells have for nuclei all points marked 0, 1, 2, or 3 and are truncated octahedra. Their vertices (the nodes) are all points marked + or −.

Table 2.

Typical Welsh tetrahedra

Points	Welsh high: 24 symmetries		Welsh medial: 6 symmetries		Welsh low: 4 symmetries
	Coordinates	Type	Coordinates	Type	Coordinates	Type
Vertices	(3/4, 3/4, 3/4)	23	(0, 0, 0)	0	(0, 0, 0)	0
	(3/4, 1/4, 1/4)	23	(3/4, 1/4, 1/4)	23	(−1/2, 1/2, 1/2)	1
	(1/4, 3/4, 1/4)	23	(1/4, 3/4, 1/4)	23	(1/4, 3/4, 1/4)	23
	(1/4, 1/4, 3/4)	23	(1/4, 1/4, 3/4)	23	(1/4, 1/4, 3/4)	23
Node	(1/2, 1/2, 1/2)	3	(11/40, 11/40, 11/40)	03	(−2/48, 17/48, 17/48)	130

Dodecahedral vocells have nuclei 23 and volume 14267/46080. Dodecatetrahedral ones have nuclei 0 or 1 and volume 8773/23040. Here 0₃ = (11/20)·0 + (9/20)·3 and 1₃₀ = (19/48)·1 + (15/48)·3 + (14/48)·0. Nodes are all points 2, 3, 0₂, 0₃, 1₂, 1₃, 0₂₁, 0₃₁, 1₂₀, or 1₃₀ with the above proportions.

Table 3.

Typical Irish tetrahedra

Points	Irish high: 8 symmetries		Irish medial: 3 symmetries		Irish low: 2 symmetries
	Coordinates	Type	Coordinates	Type	Coordinates	Type
Vertices	(−1/4, 1/2, 0)	+	(0, 0, 0)	0	(0, 0, 0)	+
	(1/4, 1/2, 0)	+	(0, 1/4, 1/2)	+	(−1/4, 1/2, 0)	+
	(0, 1/4, 1/2)	+	(1/2, 0, 1/4)	+	(1/4, 1/2, 0)	+
	(0, 3/4, 1/2)	+	(1/4, 1/2, 0)	+	(0, 1/4, 1/2)	+
Node	(0, 1/2, 1/4)	−	(5/24, 5/24, 5/24)	03	(−5/32, 0, 10/32)	−0

Dodecahedral cells have nuclei 0, 1, 2, or 3 and volume 125/1024. Dodecadihedral ones have nuclei + and volume 129/1024. Here 0₃ = (7/12)·0 + (5/12)·3 and −₀ = (5/8)·− + (3/8)·0. Nodes are all points −, 0₁, 1₂, 2₃, 3₀, 0₃, 1₀, 2₁, 3₂, −₀, −₁, −₂, or −₃ with above proportions.

Covering Problem

We now consider the determination of the optimal coverings by equal regular tetrahedra. A “covering” is an arrangement of overlapping sets that covers the entire space. The truncated tetrahedra of the primitive Welsh tessellation are obtained by removing small tetrahedra (say, of edge-length e) from larger tetrahedra of edge-length 3e. These larger, or “pretruncated Welsh,” tetrahedra, cover 3-space and have 27 times the volume (say, v) of the smaller ones, so that the volume of the truncated tetrahedra is 23v. The density of this “Welsh covering” is therefore 27/24 = 9/8 = 1.1111 …, because the object of volume 24v obtained by replacing just one of them exactly tiles space. This density is so close to 1 that the Welsh covering is very probably optimal.

We remark that the similarly defined “detruncated Scottish” octahedra almost certainly form the optimal covering of space by equal regular octahedra.

Packing Problem

We shall now pass to the problem of determining the optimal packings by equal regular tetrahedra.

Definitions.

A collection of convex bodies in d-dimensional Euclidean space ℜ^d is called a “packing” P if no two of the bodies have an interior point in common. The density Δ of a packing is the fraction of space ℜ^d covered by the bodies. In the mathematical literature, a “lattice packing” P_L of a convex body C is a packing in which the centers r₁, r₂, … of the convex bodies, each oriented in the same direction, are integer linear combinations of basis vectors. In the physical sciences, this arrangement is referred to as a “Bravais lattice.” In a lattice packing, the space ℜ^d can be geometrically divided into identical regions F called “fundamental cells,” each of which contains the center of just one body. We denote by Vol(C) and Vol(F) the volumes of the convex body and fundamental cell, respectively. The packing density of a lattice packing P_L is therefore given by

A “periodic packing” P_P of congruent copies of a convex particle C is obtained by placing a fixed nonoverlapping configuration of n particles (where n ≥ 1) in each fundamental cell of a lattice. Thus, the packing is still periodic under translations by a lattice vector, but the n particles can be positioned anywhere in the fundamental cell with arbitrary orientation subject to the nonoverlap condition. The density of such a periodic packing is given by

There are more general types of packings, but in this work we will restrict ourselves to periodic packings.

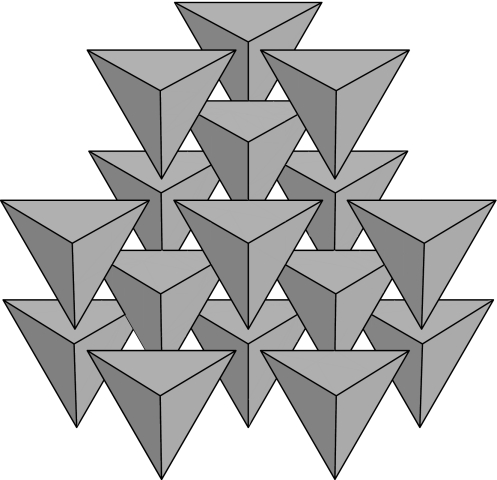
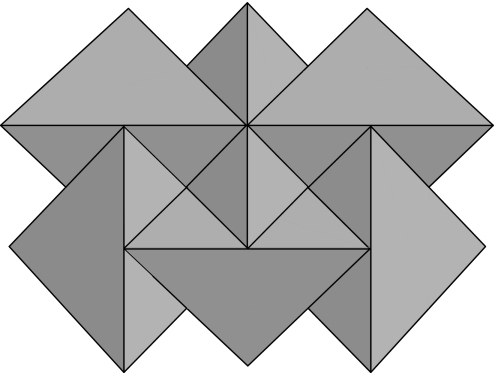
We now turn to the packing of congruent regular tetrahedra. Our first remark is that the method of (Bravais) lattice packing, which produces good packings for many other solids (including an optimal sphere packing; see ref. 2), is of no use here. The optimal lattice packing for any tetrahedron, found by Hoylman (16), has density Δ = 18/49 = 36.73 … %, and each tetrahedron meets others at 14 points (see Fig. 3). [It is noteworthy that there is a lattice packing of tetrahedra with much smaller density (Δ = 1/3) but in which each tetrahedron is in contact with 18 others (17), a rather counterintuitive result.] Clearly, denser packings can be achieved by orienting the tetrahedra in different directions. Fig. 4 shows a simple packing that achieves density Δ = 2/3 = 66.666 … %. This is the best density we have been able to achieve with a “uniform packing,” i.e., one in which the tetrahedra are embedded in the same way, meaning that there is a symmetry of the packing that takes any one tetrahedron to any other.

Fig. 3.

A portion of the densest (Bravais) lattice packing of regular tetrahedra (16). It has density Δ = 18/49 = 36.73 … %, and each tetrahedron is in contact with 14 others.

Fig. 4.

A portion of the densest uniform packing of regular tetrahedra that we have been able to find. It has density Δ = 2/3 = 66.666 … %.

Scottish and Welsh Regulars.

Another idea is to insert regular tetrahedra into one of our three systems of irregulars. From Irish irregulars, this idea produces a very low density, and from Scottish ones, a density Δ of 1/2 = 50% is produced (the regular tetrahedra in that case being obtained by shrinking the long edges of the Scottish irregulars by a factor of $\sqrt{\mathrm{1/2}}$). However, a more interesting packing can be obtained from the Scottish Vocells as follows. There is a well known way [see, e.g., Coxeter (18)] to inscribe an icosahedron in an octahedron. In fact, the icosahedron fits entirely inside the corresponding truncated octahedron (see Fig. 5) and occupies 8/9 the volume of the truncated octahedron. We obtain “Scottish icosahedra” by inscribing icosahedra in this way in all of the Scottish truncated octahedra. Each icosahedron touches eight others as in Fig. 6, the contact spots of that figure (which form the vertices of a cube) being at the centers of eight faces.

Fig. 5.

A regular icosahedron inscribed in a truncated octahedron.

Fig. 6.

Each Scottish icosahedron is placed so that its eight contact spots coincide with those of its neighbors. It has density Δ = 82.13 … %.

The tetrahedra of the Scottish regular packing (or just the “Scottish regulars”) are obtained by packing 20 tetrahedra in each icosahedron (see Appendix). This tetrahedron packing has density Δ = 45/64 = 70.3125%. We shall see later that the Scottish regulars can be displaced slightly to increase their density to >71.655%.

Another good packing is obtained from the Welsh irregulars. We retain the high ones that are already regular and put regular tetrahedra of the same size as these into each of the medial and low ones. The density of the resulting Welsh regulars is Δ = 17/24 = 70.8333 … %. Once again, there exist displacements that increase the density.

Displaced and Reformed Regulars.

We have remarked that the density of both Scottish and Welsh regulars can be improved by suitably repositioning them. The tetrahedra fall into clumps, and we can distinguish between “displacements,” which treat the clumps bodily, and “reformations,” which then move individual tetrahedra.

The Scottish regulars do not form an optimal packing because the icosahedra are related by the translations of the BCC lattice, and this lattice can be slightly deformed in a way that increases the density without causing the icosahedra to overlap. The reason, in brief, is that any icosahedron I (centered at zero) touches only eight others, namely, I± v₁, …, I ± v₄, where v₁, …, v₄ are generators of the BCC lattice that satisfy v₁ + … v₄ = 0. They can be replaced by four nearby vectors w₁, …, w₄, provided that w₁/2, …, w₄/2 lie in the same faces of the icosahedron and add to zero. Since this requirement imposes only four conditions on the lattice, whereas six parameters are needed to specify the shape of a lattice, it can be varied with two degrees of freedom, and it turns out that some values increase the density. The optimal (Bravais) lattice packing of icosahedra (the “displaced Scottish icosahedra”) was found by Betke and Henk (19); it has the density Δ = 83.63574 … % and yields the displaced Scottish packing of regular tetrahedra that has density Δ = 71.65598 … % (see Fig. 7).

Fig. 7.

For Betke and Henk’s displaced Scottish packing of icosahedra, the number of contact spots increases to 12. It has density Δ = 83.63574 … % and leads to the displaced Scottish regulars that have density Δ = 71.65598 … %.

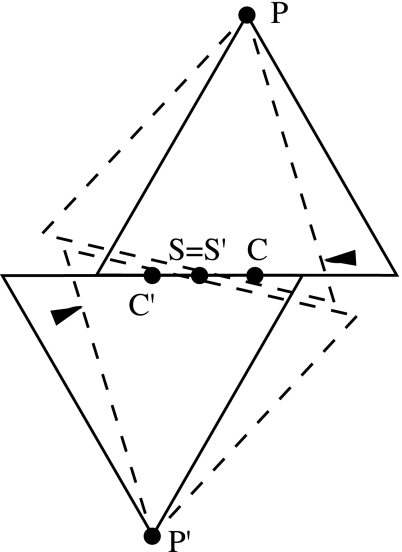
However, this density is still not optimal, because the clumps may be reformed by adjusting the individual tetrahedra so as to increase the density still further. To see this, observe that none of the “contact spots” S of Fig. 7 lies at the center C of its face.

Now consider two tetrahedra from clumps centered at P and P′, whose contact spots S and S′ presently coincide with each other, but not with the centers C and C′ of their corresponding faces. Then they can be rotated about axes through P and P′ perpendicular to the line CC′ so as to take S and S′ further away from the initial positions of C and C′.

Do likewise for all tetrahedra of every clump. After this rotation, if it is through a sufficiently small angle, the tetrahedra still do not overlap and now touch only at the centers of their clumps (see Fig. 8). The density therefore can be increased by bringing the clumps closer together.

Fig. 8.

Adjusting the Scottish regulars (a two-dimensional schematic).

It is very difficult to say exactly how dense such “reformed Scottish” packings can be (especially because they will involve slight changes to the lattice), but we suspect it will be ≈72%.

Welsh regulars also fail to be optimal, because these tetrahedra fall into “clumps” of 17, and each clump touches others only at four points. If we replace these points by universal joints, the resulting structure is not rigid, and suitable displacements increase density. One such displaced Welsh packing has density Δ = 71.7455%, the highest we have yet explicitly achieved. It is obtained by rotating the clumps alternately through ±0.1131 radians about their vertical (dyad) axes. Before this rotation, each low tetrahedron is hinged as far as possible about the edge it shares with a high one, either “centrifugally” outwards if that edge is horizontal and otherwise in the “lagging” direction (thus, each low tetrahedron goes to the place it would if the displacement of the other tetrahedra were impulsive). Again, still denser reformed Welsh packings might be obtainable by allowing individual tetrahedra to move more freely.

There are various systems of Irish regulars, obtained by repositioning (some of) the Irish irregulars. So far, we have not found any that are as dense as our Scottish or Welsh ones, but we cannot rule out this possibility. We therefore suspect that the optimal packing of regular tetrahedra will be some displacement of either the Scottish or Welsh regulars, but we do not know which! However, it appears unlikely that the density of the optimal packing of regular tetrahedra will exceed the optimal density of 74.048 … % for congruent spheres.

This raises the possibility that for packings of equal convex solids, the shape that gives the least density might be the regular tetrahedron rather than the sphere, in contradiction to Ulam’s conjecture (7).

Abbreviations

3-space

three-dimensional Euclidean space ℜ³

BCC

body-centered cubic.

Appendix

Here we describe elementary calculations concerning one of our ideas that leads to dense packings of congruent regular tetrahedra. As noted in the introduction, 20 regular tetrahedra cannot fit into a regular icosahedron that has the same side length as one of the tetrahedra. Thus, it is desired to shrink the sizes of the regular tetrahedra relative to an icosahedron such that the space packed by the 20 tetrahedra is maximized. Once this optimal shrinking is determined, the goal is then to find the densest packing of the filled icosahedra.

The volume of a regular tetrahedron V_T of side length s_T is given by

The height (distance from a vertex to the midpoint of the opposite face) is given by h = $\sqrt{\mathrm{2/3}}$s_T. The volume of a regular icosahedron V_I of side length s_I is given by

where τ = (1 + $\sqrt{5}$)/2 is the golden ratio. The “apothem” a (distance from the centroid of the icosahedron to the midpoint of one of its faces) is given by a = τ²/(2 $\sqrt{3}$)·s_I. To determine the largest regular tetrahedron that can be placed in a regular icosahedron such that one vertex of the tetrahedron is placed at the centroid of the icosahedron, set the height of the tetrahedron equal to the apothem of the icosahedron. Therefore, s_T = τ²/(2 $\sqrt{2}$)·s_I = 0.9256147 … s_I. Thus, the fraction of the icosahedral volume occupied by the 20 regular tetrahedra sharing a vertex positioned at the centroid of the icosahedron is given by

The density Δ of the Scottish icosahedron packing is 45/(8τ⁴) = 0.8214 … . This result is obtained from the fact that the associated circumscribed truncated octahedron (see Displaced and Reformed Regulars) occupies 8/9 the volume of the associated octahedron, and the icosahedron-to-octahedron volume ratio is 5/τ⁴. Packing each icosahedron with 20 tetrahedra in the fashion described above leads to a packing of congruent regular tetrahedra with density Δ = 45/(8τ⁴) × τ⁴/8 = 45/64 = 70.3125%. If the icosahedra are instead arranged on the points of the optimal (Bravais) lattice (19), which has density Δ = 0.8363574 …, then packing each icosahedron with 20 tetrahedra gives a packing of regular tetrahedra that has density Δ = 0.8363574 × 0.8567627 = 0.716559 … . Of course, it is not known whether there are denser packings of icosahedra than the optimal lattice packing.

It is useful here to specify the optimal icosahedral lattice packing (19). Let I and Λ denote the icosahedron and lattice, respectively. The optimal lattice is specified as follows:

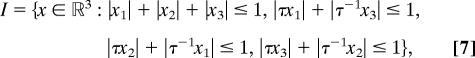where the basis vectors wⁱ(x̄) (i = 1, 2, or 3) are given by

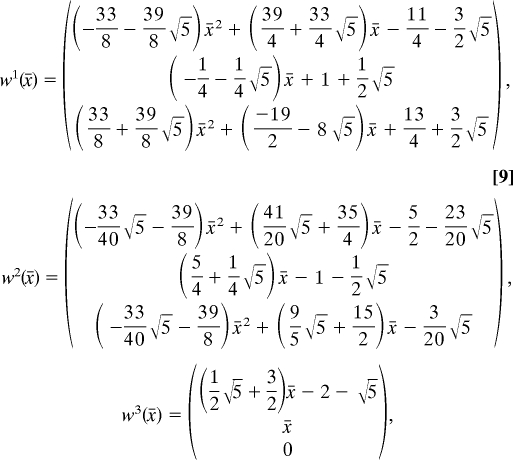and x̄ ∈ (1, 2) is the unique root of the polynomial 1,086x³ − (1,603 + 113 $\sqrt{5}$)x² + (15 $\sqrt{5}$ + 43)x + 102 + 44 $\sqrt{5}$. It is found that x̄ = 1.59160301 …, and therefore Eq. 9 yields

The density is given by

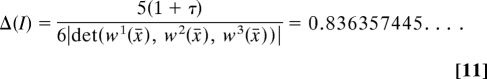The formulas for the polynomial and the density given in the original paper (19) contained typographical errors, as pointed out by one of the authors (M. Henk, personal communication).