Ligand Orientation Control in Low-Spin Six-Coordinate (Porphinato)iron(II) Species

Abstract

The synthesis of a low-spin six-coordinate iron(II) porphyrinate in which the two axial ligands are forced to have a relative perpendicular orientation has been successfully accomplished for the first time. The reaction of four-coordinate (tetramesitylporphinato)iron(II) with 2-methylimidazole leads to the preparation of [Fe(TMP)(2-MeHIm)₂] that cocrystallizes with five-coordinate [Fe(TMP)(2-MeHIm)]. The six-coordinate complex accommodates the sterically crowded pair of imidazoles with a strongly ruffled core and relative perpendicular orientation. This leads to shortened equatorial bonds of 1.963(6) Å and slightly elongated axial Fe–N bond lengths of 2.034(9) Å that are about 0.04 Å shorter and 0.03 Å longer, respectively, in comparison to bis-imidazole ligated iron(II) species with parallel oriented axial ligands. The Mössbauer spectrum shows a pair of quadrupole doublets that can be assigned to the components of the cocrystallized crystalline solid. High-spin five-coordinate [Fe(TMP)(2-MeHIm)] has ΔE_Q = 2.25 mm/s and δ = 0.90 mm/s at 15 K. The quadrupole splitting, ΔE_Q, for [Fe(TMP)(2-MeHIm)₂] is 1.71 mm/s and the isomer shift is 0.43 mm/s at 15K. The quadrupole splitting value is significantly larger than that found for low-spin iron(II) derivatives with relative parallel orientations for the two axial ligands. Mössbauer spectra thus provide a probe for ligand orientation when structural data is not otherwise available.

Introduction

Hemes (iron porphyrinate complexes) are the active component in many biologically important systems. These include the cytochrome b electron transfer proteins that are axially coordinated by two histidine ligands. For this case of heme centers coordinated to two planar histidine (imidazole) residues, there are a number of X-ray structures reported.^1–7 In each of these structures it is found that an axial histidine plane is fixed in a particular orientation with respect to its projection onto the heme plane by a combination of the covalent attachment of the imidazole ring of the histidine residue to the protein backbone, hydrogen bonding of the imidazole N–H proton to the protein residues, and the packing of other amino acid side chains in the heme pocket. For bis-histidine-coordinated heme proteins, the relative orientation of the two imidazole planes with respect to each other is important in understanding the spectroscopic and possibly also the redox properties of these heme proteins. In the current protein structures, two limiting orientations of the axial ligand planes are found: imidazole planes oriented parallel to each other, (cytochromes b₅,¹ three of the heme centers of cytochromes c₃,^2–4 the b hemes of sulfite oxidase⁵ and flavocytochrome b₂,⁶ and the heme a of cytochrome oxidase,⁷) while one of the four heme groups in cytochrome c₃ from D. vulgaris has a more staggered conformation in which the dihedral angle between the histidine planes is closer to a relative perpendicular arrangement (77°).

There are also other bis-histidine-coordinated heme proteins believed to have their axial imidazole planes orientated perpendicular to each other. They have been identified largely on the basis of spectroscopic data for the oxidized (Fe(III)) forms and includes the b hemes of mitochondrial complex III, also known as cytochrome bc₁,⁸ the similar b hemes of cytochrome b₆f of chloroplasts and the c-type heme of cytochrome c″ of Methylophilus methylotrophus.⁹ For example, studies on cytochrome c₃¹⁰ and the mitochondrial cytochromes b,8^b,11 have shown that changes in the relative orientations of the coordinated imidazole ligands cause significant changes of the observed g values for the low-spin complexes. These have large g_max EPR spectra^10,12–16 and a wider range of reduction potentials than observed for the cytochromes b₅ and b₂, and the b heme of sulfite oxidase, all of which have rhombic, typical B hemichrome EPR spectra (g_zz ~ 2.9–3.0, g_yy ~ 2.25–2.35, g_xx ~ 1.4–1.6). There is thus the possibility of a correlation between the axial ligand plane orientation and the reduction potential in hemes and heme proteins.^15,17,18

The orientations of planar axial ligands in bis-ligated hemes of iron(III) have been intensively investigated. The earliest studies showed that the relative and absolute orientations of the two axial ligands have significant effects on the electronic structure. The first example was that of [Fe(OEP)(3-ClPy)₂]ClO₄¹⁹ where two different crystalline polymorphs were isolated. The polymorphs are those of a triclinic, spin-equilibrium (S = 1/2 ⇌ S = 5/2)^{20, 21} system and a monoclinic, intermediate-spin system, S = 3/2.²² In these complexes, the two pyridines maintain a relative parallel orientation but the absolute orientation of the two axial ligands with respect to the porphinato core changed. Although this system showed large changes in the electronic structure of iron(III), controlling axial ligand orientation more likely will effect the relative energies of the three lowest d-orbitals of iron, namely the d_xy, d_xz, and d_yz orbitals.

While most bis-ligated iron(III) complexes have a characteristic rhombic EPR spectrum,²³ with three observed g-values, some iron(III) species have an unusual EPR spectrum: a single-feature low-spin EPR signal with g ≥ 3.2. This EPR spectral type has been called large g_max²⁴ or highly anisotropic low-spin (HALS).²⁵ The origin of the large g_max EPR spectrum was first studied in the complex [Fe(TPP)(2-MeHIm)₂]^+.12,15 This study showed that the spectrum resulted from mutually perpendicular axial ligands that lead to nearly degenerate iron d_π orbitals. Subsequently, a number of additional iron(III) species were shown to have the two planar ligands oriented perpendicular to each other.^{13,14,26–29} Most of these species display a large g_max EPR spectrum^13,14,16,27 and an unusually small value of the Mössbauer quadrupole splitting constant.^{13–15,26,28,29} A final case is found for strong π-accepting ligands, such as 3- and 4- cyanopyridine, where the interaction with axial ligands lowers the energy of iron d_π orbitals below d_xy so that the ground state changes to (d_xz,d_yz)⁴(d_xy)¹. This leads to a final type of EPR spectrum observed in low-spin iron(III): an axial EPR spectrum. All of the complexes with relative perpendicular ligands are found to have strongly ruffled porphyrinato cores. For these systems, this conformation allows for the possibility of a π interaction between iron and the porphyrin.

In contrast to the comparative ease in obtaining relative perpendicular orientations of planar axial ligands in iron(III), iron(II) porphyrinates are found to display significantly different orientation behavior. The same strategies used with iron(II) porphyrinates are found to yield bis-ligated species with relative parallel orientations.³⁰ Thus, for a series of substituted pyridine derivatives, binding is independent of ligand basicity, and it was concluded that insensitivity of the ligation behavior was the consequence of noninteracting d_π orbitals between iron and the axial ligands. In addition, a series of imidazole-ligated iron(II) species where the imidazoles are sterically unhindered showed relative parallel orientations for the two ligands.³¹ Clearly iron(II) and iron(III) porphyrinates with two planar axial ligands have differing orientational preferences. This leads us to pose the question: What are the electronic structure and orientation energy differences between the two oxidation states?

Another set of strategies used with great success in iron(III) to force relative perpendicular orientations is the use of sterically hindered imidazoles with a bulky 2-methyl substituent on the imidazole ring. However, for iron(II) systems, it is well-known that the use of sterically hindered imidazoles decreases the magnitude of the binding constant of the second imidazole, relative to those seen for unhindered imidazoles.³² This leads the preparation and isolation of the high-spin five-coordinate species [Fe(Porph)(R-Im)].^33–35 However, [Fe(TPP)(2-MeHIm)] is reported to bind a second 2-methylimidazole ligand at low temperature,³⁶ which suggests that the synthesis of a bis-ligated hindered imidazole should be possible. Further encouragement for the successful synthesis was provided by the electrochemical measurement of stability constants for iron(II) derivatives of tetraphenylporphyrin and tetramesitylporphyrin.¹⁸ The presence of the bulky 2,6-methyl substituents in the iron(II) tetramesitylporphyrinate species was seen to lead to an increased overall binding of two axial 2-methylimidazoles, confirming an earlier qualitative observation of Safo.³⁷ However, despite these encouraging features, no synthesis or solid-state structure of a bis(2-methylimidazole) or related complex of an Fe(II) porphyrinate has yet appeared.

As part of our program to understand the control of iron(II) porphyrinate structure and the concomitant effect on physical properties, we have again tried to synthesize and isolate bis-ligated iron(II) porphyrinates with hindered imidazoles as the axial ligands. We have now successfully synthesized and structurally characterized the bis-ligated complex of the iron(II) derivative of tetramesitylporphyrin, [Fe(TMP)(2-MeHIm)₂]. The structure determination shows that the coordination of two 2-methylimidazole ligands leads to a low-spin iron(II) derivative, with the two ligands having a relative perpendicular orientation. As expected from analogous iron(III) species, the porphyrin core is necessarily ruffled to accommodate the two ligands. Interestingly, the desired six-coordinate complex cocrystallized with the five-coordinate species [Fe(TMP)(2-MeHIm)]. The crystalline mixture has been characterized with the aid of Mössbauer spectroscopy and full synthetic, structural, and Mössbauer details are presented herein.

Experimental Section

General Information

All reactions and manipulations for the preparation of the iron(II) porphyrin derivatives (see below), were carried out under argon using a double-manifold vacuum line, Schlenkware and cannula techniques. Toluene and hexanes were distilled over sodium benzophenone ketyl. Methylene chloride was distilled over sodium hydride. Ethanethiol (Aldrich) was used as received. 2-Methylimidazole was purchased from Aldrich, recrystallized from toluene, and dried under vacuum. The free-base porphyrin ligand meso-tetramesitylporphyrin (H₂TMP), was prepared according to Lindsey et al.³⁸ The metallation of the free-base porphyrin to give [Fe(TMP)Cl] was done as previously described.³⁹ [Fe(TMP)](OH) was prepared according to a modified Fleischer preparation.⁴⁰ Mössbauer measurements were performed on a constant acceleration spectrometer from 15 K to 300 K with optional small field (Knox College).

Synthesis of [Fe(TMP)(2-MeHIm)₂]

[Fe(TMP)(OH)] (0.04 mmol) was dissolved in 3 mL of methylene chloride, and 1 mL of ethanethiol was added by syringe. The mixture was stirred at room temperature for 3 days, then a suspension of excess 2-methylimidazole (0.24 mmol) in 4 mL of hot toluene was added by cannula. The reaction mixture was then stirred for 1 h. X-Ray quality crystals were obtained in 8 mm × 250 mm sealed glass tubes by liquid diffusion using hexanes as nonsolvent after three weeks. Microcrystalline solids for Mössbauer measurements were obtained by liquid diffusion in Schlenk tubes using hexanes as the nonsolvent. The solids were isolated in an inert-atmosphere box and immobilized in Apiezon M grease.

X-ray Structure Determination

A dark red crystal with the dimensions 0.20 × 0.26 × 0.33 mm³ was used for the structure determination. The single-crystal experiment was carried out on a Bruker Apex system with graphite-monochromated Mo-K radiation (λ = 0.71073 Å). The crystalline sample was placed in inert oil, mounted on a glass pin, and transferred to the cold gas stream of the diffractometer. Crystal data were collected at 100K.

The structure was solved by direct methods using SHELXS-97⁴¹ and refined against F² using SHELXL-97;^{42, 43} subsequent difference Fourier syntheses led to the location of most of the remaining nonhydrogen atoms. For the structure refinement all data were used including negative intensities. The structure was refined as a racemic twin in space group I $\overline{4}$. The program SADABS⁴⁴ was applied for the absorption correction. Complete crystallographic details, atomic coordinates, bond distances and angles, anisotropic thermal parameters, and fixed hydrogen atom coordinates are given in the Supporting Information.

The asymmetric unit was found to contain four iron porphyrinate molecules as well as toluene, 2-methylimidazole, methylene chloride, and methanol solvates. Two of the iron porphyrinates are the desired bis-ligated species, [Fe(TMP)(2-MeHIm)₂]. These two molecules were completely ordered. These molecules will be referred to mol 1 and mol 2. The third and fourth iron porphyrinates were five-coordinate species, [Fe(TMP)(2-MeHIm)] that had cocrystallized with the desired six-coordinate species. For the third iron molecule, [Fe(TMP)(2-MeHIm)] (mol 3), the axial 2-methylimidazole was found to be disordered over two positions, a major and a minor position, which were refined isotropically as rigid groups. The temperature factors of the atoms of the minor 2-methylimidazole N(35b), N(36b), C(31b), C(32b), C(33b) and C(34b) were constrained to be the same within an effective standard deviation (0.05). The occupancy of the major imidazole orientation was found to be 55%. For the fourth molecule, [Fe(TMP)(2-MeHIm)] (mol 4), both iron and the 2-methylimidazole were found to be disordered over two position (both sides of the porphyrin plane). Both 2-methylimidazoles were refined isotropically as rigid groups. A partially occupied methylene chloride molecule (occupancy is 0.20) is found in the same region as the minor 2-methylimidazole ligand. The occupancy of the major iron and 2-methylimidazole was found to be 68%. The atoms of other partially occupied methylene chloride, 2-methylimidazole, methanol and water solvate molecules were refined isotropically. All other nonhydrogen atoms were refined anisotropically. For the porphyrin rings and the 2-methylimidazole ligands of mo1 and mol 2, hydrogen atoms were added with the standard SHELXL-97 idealization methods, other hydrogen atoms were not generated. The largest residual density (2.4 e/ų) is 1.07 Å from iron atom Fe(3). Brief crystal data and intensity collection parameters for the crystalline complex are shown in Table 1 and complete details are given in Table S1.

Table 1.

Crystallographic Details for [Fe(TMP)(2-MeHIm)₂]₂·[Fe(TMP)(2-MeHIm)]₂

formula	C259.80H259.85Cl1.40Fe4N29.88O0.76
unit cell content	8×{[Fe(TMP)(2-MeHIm)2]2·[Fe(TMP)(2-MeHIm)]2·C6H5CH3·0.94(2-MeHIm)·0.7CH2Cl2·0.34CH3OH·0.42H2O}
FW, amu	4085.99
a, Å	39.8634(3)
c, Å	28.1013(6)
V, Å3	44655.5(11)
space group	I $\overline{4}$
Z	8
Dc, g/cm3	1.216
F(000)	1729
μ, mm−1	0.334
crystal dimensions, mm	0.33 × 0.26 × 0.20
radiation	MoKα, $\overline{\lambda }=0.71073\hspace{0.17em}\mathring{A}$
temperature, K	100(2)
total data collected	194984
absorption correction	Semi-empirical from equivalents
unique data	44982 (Rint = 0.051)
unique observed data [I > 2σ(I)]	34716
refinement method	Full-matrix least-squares on F2
final R indices [I > 2σ(I)]	R1 = 0.0632, wR2 = 0.1728
final R indices (all data)	R1 = 0.0882, wR2 = 0.1903
absolute structure parameter	0.463(9)

Results

In order to obtain the bis-ligated iron(II) porphyrinates with two ligands oriented perpendicular to each other, we tried to synthesize bis-ligated Fe(II)(TMP) complexes with 2-methylimidazole or 1,2-dimethylimidazole as axial ligands. Many crystallization attempts were made with a variety of conditions and solvent in order to get good crystals. Finally, in the presence of toluene, methylene chloride and ethanethiol, single crystals of [Fe(TMP)(2-MeHIm)₂] were obtained for 2-methylimidazole, but not for 1,2-dimethylimidazole. In these crystals, it is found that the asymmetric unit contains four independent porphyrin molecules. Surprisingly, there are two different species that have cocrystallized: six-coordinate [Fe(TMP)(2-MeHIm)₂] (Figures 1 and 2) and five-coordinate [Fe(TMP)(2-MeHIm)] (Figures 3, S1 and S2). In these figures and in all tables the following atom naming convention has been used: Q(nyy), where Q is the atom type, n refers to molecules 1–4 and yy are further numbers and letters needed to completely specify the atom. Similar atoms in the four molecules have the same name except for the digit n. Selected bond distances and angles are listed in Table 2.

Figure 1.

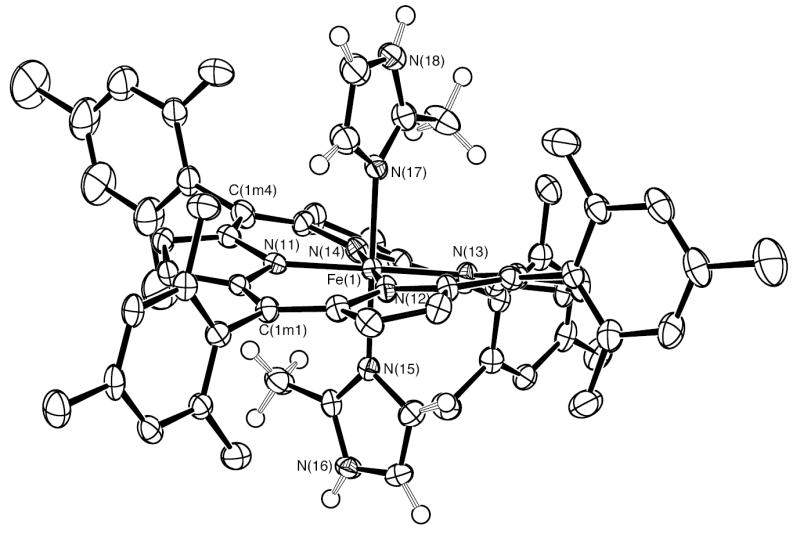
ORTEP diagram of six-coordinate [Fe(TMP)(2-MeHIm)₂] (mol 1). The hydrogen atoms of the porphyrin ligand have been omitted for clarity; the hydrogen atoms of the imidazole ligand are shown. 50% probability ellipsoids are depicted.

Figure 2.

ORTEP diagram of six-coordinate [Fe(TMP)(2-MeHIm)₂] (mol 2) The hydrogen atoms of the porphyrin ligand have been omitted for clarity; the hydrogen atoms of the imidazole ligand are shown. 50% probability ellipsoids are depicted. The orientation of the molecule in this figure and Figure 1 are chosen to show the similar conformations.

Figure 3.

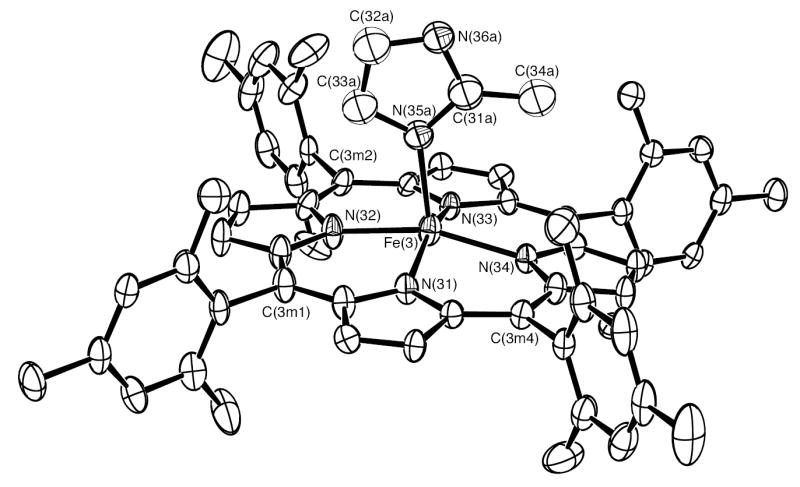
ORTEP diagram of [Fe(TMP)(2-MeHIm)] (mol 3). Only the major orientation (55%) of the imidazole ligand is shown. The hydrogen atoms have been omitted for clarity; 50% probability ellipsoids are depicted.

Table 2.

Selected Bond Lengths and Angles for [Fe(TMP)(2-MeHIm)₂]₂·[Fe(TMP)(2-MeHIm)]₂.

bond	length(Å)	bond	length (Å)
Fe(1)–N(11)	1.959(3)	Fe(1)–N(13)	1.961(3)
Fe(1)–N(12)	1.965(3)	Fe(1)–N(14)	1.971(3)
Fe(1)–N(15)	2.030(3)	Fe(1)–N(17)	2.047(3)
Fe(2)–N(24)	1.953(3)	Fe(2)–N(22)	1.958(3)
Fe(2)–N(23)	1.965(3)	Fe(2)–N(21)	1.969(3)
Fe(2)–N(27)	2.028(3)	Fe(2)–N(25)	2.032(3)
Fe(3)–N(31)	2.066(3)	Fe(3)–N(33)	2.066(3)
Fe(3)–N(34)	2.082(3)	Fe(3)–N(32)	2.084(3)
Fe(3)–N(35a)	2.123(4)	Fe(3)–N(35b)	2.204(5)
Fe(4a)–N(44)	2.062(3)	Fe(4a)–N(42)	2.065(4)
Fe(4a)–N(41)	2.073(3)	Fe(4a)–N(43)	2.104(3)
Fe(4a)–N(45a)	2.163(3)	Fe(4b)–N(42)	2.066(4)
Fe(4b)–N(44)	2.075(4)	Fe(4b)–N(43)	2.085(4)
Fe(4b)–N(45b)	2.117(9)	Fe(4b)–N(41)	2.131(4)

angle	value(°)	angle	value(°)
C(11)–N(15)–Fe(1)	132.0(3)	C(13)–N(15)–Fe(1)	122.2(3)
C(15)–N(17)–Fe(1)	133.0(3)	C(17)–N(17)–Fe(1)	120.6(3)
C(21)–N(25)–Fe(2)	133.7(3)	C(23)–N(25)–Fe(2)	119.2(3)
C(25)–N(27)–Fe(2)	133.2(3)	C(27)–N(27)–Fe(2)	121.6(3)
C(31a)–N(35a)–Fe(3)	127.1(3)	C(33a)–N(35a)–Fe(3)	126.4(3)
C(31b)–N(35b)–Fe(3)	127.9(4)	C(33b)–N(35b)–Fe(3)	124.5(4)
C(41a)–N(45a)–Fe(4a)	132.1(2)	C(43a)–N(45a)–Fe(4a)	120.3(2)

The six-coordinate species have two imidazole ligands with nearly perpendicular orientation. Equatorial bond distances (Fe–N_p) average 1.964(5) Å in mol 1 and 1.961(7) Å in mol 2. The axial bond lengths are 2.030(3) Å and 2.047(3) Å in [Fe(TMP)(2-MeHIm)₂] (mol 1), and 2.032(3) Å and 2.028(3) Å in [Fe(TMP)(2-MeHIm)₂] (mol 2).

The displacement of each atom of the porphyrin core from the 24-atom mean plane is shown in Figure 4. The orientation of the 2-MeHIm ligands including the value of the dihedral angle are also shown; the circle represents the position of the methyl group. Both six-coordinate species have significantly S₄-ruffled cores. The ligand planes make dihedral angles of 41.1°; and 41.3°; to the closest Fe–N_p axis in [Fe(TMP)(2-MeHIm)₂] (mol 1), and 44.8°; and 37.9°; in [Fe(TMP)(2-MeHIm)₂] (mol 2). This results in relative ligand orientations of 82.4°; and 84.4°; between the two imidazole planes in mol 1 and mol 2, respectively. Both ligands are almost perpendicular to the porphyrin plane with dihedral angles 88.7°; and 89.0°; for [Fe(TMP)(2-MeHIm)₂] (mol 1), and 79.9°; and 87.7°; for [Fe(TMP)(2-MeHIm)₂] (mol 2).

Figure 4.

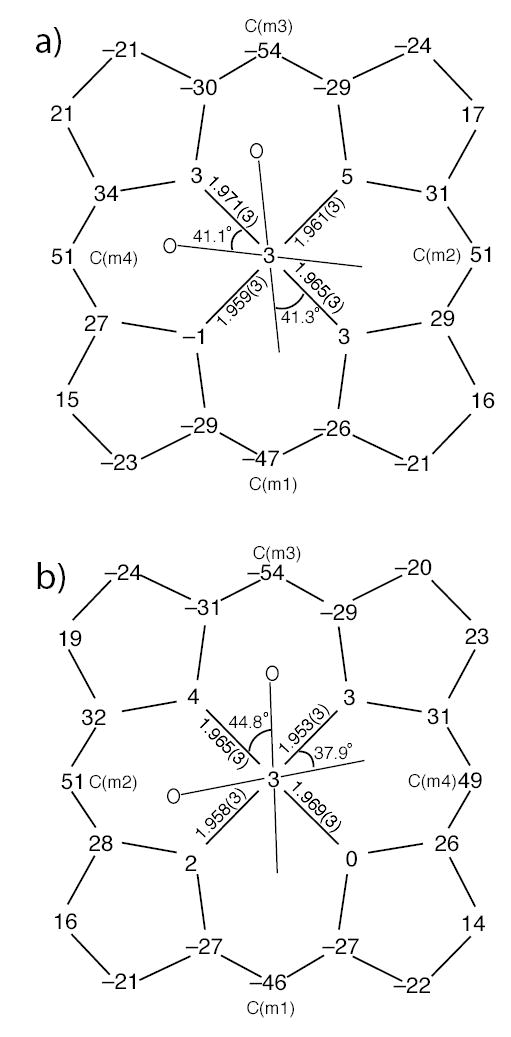
Formal diagrams of the porphyrinato cores of (a) [Fe(TMP)(2-MeHIm)₂] (mol 1), (b) [Fe(TMP)(2-MeHIm)₂] (mol 2). Illustrated are the displacements of each atom from the 24-atom core plane in units of 0.01 Å. The diagrams also show the orientation of the imidazole ligand with respect to the atoms of the porphyrin core. The position of the methyl group at the 2-carbon position is represented by the circle.

Both five-coordinate [Fe(TMP)(2-MeHIm)] molecules are disordered. For mol 3, the 2-methylimidazole is disordered over two position. Only the major position is displayed in Figure 3. For mol 4, both the iron and the 2-methylimidazole are disordered over two positions: above and below the porphyrin plane, which is shown in Figure S2. The average Fe–N_p distances are 2.074(10) Å and 2.076(19) Å in mol 3 and mol 4, respectively. The axial bond distances for the major imidazole orientation are 2.123(4) Å and 2.163(3) Å, respectively. As shown in Figure 5, iron atom displacements out of the 24-atom core are both 0.44 Å for two five-coordinate species, which is a general feature of high-spin five-coordinate Fe(II) species. The Fe–N_im–C_im angles are also listed in Table 2.

Figure 5.

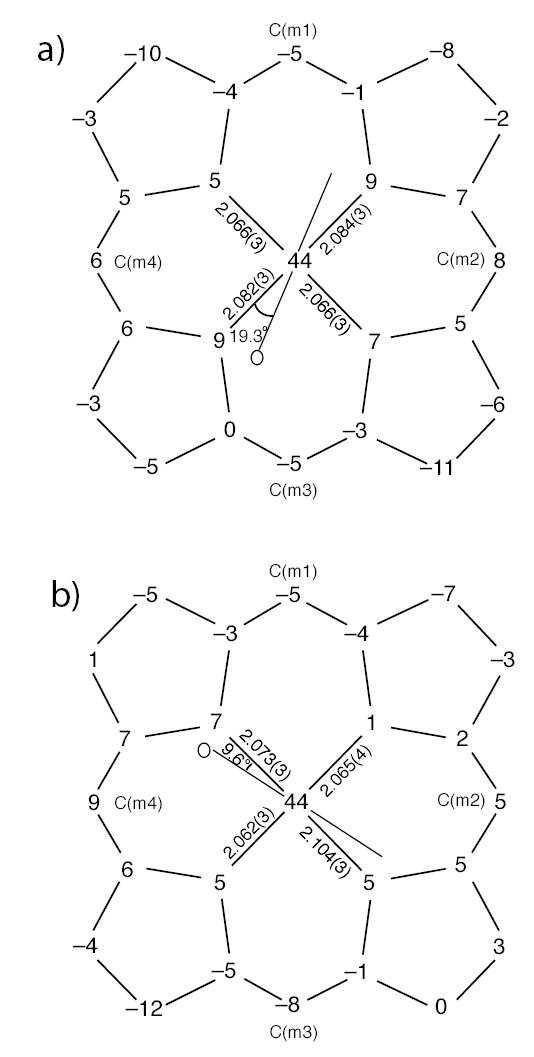
Formal diagrams of the porphyrinato cores of (a) [Fe(TMP)(2-MeHIm)] (mol 3), (b) [Fe(TMP)(2-MeHIm)] (mol 4). Illustrated are the displacements of each atom from the 24-atom core plane in units of 0.01 Å. The diagrams also show the orientation of the major imidazole ligand with respect to the atoms of the porphyrin core. The position of the methyl group at the 2-carbon position is represented by the circle.

The Mössbauer spectra of the polycrystalline compound were taken at several different temperatures from 15 K to 298 K. The observed spectra consist of two quadrupole doublets with equal area, and as will be discussed later, can be assigned to the two components of the polycrystalline derivative.

Discussion

Synthesis

One of our goals was to investigate whether a six-coordinate Fe(II) porphyrin with hindered imidazole ligands could be synthesized and isolated. If such species could be synthesized, this would appear to be a strategy for controlling the relative axial ligand orientation in iron(II) species. Coordination of sterically hindered imidazoles as the axial ligand has been used as a strategy for synthesis of five-coordinate high-spin iron(II) porphyrins, as originally reported by Collman and Reed.³³ The strategy is based on the idea that the binding constant for adding the second axial ligand can be reduced by steric effects while not significantly affecting the binding of the first ligand for the equilibrium reactions below.³²

$$\text{Fe(Porph)}+\text{L}\rightleftharpoons \text{Fe(Porph)L}+\text{L\hspace{0.17em}}\hspace{0.17em}\to \hspace{0.17em}{\text{Fe(Porph)L}}_{\text{2}}$$

However, the second binding constant K₂ is not reduced to a vanishingly small value with the use of hindered imidazoles. Thus Kassner and Wagner,³⁶ and later Brinigar et al.⁴⁵ showed, spectroscopically, that Fe(TPP) could bind two axial 2-methylimidazole ligands at low temperature. Safo³⁷ showed that the binding constant for the second 2-methylimidazole was porphyrin ligand dependent. Safo was able to spectroscopically demonstrate enhanced binding of the second axial ligand when the porphyrin ligand was tetramesitylporphyrin, even at ambient temperatures. This particular porphyrin complex appeared to be a strong candidate for the preparation of a crystalline derivative. However, Safo was unable to prepare a solid, crystalline species.³⁷

Subsequent to these experiments, Nesset et al.¹⁸ were able to measure, by electrochemical methods, the value of the second binding constant in DMF solution. They obtained a value of log(K₂) = 1.9 for the iron(II) derivative of tetra-mesitylporphyrin and 2-methylimidazole for the reaction

$$\text{Fe(TMP)\hspace{0.17em}L}+\text{L}\rightleftharpoons \hspace{0.17em}{\text{Fe(TMP)L}}_{\text{2}}$$

The equilibrium constant for binding the second hindered imidazole ligand is somewhat larger when the iron atom has been oxidized to the iron(III) oxidation state. Thus the low-spin iron(III) species, [Fe(TPP)(2-MeHIm)₂]⁺¹² and [Fe(TMP)(1,2-Me₂Im)₂]⁺²⁶ have been isolated and structurally characterized. The complex [Fe(OEP)(2-MeHIm)₂]⁺,⁴⁶ also isolated and characterized, is a high-spin derivative. The steric effects of the hindering group are always a factor and both the high-spin and low-spin species have (differing) structural features that minimize the nonbonded contacts between the hindering methyl group of the imidazole and the porphyrin core.

The relatively low value of the second binding constant (see equation below) shows part of the synthetic difficulty of preparing six-coordinate iron(II) derivatives

$${\text{K}}_{\text{2}}=\frac{[{\text{Fe(TMP)(L)}}_{\text{2}}]}{[\text{Fe(TMP)(L)}][\text{L}]}$$

where L is 2-methylimidazole. Although the value of K₂ may be larger in some nonpolar solvents, driving the the equilibrium towards complete formation of the six-coordinate species is limited by the solubility of 2-methylimidazole. Under our experimental conditions, [2-MeHIm] is about 0.03 mol/L, so the [Fe(TMP)L₂]/[Fe(TMP)L] ratio is about 2.4 in the solution. Any crystallizing solution must thus contain a mixture of the five-coordinate and six-coordinate species. Obtaining the pure crystalline six-coordinate complex would depend on finding a solvent system that favored its crystallization. The single crystals finally obtained for this system were formed in a solvent system of toluene, methylene chloride and ethanethiol, with hexane as the nonsolvent. In these crystals the five-coordinate and six-coordinate species have cocrystallized and have yielded an especially interesting structure.

[Fe(TMP)(2-MeHIm)₂] Structures

The asymmetric unit of the cell of the cocrystallized species contains four porphyrin molecules, two low-spin six-coordinate [Fe(TMP)(2-MeHIm)₂] and two high-spin five-coordinate [Fe(TMP)(2-MeHIm)] molecules. The low-spin state for [Fe(TMP)(2-MeHIm)₂] is evident from the structural parameters and from the Mössbauer studies described subsequently. With a confirmed low-spin state for the six-coordinate species, certain stereochemical features can be expected. The axial bonds to iron must be relatively short. A strongly ruffed porphyrin core is required in order to allow an appropriate close approach with the sterically bulky 2-methylimidazole ligands, with the formation of two oblong cavities at right angles on opposite sides of the porphyrin ring, and a relative perpendicular orientation of the two axial imidazole ligands. Both [Fe(TMP)(2-MeHIm)₂] mol 1 and mol 2 show such structural features. As can be seen from an examination of Figures 1 and 2, the two molecules have nearly identical core conformations and strongly similar relative and absolute axial ligand orientations. The absolute ligand orientation is given by the dihedral angle between the axial ligand plane and the closest N_axFeN_p plane and is conventionally denoted by φ. The relative ligand orientation is simply the dihedral angle between the two axial ligand planes.

Additional quantitative information is given in Figure 4 which gives detailed displacements of each porphyrin core atom (in units of 0.01 Å from the 24-atom mean plane and shows the orientation of the two axial ligands for each molecule. The figure also shows that the core conformations also display some (small) mixture of a saddling deformation. The steric interaction of the 2-methyl group adjacent to the coordinated nitrogen atom leads to a small tilting of the Fe–N_im bond from the normal to the porphyrin plane; values are 3.0, 3.5, 3.5, and 3.7°. The direction of the tilts always serves to decrease the imidazole methyl group ··· porphyrin core contacts. In addition, the methyl group leads to significantly different pairs of Fe–N_im–C_im angles; the averaged angle involving the methyl side of imidazole is 133.0(7)°, while the unhindered C_im has Fe–N_im–C_im average angles of 120.9(13)°. These are similar to those values in [Fe(TPP)(2-MeHIm)₂]^+,12 where small tilt angles(~4°) and large difference between two different Fe–N_im–C_im angles are also observed.

The ligand binding pocket formed is bounded by the 2- and 6-methyl substituents of the peripheral mesityl substituents. The ruffing of the core leads to large variation in the position of the the 2- and 6-methyl substituents with respect to the mean plane of the porphyrin core. There are effectively two classes of methyl groups: one group has an average perpendicular distance of 1.51 Å from the mean porphyrin plane, while the second has an average distance of 3.29 Å. These are clearly visible in Figures 1 and 2. These features are similar to those observed in a number of iron(III) derivatives of TMP and have been previously described.¹³ These conformational features lead to the dihedral angles between the mesityl groups and the core all being nearly 90°. The observed dihedral angles are 88.0°, 89.5°, 82.1°, 81.7°; in [Fe(TMP)(2-MeHIm)₂] (mol 1), 90.0°, 86.9°, 89.0°, 77.8° in [Fe(TMP)(2-MeHIm)₂] (mol 2).

The generally observed value for the equatorial Fe–N_p distances in low-spin six-coordinate iron(II) porphyrinates is ~2.000 Å, or about ~0.01 Å longer than than those observed for comparable iron(III) species.⁴⁷ These complexes have effectively planar porphyrin core conformations. The average equatorial distances observed in [Fe(TMP)(2-MeHIm)₂] are shorter at 1.964(5) Å (mol 1) and 1.961(7) Å (mol 2); the observed decrease (bond shortening) is the clear result of the core ruffing.

Some time ago, Hoard^{48, 49} pointed out that there should be a quantitative relationship between the degree of core ruffing and the amount of bond shortening. The shortening observed for the [Fe(TMP)(2-MeHIm)₂] derivatives are in general agreement with those expectations. We have explored the issue more quantitatively by examining the value of the equatorial Fe–N_p bond distances with the degree of ruffing in iron(II) and iron(III) derivatives. All such ruffed derivatives are axially ligated by two planar ligands with relative perpendicular orientations. We take the average absolute displacement of the methine carbon atoms from the mean plane of the 24-atom core as a quantitative measure of the ruffing of the core. A plot of average absolute C_m displacements against the equatorial Fe–N_p bond distance in the known iron(III) derivatives^{12–14,26–29,63} is given in Figure 6; detailed values are given in Table 3.^50–64 The C_m displacements vary from 0.25 to 0.72 Å and the Fe–N_p distances correspondingly range from 1.989 down to 1.937 Å. The line illustrated is the best fit to these iron (III) data. Also shown on Figure 6 are the two values for [Fe(TMP)(2-MeHIm)₂] and the one other iron(II) datum^55,65 available from the literature (shown with filled squares). The figure suggests not only the strong correlation between the degree of ruffing and the equatorial bond distance shortening but that the small difference (~0.01 Å) between iron(II) and iron(III) porphyrinate Fe–N_p bond distances remains when the derivatives have ruffed conformations.

Figure 6.

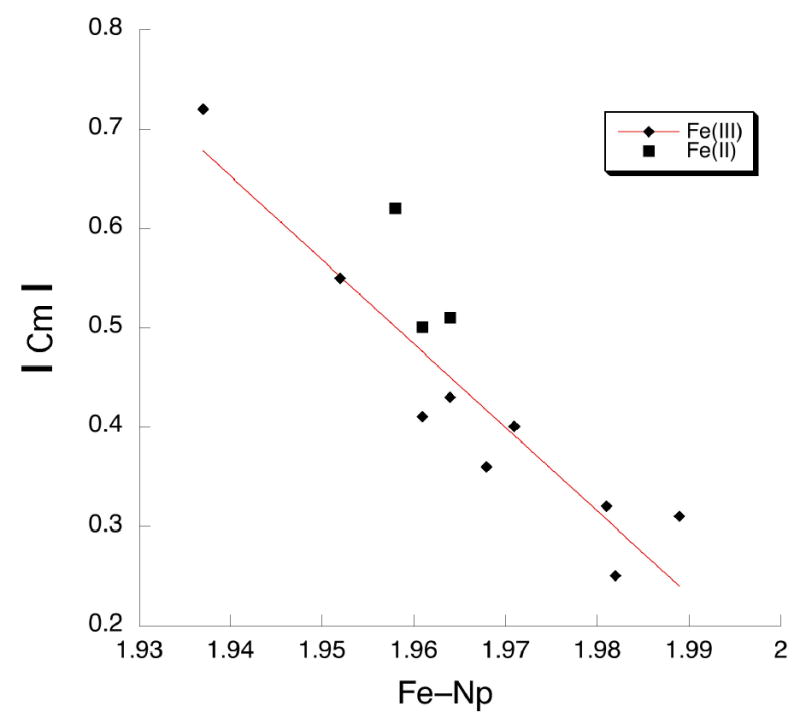
Plot of absolute meso-carbon (C_m) displacement (Å) vs the Fe–N_p bond distance (Å) for iron(II) and iron(III) porphyrinates with two axial ligands perpendicular to each other.

Table 3.

Selected Bond Distances (Å) and Angles (deg) for [Fe(TMP)(2-MeHIm)₂] (mol 1 and mol 2) and Related Species^a

Complex	Fe–Npb,c	Fe–NAxc	Cmc,d	φe,f	relative orientatione,g	ref.
Iron(II)
[Fe(TMP)(2-MeHIm)2] (mol 1)	1.964(5)	2.030(3)	0.51	41.1	82.4	tw
		2.047(3)		41.4
[Fe(TMP)(2-MeHIm)2] (mol 2)	1.961(7)	2.032(3)	0.50	44.8	84.4	tw
		2.028(3)		37.9
[Fe(TPP)(1-VinIm)2]	2.001(2)	2.004(2)		14	0h	31
[Fe(TPP)(1-BzylIm)2]	1.993(9)	2.017(4)		26	0h	31
[Fe(TPP)(1-MeIm)2]	1.997(6)	2.014(5)		15	0h	31
[Fe(TMP)(4-CNPy)2]	1.992(1)	1.996(2)		40	0h	30
[Fe(TMP)(3-CNPy)2]	1.996(0)	2.026(2)		42	0h	30
[Fe(TMP)(4-MePy)2]	1.988(0)	2.010(2)		41	0h	30
[Fe(TPP)(Py)2]·2Py	1.993(6)	2.039(1)		34.4	0h	50
[Fe(TPP)(Py)2]	2.001(2)	2.037(1)		45	0h	51
[Fe(TPP)(Pip)2]	2.004(6)	2.127(3)			0h	53
[Fe(TPP)(pyz)2]	1.987(8)	1.990(28)		3.9/37.0	40.9	52
[Fe(TFPPBr8)(Py)2]	1.963(4)	2.012(7)			90	54
[Fe((C3F7)4P)(py)2]	1.958(4)	2.002(11)	0.62	41.3/46.0	87.5	55
Iron(III)
[Fe(TMP)(1-MeIm)2]ClO4	1.988(20)	1.975(3)		23	0h	13
	1.987(1)	1.965(3)		41	0h
[Fe(TPP)(HIm)2]Cl·CHCl3	1.994(12)	1.977(3)		6	0h	56
	1.993(4)	1.964(3)		41	0h
[Fe(TPP)(4-MeHIm)2]Cl	2.000(11)	1.975(2)		3.1	0h	57
	1.995(10)	1.987(2)		4.6	0h	57
[Fe(TPP)(t-Mu)2]SbF6	1.992(5)	1.983(4)		22	0h	58
[Fe(TPP)(c-Mu)2]SbF6	1.997(1)	1.967(7)		29	0h	58
	1.995(17)	1.979(7)		15	0h
[Fe(TPP)(1-MeIm)2]ClO4	1.982(11)	1.974(6)b		22/32	11	60
[Fe(OEP)(4-NMe2Py)2]ClO4	2.002(4)	1.995(3)		36	0h	13
[Fe(Proto IX)(1-MeIm)2]	1.991(16)	1.977(16)b		3/16	13	61
paral-[Fe(TMP)(5-MeHIm)2]ClO4	1.983(4)	1.970(12)b		10/46	30	14
	1.981(5)	1.982(3)b		14/12	26
paral-[Fe(OMTPP)(1-MeIm)2]Cl	1.990(2)	1.996(29)b	0.01	12.6/6.9	19.5	62
[Fe(TPP)(HIm)2]Cl·MeOH	1.989(8)	1.974(24)b	0.31	18/39	57	63
perp-[Fe(TMP)(5-MeHIm)2]ClO4	1.981(7)	1.965(11)b	0.32	30/12	76	14
[Fe(TPP)(2-MeHIm)2]ClO4	1.971(4)	2.012(4)b	0.40	32/32	89.3	12
[Fe(TMP)(1,2-Me2Im)2]ClO4	1.937(12)	2.004(0)b	0.72	44.8/45.4	89.4	26
[Fe(TPP)(Py)2]ClO4	1.982(7)	2.003(3)b	0.25	34/38	86	27
[Fe(TMP)(3-ClPy)2]ClO4	1.968(3)	2.012(8)b	0.36	48/29	77	28
[Fe(TMP)(4-CNPy)2]ClO4	1.961(7)	2.011(14)b	0.41	43/44	90	29
[Fe(TMP)(3-EtPy)2]ClO4	1.964(4)	1.996(9)b	0.43	43/43	90	28
[Fe(TMP)(4-NMe2Py)2]ClO4	1.964(10)	1.984(8)b	0.51	37/42	79	13
[Fe(TPP)(4-CNPy)2]ClO4	1.952(7)	2.002(8)b	0.55	35/36	89	29
perp-[Fe(OMTPP)(1-MeIm)2]Cl	1.969(7)	1.982(10)	0.10	29.3	90.0h	62
[Fe(OETPP)(1-MeIm)2]Cl	1.970(7)	1.977(1)b	0.03	9.6/82.7	73	62
[Fe(OETPP)(4-NMe2Py)2]Cl	1.951(5)	2.000(22)b	0.28	9.0/29.0	70	64
[Fe(OMTPP)(4-NMe2Py)2]ClO4	1.979(3)	2.009b	0.01	1.3/2.4	84.2	78
[Fe(OMTPP)(Py)2]ClO4	1.973(3)	2.024(4)	0.18	23.4	90.0h	78
[Fe(OETPP)(4-NMe2Py)2]ClO4	1.977(2)	2.030(3)b	0.08	10.6/20.5	53.2	78

^aEstimated standard deviations are given in parentheses.

^bAveraged value.

^cin Å

^dAverage absolute values of displacements of the methine carbons from the 24-atom mean plane.

^eValue in degrees.

^fDihedral angle between the plane defined by the closest N_p–Fe–N_im and the imidazole plane.

^gDihedral angle between two axial ligands.

^hExact value required by symmetry.

It is to be noted that one of the two bis(pyridine) derivatives of iron(II) with nearly relative perpendicular pyridine ligands displayed in Table 3 is not given in these comparisons of Figure 6. The core conformation of [Fe(TFPPBr₈)(Py)₂]⁵⁴ is saddled as a result of the peripheral steric congestion. [Fe((C₃F₇)₄P)(py)₂],⁵⁵ on the other hand, has a ruffed core that is thought to result from the bulky meso-C₃F₇ groups. Even though the basis for the ruffing may be different, the compound follows the ruffing pattern.

The average value of the four axial Fe–N_im distances is 2.034(9) Å, which is slightly longer than the corresponding distances observed in other bis(imidazole-ligated) iron(II) porphyrinates with unhindered imidazoles: 2.004 Å in [Fe(TPP)(1-VinIm)₂], 2.017 ų¹ in [Fe(TPP)(1-BzylIm)₂],³¹ and 2.014 Å in [Fe(TPP)(1-MeIm)₂],⁶⁶ where the two ligand planes have a relative parallel orientation. Thus the steric crowding from the methyl group leads to a small increase in the axial Fe–N bond distance of about 0.02 Å. As shown in Table 3, the differences in axial bond lengths between hindered and unhindered imidazoles in the iron(III) derivatives appears to be a bit larger; but all iron(III) distances are shorter than those of iron(II) reflecting the effects of the oxidation state of iron.

[Fe(TMP)(2-MeHIm)] Structures

The structural features of the two five-coordinate [Fe(TMP)(2-MeHIm)] species have the common features found in other high-spin imidazole-ligated Fe(II) porphyrinates.^34,35,67 These include an expanded porphinato core, large equatorial Fe–N_p bond distances, and a significant out-of-plane displacement of the iron(II) atom. Selected structural parameters for related high-spin iron(II) derivatives are given for comparison in Table 4.^68,69 The similarities between the known structures and the two new molecules are evident. As shown in Figure 5, both five-coordinate species show core conformations with doming and some ruffing. The extent of the doming is given by the difference between the displacement of the iron atom from the four nitrogen atoms (Δ N₄ ) and the mean plane of the 24 -atom core (Δ); the values are not unusual.

Table 4.

Selected Bond Distances (Å) and Angles (deg) for [Fe(TMP)(2-MeHIm)] (mol 3 and mol 4) and Related Species^a

Complex	Fe–Npb,c	Fe–Nimc	ΔN4c,d	Δc,e	Ct· · ·Nc	Fe–N–Cf,g	Fe–N–Cf,h	θf,i	φf,j	ref.
[Fe(TMP)(2-MeHIm)] (mol 3)	2.074(10)	2.123(4)k	0.36	0.44	2.042	127.1(3)	126.4(3)	9.1	19.3	tw
[Fe(TMP)(2-MeHIm)] (mol 4)	2.076(19)	2.163(3)k	0.40	0.44	2.038	132.2(2)	120.2(2)	5.2	9.6	tw
[Fe(TPP)(1,2-Me2Im)]	2.079(8)	2.158(2)k	0.36	0.42	2.048	129.3(2)	124.9(2)	11.4	20.9	67
[Fe(TTP)(2-MeHIm)]	2.076(3)	2.144(1)	0.32	0.39	2.050	132.8(1)	121.4(1)	6.6	35.8	67
[Fe(Tp-OCH3PP)(2-MeHIm)]	2.087(7)	2.155(2)k	0.39	0.51	2.049	130.4(2)	123.4(2)	8.6	44.5	67
[Fe(Tp-OCH3PP)(1,2-Me2Im)]	2.077(6)	2.137(4)	0.35	0.38	2.046	131.9(3)	122.7(3)	6.1	20.7	67
[Fe(TPP)(2-MeHIm)](2-fold)	2.086(8)	2.161(5)	0.42	0.55	2.044	131.4(4)	122.6(4)	10.3	6.5	34
[Fe(TPP)(2-MeHIm)] ·1.5C6H5Cl	2.073(9)	2.127(3)k	0.32	0.38	2.049	131.1(2)	122.9(2)	8.3	24.0	35
[Fe(TpivPP)(2-MeHIm)]	2.072(6)	2.095(6)	0.40	0.43	2.033	132.1(8)	126.3(7)	9.6	22.8	68
[Fe(Piv2C8P)(1-MeIm)]	2.075(20)	2.13(2)	0.31	0.34	2.051	126.5	120.4	5.0	34.1	69

^aEstimated standard deviations are given in parentheses.

^bAveraged value.

^cin Å

^dDisplacement of iron from the mean plane of the four pyrrole nitrogen atoms

^eDisplacement of iron from the 24-atom mean plane of the porphyrin core.

^fValue in degrees.

^gImidazole 2-carbon, sometimes methyl substituted

^hImidazole 4-carbon.

ⁱOff-axis tilt (deg) of the Fe–N_im bond from the normal to the porphyrin

^jplane. Dihedral angle between the plane defined by the closest N_p –Fe–N_im and the imidazole plane in deg.

^kMajor imidazole orientation.

The imidazole 2-methyl group adjacent to the coordinated nitrogen atom creates a steric interaction with the porphyrin core and leads to a tilting of the Fe–N_im bond from the normal to the porphyrin plane. For these five-coordinate species, the tilt angles are 5.2 and 9.1°. There are also two types of Fe–N_im–C_im angles that serve to minimize the steric interactions. Despite the presence of the hindering methyl group, the dihedral angles between the imidazole plane and the nearest N_p–Fe–N_im plane are 19.3 and 9.6°. The orientation of the imidazole is also shown in Figure 5.

Mössbauer Spectra

Mössbauer spectra were measured from room temperature to 15 K. The spectra consist of two quadrupole doublets that are overlapped at most temperatures; spectra are illustrated in Figure 7. The two doublets have equal area as would be expected for the crystalline species that shows 1:1 stoichiometry of the two co-crystallized species. The isomer shift (δ) and quadrupole splitting ( ΔE_q) values have been obtained by fitting these data to a set of four Lorentzian lines. The pairwise assignment of lines into quadrupole doublets is based on the temperature dependence of the isomer shift. Only with the assignments of lines 1 and 3 as a doublet and lines 2 and 4 as a second doublet does one get a proper monotonic decrease of the two isomer shift values with increasing temperature. Complete results from the fitting of the temperature-dependent data is given in Tables 5 and 6. One of the doublets has a strongly temperature-dependent quadrupole splitting, with values of ΔE_q that range from 1.46 to 2.25 mm/s and isomer shift values that range from 0.79 at room temperature to 0.90 mm/s at 15K. These values are reasonable for five-coordinate high-spin Fe(II) porphyrinates.^35,67,70 Table 5 shows the strong similarity between the Mössbauer data observed for the current complex (five-coordinate [Fe(TMP)(2-MeHIm)]) and related species. The large temperature-dependence of the quadrupole splitting is presumably caused by the presence of close-lying excited states of the same or lower spin multiplicity and appears to be a general feature of all five-coordinate imidazole-ligated iron(II) porphyrinates.

Figure 7.

Solid-state Mössbauer spectra at several different temperature. Lines are numbered 1 to 4 from left to right and are clearly seen in the spectrum at 200 K.

Table 5.

Mössbauer Parameters for Five-coordinate [Fe(TMP)(2-MeHIm)] and Related Complexes

Complex	ΔEQa	δFea	T, K	ref.
Fe(TMP)(2-MeHIm)]	2.25	0.90	15	tw
	2.21	0.90	50	tw
	2.12	0.90	100	tw
	1.78	0.84	200	tw
	1.46	0.79	298	tw
[Fe(Tp-OCH3PP)(1,2-Me2Im)]	2.47	0.94	16	67
	2.28	0.92	50
	2.27	0.92	100
	2.10	0.91	150
	1.97	0.88	200
	1.88	0.90	250
	1.77	0.81	298
	−2.44	0.95	4.2
[Fe(Tp-OCH3PP)(2-MeHIm)]	−2.18	0.94	4.2	67
[Fe(TPP)(1,2-Me2Im)]	−1.93	0.92	4.2	67
[Fe(TPP)(2-MeHIm)]	−1.96	0.86	4.2	67
[Fe(TTP)(2-MeHIm)]	−1.95	0.85	4.2	67
[Fe(TTP)(1,2-Me2Im)]	−2.06	0.86	4.2	67
[Fe(TPP)(2-MeHIm)]	−2.40	0.92	4.2	35
[Fe(TPP)(2-MeHIm)(2-fold)	−2.28	0.93	4.2	70
[Fe(TPP)(1,2-Me2Im)]	−2.16	0.92	4.2	70
Hb	−2.40	0.92	4.2	70
Mb	−2.22	0.92	4.2	70

^amm/s.

Table 6.

Mössbauer Parameters for Six-coordinate [Fe(TMP)(2-MeHIm)₂] and Related Complexes.

Complex	ΔEQa	δFea	sample phase	T, K	relative orientationb	Conf.c	ref.
Fe(II) complexes
[Fe(TMP)(2-MeHIm)2]	1.71	0.43	cryst solid	15	82.4/84.4	ruf	tw
	1.70	0.42		50			tw
	1.70	0.42		100			tw
	1.76	0.40		200			tw
	1.78	0.35		298			tw
[Fe(TPP)(1-MeIm)2]	1.07	0.47	cryst solid	77	0	pla	31
[Fe(TPP)(1-AcIm)2]	0.97	0.45	cryst solid	77	d	d	31
[Fe(TPP)(1-VinIm)2]	1.02	0.45	cryst solid	77	0	pla	31
[Fe(TPP)(1-BzylIm)2]	1.02	0.45	cryst solid	77	0	pla	31
[Fe(TPP)(1-SiMe3Im)2]	1.04	0.46	cryst solid	77	d	d	31
[Fe(TPP)(Py)2]	1.15	0.40	cryst solid	77	0	pla	71
[Fe(OEP)(Py)2]	1.13	0.46	cryst solid	4.2	d	d	72
[Fe(TMP)(1-MeIm)2]	1.11	0.43	cryst solid	120	d	d	30
	1.09	0.45		4.2
[Fe(TMP)(4-CNPy)2]	1.13	0.41	cryst solid	120	0	pla	30
	1.11	0.42		4.2
[Fe(TMP)(3-ClPy)2]	1.23	0.43	cryst solid	120	0	pla	30
	1.24	0.45		4.2
[Fe(TMP)(4-MePy)2]	1.12	0.42	cryst solid	120	0	pla	30
	1.09	0.43		4.2
[Fe(TMP)(4-NMe2Py)2]	1.27	0.36	cryst solid	120	0	pla	30
	1.20	0.39		4.2
[Fe(TMP)(2-MeHIm)2]	1.64	0.39	frozen soln	77	e	e	73
[Fe(TMP)(1,2-Me2Im)2]	1.73	0.39	frozen soln	77	e	e	73
[Fe(OEP)(2-MeHIm)2]	1.67	0.34	frozen soln	77	e	e	73
[Fe(OEP)(4-NMe2Py)2]	1.02	0.45	frozen soln	77	d	d	73
[Fe(OEP)(4-CNPy)2]	1.10	0.32	frozen soln	77	d	d	73
[Fe(OEP)(1-MeIm)2]	0.96	0.46	frozen soln	77	d	d	73
Fe(III) complexes
[Fe(TMP)(4-NMe2Py)2]ClO4	1.74	0.20	cryst solid	77	79	ruf	13
perp-[Fe(TMP)(5-MeHIm)2]ClO4	1.78	0.22	cryst solid	120	76	ruf	14
[Fe(TPP)(2-MeHIm)2]ClO4	1.77	0.22	cryst solid	120	89.3	ruf	15
[Fe(TMP)(1,2-Me2Im)2]ClO4	1.26	0.17	cryst solid	120	89.4	ruf	26
[Fe(TMP)(2-MeHIm)2]ClO4	1.48	0.20	cryst solid	77	e	e	28
[Fe(TMP)(3-EtPy)2]ClO4	1.25	0.18	cryst solid	77	90	ruf	28
[Fe(TMP)(3-ClPy)2]ClO4	1.36	0.20	cryst solid	77	77	ruf	28
[Fe(TPP)(Py)2]Cl	1.25	0.16	solid	77	e	e	74
[Fe(TMP)(4-CNPy)2]ClO4	0.97	0.20	cryst solid	77	70	ruf	28
[Fe(TPP)(4-CNPy)2]ClO4	0.65	0.19	cryst solid	4.2	89	ruf	29
perp-[Fe(OMTPP)(1-MeIm)2]Cl	1.76		cryst solid		90	sad	16
[Fe(OETPP)(1-MeIm)2]Cl	1.94		cryst solid		73	sad	16
[Fe(OETPP)(4-NMe2Py)2]Cl	1.89		cryst solid		70	sad	16
[Fe(OMTPP)(4-NMe2Py)2]ClO4	1.89	0.23	cryst solid	70	84	sad	78
[Fe(OMTPP)(Py)2]ClO4	2.18	0.25	cryst solid	78	90	sad	78
[Fe(OETPP)(4-NMe2Py)2]ClO4	2.31	0.26	cryst solid	80	53,70	sad	78,64
paral-[Fe(TMP)(5-MeHIm)2]ClO4	2.56	0.22	cryst solid	120	26/30	pla	14
[Fe(TMP)(1-MeHIm)2]ClO4	2.28	0.28	cryst solid	77	0	pla	13
[Fe(OEP)(4-NMe2Py)2]ClO4	2.14	0.26	cryst solid	77	0	pla	13
[Fe(TPP)(4-MeHIm)2]Cl	2.26	0.34	cryst solid	77	0	pla	57
[Fe(TPP)(HIm)2]Cl	2.23	0.23	crystalline(?)	77	d	d	74
paral-[Fe(OMTPP)(1-MeIm)2]Cl	2.80		cryst solid		19.5	sad	16

^amm/s.

^bDihedral angle between two axial ligands.

^cPredominant core conformation contribution; pla, planar; ruf, ruffled; sad, saddled.

^dNot determined, presumed parallel and planar.

^eNot determined, presumed perpendicular and ruffled.

The second quadrupole doublet arises from the six-coordinate [Fe(TMP)(2-MeHIm)₂] component of the crystals. [Fe(TMP)(2-MeHIm)₂] data are given at the top of Table 6; values of the quadrupole splitting and isomer shift vary only slightly with temperature. The isomer shift value is that expected for a low-spin iron(II) complex. However, the quadrupole splitting value of ~1.70 mm/s is significantly larger than those previously measured for bis(imidazole) complexes as crystalline solids. The comparison with Mössbauer data given in Table 6 is generally shown at a temperature chosen to facilitate comparisons, a few systems have values shown at two temperatures. None of the iron(II) species of Table 6, when such data are available, show significant temperature dependence of quadrupole splitting. Nearly all other species whose Mössbauer spectrum has been obtained as crystalline solids have known structures. In all of these structures, save that of [Fe(TMP)(2-MeHIm)₂], the two axial ligands are in a relative parallel configuration; the absolute orientations show a wide range of φ values (values tabulated in Table 3). We can thus conclude that the quadrupole splitting value for low-spin bis(planar axial ligand) iron(II) systems is sensitive to the relative orientation of the two axial ligands. Larger values of the quadrupole splitting (≥ 1.5 mm/s) indicate the presence of relative perpendicular orientation for the two axial ligands while lower values (≤ 1.25 mm/s) indicate relative parallel orientations. Frozen solution Mössbauer data for Fe(TMP) in the presence of a hindered imidazole have also been obtained. These data are shown in the top portion of Table 6; the values of quadrupole splitting are totally consistent with the conclusion of large values of the quadrupole splitting for derivatives with perpendicular relative orientations. It is to be noted that this pattern of magnitude of the quadrupole splitting with ligand orientation in the iron(II) derivatives is the opposite of that observed for the iron(III) derivatives. In the iron(III) derivatives, the species with relative perpendicular ligand orientations have the small values of the quadrupole splitting. Thus any explanation for the pattern seen in the iron(II) derivatives must also be able to account for the pattern in iron(III) as well.

We see from Table 6 an interesting contrast between [Fe(TMP)(2-MeHIm)₂] and the other bis-ligated Fe(II) compounds of known molecular structure: only [Fe(TMP)(2-MeHIm)₂] has a ruffed core conformation whereas the remaining iron(II) derivatives have effectively planar porphyrin cores. Concomitantly, only [Fe(TMP)(2-MeHIm)₂] has a perpendicular relative orientation for the two planar axial ligands; the remainder have relative parallel orientations.

One theoretical framework for understanding the origins of the quadrupole splitting involves the dominant contributions to the electric field gradient (EFG) from the 3d electrons. The valence electron contribution to the EFG can be expressed by the Townes-Dailey approximation⁷⁵

$$\begin{array}{l}{q}_{val}=\frac{4}{5}<r^{-3}>[-N(p_z)+\frac{\text{1}}{\text{2}}(N(p_x)+N(p_y))]+\frac{4}{7}<r^{-3}>[N(d_{x^2-y^2})-N(d_{z^2})+\\ N(d_{xy})-\frac{1}{2}(N(d_{xz})+N(d_{yz})]\end{array}$$ (1)

where N_p and N_d are the effective populations of the appropriate 4p and 3d iron orbitals, respectively, and < r⁻³ > is the expectation value of 1/r³ taken over the appropriate 3d and 4p radial functions.

For low-spin 3d⁶ complexes, the t₂ orbitals (d_xz, d_yz, d_xy) are all nominally doubly occupied. If that were strictly the case, their net contribution to the EFG would be zero. And for our purposes, with a positive quadrupole splitting,⁷⁶ we need an explanation of why the d_p orbitals (which make negative contributions to the EFG) have smaller populations than the d_xy orbital, and even smaller population in a ruffed porphyrin than in a more planar one.

Grodzicki et al.⁷⁷ have done some theoretical calculations that are helpful. Their results show that for both [Fe(TMP)(1-MeIm)₂] and [Fe(TMP)(2-MeHIm)₂] the energies of the d orbitals have this order: d_yz < d_xz < d_xy < d_z² < d_x²−y². The splitting between the d_π states is very small (0.006 and 0.018 eV for the two compounds, respectively). Furthermore, the population of the d_xy orbital is very similar in the two compounds (1.982 and 1.988), and is larger than the population of d_xz (1.740 and 1.859) and d_yz (1.758 and 1.805). The latter two orbital populations are, in fact, slightly smaller for the relative perpendicular than for relative parallel ligand plane orientations. But even more significantly, Grodzicki did model calculations on two structures with hindered perpendicular imidazoles, one with a planar porphyrin core and one with a ruffed porphyrin core. The populations of the d_π orbitals were significantly smaller with the ruffed porphyrin core, thus predicting a larger quadrupole splitting.

As described in the Structure section, the six-coordinate Fe(II) complex has shortened Fe–N_p bonds that correlate with the strong ruffing. We suggest the shorter Fe–N_p bonds enhance the π interaction between the Fe(3d_π) and N_p(2p_π). The stronger π interaction will cause Fe → N_π donation, lowering N(d_xz) and N(d_yz). The resulting reduction of negative contributions to the EFG (N(d_xz) and N(d_yz)) results in the observed larger quadrupole splitting.

It is interesting to observe (Table 6) that while for Fe(II) complexes the quadrupole splitting is higher for the ruffed porphyrins with perpendicular ligand planes than for planar porphyrins with parallel ligands, the opposite is true in Fe(III) complexes. That observation calls for an explanation as well. Among the bis-ligated Fe(III) compounds, we can identify three structural/spectroscopic categories: Type I) perpendicular ligands, normally ruffed or saddled porphyrin core, with “large g_max” EPR, and quadrupole splittings in the range 1.24 to 1.78 mm/s; Type II) parallel ligands, usually planar porphyrin cores although a saddled example exists, with classic rhombic EPR and quadrupole splittings in the range 2.14 to 2.8 mm/s; and Type III) axial ligands nearly perpendicular, ruffed porphyrin core, axial EPR spectrum, very small quadrupole splitting (≤ 1.00 mm/s).

Our goal is to understand the systematics of these categories and how the resulting structures allow us to make sense of the measured EPR and Mössbauer parameters. The quadrupole splittings in particular are interesting, as the largest splittings for Fe(III) models occur with parallel ligands, while for Fe(II) models the splitting is larger for perpendicular ligands.

The EPR differences between the three groups are understood in terms of the d electron configuration differences that depend on which t₂ orbital is singly occupied (highest in energy), as determined by the crystal field of the ligands. Type III has the d_xy orbital singly occupied, a conclusion based on the fact that in the Taylor formalism,⁷⁹ a negative tetragonal crystal field is required to fit the observed g-values, such that the d_xy orbital moves above both of the d_π orbitals in energy and thus becomes singly occupied. In the Townes-Dailey approximation, the valence contribution to the EFG should be proportional to

$$\mathrm{\Delta }N(d)=N(d_{x^2-y^2})+N(d_{x}y)-N(d_{z^2})-(N(d_{xz})+N(d_{yz}))/2$$ (2)

Relative to Type I and II, Type III has roughly one more d_π electron and one fewer d_xy electron. Both of these changes will reduce the EFG’s for members of Type III, so the observed small quadrupole splitting values are to be expected.

Type I has a singly-occupied d_π orbital and, based on its g-values, must have a relatively weak rhombic crystal field, which in turn implies the two d_π orbitals will be close in energy and therefore strongly mixed by spin-orbit coupling. This results in the characteristic large g_max EPR spectrum. Type II compounds also have an unpaired d_π electron, but in contrast to Type I, they exhibit classic rhombic EPR spectra. The g-values of such spectra imply the rhombic crystal fields are much larger than for Type I species. Therefore the ground d_π orbital has much smaller admixtures of the other two t₂ orbitals. It is reasonable that the rhombic crystal field should be larger for members of this group, as the parallel configuration of the ligand planes will result in a much larger asymmetry between the x- and y-axes than for the perpendicular-plane configuration of Type I.

We understand why Types I and II should have larger quadrupole splittings than Type III, but explaining why Type II shows larger quadrupole splittings than Type I is harder. The key to understanding this effect is to note that for the ruffed and saddled hemes, the symmetry is lowered so that the porphyrin π* orbitals can mix with the iron d_xy orbital. In this case π donation out of the doubly-occupied d_xy will occur in the distorted porphyrins, while it is symmetry-forbidden in the planar complexes. The smaller N(d_xy) for Type I, as can be seen in Eqn 2, results in a smaller quadrupole splitting for these compounds than for Type II.

In Type II species with parallel ligand planes and φ ≈ 0, the axial nitrogen π orbitals have the right symmetry to mix with the iron d_π orbitals, and compete with any possible bonding between the iron and the porphyrin π orbitals. This competition makes it a challenge to assess whether iron will be a net acceptor or donor as a result of these π interactions. Toward this end, we note the following: i) It is reasonable to assume that for φ ≈ 0, the singly occupied d-orbital (call it d_yz) is likely to be along the axis of the imidazole and ii) It has been noted⁵⁶ that for [Fe(TPP)(HIm)₂]Cl the equatorial Fe–N_p bonds perpendicular to the imidazole plane are shorter than those parallel. These points are consistent with the idea that the doubly-occupied d_xz orbital has increased π donation to the porphyrin π system. The fact that most complexes with relative parallel ligands also have φ near zero argues that π interaction with iron is significant. There may well also be π donation from the imidazole into the iron orbitals. To assess the net effect on the quadrupole splitting, a theoretical calculation would be required to determine whether the result of the π interactions is increases or decreases population of the iron d_π orbitals.

We see that the quadrupole splittings seem to be slightly larger for those planar models having relative orientations slightly greater than zero (Table 6). This distortion from axial parallel alignment is expected to reduce the π interaction with the axial ligands, and the larger quadrupole splitting is consistent with reduced π donation from those ligands.

We note in Tables 3 and 6, some of the compounds have both parallel and perpendicular arrangements of the axial ligands possible. Also, for the same ligands, using different porphyrins can change the orientation from parallel to perpendicular (e.g. [Fe(TMP)(4-NMe₂Py)₂]ClO₄ vs.[Fe(OEP)(4-NMe₂Py)₂]ClO₄. A natural inference is that the transitions between the various structural forms are rather delicately poised, and may be driven one way or another by small effects such as crystal packing forces. In this case the solid-state EPR and Mössbauer spectra are very likely to differ from those one would obtain in a frozen solution.

Summary

The synthesis and isolation of a six-coordinate low-spin iron(II) porphyrinate with its axial ligands in a relative perpendicular orientation has been accomplished for the first time. Consistent with the necessary use of a hindered imidazole to achieve a relative perpendicular orientation, the porphyrin core is strongly ruffed. The complex has been characterized by an X-ray diffraction study. The equatorial Fe–N_p bonds are shorter than those found in analogous planar complexes that have the two axial imidazoles in a relative parallel orientation. However, the axial Fe–N(Im) bonds are longer than when the ligands are oriented in a relative perpendicular orientation. Owing to the relatively low binding constant for the addition of the sixth ligand, the desired complex, [Fe(TMP)(2-MeHIm)₂] cocrystallizes with the five-coordinate precursor. Nonetheless, the study shows that a perpendicular orientation of axial ligands is experimentally accessible. The complex mixture has been characterized by temperature-dependent Mössbauer spectroscopy. The Mössbauer quadrupole splitting constants of the complex with relative perpendicular orientation are significantly larger than those of derivatives with similar axial ligands and show that the Mössbauer quadrupole splitting constant can be used to evaluate the relative ligand orientation of bis-ligated iron(II) porphyrinates.

Supporting Information

Table S1. Complete Crystallographic Details for [Fe(TMP)(2-MeHIm)₂]₂·[Fe(TMP)(2-MeHIm)]₂.

Table S2. Atomic Coordinates and Equivalent Isotropic Displacement Parameters for [Fe(TMP)(2-MeHIm)₂]₂·[Fe(TMP)(2-MeHIm)]₂.

Table S3. Bond Lengths for [Fe(TMP)(2-MeHIm)₂]₂·[Fe(TMP)(2-MeHIm)]₂.

Table S4. Bond Angles for [Fe(TMP)(2-MeHIm)₂]₂·[Fe(TMP)(2-MeHIm)]₂.

Table S5. Anisotropic Displacement Parameters for [Fe(TMP)(2-MeHIm)₂]₂·[Fe(TMP)-(2-MeHIm)]₂.

Table S6. Hydrogen Coordinates and Isotropic Displacement Parameters for [Fe(TMP)-(2-MeHIm)₂]₂·[Fe(TMP)(2-MeHIm)]₂.

Captions for Supporting Information Figures

Figure S1. ORTEP diagram of [Fe(TMP)(2-MeHIm)] (mol 3) showing the two orientations of the imidazole ligand. The major (55%) orientation is drawn with heavy bonds, while the minor orientation is depicted with open bonds. 50% probability ellipsoids are depicted.

Figure S2. ORTEP diagram of [Fe(TMP)(2-MeHIm)] (mol 4) showing the two disordered parts of both iron and imidazole ligands. The major (68%) orientation is drawn with heavy bonds, while the minor orientation is depicted with open bonds. 50% probability ellipsoids are depicted.