Abstract
The tumor microenvironment is hypoxic and acidic. These conditions have a significant impact on tumor progression and response to therapies. There is strong evidence that tumor hypoxia results from inefficient perfusion due to a chaotic vasculature. Consequently, some tumor regions are well oxygenated and others are hypoxic. It is commonly believed that hypoxic regions are acidic due to a stimulation of glycolysis through hypoxia, yet this is not yet demonstrated. The current study investigates the causes of tumor acidity by determining acid production rates and the mechanism of diffusion for H+ equivalents through model systems. Two breast cancer cell lines were investigated with divergent metabolic profiles: nonmetastatic MCF-7/s and highly metastatic MDA-mb-435 cells. Glycolysis and acid production are inhibited by oxygen in MCF-7/s cells, but not in MDA-mb-435 cells. Tumors of MDAmb-435 cells are significantly more acidic than are tumors of MCF-7/s cells, suggesting that tumor acidity is primarily caused by endogenous metabolism, and not the lack of oxygen. Metabolically produced protons are shown to diffuse in association with mobile buffers, in concordance with previous studies. The metabolic and diffusion data were analyzed using a reaction-diffusion model to demonstrate that the consequent pH profiles conform well to measured pH values for tumors of these two cell lines.
Keywords: acid-base, metabolism, tumor cells, hypoxia, glycolysis
Introduction
Tumors in humans and animal models contain microenvironments that are both hypoxic [1,2] and acidic [3,4,5,6]. These environments can play a significant role in tumor progression, as hypoxia and acidity are associated with increased mutations [7,8], chromosomal instability [9], spontaneous transformation [10], resistance to apoptosis [11], and increased invasion and metastasis [12,13,14,15]. Hypoxia and acidity also cause resistance to radiotherapies and chemotherapies [1,16,17]. Thus, it is important to define the underlying causes of tumor hypoxia and acidity and the relationships between them.
It is commonly believed that hypoxia and acidity are a direct result of the chaotic and heterogeneous microvascular structure of solid tumors [18,19]. In solid tumors, there may be several layers of intervening cells and several hundreds of microns of separation between viable tumor cells and the nearest feeding blood vessel. Blood vessels are the primary mode for delivery of glucose and O2 and for the removal of metabolic H+ and lactate. Whereas some convective flow of extravascular (extracellular) fluid may occur, it is more likely the case that movement of metabolites between blood and cells occurs primarily by a simple (Fickian) diffusion mechanism. This is consistent with the recent results of Dafni [20] who showed that interstitial convective velocities in tumors were ca. 0.2 µm sec-1. Fluxes arising from such velocities would be orders of magnitude lower than diffusive fluxes for small molecules (assuming a concentration gradient of 1 mM over a distance of 0.1 mm). Diffusion generally cannot supply cells with O2 beyond ca. 170 µm from a vessel [21,22] because the heterogeneously distributed microcirculation of tumors would be expected to generate significant volumes that are hypoxic. The distributions of hypoxic volumes in tumors have been modeled in three dimensions from microcirculatory distribution and flow data obtained using intravital microscopy [23]. In these communications, the spatially dependent delivery of oxygen to cells in tumors was obtained by taking into account the vessel distributions, blood flow, hematocrit, and oxygen diffusion. These factors were spatially compared to oxygen consumption rates to yield a model for the spatial distribution of oxygen and hypoxia.
Whereas similar analyses have not been performed for tumor pH, it has generally been assumed that hypoxia and low pH are mechanistically coupled through hypoxia inducible factor (HIF-1α) or the Pasteur effect (i.e., the inhibition of glycolysis by oxygen). Perfusion heterogeneities resulting from the nonuniform microcirculatory structure of tumors coupled with diffusion limitations of O2 and lactate may contribute to significant pH gradients in tumors. Helmlinger et al. [24] have shown a relationship between pO2 and pH on average, although the relationship is not strictly observed in individual volumes.
It is commonly accepted that the acidic extracellular pH of tumors is simply a result of poor oxygenation due to heterogeneous blood supply. Hence, a goal of the present study is to better define the relationship between pO2 and pH in a well-characterized set of breast cancer cells, tumor xenografts, and model systems. In addition to the aforementioned intravital microscopy studies [24], in vivo MR maps of pH [6,12,25] have clearly demonstrated that steady-state gradients of interstitial pH (pHe) exist within tumors. The current work was undertaken to investigate further the causes underlying these pHe gradients, using two breast cancer cell lines that have significantly divergent metabolic profiles. MCF-7/s cells are lowly metastatic cells that do not produce significant amounts of lactic acid and have relatively high pHe values when grown as tumors [25]. MDA-mb-435 cells are highly metastatic, produce copious lactic acid, and have relatively low pHe values when grown as tumors [26]. In this work, we also show that glycolysis in MDA-mb-435 cells is not affected by oxygen, and thus these tumors are acidic, even when well perfused.
Theoretically, steady-state pHe gradients could be inconsistent with the high diffusion coefficient of H+ of ca. 10-4 cm2 sec-1 [27]. For comparison, water diffusion in tissue interstitium is ca. 2x10-6 cm2 sec-1 [28]. This higher apparent H+ diffusivity is usually attributed to a “Grotthus mechanism,” also described as a “proton wire,” wherein aH+ adding onto water in one environment can induce the release of a H+ from H3O+ at a divergent location. However, proton conductance in biological solutions is generally limited by the codiffusion of counterions, which is necessary to maintain charge balance [29]. Nonetheless, in the presence of sufficient mobile counterions, H+ can effectively diffuse seven times faster than other monovalent cations [30]. In the current communication, we demonstrate that, although the diffusion of free protons may be high, the flux of H+ moving by this mechanism is low due to a low driving force (i.e., the concentration difference is submicromolar). Our data indicate that most diffusive H+ fluxes occur in association with ionizable solutes (mobile buffers), which is in agreement with the theoretical work of Junge and McLaughlin [27]. The results obtained from measurements of the buffered proton diffusion coefficient in gel phantoms, the oxygen-dependent proton production rates for MCF-7/s and MDA-mb-435 cells, and the buffering capacity of tumor interstitial fluid are combined in a reaction-diffusion model to predict steady-state pHe values as a function of distance from a vessel. The pHe gradients generated by this model are consistent with steady-state pHe values measured for these two cell lines in vivo.
Materials and Methods
Cell Culture
Experiments were performed on the lowly metastatic MCF-7/s and highly metastatic MDA-mb-435 breast cancer cells. MCF-7/s cells were obtained from the Arizona Cancer Center Cell Culture Shared Service. MDA-mb-435 cells were obtained from the American Type Culture Collection, Manassas, VA (http://www.atcc.org) (CCL no. HTB 129). MCF-7 and MDA-mb-435 cells were maintained in Dulbecco's modified Eagle's medium (DMEM) supplemented with 10% fetal bovine serum [FBS; 1:1 DMEM/F-12 mixture consisting of DMEM/F12 (D0547; Sigma, St. Louis, MO) and FBS (Gibco, Invitrogen, Carlsbad, CA (http://www.lifetech.com)) in a 5% CO2 atmosphere at 37°C]. For rate measurements, cells were trypsinized, counted, and resuspended at a concentration of 1x106 cells in 20 ml, and plated at 200 µl per well of a 96-well flat-bottomed tissue culture plate or, alternately, 1x106 cells were resuspended in 24 ml of media, and 1 ml was added to each well of a 24-well tissue culture plate. Cells were then incubated at 37°C/5% CO2, until ready for assay.
Chemicals and Solutions
All chemicals were obtained from Sigma, unless otherwise noted. A modified Hank's buffer (MHB), free of bicarbonate and sugars, was prepared with the following composition in 1 l: 0.14 g, 0.00126 mol of CaCl2 anhydrous [FW=110.99]; 0.10 g, 0.000492 mol of MgCl2·6H2O [FW=203.31]; 0.4 g of KCl; 0.18 g, 0.001323 mol of KH2PO4 [FW=136.1]; 8.0 g of NaCl; 0.1436 g, 0.001011 mol of Na2HPO4 [FW=141.96]; phenol red [FW=376.4], 0.1 mM (from 0.5 mM stock solution). This buffer has 25% of the buffering capacity of bicarbonate-free Hank's buffer (i.e., it is 2.375 mM in total phosphate).
A concentration of 40 mM mannitol, glucose-free and bicarbonate-free buffer (mannitol-MHB), was prepared by adding 3.643 g of mannitol [FW=182.17] to 500 ml of MHB. A buffer that has 32 mM glucose and 8 mM mannitol (glucose-MHB) was prepared using a 4:1 mix of MHB and mannitol-MHB and by adding anhydrous glucose to the required concentration. Because glucose requires several minutes to be completely solubilized in aqueous solution, these solutions were prepared ahead of time, heated at 80°C for 10 minutes, filtered with 0.2-µm filters, divided into 50-ml aliquots, and stored at -20°C.
For titration, a carbonate-free standard NaOH solution was made by boiling distilled, deionized H2O, cooling under vacuum, and adding the appropriate mass of NaOH pellets (min 98%, S-5881; Sigma) to yield a 50% aqueous solution of NaOH. This solution was allowed to cool under constant vacuum and was sealed in a polyethylene bottle with no headspace for 1 day to allow sodium carbonate to precipitate out of the solution, leaving a carbonate-free NaOH solution. Dilutions of this 50 % aqueous NaOH were made with degassed, distilled, deionized H2O to final approximate concentrations 0.1, 0.5, and 1 M NaOH. These solutions were standardized against potassium hydrogen phthalate (Sigma-Aldrich, St. Louis, MO (http://www.sigmaaldrich.com)) by gravimetric determination of standard mass and titration with a 50-ml burette. Solutions were stored in polyethylene bottles with minimal head spaces.
Cell Cycle Analysis
A portion of the cells was prepared for cell cycle analysis just prior to the metabolism assay measurements. The MDA-mb-435 cells were 52% to 64% G0–G1, 8% to 20 % G2-M, and 27% to 28 % S phase. The MCF-7/s cells were 56% to 71% G0–G1, 8% to 20% G2-M, and 20% to 24% S phase.
Proton Production Rates
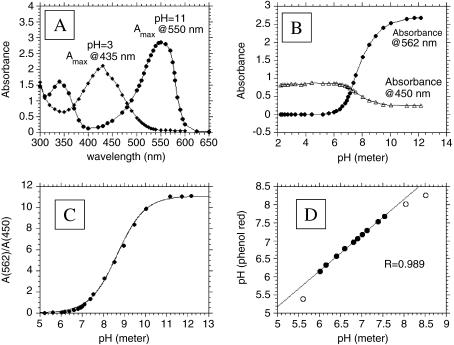
Proton production rates were measured by monitoring the optical absorbance of phenol red at two wavelengths in the buffer solution overlying the cell monolayers in 96-well plates, similar to that described previously [31]. The absorbance spectra for phenol red at low and high pH are shown in Figure 1A, showing maxima at 435 and 550 nm, respectively, with isosbestic points at 369 and 482 nm. From these data, it can be seen that absorbance changes reciprocally between pH 6 and 10 at 450 and 562 nm (Figure 1B). These values were chosen to match the filter set available in the plate reader. Thus, the ratio of absorbance at 562/450 nm can be used to generate a titration curve (Figure 1C) that can be fitted by:
Figure 1.
Determination of pH by phenol red absorption. The concentration of phenol red was 0.1 mM and the path length was 0.62 cm in each case. (A) Absorption versus wavelength spectrum for the deprotonated (pH=11) and protonated (pH=3) forms of phenol red showing maximum absorbance at 550 and 435 nm, respectively. (B) Absorbance of phenol red at 562 nm (●) and 450 nm (◆) as a function of pH. (C) Ratio of phenol red absorption, A(562 nm)/A(450 nm), as a function of pH. (D) Calibration of pH determination by comparing values from potentiometric and phenol red absorption pH determinations. R=0.99 between pH values of 6.0 and 7.5 (filled circles).
| (1) |
where 10.5 is the ratio at high pH and 0.38 is a correction factor representing the ratio of absorbance at high to low pH at the denominator wavelength (450 nm). The reliability of this method is shown in Figure 1D, which shows the correlation (r2>0.99) between the pH measured by phenol red and by electrode in the pH range 6.0 to 7.5.
At the time of an experiment, an aliquot of glucose-MHB was thawed and dilutions were made with mannitol-MHB to various glucose concentrations with a total osmotically active sugar concentration of 40 mM. An airtight glove box was constructed containing the BioTek Instruments, Winooski, VT (http://www.biotek.com) EL 311 microarray plate reader to maintain the cells under constant atmosphere and temperature for the time course spectrophotometric measurements of pH versus time. At the start of the experiment, two 96-well plates containing confluent cells were transferred from the incubator to the glove box and the chamber was sealed by attaching the Plexiglas face plate with gloved access ports to the front of the box. A normoxic atmosphere was accomplished by having a direct orifice between the glove box and the ambient laboratory air, whereas the anoxic atmosphere was accomplished by delivery of 100% N2 gas to the glove box with a slight excess of positive pressure relative to the ambient laboratory pressure. Venting ports were included in the wall of the glove box to prevent pressure buildup. The glove box was also equipped with a digital thermostat (Digital Temperature Controller, model CN320; Omega Engineering, Stamford, CT (http://www.omega.com)) interfaced with heating elements that allowed the temperature to be maintained at 37±1°C. An alcohol thermometer was suspended in a 5-ml volume of incubation solution in the glove box to independently confirm that the incubation solutions were maintained at 37°C throughout the experimental time course. The absorption of phenol red at 450 and 562 nm was calibrated against pH using a pH meter (Beckman 71) and standard NBS buffers (Beckman Coulter, Fullerton, CA (http://www.beckman.com)). Sample pH was monitored across all wells as a function of time by sequential monitoring of absorption at 450 and 562 nm using a BioTek EL311 microtiter plate reader with 20-nm bandpass optical filters for each wavelength. Typical experimental time courses spanned 150 to 210 minutes. These data were analyzed by linear regression and, after correcting for buffering capacity, were expressed as nanomoles of H+ per minute per milligram of protein.
Lactate Production and Glucose Consumption
Lactate production and glucose consumption rates were determined on cells grown to confluence in 24-well plates (Falcon, model 3047; Becton Dickinson, Franklin Lakes, NJ (http://www.bd.com)). Cells were inoculated at a density of 104 cells per well and allowed to grow for 3 to 4 days, until confluent. Lactate and glucose levels were both measured by two methods: by a glucose/ lactate analyzer (YSI model 2000) and by spectrophotometric assay kits (Sigma). The analyzer measurements required a minimum of 500 µl of solution to make a single measurement, so that only single time points could be obtained. The enzymatic assays required 10 µl to measure both glucose and lactate, allowing several sampling points per well over a 12-to 15-hour experimental time course.
Buffering Capacities (β)
Buffering capacities were determined by backtitration for all experimental solutions, as well as tumor interstitial fluid. For tumor interstitial fluid, 20 to 80 µl of tumor fluid was drawn from MDA-mb-231 SCID mouse tumors into gas-tight 1-ml syringes. For all titrations, the solutions to be tested were injected into unbuffered and degassed water that had previously been overlaid with a 2-mm layer of mineral oil. These were titrated through injection of degassed NaOH that had been standardized as described above. Solutions were maintained at 37°C and pH was measured with a combination pH electrode that had been inserted into the water prior to the addition of the mineral oil.
Proton Diffusion
Diffusion of protons through gels was measured using a stirred bath technique, as described in Ref. [32]. This technique employs two well-stirred baths separated by a gel layer. Gels were established with varying mixtures of agarose and collagen to simulate the extracellular space, and these were equilibrated for > 2 days in the apparatus with solutions of varying buffer capacities (e.g., 1.9, 3.6, and 6.4 mmol of H+ per pH unit). Measurements were begun with the addition of acid or base equivalents to the upper chamber and by monitoring the collapse of the pH gradient with time. The pH meter was connected to a PC with a 25-pin serial connection. The solution pH, solution temperature, and time were recorded automatically at 20-minute intervals using a Denver Instrument, Arvada, CO (http://www.denverinstrument.com) pH meter. To determine the number of H+ that had moved across the gel, the initial pH value was subtracted from the recorded pH at each time point, to yield a ΔpH. These data were converted to millimoles of H+ according to the equation: mmol H+ =(ΔpHxβ).
Modeling of Interstitial pH
A finite difference model similar to that of Griffiths et al. [33] was used to predict pHe as a function of distance from feeding capillaries. This model only considers the integrated flux rates due to steady-state diffusion along one dimension for both free and buffered H+ occurring for a two-dimensional sheet of cells lying between two parallel capillaries, which is similar to the situation for tumors grown in a window chamber [24]. The overall steady-state expression derived from Fick's second law, including terms for the effects of proton production and buffer-facilitated diffusion, is:
where Q is the proton production rate [µmol cm-3 sec-1], x is the distance [µm], DH is the hydronium ion diffusion coefficient, DB is the protonated buffer diffusion coefficient, and cH is the free [H+] concentration. The above expression is integrated once, applying the boundary condition that d[H+]/dx=0 at x=L, where L is half of the intervessel distance, and integrated a second time using the boundary condition that cH is the [H+] of blood at x=0, the vessel wall. Substituting for [BH] yields:
where cB is the total buffer concentration, KB is the buffer acid association constant, and M is a constant determined by the above expression when x=0. A rearrangement of the above expression yields a quadratic in cH, which was solved for cH by hand by using MathCad 6.0. In order to apply this model, proton production rate data expressed per milligram of protein were converted to per gram of tissue (or per cubic centimeter of tissue volume, assuming a tissue density of 1.03 g ml-1). This was achieved using a conversion factor of 140 mg protein (g tumor wet weight)-1.
Results
Proton Production Rates
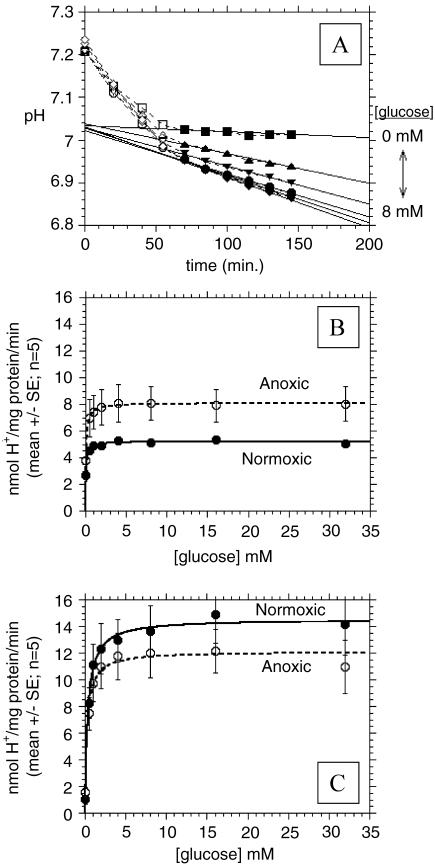
Proton production was determined from the timedependent change in the pH, as measured from spectra of phenol red in lightly buffered media, as described in Materials and Methods section. pH values were monitored in an airtight glove box at 37°C following the addition of MHB containing various concentrations of glucose. Representative plots of the decrease in buffer pH with time are shown in Figure 2A for normoxic MDA-mb-435 cells. The t=0 time point is the first measurement of phenol red absorption at 450 and 562 nm obtained immediately after washing the cells with saline and adding the assay buffers to respective wells. Each data point of pH versus time is the average of five to eight wells. Note that the rate of decrease in pH is essentially independent of glucose concentration for the first 50 minutes after washing the cells and adding the assay solutions. This is likely due to endogenous glucose or intracellular acid stores. After 50 minutes, however, the pH decreased monotonically with increasing glucose up to 4 mM. Figure 2, B and C shows the rate of H+ production by MCF-7/s and MDAmb-435 breast cancer cells, respectively, as a function of glucose concentration in the presence of atmospheric oxygen and under hypoxia, respectively. These data can be fitted with Michaelis-Menten kinetics to generate apparent Vmax and Km values (Table 1). These analyses show that the major differences occur under normoxic/normoglycemic (i.e., 5.6 mM glucose) conditions, where MDA-mb-435 cells produce H+ at a rate approximately 2.8 times faster than MCF-7/s cells. These data also show that the anoxia stimulates H+ production rates by 1.6-fold in MCF-7/s cells, whereas it has no significant effect on proton production rates in MDA-mb-435 cells. If anything, the Vmax appears lower for hypoxic MDA-mb-435 cells, although the differences were not statistically significant. These data indicate that glycolysis in MCF-7/s cells is affected by oxygen, whereas MDA-mb-435 cells exhibit a similarly high rate of H+ production in the presence or absence of O2.
Figure 2.
Proton production rates. (A) pHe determined with phenol red as a function of time for MDA-mb-435 cells incubated at 37°C and ambient O2 and 0.5, 1, 2, 4, and 8 mM glucose. (B) Proton production rates of MCF-7/s cells under normoxic and anoxic conditions as a function of incubation [glucose] in millimolar (standard error bars range from ±0.2 to 0.5 for normoxic MCF-7/s cells so that they fall within the symbols). (C) Proton production rates of MDA-mb-435 cells under normoxic and anoxic conditions as a function of incubation [glucose] in millimolar. For (B) and (C), lines represent best fits to unimolecular Michaelis-Menten equation.
Table 1.
Metabolic Profiles of MDA-mb-435 and MCF-7/s Cells.
| Substrate | MDA435 cells | MCF-7/s cells | ||
| Normoxia | Anoxia | Normoxia | Anoxia | |
| Vmax [nmol min-1 (mg protein)-1] | ||||
| Glucose consumption | 8.4 | 8.1 | 7.2 | 15.4 |
| Lactate production | 10.4 | 9.8 | 6.1 | 9.3 |
| Proton production | 14.5 | 12.1 | 5.2 | 8.1 |
| Apparent Km for glucose [mM] | ||||
| Glucose consumption | 1.75 | 1.83 | 2.0 | 2.9 |
| Lactate production | 0.57 | 0.31 | 0.22 | 0.37 |
| Proton production | 0.36 | 0.27 | 0.07 | 0.08 |
Proton production, lactate production, and glucose consumption rates were determined as described in the text and were fitted with Michaelis-Menten kinetics relative to [glucose] to yield apparent Vmax and Km values.
Lactate Production Rates
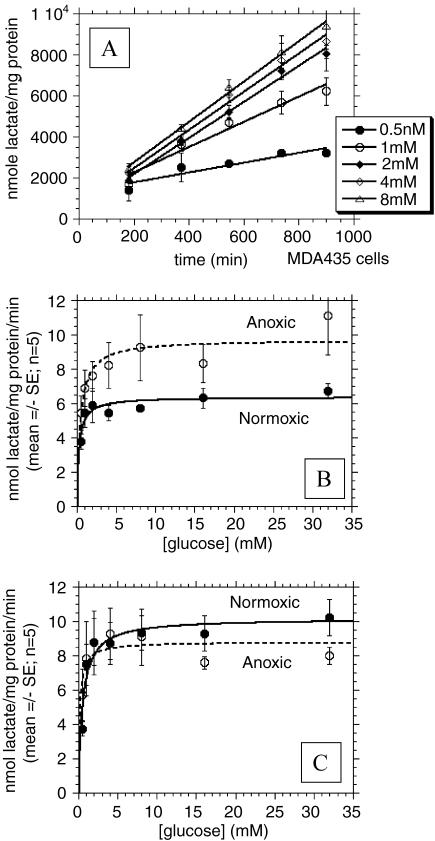
Both MDA-mb-435 and MCF-7/s cells produce lactate acid in appreciable amounts. Representative plots of the lactate concentration time course of normoxic MDA-mb-435 cells are shown in Figure 3A. The first sampling point occurs at 180 minutes after washing cells with PBS and adding the assay solutions with variable glucose concentrations. The linear least squares fits to the data are included in this plot. As shown in this figure, lactate accumulation into the assay medium increases monotonically with increasing glucose concentrations and is virtually linear for up to 15 hours. Figure 3, B and C shows the rate of lactate production by MCF-7/s and MDA-mb-435 breast cancer cells incubated with different glucose concentrations under normoxic and anoxic conditions, respectively, along with nonlinear least square fits to a simple Michaelis- Menten equation (Table 1). Under normoglycemic conditions, the anoxic/normoxic ratios for lactate production rates were nearly 1.0 for MDA-mb-435 cells but were ca. 1.5 for MCF-7/s. Hence, these data are similar to those observed with proton production and indicate that lactate production in MCF-7/s cells is sensitive to oxygen, whereas it is not in MDA-mb-435 cells. Also note that MDA-mb-435 cells produce more lactic acid compared to MCF-7/s cells under normoxic conditions.
Figure 3.
Lactate production rates. (A) Lactate production as a function of time for MDA-mb-435 cells incubated at 37°C with ambient O2 and 0.5, 1, 2, 4, and 8 mM glucose. (B) Lactate production rates of MCF-7/s cells under normoxic and anoxic conditions as a function of incubation [glucose] in millimolar. (C) Lactate production rates of MDA-mb-435 cells under normoxic and anoxic conditions as a function of incubation [glucose] in millimolar. For all plots, lines represent best fits to simple Michaelis-Menten equation.
Glucose Consumption
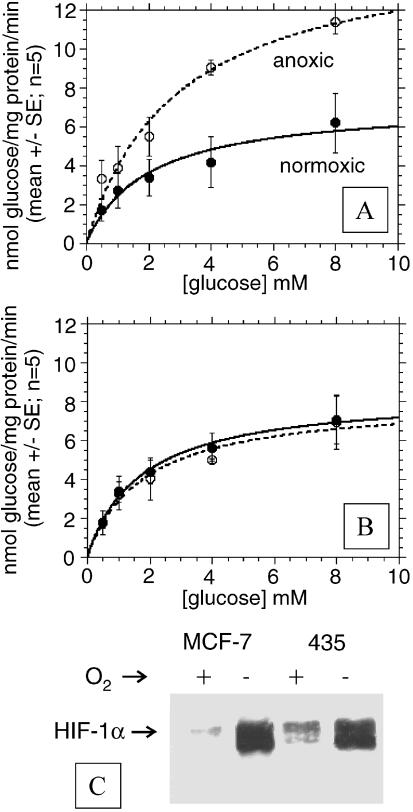
Figure 4, A and B shows the rate of glucose consumption by MDA-mb-435 and MCF-7 breast cancer cells incubated with different glucose concentrations under normoxic and anoxic conditions, respectively. Results with 16 and 32 mM [glucose] were omitted because the absorbance values where higher than the linear portion of the Trinder assay calibration curve. The steady-state glucose consumption rates under normoglycemic conditions increase significantly upon hypoxia for MCF-7 cells, but remain unchanged for MDA-mb-435 cells (Table 1). Hence, similar to the independently measured H+ and lactate production rates, these data further support that glycolysis in MCF-7/s cells is inhibited by oxygen, whereas it is not in MDA-mb-435 cells. The data in Table 1 show consistent values for glucose consumption, lactate production, and proton production for all conditions. It is notable that at Vmax, the lactate /glucose ratio varies between 0.60 and 1.2 and approaches 2.0 at glucose concentrations near the Kmapp. Furthermore, despite similarities in the apparent Vmax, proton and lactate production rates had consistently lower apparent Km values compared to glucose consumption rates.
Figure 4.
Glucose consumption rates. (A) Glucose consumption rates of MCF-7/s cells under normoxic and anoxic conditions as a function of incubation [glucose] in millimolar. (B) Glucose consumption rates of MDA-mb-435 cells under normoxic and anoxic conditions as a function of incubation [glucose] in millimolar. For all plots, lines represent best fits to simple Michaelis-Menten equation. (C) Western blot of HIF-1α expression under normoxia and hypoxia.
Diffusion of H+ through Gels and Tissues
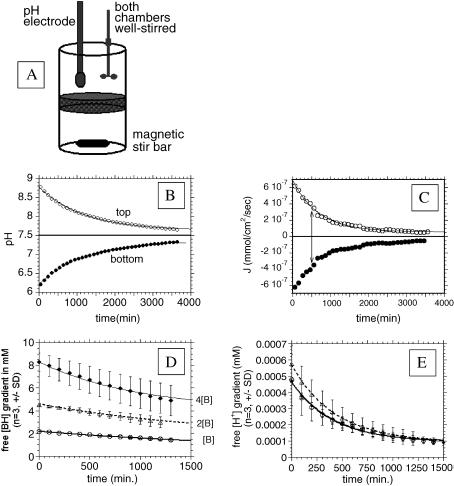
Measurements were made in gel phantoms to determine the nature of H+ movement through tissues and the feasibility of steady-state H+ gradients. Figure 5A illustrates the apparatus used to measure the movement of H+ equivalents through gels. This stirred bath was temperature-controlled to ±0.2°C and contains two well-stirred chambers separated by gels of varying composition and thickness. For the current study, gels containing 3% gelatin and 3% agarose were made, in order to make a stable thin gel layer that mimics the protein and carbohydrate content of the extracellular matrix [34]. Figure 5B illustrates a typical pH gradient decay curve from the stirred bath apparatus. In this case, the bath and gel were equilibrated at a pH of 6.2 for 3 days prior to the experiment. The experiment was initiated by the addition of base equivalents to the upper chamber, which resulted in an increase in pH to ca. 8.8. The pH of the upper chamber was measured constantly for >3500 hours, and the pH values of the lower chamber were calculated. With knowledge of the buffering capacity, the rate of movement of H+ equivalents across the gel can be determined. Buffering capacities were measured as described in Materials and Methods section. A typical titration curve for the buffer mix is shown in Figure 6A, illustrating that buffering capacity (millimolar H+ per pH unit) is constant in the range pH 6.1 to 8.75 (closed circles in figure). Table 2 shows the measured buffering capacities for all solutions used in this study. From the measured pH and β, the rate of decay in pH can be expressed in millimolar H+. Multiplying by the respective chamber volumes and dividing by the surface area of the gel layer and the time increment between pH readings (20 minutes) yielded the flux (J) of H+ across the gel in millimoles per minute per square centimeter. As shown for these data in Figure 5C, J begins at 6x10-7 mmol H+ cm-2 min-1 and decays exponentially with a time constant of ∼300 minutes. To test whether the driving force for H+ movement was affected by the pH or the buffer gradient, the proton flux rate was determined with buffers of different concentrations (Table 2). The data in Figure 5D show that the rate of collapse in the gradient of protonated buffer, [BH], increased with increasing buffering power. In contrast, plots of free [H+] gradients with time show that the rate of free proton gradient collapse was independent of buffering power (Figure 5E). As the total flux of H+ at the same pH gradient must increase with increasing β to effect the same pH change, these data imply that the flux of H+ equivalents increases with increasing gradient of buffer (BH) and not with increasing gradient of pH. To test this, the diffusion coefficient was calculated from these data according to Fick's law:
Figure 5.
Measurements of H+ diffusion. (A). Stirred bath apparatus, containing two gas-sealed well-stirred chambers separated by gelatin/agarose gel of thickness 0.2 cm and 2 cm2 surface area at 37°C. (B) Collapse of pH gradient across gel with time. Prior to experiment, the gel was equilibrated for 7 days with media in both chambers at a pH of 6.2. At t=0, the pH of the upper chamber was raised with a bolus addition of base (C). Calculated flux (J) of H+ equivalents moving from one side of the gel to the other, in both directions. (D) Collapse of [BH] gradient across the gel with time with three different buffers. (E) Collapse of free [H+] gradient across the gel with time with three different buffers. In this case, identical rates can be achieved only with increased flux, as β values are significantly different for all samples.
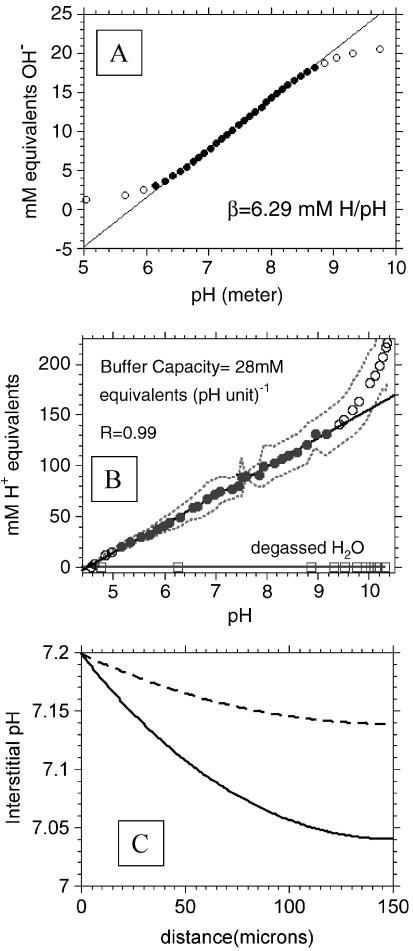
Figure 6.
Titrations and model. (A) Representative titration curve for buffers used in stirred bath experiments showing constant b over range 6 to 9. (B) Titration curve of tumor interstitial fluids to determine buffering capacity, β. Curve represents average of five determinations, with 95% confidence belts indicated with dotted line. Straight line represents regression of filled data points to yield a β of 28 mM H+ equivalents (pH unit)-1. (C) Predicted spatially dependent interstitial pH values. These data were generated using a reaction-diffusion model of Griffiths et al. [33] using values generated in the current study: a diffusion coefficient D of 2x10-6 cm2 sec-1, a buffer concentration of 28mM [i.e., β of 28mM H+ (pH unit-1)], an interstitial buffer pKa of 6.7 (approximating linearity between 6.3 and 7.3), and proton production rates of 0.53 and 1.49 µmol min-1 cm-3 (see Materials and Methods section).
Table 2.
Buffer Capacities of Proton Production Rate Buffer, Diffusion Assay Buffers, and Tumor Interstitial Fluid.
| Sample description | Buffer capacity, β [mM H+ (pH unit)-1] |
| Proton production rate assay buffer (modified Hank's buffer) |
1.12 |
| 2.5 mM gel diffusion buffer: 2.5 mM PIPES, 2.5 mM bicine |
1.89 |
| 5.0 mM gel diffusion buffer: 5 mM PIPES, 5 mM bicine |
3.56 |
| 10.0 mM gel diffusion buffer: 10 mM PIPES, 10 mM bicine |
6.39 |
| Tumor “interstitial” fluid | 28 ±4 (n=5) |
| (2) |
where dC is the instantaneous difference in concentration across the gel (driving force), X is the thickness of the gel, and D is the diffusion coefficient [cm2 sec-1]. Assuming that H+ is the diffusing species with a driving force set by an electrochemical gradient for protons, the calculated D would be 8.2±0.6x10-2 cm2 sec-1, or approximately 250 times higher than the D of water (Table 3). Such a high value is unlikely, even through a “proton wire” mechanism. Furthermore, the calculated D varied with increasing β, which is in clear violation of Fick's law. In contrast, if H+ is assumed to be diffusing along with a small, ionizable buffer species with a driving force set by the gradient of ionized and deionized species, the calculated D is 0.63±0.07x10-5 cm2 sec-1. This is consistent with a molecule having a molecular weight of 500 to 600 [32]. Furthermore, this is constant for all β, which is an expected result for Fickian diffusion.
Table 3.
Diffusion Coefficients Calculated from Stirred Bath Experiments Using the Concentration of H+ or, Alternatively, of BH as the Driving Force Behind Diffusive Movement.
| Experimental [Buffer; mm] |
Df{d[H+]/dx} [x10-5 cm2 sec-1] |
Df{d[BH]/dx} [x10-5 cm2 sec-1] |
| 2.5 (n=3) | 8,200±600 | 0.63±0.07 |
| 5 (n=3) | 16,000±2,000 | 0.60±0.1 |
| 10 (n=3) | 29,000±4,000 | 0.58±0.05 |
All values are between pH 6.0 and 7.5.
Buffering Capacities of Tumor Fluid
To determine the buffering capacity of interstitial fluid from tumors, approximately 100 µl of fluid was drawn from individual tumors into gas-sealed syringes and titrated in a closed system in the same manner as assay buffers above (see Materials and Methods section). From these titration curves, the buffering capacity of interstitial fluid was measured to be 28 mM H+ (pH unit)-1 between pH 5 and 9. The averaged titration curve from five samples is illustrated in Figure 6B. The buffering strength was constant over this range, indicating a mix of high and low pKa buffering species.
Modeling
The above data for interstitial buffer concentrations, proton production rates, and diffusion coefficients were used as a basis to calculate pHe using the reaction-diffusion finite difference approximation [33] to determine if these values were consistent with low tumor pHe observed in vivo. Figure 6C shows the predicted pHe profile for both MCF-7 and MDA-mb-435 cells as a function of distance from a feeding capillary. As these simulations were only carried out to 150 µm, only aerobic proton production values were used. This simulation illustrates that the proton production, diffusivity, and buffering capacities determined in this study are consistent with both acidification of the extracellular space and a difference in the steady-state pHe between these two cell lines. Thus, a reasonable interpretation of the data in the present study is sufficient to generate a significant extracellular acidification and pHe difference between MCF-7/s and MDA-mb-435 cells.
Discussion
The aim of this study was to investigate the mechanisms underlying the acidic pHe of tumors. Prior work in our group has established pH values for MCF-7/s and MDA-mb-435 tumors using 31P MR spectroscopy of the pHe marker, 3-aminopropylphosphonate (3-APP) [5]. Table 4 shows the intracellular (pHi) and interstitial (pHe) pH values for MCF-7/s and MDA-mb-435 tumors grown in SCID mice. Because the average pHe decreases with increasing size [25], these data are shown for tumors of similar volumes. Although the intracellular pH values are similar for both cell types, the pHe is significantly lower for the MDA-mb-435 tumors, compared to MCF-7/s tumors. These observations are consistent with the predicted pH values shown in Figure 6C. The measured pHe values are lower than those predicted, yet this is expected because large volumes exist beyond 150 µm from a feeding capillary, weighting the observation towards the acid regions.
Table 4.
Intracellular and Extracellular pH in Tumors of MCF-7/s and MDAmb-435 Cells Grown as Tumors in SCID Mice.
| Cell type | Tumor volume [mm3] | pHi | pHe | n | Reference |
| MDA-mb-435 | 324±41 | 7.37±0.07 | 6.80±0.11 | 7 | [26] |
| MCF-7/s | 362±100 | 7.32±0.09 | 7.1±0.13 | 5 | [25] |
Intracellular and extracellular pH were determined from 31P magnetic resonance spectroscopy of the chemical shifts of endogenous inorganic phosphate and exogenous 3-APP, respectively [5].
A plausible explanation is that the heterogeneous acidity is due to heterogeneous perfusion and that regions that are hypoxic are also acidic due to hypoxic induction of glycolysis. However, this is not supported by the current work. In the first part of this study, the metabolic profiles of MCF-7/s and MDA-mb-435 cells were compared. These results indicate that glycolysis in MCF-7/s cells is sensitive to oxygen and hence produce more H+ under anaerobic conditions. Conversely, MDA-mb-435 cells produce acid at a rapid rate regardless of oxygen. Notably, tumors of MDAmb-435 cells are more acidic than those of MCF-7/s cells (Table 4).
The presence and the absence of oxygen-sensitive glycolysis in MCF-7/s and MDA-mb-435 cells, respectively, were consistent among the proton production, lactate production, and glucose consumption measurements. Considering that these data were obtained from completely independent measurements, the agreement between the scalar lactate and proton production rates is notable. However, we consistently observed a discrepancy between these numbers and the glucose consumption rates. It is tempting to ascribe this difference to assay errors. However, it is possible that these differences are real and reflect that the glucose consumed is not primarily destined for glycolysis by these cells. If it were, the ratio of lactate to glucose should approach 2:1 under anaerobiosis [31]. However, the lactate/glucose Vmax ratio ranged from 0.60 (anoxic MCF-7/s) to 1.23 (normoxic MDA-mb-435), suggesting that glucose is being utilized by other processes. This is also consistent with the observation that the apparent Km for glucose consumption was much higher than that for lactate or protons production. The mechanisms underlying this discrepancy are unknown.
It is striking that the vast majority of human tumors exhibit elevated rates of fluorodeoxyglucose (FdG) uptake, as measured by positron emission tomography (PET) [35]. Elevated FdG uptake is a surrogate for high glycolysis, yet it is not known whether this is due to constitutive upregulation or is due to hypoxic induction. According to our observations, elevated glycolysis and hyperacidity of MDA-mb-435 tumors are likely constitutive, and not just a result of perfusion-limited hypoxia. Instead, it is due to an uncoupling of glycolysis from respiration in these cells, first observed by Warburg [36] in the early half of the last century [37]. Nonetheless, it should be mentioned that a number of workers have shown that glycolysis-deficient tumors can be acidic [38,39,40]. The pH values reported for these systems were near 7.0, which is significantly higher than the pH observed for the MDA-mb-435 tumors. Hence, we contend that elevated glycolysis is required for tumors to achieve a state of hyperacidity. Although they have been investigated for many years, the mechanisms of the Pasteur and Warburg effects are not understood. The Pasteur effect is an acute phenomenon and likely involves a competition between mitochondria and glycolysis for shared intermediates, cellular redox, or an AMP-activated protein kinase cascade [41,42,43]. More chronic exposure to hypoxia leads to induction of hypoxia-inducible factor HIF-1α, which induces expression of glycolytic enzymes [44,45]. Notably, HIF-1α and its induced genes are constitutively upregulated and insensitive to oxygen in MDA-mb-435 cells, compared to MCF-7/s cells (Figure 3C).
The conclusion that tumor acidity is not solely a function of poor perfusion is also supported by the recent work of Bhujwalla et al. [12]. This study investigated the relationship between perfusion, using dynamic contrast-enhanced MRI, and pHe, with MR spectroscopy in MCF-7/s and MDA-mb-231 tumors. These data were spatially registered from the same tumors and no correlations were observed between pHe and vascular volume or vascular permeability. Interestingly, the correlation appeared to be worse in the MDA-mb-231 tumors, which are metabolically similar to the MDA-mb-435 cells used here.
In the second part of this work, the existence of steadystate pHe gradients was investigated by measuring proton fluxes across protein/carbohydrate mixed gels. At a given pH gradient, the proton flux increased with increasing concentrations of ionized solutes, suggesting that these species are responsible for carrying H+ across the gel. Notably, the diffusion coefficient was a constant at ∼6x10-6 cm2 sec-1 when calculated using the protonated buffer gradient as the driving force. In contrast, the diffusion coefficient varied from 0.08 to 0.2 cm2 sec-1 when calculated using the free proton gradient as the driving force. Because these values are unbelievably high and because the diffusion coefficient should not vary with β, we conclude that protons are not moving across the gel according to a Grotthus mechanism but instead are attached to mobile ionizable species. Furthermore, the movement of uncoupled H+ would not be expected in the absence of an electrical potential. This mechanism likely exists at the quantum level, as shown by Agmon [30]. However, for such a mechanism to be important on the millimeter scale would require the presence of electrical potential differences. These can exist at the cellular level, in developing eggs and embryos, and in specialized organs, such as Torpedo electrical organ, along axons, or in specialized organelles, such as thylakoids [27,46,47]. All of these organs are highly organized and polarized, and there is little datum to support that this level of organization exists in tumors.
Alternatively, these data cannot rule out the diffusion of free H+ limited by the codiffusion of inorganic anions (e.g., Cl-) or counterdiffusion of inorganic cations (e.g., Na+). However, a gedanken experiment can rule out this explanation. Inorganic ions are unlikely to provide counterions in the steady state because protons are continuously produced in the interstitium and move to the blood, whereas no such source sink can exist for inorganic ions. Hence, gradients for these ions would be self-limiting. Thus, metabolically produced protons most likely move in concert with metabolically produced buffers, The β of interstitial fluid was determined to be 28 mM H+ (pH unit)-1 and was constant between pH 5 and 9, indicating the presence of sufficient buffering species such as HCO3- (pKa=6.24, ca. 20 mM), inorganic phosphate (pKa=6.8, ca. 1.2 mM), and various α- and ɛ-amino groups of amino acids. This is a contrast to the theoretical work of Junge and McLaughlin [27] who only considered interstitial buffers that have pKa values less than physiological pH. Previous work by us has shown that pH gradients of ca. 0.5 pH unit can exist between volumes that are ca. 0.5 cm apart [6] and that large interstitial gradients for lactate can exist in tissues and model systems [48]. These observations, combined with the current modeling, indicate that pHe gradients in tumors are consistent with theory. The pH gradients generated in our model are based on conservative parameter estimations. For example, a D of 6x10-6 cm2 sec-1 is likely an upper limit as mobile buffers carrying H+ would tend to diffuse around cells as they make their way to venules. This would justify the introduction of a “tortuosity factor” that could decrease the effective D by up to a factor of 3 [33]. Furthermore, the β measured for an interstitial fluid of 28 mM H+ (pH unit)-1 is also an upper limit because it was unprocessed and hence contained large MW buffers (e.g., proteins) as well.
In summary, the current work indicates that the acid pHe of tumors is not solely due to poor perfusion but instead is an integral property of the cancer cells themselves. These metabolically produced H+ diffuse through the interstitium in association with mobile ionizable species, such as bicarbonate, phosphate, or amino acids. The low diffusion coefficient and driving force for these species is consistent with a low flux relative to proton production rates, which demonstrates the feasibility of steady-state pH gradients in tissues.
Acknowledgements
The authors would like to thank David W. Deamer, Natarajan Raghunand, Timothy Secomb, and Dominick McIntyre for their help in data analysis and in the preparation of this manuscript.
Footnotes
This work was supported by NIH grant R01 CA77575.
References
- 1.Vaupel P, Kallinowski F, Okunieff P. Blood flow, oxygen and nutrient supply, and metabolic microenvironment of human tumors: a review. Cancer Res. 1989;49:6449–6465. [Review; 214 references] [PubMed] [Google Scholar]
- 2.Okunieff P, Dols S, Lee J, Singer S, Vaupel P, Neuringer LJ, Beshah K. Angiogenesis determines blood flow, metabolism, growth rate, and ATPase kinetics of tumors growing in an irradiated bed: 31P and 2H nuclear magnetic resonance studies. Cancer Res. 1991;51:3289–3295. [PubMed] [Google Scholar]
- 3.Wike-Hooley JL, Haveman J, Reinhold HS. The relevance of tumour pH to the treatment of malignant disease. Radiother Oncol. 1984;2:343–366. doi: 10.1016/s0167-8140(84)80077-8. [DOI] [PubMed] [Google Scholar]
- 4.Griffiths JR. Are cancer cells acidic? Br J Cancer. 1991;64:425–427. doi: 10.1038/bjc.1991.326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Gillies RJ, Liu Z, Bhujwalla Z. 31P-MRS measurements of extracellular pH of tumors using 3-aminopropylphosphonate. Am J Physiol. 1994;267:t-203. doi: 10.1152/ajpcell.1994.267.1.C195. [DOI] [PubMed] [Google Scholar]
- 6.van Sluis R, Bhujwalla ZM, Raghunand N, Ballesteros P, Alvarez J, Cerdan S, Galons JP, Gillies RJ. In vivo imaging of extracellular pH using 1H MRSI. Magn Reson Med. 1999;41:743–750. doi: 10.1002/(sici)1522-2594(199904)41:4<743::aid-mrm13>3.0.co;2-z. [DOI] [PubMed] [Google Scholar]
- 7.Yuan J, Glazer PM. Mutagenesis induced by the tumor microenvironment. Mutat Res. 1998;400:439–446. doi: 10.1016/s0027-5107(98)00042-6. [Review; 47 references] [DOI] [PubMed] [Google Scholar]
- 8.Yuan J, Narayanan L, Rockwell S, Glazer PM. Diminished DNA repair and elevated mutagenesis in mammalian cells exposed to hypoxia and low pH. Cancer Res. 2000;60:4372–4376. [PubMed] [Google Scholar]
- 9.Morita T, Nagaki T, Fukuda I, Okumura K. Clastogenicity of low pH to various cultured mammalian cells. Mutat Res. 1992;268:297–305. doi: 10.1016/0027-5107(92)90235-t. [DOI] [PubMed] [Google Scholar]
- 10.LeBoeuf RA, Kerckaert GA, Aardema MJ, Gibson DP. Multistage neoplastic transformation of Syrian hamster embryo cells cultured at pH 6.70. Cancer Res. 1990;59:3722–3729. [PubMed] [Google Scholar]
- 11.Chen EY, Mazure NM, Cooper JA, Giaccia AJ. Hypoxia activates a platelet-derived growth factor receptor/phosphatidylinositol 3-kinase/Akt pathway that results in glycogen synthase kinase-3 inactivation. Cancer Res. 2001;61:2429–2433. [PubMed] [Google Scholar]
- 12.Bhujwalla ZM, Artemov D, Ballesteros P, Cerdan S, Gillies RJ, Solaiyappan M. Combined vascular and extracellular pH imaging of solid tumors. NMR Biomed. 2002;15(2):114–119. doi: 10.1002/nbm.743. [DOI] [PubMed] [Google Scholar]
- 13.Martinez-Zaguilan R, Seftor EA, Seftor REB, Chu Y-W, Gillies RJ, Hendrix MJC. Acidic pH enhances the invasive behavior of human melanoma cells. Clin Ex Metastasis. 1996;14:176–186. doi: 10.1007/BF00121214. [DOI] [PubMed] [Google Scholar]
- 14.Rozhin J, Sameni M, Ziegler G, Sloane BF. Pericellular pH affects distribution and secretion of cathepsin B in malignant cells. Cancer Res. 1994;54:6517–6525. [PubMed] [Google Scholar]
- 15.Schlappack OK, Zimmermann A, Hill RP. Glucose starvation and acidosis: effect on experimental metastatic potential, DNA content and MTX resistance of murine tumour cells. Br J Cancer. 1991;64:663–670. doi: 10.1038/bjc.1991.378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Raghunand N, He X, van Sluis R, Mahoney B, Baggett B, Taylor CW, Paine-Murrieta G, Roe D, Bhujwalla ZM, Gillies RJ. Enhancement of chemotherapy by manipulation of tumour pH. Br J Cancer. 1999;80:1005–1011. doi: 10.1038/sj.bjc.6690455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Raghunand N, Mahoney B, van Sluis R, Baggett B, Gillies RJ. Acute metabolic alkalosis enhances response of C3H mouse mammary tumors to the weak base mitoxantrone. Neoplasia. 2001;3:227–235. doi: 10.1038/sj.neo.7900151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Dewhirst MW, Kimura H, Rehmus SW, Braun RD, Papahadjopoulos D, Hong K, Secomb TW. Microvascular studies on the origins of perfusion-limited hypoxia. Br J Cancer Suppl. 1996;27:S247–S251. [PMC free article] [PubMed] [Google Scholar]
- 19.Gillies RJ, Schornack PA, Secomb TW, Raghunand N. Causes and effects of heterogeneous perfusion in tumors. Neoplasia. 1999;1:197–207. doi: 10.1038/sj.neo.7900037. [Review; 161 references] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Dafni HI. Overexpression of vascular endothelial growth factor 165 drives peritumor interstitial convection and induces lymphatic drain: magnetic resonance imaging, confocal microscopy, and histological tracking of triple-labeled albumin. Cancer Res. 2002;62:6731–6739. [PubMed] [Google Scholar]
- 21.Thomlinson RH, Gray LH. The histological structure of some human lung cancers and the possible implications for radiotherapy. Br J Cancer. 1955;9:539–549. doi: 10.1038/bjc.1955.55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Franko AJ, Sutherland RM. Oxygen diffusion distance and development of necrosis in multicell spheroids. Radiat Res. 1979;79:439–453. [PubMed] [Google Scholar]
- 23.Secomb TW, Hsu R, Braun RD, Ross JR, Gross JF, Dewhirst MW. Theoretical simulation of oxygen transport to tumors by three-dimensional networks of microvessels. Adv Exp Med Biol. 1998;454:629–634. doi: 10.1007/978-1-4615-4863-8_74. [DOI] [PubMed] [Google Scholar]
- 24.Helmlinger G, Yuan F, Jain MD, Jain R. Interstitial pH and pO2 gradients in solid tumors in vivo: high-resolution measurements reveal a lack of correlation. Nature. 1997;3:177–182. doi: 10.1038/nm0297-177. [DOI] [PubMed] [Google Scholar]
- 25.Raghunand N, Altbach MI, van Sluis R, Baggett B, Taylor CW, Bhujwalla ZM, Gillies RJ. Plasmalemmal pH-gradients in drug-sensitive and drug-resistant MCF-7 human breast carcinoma xenografts measured by 31P magnetic resonance spectroscopy. Biochem Pharmacol. 1999;57:309–312. doi: 10.1016/s0006-2952(98)00306-2. [DOI] [PubMed] [Google Scholar]
- 26.Bhujwalla ZM, Aboagye EO, Gillies RJ, Chacko VP, Mendola CE, Backer JM. Nm23-transfected MDA-MB-435 human breast carcinoma cells form tumors with altered phospholipid metabolism and pH: a 31P nuclear magnetic resonance study in vivo and in vitro. Magn Reson Med. 1999;41:897–903. doi: 10.1002/(sici)1522-2594(199905)41:5<897::aid-mrm7>3.0.co;2-t. [DOI] [PubMed] [Google Scholar]
- 27.Junge W, McLaughlin S. Effect of fixed or mobile buffer ions on proton mobility. Biochim Biophys Acta. 1987;890:1–5. doi: 10.1016/0005-2728(87)90061-2. [DOI] [PubMed] [Google Scholar]
- 28.Latour LL, Svoboda K, Mitra PP, Sotak CH. Time-dependent diffusion of water in a biological model system. Proc Natl Acad Sci USA. 1994;91:1229–1233. doi: 10.1073/pnas.91.4.1229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Engasser JM, Horvath C. Buffer-facilitated proton transport pH profile of bound enzymes. Biochim Biophys Acta. 1974;358:178–192. doi: 10.1016/0005-2744(74)90269-1. [DOI] [PubMed] [Google Scholar]
- 30.Agmon N. The Grotthuss mechanism. Chem Phys Lett. 2002;244:456–462. [Google Scholar]
- 31.Gillies RJ, Martinez-Zaguilan R, Martinez GM, Serrano R, Perona R. Tumorigenic 3T3 cells maintain an alkaline intracellular pH under physiological conditions. Proc Natl Acad Sci USA. 1990;87:7414–7418. doi: 10.1073/pnas.87.19.7414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Chresand TJ, Dale BE, Hanson SL, Gillies RJ. A stirred bath technique for diffusivity measurements in cell matrices. Biotechnol Bioeng. 1988;32:1029–1036. doi: 10.1002/bit.260320810. [DOI] [PubMed] [Google Scholar]
- 33.Griffiths JR, McIntyre DJ, Howe FA, Stubbs M. Why are cancers acidic? A carrier-mediated diffusion model for H+ transport in the interstitial fluid. Novartis Found Symp. 2001;240:46–62. doi: 10.1002/0470868716.ch4. [discussion 62–67, 152–153] [DOI] [PubMed] [Google Scholar]
- 34.Alberts B, Bray D, Lewis J, Raff M, Roberts K, Watson JD. Molecular Biology of the Cell. New York and London: Garland Publishing; 1994. [Google Scholar]
- 35.Gambhir SS, Czernin J, Schwimmer J, Silverman DH, Coleman RE, Phelps ME. A tabulated summary of the FDG PET literature. J Nucl Med. 2001;42:1S–93S. [PubMed] [Google Scholar]
- 36.Warburg O. On the origin of cancer cells. Science. 1956;123:309–314. doi: 10.1126/science.123.3191.309. [DOI] [PubMed] [Google Scholar]
- 37.Racker E, Spector M. Warburg effect revisited: merger of biochemistry and molecular biology. Science. 1981;213:303–307. doi: 10.1126/science.6264596. [DOI] [PubMed] [Google Scholar]
- 38.Helmlinger G, Sckell A, Dellian M, Forbes NS, Jain RK. Acid production in glycolysis-impaired tumors provides new insights into tumor metabolism. Clin Cancer Res. 2002;8:1284–1291. [PubMed] [Google Scholar]
- 39.Newell KJ, Tannock IF. Reduction of intracellular pH as a possible mechanism for killing cells in acidic regions of solid tumors: effects of carbonylcyanide-3-chlorophenylhydrazone. Cancer Res. 1989;49:4477–4482. [PubMed] [Google Scholar]
- 40.Yamagata M, Hasuda K, Stamato T, Tannock IF. The contribution of lactic acid to acidification of tumours: studies of variant cells lacking lactate dehydrogenase. Br J Cancer. 1998;77:1726–1731. doi: 10.1038/bjc.1998.289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Ainscow EK, Brand MD. Top-down control analysis of ATP turnover, glycolysis and oxidative phosphorylation in rat hepatocytes. Eur J Biochem. 1999;263:671–685. doi: 10.1046/j.1432-1327.1999.00534.x. [DOI] [PubMed] [Google Scholar]
- 42.Hardie DG. Metabolic control: a new solution to an old problem. Curr Biol. 2000;10:757–759. doi: 10.1016/s0960-9822(00)00744-2. [DOI] [PubMed] [Google Scholar]
- 43.Marsin AS, Bertrand L, Rider MH, Deprez J, Beauloye C, Vincint MF, van den Berghe G, Carling D, Julius D. Phosphorylation and activation of heart PFK-2 by AMPK has a role in the stimulation of glycolysis during ischaemia. Curr Biol. 2000;10:1247–1255. doi: 10.1016/s0960-9822(00)00742-9. [DOI] [PubMed] [Google Scholar]
- 44.Seagroves T, Ryan HE, Lu H, Wouters BG, Knapp AG, Thibault P, Laderoute K, Johnson RS. Transcription factor HIF-1 is a necessary mediator of the Pasteur effect in mammalian cells. Mol Cell Biol. 2001;21:3436–3444. doi: 10.1128/MCB.21.10.3436-3444.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Zhong H, De Marzo AM, Laughner E, Lim M, Hilton DA, Zagzag D, Buechler P, Isaacs WB, Semenza GL, Simons JW. Overexpression of hypoxia-inducible factor 1alpha in common human cancers and their metastases. Cancer Res. 1999;59:5830–5835. [PubMed] [Google Scholar]
- 46.Nuccitelli R, Jaffe LF. Current pulses involving chloride and potassium efflux relieve pressure in pelvetia embryos. Planta (Berlin) 1976;131:315–320. doi: 10.1007/BF00385433. [DOI] [PubMed] [Google Scholar]
- 47.Nuccitelli R, Jaffe LF. The ionic components of the current pulses generated by developing fucoid eggs. Dev Biol. 1976;49:518–531. doi: 10.1016/0012-1606(76)90193-7. [DOI] [PubMed] [Google Scholar]
- 48.Chresand TJ, Gillies RJ, Dale BE. Optimum fiber spacing in a hollow fiber bioreactor. Biotechnol Bioeng. 1988;32:983–992. doi: 10.1002/bit.260320806. [DOI] [PubMed] [Google Scholar]