The solid-state architecture of a metallosupramolecular polyelectrolyte

Abstract

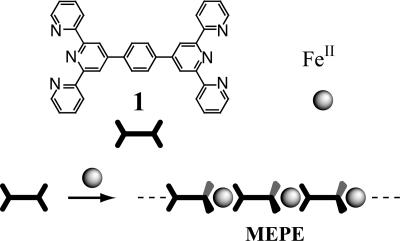
Self-assembly of Fe(II) and the ditopic ligand 1,4-bis(2,2′:6′,2″-terpyridine-4′-yl)benzene results in equilibrium structures in solutions, so-called metallosupramolecular coordination polyelectrolytes (MEPEs). It is exceedingly difficult to characterize such macromolecular assemblies, because of the dynamic nature. Therefore, hardly any structural information is available for this type of material. Here, we show that from dilute solutions, where small aggregates predominate, it is possible to grow nanoscopic crystals at an interface. A near atomic resolution structure of MEPE is obtained by investigating the nanoscopic crystals with electron diffraction in combination with molecular modeling. The analysis reveals a primitive monoclinic unit cell (P2₁/c space group, a = 10.4 Å, b = 10.7 Å, c = 34.0 Å, α = γ = 90°, β = 95°, ρ = 1.26 g/cm³, and Z = 4). The MEPE forms linear rods, which are organized into sheets. Four sheets intersect the unit cell, while adjacent sheets are rotated by 90° with respect to each other. The pseudooctahedral coordination geometry of the Fe(II) centers is confirmed by Mössbauer spectroscopy. The combination of diffraction and molecular modeling presented here may be of general utility to address problems in structural materials science.

Weak competing interactions provide an efficient and elegant route to self-assemble supramolecular modules in tailored architectures with a tremendous range of value-adding (1) and dynamic (2) properties. Metal ion-assisted self-assembly is one of the major recognition motives in supramolecular chemistry (3). The resulting metallosupramolecular modules possess structural, kinetic, magnetic, optic, electronic, and reactive properties that are relevant for functional devices and materials of technological interest (4).

Although polymers based on kinetically inert transition-metal complexes are readily characterized in solution by standard analytical means, polymeric assemblies formed by kinetically labile transition-metal complexes have successfully evaded characterization in solution (5). The overwhelming majority of metal-organic frameworks are isolated and characterized as crystalline solids (6). The diversity of the resulting framework architectures is remarkable (7). Solids with well defined voids with molecular dimensions give an opportunity to manipulate, separate, arrange, and react molecules. Now, there are a large number of porous solids available that exhibit permanent porosity suitable for technological applications (8–10).

In 1992, Constable et al. (11) published the synthesis and characterization of various multinucleating terpyridines (tpy), including 1,4-bis(2,2′:6′,2″-terpyridine-4′-yl)benzene (11). A high binding affinity to many transition metal ions and a well defined stereochemistry make this building block an attractive component for the assembly of dynamic and functional metallosupramolecular polyelectrolytes (MEPEs) (Scheme 1) (12). The ditopic tpy-ligand used here forms stable macromolecular assemblies in solution, so the availability of processable MEPEs stimulated research concerning nanostructures (13), Langmuir (14) and Langmuir–Blodgett (15) layers, thin films (16), capsules (17) and liquid crystals (18), electrochromic windows (19), rheological fluids (20, 21), and magnetic materials (22). To establish structure–property relationships in these semiordered materials, it is of pivotal importance to obtain most accurate structural information.

Scheme 1.

Metal ion-induced self-assembly of iron acetate and 1,4-bis(2,2′:6′,2″-terpyridine-4′-yl)benzene, 1, results in the metallosupramolecular polyelectrolyte (MEPE). Because of the octahedral coordination geometry (indicated by the wedges), a linear, positively charged macroassembly is formed.

In the case of kinetically labile transition metal ions such as Fe, Ni, or Co, MEPEs form extended macromolecular equilibrium structures in solution. The mean molar mass of the assemblies depends on the concentrations of the constituents and is determined by the dynamic equilibrium of association and dissociation. On increasing the concentration, the mean length is shifted to larger assemblies (23). The theory of self-assembly of two components predicts an exponential growth as a function of concentration. For these reasons, it is generally difficult to grow suitable single crystals for structure analysis in particular at supersaturation typically used for crystallization. As a result, structural information on the molecular level is hardly available for these materials (24, 25).

Nevertheless, there are two aspects that can be taken into consideration. If the stoichiometry of the two constituents, that is the ratio of metal ions to ligands, deviates from one, the length of the aggregates is finite (26). Above a certain concentration, the length of the aggregates reaches a threshold value and becomes independent of concentration. The deficient constituent is eventually consumed in the aggregates, so that growth comes to an end. Because of experimental errors the stoichiometry will generally deviate from one. In addition, in solutions of self-aggregating polymers, a surface region is predominantly occupied by shorter assemblies. In the absence of strong polymer–surface interactions, long chains experience a larger entropy loss than shorter ones, so the surface region is predominantly occupied by short chains. Therefore, it should be possible to crystallize the constituents at low concentration at an interface. Based on these considerations, we attempted crystal growth from dilute solutions directly on carbon-covered transmission electron microscopy grids to interrogate the solid-state structure. Electron diffraction was used to analyze the resulting nanoscopic crystals. The occurrence of metal ions in MEPEs is a fortunate coincidence because they enhance contrast for diffraction. We have chosen Fe(II) as central metal ion to use Mössbauer spectroscopy as a complementary tool to probe the coordination environment of the metal complexes. Similar to protein crystallography, we use a combination of diffraction data and molecular modeling to refine the structure to near atomic resolution (27).

Results and Discussion

Mössbauer Spectroscopy.

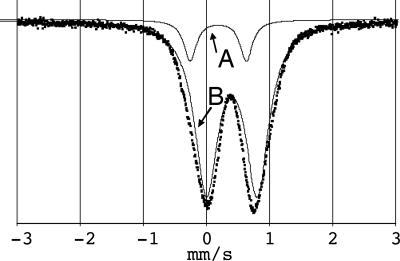
To confirm the pseudooctahedral coordination geometry, the predominant coordination motive found for Fe(II) bis-terpyridine complexes, powder samples of MEPE were subjected to analysis by Mössbauer spectroscopy. A representative Mössbauer spectrum of the precipitated solid MEPE taken at room temperature and fitted with two quadrupole doublets, named A and B, is shown in Fig. 1. The values of the Mössbauer parameters are summarized in Table 1.

Fig. 1.

Representative Mössbauer spectrum of Fe-MEPE at room temperature. The data (dots) is fitted by two quadrupole doublets (solid lines) named A and B.

Table 1.

Mössbauer parameters of Fe-MEPE at 295 K

Doublet	Isomer shift, mm/s	Quadrupole splitting, mm/s	Relative area, %
A	0.18	0.88	12
B	0.40	0.80	88

The doublet B is assigned to pseudooctahedral Fe(II) sites with a diamagnetic low spin electronic configuration typical for Fe(II) bis-terpyridine complexes (28).^h The doublet A has a larger quadrupole splitting indicating a species of lower symmetry. These sites are considered as defects such as kinks or end-groups, in which the coordination geometry deviates from the pseudooctahedral geometry of bis-terpyridine Fe(II) complexes. Presumably, the defects represent Fe(II) end groups, in which the metal ion is situated in a fivefold coordination geometry associated with one terpyridine ligand and the two counter ions.ⁱ.

A quantitative analysis of the Mössbauer spectra reveals that the fraction of the sixfold coordinated segment of MEPE consists in average of eight repeat units. According to molecular modeling the metal ion-metal ion distance is ≈1.55 nm (29). Therefore, the average length of a continuous segment of MEPE is ≈12.4 nm.^j Note that within the experimental error the presence of Fe(III) can be excluded based on the Mössbauer analysis.

Apparently, precipitation from solution results in many defects in the resulting architecture. To make highly ordered materials suitable for structural analysis, we considered a different approach described in the next section.

Crystal Growth.

To verify the above-mentioned hypothesis to grow crystals from dilute solutions where molecular and aggregated species coexist, we investigate the adsorption of MEPE on solid surfaces (data not shown). Initially, the surface coverage, Γ, of MEPE increases steeply and independently of the bulk concentration (between 10⁻⁶ and 10⁻⁴ mol/liter) with the immersion time of the substrate in the MEPE solution and reaches a plateau after ≈60 min. The surface coverage at the very beginning of the adsorption process, when each species that reaches the surface finds an adsorption site, can be described by a square root time dependence given by Γ = 2cN_A$\sqrt{\mathrm{Dt}/\pi }$ (where c is the bulk concentration, N_A is Avogadro’s constant, D is the bulk diffusion constant, and t is the immersion time). Within the experimental error, we obtain for Γ/$\sqrt{t}$ a constant value of 1.7 × 10¹⁵ m²/s^1/2 that is the surface coverage in the initial stage of the adsorption is more or less independent of concentration c.

From these data, we can estimate the diffusion coefficient. We assume here that a repeat unit of MEPE consists of one ligand and one metal ion. The binding constant of terpyridine and Fe(II) has been determined to be pK = 21 (53.4 kJ/mol) (30). As pointed out above, a deviation from a 1:1 stoichiometry reduces the chain length. We assume that the concentration of Fe(II) is generally less than that of the ligand, because Fe(II)OAc₂ is susceptible to oxidation to Fe(III). Because Fe(III) does not bind to terpyridine strongly, this will reduce the overall chain length. At a concentration, c, of 10⁻⁵ mol/liter, and assuming that the concentration of Fe(II) is 10% less than that of the ligand, the concentration of monomers is calculated to be 10⁻⁷ mol/liter, that of dimers is calculated to be 0.9 × 10⁻⁷ mol/liter, and that of trimers is calculated to be 0.8 × 10⁻⁷ mol/liter, which amounts to diffusion coefficients of 6 × 10⁻¹⁰ to 10⁻⁹ m²/s (23). For comparison, the diffusion coefficient of glucose is 4.5 × 10⁻¹⁰ m²/s, indicating that the estimated values are in the right order of magnitude. This simplified analysis suggests that the aggregates that adsorb at the interface are small species that are mobile enough to diffuse to the surface and to assemble to a crystal (vide infra). Therefore, it is not surprising that after a few hours immersion time, small crystals begin to form, ≈50 × 100 nm² in size and a few nanometers in height, which confirms the idea that crystals of MEPEs, even though very small, can be grown from dilute solution.

Electron Diffraction.

It is not possible to subject these crystals to x-ray diffraction techniques because of their exceedingly small size. A technique more suitable to study such small crystals is electron diffraction, because electrons strongly interact with matter (31). It is possible to select (in real space) individual crystals for analysis because the beam diameter can be reduced to a few nanometers. In contrast to powder diffraction, the Bragg peaks can be unambiguously correlated with the lattice planes. Because of the small wavelength of the electrons (0.03 Å) with respect to the cell dimensions, many Bragg peaks of one lattice plane can be observed simultaneously, with sub-angstrom spatial resolution. Rotating the sample around a lattice axis, that is recording a tilt series, provides access to three-dimensional information. However, because of geometric constrictions within the instrument, the access to reciprocal space is limited (missing cone problem) (32). Dynamical or multiple scattering can complicate space group determination and intensity quantification, which is, however, not so severe in the case of anisometric crystals (33).

The data analysis is based on the following approach. From the symmetry and the peak positions of diffraction patterns obtained from different orientations of a crystal, cell parameters and possible space groups are determined. To eliminate space groups, we use a low-resolution molecular model, which allows fast and efficient sampling over large areas of configurational space. Molecular models where all atoms are mobile provide a more accurate energy description that is particularly useful in describing the details of the molecular structure but is limited with respect to extensive conformation sampling.

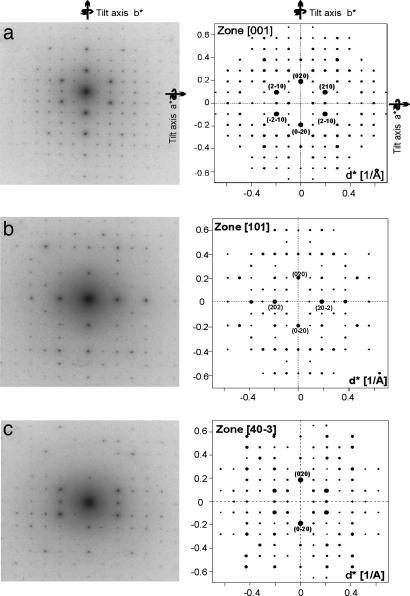
Representative transmission electron diffraction patterns of a MEPE nanocrystal, which are found to crystallize all in the same orientation on the carbon support, are shown in Fig. 2. The diffraction pattern at 0° (Fig. 2a) exhibits a rectangular symmetry with two mirror planes along a* and b*, therefore γ is 90° and the zone is identified as [001]. Notably, we observe an extinction of the odd reflections along the b* axis. The peaks at (020), (0−20), (210), (−210), (2−10), and (−2−10) are especially bright.

Fig. 2.

Experimental (Left) and simulated (Right) MEPE diffraction patterns: zone [001] (a); zone [101] (b); zone [40−3] (c).

Tilt series are obtained by orienting a* and b*, respectively, along the goniometer axis and by subsequent tilting in ± direction. We obtain seven additional diffraction patterns for a*-tilt ([021]/[02−1] at ±32°, [043]/[04−3] at ±22°, [023]/[02−3] at ±11°) and for b*-tilt ([403]/[40−3] at 22.5°/−21°, [101]/[10−1] at 17°/−15°, [20−3] at −11°, and [30−1] at −39°). The diffraction patterns obtained at 17° and 22° tilted with respect to the b* axis (Fig. 2 b and c) exhibit along the b* axis an extinction of odd reflections (k = 2n + 1; n = 0, 1, 2, …). Note that all zones imaged after the tilt about the b* axis exhibit a rectangular symmetry indicating α to be 90°. During the tilt about a* the angle between the tilt axis and the second reciprocal vector deviates from 90° leading to β = 95°. Furthermore, the diffraction patterns in both tilt directions are identical, which confirms α to be 90°. Note that in zone [101] at 17° (Fig. 2b) beside the extinctions along b* the odd reflections along (10−1)* are very weak. This can be explained by a superstructure along c. This geometrical analysis routine leads to a primitive monoclinic cell with a = 10.4 Å, b = 10.7 Å, c = 34.0 Å, α = γ = 90°, β = 95°, ρ = 1.26 g/cm³, and Z = 4. The accuracy of the cell dimensions is ±0.05 Å. The above-mentioned extinctions along b* indicate a 180° screw axis along b, leaving P2₁, P2₁/m, and P2₁/c as possible space groups.

To begin the molecular modeling refinement, the starting configuration is based on the x-ray single-crystal structure of bis(2,2′:6′,2″-terpyridine)-iron(II) diperchlorate monohydrate, Fe^II(tpy)₂(ClO₄)₂, which resembles the Fe^II-octahedron (24). Based on the Mössbauer results, this is a reasonable assumption. To build the MEPE repeat unit, defined here as -terpy-Fe^II-tpy-ph-, a phenyl group is added in the 4-position of the central pyridine ring. The repeat unit is positioned into the unit cell such that a polymer is formed. Subsequently, two acetate counter ions are placed manually into the biggest remaining cavities. The packing is energy minimized by force-field calculations. The bis(tpy)Fe^II units as well as the bridging phenyl rings are maintained as rigid bodies, which can rotate with respect to each other. Each MEPE is allowed to translate in the cell. No constraints are applied to the acetate ions. For space groups P2₁ and P2₁/c, the minimization of the packing energy results in a stable structure with negative energies (vide infra). For space group P2₁/m, the packing energy is strongly positive indicating that reasonable packing is not possible; therefore this space group is discarded.

The energy-minimized model is then further refined in an iterative procedure by comparing kinematically calculated with digitized experimental diffraction data in terms of their intensities as described above. For space group P2₁, the refinement results are in excellent agreement as can be seen in Fig. 2; we find equally good agreement for the other zones (data not shown). The packing energy of the final model, the structure of which is shown in Fig. 3, amounts to −156 kcal/mol for one cell or −39 kcal/mol per monomer. This value is in good agreement with the packing energy of the mononuclear complex, Fe^II(tpy)₂(ClO₄)₂ (34), calculated with the same force field and partial charges as in the minimization process of MEPE, which amounts to −217 kcal/mol for one cell and −54 kcal/mol per unit, respectively.

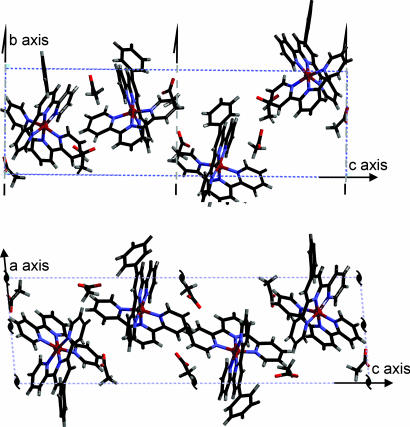
Fig. 3.

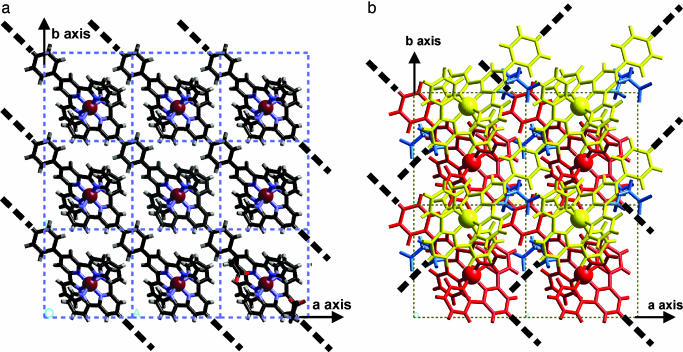
Crystal structure of MEPE. (a) View along c showing a single layer of parallel oriented MEPE chains. For brevity the acetate counter ions are shown in one unit cell only at the lower right of the figure. Note that the main axes of MEPE are always within the ab plane. (b) Same view showing two subsequent MEPE layers rotated 90° relative to each other. The bold dotted lines indicate the direction of the MEPE rods.

For brevity, Fig. 3a shows a single plane of MEPE. The view along the c axis, parallel to the probe beam, reveals polymer chains approximately oriented along the diagonal between a and b axes. As one can see, parallel-oriented MEPE rods form a single plane. Notably, the distance between acetate counter ions and Fe^II centers in MEPE is 5–6 Å, which is comparable with the corresponding distances in Fe(tpy)₂(ClO₄)₂. The torsion angle of the phenyl rings to the central pyridine ring ranges from 36° to 40°. The terpyridine groups of one ditopic ligand are perpendicular to each other in agreement with the spatial boundaries of the unit cell dimensions. Four such layers intersect the unit cell. For the stacking of the layers along the c axis, the following rules apply. The second layer is rotated by 90° around the c axis. The two layers viewed from the top resemble a Scottish tartan, as shown in Fig. 3b. The next two layers are generated by applying to the first two layers a 180° rotation around b followed by a shift of b/2 in the direction of b, which causes the extinctions along b* as described above. The complete unit cell with all four layers is shown in Fig. 4.

Fig. 4.

View along a (Upper) and b (Lower) of MEPE unit cell structure. Note that the monoclinic angle between a and c is 95°. Each unit cell contains four MEPE monomer units, each belonging to a different layer. The 2₁ screw axis along b correlating the two double layers within the unit cell is indicated in each figure.

Conclusions

In summary, we describe the solid-state organization of a dynamic equilibrium metallosupramolecular coordination polyelectrolyte using Mössbauer spectroscopy, electron diffraction, and molecular modeling. Although the dynamic nature provides a plethora of interesting effects and potential applications, it is difficult to establish structure–property relationships. To overcome this problem, we employ the following strategy to obtain crystals. From the theory of self-assembly it follows that at dilute conditions in the proximity of a surface predominantly small species exist, which are mobile enough to assemble at the interface to nanoscopic crystals. This approach may be of general utility to address a fundamental question concerning growth and analysis of nanocrystalline particulates in the initial state of crystallization of all kinds of solid-state architectures including metal-organic frameworks. Electron diffraction turns out to be the method of choice to interrogate the structure of these single crystals. The metal ions enhance contrast, individual crystals can be selected and subjected to analysis and tilt-series in combination with molecular modeling provide a three-dimensional structure with near atomic resolution. The Fe-MEPE crystallizes in linear rods (space group P2₁; a = 10.2Å, b = 10.5 Å, c = 34.0 Å, β = 95°, Z = 4). The linear arrays are organized in sheets, which are stacked, each rotated by 90°. Independently, Mössbauer spectroscopy of amorphous powders was used to confirm the pseudooctahedral coordination environment of the Fe(II) centers. Using this approach, we hope to address materials science-related structure–property relationships such as perturbation-induced structural changes in MEPEs, for instance as they occur in spin transitions (35).

Materials and Methods

The ligand (11) and MEPE (12) were prepared according to literature procedures. Solid MEPE was prepared by precipitation from aqueous solution. Nanoscopic crystals of MEPE with dimensions of 800–1,700 nm in width and 10 nm in height were crystallized on carbon coated copper grids from dilute aqueous solution (10⁻⁶ to 10⁻⁴ mol/liter) by slow evaporation during 3 days at 8°C. The best crystals were obtained at a concentration of 10⁻⁵ mol/liter.

The surface coverage was determined by immersing the substrate for a specified time into the MEPE solution (aqueous, 10⁻⁶ to 10⁻⁴ mol/liter), after which the adsorption of the metal-to-ligand charge-transfer band was measured by UV-vis spectroscopy.

Electron diffraction tilt series were performed by using a Philips EM300 at 100 kV with a rotation tilt holder (maximum tilt angle ±60°) (36). Thallium chloride is used as internal calibration standard (37). X-ray powder diffraction data were measured with a Siemens D500, Cu-K_α radiation in Θ/2Θ mode.

Absorption spectra were recorded with a PerkinElmer Lambda 900 spectrometer. The extinction coefficient of the MEPE was found to be 2.15 × 10¹⁰ mm²/mol.

Molecular modeling was done with CERIUS 2, using the DREIDING2.21 force field. Atomic charges were obtained by semiempirical, quantum-mechanical calculations using the self-consistent field (1SCF) approach and PM3 parameters in mopac6.0 (a general-purpose molecular orbital package; Quantum Chemistry Program Exchange). Because no force-field parameters for Fe^II were available, it was substituted by Ca^II in the low-resolution molecular model (38).

The Mössbauer spectra were recorded at room temperature with a constant-acceleration 1,024-channel Mössbauer spectrometer (type CM 2201; produced by the Institute for Analytical Instrumentation of the Academy of Sciences of Russia) using a Mössbauer source of ⁵⁷Co in chromium matrix with a present activity of 0.55 GBq. A proportional counter (LND, INC.; tube type 45431) was used with a voltage of 1,800 V to detect the spectrum. The sample (71.8 mg) was placed into a sealable cylindrical polyethylene sample compartment with an inner diameter of d = 19 mm. The Mössbauer spectra were recorded with a maximum velocity of ±3.1 mm/s and referred to a standard Fe-foil (Goodfellow).

Abbreviations

MEPE

metallosupramolecular coordination polyelectrolyte.