Multiple routes lead to the native state in the energy landscape of the β-trefoil family

Abstract

In general, the energy landscapes of real proteins are sufficiently well designed that the depths of local energetic minima are small compared with the global bias of the native state. Because of the funneled nature of energy landscapes, models that lack energetic frustration have been able to capture the main structural features of the transition states and intermediates found in experimental studies of both small and large proteins. In this study we ask: Are the experimental differences in folding mechanisms among members of a particular structural family due to local topological constraints that deviate from the tertiary fold common to the family? The β-trefoil structural family members IL-1β, hisactophilin, and acidic/basic FGFs were chosen to address this question. It has been observed that the topological landscape of the β-trefoils allows for the population of diverse, geometrically disconnected routes that provide energetically similar but structurally distinct ways for this family to fold. Small changes in topology or energetics can alter the preferred route. Taken together, these results indicate that the global fold of the β-trefoil family determines the energy landscape but that the routes accessed on that landscape might differ as a result of functional requirements of the individual family members.

Most proteins have an energy landscape that is low in energetic frustration, with few traps to compete with the energy state of their native fold. Consequently, their energy landscapes are funneled, and the topology of their respective folds becomes a key factor in determining the folding mechanism. Recent studies of fast-folding, single-domain proteins have reinforced the funneled landscape theory (1–11). Many groups have designed structure-based protein models that assign only native contacts an attractive interaction (5–11), making the landscape perfectly funneled. These energetically unfrustrated, structure-based (12) potentials have successfully captured the folding mechanisms of not only small, single-domain two-state proteins but also larger multistate folders and dimeric proteins (13–17). Because energetic roughness is sufficiently small in proteins, topology becomes the main reason for structural heterogeneity in folding mechanisms, which leads to the question: Are protein homologs that are reported to fold through very different routes accessing different regions of a similarly shaped energy landscape determined by their common global fold, or do the specifics of the amino acid sequence create enough differences to sculpt a unique landscape for each protein in the family (18–21)? We address this question by investigating the energy landscapes of four members of the β-trefoil family with diverse biological functions and folding mechanisms: IL-1β, the acidic FGFs (aFGFs), the basic FGFs (bFGFs), and hisactophilin (His). These four proteins have little sequence similarity (<17%), but they have the same global fold, called a β-trefoil, which is composed of a repeating structure, the trefoil unit (βββ loop β-motif), forming a six-stranded β barrel capped by a hairpin triplet (Fig. 1 a–c) (22).

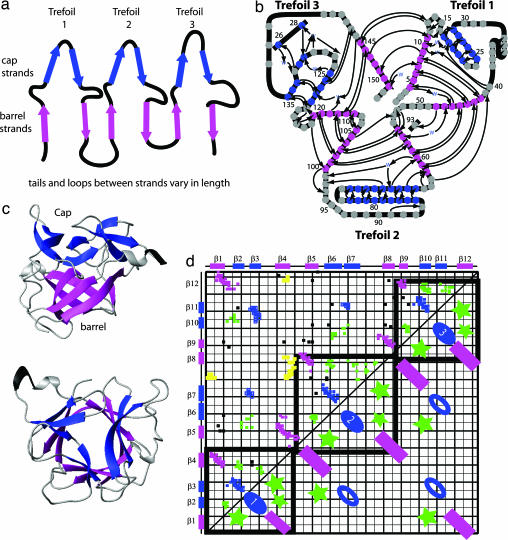
Fig. 1.

β-Trefoil structure. (a) β-Trefoils are formed from 12 β-strands divided into three trefoils. Each trefoil is composed of a hairpin and a β-sheet. Throughout the diagram, β-strands found in the cap are colored blue, and those forming the barrel are pink. (b) A splay diagram of the protein shows the threefold pseudosymmetry of the trefoil units. (c) Two views of IL-1β. (d) Contact map for β-trefoil. The axes show the primary sequence. The upper triangle shows the contact map of IL-1β. The lower triangle shows the contacts that form structures common to the entire β-trefoil family. Contacts between β-strands forming the barrel are shown as pink rectangles. The blue ovals represent contacts forming the cap. Green stars indicate contacts within local loops or between local loops found at the intersection of the cap and barrel. The heavy black lines outline the contacts contained within each of the three trefoils. Contacts outside the lines represent intertrefoil interactions. In the upper triangle, contacts unique to the β-bulge of IL-1β are shown in yellow.

We focus on folding kinetics and find that members of the β-trefoil family can fold into their respective native states along three dominant routes. First, a direct route is observed in which the formation of local contacts within turns gradually leads to the formation of tertiary structure (13). This finding is consistent with the idea that local contacts serve to decrease the effective loop length of longer-range contacts and facilitate folding (23, 24). Second, we observe a variation in the above route in which two subsets of contacts compete with each other, resulting in the unfolding of one subset of native contacts and their subsequent refolding later along the folding coordinate. We term this behavior “backtracking” (25), as opposed to misfolding, because no nonnative contacts are formed. Third, we describe a route where folding initiates with the β-trefoil bringing its N and C termini together despite the high entropic cost.

We find that our energetically unfrustrated, native structure-based model captures the diversity of experimentally observed routes on the β-trefoil energy landscape. As a family, the β-trefoils fold by means of three routes, two of which are geometrically disconnected; that is, due to geometric constraints, it is impossible for the protein to interconvert between these two folding routes at intermediate stages of the folding process. Small alterations to the wild-type energetics can change the preferred route used by an individual protein to the preferred route of a different family member. Therefore, one route may dominate the landscape in a specific family member, but the overall landscape is the same for the structural family. The global fold of the family determines the energy landscape, whereas the details of the amino acid sequence determine which route is most used within that landscape. This observation introduces an interesting twist to our understanding of protein folding: Diverse transition states and folding mechanisms may be alternative folding routes on the same energy landscape.

Results and Discussion

Comparing the Family Members.

The β-trefoil fold is formed by three trefoil units and was first described for the soybean trypsin inhibitor by Chothia and colleagues (22). Starting from the N terminus to C terminus, we number the trefoils 1, 2, and 3 (Fig. 1). Members of the fold family include IL-1β, His, aFGF, bFGF, the β-chain of the toxin ricin, and the family of soy and winged bean Kunitz inhibitors. For this study, we selected proteins based on the availability of experimental folding studies and chose IL-1β, His, aFGF, and bFGF. Their size ranges from 118 (His) to 153 (IL-1β) residues; the length of the β-strands, intervening loops, and turns vary across the family. Interestingly, these proteins all have a low relative contact order at odds with their observed slow folding rates (26).

Experimental studies of their folding routes show distinct mechanisms among the family members. Pulse labeling of IL-1β shows that it forms its central core early and has a well populated kinetic intermediate (13, 27–29). In contrast, aFGF folds by bringing the N and C termini together to form an intermediate that is structurally distinct from that of IL-1β (30). Experiments on bFGF show that it is also a three-state folder, but structural details of the intermediate are unavailable (31). His displays predominantly two-state folding with intermediates observed only under specific conditions (32–34).

To investigate whether the experimentally observed folding mechanisms are a result of the particular geometric constraints of each family member or differently shaped energy landscapes, we analyzed their computational folding trajectories. We found the free-energy profiles for all four proteins (Fig. 4, which is published as supporting information on the PNAS web site) by using kinetic simulations and a modified multicanonical sampling method (see Methods and ref. 25). Generally, the β-trefoils have high and broad free-energy barriers, with His having a broad barrier broken in height by a plateau early in folding. In these reduced model simulations, no single kinetic intermediate is regularly populated in any of the trajectories. Rather, the unusually broad free-energy barrier represents a continuum of states in which partially structured formations populate the entire transition state region between the unfolded and folded states, consistent with experimental studies (35). The broad barrier indicates that minor energetic or geometric details, which are not present in the reduced representation used for these simulations, can be responsible for the creation of different intermediates, or even traps, that may depend on sequence or folding conditions.

A β-Trefoil Protein May Fold by Multiple Routes.

To compare the data from each homolog, we use contact maps (Fig. 1d). The two-dimensional contact map shows the residue number of the amino acid sequence of a given protein numbered on the x and y axes, with points plotted within the map to represent each native contact between two residues. The color of each point in Figs. 2 and 3 corresponds to how frequently that contact is formed in the stated ensemble. To observe how these proteins traverse the landscape, we chose the reaction coordinate Q, the fraction of native contacts, because it has been shown to be an accurate reaction coordinate for minimalist Go models (36–39). Q ranges from 0, completely denatured, to 1, the fully folded protein. We limited our analysis to trajectories that resulted in folding, and we grouped individual trajectories together by folding patterns (Fig. 5, which is published as supporting information on the PNAS web site).

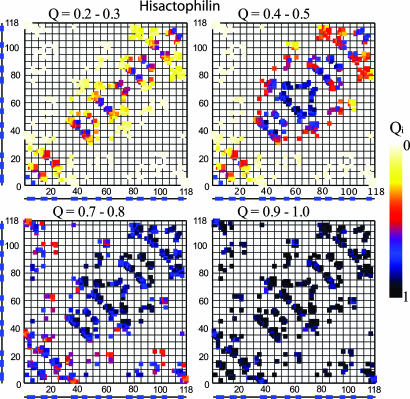
Fig. 2.

His folds exclusively by means of the direct route of the β-trefoil family. Folding initiates in turns and continues with the stabilization of trefoils 2 and 3. Trefoil 1 and connections between the trefoils form concurrently. The folding progresses, with contacts having a smaller loop length forming first and longer-range contacts forming later after their effective loop length has decreased.

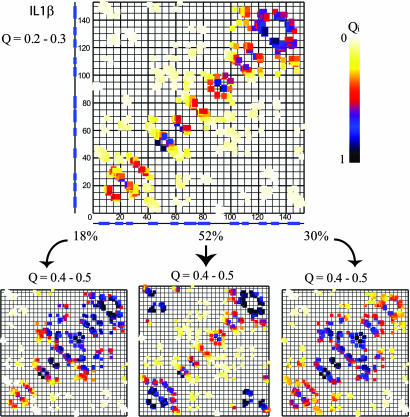
Fig. 3.

The multiple routes of IL-1β. (Left) IL-1β starts and sometimes continues to fold similarly to His. (Center) More often, contacts connecting trefoils 1 and 3, which are entropically disfavored, come together and stick. The remainder of the barrel and cap structure then forms. (Right) Another route involving the unfolding of trefoil 3 contacts and the stabilization of trefoil 2 also leads to folding. Trefoil 3 reforms, and the route continues similarly to His.

Results for His are shown in Fig. 2. At Q = 0.2–0.3, the formation and stability of turns is evident from the high probability of contact formation close to the diagonal (proximity to the diagonal represents the local contacts of turns). At this point, the protein lacks stable, long-range interactions. At Q = 0.4–0.5, the progressive stabilization of turns and the development of medium- and long-range interactions in trefoils 2 and 3 are apparent. By Q = 0.8–0.9, the majority of the protein is folded, with the exception of the contacts between the hairpin caps and the trefoil barrel. In this route, trefoils 2 and 3 fold to make a nascent barrel with partial cap formation. The final step is the packing of the barrel and cap into the native fold. We label this route the “direct route.” This mechanism also describes the observed results for aFGF. bFGF, however, uses this route only ≈30% of the time and mostly folds along a similar and symmetric route, with trefoils 1 and 2 partnering to form the nascent barrel (40).

The symmetry-related routes discussed above result from the pseudothreefold symmetry of the β-trefoil fold. We observe that folding frequently begins with the formation of the β-turns in the hairpins and the barrel connections of trefoils 2 and 3 (less often, trefoils 2 and 1), with longer-range contacts between the two trefoils quickly following. Experiments also observe early structure most commonly in trefoils 2 and 3 (33). The pairing of trefoil 2 with either trefoil 1 or 3 may depend on relative contact strength or number. For instance, aFGF has more intertrefoil contacts between trefoils 2 and 3 than between 1 and 2, and in aFGF, trefoils 2 and 3 partner to form the nascent barrel. In bFGF, the contacts are more uniformly distributed across the molecule. In our course-grained model of bFGF, whether trefoil 2 pairs with trefoil 1 or 3 may simply depend on which trefoil it encounters first, because there is nothing energetically included in the model to break the symmetry.

IL-1β can access the routes discussed above; however, two alternate routes emerge (Fig. 3). One involves the formation of trefoil 3, then local unfolding of this same trefoil, and the formation of trefoil 2. Folding then continues as described for His. In the other alternate route, trefoil 3 forms, followed by trefoil 1. The stabilization of trefoils 1 and 3 allows the ends to come together to form the nascent barrel, and the rest of the protein then arranges into the native fold. These two routes appear to compete with each other. The use of multiple folding routes in IL-1β is also reflected in the route measure (see Figs. 6 and 7, which are published as supporting information on the PNAS web site, for a description of route measure and the route measure of each protein). IL-1β traverses its three routes at the following frequencies: direct route, 18%; backtracking route, 30%; ends-together route, 52%.

These alternate routes are thought to be in use because of a set of contacts unique to IL-1β (see Fig. 1d, yellow contacts). IL-1β has a β-bulge at residues 48–53, which is caused by a misalignment in hydrogen bonds between β-strands 4 and 5. This region interacts with a loop composed of residues 90–100, which is involved in a functionally relevant binding site (41). These contacts cause topological frustration in the direct folding route, making the alternative routes more likely. The ends-together route has been experimentally observed for one member of the β-trefoil family: aFGF has been observed to have an intermediate structure formed by hydrogen bonds between its termini (30).

Energetic Perturbations Alter the Dominant Folding Route.

Because folding routes of real proteins can be experimentally altered (42–46), we investigated whether we could model this experimental observation with subtle changes in the overall energy of the β-trefoils in silico. In our model of IL-1β, we perturbed the energetics by altering the definition of the contact map, which changed the total number of native contacts from 433 to 422. The 11 omitted contacts are uniformly distributed across the molecule. We found that although the overall landscape remains the same, the dominant route shifts from the ends-together route to the backtracking route. The early stages in folding of the IL-1β-422 model (at Q = 0.2–0.3) remain consistent with the early structure of the IL-1β-433 model, with formation of turns and trefoil 3 occurring first. Then, between Q = 0.4 and Q = 0.5, ≈30% of the molecules proceed along the direct route observed for His with stabilization in trefoils 2 and 3, 60% proceed along the backtracking route, and 10% take the ends-together route. The partition between the protein populations folding by means of the ends-together route and those taking the backtracking route may depend on the precise definition of the contact map. As discussed earlier, our reduced representation of IL-1β provides a qualitative view of the accessed routes on the energy landscape of this more complex fold, but selecting the dominant route may depend on quantitative details that are beyond the scope of this model.

His folds along the direct route, built by closing local loops, because it lacks the topological frustration of IL-1β. His can be forced to fold by means of the ends-together route by adding energetic heterogeneity to the contact energy potential. We increased the energy in the cluster of contacts within and between trefoils 1 and 3 and reduced the energy of all other contacts to maintain the total native contact energy found in the homogeneous model. The direct route is so favorable that a 10% shift in energy distribution is required for His to fold by means of the ends-together route. These data are shown in Fig. 8, which is published as supporting information on the PNAS web site.

Multiple Routes in the β-Trefoil Family.

Multiple routes have been observed in studies of individual proteins (47, 48). Here, we present a detailed analysis of a structurally homologous family and show that family members may fold by means of multiple routes on a shared energy landscape. The theoretical results capture all of the folding routes that are seen experimentally. The resolution of the C_α model with an energetically unfrustrated potential is not sufficient to quantitatively predict the dominant route that is experimentally observed for a specific family member, because such a prediction may require details that are specific to its amino acid sequence and not simply its global fold (42–46, 49). Because experimental observations are based on ensemble averages of a protein, only the dominant route is likely to be observed, and events such as backtracking are hard to directly probe. The theoretical evidence, however, provides an understanding of how topology determines the overall shape of the free-energy landscape, whereas energetic and structural nuances may determine which route is used to fold to the native state. The presence of multiple routes indicates a robust landscape in which a protein can fold by accessing one of several routes. The traversal of different routes of the family as a whole, and the studies on IL-1β in particular, show that a small change in sequence or environment allows one of several possible routes to dominate. If a small change makes the most direct route unavailable, a previously disfavored route may be accessed.

Conclusions

The funnel shape of the landscape arises because the interactions present in the native structure of natural proteins conflict with each other much less than would be expected if there were no constraints of evolutionary design to achieve reliable and relatively fast folding. In small, fast-folding proteins, the kinetics of folding can be best considered as a progressive organization of an ensemble of partially folded structures through which the protein passes on its way to the folded structure (a single route). The family of larger proteins discussed here still has a sufficiently energetically smooth, funnel-like landscape, but its complexity creates geometrical constraints that partition the funnel landscape into disconnected regions. Folding now can proceed by means of not one, but several, energetically similar routes.

The energy landscape of the β-trefoil family displays heterogeneity in folding routes, two of which are globally distinct (see Fig. 9, which is published as supporting information on the PNAS web site). The direct global route initiates with the formation of trefoils 2 and 3 (13, 33). A variation unique to IL-1β involves the local backtracking of a subset of contacts, perhaps due to a topological discontinuity involving the formation of the β-barrel and the structuring of two functional loops. The ends-together route differs greatly. The two routes are on the same energy landscape but are separated in configuration space: To change from one route to another midway through folding, the protein would have to globally unfold and refold (50). These multiple routes may be necessary in more complex folds with greater amounts of topological frustration. The diversity of folding mechanisms is further testimony to the robustness of funneled landscapes: If one route is inaccessible, the protein may choose “the one less traveled by” (51).

Methods

Model.

A C_α model is used to represent the protein, where each residue is represented by its C_α atom. The energy potential is called an energetically unfrustrated, native structure-based (or Go) potential and is set by using the coordinates found in the protein database [His, 1HCE; aFGF, 2AFG; bFGF, 2FGF; IL-1β, 6I1B (52–55)]. Each native contact is given an energy weighting of 1ε (1ε = 1 kcal/mol) (1 kcal = 4.18 kJ). The potential is described in detail by Clementi et al. (9) and in ref. 25.

Simulations.

Even with a minimalist, native structure-based potential, the inherent slow folding of β-trefoil proteins makes it difficult to capture many folding and unfolding events at equilibrium conditions by using standard molecular dynamics [run with amber (56)]. To combat this computational expense, we used the following sampling techniques developed in our laboratory and described in detail in ref. 25. Temperature is given in units of ε (1 kcal/mol).

Kinetic runs.

We analyzed at least 20 kinetic runs that resulted in folding for each protein. Each simulation begins with a short run at a high temperature (1.5ε) to denature the protein and then continues for 675 ns at a common temperature, 1.1ε. This temperature is slightly below the folding (equilibrium) temperature (1.134–1.17ε) for all of the proteins. The folding temperature was determined by using a modified multicanonical algorithm that is described below.

Thermodynamic sampling.

To access the thermodynamics of the proteins at their folding temperature, we used a modified multicanonical method (25). In this method, a potential is introduced to reweight the force in the molecular dynamics simulator and push the protein into the transition region, the least populated region of the configuration space. Subsequently, a reweighting factor is used to regain the thermodynamic distribution of the canonical system.

Contact Map Definition.

Two distinct reasons were postulated for the change between the 433 and 422 contact models. The two contact maps were generated by either including or excluding the nonsymmetric contacts in the csu analysis readout (57). The 11 additional contacts found in the 433 contact model could either specifically stabilize the ends-together folding route or subtly shift the balance of energy between the secondary and tertiary interactions. In the C_α model, the secondary structure is determined by the dihedral term in the energetic potential. A change of 11 contacts shifts the total energy contained in the native contacts (∝ the number of contacts) to that contained in the dihedrals (∝ the number of dihedrals, which is unchanged). Additionally, the route populations may vary with temperature, and the change of 11 contacts could alter the folding temperature of IL-1β. To investigate the reason for the shift in route traversal, we ran several models: (i) a model with 422 contacts, with each contact energy increased to have the same total contact energy as the 433 contact model, (ii) a model with 433 contacts, with each contact energy decreased to mimic the 422 contact model, and (iii) a model with 11 random contacts removed from the structure. Model i favored the ends-together route. Models ii and iii used the ends-together route infrequently and preferred either the backtracking or direct route. We speculate that having more energy in the native contacts allows the protein to overcome the stiffness of the secondary structure due to the dihedral potential and make contacts between the N and C termini more readily. The temperature of the kinetic runs was varied from 1.1ε to 1.08ε to compensate for the change in folding temperature from 1.156ε to 1.134ε. Changing the temperature affected the total number of successful folding events, but not the frequency of route traversal. These studies support the change in energy balance as the reason for the observed shift in folding route frequency.

Abbreviations

His

hisactophilin

aFGF

acidic FGF

bFGF

basic FGF.