Endocytic vesicle scission by lipid phase boundary forces

Abstract

Endocytosis in budding yeast is thought to occur in several phases. First, the membrane invaginates and then elongates into a tube. A vesicle forms at the end of the tube, eventually pinching off to form a “free” vesicle. Experiments show that actin polymerization is an active participant in the endocytic process, along with a number of membrane-associated proteins. Here we investigate the possible roles of these components in driving vesiculation by constructing a quantitative model of the process beginning at the stage where the membrane invagination has elongated into a tube encased in a sheath of membrane-associated protein. This protein sheath brings about the scission step where the vesicle separates from the tube. When the protein sheath is dynamin, it is commonly assumed that scission is brought about by the constriction of the sheath. Here, we show that an alternative scenario can work as well: The protein sheath acts as a “filter” to effect a phase separation of lipid species. The resulting line tension tends to minimize the interface between the tube region and the vesicle region. Interestingly, large vesicle size can further facilitate the reduction of the interfacial diameter down to a few nanometers, small enough so that thermal fluctuations can fuse the membrane and pinch off the vesicle. To deform the membrane into the tubular vesicle shape, the membrane elastic resistance forces must be balanced by some additional forces that we show can be generated by actin polymerization and/or myosin I. These active forces are shown to be important in successful scission processes as well.

Internalization of plasma membrane and cell-surface proteins during endocytosis is an indispensable metabolic process in nearly all eukaryotic cells. Nutrient uptake, membrane recycling, and signal transduction are but a few of the essential cellular processes that depend on endocytosis. The internalization process is characterized by precisely regulated changes in membrane geometry and sequential recruitments of proteins to the internalization sites during vesicle formation, vesicle scission, and trafficking to the cell interior (for recent reviews, see refs. 1–3).

The classical model for formation of coated endocytic vesicles proposes a critical role for a large GTPase dynamin in vesicle scission. Dynamin oligomerizes at the neck of the endocytic membrane invaginations and facilitates vesicle scission upon GTP hydrolysis (4, 5). Dynamin has been suggested to function either as a regulatory GTPase that coordinates the timing of events leading to scission at the endocytic site or as a mechanoenzyme that uses the energy from hydrolysis to drive scission. As a mechanoenzyme, dynamin has been proposed to drive scission by constricting the membrane tube connecting the budding vesicle to the plasma membrane. However, recent in vitro experiments have questioned whether dynamin sheath constriction alone can drive scission (6). Furthermore, endocytic internalization can take place without dynamin in budding yeast, establishing that dynamin is not always essential for scission (7, 8).

Here, we propose an alternative theoretical model for the scission process during endocytosis in budding yeast. The model is based on the following assumptions, which are based largely on evidence from studies of endocytosis in yeast cells and on in vitro studies.

1. Endocytosis is initiated by an invagination of the plasma membrane that progressively deforms into a tubular bud-like ingression. On average, the tube is ≈35–45 nm in diameter and 150–250 nm long (9).

2. The invaginated membrane consists of regions along the tubular bud, each concentrating different proteins. Clathrin and other “coat proteins” localize to the tip of the invagination, whereas amphiphysin-like proteins Rvs161 and Rvs167 localize along the tubular “neck” region of the invagination (10). We assume that the different membrane lipids are also differentially localized to these different membrane domains. In vitro experiments also suggest that the tubular membrane might consist of multiple regions that could contribute to membrane fission (11, 12). Therefore, there could be a substantial interfacial tension between the bud region and the rest of the tube membrane.

3. The membrane mechanics of different regions could be quite different. The bending modulus and the surface tension of lipid raft domains are known to be larger than those of liquid disordered phases (13). Different membrane-associated proteins such as clathrin coat proteins and amphiphysin likely affect the local curvatures of the different membrane phases (14–18); therefore, different phases along the tubular membrane may assume different spontaneous curvatures.

4. In yeast, the surface of the invaginated membrane at the endocytosis site is surrounded by a cortical actin patch composed of branched actin filaments (9, 19, 20). In yeast, actin polymerization is essential for endocytosis (21, 22). The barbed ends of actin filaments are oriented toward the plasma membrane (19, 22). The F-actin at the endocytic sites could bind to the corresponding cell membrane via adaptor proteins (e.g., Sla2p) that simultaneously bind the coat proteins (22). The endocytic sites also promote actin polymerization by sequentially recruiting myosin (23, 24) and Arp2/3 activator proteins (22, 25). Actin polymerization is coincident with the formation of the invaginated membrane and is followed by release of a newly formed vesicle (26). Overall, these experimental observations strongly suggest that the polymerization of actin filaments actively deforms the membrane at the endocytosis site into a tubular invagination, pushing and/or pulling the invaginated membrane inward.

The above findings suggest that membrane heterogeneities and active forces may be two major determinants for the scission of the carrier bud from the tubular membrane invagination during endocytosis. Indeed, recent in vitro experiments and theories confirm the existence of a membrane fission mechanism driven by phase separation along the membrane tube (11, 12). However, Allain et al. (12) considered only the interfacial behavior by simplifying the two regions along the invaginated membrane into two infinite membrane tubes. They do not address the effects of the forces that deform the membrane into a tubular invagination and the size of the bud region on the scission process. Here, we present a general theoretical model for the scission process during endocytosis for yeast cells, specifically focusing on the influence of the bud size and the interplay between membrane lateral heterogeneities and active forces on the scission process of the bud.

Theoretical Model

The central notion of the model is that the protein sheath around the membrane tube acts as a “filter” that traps one lipid species while allowing other species to diffuse relatively unhindered. The trapping is most likely due to charge, so that if the protein is attached to the membrane by a surface carrying a net positive charge, then negatively charged lipids (e.g., phosphatidylinositols or phosphatidylserines) will be captured, whereas neutral lipids (e.g., phosphatidylcholine) diffuse more freely through the tube to the bud. Thus, the presence of the protein sheath induces a phase separation between lipids forming the tube and those comprising the budding vesicle. [Lipid phase segregation can be facilitated by their intrinsic incompatibilities, such as “hydrophobic mismatch” in their chain lengths (27).] This phase separation can be further facilitated by coat proteins, such as Sla2, epsins, and AP-2, which specifically bind PIP2. The resulting line tension constricts the interface down to a dimension where thermal fluctuations are sufficient to complete the scission of the bud from the tube. This process is assisted, and completed, by the axial thrust of the actin filaments that polymerize centripetally from the plasma membrane and are attached to the growing vesicle (10, 22).

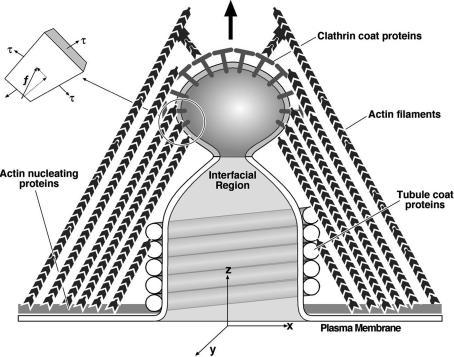
In our theoretical model, the cell plasma membrane at the endocytic site is modeled as an axisymmetric tubular invagination as shown in Fig. 1. The shape of the tubular membrane is determined by the “active” forces arising from actin polymerization and/or by myosin motors acting on F-actin. We assume that all of the active forces all over the membrane surface are constant and uniformly distributed. Also, the forces on the membrane are exerted at the same fixed angle with regard to the base membrane. The fixed magnitude and the fixed angle of the forces reflect their mean values for the fluctuating environment in real cells. Along the tubular membrane, a well defined phase boundary separates the bud region (phase 2) from the rest of tubular membrane (phase 1). We also assume that the time scale for the formation of the phase boundary is much faster than the scission process, so that we can treat the membrane shape as a sequence of elastic equilibrium states (12).

Fig. 1.

Schematic picture of the theoretical model for endocytosis. (Inset) The actin filaments exert protrusive surface stresses on the bud and tubule. The tubule coat proteins create a lipid phase boundary between the bud and the tubule. The clathrin adaptor proteins may add to the bending modulus and spontaneous curvature of the bud region.

Each phase along the tubular membrane is characterized by its surface tension, bending rigidity, and spontaneous curvature, all of which are assumed to be constant. This assumption is in part based on the fact that at least animal cells maintain the surface tensions of most of their membranes at a constant level via membrane reservoirs (28). We assume that this conclusion applies also to yeast cells, where the observed folding of the plasma membrane could provide the membrane reservoirs (9). To minimize the energetically unfavorable contacts between the two phases, the interfacial line tension minimizes the interface, which leads to a phase boundary characterized by a well defined circle perpendicular to the tube axis.

We use the Helfrich elastic membrane free energy to calculate numerically the equilibrium shape of the tubular membrane at the endocytosis site (29). The free energy of the system is given by the equation below.^§

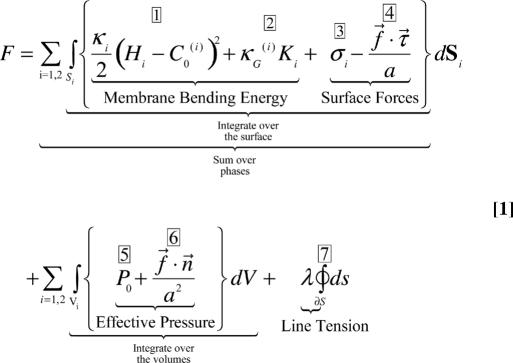For each phase i, the integrations are over its membrane surface (S_i) and its enclosed volume (V_i). The terms in Eq. 1 are as follows:

1. The bending energy associated with the mean curvature of the membrane, H_i. C₀⁽ⁱ⁾ is the spontaneous curvature originating from coat proteins and/or lipids for each phase, and κ_i is the mean bending rigidity for each phase, i = 1, 2.

2. The bending energy associated with the Gaussian curvature of the membrane, K_i, and κ_G⁽ⁱ⁾ is the Gaussian bending rigidity for each membrane phase, i = 1, 2. The Gaussian curvature is negative only in the scission region where the surface is saddle-shaped.

3. The surface tensions, σ_i, of each membrane phase.

4. The tangential stress (force per unit area) exerted by the actin filaments on the membrane surface. The term f⃗ · τ⃗ is the tangential component of the force from each F-actin, where τ⃗ is a unit tangent to the surface. a is the diameter of the cross section over which the individual force, f⃗, is applied on the membrane surface; it is roughly the same as the diameter of an individual F-actin filament at ≈5 nm.

5. The osmotic pressure difference across the membrane (with the positive direction defined as from inside the cell to the outside).

6. The normal stress (force per unit area) exerted by the actin filaments on the membrane surface, where f⃗ is the force and a² is the area on which it is exerted (roughly, the cross-sectional area of an actin filament).

7. The interfacial line tension that squeezes the neck of the tubule into its saddle-shape (the negative Gaussian curvature in term 2). The integral is over the interfacial line, ∂S.

Using Euler–Lagrange variational methods (30), the shape equation of the membrane surface can be computed by minimization of the free-energy functional (Eq. 1) under the constraints. The constraints include: (i) constant line tension at the interface λ; (ii) constant bending moduli, κ_i, and constant surface tensions, σ_i, for each phase, respectively; (iii) constant active force, f, per actin filament; and (iv) constant osmotic pressure, P₀. To examine the effects of bud size alone on the scission process, we fix the surface area for the tube region (phase 1) and allow only the bud region (phase 2) to vary. The calculation is detailed in the Supporting Appendices A and B, which are published as supporting information on the PNAS web site.

The coat proteins at the bud region and the protein sheaths at the tube region may provide rigid scaffolds attached to the underlying cell membrane. In the simplest approximation, these effects can be implicitly incorporated into the effective bending moduli of the cell membranes. Therefore, in all of the following calculations, we choose κ₁ = 50 k_BT, and κ₂ = 100 k_BT, which are much larger than that of pure lipid bilayers ≈10 k_BT. Also, we choose σ₁ = 5 × 10⁻⁵ N/m, σ₂ = 1 × 10⁻⁴ N/m, λ = 10 − 60 pN, P₀ = 0, f ≈ 1 pN as well as C₁⁽⁰⁾ = C₂⁽⁰⁾ = 0. All of the parameter values are summarized in Table 1. We fix the surface area of the tube region at 5,000 nm²; the total length of the tubular vesicles before scission are ≈100–150 nm, and the largest diameters are ≈50 nm, both of which are in accordance to the experimental observations. Varying the tube size does not change the qualitative results.

Table 1.

Model parameter values

Symbol	Meaning	Values	Reference
κi (i=1, 2)	Bending rigidity for phase i along the membrane invagination	10–400 kBT	11–13, 41–43
σi (i=1, 2)	Surface tension for phase i along the membrane invagination	10−5−10−3 N/m	11–13, 41–43
f	Polymerization force per actin filament	≤2.0 pN	34, 36, 44, 45
	Force per myosin power stroke	4 ∼ 8 pN	37, 44, 46, 47
a	Diameter of the area to which the active forces are applied	2–7 nm	37, 44
λ	Line tension between the bud and tube regions	10–100 pN	42, 48, 49
P0	Osmotic pressure difference across the membrane	−103 Pa	38

We have not treated the membrane as a true fluid bilayer but as an elastic sheet endowed with a bending resistance and surface tension. Thus, we cannot treat the scission of the bud from the tube explicitly; instead, we impose a criterion to decide when the actual scission takes place. It is known that monolayer fusion can take place spontaneously if bilayers are held within thermal fluctuation distance (31). Therefore, the natural linear length scale cutoff for our coarse-grained model for the bilayer is ≈5 nm, the width of a cell membrane. When the line tension around the neck of the bud squeezes the model to this diameter, we can safely assume that membrane fusion and budding of the vesicle will ensue spontaneously.

Results

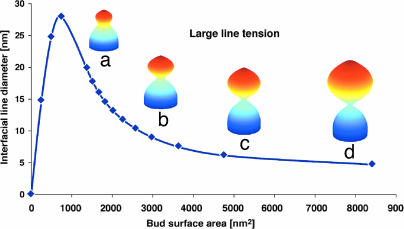
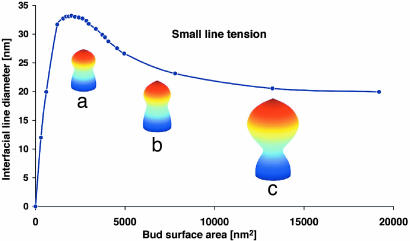
Fig. 2 shows that, for a reasonable range of (f, σ_i, κ_i, κ_G⁽ⁱ⁾), when the line tension, λ, is very large (λ ≈ 60 pN), the diameter of the interface between the bud region and the neck region decreases sharply as the surface area of the bud region increases. As the surface area of the bud grows very large, the diameter of the interfacial line can be as small as 6–7 nm. At this point, the distance between the two inner surfaces is actually ≈1–2 nm, and thermal fluctuations alone can pinch the bud off the membrane tube. On the other hand, when the line tension is very small (λ ≈ 10 pN), the diameter of the interfacial line asymptotes to ≈15 nm no matter how large the bud grows (Fig. 3). At this dimension, the two inner leaflets are still >10 nm away from each other, and thermal fluctuations alone cannot pinch the bud off from the membrane tube. The interface diameter is controlled by the competition between line tension, surface tension, and bending rigidity. Line tension and surface tension tend to minimize the interface so as to decrease the interfacial line length and the surface area, while bending rigidity opposes these forces because of the large mean curvature developing at the interface. As the surface area of the bud increases, the bending energy per unit area decreases, the neck becomes an insignificant fraction of the surface area, and the bending energy penalty per unit area for this region decreases. Consequently, the relative strength of bending rigidity is reduced. Physically, this property means that, as the surface area increases, there is more room to relax the stress from the bending energy, and the line tension and surface tension come to dominate the bending rigidity as the surface area grows and the diameter of the interface neck decreases.

Fig. 2.

The decrease in the diameter of the interfacial line as the surface area of the bud increases for large interfacial line tension λ = 60 pN. The series of equilibrium membrane shapes is obtained by means of the variational method with the constraints that the mechanical forces applied to the membrane surface by the actin filaments is constant. The membrane parameters are as follows: bending rigidities κ₁ = 50 k_BT, κ₂ = 100 k_BT; the Gaussian bending rigidities κ_G⁽¹⁾ = κ_G⁽²⁾; the surface tensions σ₁ = 5 × 10⁻⁵ N/m, σ₂ = 1 × 10⁻⁴ N/m; the active force ƒ = 1.0 pN, α = 2π/3; the osmotic pressure P₀ = 0. The surface areas of the buds are as follows: 1,668 nm² (a); 2,980 nm² (b); 4,760 nm² (c); and 8,415 nm² (d). The corresponding diameters of the interfacial line are as follows: 16.00 nm (a); 8.94 nm (b); 6.14 nm (c); and 4.71 nm (d). The natural length cutoff in this model is the width of the membrane, ≈5 nm. Therefore, the actual distance between the two inner leaflets at the interface for d is negative, i.e., the bud is already pinched off. The line is fit to the computed points (♦). Note that as the surface area of the bud region approaches zero, the diameter of the interface does as well. Because the surface area of the bud region is very small, the bending energy per area dominates the line tension; consequently, increasing the interfacial line dominates bending the membrane surface. Conversely, when the surface area of the bud is very large, the bending energy per area is dominated by the line tension, and the interface will shrink, making the membrane bend more. Therefore, the peak in the plot corresponds to the point where the bending energy per area is comparable to the line tension. We restrict ourselves to line tensions that dominate, corresponding to the case where the interfacial diameter decreases as the bud size increases.

Fig. 3.

The decrease in the diameter of the interfacial line upon increasing the surface area of the bud for small interfacial line tension λ = 30 pN, using the same parameters as in Fig. 2. The surface areas of the buds are as follows: 3,371 nm² (a); 4,952 nm² (b); and 13,235 nm² (c). The corresponding diameters of the interfacial line are as follows: 30.9 nm (a); 26.6 nm (b); and 20.55 nm (c). Using the same cutoff length of 5 nm as in Fig. 2, the actual distances between the two inner leaflets at the interface for a, b, and c are 25.92, 21.61, and 15.55 nm, respectively. Line is fit to the computed points (●).

When the surface area of the bud is relatively small, (e.g., <2,000 nm², where the diameter of the bud is <≈20 nm), the decrease in the interface diameter is limited by the increase of the interfacial line tension, and the interface can no longer decrease to nanometer size (data not shown), suggesting that a large bud may be necessary for successful scission in real cells. Qualitatively, this requirement is because the line tension is not large enough to overcome the huge bending stress of a small bud because, as noted earlier, the bending stress per area varies inversely with the surface area of the bud. In our calculations, a line tension of >200 pN was required, which is beyond the physical limits of cell membranes. On the other hand, bilayer line tensions are generally <100 pN, but spontaneous membrane fissions are easily observed in synthetic membranes (11–13). This feature is in sharp contrast to the highly regulated membrane fission events that characterize in vivo systems (22, 32). This phenomenon could be attributed to the much larger length scale (≈1 μm) for synthetic membrane systems that results in a much smaller bending energy barrier opposing the line tension, making the scission much easier. This finding has two implications. First, the size of the bud is a key factor in controlling successful scission of the bud during endocytosis in vivo. This conclusion augments the recent theoretical work by Allain et al. (12) who examined only the interplay of the mechanical forces at the interface without considering the finite size effect of the bud region (12). Second, given the small size of the bud in vivo and the physical range of membrane mechanical properties, an active cellular process is required to assist the line tension in pinching off the bud. This conclusion suggests the important role of actin-generated forces (polymerization and/or myosin driven) in the endocytic process.

If the bud region assumes a higher surface tension than the tube, it is conceivable that Marangoni flows could contribute to the growth of the bud (33). The increase in the surface area of the bud region can be driven by active forces derived from actin filament polymerization (22) and/or by power strokes of myosin 1 (23). For example, the F-actin could bind to the corresponding cell membrane via adaptor proteins (e.g., Sla2p) that simultaneously bind the coat proteins (22). The polymerization of the F-actin could then push and/or pull the underlying bud region, which creates vacancies for other membrane components to move in. Thermodynamically, this phenomenon corresponds to a lower chemical potential at the bud region so that more adaptor proteins, and hence more F-actin, bind to the bud, and additional polymerization forces are generated. If phase segregation occurs on much faster time scales than those for force generation and membrane shape changes (18, 19), then the equilibrium bud size is determined by the force balance between the total active forces and the elastic restoring forces of the membrane itself. Furthermore, if the membrane shape changes are much faster than the force generation, the system should have sufficient time to relax to its equilibrium shape. Then our calculation of the bud growth as a sequence of equilibrium shapes provides a good qualitative indication of the scission dynamics of the bud. A complete study of endocytosis dynamics will be the subject of a subsequent study.

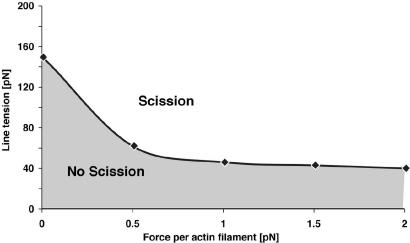
Fig. 4 quantifies the role of the active forces in driving a successful scission of the bud during endocytosis. Fig. 4 is a phase diagram (f vs. λ) showing the combinations of active forces and line tension required for successful scission of the bud given a given reasonable window for the membrane mechanical properties (λ_i, κ_i, κ_G⁽ⁱ⁾). The criteria chosen for the successful scission of the bud is that the diameter of the interface must decrease below 5 nm as the bud size is <2 × 10⁴ nm². We chose this value for the bud size cutoff because bud diameters >80 nm are very rare in yeast cells. When the actin-generated forces vanish (f = 0), the required interfacial line tension for successful scission is ≈150 pN, which is quite high for a cell membrane. However, a small increase in the active force (from 0 to 0.5 pN) reduces the required line tension for successful scission by 2.5 times, down to 60 pN. Note that, 0.5 pN per F-actin is less than the maximum force that a polymerizing actin filament can exert (34–36), and much less than the force from a myosin motor (37). The dependence of successful scission of the bud on the active forces arises because the active force exerts force parallel and perpendicular to the membrane tube and contributes to reducing the equilibrium radius of the tube (see Supporting Appendix B). Of course, this effect also depends on the angle, α, between the membrane normal and the active force vector; if α = π/2, there is no normal force at all. The existence of normal forces is supported by the observation that the whole tubular membrane invagination swings back and forth, hinging around its base transverse to the z axis (10). In our calculations, we chose α = 2π/3. The forces from the actin polymerization might not be exerted directly on the tube region of the invaginated plasma membrane but may bind to rigid coat proteins, which transmit the force to the membrane via anchoring proteins. The diverse origins of the active forces and the variations in the distributions of the active forces over the membrane surface are not considered in this paper.

Fig. 4.

The phase diagram (line tension, λ, vs. surface active force, ƒ) for the successful scission of the bud for a given set of the membrane mechanical forces. Large line tension and large active forces are needed for successful scission of the vesicle. The membrane mechanical constants are κ₁ = 50 k_BT, κ₂ = 100 k_BT; κ_G⁽¹⁾ = κ_G⁽²⁾; σ₁ = 5 × 10⁻⁵ N/m, σ₂ = 1 × 10⁻⁴ N/m; ƒ = 1.0 pN, α = 2π/3; P₀ = 0, and α = 2π/3. The criteria for successful scission of the bud is when the actual distance between the two inner leaflets at the interface is less than zero for the surface area of the bud <2 × 10⁴ nm².

The above calculations suggest that the interfacial line tension may be very important for a successful scission of the bud in endocytosis processes (Fig. 4). Many cellular events, such as the binding of proteins (e.g., AP-2, epsins, amphiphysin) to specific lipids, could induce the phase segregation along the tubular membrane at the endocytic sites to create the interfacial line tension. Indeed, any protein that can promote lipid phase separation will create a line tension that can perform the same function as the dynamin. In our coarse-grained model, we do not specify this level of detail.

Some simplifications are adopted in this paper and should be clarified. First, the spontaneous curvatures of both membrane (lipid) and coat protein (e.g., clathrin) components were chosen to be zero. Given the presence of the active forces impinging on the invaginated membrane, it was difficult to distinguish whether the coat proteins cause the membrane to bend or simply adopt the resulting local curvature. Furthermore, in our experiments on budding yeast, endocytosis still takes place in clathrin knockout strain (10). Therefore, clathrin may not be essential for endocytosis in budding yeasts. Nonetheless, we discuss the role of spontaneous curvature on the bud scission process in Supporting Appendix C.

Second, the Gaussian bending rigidities of the two phases have been taken to be equal, and the osmotic pressure term is neglected. This assumption is because we have chosen the active force per filament f ≈1 pN, so its contribution to the pressure term is ƒ/a² ≈ 4 × 10⁴ Pa ≫ P₀ ≈ 10³ Pa for resting cells (38). However, successful endocytosis requires an osmotic pressure lower than a threshold value (38). The detailed investigation for osmotic pressure will be carried out in the future.

Third, in our simulations, a small radius curvature can develop at the tip of the bud region. This unphysical singularity arises in the model because a force is applied at the tip (coarse-grained over a region ≈5 nm) (see also refs. 39 and 40). This small curvature at the “north pole” of the bud could lead to the rupture of membrane. This singularity could be prevented by a more smooth distribution of the actin filament forces by coat proteins covering a larger area of the bud or by lipid rafts as discussed in ref. 39. We believe this sharp tip region (<5 nm in diameter) does not greatly affect the diameter of the interface; therefore, we neglect this detail in the equilibrium shape and artificially replace the tip region with a harmonic surface in the figures for illustration purposes.

Discussion

We have constructed a theoretical model to investigate the effects of mechanical forces on the endocytic scission process in budding yeast. Our central hypothesis is that scission of the vesicle from the tube that connects it to the plasma membrane is accomplished by a separation of lipid phases between the tube and the growing bud. This separation could be accomplished by membrane-associated proteins, such as amphiphysin, which line the tubule and trap particular (e.g., negatively charged) lipids while allowing other lipid species to diffuse through to the vesicle bud. Using variational methods and an elastic-free energy describing multiple phases along the invaginated membrane, we calculate a series of equilibrium shapes of the membrane invaginations as the bud grows. The membrane with multiple phases is characterized by the different surface tensions, different bending rigidities, and the line tension between the bud region and the tube region. We find that phase segregation along the tubular membrane creates a large interfacial line tension that promotes scission of the bud during the endocytosis process. This conclusion is in agreement with the recent theoretical studies and in vitro experiments (11, 12).

For a small bud, the reduction in the diameter of the interface by line tension is limited because it is opposed by the large bending energy stored in the small diameter bud. However, as the surface area of the bud grows, the neck will constrict at the interface because the bending energy of the bud will be distributed over a larger area with smaller curvature. Thus the line tension will grow more dominant over the bending stress at the interfacial line. With reasonable values of the membrane mechanical properties, the growth of the bud can further reduce the diameter of the interface to be as small as several nanometers. At such small separation between the two inner leaflets of the membrane, thermal fluctuations are sufficient to fuse the leaflets and pinch off the bud from the membrane tubule. The model augments previous theoretical studies on line tension induced scission of membrane tubules (12) to include the size of the bud and active surface forces for the successful scission during endocytosis in living cells (12).

We found that active forces generated by actin polymerization and/or myosin on the membrane surface greatly facilitate the scission of the bud. A phase diagram of the active force vs. line tension delineates the region where scission is possible. A fairly small active force per F-actin filament of ≈0.5 pN will reduce the line tension required for successful scission from ≈150 pN to ≈60 pN, thus requiring a weaker lipid phase separation and possibly a faster pinching off process. Thus, complete scission of the bud can be achieved by increasing the line tension and/or the active force; however, the effect of the active forces asymptotes >≈0.5 pN per filament, above which not much further effect is obtained.

In summary, the coordinated effect of protein-induced lipid phase segregation along the tubule, growth of the vesicle bud, and the action of actin-generated surface forces on the invaginating membrane is sufficient for successful vesicle scission during endocytosis. Although our model is largely based on observations of the endocytic process in budding yeast, similar principles could also apply for endocytic events in more complex organisms, and for other vesicle scission events.