Dynamic evidence for metal ion catalysis in the reaction mediated by a flap endonuclease

Abstract

On the basis of structural work, metal ions are proposed to play a catalytic role in reactions mediated by many phosphoryl transfer enzymes. To gain dynamic support for such mechanisms, the role of metal ion cofactors in phosphate diester hydrolysis catalysed by a flap endonuclease has been studied. The pH maximal rate profiles were measured in the presence of various metal ion cofactors; in each case, a single ionic form of the enzyme/cofactor accounts for the pH dependence. The kinetic pK_as display good correlation with the acidity of the corresponding hexahydrated metal ions, which strongly suggests a role for metal-bound hydroxide, or its equivalent ionic species, in the reaction. Comparing rates of reaction in the pH-independent regions, a small negative β_nuc value is observed. This suggests that expected trends in the nucleophilicity of the various metal-bound hydroxides are balanced by a second form of metal ion catalysis that is related to the acidity of the hexahydrated metal ion. This is likely to be either electrophilic catalysis or leaving group activation.

Introduction

Key cellular processes in all living organisms are controlled by the action of enzymes that often require divalent metal ion cofactors for activity. Phosphoryl transferases are one important family of enzymes that are essential for the synthesis, metabolism and repair of the genetic material (DNA and RNA) and for cellular signalling mechanisms. Examples of metal ion-dependent phosphoryl transferases include polymerases (Steitz, 1993), phosphatases (Hengge, 1998), nucleases (Williams, 1998) and catalytic RNA molecules (Grasby, 1998). This group of enzymes can be divided into two broad mechanistic classes. In one group of enzymes, metal ions are thought to play the role of electrophilic catalyst (Figure 1C), but rate enhancements are also brought about by the direct participation of amino acid side chains as general acid and general base catalysts in the reaction mechanism. Examples of this class of phosphoryl transfer enzymes include staphyloccocal nuclease, bovine pancreatic DNase I and Serratia nuclease (Williams, 1998). However, for reactions catalysed by another group of divalent metal ion-dependent phosphoryl transferases, it has been proposed that active site amino acids do not participate directly in catalysis. Instead, metal ions alone are suggested to be responsible for the observed rate enhancements (Beese and Steitz, 1991; Davies et al., 1991; Kim and Wyckoff, 1991; Steitz and Steitz, 1993; Kim et al., 1995; Kostrewa and Winkler, 1995; Rice et al., 1996; Newman et al., 1998; Hopfner et al., 2001; Hadden et al., 2002).

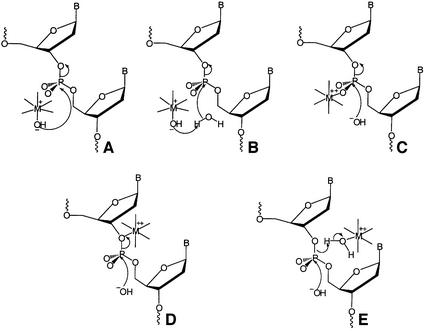
Fig. 1. Possible roles for divalent metal ions in phosphate diester hydrolysis. Double bonds at the phosphorus centre have been omitted for clarity. (A) Metal-bound hydroxide is the nucleophile in the reaction. (B) Metal-bound hydroxide acts as a general base. (C) A metal ion binds to one of the non-bridging oxygens of the scissile bond, acting as a Lewis acid catalyst. (D) A metal ion activates the leaving group. (E) Metal-bound water acts as a general acid. Hydroxide is shown as the attacking nucleophile in (C–E), for the purposes of illustration only. These possible roles for metal ions are not mutually exclusive. For example, the same metal ion may act as a source of hydroxide (A) and a Lewis acid catalyst (C), or as a Lewis acid catalyst (C) and activate the leaving group (D). However, the same metal ion cannot fulfil the role of nucleophile or general base (A or B), and leaving group activation or general acid (D and E), but two metal ions could fulfil these requirements.

Metal ions have the potential to participate in the enzymatic catalysis of phosphate diester hydrolysis reactions in several ways (Figure 1). These include providing metal-bound hydroxide as the nucleophile (Figure 1A) or general base (Figure 1B). Electrophilic catalysis by coordination to one of the non-bridging oxygens of the scissile phosphate diester (Figure 1C), leaving group activation (Figure 1D) or general acid catalysis by metal-bound water (Figure 1E) are also possibilities. Combinations of more than one mode of catalysis and/or the involvement of multiple metal ions are also likely. For example, the two-metal ion mechanism invoked for the 3′–5′ exonuclease domain of the Klenow fragment proposes that one metal ion acts as a source of nucleophilic hydroxide and as an electrophilic catalyst, whilst a second metal ion activates the leaving group and acts as an electrophilic catalyst (Beese and Steitz, 1991). Examples of other enzymes where similar types of metal ion catalysis have been proposed include alkaline phosphatase (Kim and Wyckoff, 1991), restriction endonucleases (Kostrewa and Winkler, 1995; Newman et al., 1998), the double-strand break repair nuclease Mre11 (Hopfner et al., 2001), large and small ribozymes (Pyle, 1993; Yarus, 1993), retroviral integrases (Rice et al., 1996), junction-resolving enzymes (Hadden et al., 2002) and RNase H (Davies et al., 1991).

Mechanistic proposals for metal ion catalysis are derived largely from crystallographic studies of a few ground state product–metal ion–protein ternary complexes (Beese and Steitz, 1991; Kim and Wyckoff, 1991; Kostrewa and Winkler, 1995; Newman et al., 1998; Hopfner et al., 2001) that have been extended to a number of enzymes that lack such detailed structural data, but have metal ion requirements (Davies et al., 1991; Steitz and Steitz, 1993; Kim et al., 1995; Rice et al., 1996; Hadden et al., 2002). Dynamic studies that support these proposals have concentrated mainly on eliminating the possibility of the direct participation of amino acids in catalysis. For example, it has been demonstrated that an active site tyrosine in Klenow fragment 3′–5′ exonuclease does not play a catalytic role (Derbyshire et al., 1991). In some notable cases, solution studies have revealed that proposals for metal ion catalysis are not plausible (Jou and Cowan, 1991; Hampel and Cowan, 1997; Nesbitt et al., 1997; Young et al., 1997). In contrast, dynamic approaches to provide positive experimental support for metal ion catalysis have been elusive, even though such studies are required to test these mechanistic proposals.

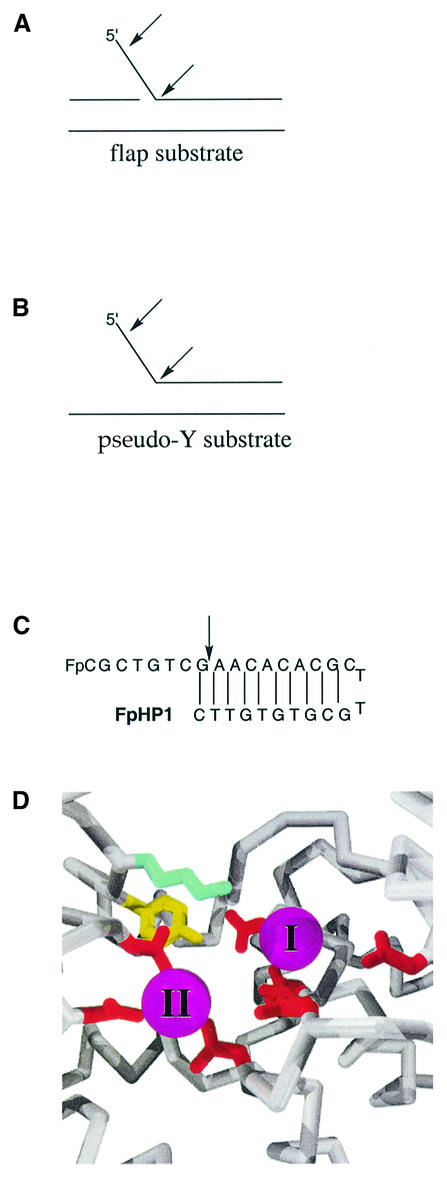
One family of enzymes that have an absolute requirement for divalent metal ion cofactors are the flap endonucleases (FENs). FENs catalyse the hydrolysis of nucleic acids at key steps during DNA replication and repair, and are present in organisms as diverse as bacteriophage and humans. The importance of FEN proteins is underlined by the fact that defective FEN genes cause the rapid progression of some tumours and are embryonic lethal (Kucherlapati et al., 2002). FEN proteins catalyse both the 5′-exonucleolytic and structure-specific endonucleolytic hydrolysis of nucleic acid substrates to generate products terminating in a 5′-phosphate monoester and a 3′-hydroxyl group. Structure-specific activity occurs at double strand–single strand junctions in bifurcated nucleic acid substrates such as flap (Figure 2A), pseudo-Y (Figure 2B) and 5′-overhanging hairpin substrates (Figure 2C) (Lyamichev et al., 1993; Harrington and Lieber, 1994; Garforth and Sayers, 1997; Pickering et al., 1999b). During DNA replication, FEN proteins are involved in the removal of RNA primers from Okazaki fragments (Rumbaugh et al., 1997; Bhagwat and Nossal, 2001).

Fig. 2. (A) A generic flap structure. Arrows indicate sites of 5′-exonucleolytic and endonucleolytic cleavage. (B) A generic pseudo-Y structure. Arrows indicate the sites of endo- and 5′-exonucleolytic cleavage. (C) The 5′-fluoresent overhanging DNA hairpin (FpHP1) is an empirically derived single cleavage substrate (Patel et al., 2002). An arrow indicates the site of reaction. (D) The structure of the active site of T5 FEN (Ceska et al., 1996) illustrating the location of metal II (magenta, foreground) and metal I (magenta, further back), Tyr82 (yellow) and Lys83 (light blue). Aspartic acid residues are shown in red. Previous experiments eliminated Lys83 and Tyr82 as the titrating moiety in the pH rate profile of k_cat (Pickering et al., 1999a; Patel et al., 2002).

Six FEN crystal structures currently are known (Kim et al., 1995; Ceska et al., 1996; Mueser et al., 1996; Hosfield et al., 1998; Hwang et al., 1998; Matsui et al., 2002). To date, no enzyme–substrate or enzyme–product co-crystal structures have been reported. However, the structure of the T5 FEN revealed a novel structural motif: a helical arch, through which single-stranded but not double-stranded nucleic acids can thread, allowing the enzyme to discriminate between potential substrates (Ceska et al., 1996). The T5 FEN active site is located at the bottom of the helical arch. A model of the DNA–protein complex was proposed that accounts for the observed endonucleolytic specificity of the FEN proteins (Ceska et al., 1996). This model has been revised recently, re-orientating the double-stranded portion of the DNA on the protein, but retaining the role of the helical arch (Dervan et al., 2002). Most of the available FEN structures, including that of T5 FEN (Figure 2D), reveal binding sites for two divalent metal ions (Ceska et al., 1996; Mueser et al., 1996; Hosfield et al., 1998; Hwang et al., 1998). In solution studies, two metal ions have been found to bind to the murine homologue (mFEN) using isothermal titration calorimetry (Zheng et al., 2002).

Previous mechanistic studies have used a single cleavage 5′-overhanging hairpin substrate for T5 FEN to characterize the pH dependence of the enzyme-catalysed reaction (Pickering et al., 1999a,b). The pH rate profile of log k_cat/K_M is bell-shaped as the consequence of the association constant of the enzyme reaching a maximum at low pH, whereas the turnover number of the enzyme is maximal at high pH. The pH dependence of DNA binding is the result of a requirement for protonation of an active site lysine residue, Lys83 (Figure 2D) (Pickering et al., 1999a). Mutation of another active site amino acid, Tyr82 (Figure 2D), does not significantly alter the pH rate profile of the enzyme (Patel et al., 2002). A catalytic role for metal ions in the T5 FEN reaction has been suggested, based on the premise that no other candidate amino acid residues within the active site could account for the pH rate profile of the enzyme (Pickering et al., 1999a; Patel et al., 2002).

Here, we describe experiments designed to investigate the role of metal ions in the FEN reaction. These studies have exploited the wide cofactor tolerance of T5 FEN (Garforth et al., 2001). The effects of varying the metal ion cofactor on the pH rate profiles of the enzyme-catalysed reaction have been quantified. These studies produced clear dynamic evidence in support of a catalytic role for metal ions in this reaction.

Results

Comparison of the T5 FEN-catalysed reactions supported by Mg²⁺, Mn²⁺ and Co²⁺ cofactors

Previous studies have demonstrated that Mn²⁺, Mg²⁺ and Co²⁺ ions support the T5 FEN-catalysed exonucleolytic and endonucleolytic hydrolysis of DNA flap substrates, with Mn²⁺ and Mg²⁺ cofactors producing the most efficient reactions (Garforth et al., 2001). To quantify the effects of varying the metal ion cofactor on the steady-state catalytic parameters of T5 FEN, a fluorescent 5′-overhanging DNA hairpin substrate (FpHP1, Figure 2C) was employed. This 29mer 5′-fluorescent substrate undergoes a single endonucleolytic cleavage reaction catalysed by T5 FEN, to generate a fluorescent 8mer product and a 21mer product, and has been used previously to characterize the enzyme (Pickering et al., 1999b; Patel et al., 2002). The fluorescent product and substrate were separated and quantified using denaturing HPLC (dHPLC) equipped with a fluorescence detector. Initial rates of reaction at various substrate concentrations, under the standard assay conditions of 25 mM buffer pH 9.3, 50 mM KCl, 0.2 mg/ml bovine serum albumin (BSA) and 10 mM divalent metal ion chloride, were used to generate the Michaelis–Menten parameters shown in Table I. Under steady-state conditions ([E]<[S]), the turnover number of the enzyme is greatest with Mn²⁺ as the cofactor, and slowest with Co²⁺. Small variations in the Michaelis constant upon changing cofactor are also observed. The most stable ternary complexes are formed when Co²⁺ is the metal ion component, but the highest value observed with Mn²⁺ is only 2-fold greater.

Table I. Results of evaluation of the catalytic parameters of T5 FEN with Co²⁺, Mn²⁺ and Mg²⁺ cofactors.

Metal ion cofactor	kcat (per min)	KM (nM)	pKa M(H2O)62+
Co2+	58 ± 4	39 ± 10	9.65
Mn2+	336 ± 48	86 ± 28	10.46
Mg2+	155 ± 9	53 ± 10	11.44

The pK_a M(H₂O)₆²⁺ is taken from Dean (1985). Full experimental details are provided in Materials and methods.

Metal ion dissociation constants of T5 FEN

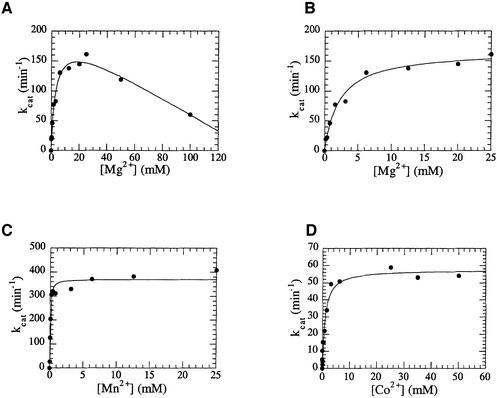
Metal ion dissociation constants for each cofactor were also determined by examining the metal ion dependence of k_cat. These experiments were carried out with 1 µM FpHP1, >10-fold in excess of the observed K_M values with each cofactor, to ensure that the maximal rate of reaction under steady-state conditions was measured. Higher metal ion concentrations (>25 mM) were found to inhibit the reaction (Figure 3A). The inhibitory effects of divalent metal ions have been noted previously for FENs (Paul and Lehman, 1966; Zheng et al., 2002) and other nucleases (Groll et al., 1997), and may arise from metal ions bound to the DNA that must be displaced before interaction with the enzyme. It is also possible that, as has been proposed for RNase H, higher concentrations of metal ion cofactor facilitate the binding of another metal ion that attenuates activity (Keck et al., 1998), or that inhibition of activity is the result of elevated ionic strength. Below 25 mM metal ions, the data shown in Figure 3B–D fit simple binding isotherms well (Equation 2). Although the crystal structure of T5 FEN (Ceska et al., 1996) has two bound metal ions, there is no evidence for the binding of multiple metal ions from these titrations. However, these experiments were undertaken to determine K_D^M2+ for the purposes of selecting saturating metal concentrations for further experiments. They did not measure rates of reaction at very low metal concentrations (<1/8 K_D^M2+), where the binding of multiple metal ions may be evident. Mn²⁺ ions bind most strongly to the protein, whilst metal ion dissociation constants for Co²⁺ and Mg²⁺ are comparable and an order of magnitude greater.

Fig. 3. Metal ion dependence of the turnover number of T5 FEN with Mg²⁺, Mn²⁺ and Co²⁺ cofactors. (A) High concentrations of magnesium ions inhibit the reaction. (B) Mg²⁺ dependence of k_cat. Data were collected up to 25 mM MgCl₂. In this range, the data fitted a simple binding isotherm (Equation 2) to yield K_D^M2+ = 2.2 ± 0.34 mM and a maximal rate of reaction of 167 ± 7/min. (C) Mn²⁺ dependence of k_cat. Data were collected up to 25 mM MnCl₂. In this range, the data fitted a simple binding isotherm to yield K_D^M2+ = 0.05 ± 0.01 mM and a maximal rate of reaction of 370 ± 12/min. (D) Co²⁺ dependence of k_cat. Data were collected up to 25 mM CoCl₂. In this range, the data fitted a simple binding isotherm to yield K_D^M2+ = 0.93 ± 0.18 mM and a maximal rate of reaction of 58 ± 3/min. Experimental details are described in Materials and methods.

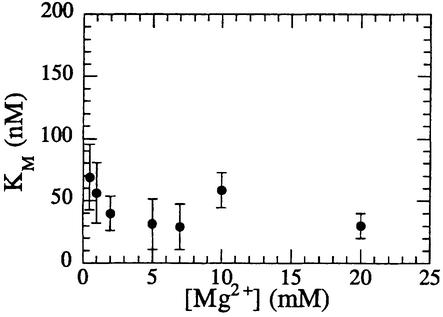
The magnesium ion dependence of both steady-state parameters was also determined by analysis of the catalytic parameters at various metal ion concentrations (Figure 4). In contrast to k_cat, K_M is virtually metal ion independent in the 0.5–20 mM Mg²⁺ ion range, with <3-fold variation in the Michaelis constant (Figure 4). The K_M ranged from 30 to 70 nM at 0.5 and 7 mM MgCl₂, respectively. Shen and colleagues recently described variation in the Michaelis constant for the endonucleolytic activity of mFEN on a DNA flap substrate (Zheng et al., 2002). In their study, this parameter varied from 90 nM (20 mM MgCl₂) to 37 nM (5 mM MgCl₂), with a value of 89 nM at 0.01 mM MgCl₂. This broadly agrees with values reported here for T5 FEN on a 5′-overhanging hairpin substrate. Shen et al. have suggested that the observed variation in Michaelis constant is evidence that the binding of metal ions modulates the substrate binding ability of FENs (Zheng et al., 2002). However, the small changes in this parameter are often in line with the experimental errors of such measurements and do not appear to merit this conclusion.

Fig. 4. Variation in the Michaelis constant (K_M)_.of T5 FEN with magnesium ion concentration. Michaeli–Menten parameters were determined at magnesium ion concentrations from 0.5 to 20 mM. Less than 3-fold variation in K_M is observed in this range. Experimental details are described in Materials and methods.

The pH dependence of the rate of reaction with Mg²⁺, Mn²⁺ and Co²⁺ cofactors

The effect of changing the metal ion cofactor employed in the enzyme reaction was selected as a test for a possible catalytic role for metal ions. At any given pH, the ionization state of water coordinated to a hydrated divalent metal ion is quantified by the solution pK_a (Table I) (Dean, 1985), which decreases as the Lewis acidity of the ion increases. If metal ions play a catalytic role in the reaction, the ability to support the reaction will be dependent on the ionization state of metal-bound water and/or its Lewis acidity. Moreover, if metal-bound water is the titrating moiety in the pH rate profile, changing the cofactor in the reaction should shift the experimentally observed pK_a in a manner predictable from its solution value.

For a comparison of the reaction rates with various cofactors to be valid, it is essential that the maximal rate of phosphate diester hydrolysis is determined for each cofactor examined. As previous work demonstrated that the rate of the T5 FEN-catalysed reaction is partially limited by product release in the presence of Mg²⁺ ions (Patel et al., 2002), these experiments had to be carried out under single turnover conditions, where product release is not measured. The fast rates of T5 FEN-catalysed reactions necessitated the use of quench flow apparatus. Steady-state catalytic parameters (Table I) were used to select concentrations of enzyme and substrate that would produce maximal rates under single turnover conditions. Furthermore, to ensure maximal rates of phosphate diester hydrolysis with each metal ion cofactor, it is also essential that the concentration of metal ions used does not limit the rate of reaction. Thus, investigations were carried out at metal ion concentrations in excess of the experimentally derived K_D^M2+ (Figure 3).

Practical limitations restricted the feasibility of our studies, as elevated concentrations of divalent metal ions are known to cause precipitation of enzyme. Furthermore, the redox properties and reactivity of transition metals, particularly significant at high pH, limited the metal ion concentrations that could be used. Nevertheless, within these limitations, we were able to carry out pH titrations in the presence of cofactor concentrations 5-fold greater than the metal ion dissociation constants. For reactions involving Mn²⁺ and Co²⁺, an acidic quench had to be used to stop the reaction and prevent the formation of precipitates, whereas a basic quench was employed with Mg²⁺ ions. In both cases, EDTA was added to the quench to preserve the lifetime of the dHPLC column. Previous work has demonstrated that EDTA alone is not a fast enough quench for T5 FEN reactions (Patel et al., 2002). The concentration of enzyme used to ensure maximal single turnover rates was at least 5-fold higher than the K_M, and the concentration of substrate was at least 20-fold lower than the K_M.

Since K_M is maximal at high pH (Pickering et al., 1999a), the use of parameters obtained at pH 9.3 to set substrate concentrations designed to produce a maximal rate at lower pH values is valid. Reactions using low concentrations of substrate (1 nM) could be analysed easily by dHPLC, where the injection volume could be varied to compensate for the dilute solutions. Single turnover first-order rates of reaction (k_c) were measured by taking at least eight time points on the millisecond scale. Experiments were repeated at 12 or more different pH values in the range 5.5–9.3 (Co²⁺), 5.5–9.3 (Mn²⁺) and 6.3–10.5 (Mg²⁺), using MES, HEPES, EPPS, potassium bicinate, CHES, potassium glycinate or CAPS buffers. Some buffers appeared to form insoluble complexes with specific metal ions. When this was the case, an alternative buffer was employed. For each pH studied, the first-order rate constant was determined from a plot of product versus time on at least three separate occasions (Equation 3).

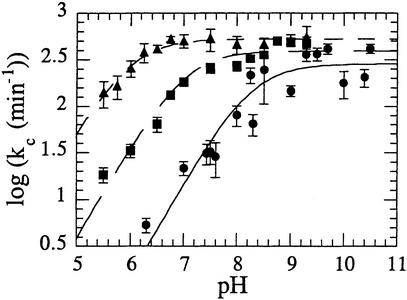
The pH dependence of log k_c is illustrated in Figure 5 for reactions involving Co²⁺, Mn²⁺ or Mg²⁺ cofactors. At lower pH values, the rate of reaction is dependent on hydroxide ion concentration, until a pH-independent region is reached. The pH-dependent regions of the Mn²⁺ and Mg²⁺ curves have a slope close to unity, indicating that a single ionization event is taking place. By necessity, the data in this region of the Co²⁺ profile are minimal but, by analogy, a single titrating residue was assumed. The data have therefore been fitted to a model that assumes the enzyme–metal ion–DNA complex exists in a protonated and deprotonated state, but that only the deprotonated form is catalytically competent. The results of this analysis reveal that with Mg²⁺ as a cofactor, the ternary complex has a pK_a of 8.3 ± 0.13. The pK_a derived from this analysis is in excellent agreement with a previous study under steady-state conditions that used Mg²⁺ as cofactor and reported a pK_a value of 8.3 ± 0.10 (Pickering et al., 1999a). With Mn²⁺ as cofactor, the pK_a value observed for the ternary complex is lowered to 7.0 ± 0.09, and with Co²⁺ as the cofactor, the observed pK_a value is lowered further to 6.0 ± 0.05.

Fig. 5. Combined plot of the pH dependence of the logarithmic single turnover rate (k_c) of T5 FEN with various cofactors. Plots of log k_c versus pH have been fitted to a single ionization model that assumes the DNA–protein–metal ion ternary complex can exist in two states, one protonated and another deprotonated, but only the deprotonated form is catalytically competent. This curve fitting yields the pK_a of the ternary substrate–metal ion–protein complex and (k_c)₀, the maximal rate of reaction of catalytically competent complex. With Co²⁺ (triangles), this curve fitting yields pK_a = 6.0 ± 0.05 and (k_c)₀ = 531 ± 1/min. With Mn²⁺ (squares) as the cofactor, curve fitting yields pK_a = 7.0 ± 0.09 and (k_c)₀ = 395 ± 1/min. With Mg²⁺ (circles) as the cofactor, curve fitting yields pK_a = 8.3 ± 0.13 and (k_c)₀ = 286 ± 1/min. Experimental details are provided in Materials and methods.

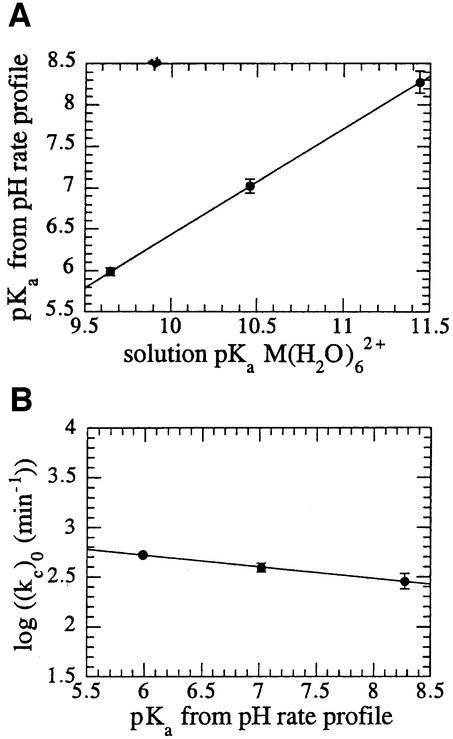
At pH values below the respective pK_as of the ternary complexes, rates of reaction follow the same trend as the acidity of the corresponding metal ion in solution, with rates of reaction greatest with Co²⁺ and slowest with Mg²⁺. To examine the possibility that the titrating moiety in the pH rate profiles is metal-bound water, the pK_as observed in the pH rate profiles were plotted against the solution pK_as of the hexa-aqua metal (Figure 6A). A good correlation exists, strongly indicating a role for metal-bound hydrox ide, or its ionic equivalent, in the reaction catalysed by T5 FEN. However, the maximal rates of reaction reached in the pH-independent region of the pH rate profile are similar for each cofactor. For reactions that involve transition states where significant bond formation between the attacking nucleophile and the reactants takes place, the rate of reaction is highly dependent on the basicity of the attacking nucleophile. This effect is quantified as the value of β_nuc using Brønsted analysis. A small β_nuc value of –0.12 is observed when the logarithmic rates of reaction derived from the pH-independent region of the profiles (Figure 5) are plotted against their respective ternary complex pK_as (Figure 6B).

Fig. 6. (A) Plot of the pK_a derived from the T5 FEN pH rate profile (Figure 5) in the presence of Co²⁺, Mn²⁺ and Mg²⁺ against the solution pK_a of the divalent metal ion hexahydrate (Dean, 1985). The slope and R-factor are 1.3 and 1.0, respectively. (B) Logarithmic maximal rate of reaction derived from the pH-independent region of the T5 FEN pH rate profile [(k_c)₀ (Figure 5)] versus the pK_a derived from the same pH rate profile. The β_nuc value (slope) and R-factor are –0.12 and 0.99, respectively.

A metal ion-dependent conformational change is unlikely to limit the rate of the T5 FEN-catalysed reaction

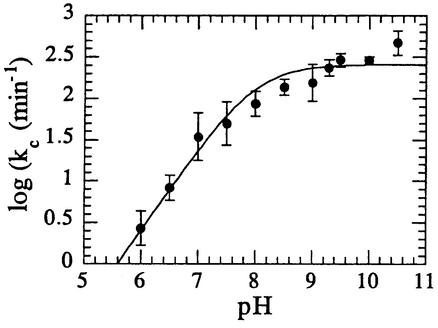
A metal ion-dependent conformational change has been proposed to limit the rate of reaction of human FEN-1 (hFEN) (Nolan et al., 1996). This suggestion is based upon the very low turnover numbers observed with mammalian FENs of 0.15/min (mFEN) (Zheng et al., 2002) and 6/min (hFEN) (Nolan et al., 1996), not a factor with T5 FEN where rates of reaction are orders of magnitude greater. Recently, it has been suggested that the binding of metal ions to the murine protein alone brings about a structural change (Zheng et al., 2002). Our single turnover quench-flow experiments were initiated by mixing enzyme with a solution of DNA plus metal ion, and could therefore measure the rate of such a conformational change. To test this possibility, we pre-incubated enzyme with metal ions and then initiated the reaction by addition of substrate. The observed reaction rates and pH rate profiles from these experiments were very similar to those observed with the alternative mixing protocol (Figures 5 and 7), so we can rule out a metal-dependent conformational change as the rate-limiting step in this reaction.

Fig. 7. pH dependence of the logarithmic single turnover rate (k_c) of T5 FEN with Mg²⁺ added to enzyme prior to mixing enzyme and substrate in a quench-flow apparatus. Experimental details are provided in Materials and methods. Curve fitting (Equation 4) yields pK_a = 8.0 ± 0.11, (k_c)₀ = 256 ± 1/min. The similarity of these results to those obtained when Mg²⁺ is pre-mixed with substrate (Figure 5) indicates that an Mg²⁺-dependent conformational change does not limit the rate of reaction catalysed by T5 FEN.

Discussion

To investigate the role of metal ions in the reaction catalysed by FENs, we have measured the pH rate profiles of the T5 enzyme with three different cofactors, Co²⁺, Mn²⁺ and Mg²⁺. To reach mechanistic conclusions from such an experiment, it is critical that, for each cofactor studied, the maximal chemical rate of reaction is measured at all pH values. Several factors required consideration to satisfy these criteria. First, to avoid product release as a factor in the measured rates, reactions had to be carried out under single turnover conditions. Secondly, all experiments were carried out under saturating concentration of metal ions.

The standard assay conditions for T5 FEN use a pH of 9.3. Comparing maximal rates of reaction under single and multiple turnover conditions at pH 9.3 demonstrates that the rate of reaction with Co²⁺, like that with Mg²⁺, is limited by product release, whereas the reaction with Mn²⁺ is not. These results imply that the ternary product–metal ion–protein complex is more stable with Co²⁺ and Mg²⁺ than it is with Mn²⁺. Interestingly, this order of stability is also observed in the K_M values determined (Table I), suggesting that Co²⁺ and Mg²⁺ complexes are twice as stable as the Mn²⁺ complex. These results contrast with findings reported by Baldwin et al. (1999) for EcoRV endonuclease. In the case of EcoRV, K_M values are much smaller with Mn²⁺ and Co²⁺ than with Mg²⁺. Many phosphoryl transferases catalyse aberrant reactions in the presence of Mn²⁺ cofactors, including the star activities of restriction enzymes (Vermote and Halford, 1992) and the infidelity of DNA polymerases (Campbell et al., 2002). T5 FEN also exhibits this type of behaviour, cleaving double-stranded closed-circular plasmid substrates efficiently with an Mn²⁺ cofactor (Garforth et al., 2001), an unexpected result given the lack of a single-stranded end. One explanation for the promiscuous behaviour of phosphoryl transferases in the presence of Mn²⁺ ions is suggested to be an enhanced stability of complexes with this cofactor, coupled with enhanced reaction rates (Baldwin et al., 1999). However, results presented here suggest that the stability of ternary complexes with Mn²⁺ cannot be the reason for this behaviour with T5 FEN. Instead, the stimulation of such aberrant reactions with Mn²⁺ ions is likely to be the consequence of increased chemical reactivity and ease of product release in the case of this FEN.

Previous studies have attempted to elucidate a catalytic role for metal ions in nuclease reactions by relating the effects of varying the metal ion cofactor on rate of reaction at a single pH value to the known solution pK_as for hexa-aqua divalent metal ions (Baldwin et al., 1999; Campbell et al., 2002). However, as metal ion catalysis is clearly a pH-dependent process that varies with the cation selected, we studied the maximal rate of reaction over a full range of pH values. In line with previous experiments on T5 FEN that determined the pH dependence of k_cat in the presence of Mg²⁺ ions, the pH dependence of the maximal single turnover rate of reaction, regardless of cofactor, results from the titration of a single moiety. Reaction rates reach a maximal value at high pH, demonstrating that the catalytically active form of the ternary complex is a deprotonated state. As the divalent metal ion cofactor used in the reaction becomes more acidic, the observed pK_a values in the pH rate profile are decreased. Moreover, when the observed pK_a in the pH rate profile is plotted against the pK_a of the hexa-aqua metal ion, an excellent correlation exists. Together, these results provide strong evidence that the titrating moiety in the pH rate profile is metal-bound hydroxide, or its ionic equivalent.

At high pH values, rates of reactions are pH independent, as all the metal-bound water is fully deprotonated. In this pH-independent region, the observed rates should reflect the nucleophilicity of hydroxide bound to the various metal ions. Since the conjugate base of a strong acid is a weak base, it follows that a more acidic hydrated metal ion would produce a poorer base or nucleophile when deprotonated. Thus, the expected trend in this region of the pH rate profile is that the rate of reaction would be fastest with Mg²⁺. However, the maximal rates of reaction reached in the pH-independent region of the pH rate profile are similar for each cofactor, and yield a surprisingly low β_nuc value of –0.12 (Figure 6B). One explanation of this behaviour is that the relevant transition state involves very little bond formation, but this would contradict previously established data for the reactions of phosphate diesters (Dalby et al., 1993). It is more plausible that the metal ion(s) play(s) a second role in the reaction, which is dependent on the acidity of the hydrated metal ion(s) and compensates for the expected basicity trend. Electrophilic catalysis (Figure 1C) or leaving group activation (Figure 1D), where a metal ion coordinates to one of the non-bridging oxygens of the phosphate diester or to the leaving group, are often proposed as modes of catalysis in metallonucleases. The effectiveness of electrophilic catalysis, or activation of a leaving group, is related to the metal’s ability to stabilize negative charge. This phenomenon can be quantified by measuring the pK_a of metal-bound water. Therefore, both of these types of catalysis would follow the acidity trend of the metal ion employed.

In summary, a full explanation of the pH rate profiles observed with the various metal cofactors is as follows. At lower pH, the rate of reaction is dominated by the concentration of metal-bound hydroxide, which increases in a linear fashion with pH, and so, in this region of the profile, the rate of reaction is Co²⁺>Mn²⁺>Mg²⁺. Above the pK_a of each metal species, two effects balance to produce similar rates of reaction for all metal cofactors. On the one hand, reactivity of the metal-bound hydroxide will follow the order Mg²⁺>Mn²⁺>Co²⁺, whereas electrophilic catalysis or leaving group activation will follow the opposite trend Co²⁺>Mn²⁺>Mg²⁺. In this region of the profile, the effects compensate and produce a small value of β_nuc.

Electrophilic catalysis at the unesterified phosphate oxygens, combined with metal hydroxide as the nucleophile, could be carried out by the same metal ion. However, a combination of metal hydroxide as the nucleophile and leaving group coordination carried out by a single metal ion would require a large movement of the metal ion during the reaction (Figure 1). This appears unlikely, and therefore two metal ions are likely to be required to combine these two modes of catalysis. A further possibility is that a metal ion activates the nucleophile (metal 1), a second metal ion activates the leaving group (metal 2), and one or both metal ions act as electrophilic catalysts in analogy to the mechanism proposed for the Klenow fragment 3′–5′ exonuclease (Beese and Steitz, 1991). Indeed, many of the crystal structures of FENs demonstrate two bound metal ions, suggesting that this is possible (Ceska et al., 1996; Mueser et al., 1996; Hosfield et al., 1998; Hwang et al., 1998). However, in each crystal structure, the metal–metal distance is greater than the 4 Å required for bridging the same phosphodiester bond in a two-metal ion mechanism. Notwithstanding, conformational change upon substrate binding could bring the two metal sites closer together.

The acidic amino acid ligands that coordinate metal I in FENs cannot be mutated without totally abolishing catalytic activity but retaining DNA binding ability (Shen et al., 1996; Bhagwat et al., 1997), suggesting a catalytic role for this metal ion. Distinguishing between a one-metal ion (metal hydroxide plus electrophilic catalysis) and a two-metal ion mechanism (metal hydroxide plus leaving group activation, with or without electrophilic catalysis) requires insight into the role of metal II in the FEN reaction. Current evidence suggests that metal II does not play a catalytic role, favouring a one-metal ion mechanism (Bhagwat et al., 1997; Amblar et al., 2002; Zheng et al., 2002), although this question is still not entirely resolved.

The inferences made above hold only if chemistry is the rate-limiting step in the T5 FEN-catalysed reaction over the entire pH range studied. Two alternative possibilities deserve consideration. First, the observed pK_a may be a kinetic pK_a resulting from a change in the rate-limiting step. However, we have studied the pH rate profile of a K83A mutant of T5 FEN (Pickering et al., 1999a). This mutation produces a 10³-fold decrease in k_cat over the entire pH range and exhibits a pH dependence similar to the wild-type enzyme for this parameter, albeit at a greatly reduced rate. Thus, if a change from one rate-determining step to another is observed, the mutation K83A must produce identical effects on both these steps. This is unlikely. Secondly, the possibility that a conformational change limits the rate of reaction must also be considered. This can be ruled out, as an alternative mixing protocol produces similar results (Figure 7).

Surprising patterns of reactivity observed with various cofactors that have been described in other work addressing the role of metal ions in nuclease reactions may be explained by this study (Baldwin et al., 1999; Campbell et al., 2002). The rates of reaction observed here under steady-state conditions, where Co²⁺ ions produce the slowest reaction, display no relationship to the acidity of the hydrated metal ion in solution. This underlines the importance of eliminating product release as a rate-limiting step in the reaction by using single turnover experiments. Similarly, the differing metal ion dissociation constants of the ternary complexes may have led to confusing patterns of reactivity, as conditions under which manganese ions produce maximal rates would not fulfil this requirement with other metal cofactors. The assumption that metal ion dissociation constants are similar is likely to produce erroneous interpretations. Even with these two problems addressed, measuring the rate of reaction at a single pH value may well produce inaccurate relationships. For example, if we had compared maximal single turnover rates at pH 9.3, the standard assay condition for T5 FEN, we would have been led to the conclusion that the identity of the metal ion is unimportant. Furthermore, even comparing rates of reaction at values below the pK_as of all the ternary complexes, which do display a relationship to the acidity of the metal ion cofactor, we could not have discriminated between modes of catalysis, as any form of metal ion catalysis potentially could produce this result.

In conclusion, dynamic evidence for at least two roles for metal ions in the T5 FEN-catalysed reaction is reported. These results demonstrate that previous proposals for metal ion catalysis in a range of enzyme-catalysed phosphoryl transfer reactions that derive from static structural work are plausible. It has been suggested that metal ion catalysis is a primitive answer to the problem of accelerating the rate of hydrolytic reactions, requiring only the correct positioning of metal ions (Beese and Steitz, 1991). Modern day nucleases typically utilize magnesium ion cofactors. The rather high solution pK_a of magnesium-bound water, [Mg(H₂O)₆]²⁺ pK_a = 11.44 (Dean, 1985), with resultant low concentrations of metal-bound hydroxide at lower pH, does not appear attractive for this type of catalysis. However, the results presented here demonstrate that enzymes have evolved to lower the pK_a of magnesium-bound water. The decreases in basicity or nucleophilicity of the conjugate base associated with lowered pK_a are compensated for by using Lewis acidity of metal ions to enhance reaction rates further. Hence, metallonucleases produce life-sustaining rates of reaction and operate under conditions that support present day cellular requirements.

Materials and methods

Production of T5 FEN

T5 FEN was purified to homogeneity as described previously (Sayers and Eckstein, 1990).

Synthesis, purification and characterization of fluorescein-labelled HP1 (FpHP1)

Fluorescent 5′-overhanging hairpin oligonucleotide substrate [FpHP1: 5′ fluorescein-pd(pCGCTGTCGAACACACGCTTGCGTGTGTTC)] was synthesized, purified and characterized as described previously (Patel et al., 2002).

Determination of steady-state parameters

Reaction mixtures containing appropriate concentrations of FpHP1 in 25 mM potassium glycinate pH 9.3, 50 mM KCl, 0.2 mg/ml BSA, 10 mM M²⁺Cl₂ (MgCl_2, MnCl₂ or CoCl₂) were heated to 90°C for 1 min and cooled to 37°C to pre-fold the substrate. Enzyme stock was diluted in 25 mM potassium glycinate pH 9.3, 50 mM KCl, 0.2 mg/ml BSA plus appropriate M²⁺Cl₂, and kept on ice until used. Reactions were initiated by addition of enzyme and brief vortexing. Final concentrations of 10–400 nM (Mn²⁺, Mg²⁺), 2–640 nM (Co²⁺), substrate and 4.1–82.2 pM enzyme were used. Aliquots were removed at eight time intervals and quenched with an equal volume of 20 mM EDTA. dHPLC (Wave® fragment analysis system with a fluorescence detector; Transgenomic, Warrington, UK) was used to separate and quantify the fluorescent product from FpHP1 substrate. A DNA Sep® column was used with the following buffers: buffer A, 2.5 mM tetrabutyl ammonium bromide, 1 mM EDTA, 0.1% acetonitrile; buffer B, 2.5 mM tetrabutyl ammonium bromide, 1 mM EDTA, 70% acetonitrile; gradient, t = 0 min, 50% B; t = 13 min, 80% B; retention times, fluorescent 8mer product 3.5 min, fluorescent 29mer substrate 7.2 min.

Initial rates of reaction at the various substrate concentrations were determined and the kinetic parameters were calculated by non-linear regression fitting of the data to the Michaelis–Menten equation (Equation 1). All curve fitting was carried out using Kaleidagraph software (Synergy Software, Reading, PA).

v is the initial rate, [S] is the substrate concentration and [E] is the total enzyme concentration.

Steady-state reactions with magnesium ions as the cofactor were also undertaken at a range of K_D^M2+ concentrations.

Measuring the metal ion dissociation constants of T5 FEN

Aliquots of 1 µM FpHP1 in 25 mM potassium glycinate pH 9.3, 50 mM KCl, 0.2 mg/ml BSA, plus 0.006–100 mM M²⁺Cl₂ (MgCl₂, MnCl₂ or CoCl₂) were heated to 90°C for 1 min and cooled to 37°C. The concentration of FpHP1 was chosen to produce the maximal rate of reaction, k_cat. Enzyme stock was diluted in 25 mM potassium glycinate pH 9.3, 50 mM KCl, 0.2 mg/ml BSA, and kept on ice until used. Reactions were initiated by addition of enzyme and brief vortexing. Enzyme was used at a final concentration of 20 pM. Aliquots were removed at eight time intervals and quenched with an equal volume of 20 mM EDTA. dHPLC was used to separate and quantify fluorescent product from FpHP1 as described for determining the steady-state parameters (above).

Normalized initial rates of reaction, k_cat, at the various metal ion concentrations were determined. This allowed the metal ion dissociation constant to be calculated by non-linear regression fitting of the data to Equation 2:

where K_D^M2+ is the metal ion dissociation constant, k_cat (v/[E]) is the normalized initial rate, [M²⁺] is the concentration of metal ion cofactor, and k_cat(max) is the maximal rate at saturating metal ion concentration.

pH rate profiles

pH rate profiles were carried out under single turnover conditions using an RQF-63 rapid quench flow device (Hi-Tech Ltd; Salisbury, UK). An 80 µl aliquot of enzyme in reaction buffer (25 mM buffer, 50 mM KCl, 0.2 mg/ml BSA) was mixed with an equal volume of pre-folded FpHP1 substrate in reaction buffer plus the appropriate metal ion cofactor (20 mM MgCl₂, 2 mM MnCl₂ or 10 mM CoCl₂; final concentrations were 10, 1 and 5 mM, respectively). Buffers employed to maintain pH were pH 5.5–6.25 MES, pH 6.5–8.0 HEPES, pH 8.0–8.4 EPPS, pH 8.5–9.0 potassium bicinate, pH 9–10 CHES, pH 9.3 potassium glycinate and pH 10–10.5 CAPS. Enzyme and FpHP1 were used at final concentrations of 410 and 1 nM, respectively. After a controlled time delay of between 9 ms and 6.4 s, 80 µl of quench (1.5 M NaOH, 60 mM EDTA for Mg²⁺, 1.0 M HCl, 60 mM EDTA for Mn²⁺ and Co²⁺) was added. Solutions of enzyme, substrate and quench were held at 37°C in a thermostated water bath within the instrument during the reactions. Quenched samples were analysed by dHPLC as described for the steady-state analyses. The first-order rate of the reaction was determined by plotting the appearance of product against time and by non-linear regression fitting to Equation 3:

P_t = P_∞ (1 – exp^–kct)(3)

where P_t is the amount of product at time t, P_∞ is the amount of product at t_∞, and k_c is the rate of reaction.

The pH dependence of k_c was fitted to a single ionization using Equation 4:

where K_ES is the acid dissociation constant of the ternary (enzyme– substrate–metal ion) complex, k_c is the first-order rate at a given pH, and (k_c)₀ is the maximal first-order rate constant of the catalytically competent form of the enzyme.

Alternative mixing protocol. Analogous experiments to the pH rate profiles described above were conducted with Mg²⁺ cofactor using an alternative mixing protocol to test whether a metal ion-dependent conformational change takes place. An 80 µl aliquot of enzyme in reaction buffer (25 mM buffer, 50 mM KCl, 0.2 mg/ml BSA) and 20 mM MgCl₂ was mixed with 80 µl of pre-folded FpHP1 substrate in reaction buffer (no divalent metal ion). All other procedures were carried out as above.