Structural origins of adenine-tract bending

Abstract

DNA sequences containing short adenine tracts are intrinsically curved and play a role in transcriptional regulation. Despite many high-resolution NMR and x-ray studies, the origins of curvature remain disputed. Long-range restraints provided by 85 residual dipolar couplings were measured for a DNA decamer containing an adenine (A)₄-tract and used to refine the structure. The overall bend in the molecule is a result of in-phase negative roll in the A-tract and positive roll at its 5′ junction, as well as positive and negative tilt inside the A-tract and near its junctions. The bend magnitude and direction obtained from NMR structures is 9.0° into the minor groove in a coordinate frame located at the third AT base pair. We evaluated long-range and wedge models for DNA curvature and concluded that our data for A-tract curvature are best explained by a “delocalized bend” model. The global bend magnitude and direction of the NMR structure are in excellent agreement with the junction model parameters used to rationalize gel electrophoretic data and with preliminary results of a cyclization kinetics assay from our laboratory.

It has been known for ≈20 years that DNA molecules containing four to six consecutive adenine–thymine base pairs exhibit intrinsic curvature (1). This curvature can play a significant role in transcriptional activation by affecting promoter geometry. Many transcriptional activators are DNA-bending proteins that can either recognize DNA bases (direct recognition) or specific DNA properties such as flexibility (indirect recognition) (2). Escherichia coli promoters frequently contain an adenine (A)-tract region, mostly centered around the −44 region, which when mutated has been shown to reduce transcription (3). In some cases, substitution of an entire promoter region by properly curved DNA can activate in vitro transcription (4, 5). More recent work indicates that these sequences function as upstream recognition elements (UP elements), the curvatures of which play an unknown role (6). In addition, HIV-1 reverse transcriptase termination of the (+) strand DNA synthesis is thought to occur because of minor groove compression of duplex DNA caused by the A-tracts (7, 8). Understanding A-tract geometry can therefore play an important role in our understanding of gene expression. Despite many structural efforts, no consensus about the stereochemical origins of the bend has yet emerged. A-tract molecules studied by x-ray crystallography are all bent in directions orthogonal to that established by gel and solution studies (1). Solution NMR, which is not prone to the artifacts of the crystal environment, has only recently been able to provide the long-range restraints necessary to determine global DNA properties (9). We present application of dipolar couplings to determination of DNA bending of an A₄-tract and discuss implications for DNA-bending models and stereochemical origins of curvature. Because reliable values for the magnitude and direction of DNA bends can be obtained by cyclization kinetics (10) and comparative gel electrophoresis (11, 12), we verified the bending properties of the same molecule by comparison with a preliminary cyclization kinetics assay (Y. Zhang, A.B., and D.M.C., unpublished results).

Methods

Synthesis of NMR Samples.

Unlabeled DNA oligomers were synthesized by standard phosphoramidite chemistry at the Keck Foundation Center of Yale University. Uniformly ¹³C¹⁵N-labeled samples were obtained using a primer extension method (13). All samples were dialyzed into a 20 mM sodium phosphate buffer (pH 7.0), 200 mM NaCl, and 0.5 mM EDTA.

NMR Spectroscopy.

All assignments were made using 2D and 3D homonuclear and heteronuclear NMR spectroscopy, including HCCH correlated spectroscopy (COSY) and HCCH total correlation spectroscopy (TOCSY) (14). Standard 2D NOESY spectra were acquired at 600 MHz in D₂O at mixing times of 100 and 250 ms. A recycle delay of 10 s was used in both experiments to give the adenine H2 protons sufficient time for T₁ relaxation. In all experiments in D₂O, the proton carrier frequency was set to the HDO frequency (4.76 ppm). Jump–return spin-echo H₂O NOESY spectra and double-quantum filtered (DQF)-COSY experiments were acquired on a 500-MHz Varian Unity spectrometer. Spectral width was 4,000 Hz in t₁ and t₂ dimensions. The recycle delay used was 2 s. Two-dimensional HCCH-E.COSY (E, exclusive) spectra were acquired on labeled samples with a spectral width of 4,000 Hz and 512 complex data points in t₂ (14). Two hundred fifty-six complex points were collected over a spectral width of 8,000 Hz in t₁. GARP decoupling was applied to the phosphorus channel during the constant-time period and to the carbon and phosphorus channels during acquisition. On extraction of the cross-peaks for determination of the J couplings, the digital resolution was increased 8-fold to 0.24 Hz per point in ω₂. Three-dimensional HCCH-E.COSY spectra were collected on labeled samples with a spectral width of 3,600 Hz and 64 complex points in t₁ (14). A spectral width of 3,125 Hz was covered in t₂ by collecting 42 complex points. A 3,600-Hz spectral width was covered in t₃ with 256 complex points. GARP decoupling was applied to phosphorus during the constant-time period and to carbon and phosphorus during t₃. For determination of J couplings, the digital resolution was increased 32-fold in the detection dimension. We collected 85 C–H dipolar couplings by using a gradient-enhanced, gradient-selected heteronuclear single quantum coherence (HSQC) pulse sequence (15, 16) on a 3-mM unlabeled DNA sample. All spectra were recorded on an 800-MHz Varian Inova spectrometer by using an HCN probe with z gradients. For measurement of dipolar couplings, no decoupling in the t₁ dimension was used. Sweep widths were set to 6,400 Hz and 8,247 Hz in ¹H and ¹³C dimensions, respectively. For each spectrum, 400 t₁ increments were collected. The anisotropic sample contained ≈22 mg⋅ml⁻¹ of Pseudomonas aeruginosa bacteriophage Pf1, which was obtained from American Type Tissue Collection and prepared according to published procedures (17). Couplings were measured from peak splittings in the indirect dimension. Measured ¹J_CH couplings showed excellent correlation with couplings obtained from J-modulated HSQC experiments at the same magnetic field strength (data not shown).

Structural Restraints.

We have obtained a large number of restraints to adequately restrain our decamer (Table 1). Tight distance restraints were chosen to maintain correct hydrogen bonding distances (18). A hybrid relaxation matrix approach was used to determine 271 distance restraints for the nonexchangeable protons in the DNA molecule. We used yarm [Yet Another Relaxation Matrix program (19)] to convert the observed NOE cross-peak volumes to distances. In most cases, the difference between the 100- and 250-ms-derived distances was larger than 5% of the average distance and the two calculated distances were used as upper and lower bounds. The new distances computed by yarm were then used in our structure-determination protocol. Deoxyribose torsion angles were determined from 2D and 3D HCCH-E.COSY experiments (14, 20). Amplitudes and ranges of sugar puckers were determined and converted to torsion angles ν₀–ν₄ by using the appropriate Karplus relationships (21). Based on HCCH-E.COSY and DQF-COSY observations, all sugar puckers are within the South region of the pseudorotation cycle. The sugar pucker restraints were allowed the conservative range of 100–200° for most nucleotides because we did not want to unreasonably restrain the sugars, which have substantial conformational flexibility. The phosphorus spectrum was very poorly resolved, leading us to believe that α and ζ backbone torsion angles are nearly identical throughout the DNA sequence. Tight backbone torsion angle restraints (α = −60 ± 30°, β = 180 ± 30°, and ζ = −90 ± 30°) were used in the final calculation (18). To better determine global properties of the DNA duplex, 85 C–H dipolar couplings were measured in the presence of P. aeruginosa bacteriophage Pf1 (17) from peak splittings in the indirect (¹³C) dimension. Two or three sets of spectra were collected for isotropic and anisotropic samples. Standard deviations obtained from averaging of apparent ²J_CH couplings from the isotropic and anisotropic spectra were added to obtain the errors. Wherever the error was <2 Hz, it was automatically set to 2 Hz, which was estimated to be the maximum accuracy of the measurement (9).

Table 1.

Restraints used in structure calculation

Restraint type	Relaxation matrix*	Overlapped†	H2O NOESY†	Total
NOE
Intranucleotide	149	73	0	222
Sequential	117	36	11	164
Cross-strand	5	1	22	28
H bond				52
Total				466
Dihedral angles				189
Dipolar couplings (C–H)‡				85
Base planarity‡				20
Total restraints				761
Restraints per nucleotide				38.05

^*Converted to distances using a relaxation matrix program. 

^† Given lower and upper limits of 1.6 and 5.6 Å, respectively. 

^‡ Used in refinement stage only. 

Structure Refinement.

Structures were calculated using cns (22), with a refinement protocol similar to those of Stein et al. (23) and Stallings and Moore (24). Square-well potentials were used for all experimental restraints, including dipolar couplings. In the first stage, duplex molecules were annealed from two randomized single strands and cooled using torsion angle molecular dynamics (TAMD) followed by a second Cartesian cooling stage. No dipolar couplings were used in this first stage. Thirty converged molecules were further refined using restrained Cartesian molecular dynamics (MD) at 300 K, during which dipolar couplings were introduced. To avoid deformations of local geometry to accommodate dipolar coupling restraints, the force constant for dipolar couplings was slowly increased from 1 × 10⁻⁵ to 0.20 over 25 ps. The molecules were then allowed to relax over 15 ps with all force constants unchanged. Base planarity restraints were used in this stage to keep individual bases planar. The rhombicity (R) and axial component (D_a) of the alignment tensor were determined to be 0.15 and 35 Hz (25), respectively, using a grid search procedure (26) where sets of refinements are carried out with different values of D_a and R. The final value for the dipolar coupling force constant was obtained by calibration (27). The ten lowest-energy structures were selected for analysis. Structural statistics of the final set of 10 structures are summarized in Table 2.

Table 2.

Structural statistics for 10 lowest-energy A4 conformers

Average rms deviations (rmsd) from experimental data
NOEs, Å	0.053  ± 0.001
Torsion angles, °	0.655  ± 0.031
Dipolar couplings, Hz	2.64  ± 0.05
Average restraint violations
NOEs >0.5 Å	0  ± 0
Torsion angles >5°	0  ± 0
Dipolar couplings >2 Hz*	2.9  ± 1.0
Average rmsd from ideal stereochemistry
rmsd from bonds, Å	0.0142  ± 0.0002
rmsd from angles, °	3.47  ± 0.07
rmsd from impropers, °	1.52  ± 0.08
Coordinate precision
All 10 bp (all atoms)
Pairwise rmsd of 10 structures, Å	0.99
rmsd to average structure, Å	0.86
Inner 8 bp (all atoms)
Pairwise rmsd of 10 structures, Å	0.74
rmsd to average structure, Å	0.60

^*Outside of specified error bounds. 

Measurement of Curvature with madbend.

madbend (ref. 36; Version April 24, 2002) was used as described, with the following exception to determine the correct calculation of the bend magnitude, the reference plane had to be placed outside of the molecule. The reference plane position as output by madbend is 0.5 bp offset from the actual position, which was identified by running the program with several simple test input files with obvious bend directions.

Results

Description of the A-tract Structure.

Because our molecule (from now on referred to as A4) is in B-DNA helical form (Fig. 1), it is best to explain its structural features by using helical and base pair parameters. All helical and base pair parameters were calculated with 3DNA (28), which, to our knowledge, is the only DNA structure analysis program that strictly adheres to the “standard” base pair reference frame (29). Lu and Olson (30) have shown that it is the choice of the base pair reference frame, rather than the choice of algorithm, that causes different DNA analysis programs to yield different results.

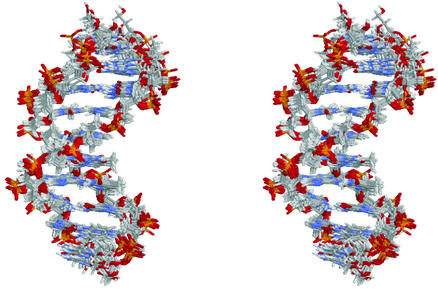
Figure 1.

Stereo view of the 10 lowest-energy A4 decamer structures calculated with dipolar couplings superimposed on inner 8 bp. The A-tract strand is facing toward the reader.

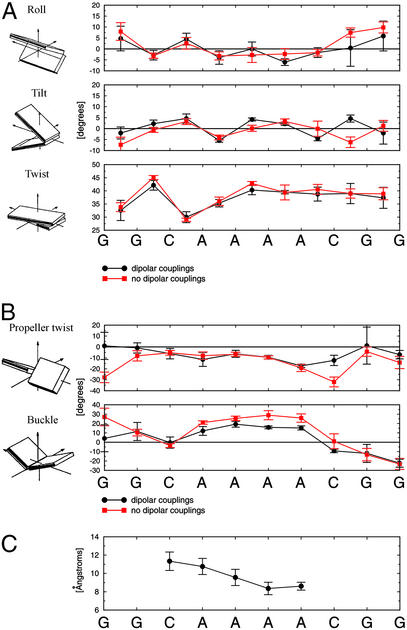
Structural parameters for the 10 lowest-energy A4 structures show that the structures exhibit relatively small degrees of roll and tilt between individual base pairs (Fig. 2A, Table 3). The molecule is slightly overwound, with an average value of twist of 37.8° (≈9.5 bp per turn). This is less than the 10.34 bp per turn determined by gel electrophoretic mobility studies (31). We believe this is a result of the inability of dipolar couplings to define the helical twist well because of redundancy of C–H vector orientations around the principal axis of the alignment tensor, which is parallel to the helical axis. All A-tract crystal structures have exhibited high degrees of propeller twist, which has been associated with potential bifurcated hydrogen bonding (32, 33). Compared with other structures, the A-tract in A4 exhibits less propeller twist, with an average value of −11° (Fig. 2B). The magnitude of this propeller twist is not large enough (close to −20°) to support formation of bifurcated hydrogen bonds. Bifurcated hydrogen bonds, however, are not necessary for A-tract curvature (34). Buckle may play an important role in bending of A-tracts and has been observed before in AATT tracts (35). We observe a significant change (12° at the 5′ end and 25° at the 3′ end) of buckling from one base pair to the next at the junctions (Fig. 2B). The buckle may offset the loss of favorable stacking interactions, which result from the presence of helical tilt at the junctions of the A-tract. Calculations with simulated data showed that buckle can be determined to a very high accuracy (data not shown). The minor groove of the A-tract progressively narrows toward the 3′ end, which has been previously observed by several techniques, including hydroxyl radical footprinting, x-ray crystallography, and NMR (1). A4 shares this compression of the minor groove (Fig. 2C).

Figure 2.

Structural parameters of 10 best A4 structures calculated with (black circles) and without (red squares) dipolar couplings. (A) local helical parameters. (B) Propeller twist and buckle. (C) Minor groove width (P–P distances). All parameters were calculated with 3DNA (28). Error bars represent three standard deviations of the mean.

Table 3.

Average helical and base pair parameters of 10 best A4 structures

Local helical parameters					Base pair parameters
Base pair step	Roll, °	Tilt, °	Twist, °	Slide, Å	Base pair	Buckle, °	Propeller twist, °
G1-G2	4.7  ± 1.9	−2.0  ± 0.9	32.5  ± 1.3	−0.32  ± 0.34	G1⋅C20	4.1  ± 4.8	1.0  ± 4.1
G2-C3	−2.9  ± 0.7	2.2  ± 0.6	42.1  ± 0.6	−0.21  ± 0.16	G2⋅C19	11.5  ± 3.2	−0.8  ± 1.6
C3-A4	4.5  ± 0.9	4.6  ± 0.7	30.0  ± 0.7	−0.78  ± 0.23	C3⋅G18	−0.4  ± 2.0	−6.1  ± 1.6
A4-A5	−3.9  ± 1.0	−5.5  ± 0.2	35.3  ± 0.5	−0.48  ± 0.16	A4⋅T17	12.0  ± 1.6	−11.5  ± 2.1
A5-A6	0.0  ± 1.1	4.2  ± 0.2	40.3  ± 0.6	−1.29  ± 0.24	A5⋅T16	19.2  ± 1.0	−6.3  ± 1.1
A6-A7	−6.0  ± 0.5	2.2  ± 0.2	39.5  ± 0.2	0.61  ± 0.04	A6⋅T15	15.8  ± 0.5	−9.4  ± 0.6
A7-C8	−1.7  ± 0.7	−4.6  ± 0.3	38.7  ± 0.9	−0.85  ± 0.22	A7⋅T14	15.2  ± 0.7	−17.3  ± 0.5
C8-G9	0.4  ± 2.8	4.6  ± 0.5	38.9  ± 1.3	−0.20  ± 0.41	C8⋅G13	−9.4  ± 0.6	−12.3  ± 1.6
G9-G10	5.9  ± 2.3	−2.0  ± 1.7	37.3  ± 1.3	−0.03  ± 0.57	G9⋅C12	−11.9  ± 3.2	1.2  ± 6.0
					G10⋅C11	−22.4  ± 1.4	−7.1  ± 1.3

Calculated with 3DNA. A-tract parameters are shown in bold. Errors represent standard deviations of the mean. 

Global Bend Magnitude and Direction.

To facilitate comparison with cyclization kinetics experiments (where global curvature is modeled as a vectorial sum of roll and tilt), global bend direction and magnitude were calculated using the program madbend. madbend calculates global roll (Θ_R) and global tilt (Θ_T) with respect to a specified reference plane from an input file with values of local helical roll, tilt, and twist. Because of end effects, only the inner 8 bp were included in the calculation of the overall bend. The average bend magnitude of the inner 8 bp of the 10 best A4 structures is ≈9.0 ± 1.3° into the minor groove in a reference frame exactly at the A6⋅T15 base pair (Table 4). This is in excellent agreement with the 9.4 ± 1.5° bend into the minor groove in a reference frame displaced 0.3 bp from the A6⋅T15 base pair obtained from our preliminary cyclization kinetics assay (Y. Zhang, A.B., and D.M.C., unpublished results). Based on a quadratic relation between bend magnitude and gel electrophoretic mobility (37), an A₄-tract should be bent by ≈11.5 ± 1°. Within the error, this value is consistent with the results observed in this work. Contributions to curvature can be explained by examining roll and tilt while assuming a helical repeat of ≈10 bp per turn (close to our experimental value of 9.5 bp per turn). Clearly, roll and tilt from several steps contribute to the bend (Fig. 2A). Contributions from roll come from small degrees of negative roll at A4-A5 (−3.9°) and A6-A7 (−6.0°) steps. Negative roll means bending into the minor groove, so these bends are in phase with the expected overall bend (into the minor groove approximately at the center of the A-tract; see text below). The average roll inside the A-tract is −3.3°. Tilt also contributes to the bend. Both positive tilts at the G2-C3 (+2.2°) and C3-A4 (+4.6°) steps are in phase with the overall bend, as is the negative tilt at A7-C8 (−4.6°). Negative tilt inside the A-tract at the A4-A5 step (−5.5°) and positive tilt at A5-A6 step (+4.2°) oppose the overall bend. Overall, contributions from tilt to the overall bend are quite significant. The contribution of the A4-A5, A5-A6, and A6-A7 dinucleotide steps in the A-tract to the overall bend is 4.0° into the minor groove in a coordinate frame located 0.3 bp between A6 and A7 base pair steps.

Table 4.

Comparisons of bend magnitudes and directions for A4 (inner 8 bp)

	Bend magnitude, °	Bend position, bp*
Method
NMR	9.0 ± 1.3	6.0 ± 0.4
Cyclization kinetics†	9.4 ± 1.5	6.3 ± 0.2
Long-range models
Junction model‡	11.6	6.1
Nearest-neighbor models
Bolshoy et al. (38)‡	20.9	5.2
De Santis et al. (39)‡	15.9	5.3
Gorin et al. (40)‡	13.6	2.9

NMR and cyclization kinetics are experimentally determined values. Bends from NMR structures and predictive models were calculated using madbend. Errors were estimated from standard deviations of the mean. 

^*Bend position indicates the location of the coordinate frame where the bend is into the minor groove. Numbering is with respect to the 10-mer, with the first G⋅C basepair having the value 1.0 and the last 10.0. 

^† Preliminary results (Y. Zhang, A.B., and D.M.C., unpublished results). Errors were estimated from reproducibility of kinetic data. 

^‡ Prediction of a model. 

Discussion

Evaluation of Bending Models.

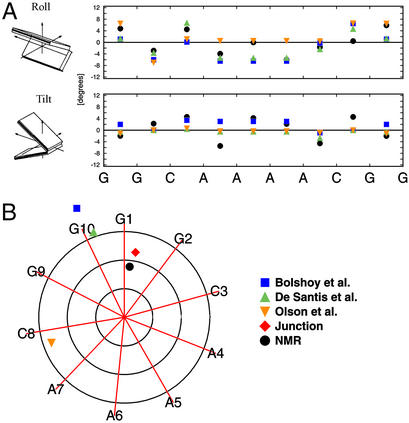
Two types of A-tract bending models have been proposed in the literature: nearest-neighbor (wedge) and long-range (cooperative; e.g., the junction model). Nearest-neighbor models [e.g., that of Bolshoy et al. (38), De Santis et al. (39), and Gorin et al. (40)] assume that local structure is not affected by any long-range effects. Because of their nature, none of the dinucleotide models can predict the changes of tilt and roll within identical A-A steps in the A-tract. Most of the models, however, do quite well in the G-C, C-A, and A-C steps (we omit G-G steps because of the inability of NMR to provide reliable parameters for terminal base pairs). The models of Bolshoy et al. (38) and De Santis et al. (39), which are derived on the basis of theory and gel electrophoretic mobility data, seem to better fit our experimental parameters than the model of Gorin et al. (40), which is derived from a database of DNA crystal structures (Fig. 3A). Contributions to the global bend of our NMR structures come from the tilt close to the junctions of the A₄-tract. In addition, the negative roll in the A-tract is in-phase with the net contribution from tilt; they all produce a bend with a net direction of roll into the minor groove at the center of the A-tract. This explanation is consistent with the junction model of Koo et al. (37, 41), which explains the bend as a deflection of the helical axis in the direction of tilt at the junctions of the A-tract, with an additional contribution from a deflection in the direction of roll at the 5′ end. The junction model does not explicitly require bends such as negative roll in the A-tract; one must remember that it predicts overall geometry of the molecule only and is therefore only modeled by helix axis deflections at the junctions.

Figure 3.

Comparisons of experimental results with predictions of various models (for identical inner 8 bp of the A4 sequence). (A) Local helical parameters. (B) Global bend magnitudes and directions. Axes point in the direction of major groove at each base pair. Circles represent bends of 5, 10, and 15°. Global bends were modeled with madbend (36).

Dinucleotide and junction models can be used to calculate overall magnitude and direction of DNA curvature with madbend (36). The bend magnitude (11.6°) and direction (6.1 bp) predicted by the junction model are closest to the bend obtained both from NMR data (9.0° at position 6.0 bp) and cyclization kinetics assay (9.4° at position 6.3 bp) (Fig. 3B, Table 4). Of the dinucleotide models, the model of De Santis et al. (39) comes closest to the proper bend direction, but overestimates the magnitude by almost 7°, whereas the similar model of Bolshoy et al. (38) overestimates the bend magnitude by almost 12°. The crystal structure model of Gorin et al. (40) misses the direction of the bend by >90°, and the magnitude of the bend (13.6°) is ≈5° too large. This should not come as a surprise given that most x-ray crystal structures of A-tract DNA oligomers have exhibited a bend direction that is 90° or more away from the bend observed in solution.

Delocalized Bend Model.

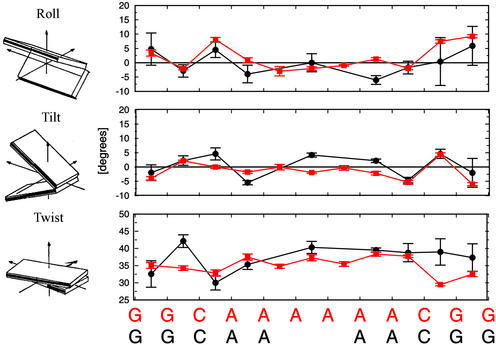
Because there is no decisive helical parameter that causes the bend in the molecule, we support a model that combines ideas contained in the wedge and junction models and was first proposed by Crothers and Shakked (1). This model explains A-tract curvature as being delocalized. It is a result of phased combinations of roll (negative inside the A-tract and positive outside the A-tract) and tilt (positive near the 5′ junction and negative near the 3′ junction). Because roll and tilt have several positive and negative components of relatively small magnitudes that all contribute to the bend, we call this the delocalized bend (DB) model. This DB model is also supported by a recent NMR structure of an A₆-tract (A6) (42). Using our structure analysis methodology (3DNA/madbend), we find the inner 10 bp of this dodecamer to be bent by 15.7° into the minor groove between the third and fourth A⋅T base pairs. The A6 molecule shows large contributions to the bend from the positive roll (+8.1°) at the 5′ junction of the A-tract and at the C10-G11 step (+7.4°). The average roll within the A-tract is −0.8°. Contributions from helical tilt are smaller than in A4, with a small contribution from positive tilt near the 5′ junction (+2.1°) at the G2-C3 step and negative tilt at the A8-A9 (−2.2°) and A9-C10 (−5.4°) steps, at and near the 3′ junction. If this negative tilt at the A9-C10 step is combined with the positive tilt at the C10-G11 step (+4.3°), it produces a net bend in the direction of the minor groove near the center of the A-tract (Fig. 4). In A4, roll components produce a bend of 7.5° into the minor groove at position 6.3 bp, whereas the tilt components add up to a 2.2° bend into the minor groove at position 5.2 bp. Similarly, roll in A6 produces a bend of 9.9° into the minor groove at position 6.7 bp, whereas tilt components add to a 7.6° bend into the minor groove at position 5.2 bp. Directions of roll-only and tilt-only contributions to the bend flank the overall bend directions for both A4 and A6. Although major single-step contributions from tilt and roll are of different magnitudes in A4 and A6, this should not come as a surprise because the A-tracts are of different lengths (A₄ vs. A₆). This requires different phasing of tilt and roll components with respect to the A-tract and a difference in overall bend magnitude of ≈7°.

Figure 4.

Comparisons of local base pair parameters of A4 (black circles) and A6 (red squares) (42) structures. Values of the A4 decamer have been translated onto the A6 dodecamer. All parameters were calculated with 3DNA (28).

Although it is reassuring that NMR yields a structure for A4 whose global properties are in good agreement with gel electrophoretic and cyclization kinetic determinations of curvature and bend direction, an important generalization remains poorly understood: Why is it that the curvature induced by A-tracts depends so little on the nature of the sequences that separate the A-tracts (43)? It appears that some feature of A-tracts gives them a dominant influence over structure in adjacent sequences. Candidates for this role include the extensive buckle in the A-tract and the abrupt change in buckle at the junctions, particularly at the 3′ end. Narrowing of the minor groove at the 3′ end could also contribute. Further work is needed to provide a basis for this general phenomenon.

Coordinates.

Coordinates for the 10 lowest-energy A4 structures have been deposited in the Protein Data Bank (PDB ID code 1NEV).

Abbreviation

A-tract

adenine tract