A Probabilistic Model of Glenohumeral External Rotation Strength for Healthy Normals and Rotator Cuff Tear Cases

Abstract

The reigning paradigm of musculoskeletal modeling is to construct deterministic models from parameters of an “average” subject and make predictions for muscle forces and joint torques with this model. This approach is limited because it does not perform well for outliers, and it does not model the effects of population parameter variability. The purpose of this study was to simulate variability in musculoskeletal parameters on glenohumeral external rotation strength in healthy normals, and in rotator cuff tear cases using a Monte Carlo model. The goal was to determine if variability in musculoskeletal parameters could quantifiably explain variability in glenohumeral external rotation strength. Multivariate Gamma distributions for musculoskeletal architecture and moment arm were constructed from empirical data. Gamma distributions of measured joint strength were constructed. Parameters were sampled from the distributions and input to the model to predict muscle forces and joint torques. The model predicted measured joint torques for healthy normals, subjects with supraspinatus tears, and subjects with infraspinatus–supraspinatus tears with small error. Muscle forces for the three conditions were predicted and compared. Variability in measured torques can be explained by differences in parameter variability.

INTRODUCTION

Healthy normal subjects demonstrate remarkable variability in maximum glenohumeral external rotation strength. For example, the standard deviation of external rotation strength can be 41% of the mean.³³ Additionally, with rotator cuff tear there is variability in the amount of strength deficit which appears to depend on factors other than cuff tear size.^{12,13,40,41,74} Current musculoskeletal modeling paradigms have been unable to explain the variation in strength, or the strength deficit. Observations of musculoskeletal parameters also exhibit variability.^1,6,61,77 One might hypothesize that the variation in strength can be explained via quantifiable differences in musculoskeletal parameter variability, specifically physiologic cross-sectional areas (PCSA), moment arms and the muscle length–tension relationships.

The historical approach to musculoskeletal modeling has been to construct deterministic models from parameter means of a sample assumed to be representative of the general population. Deterministic models have been made for many joint systems including the hand,¹⁷ elbow,^11,34,54 shoulder,^28,76 spine,^18,26,73 and lower extremity.^31,39,49,69 Such models have been used with great success to predict joint torques and muscle forces for the “average” subject. However this approach does not reflect the inherent variability in musculoskeletal parameters which ultimately results in variability in muscle force and joint strength. Consequently, it is questionable how well these models predict muscle forces and joint torques across the population, in particular for subjects quite different than the sample mean.

Monte Carlo methods are a means for modeling naturally occurring variability and uncertainty in a population. A few Monte Carlo models have been developed to model biomechanical and musculoskeletal phenomena,^{14,20,32,55,56,59,75} but such work has been limited. Monte Carlo methods utilize input parameter distributions to model intersubject variability, and therefore provide distributions of output values. Monte Carlo simulations are useful because the distribution of muscle forces in a population can be predicted. Muscle–force distributions are necessary for understanding the mechanical and biological responses to external loads placed on the human body. The question of why some athletes or laborers develop pathologies like rotator cuff tendon tear while performing a task, while others executing the same task do not develop the pathology, has not been answered with deterministic models based on average parameter data. Subject specific models could potentially answer these questions,³ but require large numbers of subjects to understand the affects of variability across the population. Such large studies are costly in terms of time and experimental involvement. Furthermore, another strength of Monte Carlo methods is that the limitations of traditional methods utilizing average values are avoided,⁷⁵ and conclusions can be made concerning output probability.

The purpose of this study was to probabilistically simulate the effects of variability in PCSAs, moment arms and the muscle length–tension relationships on predicted muscle forces and joint torque. The aim was to develop a model tuned to available data for glenohumeral external rotation strength and, if the model predicts the torques with small errors, then there is potential for predicting and analyzing muscle force distributions in different populations. Additionally, simulations such as this may help describe why some subjects retain strength in the presence of rotator cuff tear, while other subjects do not maintain strength, and may help guide clinical management of cuff tear injuries.

There were three objectives for this study: (1) to develop a stochastic model of isometric glenohumeral external rotation; (2) to tune the model to predict isometric external rotation torques, and to compare predicted and measured torques; and (3) to estimate and compare external rotation muscle force distributions for normal subjects and for subjects with supraspinatus, and infraspinatus–supraspinatus rotator cuff tears.

METHODS

Variability in musculoskeletal parameters and their effects on glenohumeral external rotation strength in healthy normals and in rotator cuff tear cases was simulated using a Monte Carlo model (Fig. 1). Multivariate Gamma distributions were generated from summary statistics of empirical moment arm, PCSA, and the muscle length–tension dependencies (Fig. 1A). Gamma distributions for joint strength were constructed from external rotation joint strength also measured in the laboratory (1B). Predicted muscle force and joint strength relationships described in the text were used to make predictions from parameters sampled from the distributions (1C). Muscle specific tension was predicted for the healthy normal case by sampling from the distributions and using a least squares method to minimize the sum of squared errors between measured and predicted strength (1D). A nonparametric 95% confidence interval adjustment of PCSA input distributions was used to ensure measured and predicted torques matched for the two rotator cuff tear cases (1E). Muscle forces and joint strength distributions were then predicted with the model for the healthy normal case, for isolated supraspinatus tear, and for supraspinatus with infraspinatus tear (1F).

FIGURE 1.

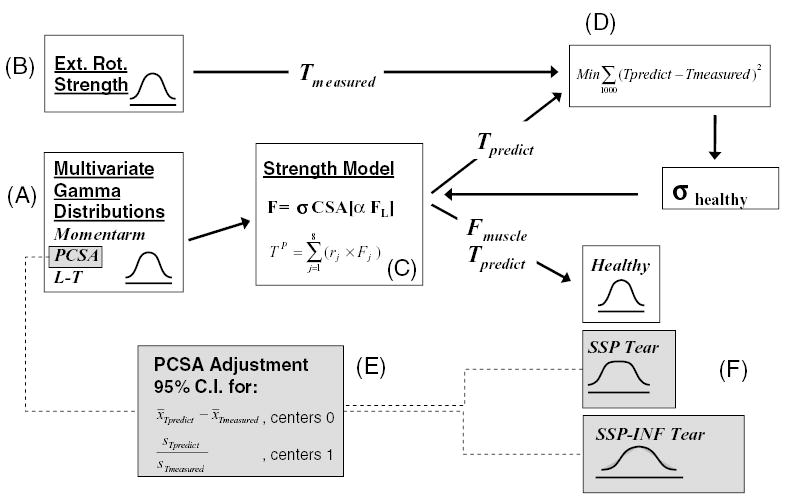
Diagram depicting the Monte Carlo model. (A) Multivariate Gamma distributions generated from summary statistics of moment arm, PCSA, and the muscle length–tension dependencies measured in our lab. (B) Gamma distributions for joint strength constructed from measured external rotation joint strength. (C) Predicted muscle force and joint strength relationships described in the text. (D) Muscle specific tension predicted for the healthy normal case (and assumed for all cases) using the method of Chang et al.¹⁴ (E) The nonparametric 95% confidence interval adjustment of PCSA input distributions to ensure measured and predicted torques matched for the two rotator cuff tear cases. (F) Muscle force and joint torque distributions predicted with the model for the three cases.

Musculoskeletal Model

An isometric model of glenohumeral external rotation was developed that simulates maximum isometric external rotation strength for the position of 15° humeral abduction at neutral glenohumeral rotation. This position was chosen because it is relevant for functional activities, is easily testable and frequently tested in a clinical setting, and is a position for which isometric strength data is available. Three agonist muscles are included: supraspinatus, infraspinatus and teres minor. Infraspinatus was represented with four subregions, supraspinatus with three subregions, and teres minor as one subregion (Fig. 2). The isometric force and torque-generating capacity of these muscles/subregions were described by the physiologic cross-sectional area, the length–tension relationships, and muscle moment arms from empirical data collected in our laboratory.^44–46

FIGURE 2.

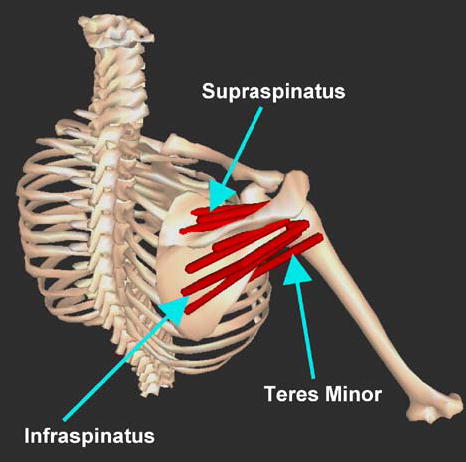
Muscles simulated in this model. Individual muscles/subregion paths are depicted as red segments; Supraspinatus: three subregions, infraspinatus: four subregions, teres minor: one region.

Glenohumeral external rotation joint torque (T^P) was predicted with a biomechanical model as the summation of the products of muscle moment arm (r_j) and muscle force (F_j) at the joint angle position simulated in this study:

$$T^{\text{p}}=\sum _{j=1}^8(r_j\times F_j)$$ (1)

Muscle force was modeled as a function of the current muscle length, the level of neuromuscular activation (α), muscle physiologic cross-sectional area (PCSA), and muscle specific tension (σ) [Fig. (1C)]. Eq. (2) represents the dependence of muscle force on these factors. Formulations from the literature⁸² are used to model the dependency of active muscle force (F_L) on muscle length.

$$F=\sigma \text{PCSA}[\alpha \hspace{0.17em}{F}_{\text{L}}]$$ (2)

The level of neuromuscular activation was fixed at unity since strength measurements, described in the next section, were obtained at conditions of maximum voluntary isometric contraction. Tendons were modeled as inelastic which is a reasonable assumption for an isometric model at one joint angle position. Incorporation of tendon stiffness results in maximum tendon strain of 3.3%,⁸² and 1.99–3.68%⁵⁰ at maximum isometric muscle force. Chang et al., 1999¹⁵ found the discrepancy in muscle strain to be less than 3% when tendon was modeled as elastic versus inelastic. For the muscles modeled here which are operating near the peak of the length–tension curve (normalized force approximately 0.9) a nominal muscle strain discrepancy of 3% introduces an error of less than 5% for muscle force.

Strength Data

Isometric external rotation strength data for healthy normals,³³ and for patients with rotator cuff tears (unpublished data) was collected in the laboratory. The data collected on rotator cuff tear patients was collected by the same authors (Biomechanics Laboratory, Mayo Clinic, Rochester, MN), under the same conditions as the healthy normal data. All data were collected with an institutional review board approved protocol. In each study, strength was measured with a Cybex II isokinetic dynamometer (Cybex, Ronkonkoma, New York). During testing, the elbow was flexed to 90° and secured with an Orthoplast splint (AliMed Inc., Dedham, Massachusetts) to allow measurement of isolated glenohumeral strength. One-hundred and twenty subjects (60 men and 60 women, mean 44, SD: 15 years) were tested for the healthy normal case, and 46 subjects (34 men, 12 women, mean: 59, SD: 11 years) were tested for the cuff tear cases. Of the 46 subjects with cuff tears, 41 tears were full thickness tears, five tears were partial thickness. Isolated supraspinatus tears were present in 23 subjects, and 23 subjects had combined supraspinatus and infraspinatus tears established via intraoperative observation.

Monte Carlo Simulation

Variability in musculoskeletal architecture and muscle moment arm were modeled as random variates with a Monte Carlo method (Fig. 1). Summary statistics of empirical data collected in our lab^44–46 were used to construct multivariate Gamma probability distributions. Muscles and tendons of supraspinatus and infraspinatus were subdivided into three and four equal width regions respectively. Excursions of these tendon subregions and teres minor were measured for full ranges of rotation on 10 independent glenohumeral cadaver specimens with the humerus abducted in the scapular plane at the position simulated with this model. Moment arms were determined from tendon excursion via the principle of virtual work.² On the same 10 specimens, muscle fascicle lengths, sarcomere lengths, pennation angles, and muscle volumes were measured. From these parameter measurements and tendon excursions, optimal fascicle length, physiological cross-sectional area (PCSA), and muscle length–tension dependence were calculated. Summary statistics of these parameters are reported in Table 1 (healthy normal case).

TABLE 1.

Musculoskeletal input parameters (mean and SD).

	Healthy normal			Supraspinatus tear	Infraspinatus–supraspinatus tear
	Moment arm (cm)	Normalized muscle force	PCSA (cm2)	PCSA (cm2)	PCSA (cm2)
Anterior-SSP	−0.19 (0.15)	0.94 (0.07)	1.36 (0.40)
Middle-SSP	0.27 (0.24)	0.94 (0.08)	1.27 (0.34)
Posterior-SSP	0.76 (0.45)	0.94 (0.08)	0.97 (0.40)
Superior-INF	1.51 (0.27)	0.90 (0.10)	1.83 (0.66)	0.89 (0.77)
Sup.Mid.-INF	1.58 (0.27)	0.89 (0.08)	1.80 (0.73)	0.88 (0.84)
Inf.Mid.-INF	1.97 (0.27)	0.91 (0.08)	2.08 (0.92)	1.02 (1.07)
Inferior-INF	2.04 (0.40)	0.93 (0.06)	1.47 (0.51)	0.72 (0.59)
Teres minor	1.43 (0.39)	0.96 (0.06)	2.02 (0.80)	0.99 (0.93)	3.90 (2.41)

Note. Parameters for the healthy normal case were measured in our laboratory from 10 cadaver specimens. Moment arms and normalized muscle force (from calculated muscle length–tension relationships) were for the position simulated with this model. Covariance between moment arm, PCSA and normalized force was determined and used to model multivariate gamma input distributions formed from the mean and standard deviation of measured parameters. PCSA for the tear cases are the values for which the model was tuned to make measured and predicted torque distributions equivalent (p > 0.05).

Because natural correlation exists among PCSA, the muscle length–tension relationship and muscle moment arms, parameter covariance was established by calculating covariance matrices of PCSA, normalized muscle force, and muscle moment arm. Frequently, the calculated covariance matrix was nonpositive definite. With small sample size, sample covariance may be nonpositive definite due to mere sampling fluctuation. An additional more likely cause of nonpositive definiteness is colinearities between vectors of the data from which the covariance is calculated. The colinearities result in a covariance matrix which lacks information, is mathematically rank deficient, and cannot be inverted. Nonpositive definite covariance matrices were made positive definite by smoothing. Ridge smoothing was accomplished by adding 10% to the diagonal terms.⁸⁰ Multivariate parameter distributions were generated with the positive definite covariance matrix [Fig. (1A)].^22,37,58 The covariance of the resulting multivariate distributions were asymptotic to empirically determined covariance with sample size. At small sample size, covariance of the model generated distribution did not match empirical covariance, but as sample size approached infinity, the empirical covariance was attained. At sample size of 1000, modeled and empirical covariances were identical and any additional samples did not increase agreement. Mean and variance of the generated distributions exactly matched summary statistics of the empirical data. Equivalency of the generated distributions and the empirical data were assessed with Komolgorov–Smirnov goodness-of-fit tests and were always equivalent (p > 0.05).

Since glenohumeral external rotation strength also exhibits variability among subjects, measured torque was also modeled as a random variate. Gamma probability distributions were constructed from summary statistics for strength from sources described earlier [Fig. (1B)]. Gamma distributions were chosen because, while exact distributions are unknown, PCSA, moment arm, normalized muscle force, and glenohumeral external rotation strength are all nonnegative. Two rotator cuff tear cases were simulated in this study; supraspinatus tendon tear, and infraspinatus with supraspinatus tendon tear. The mean strength losses were 51 and 64% for the two cases, respectively (Fig. 3). Cuff tears were mathematically induced by setting PCSA for the involved muscles equal to zero. The mean and variance of constructed gamma strength distributions matched the mean and variance of measured strengths (Fig. 3), and Komolgorov–Smirnov goodness-of-fit tests failed to detect differences between measured strength data and constructed strength distributions (p > 0.05).

FIGURE 3.

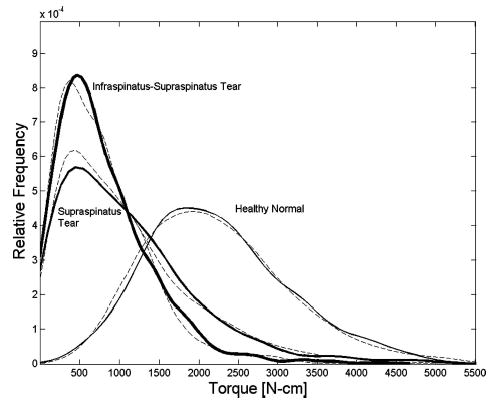
Probability distribution of measured (dashed lines) and predicted (solid lines) external rotation strength. Measured joint strength: Healthy normal (mean: 22.0, SD, 9.0 N m), 60 male, 60 female. Supraspinatus tear (mean: 10.8, SD, 8.5 N m). 16 male, 7 female. Infraspinatus–supraspinatus tear (mean: 7.9, SD, 6.1 N m), 18 male, 5 female.

A random number generator chose samples from the distributions for musculoskeletal parameters and measured torques. All simulations and data analysis were performed with the statistics toolbox in Matlab 6.5 (Mathworks, Natick, MA). The simulation was conducted for the healthy normal case and the cuff tear cases. This modeling and simulation was conducted in three phases: model tuning, muscle specific tension prediction, and muscle force prediction. Specific tension and muscle forces were predicted in the manner of Chang et al.¹⁴ [Fig. (1D)], by first sampling from the distributions and using a least-squares method to minimize the sum of squared errors between measured and predicted strength in order to predict specific tension, and then re-sampling from the distributions and using the predicted specific tension to predict muscle forces.

Specific Tension Prediction

Muscle-specific tension was determined for the healthy normal case [Fig. (1D)]. In the manner described earlier, samples were selected at random from input parameter distributions and used to predict muscle forces and external rotation torques resulting in a distribution of 1000 samples of predicted external rotation strength. Specific tension was assumed equal for all muscles, and was the least-squares solution to the problem of minimizing RMS error between the predicted torque distribution and a distribution of 1000 torques sampled from the measured torque distribution. Specific tension for the cuff tear cases was assumed equal to healthy normal specific tension. Following specific tension prediction a nonparametric two-sided Wilcoxon rank sum test was performed to test if there was a difference between median measured and predicted torques. Equivalency of the predicted and measured torque distributions were tested with a Komolgorov–Smirnov (K–S) goodness-of-fit test. These tests were performed for each of the three cases.

Model Tuning

For the healthy normal cases no model tuning was necessary or conducted since the confidence intervals constructed included the target difference and ratio respectively. For the cuff tear cases, the model was tuned by adjusting model input parameters to match predicted torque to empirical measurements of glenohumeral external rotation torque. These techniques are commonly utilized in discrete event simulation⁴⁷ to equate a model and a real-world system. Muscle architecture and moment arms were randomly chosen from the distributions and input to the muscle force and joint torque models to predict muscle forces and glenohumeral external rotation torque. Because the model and the system under consideration are inherently not the same,⁴⁷ the means of measured and predicted torques and their distributions were evaluated for equivalency with a confidence interval approach [Fig. (1E)]. One hundred distributions for predicted and measured torque were constructed, each distribution consisting of 1000 torque samples. Predicted and measured torque distributions were compared by forming 95% nonparametric confidence intervals (CI) for the difference in means, and ratio of standard deviations for the healthy normal and cuff tear cases, respectively. For the supraspinatus tear case, mean and standard deviations for PCSA of all remaining muscles were iteratively decreased (mean), and increased (SD) until the CI for the difference in means centered zero Newton-meters, and the CI for the ratio of standard deviations centered unity, within the confidence intervals. For the infraspinatus–supraspinatus tear case, the teres minor mean and standard deviation of PCSA were both iteratively increased. RMS error between the measured and predicted torque distributions was also drastically reduced via this tuning process.

Muscle Force Prediction

Following determination of a tuned model with known specific tension which predicted joint torque distributions equivalent to measured torque, the model was used to predict muscle forces for another 1000 iterations of the simulation for the healthy normal case and supraspinatus and infraspinatus–supraspinatus tear case, respectively [Fig. (1F)]. To assess normality of muscle force distributions, K–S tests were used to compare each force distribution to a normal distribution with the same mean and variance. Sample size of each distribution was equal to avoid inflating degrees of freedom for the test. Muscle forces for the healthy normal and cuff tear cases were compared by utilizing two-sided Wilcoxon rank sum tests to test for differences in median muscle forces, and K–S tests were applied to test for differences in muscle force distributions.

RESULTS

Following determination of specific tension, no input parameter tuning was performed for the healthy normal case because measured and predicted torque distributions, as well as mean torques, were identical. For supraspinatus tendon tear, mean PCSA in the remaining muscles was decreased by 51%, and the standard deviation of PCSA was increased by 16% to match predicted torque distribution to the measured distribution. With infraspinatus–supraspinatus tendon tear, mean PCSA of the remaining muscle, teres minor, was increased 93%, and the standard deviation of teres minor PCSA was increased by a factor of 3 in order to predict the measured external rotation distributions (Table 1). For the healthy normal case summary statistics for moment arms and the normalized force from the length–tension relationship (Table 1) were equal to measurements made in our lab. Confidence interval widths for the difference in mean measured and predicted torques were 0.12, 0.09, and 0.09 N m wide for the healthy normal, supraspinatus, and infraspinatus–supraspinatus tear cases respectively. The confidence interval widths for the ratio of measured and predicted standard deviations were 0.13, 0.15, and 0.17 wide, respectively.

Muscle specific tension for the healthy normal case determined with the least squares approach was 1.43 MPa, and was assumed for the cuff tear cases. Equivalent distributions for predicted and measured torques were determined with RMS error of 0.10 N m (Fig. 3) for the healthy normal and cuff tear cases. The Wilcoxon rank sum tests indicated that median predicted and measured torques were not significantly different for the healthy normal (p = 0.5), supraspinatus tear (p = 0.8), and infraspinatus–supraspinatus tear (p = 0.7) cases. Furthermore, distributions of predicted and measured joint torque were not significantly different for the healthy normal (p = 0.8), supraspinatus tear (p = 0.7), and infraspinatus–supraspinatus tear (p = 0.4) cases.

With supraspinatus tear, muscle forces in all regions of infraspinatus and teres minor were reduced as compared to the healthy normal cases (Fig. 4). For the infraspinatus–supraspinatus tear case, teres minor force was elevated compared to healthy normal. Muscle forces for the healthy normal case were normally distributed (p > 0.05), except for posterior supraspinatus (p = 0.02). Conversely, force distributions for both cuff tear cases were not normally distributed (p < 0.001). Muscle force distributions were significantly different (p < 0.001) between the healthy normal and rotator cuff tear cases (Fig. 4). Median forces for all muscles were significantly different (p < 0.001) between the healthy normal and rotator cuff tear cases (Table 2).

FIGURE 4.

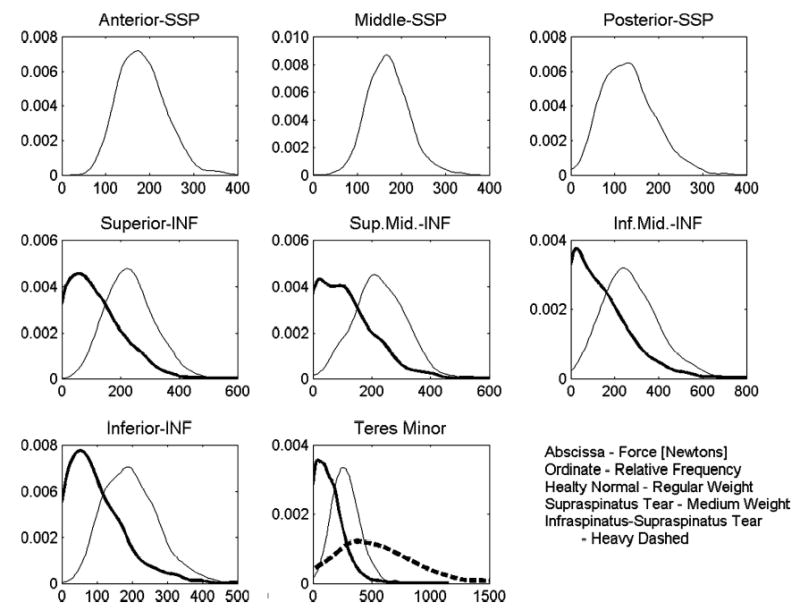
Probability distribution of muscle forces for the healthy normal, supraspinatus tendon tear, and infraspinatus–supraspinatus tendon tear cases.

TABLE 2.

Predicted glenohumeral external rotation muscle forces (Newtons) (median and SD).

	Healthy normal	Supraspinatus tear	Infraspinatus–supraspinatus tear
Anterior-SSP	177.3 (52.9)
Middle-SSP	168.2 (46.5)
Posterior-SSP	128.2 (59.8)
Superior-INF	228.9 (83.2)	96.8 (92.7)
Sup.Mid.-INF	222.4 (87.4)	98.5 (95.8)
Inf.Mid.-INF	260.0 (128.4)	110.8 (141.3)
Inferior-INF	191.1 (77.7)	80.2 (85.2)
Teres minor	271.8 (117.2)	119.1 (126.9)	503.9 (344.6)

Probabilities that muscle forces for the supraspinatus tear case were less than the median muscle forces for the healthy normal case are 0.88, 0.86, 0.83, 0.88, and 0.88 for superior infraspinatus, superior middle infraspinatus, inferior middle infraspinatus, inferior infraspinatus and teres minor, respectively. For the infraspinatus–supraspinatus tear case, the probability that teres minor force is greater than the median healthy normal teres minor force, (271.8 N) is 0.79 (Fig. 5).

FIGURE 5.

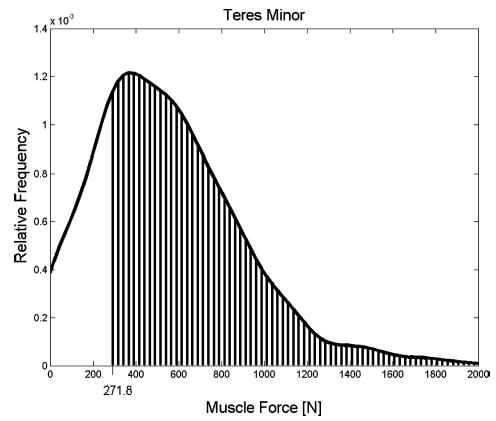
The probability that teres minor muscle force for the infraspinatus–supraspinatus tear case exceeds the median force for the healthy normal case is 0.79, and is depicted graphically as the area under the probability distribution greater than 271.8 N.

DISCUSSION

In this study a probabilistic model was used to predict measured torque distributions with small error. For the healthy normal case predicted torque distributions matched measured distributions of torque with no tuning of input parameters aside from determination of specific tension. The strong agreement between measured and predicted torque distributions illustrates how variability of muscle architecture and moment arm can explain variability in glenohumeral external rotation strength as measured in healthy normal subjects. This result demonstrates strong potential for utilizing probabilistic musculoskeletal models to predict muscle forces for two different populations.

For rotator cuff tears, the model was tuned by adjusting the distributions for muscle physiologic cross-sectional area in order to predict torque distributions with small error. For the supraspinatus tear case the PCSA was reduced by an average of 51%. Such a decrease in PCSA explains reduced ability of the infraspinatus and teres minor to generate force. Reduced muscle force capacity of these muscles of course translates to reduced external rotation strength and a disruption of the force balance necessary for maintaining static equilibrium of the humeral head relative to the glenoid. For the infraspinatus–supraspinatus tear case mean PCSA was increased by 93%. The increase in teres minor PCSA results in increased force required for generation of measured external rotation strength. Looking at the distributions of predicted muscle forces one can see that with infraspinatus tendon tear, the median muscle force in the remaining muscles is reduced compared to healthy normals. Additionally, the model in this study allows for the calculation of the probabilities that muscle forces for tear cases are different than muscle forces for healthy normals. The model predicts high probability that infraspinatus forces are reduced compared to healthy normals in the case of supraspinatus tendon tear. Likewise, for the infraspinatus–supraspinatus tear case the model predicts high probability of greater teres minor muscle force as compared to the healthy normal force. Results or insights such as these are previously un-elucidated utilizing deterministic models based on average or subject specific parameters, and highlight some strengths of stochastic modeling.

The parameter variability found via the tuning process is not known to be exact, but presents intriguing questions given the probabilistic nature of measured parameters. In the future it would be interesting to measure these, and other parameters, in healthy normal subjects and subjects with pathological conditions in order to better understand parameter variance. Measurement of parameters for estimating muscle force and torque generating capacity, particularly the muscle length–tension relationship, has primarily occurred in cadaveric models.^51,61 However, in vivo methods have recently been developed which approach the ability to measure the parameters for representing relationships modeled here.^5,67 This study is the first to quantify the effects of muscle architecture and moment arm variability on muscle strength. With advances in imaging techniques it might one day be possible to measure these parameters in vivo. The methodology utilized here can quantify the effects of parameter variability when such data becomes available. Additionally, it would be interesting to simulate alterations in other parameters such as moment arm and muscle length–tension relationships in a manner similar to how muscle hypertrophy/atrophy was simulated here. However, in this model we did not simulate these parameter changes with cuff tear because there is not experimental or clinical evidence for these alterations at the present time.

The result of this study that muscle PCSA for the supraspinatus tear case was reduced agrees with clinical findings following cuff tear with degradation of rotator cuff muscles due to muscle atrophy via fatty infiltration.^57,63,72 Of course, some period of time is necessary following injury for the atrophy to appear. Clinically, infraspinatus degradation can occur in supraspinatus tendon tear cases even if the infraspinatus tendon is intact.²⁵ This model supports clinical observations. Additionally, the reduction in infraspinatus PCSA and force is suggestive of reduced ability of infraspinatus to generate inferiorly directed force necessary to resist superior humeral head superior translation and impingement with the acromion in the case of supraspinatus tendon tear.⁷¹

For the infraspinatus–supraspinatus tear case, the data are more limited. However, the model developed here supports clinical observations in some patients with supraspinatus and infraspinatus tendon tear. Hypertrophy of teres minor allows for retention of some external rotation strength in patients with the dual tear case, and has been linked to patients who are able to function in the presence of dual cuff tear.⁷⁸ Biomechanically, in healthy normal subjects, teres minor contributes about 50% to external rotation strength.¹⁹ Hypertrophy of teres minor might allow patients to present relatively normal or minimal reduction in external rotation strength with infraspinatus–supraspinatus tendon tear as was modeled here.

A strength of this model is the consideration of correlations among muscle architecture and moment arm. In this simulation correlation between PCSA, moment arms, and the muscle length–tension relationship was incorporated by utilizing multivariate distributions to model these parameters. Use of multivariate distributions requires original empirical data for calculation of covariance, or access to determined parameter covariance. During the model development phase a univariate model, in which covariance among input parameters was ignored, was constructed and used to make predictions for the healthy normal case. The univariate model predicted a joint torque distribution with standard deviation of one-half the measured torque standard deviation, but with identical means for predicted and measured torques. From this result it can be concluded that covariance is important for realistically modeling input parameters in order to build a valid model which predicts torque distributions matched to measured distributions for the real-world system. This finding is in agreement with others who found that multivariate distributions contain important information, and therefore perform better than univariate input distributions when attempting to predict distributions of muscle forces and joint torques.^32,58 Measurements of muscle architecture and moment arms in vivo and in cadavera have begun to address issues of parameter covariance.^30,62,79

Several limitations exist in this study. We assumed that all contractions were conducted under conditions of 100% muscle activation. It is possible there exists some variability in muscle activation even under conditions of maximum exertion. Incorporation of an EMG-Activation model would be a reasonable improvement given limited availability of EMG data.⁷⁰ However deterministic musculoskeletal models commonly assume 100% muscle activation when EMG data were not recorded.^38,64,76 For our isometric stochastic model, the order of magnitude of errors associated with this assumption is comparable. An additional limitation of this simulation is that we did not model the effect of age, or control for the effect of gender on external rotation strength. Each of these variables could be controlled for using a normalization procedure, or by incorporating age and gender as multivariate model input parameters. Future models will require larger datasets to ensure the multivariate nature of these parameters can be effectively modeled. We did not include the effect of cocontraction of the subscapularis or other antagonist muscles. Incorporation of these muscles would allow loading across the joint to be determined.

According to other sources, posterior deltoid accounts for about 11% of the external rotation torque in the position simulated here.⁴³ However, posterior deltoid was not included in this model for several reasons. First, we do not have confidence in that data because there are no standard deviations reported. Additionally, our method for measuring muscle moment arms differed from the methods of Kuechle et al. in a significant respect. In the other study, muscles remained attached to the specimens and cords were routed along the surface of the muscle bellies. Cord paths were further from the joint center of rotation than physiologic muscle and tendon centroids. Consequently, moment arms were overpredicted since a longer cord path results in a greater excursion for a given rotation angle. In our study, we dissected muscles from the specimens and approximated the muscle-tendon paths with custom made low friction nylon guides to route the cords.⁴⁶ This technique is a better model since the cord path is more aligned with muscle and tendon centroids. In an early pilot test specimen we measured the moment arm of poster deltoid in one specimen for three trials and concluded that posterior deltoid does not play a significant role in rotation strength for the position simulated here since moment arm is less than 10% of moment arm for infraspinatus, and posterior deltoid PCSA is equal to infraspinatus. Our results, agree with conclusions made by others⁶⁶ that posterior deltoid does not play a significant role in external rotation.

It is important to note that this model does not consider that residual force generated in a cuff muscle tendon rupture might contribute to joint strength via lateral force transmission through an adjacent muscle or tendon. This simulation neglects these types of forces. Experimental models have demonstrated lateral force transmission between adjacent muscles.^{4,7,21,35,48,52} While the tools for modeling lateral forces in muscle exist,⁸¹ the changes in the muscle moment arm with cuff tear, and the analytical tools for modeling the change, are not well understood.

Additionally, there is evidence that with rotator cuff tear muscle activation could be altered due to pain or other factors not completely understood. Recently, a trend has been found towards increased muscle activation in asymptomatic and symptomatic rotator cuff tear patients compared to healthy controls.⁴⁰ This model neglects such alterations in muscle activation.

The muscle specific tension determined in this simulation, 1.43 MPa, is at the upper bound of values described in the literature.^{8,16,23,36,65,68,76} Specific tension, like muscle activation could be modeled as a random variable. However, in this study it was decided to model specific tension deterministically, with the assumption that the probabilistic aspects of the parameter would be captured by modeling PCSA stochastically. With a limited understanding of specific tension differences among healthy normals,⁹ it is reasonable to model specific tension as equal for all cases. Specific tension was determined for the healthy normal case using a common, simple mechanical model to ensure predicted joint torques match externally measured joint torques with small errors.^{9,14,15,27,54} With reduced specific tension, and consequently reduced muscle forces, the model would not have predicted measured joint torques with small error. However, others have found the same relative value for specific tension of elbow and shoulder muscles determined with similar modeling approaches,^9,10 including a recent-deterministic model which utilized 1.4 MPa for specific tension in order to match predicted moments to measured values.²⁹

The muscle forces predicted here have not yet been validated by direct measurement, or predicted by models using kinematic and muscle activation data collected in vivo as inputs. Current models of the glenohumeral joint have been used to make muscle force predictions for other motions.^28,53,76 In the future it would be interesting to conduct an experiment to obtain in vivo data for estimating muscle forces during external rotation as has been done for other joints and other motions.

Input parameters are not, most likely, Gamma distributed. However, owing to small sample size for the input parameters in particular, we found it necessary to assume Gamma distributions for these parameters. Gamma distributions result in generation of non-negative random variates, which is favorable since PCSA, agonist moment arms, and normalized muscle force are all non-negative. Ideally, in the future it is possible that a larger data set will allow for an easing of this assumption allowing parameters to be modeled non-parametrically. By utilizing a Gamma distribution of 1000 samples more information is added to the simulation concerning the input distribution than is actually known. In fact, when distribution sample size exceeds sample size of the empirical data, degrees of freedom are artificially inflated, and assumed distributions become less realistic.

Another method for simulating relationships between input parameters and their effect on model output is a bootstrap model.^24,60 Bootstrap models are attractive because the system under consideration is modeled directly from empirical data in a nonparametric fashion. During the model development phase of this study a bootstrap model was constructed in which input parameters were sampled at random with replacement from the original empirical data describing muscle PCSA’s, moment arms and normalized force from length–tension relationships. In this manner covariance was modeled directly since parameters were sampled as vectors corresponding to each specimen from which data was collected. Means and distributions of predicted torques matched measured torque means and distributions for the healthy normal case determined by the confidence level approach described earlier. This result demonstrates strong potential for multivariate probabilistic models.

More work is needed to determine how to utilize probabilitistic models to analyze differences in populations. For example, a random component exists to physical performance of labor and athletic tasks. If different people perform the same task many times, task performance will differ both within a subject, and between subjects. Additionally, it is possible that combinations of outlying parameters with low probabilities of occurrence within a population (short moment arm, large PCSA) may lead to pathological conditions such as rotator cuff tear. Furthermore, there is increasing evidence that mechanics of force generation at the sarcomere level is probabilistic,⁴² rather than deterministic as previously thought. Yet, little is understood concerning how the probabilistic nature of these properties might contribute to pathologies such as rotator cuff tear. Additionally, more work is needed to understand how models can explain the links between the degree of randomness and the likelihood of pathological condition.

In conclusion, in this study we incorporated the effects of population variability into a musculoskeletal model of glenohumeral external rotation strength. Muscle forces were predicted with the model. Forces for healthy normal subjects and two rotator cuff tear cases were compared. Differences in variability of measured torques for the three cases analyzed here are explained by differences in means and distributions of muscle cross-sectional area. This study furthers our understanding of effects of parameter variability on variability in muscle force and shoulder external rotation strength. The stochastic method accounts for differences in musculoskeletal parameters across a population and has potential for modeling other joint systems, and for increasing our understanding of differences between populations.