Vibrational Dynamics of Biological Molecules: Multi-quantum Contributions

Abstract

High-resolution X-ray measurements near a nuclear resonance reveal the complete vibrational spectrum of the probe nucleus. Because of this, nuclear resonance vibrational spectroscopy (NRVS) is a uniquely quantitative probe of the vibrational dynamics of reactive iron sites in proteins and other complex molecules. Our measurements of vibrational fundamentals have revealed both frequencies and amplitudes of ⁵⁷Fe vibrations in proteins and model compounds. Information on the direction of Fe motion has also been obtained from measurements on oriented single crystals, and provides an essential test of normal mode predictions. Here, we report the observation of weaker two-quantum vibrational excitations (overtones and combinations) for compounds that mimic the active site of heme proteins. The predicted intensities depend strongly on the direction of Fe motion. We compare the observed features with predictions based on the observed fundamentals, using information on the direction of Fe motion obtained either from DFT predictions or from single crystal measurements. Two-quantum excitations may become a useful tool to identify the directions of the Fe oscillations when single crystals are not available.

1. Introduction

Many essential biological processes take place at localized sites in proteins, which often incorporate metal ions. Site-selective vibrational spectroscopies [2-5] have proven to be particularly revealing probes of the structure, dynamics and reactivity of protein active sites. Nuclear resonance vibrational spectroscopy (NRVS) [6-30] is a relatively new technique that takes advantage of remarkable properties of synchrotron radiation, including time-pulsed structure, tunability, narrow bandwidth, and high brilliance, to reveal the complete vibrational spectrum of a probe nucleus. NRVS achieves the ultimate goal in selectivity, by targeting a single atom in a complex molecule. This method is particularly promising for characterizing the vibrational dynamics of ⁵⁷Fe in biological macromolecules [11,15,21,22,25-27], and in small molecules designed to model protein active sites [16,19,20,24,28].

Unlike traditional vibrational spectroscopies, NRVS is highly quantitative, revealing not only the frequencies, but also the amplitudes of ⁵⁷Fe vibrations. Measurements on oriented samples, such as single crystals, also yield the direction of vibrational motions [10,12,14,18,23,20,26,28]. Other names used for this technique include phonon assisted Mössbauer effect [21,22,25,26], inelastic X-ray scattering of synchrotron radiation [11], nuclear inelastic scattering [18], nuclear inelastic absorption [9], and nuclear resonant inelastic X-ray scattering [29].

One distinguishing feature of NRVS is the presence of multiquantum vibrational excitations, even for a strictly harmonic system. These multiquantum contributions are often removed numerically to determine a vibrational density of states [7,17]. Chumakov and coworkers recently used multiquantum features to distinguish vibrational contributions from individual sites [30]. Here, we investigate two compounds, Fe(TPP)(2-MeIm) and Fe(TPP)(1-MeIm)(CO) (Fig. 1), designed to model the active sites of heme proteins. The high ⁵⁷Fe concentrations achieved for these small molecules, relative to proteins, enable us to detect weak vibrational overtones and combinations. We explore the sensitivity of these two-quantum excitations to the direction of vibrational motion.

Fig. 1.

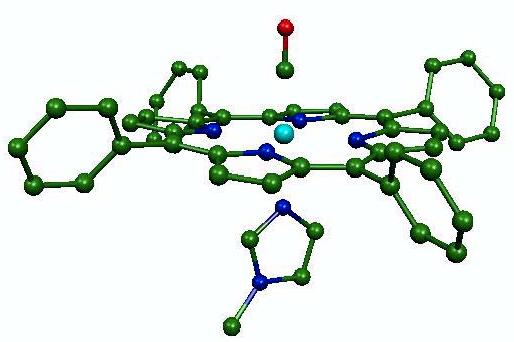
Calculated structure of Fe(TPP)(1-MeIm)(CO), resulting from geometric optimization with the B3LYP functional. Color scheme: cyan = iron, green = carbon, blue = nitrogen, red = oxygen. Hydrogen atoms are omitted for clarity.

2. Methods

2.1. NRVS measurements

⁵⁷Fe NRVS measurements were performed at sector 3-ID-D of the Advanced Photon Source at Argonne National Laboratory. A tunable high-resolution monochromator [32] selected X-rays in a 7 cm^-1 (0.85 meV) energy interval near 14.4 keV, and an avalanche photodiode detected photons emitted from a sample placed in the resulting monochromatic beam. Rejection of events detected during a time window containing the arrival time of the X-ray pulse discriminated photons emitted over the 141 ns lifetime of the ⁵⁷Fe nucleus from the large background of electronically scattered photons, which arrive coincident with the X-ray pulse. The spectrum recorded as a function of incident energy consists of a central resonance, due to recoilless excitation of the ⁵⁷Fe nuclear excited state at 14.4 keV, accompanied by a series of sidebands corresponding to creation or annihilation of vibrational quanta of frequency v̄, displaced from the recoilless absorption by an energy hcv̄. Normalization of the spectrum according to Lipkin’s sum rule [33] yields an excitation probability S(v̄), with peak areas for each mode proportional to the mean square displacement of the Fe atom. In particular, features due to a single excitation of a mode of frequency v̄ , displaced by from the recoilless absorption by an energy hcv̄, dominate the observed spectrum. Here, we focus on multi-quantum contributions to S(v̄).

2.2. Sample preparation

The synthesis of 95% ⁵⁷Fe-enriched ferrous tetraphenylporphyrin with either 2-methylimidazole or 1-methylimidazole and carbon monoxide as axial iron ligands, Fe(TPP)(2-MeIm) and Fe(TPP)(1-MeIm)(CO), respectively, was described previously [31,24]. For NRVS measurements, polycrystalline powders of both compounds were loaded into a polyethylene sample cup and mounted in a helium flow cryostat, with X-ray access through a beryllium dome. The five-coordinate compound Fe(TPP)(2-MeIm) crystallized in space group P1 [31], with the plane of both porphyin molecules in the unit cell, related by inversion symmetry, lying parallel to the (208) plane of the crystal. As decsribed previously, a single crystal Fe(TPP)(2-MeIm) with dimensions 1.7×0.7×0.6 mm³ was sealed in an X-ray capillary under an inert atmosphere, and then mounted on a copper wire on a eucentric goniometer. Coarse adjustment using the copper wire and fine adjustments with the angle adjustments on the goniometer head.allowed adjustment of the crystal orientation to make the (208) plane containing the porphyrin planes coplanar with the goniometer rotation axis and the orthogonal X-ray beam direction. In-plane NRVS data were recorded in this orientation and out-of-plane NRVS data were recorded following a 90° rotation of the goniometer axis. The capillary was immersed in a cold nitrogen gas stream to maintain sample temperature. Quantitative analysis of the relative signal above and below the recoilless resonance confirmed sample temperatures of 20 K for Fe(TPP)(1-MeIm)(CO) and Fe(TPP)(2-MeIm) powders, 114 K for Fe(TPP)(2-MeIm) crystal (in-plane orientation), and 95 K for Fe(TPP)(2-MeIm) crystal (out-of-plane orientation).

2.3. Computational methods

DFT calculations on the six-coordinate model compound Fe(TPP)(1-MeIm)(CO) yield the optimized structure shown in Figure 1, and also provide detailed vibrational predictions. Calculations were performed with Gaussian 98 [34], using the 6-31G basis set for N, O, C, and H atoms, Ahlrich’s VTZ basis set for the Fe atom [35], and the Becke-Lee-Yang-Parr composite exchange correlation functional (B3LYP) [36,37]. Vibrational properties of the 91-atom molecule are determined from the relative Cartesian displacements of each atom for each of the 267 vibrational modes, as described previously [28].

3. Results and discussion

3.1. One-quantum transitions

The top half of Fig. 2 displays the NRVS signal recorded for a randomly oriented polycrystalline sample of Fe(TPP)(1-MeIm)(CO) at 20 K. This compound is a simple model for the active site of heme proteins that bind the diatomic ligand CO. Previously, assignments for the vibrational fundamentals were proposed by adjusting the parameters in an empirical potential to reproduce the observed frequencies and amplitudes [24]. Two quantum excitations are likely to contribute to a number of weak features observed above 600 cm^-1 (expanded vertical scale in Fig. 2), which were not explicitly discussed previously. Before attempting to understand these features, we first discuss the one-quantum transitions that dominate the NRVS signal below 200 cm^-1.

Fig. 2.

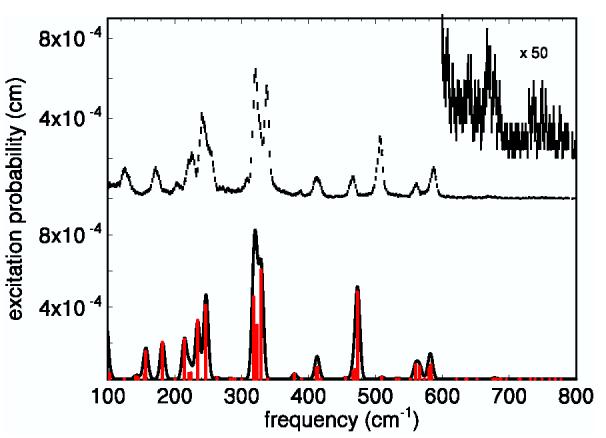
Measured and predicted Fe vibrational spectra for Fe(TPP)(1-MeIm)(CO). Upper scale: Measured excitation probability S(v̄) with error bars. Lower scale: One-phonon contribution predicted by DFT. The red bars represent the relative areas of the individual 8 cm^-1 FWHM Gaussian contributions to the solid curve, calculated from Eq. 2.

Density functional theory (DFT) methods predict many ground-state properties of molecules, including equilibrium geometries (Fig. 1) and detailed descriptions of vibrational dynamics [38-41,23]. The vibrational predictions do not rely on empirical potentials or require prior knowledge of related molecules to constrain the potential. The quantitative set of frequencies, amplitudes, and directions provided by NRVS rigorously test vibrational predictions for transition metals at protein active sites. In particular, DFT predictions were shown to be a useful guide to the vibrational modes observed in NRVS data for the model compound Fe(TPP)(NO) [28].

The lower half of Fig. 2 shows the one-quantum excitations (n_α → n_α +1) predicted for the optimized structure of Fe(TPP)(1-MeIm)(CO) shown in Fig. 1. In the harmonic approximation, these transitions dominate S (v̄) at low temperature and contribute a series of peaks, located at each of the normal mode frequencies v̄_α, with areas [16]

$${\varphi }_{\alpha }=({\overline{n}}_{\alpha }+1)f\left(\frac{{\overline{\nu }}_R}{{\overline{\nu }}_{\alpha }}\right)\langle {(\widehat{k}\cdot e_{j\alpha })}^2\rangle$$ (1)

proportional to the mean squared displacement of the probe nucleus j along the direction k̂ of the X-ray beam. Here, n̄_α = [exp(hcv̄_α/k_BT )1]^-1 is the mean occupation number for mode α-at temperature T , and v̄_R = 15.8 cm^-1 is the recoil energy of ⁵⁷Fe nucleus at 14.4 keV.

The partial excitation probability S⁰(v̄) determined by subtraction of the recoilless line provides an estimate of the recoilless fraction$f=1-\int d\overline{\nu }{S}^{\prime }\left(\overline{\nu }\right)$ We find f = 0.86 for Fe(TPP)(1-MeIm)(CO) powder at 28 K, f = 0.85 for Fe(TPP)(2-MeIm) powder at 20 K, f = 0.55 for Fe(TPP)(2-MeIm)crystal (in-plane) at 114 K, and f = 0.57 for Fe(TPP)(2-MeIm) crystal (out-of-plane) at 95 K.

Evaluation of the angular average$\langle {(\widehat{k}\cdot e_{j\alpha })}^2\rangle$for a randomly oriented sample, such as the polycrystalline powder considered here, reveals that the “recoil fraction”

$${\varphi }_{\alpha }=\frac{1}{3}({\overline{n}}_{\alpha }+1)f\left(\frac{{\overline{\nu }}_R}{{\overline{\nu }}_{\alpha }}\right)e_{Fe}^2$$ (2)

is proportional to a mode composition factor e²_Fe, which is the fraction of the mode energy associated with motion of the probe atom. In what follows, we suppress the mode index α and use j =Fe for ⁵⁷Fe NRVS. Eq. 2 determines the areas of the features contributing to the predicted excitation probability shown in Fig. 2, using e²_Fe values determined from the calculated atomic displacements, as discussed previously [28].

The optimized structure of Fe(TPP)(1-MeIm)(CO) (Fig. 1) reproduces reported structural features [42], including the almost linear FeCO unit [39,43-49]. The nearest neighbors of the Fe are approximately four-fold rotationally symmetric about an axis perpendicular to the plane of the molecule, and most of the predicted vibrational features occur either as single modes with Fe motion perpendicular to the plane, or as nearly degenerate pairs of modes with Fe motion along orthogonal directions within the plane. Out-of-plane modes (θ ≈ 0°) contribute predominantly to the region below 220 cm^-1 and to the Fe-CO stretching mode observed at 507 cm^-1, while in-plane motion (θ ≈ 90°) dominates the remaining modes (Table 1). The molecular structure beyond the nearest neighbors deviates from four-fold symmetry and lifts the degeneracy of the in-plane modes, but the predicted frequency splitting lies within the 7 cm^-1 experimental resolution in most cases, as previously reported for the related molecule Fe(TPP)(NO) [28]. The pair of experimental features at 321 and 338 cm^-1 may form an exception to this picture. A total of five modes, including one out-of-plane mode, contribute to the corresponding feature of the predicted spectrum, with some frequency variations large enough to be distinguishable at the experimental resolution.

Table 1.

Proposed correspondence of observed Fe(TPP)(1- MeIm)(CO) vibrational features with normal modes predicted on the basis of DFT calculation. Directions are specified as polar and azimuthal angles in a coordinate system with the z-axis normal to the mean porphyrin plane.

frequency (cm-1)
measured	predicted	e2Fe	θ	ϕ
125	157	0.05	148°	16°
172	182	0.07	18°	3°
224	214	0.09	5°	3°
242	234	0.14	90°	25°
253	247	0.19	89°	117°
321	318	0.27	90°	41°
321	320	0.11	4°	68°
321	321	0.02	70°	1°
321	323	0.18	87°	21°
338	329	0.37	89°	121°
413	412	0.05	90°	138°
413	413	0.05	89°	46°
466	467	0.04	89°	12°
466	469	0.05	92°	99°
507	473	0.43	1°	18°
561	560	0.08	90°	66°
561	566	0.08	89°	154°
586	580	0.06	89°	102°
586	583	0.09	85°	7°

Although there are frequency errors, as large as 34 cm^-1 for the Fe-CO stretching mode observed at 507 cm^-1, successsful prediction of the pattern of vibrational amplitudes on an absolute scale as a function of frequency (Fig. 2) suggests that the calculation provides a reliable guide to the character of the individual modes. This includes observed features at 507 cm^-1, 561 cm^-1, and 586 cm^-1,associated with Fe-CO stretching and FeCO bending, as previously seen in numerous heme proteins [50-60]. A more detailed description of these modes, together with measurements on related compounds, will appear elsewhere. Table 1 summarizes the frequencies, amplitudes, and directions of Fe motion for predicted modes, together with corresponding observed features. Below, we use the proposed correspondence to evaluate the contributions of two-quantum transitions to weak experimental features observed in the high-frequency region of the experimental data (Fig. 2).

The five-coordinate iron complex Fe(TPP)(2-MeIm) differs from Fe(TPP)(1-MeIm)(CO) by the loss of the CO and placement of the imidazole methyl group closer to the porphyrin. The NRVS signal is less complex (Fig. 3b) and lacks the characteristic FeCO vibrations above 500 cm^-1. The Fe-N_pyr and Fe-N_Im bonds are approximately 7 pm longer in Fe(TPP)(2-MeIm) than in Fe(TPP)(1-MeIm)(CO) [31,42], and thus both the in-plane and out-of-plane modes are expected at lower frequencies than in the CO complex. Again, a number of weaker features at higher frequency (Fig 3a) are candidates for two-quantum transitions.

Fig. 3.

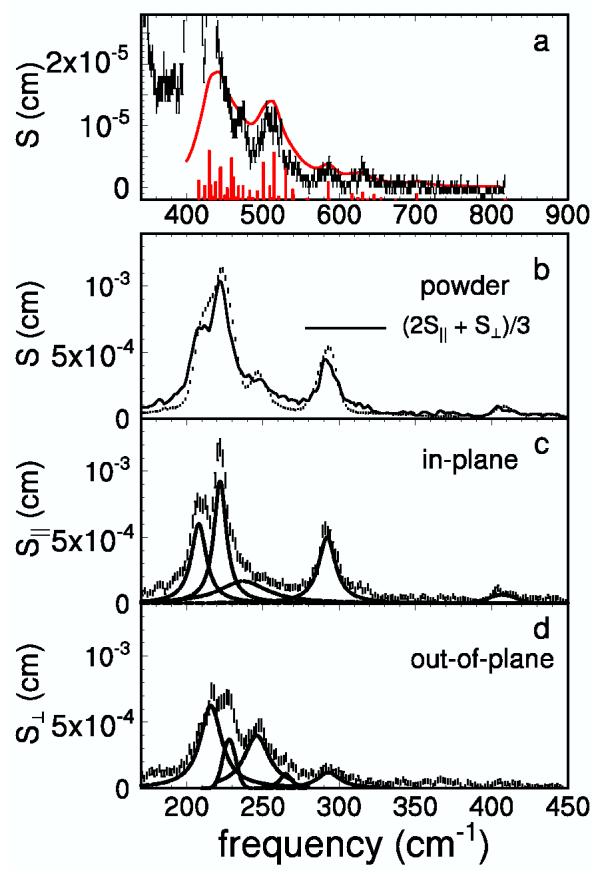
NRVS data recorded on a polycrystalline powder (a and b) and on an oriented single crystal (c and d) of Fe(TPP)(2-MeIm). The individual peaks are represented by dashed lines in c and d. The predicted two-quantum contribution, plotted as a red trace in a, has been convolved with Lorentzians of linewidth equal to the average of the linewidths of the contributing fundamentals. The red bars in a have heights proportional to the areas of the overtones and combinations.

Although no DFT prediction is available for Fe(TPP)(2-MeIm), measurements on an oriented single crystal (Fig. 3c, d) identify the contributions of Fe vibrations parallel and perpendicular to the heme plane. Although only two directions are measured, the results on Fe(TPP)(1-MeIm)(CO) suggest that deviations from fourfold symmetry and the resulting differences between the two in-plane directions will be small. In order to test this assumption, Fig. 3b compares the signal measured on a polycrystalline sample with the signal

$$S\left(\overline{\nu }\right)=\frac{1}{3}[2S_{\parallel }\left(\overline{\nu }\right)+S_{\perp }\left(\overline{\nu }\right)]$$ (3)

averaged over single crystal measurements parallel and perpendicular to the porphyrin plane. The agreement indicates that it is reasonable to neglect differences between the two in-plane directions.

We fitted the experimental single crystal spectra of Fe(TPP)(2-MeIm) in order to determine the frequencies v̄ and mode composition factors e²_Fe for each fundamental transition, using Eq.2. Lorentzian line shapes were used, with the exception of a Gaussian band at 228 cm^-1 in the out-of-plane spectrum. We further assume four-fold symmetry, so that Fe motion is perpendicular to the porphyrin plane for each feature observed in S_⊥ (v̄), and observed features in S_∥ (v̄) result from degenerate pairs of modes with kFe motion along two orthogonal in-plane directions. We use these results, compiled in Table 2, as a basis for evaluating the two-quantum transitions for Fe(TPP)(2-MeIm).

Table 2.

Vibrational analysis of a single Fe(TPP)(2-MeIm) crystal. The sum σe_Fe² includes all modes that contribute to the experimental feature.

frequency (cm-1)	σeFe2	character
208	0.52	in-plane
222	0.74	in-plane
237	0.44	in-plane
293	0.68	in-plane
409	0.12	in-plane
216	0.33	out-of-plane
228	0.09	out-of-plane
246	0.30	out-of-plane
265	0.03	out-of-plane
293	0.07	out-of-plane

3.2. Two-quantum transitions

In the harmonic approximation, the energies and the amplitudes of the multi-quantum transitions are dictated by the frequencies, amplitudes, and directions of Fe vibrations corresponding to the one-quantum transitions. The contributions of the first overtone (n_α → n_α +2), at energy 2v̄_α, and combination (n_α n_α +1), (n_β n_β +1), at energy v̄_α +v̄ , to→ →${\overline{\nu }}_{\alpha }+{\overline{\nu }}_{\beta }$, the total spectral area are given by [16]

$${\varphi }_{\alpha \alpha }=\frac{9}{10}{\varphi }_{\alpha }^2∕f$$ (4)

$${\varphi }_{\alpha \beta }=\frac{3}{5}({\varphi }_{\alpha }{\varphi }_{\beta }∕f)(1+2{\cos }^2{\xi }_{\alpha \beta }),$$ (5)

respectively, where ξ_αβ is the angle between the Fe displacements in modes α and β.

We use Eqs. 2, 4, and 5, together with the information in Table 1, to simulate the 2-quantum contributions to the Fe(TPP)(1-MeIm)(CO) NRVS signal. Because the predicted frequencies differ somewhat from observed values, we use experimental values for the frequencies (column 1), and predicted values for iron amplitudes (e²_Fe; column 3) and relative directions (ξ_αβ; columns 4 and 5).

In several cases, DFT predicts multiple unresolved contributions to an experimental feature. In particular, DFT calculations predict pairs of in-plane modes corresponding to observed 413, 466, 561 and 586 cm^-1 NRVS peaks, with frequencies too close to be resolved experimentally. In such cases, we predict a single feature at the corresponding two-quantum frequency, and sum the areas predicted for each overtone and combination (Eqs. 4-5). The simulated two-quantum curve shown in Fig. 4 uses these frequencies and areas. In principle, inhomogeneous broadening or increased vibrational dephasing might lead to larger linewidths for the two-quantum transitions than for the corresponding fundamental transitions. However, instrumental broadening appears to be the main contribution to the one-quantum line-shape for Fe(TPP)(1-MeIm)(CO), and we therefore approximated the two-quantum linewidths as the average of the linewidths of the corresponding fundamentals. Fig. 4 suggests that two-quantum excitations dominate the experimental signal at most frequencies above 630 cm^-1. However, three weak fundamentals predicted at 676, 678 and 679 cm^-1 with a total e²_Fe = 0.011 may contribute to the apparent shortfall of the two-quantum prediction near 670 cm^-1.

Fig. 4.

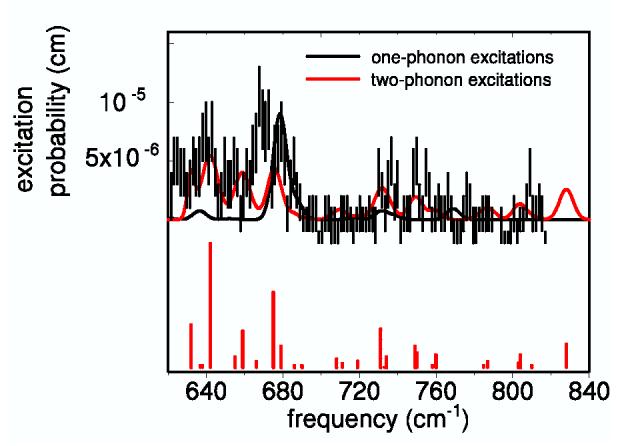
Comparison of the high-frequency spectrum of Fe(TPP)(1-MeIm)(CO) with the simulated one- and two-phonon contributions. The linewidth of each overtone and combination is the sum of the linewidths of the contributing fundamentals. The bars have heights proportional to the areas of the overtones and combinations.

DFT predictions are not available for (Fe)(TPP)(2-MeIm), but oriented single crystal measurements partially specify the direction of Fe motion. The x-y splitting of the in-plane modes for (Fe)(TPP)(2-MeIm) is too small to be observed experimentally, and we assumed that each peak in the in-plane spectrum results from two degenerate modes with equal spectral areas and orthogonal Fe displacements. The predicted curve, plotted against the experimental spectrum in Fig. 3a, again uses the average linewidth of the corresponding fundamental transitions.

Well-resolved modes that contribute strongly to the fundamental region also contribute two-quantum features to the spectrum above 450 cm^-1. Indeed, the dominant features in this region are the overtone of the 293 cm^-1 mode, and combinations between the prominent feature at 200-240 cm^-1 (mostly due to the 208 cm^-1 and 222 cm^-1 in-plane modes) and the in-plane peaks at 293 cm^-1 and 409 cm^-1.

Features at 432 cm^-1 and 474 cm^-1 significantly exceed the two-quantum simulation, and may correspond to additional fundamental transitions with small Fe amplitudes.

3.3. Directional effects

Because vibrational frequencies can be highly sensitive to structural and environmental changes, the characterization of molecular vibrations is an important challenge. NRVS measurements yield valuable quantitative information on vibrational amplitudes as well as frequencies. By itself, this information is not sufficient to characterize the vibrations of a complex molecule, and previous investigations have relied on additional information from single crystal measurements or normal mode calculations. Here, we suggest the potential use of quantitative measurements of two-quantum vibrational vibrations to provide additional information regarding the direction of Fe motion and unresolved vibrational structure.

We have previously noted the sensitivity of two-quantum transitions to the relative direction of Fe motion in the contributing modes (Eq. 5) [16]. An interesting consequence is that unresolved vibrational structure can affect the area of two-quantum features. Although the area predicted for a pure vibrational overtone (Eq. 4) does not depend on the direction of Fe motion, unresolved vibrational structure can lead to a more complex situation. As noted above, the spectrum of iron vibrations within a fourfold symmetric environment includes degenerate in-plane modes with orthogonal Fe motion (ξ = 90°), each of which contribute half of the observed area ϕ_α of the one-quantum feature at frequency v̄_α. The corresponding two-quantum feature will include contributions from two pure overtones (Eq. 4), each with area (9/10) ϕ²_α/4f , and the combination (Eq. 5), with area (3/5){ϕ²_α/4f , so that the total area

$$\varphi =\frac{3}{5}({\varphi }_{\alpha }^2∕f)$$ (6)

predicted for the feature at frequency 2v̄_α is reduced from the area predicted for a pure overtone (Eq. 4) by a factor 2/3.

Similarly, unresolved vibrational structure will affect the area predicted for a two-quantum transition involving fundamental features at v̄_α and v̄_β. Again considering the case of Fe located on an axis of fourfold symmetry, these frequencies may correspond either to isolated modes with Fe motion along the symmetry axis (i.e., perpendicular to the porphyrin plane), or degenerate in-plane mode pairs. For an in-plane mode pair at frequency v̄_α and an out-of-plane mode at frequency v̄_β, Eq. 5 predicts that each of the two combination transitions will contribute an area (3/5)$({\varphi }_{\alpha }{\varphi }_{\beta }∕2f)$ resulting in a total area

$$\varphi =\frac{3}{5}({\varphi }_{\alpha }{\varphi }_{\beta }∕f)$$ (7)

predicted for the two-quantum feature located at ${\overline{\nu }}_{\alpha }+{\overline{\nu }}_{\beta }$. This is a factor 3 lower than the area predicted by Eq. 5 for the combination of two out-of-plane modes, for which ξ_αβ = 0°.

If features at frequencies ${\overline{\nu }}_{\alpha }$ and ${\overline{\nu }}_{\beta }$ both correspond to fundamental transitions of in-plane mode pairs, a total of four two-quantum transitions will contribute to the feature at v̄_α + v̄_β. Two transitions involving orthogonal Fe motion (ξ = 90°) each contribute a predicted area (3/5)$({\varphi }_{\alpha }{\varphi }_{\beta }∕4f)$ and two transitions involving parallel Fe motion (ξ = 0°) each contribute (9/5)$({\varphi }_{\alpha }{\varphi }_{\beta }∕4f)$, yielding a total area

$$\varphi =\frac{6}{5}({\varphi }_{\alpha }{\varphi }_{\beta }∕f)$$ (8)

intermediate between the areas predicted for in-plane/out-of-plane (Eq. 7) and out-of-plane/out-of-plane (Eq. 5, with ξ_αβ = 0°) combinations.

4. Conclusions

NRVS provides a detailed picture of the vibrational dynamics of Fe in biological molecules, including porphyrins and heme proteins. Measurements on oriented crystals and comparison with quantitative theoretical predictions enrich this picture with information on the direction of Fe motion and on the motion of other atoms, respectively. In addition to vibrational fundamentals, vibrational overtones and combinations are observed in the NRVS signal. The intensity of these two-quantum excitations depends on the direction of Fe motion of the corresponding fundamental vibrations. With continuing improvements in experimental count rates, we anticipate that this may become a useful method for identifying the directions of Fe vibrations when oriented samples such as crystals are not available.