Kinetic evidence for an on-pathway intermediate in the folding of cytochrome c

Abstract

An early folding event of cytochrome c populates a helix-containing intermediate (I_NC) because of a pH-dependent misligation between the heme iron and nonnative ligands in the unfolded state (U). For folding to proceed, the nonnative ligation error must first be corrected. It is not known whether I is on-pathway, with folding to the native state (N) as in U ↔ I_NC ↔ N, or whether the I must first move back through the U and then fold to the N through some alternative path (I_NC ↔ U ↔ N). By means of a kinetic test, it is shown here that the cytochrome c I does not first unfold to U. The method used provides an experimental criterion for rejecting the off-pathway I ↔ U ↔ N option.

Perhaps the most elusive question in protein folding is whether experimentally observed intermediates (I) are on- or off-pathway (1–4). During the last 10 years, a number of protein-folding I have been characterized in some detail (5–10), but it has not been possible to demonstrate convincingly whether they are on-pathway, defined as unfolded state (U) ↔ I ↔ native state (N) or off-pathway I ↔ U ↔ N (2, 11).

The folding and unfolding process of cytochrome c (Cyt c) has been studied in detail (5, 12–18). Cyt c folding is heterogeneous and sensitive to pH. At pH 6 and higher, a large fraction of the molecules fold slowly and populate an I state in which the amino and carboxyl helices are folded (I_NC) (5). In contrast, at pH 5.0 and lower, most of the molecules fold quickly without populating any I state (14, 15). At elevated pH, a nonnative ligation between the heme iron and a peripheral histidine side chain in its neutral form erects a barrier that slows folding and causes I_NC to accumulate (14–17). It is not known whether I_NC is a dead-end, off-pathway I that has to unfold first and then refold through an alternative pathway (I_NC ↔ U ↔ N) or whether it represents an on-pathway step directly to the N (U ↔ I_NC ↔ N).

This paper describes a kinetic test that can be helpful under favorable conditions. If it can be shown that the rate for I → N is greater than that for I → U, then the off-pathway model can be rejected. The I_NC of Cyt c meets this criterion.

MATERIALS AND METHODS

Horse-heart Cyt c (type IV) was purchased from Sigma, treated with ferricyanide to oxidize the residual ferrous form, and further purified on a G-25 Sephadex column (Amersham Pharmacia). Ultrapure guanidinium chloride (GdmCl) was from Sigma. GdmCl concentrations were determined from a refractive index (19). ²H₂O (D₂O; 99.8% D) was from Cambridge Isotope Laboratories (Cambridge, MA). Deuterated GdmCl was prepared by evaporating the solvent D₂O in 6 M GdmCl solution three times with a rotary evaporator.

Stopped-flow fluorescence and absorbance experiments were performed with a Biologic SFM-4 (Grenoble, France). The fluorescence excitation wavelength was 280 nm, and the emission was collected through a 320-nm cut-off filter. For both folding and unfolding experiments, three syringes (numbered 2, 3, and 4) were used to keep the final protein concentration constant while the concentration of denaturant was varied. Refolding experiments were initiated by mixing protein solution in 4 M GdmCl (in syringe 4) with 0.1 M NaOAc buffer solution (in syringe 2) and 6.0 M GdmCl solution (in syringe 3). Each shot contained 0.1 ml of protein solution from syringe 4 and a 0.9-ml mixture from syringe 2 and syringe 3 with an appropriate ratio of the two solutions to yield different concentrations of GdmCl in the final solution. All solutions contained 0.1 M NaOAc at pH 6.2. The final protein concentration in the stopped-flow fluorescence experiments was ≈30 μM. Final data were obtained by averaging two shots. A 0.2-cm path-length cuvette (FC-20) was used. Mixing dead time was ≈8 ms. Kinetic-unfolding experiments were performed similarly, except that the solution in syringe 4 did not contain GdmCl. In the refolding experiments in D₂O at 30°C and pD 7.0, syringe 4 contained a Cyt c in 4 M GdmCl, 0.5 M KCl, and 0.1 M KH₂PO₄. Syringe 3 and syringe 2 contained 0.5 M KCl and 0.1 M KH₂PO₄. The refolding experiment was initiated by mixing 0.175 ml of solution in syringe 4 with 0.4 ml of solution in syringe 3 and 0.425 ml of solution in syringe 2. The dead time was ≈3 ms. Stopped-flow absorbance monitored at a 695-nm wavelength was initiated by mixing protein solution in 4.0 M GdmCl with 0.1 M NaOAc buffer solution to yield a final solution of 0.7 M GdmCl and 26 μM protein. A 1.0-cm path-length cuvette (TC-100/15) was used in this experiment.

The kinetic refolding and unfolding curves from stopped-flow fluorescence experiments were fitted with three exponential phases and a single exponential phase, respectively, by using a simplex algorithm (biokine from Biologic). The kinetic refolding curve from the absorbance experiment at a 695-nm wavelength was fitted with two exponential phases. Equilibrium unfolding data were obtained from the baselines of the kinetic-unfolding traces. The unfolding free energy ΔG_NU was assumed to be a linear function of GdmCl concentration, i.e., ΔG_NU([GdmCl]) = ΔG_NU(H₂O) − m_NU[GdmCl] (19). The parameters in the above equation were obtained by fitting the equilibrium unfolding data to the equation of Santoro and Bolen (20). ΔG_NU measured in this way does not include a contribution from the population of nonnative peptide conformations of prolines in U. Therefore, its value is slightly larger (≈0.5 kcal/mol) than that obtained from a slow equilibrium unfolding experiment (21). The GdmCl dependence of unfolding rate constants near the transition region was assumed to be linear on a logarithmic scale, i.e., log k_NI = log k_NI^H_2O − m‡_NI[GdmCl] (6). Linear extrapolation was used to obtain k_NI at 1.0 M GdmCl.

RESULTS

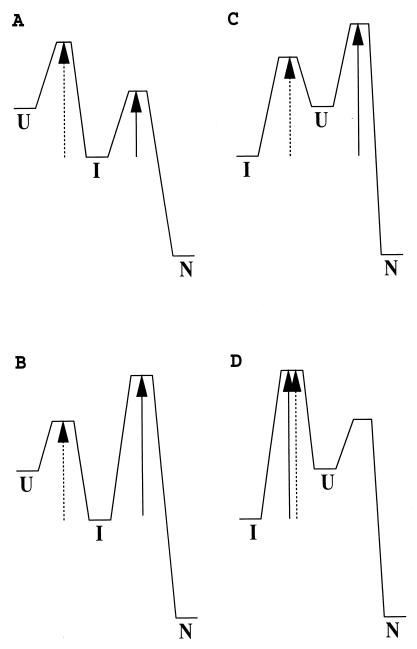
Fig. 1 illustrates the kinetic picture for on- and off-pathway folding when an I is populated. An off-pathway I must pass through the U to arrive at the N. In this mode, the time it takes for I to reach N cannot be shorter than the time for U to reach N. If the reverse condition holds, i.e., k_IN > k_IU, then the off-pathway option can be rejected. When an I is clearly populated in kinetic folding, the apparent rate constant, k_IN, for conversion from I to N (through U in the off-pathway case) normally can be measured directly. Therefore, to make the desired comparison, the key is to obtain the unfolding rate constant from I to U, k_IU, under native folding conditions. This paper shows how k_IU can be obtained indirectly from several experimental approaches by using the relationship ΔG_IU = −RT ln(K_IU) = −RT ln (k_IU/k_UI).

Figure 1.

Illustration of the kinetic difference between an on-pathway and an off-pathway reaction for an apparent three-state system. The effective kinetic barrier from I to N is indicated by the solid arrow and from I to U by the dashed arrow. (A and B) On-pathway reaction. (C and D) Off-pathway reaction. Only in A is k_IN > k_IU. This characteristic allows one to identify an on-pathway I. This is a sufficient but not a necessary condition. Even though k_IN < k_IU, I can still be on-pathway as in B. (C) The refolding I can be populated quickly, and a lag phase may be generated before the formation of N. In this case, U is not observable during the folding from I to N even though I must pass through U. Therefore, the appearance of a lag phase of I before formation of N does not necessarily indicate an on-pathway I (33). (D) Refolding may seem to be two-state, although a stable off-pathway I exists. Therefore, apparent two-state folding does not exclude the possibility that an equilibrium I may be observed. Similarly apparent two-state folding, as in A, can conceal the presence of an on-pathway I.

Direct Measurement of k_IN.

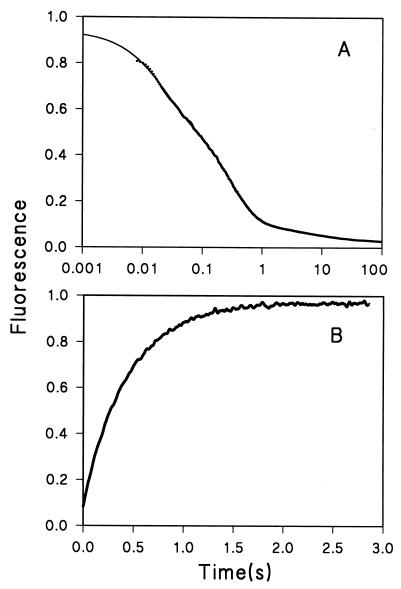
Cyt c folding and unfolding experiments were carried out at pH 6.2 and 10°C, as were earlier pulse-labeling experiments (5). Fig. 2 A and B shows typical kinetic traces for folding in 1.0 M GdmCl and unfolding in 3.0 M GdmCl. The folding trace can be fitted with three exponential phases. Previous experiments under similar conditions showed that the fast phase represents the folding process from U to I_NC (5, 22). Also, some small fraction of the protein population becomes N at this same rate (5, 15). The middle phase corresponds to folding from I_NC to N, shown specifically by the loss of the I_NC and the rise of the absorbance band at 695 nm (Fig. 3; refs. 5 and 22), a specific probe for the Cyt c N (23). The very slow phase represents a small fraction of the protein that may be blocked by a prolyl cis–trans isomerization process (13). We are interested here in the I_NC to N transition. The rate constants k_UI and k_IN can be measured directly from these results. Other states, both those seen in Fig. 2 and others that are invisible to these measurements (5, 9, 18, 24, 25) do not affect the present considerations.

Figure 2.

Kinetic traces of refolding and unfolding. The unit of fluorescence is arbitrary. (A) Refolding at 1.0 M GdmCl. A three-exponential fitting yields a residual signal that is 1/70 that of the total amplitude. The apparent relaxation rate constants are λ₁ = 50 sec⁻¹, λ₂ = 3.5 sec⁻¹, and λ₃ = 0.1 sec⁻¹. The solid line is the fitting curve. (B) Unfolding at 3.0 M GdmCl. The data fitted with a single exponential have a residual 1/20 that of the total amplitude. The solid line is the fitting curve.

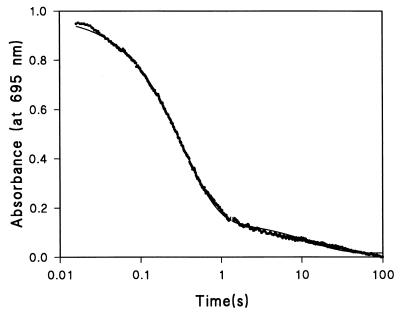
Figure 3.

Kinetic trace of refolding of Cyt c monitored at 695-nm wavelength by absorbance in arbitrary unit. The final concentrations of Cyt c and GdmCl are 26 μM and 0.7 M, respectively. The major phase of the refolding yields a rate constant k_IN of 2.9 sec⁻¹, which is in excellent agreement with the value of 2.7 sec⁻¹ from the stopped-flow fluorescence experiment (see Table 1).

Experiments like those in Fig. 2 were performed between 1.0 M and 3.5 M GdmCl, where the equilibrium unfolding free energy is known to be a linear function of denaturant. At 1.0 M GdmCl, the fast kinetic phase in Fig. 2A gives a rate constant λ₁ = 50 sec⁻¹, and the second kinetic phase yields an apparent rate constant λ₂ = 3.5 sec⁻¹. Because λ₁ is 15 times larger than λ₂, the two events are decoupled well kinetically and can be measured separately (26). Because I_NC is generated from U, and N is formed subsequently as the final stable product, λ₁ = k_UI + k_IU and λ₂ = k_IN + k_NI. The apparent folding rate constant from I_NC to N is then obtained directly as k_IN = λ₂ = 3.5 sec⁻¹, because the unfolding rate constant, k_NI, is negligibly small (≈10⁻³ sec⁻¹) under this native condition (see Fig. 4B). Similarly, for most purposes, k_UI is generally equal to λ_1.

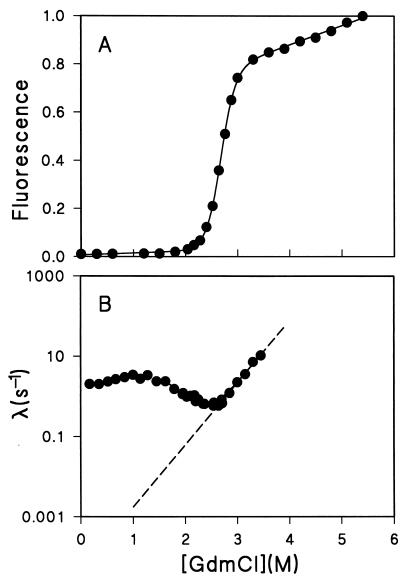
Figure 4.

Equilibrium and kinetic unfolding and refolding of Cyt c. (A) Equilibrium unfolding by fluorescence. The unit is defined arbitrarily with the last point at 5.4 M GdmCl taken as 1.0. The global unfolding data, fitted with a linear extrapolation (solid line; refs. 19 and 20), yield a ΔG_NU (1.0 M) = 6.7 ± 0.2 kcal/mol and a linear equation of ΔG_NU ([GdmCl]) = 10.7 ± 0.3 kcal/mol − (4.0 ± 0.1) (kcal/mol⋅M) [GdmCl](M). (B) The rate constants of the kinetic unfolding and the middle phase of the kinetic refolding as a function of GdmCl concentration. The dashed line represents the linear extrapolation of k_NI in logarithmic scale to 1.0 M GdmCl, which yields a value of k_NI 1.7 ± 0.6 × 10⁻³ sec⁻¹.

Indirect Measurement of k_IU.

To apply the kinetic criterion considered here, we want to compare k_IN to k_IU. The rate constant k_IU refers to melting of the stable I to the U under native conditions. It can only be determined indirectly. The value for k_IU can be determined in three independent ways. In all three approaches, λ₁ = k_UI + k_IU is obtained directly from refolding experiments under three-state conditions, as above. ΔG_IU, the stability of the I at native conditions, can be obtained from either of two different kinds of hydrogen-exchange experiments and independently from extrapolation of kinetic folding and kinetic unfolding data. The value of k_IU can then be obtained by algebra from λ₁ = k_UI + k_IU and ΔG_IU = −RT ln K_IU = −RT ln (k_IU/k_UI).

Elöve and Roder (27) measured ΔG_IU at 3 kcal/mol (pH 6.2, 10°C, 0.7 M GdmCl) by using the hydrogen-exchange pulse-labeling method with variable pulse pH. Independently, the N hydrogen-exchange results of Bai et al. (9) yield 2.3 kcal/mol for ΔG_IU at pD 7.0, 30°C, 0.7 M GdmCl. Kinetic experiments like those in Fig. 2A, done under these same conditions, provide k_UI and k_IN as described above. These values and the values for k_IU derived from them are listed in Table 1.

Table 1.

Thermodynamic and kinetic parameters of I_NC

Method	Conditions	ΔGIU, kcal/mol	kUI, sec−1	kIU, sec−1	kIN, sec−1
H/D pulse labeling (27)	pH 6.2, 10°C, 0.7 M GdmCl	3.0	55	0.3	2.7
N hydrogen-exchange (9)	pD 7.0, 30°C, 0.7 M GdmCl	2.3	61	1.3	10.0
Linear extrapolation	pH 6.2, 10°C, 1.0 M GdmCl	2.5	50	0.6	3.5

ΔG_IU values, obtained from hydrogen-exchange pulse labeling (27) or by the N hydrogen-exchange method (9) were taken from the literature where indicated or were computed from equilibrium unfolding data and the extrapolation of kinetic folding data as in Fig. 4. Values for k_UI were measured directly from the early phase of kinetic stopped-flow experiments done under three-state folding conditions, as in Fig. 2A. From these parameters, k_IU was evaluated by using ΔG_IU = −RT ln (k_IU/k_UI) and then compared with k_IN, measured from the later phase of the same stopped-flow experiments as for k_UI. These multiple comparisons all show that k_IN > k_IU, ruling out the off-pathway option, I ↔ U ↔ N. 

In a third approach, ΔG_IU was obtained from a linear extrapolation of kinetic data and the relationship ΔG_IU = ΔG_NU − ΔG_NI. ΔG_NU was obtained from equilibrium GdmCl unfolding and linear extrapolation to 1.0 M GdmCl (Fig. 4A; refs. 19, 20). ΔG_NI was measured by performing kinetic refolding and unfolding experiments as a function of GdmCl in the transition zone by using the method of Matoushek et al. (6). The unfolding rate constant k_NI at 1.0 M was obtained based on linear extrapolation of the right limb of the chevron curve in the transition zone where I are not populated (Fig. 4B; ref. 6). ΔG_NI was then calculated by using ΔG_NI = −RT ln(k_NI/k_IN). It leads to a value of ΔG_NI (1.0 M) 4.2 ± 0.1 kcal/mol. ΔG_IU (1.0 M) was then calculated to be 2.5 ± 0.2 kcal/mol. Finally, by using ΔG_IU = −RT ln(k_IU/k_UI) and λ₁ = k_UI + k_IU, the rate constant k_IU was determined to be 0.6 sec⁻¹ (Table 1). The consistent results from three independent methods show that the value of k_NI at 1.0 M GdmCl, based on the above linear extrapolation, seems correct.

The above calculations used linear extrapolation in the short range between 1.0 M and 2.3 M. In the case of Cyt c, it is known to be valid in this region (21). In fact, nonlinear behavior of unfolding free energy and the logarithm of kinetic unfolding rate constant as a function of the denaturant concentration do not affect the above analysis. It is because linear extrapolation underestimates the true unfolding free energy (21, 28–30). When a nonlinear effect is considered, it will favor the conclusion even more.

DISCUSSION

The results obtained here are summarized in Table 1. The three different methods yield the same conclusion, namely that I_NC of Cyt c moves to N significantly faster (about 7 times faster under the conditions tested) than it moves to U. Thus, I_NC cannot go through the U state on its way to N. I_NC is not an off-pathway I, according to the classical description (2, 31). Although I_NC does not unfold fully before folding to N, it may unfold partially, as it seems to do judging from the small but detectable negative dependence on GdmCl seen in Fig. 4B. Some unfolding, measured as increased surface exposure, occurs in the transition state leading from I to N. It was interpreted by Sosnick et al. (14) as a necessary partial unfolding to reorganize a misfolded and trapped segment before going forward. The present results show that in this partial unfolding, the previously formed native-like N and C helices do not unfold.

The problem of whether an I is on- or off-pathway has been considered since the earliest protein-folding work began (13, 31, 32), but we still do not know how to make this distinction. A number of suggestions as to how we might do so have been put forward: (i) compare the φ values of the I and transition states (1); (ii) look for a lag phase during which I accumulates before the acquisition of the final N (33, 34); and (iii) check for a negative dependence of folding rate on denaturant concentration (2, 35). However, in no case has the true situation been shown. Recently, a folding I of hen egg-white lysozyme with the α-domain folded I_α was suggested to be on-pathway, based on the denaturant dependence of rate in the low-concentration range (35). Although an off-pathway I may be consistent with such behavior, so is an on-pathway I with a transition state that exposes increased surface area, as has been suggested for Cyt c (14). The lysozyme work also assumed that the logarithms of the folding and unfolding rate constants are linear functions of GdmCl over a broad concentration range, but only a limited data set was used for the fitting. When a complete data set is used, the fitting for the triangle mechanism proposed deviates dramatically from the experimental data (unpublished results).

The approach shown in the present paper characterizes the folding and unfolding events by using multiple experimental methods. If an apparent three-state system can be isolated from other folding/unfolding events because of differences in time scales or populations, then a further test for a possible on-pathway I can be made, as described here. This avoids the uncertainty inherent in brute-force fitting.

ABBREVIATIONS

Cyt c

cytochrome c

GdmCl

guanidinium chloride

I

intermediate

N

native state

U

unfolded state

Note

Recently, Baldwin and coworkers (36) have shown that the late folding I_N of ribonuclease A is on the folding pathway. This I can also be shown to be on-pathway by using the kinetic criterion presented here, because the rate constant of I_N → N is 400 times larger than the rate constant of I_N → U.