Population Pharmacokinetic Analysis of Nonlinear Behavior of Piperacillin during Intermittent or Continuous Infusion in Patients with Cystic Fibrosis

Abstract

The purpose of this study was to describe the nonlinear pharmacokinetics of piperacillin observed during intermittent infusion and continuous infusion by using a nonparametric population modeling approach. Data were 120 serum piperacillin concentration measurements from eight adult cystic fibrosis (CF) patients. Individual pharmacokinetic parameter estimates during intermittent infusion or continuous infusion were calculated by noncompartmental analysis and with a maximum iterative two-stage Bayesian estimator. To simultaneously describe concentration-time data during intermittent infusion and continuous infusion, nonlinear models were parameterized as two-compartment Michaelis-Menten models. Models were fit to the data with the nonparametric expectation maximization algorithm. The calculations were executed on a remote supercomputer. Nonlinear models were evaluated by log-likelihood estimates, residual plots, and R² values, and predictive performance was based on bias (mean weighted error [MWE]) and precision (mean weighted square error [MWSE]). A linear pharmacokinetic model could not describe combined intermittent infusion and continuous infusion data well. A good population model fit to the intermittent infusion and continuous infusion data was obtained with the constructed nonlinear models. Maximum a posteriori probability (MAP) Bayesian R² values for the nonlinear models were 0.96 to 0.97. Median parameter estimates for the best nonlinear model were as follows: K_m, 58 ± 75 mg/liter (mean and standard deviation); V_max, 1,904 ± 1,009 mg/h; volume of distribution of the central compartment, 14.1 ± 3.0 liters; k₁₂, 0.63 ± 0.41 h⁻¹; and k₂₁, 0.37 ± 0.19 h⁻¹. The median bias (MWE) and precision (MWSE) values for MAP Bayesian estimation with the Michaelis-Menten model were 0.05 and 4.6 mg/liters, respectively. The developed nonlinear pharmacokinetic models can be used to optimize piperacillin therapy administered via continuous infusion in patients with CF and have distinct advantages over conventional linear models.

Piperacillin-tazobactam is a parenterally administered combination of a β-lactam antibiotic with a β-lactamase inhibitor (4). This drug combination is frequently used in the treatment of pulmonary exacerbations in patients with cystic fibrosis (CF) because of its good bactericidal activity against Pseudomonas aeruginosa and gram-positive microorganisms (20). Piperacillin, like other β-lactam antibiotics, exhibits time-dependent killing, and the parameter for the bactericidal effect is the time during which the concentration of the drug exceeds the MIC (5). As shown for ceftazidime (23), continuous infusion of piperacillin-tazobactam may result in superior efficacy with equal or lower total daily doses. Administration by continuous infusion also has distinct advantages in CF home treatment programs (24). A recent report on continuous intravenous administration of vancomycin also emphasized this point (27).

Data on the pharmacokinetics of piperacillin in patients with CF are scarce (12; J. S. Bertino, M. D. Reed, C. Meyers, and J. L. Blumer, ediatr. Res. 16:1210A, abstr. 254, 1982), while data for the combination are lacking. Piperacillin-tazobactam is commonly administered by intermittent infusion. In non-CF patient populations and with this mode of administration, the pharmacokinetics of the β-lactamase inhibitor- antibiotic combination appeared to be linear (1), although nonlinear analysis was not addressed. Some authors, however, have argued for nonlinear behavior, and studies have documented evidence for decreasing clearance with increasing concentrations (2, 3, 19). Piperacillin is, for the most part, excreted through the kidneys by active tubular secretion and by glomerular filtration. A typical characteristic of the active secretion process is a limitation in the capacity of this process. This behavior can be described in terms of Michaelis-Menten (MM) kinetics, where the rate of active transport increases toward a maximum value (V_max) with increasing plasma drug concentrations (11). The concentration at which the rate is 50% of its maximum is the K_m. At concentrations well below the K_m, the rate of excretion and the concentration vary in direct proportion. Drug clearance decreases in a nonlinear fashion with increasing concentrations, most notably at concentrations exceeding the K_m. In patients with CF, drugs that are extensively excreted by renal tubules (such as penicillins) show enhanced renal clearance (20). Using multiple constant-rate infusions of ticarcillin, Wang et al. (25) showed that renal clearance was enhanced due to increased affinity of the renal secretory system. Typically, secretory capacity was unaltered, but K_m values were significantly lower than those of controls.

Recently, while studying the pharmacokinetics and efficacy of high-dose piperacillin-tazobactam delivered via continuous infusion in patients with CF, den Hollander et al. observed significantly higher piperacillin clearance during continuous infusion than during intermittent infusion (J. G. den Hollander, S. E. Overbeek, A. A. Vinks, H. A. Verbrugh, and J. W. Mouton, Abstr. Proc. 20th Int. Congr. Chemother., abstr. 3071, 1997). This observation led us to hypothesize that the observed differences may be explained by a mechanism similar to that described for ticarcillin. As nonlinearity is a concentration-dependent phenomenon, it will be influenced by the mode of administration, especially when dosing regimens lead to very different concentrations. The high concentrations in serum during intermittent infusion may saturate the tubular secretion process, while the relatively low concentrations during continuous infusion (which remain below the K_m) may explain the observed differences in clearance. This scenario may have important clinical implications for the dosing of piperacillin administered via continuous infusion.

Until recently, it was not possible to analyze such nonlinear data, as appropriate software was lacking. With the development of a resource for the modeling of nonlinear pharmacokinetic-pharmacodynamic systems via the Internet, such an analysis has become feasible. The purpose of the present investigation was to analyze the nonlinear pharmacokinetics of piperacillin during intermittent infusion and continuous infusion in patients with CF by using a nonparametric population modeling approach. As tazobactam concentrations did not have nonlinear characteristics, these data were not part of the study.

MATERIALS AND METHODS

Patients.

Data were 120 serum concentration measurements obtained from eight adult CF patients (six women and two men) during intermittent infusion and continuous infusion of a piperacillin-tazobactam combination (Tazocin; AHP, Hoofddorp, The Netherlands). Patients participated in a clinical trial that was conducted at University Hospital Dijkzigt, Rotterdam, The Netherlands, and that was designed to evaluate the clinical efficacy, safety, and pharmacokinetics of piperacillin-tazobactam in CF patients during intermittent infusion and continuous infusion. Patients were treated for an acute exacerbation of their chronic P. aeruginosa infection with high doses of piperacillin-tazobactam. The total daily doses were 300 mg of piperacillin/kg of body weight/day (16 g) and 37.5 mg of tazobactam/kg/day (2 g). Patients received the piperacillin-tazobactam combination (piperacillin, 4,000 mg; tazobactam, 500 mg) in a crossover fashion either via intermittent infusion (piperacillin, 4 g; tazobactam, 0.5 g) every 6 h or via continuous infusion (piperacillin, 16 g; tazobactam, 2 g) over 24 h with an infusion pump. Prior to treatment, patients were randomized to either one of the regimens and were switched to the alternative regimen after 48 h.

Venous blood samples for drug assays were obtained from the arm opposite that used for the infusion of the antibiotic by using an indwelling needle. During intermittent infusion, samples were taken on day 2 prior to the sixth dose (time zero) and at 5, 30, 45, and 60 min and 1.5, 2, 3, 4, 5, and 6 h after the start of infusion. The duration of intermittent infusion was 30 min. During continuous infusion, samples were taken on the second day of continuous infusion treatment, just prior to the changing of the infusion reservoir (time zero), and at 2, 4, and 6 h into the infusion regimen. After samples were obtained, the blood was allowed to clot on ice for 20 min. It was then centrifuged, and the serum was stored at −70°C until analysis.

The study was approved by the Institutional Review Board of the University Hospital Dijkzigt, and written informed consent was obtained from each patient.

Drug assay.

Piperacillin concentrations in serum were analyzed by high-performance liquid chromatography by a modification of the method of Reed et al. (14). For piperacillin, briefly, 0.2 ml of a methanol solution containing 50 mg of methicillin/liter as an internal standard was added to an equal volume of serum sample, and the mixture was centrifuged. The supernatant was injected into a C₁₈ reversed-phase column (Chrompack, Middelburg, The Netherlands) with 0.05 M KH₂PO₄-0.05 M K₂HPO₄ (pH 6.9) containing 16% (vol/vol) acetonitrile as the mobile phase. Detection was done at 215 nm. The method was validated by using published guidelines (22). The lower limit of quantitation was 0.5 mg/liter and was determined by the method of Kucharczyk (10). All high-performance liquid chromatography measurements were obtained at 4°C.

In order to weight each serum drug concentration correctly by the reciprocal of its variance (Fisher information), the assay standard deviation (SD) was determined over the working range of the assay as described by Jelliffe et al. (9). The assay variance was estimated by regression modeling on the basis of four different concentrations over the working range. The assay error pattern was fitted best by the polynomial equation SD = 0.71470 + (0.030110 × C) + (0.000245 × C²), where the SD for the assay is given in milligrams per liter, C is the measured piperacillin concentration, and C² is the square of C. This polynomial equation for the assay error was also incorporated into the appropriate sections of the iterative two-stage Bayesian (IT2B) program and the nonparametric expectation maximization algorithm (NPEM3) program for population analysis (User Manual for Version 10.7 of the USC∗PACK Collection of PC Programs, Laboratory of Applied Pharmacokinetics, School of Medicine, University of Southern California, Los Angeles).

Pharmacokinetic parameter estimates.

Serum piperacillin concentration-time data (intermittent infusion and continuous infusion data) were analyzed by noncompartmental analysis (KINFIT, MW/PHARM, version 3.50; MediWare, Groningen, The Netherlands) (13) and by IT2B estimation (front part of NPEM3; intermittent infusion data) (User Manual for Version 10.7 of the USC∗PACK Collection of PC Programs). IT2B modeling included one- and two-compartment open-model analyses with zero-order input and first-order elimination from the central compartment. Parameters in the model were volume of distribution of the central compartment (V_c) (in liters), the elimination rate constant k_el (in hour⁻¹), and the intercompartmental rate constants k₁₂ and k₂₁ (in hour⁻¹), if applicable. The inverse of the estimated assay variance was used as the weighting in the pharmacokinetic modeling throughout. The goodness of fit was assessed by visual inspection of the predicted concentration-time profiles, log-likelihood estimates, residual analyses, and coefficients of determination. Model discrimination was performed by using Akaike's information criterion (AIC) (28). The Wilcoxon signed rank test was used to compare individual pharmacokinetic parameter estimates during intermittent infusion and continuous infusion. A P value of <0.05 was considered significant.

The IT2B individual pharmacokinetic parameter estimates were used in the simulation module of MW/PHARM to obtain piperacillin concentration estimates during continuous infusion.

Population pharmacokinetic analysis.

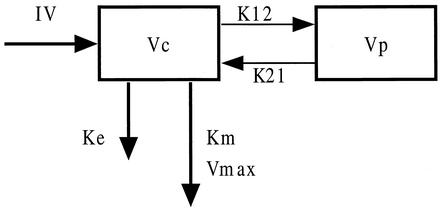
Based on the IT2B analysis and to mimic the renal elimination pathways for piperacillin, tubular secretion and glomerular filtration (25), models were parameterized as two-compartment models with elimination from the central compartment modeled as an MM process, as an MM process in combination with first-order elimination, or as a first-order elimination process only (Fig. 1).

FIG. 1.

Two-compartment open model used to fit piperacillin data. IV, zero-order infusion rate; Vc, central compartment; Vp, peripheral compartment; Ke, first-order rate constant; Km, MM constant; Vmax, maximum excretion rate; k₁₂ and k₂₁, intercompartmental rate constants. Structural models evaluated in this study had either first-order elimination (Ke), MM elimination, or a combination of MM and first-order elimination.

The general differential equation for the models was as follows:

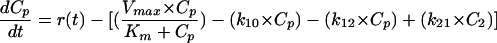where K_m is the MM constant (in milligrams per liter), V_max is the maximum elimination rate (in milligrams per hour), C_p is the plasma drug concentration (in milligrams per liter), C₂ is the concentration in the peripheral compartment, k_el is the first-order elimination rate constant (in hour⁻¹), k₁₂ and k₂₁ are distribution rate constants, and r(t) is the zero-order drug input rate in the central compartment (in milligrams per hour). In one model, the elimination rate constant k_e was defined as a function of the creatinine clearance (CL_CR) by the equation k_el = K_i + (K_s × CL_CR), where K_i is the intercept (representing residual nonrenal elimination) and K_s is the slope factor.

Differential equations for the models were defined in BOXES (USC∗PACK PC programs, version 10.7) (User Manual for Version 10.7 of the USC∗PACK Collection of PC Programs). Four different models were used in the final analysis (Fig. 1). (i) The MM model includes no first-order elimination from the central compartment. (ii) The MM-k_el combination model includes first-order elimination (k_el) from the central compartment, defined as k_el = 0.01 + (K_s × CL_CR), with K_s fixed at 0.0052 h⁻¹, according to published data (18). The value chosen for K_i corresponds to the residual k_el in dialysis patients (CL_CR, ∼0; half-life, ∼70 h). K_s is the mean slope value, as reported for people with normal renal function (CL_CR, ∼120 ml/min) (18). This model was evaluated to include CL_CR as a potential useful clinical descriptor. (ii) The MM-Ke combination model includes first-order elimination (k_el) from the central compartment, with no descriptors for k_el. (iv) The linear k_el model includes no MM elimination.

All models include V_c, k₁₂, and k₂₁ as additional parameters. In the modeling, the ranges for K_m and V_max were set at 0 to 750 mg/liter and 0 to 4,000 mg/h, respectively. Models were fit to the combined intermittent infusion and continuous infusion data with the Big-NPEM program (NPEM3) developed by R. W. Jelliffe and A. Schumitzky (16). To enable comparison with the IT2B analysis of intermittent infusion data, the best nonlinear model (MM model) was also fit to the intermittent infusion data. NPEM3 resides on the Cray T3E supercomputer at the San Diego Supercomputer Center and can be accessed over the Internet through the file transmission protocol. This resource can also be accessed more easily from its own web site (https://gridport.npaci.edu/LAPK/). Similar but smaller parallel computing facilities can now also be accessed at the University of Southern California Laboratory of Applied Pharmacokinetics modeling resource at www.lapk.org. Calculations were executed on the remote mainframe computer by up- and downloading of data and results via the Big-NPEM protocol and through the file transmission protocol. The inverse of the estimated assay variance was used as the weighting. With NPEM3, the total observation variance is approximated by the assay variance. Models were evaluated by residual analyses, coefficients of determination, AIC, and log-likelihood values. Finally, maximum a posteriori probability (MAP) Bayesian estimation was used to generate parameter estimates for each patient. Predictive performance evaluation was based on bias (mean weighted error [MWE]) and precision (mean weighted square error [MWSE]) (17; User Manual for Version 10.7 of the USC∗PACK Collection of PC Programs).

RESULTS

Pharmacokinetic parameter estimates.

The demographic data and genotypes for the patients are given in Tables 1 and 2, respectively.

TABLE 1.

Demographic and clinical data for eight adult patients with CF and participating in this study

Characteristic	Valuea
No. of patients	8
No. of men/women	2/6
Age (yr)	25.8 ± 3.6
Height (cm)	171.3 ± 5.3
Wt (kg)	57.0 ± 9.9
LBM (kg)b	56.5 ± 9.3
BSA (m2)c	1.67 ± 0.16
BMI (kg/m2)d	20.5 ± 0.6
CLCR (ml/min/1.73 m2)e	96.1 ± 20.7

^aData are expressed as mean and SD, unless otherwise indicated.

^bLBM, lean body mass, calculated by the method of Hallynck et al. (7).

^cBSA, body surface area, calculated by the method of DuBois and DuBois (6).

^dBMI, body mass index, calculated as weight in kilograms/(height in meters)².

^eCalculated according to the formula of Jelliffe and Jelliffe as described previously (21).

TABLE 2.

Genotypes for patients in this study

Patient with CF	Mutationa
1	ΔF508 and ΔF508
2	L927P and DE1260
3	ΔF508 and W1282
4	ΔF508 and unknown
5	ΔF508 and 1717-1A
6	Unknown and unknown
7	ΔF508 and unknown
8	ΔF508 and ΔF508

^aBoth alleles of the CF gene have this mutation, or one allele of the CF gene has this mutation and the mutation of the other allele is unknown. ΔF508 CF gene mutation that results from the deletion of phenylalanine at position 508 of the cystic fibrosis transmembrane conductance regulator gene.

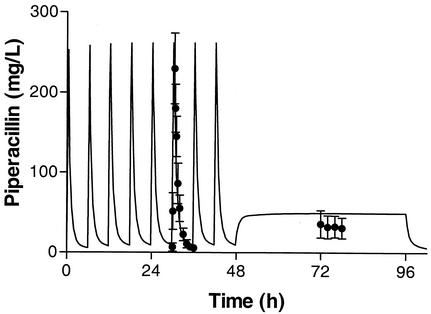
In the IT2B modeling, a two-compartment model best described the data for most of the patients (six of eight), based on the AIC, and was therefore chosen as the most appropriate for the population analysis. Mean piperacillin pharmacokinetic values based on separate intermittent infusion and continuous infusion noncompartmental data analyses are summarized in Table 3. Piperacillin clearance during continuous infusion (24.4 ± 11.7 liters/h) (mean and SD) was significantly higher than that during intermittent infusion (13.1 ± 2.3 liters/h) (P < 0.02). The mean and median parameter estimates for the IT2B modeling with intermittent infusion data only are shown in Table 4. These estimates were used to predict piperacillin concentrations during continuous infusion. However, as shown in Fig. 2, the observed piperacillin concentrations during continuous infusion (32.8 ± 14.4 mg/liter) (mean and SD) were significantly lower than those predicted (54.3 ± 12.1 mg/liter) (P < 0.001) by the individual IT2B pharmacokinetic values.

TABLE 3.

Pharmacokinetic parameter estimates obtained by noncompartmental analysis^a

Infusion	AUC0-6 (mg · h/liter)	CL (liters/h)	Vss (liters)	t1/2 (h)
Intermittent	313.0 (56.2)	13.1 (2.3)	16.9 (6.1)	1.2 (0.9)
Continuous	196.0 (83.1)	24.4 (11.7)	NA	NA

^aValues are reported as mean (SD). AUC_0-6, area under the curve from 0 to 6 h; CL, clearance; V_ss, volume of distribution at steady state; t_1/2, half-life; NA, not applicable. P values for intermittent infusion versus continuous infusion were <0.001 and <0.02 for AUC_0-6 and CL, respectively.

TABLE 4.

Piperacillin IT2B pharmacokinetic parameter estimates^a obtained with a linear pharmacokinetic model

Parameter	Vc (liters)	kel (h−1)	k12 (h−1)	k21 (h−1)
Mean	12.04	1.053	0.531	0.905
Median	11.91	1.036	0.325	0.198
SD	1.83	0.162	0.510	1.207

^aBased on intermittent infusion data.

FIG. 2.

Mean (and SD) piperacillin concentration-time profile during intermittent infusion (piperacillin, 4 g; tazobactam, 0.5 g; every 6 h) and continuous infusion (piperacillin, 16 g; tazobactam, 2 g; over 24 h) with the linear model. The solid line represents the fit with the linear model based on the intermittent pharmacokinetic data. For clarity, drug regimen crossover data are presented similarly (intermittent infusion followed by continuous infusion).

Population modeling.

The median and mean population parameter estimates and associated dispersion factors generated by NPEM3 are shown in Table 5. Parameter values were not significantly different among nonlinear models. In contrast, mean and median estimates for volume of distribution in the linear model (e.g., median V_c, 23.1 ± 13.5 liters) were significantly higher than the nonlinear model estimates (e.g., median V_c, 13.7 ± 3.3 liters for the MM model) (P < 0.04).

TABLE 5.

Piperacillin population pharmacokinetic parameter estimates obtained by NPEM3 analysis^a

Model and parameter	Km (mg/liter)	Vmax (mg/h)	kel (h−1)	Vc (liters)	k12 (h−1)	k21 (h−1)
MM
Mean	92.3 (85.6)	2,284 (1,046)	NA	13.67 (3.28)	0.600 (0.369)	0.410 (0.280)
Median	57.8 (74.8)	1,904 (1,009)	NA	14.08 (2.98)	0.630 (0.413)	0.367 (0.194)
MM-kel combination (no descriptors for kel)
Mean	83.8 (94.3)	1,836 (785)	0.0033 (0.0027)	13.78 (4.00)	1.030 (0.950)	0.433 (0.827)
Median	44.9 (62.1)	1,401 (859)	0.0023 (0.0031)	11.75 (4.40)	0.575 (1.129)	0.825 (0.750)
MM-kel combination (kel as a function of CLCR)b
Mean	77.2 (117.0)	1,572 (1,150)	NA	10.99 (3.07)	1.327 (1.222)	0.810 (0.580)
Median	32.9 (64.6)	1,151 (655)	NA	10.75 (2.32)	0.950 (1.120)	0.591 (0.598)
Linear kel
Mean	NA	NA	0.846 (0.197)	23.09 (13.45)	0.883 (1.181)	0.846 (0.197)
Median	NA	NA	0.953 (0.209)	17.59 (10.87)	0.447 (0.847)	0.953 (0.209)

^aParameters are expressed as follows: mean and median, standard deviation, as defined in User Manual for Version 10.7 of the USC*PACK Collection of PC Programs; NA, not applicable.

^bCalculated as 0.01 + (k_s × CL_CR), with k_s fixed at 0.0052 h⁻¹.

Evaluation of predictive performance.

Table 6 summarizes log-likelihood values, coefficients of determination (R²), and predictive performance of the three nonlinear models and the linear model, determined with mean error (measure of bias) and mean square error (measure of precision). Based on the log-likelihood values, the MM model describes the data best. The bias and precision estimates of the nonlinear models were in the same range, but all were significantly better (P < 0.01) than those of the linear model, as is evident from the smaller MWE and MWSE values.

TABLE 6.

Evaluation of the predictive performance of piperacillin population models^a

Model	Log likelihood	R2	Bias (ME, mg/liter)	MWE (mg/liter)	Precision (MSE [mg/liter]2)	MWSE (mg/liter)
MM	−485.9	0.973	0.37	0.05	143.3	4.55
MM-kel combination (kel as a function of CLCR)b	−645.7	0.956	0.17	−0.42	270.0	7.12
MM-kel combination (no descriptors for kel)	−700.9	0.960	−5.23	−0.93	227.7	8.26
Linear kel	−1,246.3	0.881	−11.74	−0.11	905.1	29.94

^aME, mean error; MSE, mean squared error.

^bCalculated as 0.01 + (k_s × CL_CR), with k_s fixed at 0.0052 h⁻¹.

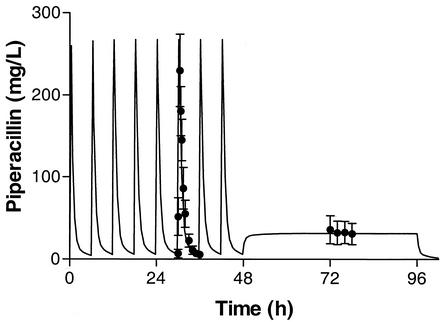
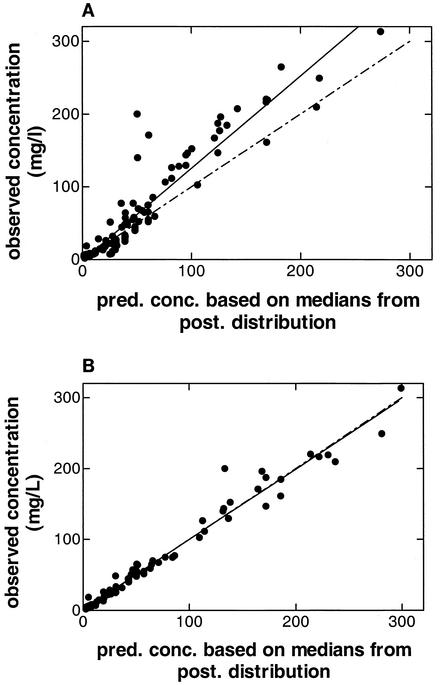
The MM model based on intermittent infusion data fit the data better than the linear model (Fig. 3). This fit was almost identical to that obtained with the MM model based on combined intermittent infusion and continuous infusion data (Tables 5 and 6). Figure 4 shows the relationship between the observed piperacillin concentrations (y axis) and the MAP Bayesian-predicted concentrations obtained with the linear and MM models (x axis) for all 120 observations in the eight patients. In the Bayesian estimation, median values were used for each parameter as the measure of central tendency. This strategy has been found to improve predictive performance (R. W. Jelliffe, personal communication). As determined by weighted linear regression analysis, the line of best fit (solid line) for the linear k_el model differed significantly from the line of identity (broken line) (Fig. 4A). The line of best fit (solid line) for the MM model did not differ from the line of identity (broken line), and the intercept did not differ significantly from 0.0 (Fig. 4A). The coefficient of determination (R²) was 0.973. Predictive performance relationships for the other nonlinear combination models were comparable to those for the MM model (R², 0.956 and 0.960).

FIG. 3.

Mean (and SD) piperacillin concentration-time profile during intermittent infusion (piperacillin, 4 g; tazobactam, 0.5 g; every 6 h) and continuous infusion (piperacillin, 16 g; tazobactam, 2 g; over 24 h) with the MM model. The solid line represents the fit with the MM model based on the intermittent pharmacokinetic data.

FIG. 4.

Scatter plot of observed versus MAP Bayesian-predicted concentrations obtained with the population model median parameter estimates for the linear model and the best nonlinear model (MM model). (A) For the k_el model, the slope and the intercept of the line of best fit (solid line) are significantly different from 1.0 and 0.0 (broken line), respectively. The R² value is 0.88. (B) For the MM model, the slope and the intercept of the line of best fit (solid line) are not different from identity and 0.0 (broken line), respectively. The R² value is 0.97. pred. conc., predicted concentration; post., a posteriori.

DISCUSSION

The purpose of this study was to describe the nonlinear behavior of piperacillin observed when the drug was administered via two distinct dosing methods, intermittent infusion and continuous infusion (Den Hollander et al., Abstr. Proc. 20th Int. Congr. Chemother.). During continuous infusion of the same total daily dose, piperacillin steady-state concentrations were, on average, 40% (range, 6 to 69%) lower than expected based on intermittent infusion pharmacokinetic parameter estimates. The results indicate that a nonlinear model better describes piperacillin pharmacokinetics in patients with CF than does a linear model (Fig. 4 and Table 6). With the increasing use of β-lactam antibiotics administered by continuous infusion, this finding has important clinical implications. Most dosing guidelines for continuous infusion of antibiotics are not based on clinical efficacy studies but are typically derived from the total daily intermittent infusion dose (24). As the renal clearance of ticarcillin, a related acylureido-penicillin derivative, was increased in patients with CF as a result of increased tubular secretion compared to that in healthy volunteers (25), we hypothesized the existence of a similarly affected renal anion excretion system for piperacillin. Recently, more theoretical evidence for this phenomenon was provided. Investigators studying CF were able to simulate an increased rate of renal organic anion secretion in the renal tubules and hence, due to enhanced tubular secretion, lower steady-state serum drug concentrations (26). An enhanced affinity for the secretory site(s) similar to that shown for ticarcillin in patients with CF and lower K_m values may very well explain our observations for piperacillin. In fact, with our nonlinear modeling approach, the K_m and V_max estimates obtained in the present study correspond well to those reported for ticarcillin. In the study of Wang et al. (25), unbound ticarcillin K_m and V_max estimates were 33.7 mg/liter (coefficient of variation, 36%) and 950 mg/h (coefficient of variation, 48%), respectively. However, when corrected for the concentration-dependent protein binding (37 to 57%) of ticarcillin, the corresponding K_m and V_max estimates for total ticarcillin are in the ranges of 91 mg/liter and 1,667 to 2,568 mg/h, respectively, and are in good agreement with our data for piperacillin (Table 5).

Over the past decades, there has been controversy over the proposed nonlinear elimination of piperacillin. Interestingly, for healthy volunteers, a recent population pharmacokinetic analysis claimed linear pharmacokinetics for piperacillin after multiple doses (1). An explanation for the inconsistent findings may be related to study design. In the present study, we used the same dose administered via two different modes of administration, intermittent infusion and continuous infusion, in a crossover fashion. Pharmacokinetic modeling of piperacillin after intermittent administration did not show obvious nonlinear or “hockey stick” behavior indicative of nonlinear elimination. As the elimination of piperacillin is, for the most part, governed by two processes, nonlinear secretion and linear filtration, changes in tubular secretion at the point at which concentrations approach saturation may very well be compensated for by increases in the filtration clearance of unbound drug. Only at concentrations well below the K_m may these effects on clearance become most obvious.

Although the objective of this study was to model the nonlinear behavior of piperacillin, we also estimated clearance and other pharmacokinetic parameters after multiple doses by linear modeling. The calculated pharmacokinetic parameter values after intermittent infusion are different from earlier observations in young patients with CF. Reed et al. (15) and Bertino et al. (Pediatr. Res. 16:121A, abstr. 254), using high-dose therapy (600 to 900 mg/kg/day), found mean total body clearance values of 305.6 and 341.6 ml/min/1.73 m², respectively, values that are higher than the 226.2 ml/min/1.73 m² found in this study. The main reason for this discrepancy is most likely the older age of our patients, as with age, renal elimination gradually diminishes. Besides age, the CF genotype may play an important role in potential pharmacokinetic differences, as was recently shown for tobramycin pharmacokinetics (P. M. Beringer, A. A. Vinks, R. W. Jelliffe, H. G. M. Heijerman, and B. J. Shapiro, Pediatr. Pulmonol., abstr. 342, 28(S19):261, 1999). In fact, the oldest patient in our study was 31 years old but did not show a large difference between predicted and observed steady-state piperacillin concentrations. Although the patient had a positive sweat test, the genotype was not known, and it is tempting to speculate that this patient may have had a mild mutation. This mild mutation may have resulted in less of an effect or a different effect on tubular piperacillin processing.

We chose to model our data in accordance with the major renal elimination processes, tubular secretion and filtration. Reabsorption is assumed to be negligible on the basis of the pK_a values of piperacillin, which indicate that most of the drug is in its ionized form at normal urinary pHs, thus preventing reabsorption. The models in which the rate of excretion was determined by tubular secretion and glomerular filtration also performed well.

A comparison by linear regression of observed versus predicted piperacillin concentrations resulted in nearly identical plots, such as the one shown in Fig. 4, for all three nonlinear models. CL_CR is an attractive descriptor in the model that can be useful clinically. Unfortunately, only a small range of CL_CR values was available, making further validation with a larger population over a broad range of clearance values necessary.

Despite the good ability of the MAP Bayesian estimator to predict observed concentrations, as indicated by low bias and relatively good precision, the parameter estimates showed large interindividual variability. This result may have been partly due to genotypic variability, as the highest K_m and V_max values were associated with non-ΔF508 mutations (Table 2, patients 2 and 6). Further studies are necessary to determine whether a direct relationship exists between genotype and piperacillin clearance.

In summary, for this group of CF patients, the nonlinear population modeling approach could describe piperacillin data well and was superior to the linear model. The population pharmacokinetic models can be used to design effective continuous infusion dosage regimens for the treatment of patients with CF. Models can also be used as a priori information in Bayesian feedback programs for further piperacillin dosage optimization. The modeling method using a remote supercomputer provides a new tool and a research resource for describing the behavior of large nonlinear systems. Recent new methods for access to the system and for improving the computations themselves have greatly improved the ease of access and the speed of the computations (A. Botnen, R. W. Jelliffe, M. Thomas, and N. Hoem, Abstr. 14th IEEE Symp. Comput. Based Med. Syst., p. 163, 2001; R. Leary, R. W. Jelliffe, A. Schumitzky, and M. Van Guilder, Abstr. 14th IEEE Symp. Comput. Based Med. Syst., p. 389, 2001).