Elastic Response, Buckling, and Instability of Microtubules under Radial Indentation

Abstract

We tested the mechanical properties of single microtubules by lateral indentation with the tip of an atomic force microscope. Indentations up to ∼3.6 nm, i.e., 15% of the microtubule diameter, resulted in an approximately linear elastic response, and indentations were reversible without hysteresis. At an indentation force of around 0.3 nN we observed an instability corresponding to an ∼1-nm indentation step in the taxol-stabilized microtubules, which could be due to partial or complete rupture of a relatively small number of lateral or axial tubulin-tubulin bonds. These indentations were reversible with hysteresis when the tip was retracted and no trace of damage was observed in subsequent high-resolution images. Higher forces caused substantial damage to the microtubules, which either led to depolymerization or, occasionally, to slowly reannealing holes in the microtubule wall. We modeled the experimental results using finite-element methods and find that the simple assumption of a homogeneous isotropic material, albeit structured with the characteristic protofilament corrugations, is sufficient to explain the linear elastic response of microtubules.

INTRODUCTION

Microtubules

In most eukaryotic cells a combination of three types of protein filaments—F-actin, microtubules (MTs), and intermediate filaments—and their accessory proteins make up a three-dimensional polymer network, the cytoskeleton. The cytoskeleton acts as a mechanical framework for the cell, providing rigidity and shape. It is involved in many complex active cellular tasks such as motility, growth, and mitosis/meiosis (1). The polymeric construction materials of the cytoskeleton differ in many ways from common technical polymers; for one thing, most are “semi-flexible” or rather rigid as single filaments. Considerable progress has been made in understanding the relationship between molecular and collective structure and function (2). Basic to understanding the whole cytoskeleton is an understanding of the individual filaments.

MTs are the most rigid of the cytoskeletal filaments and have the most complex structure. Their outer diameter is ∼25 nm, whereas length can vary from tens of nanometers to tens or even hundreds of micrometers, frequently spanning the whole cell (1). In vivo MTs are composed of 13 parallel protofilaments (3), which are connected laterally into hollow tubes (Fig. 1 a). The number of protofilaments of in vitro polymerized MTs has been found to vary between 11 and 17, depending on buffer conditions (4). Protofilaments consist of head-to-tail connected dimers of α and β tubulin (55 kD each). The atomic structure of tubulin has been solved by electron crystallography (5), and the whole MT structure has subsequently been reconstructed by electron microscopy (EM) (6).

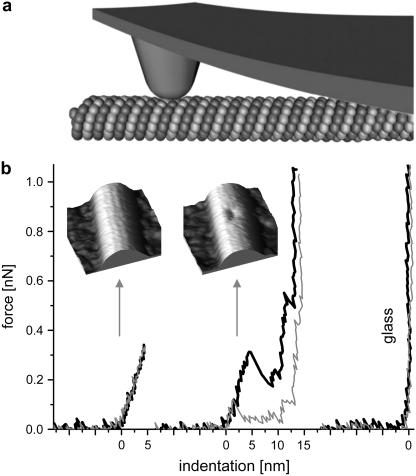
FIGURE 1.

(a) Sketch of the experiment (not to scale). The MT is built from tubulin proteins arranged in a tube. The AFM tip mounted on a cantilever deforms the MT locally. (b) Typical force-versus-indentation curves: black is the pushing curve, gray the retraction curve. The left curve shows that the MT deformed linearly and reversibly for forces up to 0.3 nN. The inset scan shows an MT after the pushing experiment. For the middle curve, more force was applied. The MT collapsed and the backward curve shows that the deformation is irreversible. The inset image shows the damaged MT afterward. The right curve was performed on glass.

Resistance to bending is clearly an important property of microtubules in many of their functions. During mitosis, MTs form the mitotic spindle. Many single cellular eukaryotic organisms and also many cells of higher eukaryotes (such as sperm cells or lung epithelial cells) possess cilia or flagella, specialized bundles of microtubules, to propel themselves or to pump fluid. Microtubules also form the core of neuronal axons.

Mechanical measurements

The bending stiffness of MTs has been measured both passively, by analyzing thermal fluctuations in shape, and actively, using optical tweezers (for an overview, see van Buren et al. (7)). Published values for the flexural rigidity range all the way from 1 × 10⁻²⁴ to 32 × 10⁻²⁴ Nm². Complementary to bending of MTs, it is possible to explore how they respond under a very different force, namely one leading to a radial indentation. We recently tested MT elasticity by indentation with atomic force microscopy (AFM) and modeled the tubes with a thin-shell finite-element model (8).

In this article, we describe in more detail the linear elastic response of microtubules tested in the same way. We demonstrate that the results can be very well described using macroscopic continuum mechanics. We have extended the finite-element modeling beyond thin-shell dynamics to explore buckling and to explain the effect of the protofilaments as axial reinforcements. We furthermore control for the effect of the finite AFM tip size. At higher forces we observed instabilities and breakage events of the microtubule wall in the experiments, likely representing either bond rearrangements or breakage of a few protein bonds, which were remarkably reversible as long as the damage was limited.

METHODS

Sample preparation

Tubulin was purified from porcine brain using standard methods (9), and polymerized at 3 mg/ml concentration by adding 10% glycerol and 1 mM guanosine triphosphate, and then incubated at 36°C for 30 min. MTs were diluted to 10 μg/ml in buffer (80 mM Pipes, pH 6.9, 1 mM EGTA, 2 mM MgCl₂, 10 μM paclitaxel (Sigma Aldrich, Zwijndrecht, The Netherlands).

To immobilize the negatively charged MTs on a surface, clean glass coverslips were derivatized with a positively charged silane by immersing in a 0.1% solution of aminopropyl-triethoxy-silane (Sigma Aldrich) or trimethoxysilylpropyl-diethylenetriamine (Sigma Aldrich). They were then rinsed with water and dried at, respectively, 65°C or 110°C.

A 20-μl amount of MT sample was incubated for 10 min on the silanized surface. The sample was then washed with multiple volumes of buffer to remove the unbound MTs, and mounted on the AFM, without letting the sample dry out. All experiments were performed at room temperature.

AFM imaging

To minimize damage induced by scanning, we operated the AFM in “jumping mode” (10), which we found suitable for obtaining single-protein resolution in liquid while maintaining the structural integrity of the MTs (11). In this mode, the AFM performs a force-distance curve (FZ) at every point of a raster scan, with a maximum vertical force that is set as a parameter. For each point, the vertical sample position at this set force is recorded. The tip is then elevated to ∼30 nm from the surface before performing the lateral motion to the next point, thereby minimizing lateral drag forces on the sample.

Force-versus-distance curves

First we imaged an intact MT in a scan area of ∼150 × 150 nm². While recording the next image, an FZ curve was performed in the center of the MT, which was located from a preceding scanline. To perform an FZ curve, the scanner piezo stopped xy scanning and performed a ramp in the z direction starting from a predefined distance. Force corresponds to the deflection of the cantilever, which is detected by a reflected laser beam on a split photo detector and is recorded as function of the z motion.

Diode signals (in Volts) were converted to absolute deflection (in nm) using an FZ curve on the glass substrate (using the fact that the glass is incompressible). This deflection signal is converted to force via the known cantilever stiffness.

Typically we started an FZ curve with the tip elevated 30 nm above the MT, and used a z displacement between 35 and 70 nm. Every FZ curve was sampled with 3000–10,000 sample points at 15 KHz, and every point of the plotted curves was averaged from ∼30 sample points.

Varying the approach speed from 30 to 160 nm/s did not result in differences in elastic behavior or breakage events.

Force-versus-indentation curves

When performing an FZ curve on top of an MT, the cantilever and the MT can be regarded as two springs in a series (Eq. 1):

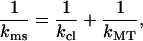(1)

which gives, for k_MT,

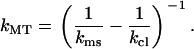(2)

Assuming that both springs are linear, the MT spring constant k_MT can be simply calculated by filling in k_ms and the known spring constant for the cantilever k_cl in Eq. 2. If the measured response is not linear, i.e., k_ms is not a constant, a data analysis program can be used to subtract the cantilever deflection from every measured data point.

Stiffness maps

To visualize the stiffness distribution during imaging in jumping mode, a development version of the WSxM scanning software was used (Nanotec, Madrid, Spain) (see also A-Hassan et al. (12). For each scanpoint, an FZ curve (∼40 nm in 10 ms) is performed with the force limited to ∼100 pN to prevent damage. A linear fit is performed to the contact part of the retraction curves (the region for fitting is selected by the user), normally sampled with ∼10 points counted from the point of maximum cantilever deflection and its slope is stored. The acquisition of every xy coordinate, for which both the height and slope are stored, takes ∼20 ms. Afterward, the spring constant can be calculated as shown previously.

Cantilevers

To test the independence of the results of the type of cantilevers used for the experiment, we used two different rectangular cantilevers from Olympus (RC800PSA, 200 × 20 μm, 0.05 N/m; and BL-RC150VB, 60 × 30 μm, 0.03 N/m). Of most cantilever batches we calibrated a few using the Saders method (13); otherwise, we used the stiffness values given by Olympus.

Finite-element modeling

For finite-element modeling, we used FEMLAB 3.1i (Comsol, Zoetermeer, Netherlands). We created several models to test the importance of the boundary conditions and tube geometry.

1. We first calculated the response of a thin-shell long tube made of a homogeneous elastic material, where compression in the normal direction of the shell, i.e., thickness variation, is ignored. The model uses the approximation R ≫ t, i.e., it ignores terms higher than those of the lowest order in t/R wherever possible. Buckling also does not occur in this model. The model consisted of ∼7000 elements, and the element size was set smallest (0.3 nm) close to the loading point and increased with the distance from the loading point. The thin-shell tube model was subjected to two opposing, radially applied point forces.

2. The same thin-shell tube model was fixed at the bottom rib over its whole length and the point force was applied at the top.

3. We replaced the point force with a parabolic tip. We used a contact-penalty stiffness method. Nonlinear springs connected the tip with the tube surface. During periods of noncontact, these springs have a very low stiffness and do not contribute to the deformation. When the gap between the tip and tube closes, the springs become very stiff and the tube gets indented such that it respects the boundary set by the tip shape. By integrating the vertical component of the load over the total contact area, the force is obtained (the horizontal components cancel out due to symmetry). Models were solved using the parametric nonlinear solver of FEMLAB, where the parameter solved for is the stepwise lowering of the tip onto the tube. We validated this approach by finding that a parabolic tip with a small radius (2 nm) gives similar results as indentation with a point force up to ∼10 nm indentation. For bigger tip radii (up to 60 nm) we found that the deformed tube surface did not intersect the tip surface.

4. We replaced the thin shell by three-dimensional “brick elements” where both, compression in the normal direction and buckling occur, and indented with a parabolic tip. The model consisted of ∼25,000 elements, with smaller elements close to the loading point.

5. The model described in item 4 was modified by making the outer surface of the tube corrugated to simulate the effects of the protofilaments (see Fig. 9, inset). The model consisted of ∼55,000 elements, with smaller elements close to the loading point.

FIGURE 9.

MT model including the protofilaments. The Young's modulus was set to 0.6 GPa. The behavior was very similar to that of the thick-walled tubes. The graph shows the difference in response between pushing on top of the protofilament or between two protofilaments (by rotating the model). The difference is ∼13% and was also visible in our experiments (Fig. 4).

To reduce computing time, all models were reduced to quarter-tubes taking advantage of the two mirror planes of symmetry perpendicular to the supporting surface, one parallel and one perpendicular to the tube axis. Computation time on a standard PC could still reach days for the thick-shell models.

RESULTS

Linear response

The mechanical response of an object to an external force depends on both geometry and the material properties of the object. The elastic behavior we measured for MTs is determined by their tubular shape and by the elastic properties of the tube wall material, the tubulin proteins. For a macroscopic cylindrical shell made from a homogeneous isotropic material and subjected to a point load, a linear elastic response is expected for deformations on the order of the shell thickness. In general there is also a viscous component of the response, but for the compression rates used here, the viscous drag forces against the fluid are negligible.

Fig. 1 b shows that MTs, although they are only 25 nm in diameter, responded like macroscopic tubes for forces up to ∼0.3 nN, which corresponded to a 15% deformation. The response was linear and reversible. Only at higher forces sudden steps in the indentation were seen, and the deformation was no longer reversible. To determine the reproducibility of the linear elastic part of the deformation, we recorded >100 FZ curves during multiple experiments and used two different types of cantilevers (Fig. 2). Although the cantilevers had different dimensions and spring constants, the values found for the MT response were independent of the cantilevers. To quantify the spring constant, a fit was performed to the linear part of the deformation, resulting in a value of 0.074 N/m ± 17% (mean ± SD). The average standard deviation found in the individual experiments (set of measurements performed with the same cantilever) was 13%, showing that variations in the cantilever spring constant contribute roughly equally to the observed variation. The remaining sources of variability can include boundary conditions (MT attachment) and the fitting procedure, but also (local) differences in MT elasticity.

FIGURE 2.

Microtubule spring constants measured using two different types of cantilevers (0.03 N/m, n = 57, and 0.05 N/m, n = 50). The 14 experiments were performed on two different AFMs, each time using new cantilevers and samples. The Gaussian fit (performed on the cumulative histogram) gives 0.074 N/m ± 17% (mean ± SD).

Several EM studies (14,15) have reported transitions in the number of protofilaments with a frequency of about one per 15–17 μm, which should give a variation in MT diameter and a clear difference in stiffness. In the hundreds of micrometers of MTs scanned we never found clear evidence for a variation in the protofilament number, which should show up as a combination of a changed height and stiffness and protofilaments forming an angle with the MT axis.

It is expected that the deformed region of a tube under a point load will extend to both sides in the axial direction for several tens of nanometers (8). We confirmed this estimate by finite-element modeling (see below). This implies that the end of an MT should appear softer. To probe this, we cut MTs (by scanning at high force >0.3 nN) and obtained FZ curves close to the cut ends. Fig. 3 shows that, in agreement with the modeling, this effect is not seen until ∼50 nm distance from the end. Experimentally it was difficult to probe closer to the end.

FIGURE 3.

Indentation experiments were performed close to a previously cut end of an MT (see inset). The graph shows spring constants (normalized to values obtained on the same MT far from the cut) and the force at which the MT collapsed. At distances >∼50 nm from the end of the MT, no effect was measurable; at lower distances, the MT rigidity seemed affected. The curve gives the spring constant predicted by FEM, using the thin-shell model, which also shows that end effects occurred only at distances <∼50 nm.

To check for more local variations in the stiffness on the MT surface, we recorded stiffness maps (see Methods). In Fig. 4 b, such a stiffness map shows a fairly homogenous distribution of the MT stiffness over its surface. The stiffness in the center and up to a few nm to each side was constant and than decreased slightly toward its sides. This behavior was qualitatively reproduced in finite-element modeling with a finite tip size and involves contact with the side of the tip and lateral deformation, the response to which in turn depends on not well-controlled surface-attachment conditions (data not shown). Thus, overall, the probed elasticity is relatively insensitive to the exact location and does not rely on nanometrically accurate positioning of the probe exactly at the center of the tubes. The stiffness map in Fig. 4 b also shows an axial pattern representing the protofilaments. When overlaying the stiffness maps with the simultaneously recorded topography images (Fig. 4 a), it becomes evident that the stiffness is slightly higher when probed between two protofilaments than when probed on top of one protofilament, which we discuss in Modeling. The observed difference in stiffness (∼10%) is close to the noise in the measurements so it does not show in the histogram of Fig. 2.

FIGURE 4.

(a) MT topography and (b) simultaneously acquired stiffness map, with the darker colors representing softer regions. The MT was clearly softer than the background, and the stiffness on the MT was homogeneously distributed over its surface. Toward the sides, the stiffness was slightly reduced. Also the MT appeared stiffer when probed between the protofilaments, as indicated by the lines.

Nonlinear response

An ideal thin-walled tube shows a linear response to an indentation depth on the scale of the wall thickness. For larger indentations, buckling occurs accompanied by an inversion of curvature from convex to concave in the radial direction (16). Note that, in contrast to spherical shells, curvature in the axial direction will immediately be concave. In our experiments, the situation will be modified in several ways. 1), Thermal fluctuation of the cantilever (root-mean-square deflection of the tip by ∼0.5 nm) will cause a smooth transition to contact. 2), Insertion of the tip into the finite-thickness wall (Hertzian contact (17)) will cause a gradual stiffening on a scale of, in our case, not more than ∼1 nm. Over this distance the compression of the wall dominates the total indentation. 3), The finite tip size causes an increasing contact area and becomes strongly noticeable at large indentations, where it tends to cancel the effects of buckling.

Fig. 1 b shows that the measured response remained very close to linear up to deformations of ∼3.6 nm and exhibited no clear signs of nonlinearities before collapse. Collapse of the tubes is expected when the stress exceeds the ultimate strength of the material. For the MT, this happened at tip forces >∼0.3 nN, where the deformation became clearly nonlinear and irreversible. The breakage itself was most likely caused by the rupture of protein bonds between the tubulin subunits.

To investigate the events near collapse, we limited the applied force to 0.3–0.4 nN and then sampled with high temporal resolution. Surprisingly, this revealed an instability resulting in a well-defined ∼1-nm step of the tip at 0.27 nN ± 30% (mean ± SD) preceding the catastrophic collapse of the MTs (Fig. 5 a). In Fig. 5 b, we applied just enough force to see the step but to avoid the collapse of the MT. These force-indentation curves show that the step was reversible; the retraction curves show the backward steps occurring at a slightly lower force of 0.21 nN ± 20%. Subsequent imaging did not reveal any damage in the MTs. In most cases, we could perform multiple such curves at a single location without seeing damage in the images afterwards, suggesting a self-healing mechanism.

FIGURE 5.

(a) Twenty-four indentation curves from five different experiments. The curves are shifted such that the first steps superimpose. At an average force of 0.27 nN a stepwise indentation of 1 nm is clearly visible, after which the deformation continues with a comparable slope. Then, at an average force of 0.35 nN, a sequence of multiple steps is seen, the collapse of the MT. (b) Individual curves on different MTs from different experiments. The gray curves show that the backward curves are almost identical to the forward, except that the backward jumps occurred at a lower force of 0.21 nN on average.

On a few occasions, we even found that this self-repairing mechanism was not limited to the small initial instability. Fig. 6 shows an experiment where substantial collapse was seen in the indentation curve. The image made directly afterward shows the damage as a hole in the MT, with two protofilaments clearly disrupted. Subsequent imaging showed that the hole was slowly reannealing. The experimental conditions were such that there was no free tubulin in solution. Therefore, the self-repairing likely depended on the reconnection of the disrupted protein bonds.

FIGURE 6.

Self-healing MT. (a) The curve shows the force-versus-indentation preceding image b, where the tip indented the MT by 10 nm. (b–d) This sequence of images shows that the MT closed over a period of 4 min (the fuzziness in the middle image is caused by the tip being almost out of contact, as a result of the low scan forces). Fiducial marks (highlighted in the background) were used to compensate for sample drift. No free tubulin was present in the solution, indicating that the reannealing must be due to reconnecting tubulin bonds.

Modeling

To quantitatively relate our measured force versus indentation curves to the material parameters of the protein assembly making up the MTs, we used a combination of complementary analytic and computational finite-element methods (FEM, see methods). We begin in both cases by modeling MTs as homogeneous elastic shells with dimensions (e.g., inner and outer radii) based on an axial projection of the electron-density map of MTs (kindly provided by K. Downing; see also Fig. 9). Using FEM, this model has also been extended to account for the most prominent inhomogeneities in the MT structure, namely the longitudinal, rib-like structures of the protofilaments.

The elastic response of an MT to an AFM tip depends not only on the local elastic properties and geometry of the MT but also on the boundary conditions. For instance, the force-indentation relationship is expected to depend sensitively on the proximity of the probe tip to the MT ends. For simplicity, we begin with the response of a long MT, for which end effects are not important. Thus, we model the MT as a cylinder that is uniform along its axis.

For the same boundary conditions, probe-tip shape, and geometry of an elastic cylinder, the linear force-indentation relationship, i.e., effective spring constant k, must be proportional to the Young's modulus E of the material. On dimensional grounds, we can expect that the spring constant for indenting a homogeneous cylindrical shell of thickness t and radius R with a point-like probe tip must be of the form 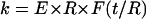, where F is a dimensionless function of t/R. In the limit of a thin shell (R ≫ t), we can ignore compression in the tube wall in its normal direction, and the tube deformation is characterized entirely by bending and in-plane compression and shear. In this limit, we previously found that

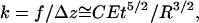(3)

where the prefactor C depends on the particular boundary conditions and only weakly on t/R. For equal and opposite point forces, this can be calculated analytically (8) based on the methods of thin-shell elasticity theory (18). The results of the calculation agree with our FEM results. There are two principal results of the theoretical analysis. First, the spring constant k varies with tube thickness and radius approximately as in Eq. 3. Specifically, as shown in Fig. 7, a and inset, 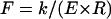varies as (t/R)^5/2 with a prefactor C that is constant to within 2% for t/R < 0.1. Second, the characteristic axial length of deformation is identified as

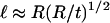(4)

away from the point force. In Fig. 7 b, we compare the deformation length ℓ obtained from both methods. In the case of the analytic calculation, this length is determined from the axial decay length of the most extended mode of deformation (found to decay exponentially in the axial direction). For the FEM results, this is determined by an exponential fit of the deformation profile (using the form 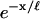, where x is the axial distance from the point of indentation). We find that to within 10% over the range 0.005 < t/R < 0.1.

FIGURE 7.

Comparison of the scaling behavior of the analytical model and the FEM calculations. (a) Dependence of the tube's spring constant on t/R. The black curve shows the analytical result for 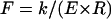, which varies as (t/R)^5/2 with a prefactor C = 1.38 (inset) to within <2% for t/R < 0.1. The corresponding FEM results for a symmetrically-loaded tube are shown in red. Also the FEM results for the tube that was loaded from the top and supported at the bottom over its whole length are shown in green. The scaling behavior for all models is identical, except that the prefactors depend on the boundary conditions. (b) Dependence of the deformed axial length on t/R. The black curve shows the analytical result. The prefactor was ∼0.7 (see inset). The FEM results for a symmetrically-loaded tube are shown in red and those for a top-loaded tube in green. The scaling behavior for all models is identical, except that the prefactors depend on the boundary conditions. For the top-loaded tube we found a prefactor of 1.2. The blue point gives the deformed length from the MT with protofilaments (where we used 1.1 nm for t (see also Fig. 9)); it shows that the presence of protofilaments do not cause a substantial shift in ℓ/R.

Although the above results were calculated for opposing point forces, we find from our FEM analysis that the scaling relationships above for both k and ℓ hold for different boundary conditions. In the same thin-shell limit, using FEM for a long tube composed of thin plates (8) subjected to a radially applied point force from the top and supported over its whole length by a flat substrate, we find a prefactor C = 1.2.

Thin shell, radially indented by tips of varying radius

Because the axial deformed length exceeds the AFM tip radius (∼20 nm), and because for small indentations the cross-sectional shape of the tube remains convex, the assumption of a point load seems justified for small indentations. This is not necessarily true for large indentations. To investigate the effects of a more realistic load distribution, we modeled the indentation of the tube with a parabolic tip. Thin-shell FEM gives a nonlinear response because the contact area will increase with indentation. Fig. 8 a shows the calculated force-versus-indentation curves for different tip sizes. They show the expected nonlinearity: the spring constant increases with the indentation, and this effect is stronger for bigger tips. For deformations up to 4 nm (the measured indentations before collapse), this effect is <10%. In any case, this tip effect is expected to occur after buckling, i.e., after the inversion of radial curvature under the tip. Buckling, however, is not captured by our thin-shell FEM model, so the result is only qualitatively valid in the sense that the force-versus-indentation curves will shift upward at indentations >∼4 nm with increasing tip size.

FIGURE 8.

Effects of the finite tip size and wall thickness on the tube response. The tubes, with a 10-nm radius, were loaded from the top and supported over their whole length at the bottom. (a) Thin-shell model: effect of tip radius on the response of a tube with a wall thickness of 1.6 nm and a Young's modulus of 0.6 GPa. At indentations up to 4 nm, with realistic tip sizes up to 40 nm, the effects are small, at most 10%. At larger deformations, the effects of the tip size become evident. (b) Thick-shell model: dependence of the response on the wall thickness. The Young's modulus was calculated using Eq. 3. The tube softens (buckles) at small deformations. This effect is most obvious for the thinnest wall. The critical indentation for buckling scales with the wall thickness. Indenting with a bigger tip radius partly masks this effect. This masking is stronger for bigger wall thicknesses.

Thick-wall model

MTs do have a wall thickness that is not negligible compared to their radius (t/R ∼0.2). Therefore, thick-shell FEM seems a more appropriate approach. Thick-shell FEM also accounts for buckling. We created a series of models composed of three-dimensional brick elements. We expect two effects: First, the total response should be softer than predicted by thin-shell modeling because of compression of the tube wall. Second, buckling will result in softening at larger indentations. Due to the compressible nature of the tube wall, indentation with a very localized force resulted in numerical instabilities. Therefore, we only simulated parabolic tips with a tip radius >5 nm.

Fig. 8 b gives the force-versus-indentation curves for different wall thicknesses and tip radii. At small indentations, the response is indeed softer than that calculated by the thin-shell model for the same wall thickness and Young's modulus. The discrepancy is stronger for thicker walls and sharper tips. The flattening of the curves (buckling) occurs at an indentation about equal to the wall thickness, as expected, and the transition region is extended with increasing wall thickness. As shown in Fig. 8 a, the finite tip size causes an upward shift in the curves, which partially compensates for the effect of buckling. At higher wall thicknesses, the tip size has more of an effect because the deformed length decreases (Eq. 4) so that the tip-tube contact area is larger.

Protofilaments

Modeling the MTs as smooth homogenous tubes ignores an important structural feature of the MTs. MTs are assembled from linear protofilaments and show deep axial grooves on the outside, whereas the inside is relatively smooth. Nevertheless, the initial modeling of the MTs as unstructured shells is not as unrealistic as it may seem, because most of the strain is localized to the bridges between the protofilaments, and the homogenous model uses an effective wall thickness close to that of the bridges. To approximate reality better, we composed a model that includes the protofilaments as axial ribs, with dimensions based on an axial projection of the electron-density map of MTs (kindly provided by K. Downing). This model consists of a core tube on which the protofilaments are mounted as external ribs. In Fig. 9, the model and the response curves calculated with it are shown. The force-versus-indentation curves look very similar to those of the thick-walled tubes. Again, the tip radius had hardly any effect on the deformation at small indentations.

DISCUSSION

Still under the assumption of a homogeneous material, we can compare finite element modeling with the indentation data while varying the Young's modulus of the material to fit the data. Using the most realistic model including protofilaments we find the best fit with a Young's modulus of 0.6 GPa. But even the very simplified thin-shell model describing an MT as a smooth homogenous tube, ignoring tip size and buckling, gives very similar numbers when one uses a value of t close to that of the 1.1-nm thickness of the interprotofilament bonds. When we fixed the inner radius of the tube to 8.4 nm (Fig. 9, inset) and the Young's modulus at 0.6 GPa, we found an effective wall thickness of 1.54 nm.

For comparison, an effective Young's modulus can also be calculated from MT bending experiments. Values reported for the flexural rigidity range from 1 × 10⁻²⁴ to 32 × 10⁻²⁴ Nm², with most measurements leaning toward the high end of this range (7). To extract the Young's modulus E from the flexural rigidity EI, the moment of inertia I for the cross section of the tube must be known (19). This can be numerically calculated from the EM cross section we also used for the model in Fig. 9, and gives 2.7 × 10⁻³² m⁴. This, in turn, predicts Young's moduli between 0.04 and 1.2 GPa from the bending experiments. Considering that the most reported values are at the high end of the range, this agrees very well with the value we found from indenting the MT. This result is remarkable since the response to deformation in the two geometries, axial bending and radial indentation, is dominated by different parts of the microtubule structure. In bending experiments, the flexural rigidity is dominated by the protofilaments, whereas for indenting experiments, most strain is localized in the thin connections between the protofilaments. Given the similar values obtained for E, this suggests that the material properties of tubulin do not vary considerably between the centers of the protofilaments and the bond region between them. This finding is in contrast to results from osmotic compression of microtubules, where the authors report evidence for material orders of magnitude more compliant between the protofilaments (20).

It is instructive to compare our model with the, by now, textbook (19) modeling that has been applied to interpret MT bending experiments. The most simplifying description for the geometry of the microtubules is that of a homogeneous hollow cylinder with some inner and outer diameter. This ignores all monomer, dimer, or protofilament substructure. The simplest assumption about the material properties of microtubules is that they consist of a homogeneous solid material with a constant Young's modulus everywhere. Maintaining this assumption throughout, Howard gives a number of different prefactors describing the true geometry of microtubules in more detail (19), the most realistic of which includes protofilaments as perfect cylindrical rods just touching each other. The difference between the simple shell and the protofilament model for the bending rigidity is negligible, but the latter model makes it more straightforward to calculate the rigidity for different numbers of protofilaments. For indentation experiments, however, the predictions of the two models are extremely different: The protofilament model with zero-contact bridge thickness would predict zero linear response stiffness with a strongly nonlinear continuation, whereas the solid homogeneous wall model gives the maximal indentation stiffness possible. The existing textbook model had thus to be extended to be relevant for our experiment, which serves to emphasize the uniqueness of this approach to test MT mechanics.

Our model of the microtubules as thick shells is also basically similar to that used by Hunyadi et al. (21) to estimate the excess in free energy due to bending and torsion of protofilaments and to shear between neighboring protofilaments in microtubules with protofilament numbers different from 13. In their case, the thickness of the bridges between protofilament was mainly relevant for the shear energy, but they only extracted a collective parameter from a fit to the data, from which no concrete number was calculated to compare to our results. They also didn't make any predictions about the elastic properties of a 3-start-helix 13-protofilament microtubule, because the main interest was in the difference in stored elastic energies between those and the ones with more or less than 13 protofilaments. Prestress in the lattice, which occurs in all microtubules that are not 3-start-helical with 13 protofilaments, would only change the elastic response parameters of the microtubules if the material was stressed into a nonlinear response regime. It is unknown if this is the case, but it would be an interesting application of our indentation method to search for such changed elastic properties in different microtubule conformations. We haven't been able to observe any microtubules other than those with 13 protofilaments. The reason for that might be that the ones with other protofilament numbers are so unstable, despite the presence of taxol, that they cannot be imaged and tested with our AFM.

Compression experiments of microtubules by AFM have been performed before on MTs covalently cross-linked with glutaraldehyde (22). The observed stiffness was strongly affected by the cross-linking, and imaging without cross-linking was not possible. Only recent progress in AFM methods, in particular “jumping mode” in liquid (11,23) or “tapping mode” in liquid using very small cantilevers (24), has made it possible to scan the fragile microtubules without destroying them and has thereby made it possible to study the elastic properties without chemical cross-linking. Without any stabilization, however, MTs depolymerize spontaneously. Therefore, we used taxol-stabilized MTs. The effect of taxol on bending rigidity has been controversial (25–27). It has been proposed that taxol, binding close to the lateral β-tubulin contacts, stabilizes these lateral contacts. Alternatively, or perhaps in addition, it may hold the protofilaments in a straight stable conformation (28). Taxol is a small molecule, and thus, although it binds close to the lateral bonds, it is not expected to add much to the mass density, which could affect the response to indentation.

In the stiffness maps (Fig. 4), the protofilaments appeared softer than the gaps between them. This seems at first glance counterintuitive to the protofilaments being the thickest part of the tube wall. The phenomenon is, however, consistent with the description we have developed so far, and is also reproduced by modeling. When pushing between the protofilaments with a tip of 20-nm radius, the load gets distributed over two protofilaments, and the apparent stiffness of the tube is slightly higher than when pushing on exactly one protofilament. Furthermore the observed boundary effects when pushing close to the MT ends or toward the sides are confirmed by our finite-element models (data not shown).

For larger indentations, we found nonlinear behavior, as expected. Nonlinearity due to geometry, i.e., buckling of the tube wall, gave a gentle change in slope in the FEM results, which was more or less compensated by the finite size of the tip, which causes the load to be spread laterally over the tube. Modeling also showed that buckling becomes less pronounced for higher wall thickness, or in the presence of protofilaments.

When we included the protofilaments in the finite-element model, we saw that the tip only contacted the ridges of the upper, or the upper two, protofilaments, getting less embedded in the tube wall than is the case for the homogenous tube models. This resulted in a larger degree of independence of the tip radius. For large deformations (5.5 nm for a 20-nm tip pushing on top of a single protofilament), the tip started to contact the neighboring protofilaments as well, which resulted in a stiffening of the response. In the actual experiments, however, the MT collapsed before that point was reached.

Besides the geometrical nonlinearities, there was clear evidence of structural transitions or damage to the MTs as described above. After irreversible failure, one could usually see the damage to the MTs in images taken after the pushing experiments. This damage usually involved removal of parts of the top protofilaments, which implies breakage of tubulin bonds in and between the upper protofilaments. Given that MTs are inherently unstable, it was not surprising that they mostly kept disintegrating under repeated imaging after this type of damage. The small and reversible step in indentation we found preceding the full collapse (Fig. 5), was likely caused by only a partial rearrangement of bonds or a limited opening of bonds. From finite-element modeling we know that buckling of the tube wall will not show such sudden transitions. The weakest connections in the MT structure (29) seem to be the ones between the protofilaments. This is also confirmed by the different ways in which tubulin can organize (rings, sheets, MTs with different protofilament numbers, double-walled MTs, and more) (30). We can estimate the energy dissipation involved in the observed instability in the MT wall from the area under the force-versus-indentation curve highlighted in Fig. 10. This area represents the difference in work between deforming an MT without and deforming one with the change causing the instability. Given that the 1-nm step occurs, on average, at ∼0.27 nN, this gives 1.35 × 10⁻¹⁹ J (32.8 k_BT) for the energy necessary to cause the change.

FIGURE 10.

Force-indentation curve showing the 1-nm step. The shaded part indicates the work needed for the observed instability. The work was measured by the difference between the measured force-indentation curve and backward-extrapolated from the curve section after the step. This gives 1.35 × 10⁻¹⁹ J (32.8 k_BT).

One can speculate on different scenarios that could explain the observed reversible 1-nm step:

1. The weakest connections, the lateral bonds between the protofilaments, give way and the MT splits open like a zipper. After the load is released they reanneal. The observation of a well-defined 1-nm step, followed by further sudden steps at higher loads, argues against this scenario. It would be difficult to understand why the unzippering process does not continue smoothly.

2. The MT lattice might have alternative bistable confirmations. EM studies (31) have shown that the axial shift between neighboring tubulin subunits can switch between two states under stress, and the energy cost for this switch has been estimated by Hunyadi et al. (21) to be ∼7 kT per dimer. Thus, one could in principle explain the observed step in indentation by the switching of approximately five dimers. It is not obvious, however, how an axial shift between the neighboring dimers would minimize energy in the lattice indented under the AFM tip without a concurrent change in the axial spacing of dimers in one protofilament. Recently it has been shown (32) that for sheets with an inverted radius of curvature (GMPCPP ribbons), protofilaments arrange in pairs with the lateral bonds between protofilaments exhibiting two different and alternating conformations of a different kind. Within a pair, the lateral bonds are indistinguishable from those of an intact MT and the protofilaments have the usual inward curvature, whereas between the pairs, the bonds are rearranged and curvature is inverted. One could speculate that such an instability is much more likely to occur in our experiments over the deformed length of the MT, a limited distance on the order of 100–200 nm (where curvature is inverted). Using the work calculated from the data, this gives an energy of ∼2 k_BT per pair of tubulin dimers that have their conformation flipped if one line of bonds is involved, 1/n^th of this value if n protofilament pairs are flipped. This energy is less than that of a single lateral dimer bond (see below), which is consistent.

3. The 1-nm step is caused by total disruption of tubulin-tubulin bonds. It has been estimated by modeling that the lateral bonds (3.2–5.7 k_BT) between dimers are ∼5.2 times weaker than the axial bonds (18.5–27.8 k_BT) (33). This is supported by EM reconstructions of MTs that show much thinner lateral than axial connections (29) and by the way MTs shorten, with the protofilaments fraying out at the depolymerizing ends, showing that the lateral bonds dissociate before the axial bonds (34). Pushing one tubulin dimer out of the microtubule lattice would involve disruption of one axial bond and two lateral dimer bonds, leaving the dimer retained on one (axial) side. Such a mode of rupture is consistent with Fig. 6 b, where a strong indentation caused the (in this case reversible) disruption of two parallel axial bonds. Rapidly reannealing damage would of course have disappeared before the first image was recorded after producing damage. Using the ratio of 5.2, we get 18.5 k_BT for the axial bond and 3.6 k_BT for the lateral bonds between dimers from our data. These experimentally derived values are upper limits, as they were obtained by assuming a minimum disruption of bonds, but they do agree remarkably well with the previously calculated values for binding energies (33).

In vivo, MTs are decorated with a multitude of accessory proteins (35). Many of these might have as yet unknown mechanical functions. One prediction can be made from our results: when an accessory protein binds on the ridges of the protofilaments as, for example, predicted for tau (36), the resistance against compression will hardly change, whereas the flexural rigidity would likely increase. This has been observed for tau (25,37). To make MTs rigid against radial compression, the proteins should fill up the grooves between the protofilaments.

The AFM indentation experiments we have presented here access a mode of deformation of microtubules that is different from bending experiments. The focus is on different parts of the microtubule structure, the grooves between the protofilaments, and the deformation is localized on the scale of ∼100 nm. We expect that this will enable further research into local variations of microtubule mechanics under various circumstances and into the local mechanical effects of microtubule binding proteins.