Direct Evidence of Multicompartment Aggregates in Polyelectrolyte-Charged Liposome Complexes

Abstract

By means of the combined use of dynamic light scattering and transmission electron microscopy measurements, we provide a direct evidence for the existence of an equilibrium cluster phase in the polyion-induced liposome aggregation, where the liposomes maintain their integrity, with the ability of preserving the aqueous core content from the external medium. We prepared single liposomes containing, in their interior, different CsCl electrolyte solutions at different concentrations (0.1 and 0.01 M, respectively). During the polyion-induced complexation of a mixture of these two differently loaded liposomes, reversible aggregates form, whose multicompartmental structure reveals the simultaneous presence of nonfused liposomes. Clusters composed by mesoscopic-sized vesicles and realized by charged lipids coupled to oppositely charged polyions are playing an increasingly important role as model systems in a variety of phenomena in soft matter and for their potential use in biomedical applications as drug delivery systems. Aggregates of liposomes such as those described in this article, where the electrostatic interactions are the primary driving forces promoting aggregation, may represent a new and interesting class of colloids which give rise to a rich phenomenology with several unusual colloidal behaviors that deserve to be further investigated.

INTRODUCTION

The complexation of charged spherical particles of mesoscopic size induced by oppositely charged polyions has been extensively investigated both theoretically and experimentally, owing to its importance in many fields of physical chemistry (1,2) and in soft-matter physics (3–5). The resulting aggregates possess new and not yet completely understood properties. Among these structures, cationic lipid-DNA complexes (lipoplexes) have witnessed an increasing acceptance as preferential DNA delivery vehicles in gene therapy (6–8), because of their enhanced permeability through the membrane bilayers, favoring the delivery of DNA into the cells.

The equilibrium structures that, for different compositions of the lipid phase, form in the close proximity of the isoelectric point (where the stoichiometric charge of DNA counterbalances the stoichiometric charge of the lipid phase) have been thoroughly investigated (9–14). However, these systems, showing different self-assembling structures, exhibit a much richer and interesting phenomenology, far from being completely understood.

Although there is evidence that, in the case of cationic liposome-DNA systems, a liposome restructuring occurs during the lipoplex formation, consisting in a liposome fusion (15) with a consequent release of their aqueous content (16) (the equilibrium structures being multilamellar or cylindrical phases (9–11)), we have recently shown (17) that there is also evidence, at least in a low concentration range, for aggregates where liposomes maintain their individuality.

Although the integrity of the single vesicles in complexation of synthetic cationic polyions with oppositely charged lipid vesicles was reported in several works dated back many years ago (18–20), this topic aroused a renewed interest since some experimental evidences, based on small-angle x-ray scattering and cryoelectron microscopy (9,21,22), have shown that complexes of anionic polyions, such as DNA, with double-tailed cationic lipids form an intercalated lamellar phase, where DNA chains are sandwiched between the lipid bilayer. These structures, which have a highly ordered arrangement, are induced by the intercalation of a monomolecular layer of DNA in multilamellar stacks of lipid bilayers, and have received much attention because of their potential use as nonviral gene carriers. However, several other experimental studies suggest another possible class of complex morphologies, and it is not entirely clear whether these aggregates are thermodynamically stable or metastable intermediates.

This seeming inconsistency among the different structures revealed by different experiments is probably due to the different bulk lipid concentration and to the different procedures for sample preparation, required by the different experimental techniques. Our results clearly demonstrate that, in the range of dilute systems, with concentration lower than few milligrams per ml, polyions (polyanions) induce clusterization of intact cationic liposomes. The existence of different structural arrangements in different concentration intervals might account for some unsuccessful attempts to optimize lipoplexes for gene delivery since, in therapeutic concentration ranges, the structures may be different from those hypothesized.

In a series of recent works (17,23–25), we showed that, in a broad polyelectrolyte concentration range around the point of charge inversion (isoelectric point), polyion-coated liposomes form clusters that are equilibrium aggregates. This reversible aggregation is due to a balance of long-range electrostatic repulsion and of short-range attraction (17,25), arising from the correlated adsorption of polyions at the liposome surface, where polyion domains alternate with oppositely charged, polyion-free domains (charge-patch attraction (26–29)).

There is now substantial evidence that, by adding polyions to a suspension of oppositely charged liposomes, polyion chains rapidly adsorb at the liposome surface (30–33). To gain some energy, the adsorbed chains, repelling each other, reconfigure themselves at the surface in more or less orderly patterns (3,4). Thanks to this lateral correlation, with the increase of the polyion concentration, the polyelectrolyte-decorated liposomes (pd-liposomes) are not only progressively neutralized but, depending on the relative size and valence of the oppositely charged macroions, the neat charge of the whole assembly can even be inverted. This phenomenon, described as a “giant charge inversion” (5), has been recently shown to occur in polyelectrolyte-charged liposome systems by small-angle neutron scattering (34).

It remains to be clarified if this aggregation process results in a new multicompartment cluster phase that is thermodynamically stable, or only in a dynamically entrapped phase. However, this new phase appears very interesting, both for applications and for further advances in the understanding of colloid physics.

No matter how complex the mechanism of stabilization of the multicompartment phase may be, it is important to give a further direct and convincing evidence of it. In this article, we present direct evidence that, in the aggregation process induced by polyions resulting in polyion-coated liposome complexes, the liposomes maintain their individuality within the aggregates, without any appreciable fusion or rearranging of their individual structures. We give direct evidence of this showing a series of transmission electron microscopy (TEM) images, where single liposomes, assembled into multicompartment aggregates, owing to the different concentrations of Cs⁺ ions in their aqueous core, are clearly recognizable.

There has recently been a renewed interest in colloidal systems with short-range attraction and screened electrostatic repulsion (see, for example, (35–40)). In this context, pd-liposomes appear as a good model system to experimentally investigate the role of interparticle interactions in controlling the structure and dynamics of the colloidal dispersion. Moreover, the circumstance that, in this case, both repulsion and attraction share a common electrostatic origin, makes pd-liposomes particularly intriguing.

This cluster phase also shows very interesting features in view of possible biomedical applications. Despite the possible intrinsic nonequilibrium nature of the composing elements (the liposomes), their aggregation, being reversible (25), is an equilibrium process. For this reason, the aggregation can be, in principle, easily controlled by varying environmental parameters such as temperature or ionic strength of the suspending medium. The existence of such a peculiar phase, with liposomes reversibly glued-together by a nonuniform distribution of adsorbed polyelectrolytes, opens interesting perspectives for the application of these multicompartment liposomal aggregates as effective multidrug delivery vectors (41–43).

EXPERIMENTAL SECTION

Materials

Liposomes were built up with 1,2-dioleoyl-3-trimethyl ammonium-propane (DOTAP), a cationic lipid which is quite popular in transfection protocols. DOTAP was purchased from Avanti Polar Lipids (Alabaster, AL) and used without further purification. The anionic polyelectrolyte employed to induce aggregation was sodium polyacrylate (NaPA), a highly charged, flexible polyelectrolyte with a simple structure, [−CH₂ −CH(CO₂Na)−]_n, and with a nominal weight of 60 kDa. NaPA was purchased from Polysciences (Warrington, PA), as a 0.25 (wt/wt) solution in water. Double-stranded DNA from herring sperm was purchased from Boehringer Mannheim (Amsterdam, The Netherlands). Cesium chloride, analytical grade, was from Merck (Darmstadt, Germany). For all preparations, Milli-Q grade (Millipore, Billerica, MA) deionized water was employed.

Liposome preparation

We have prepared DOTAP liposomes in aqueous suspensions at two different CsCl electrolyte concentrations, following the standard procedure. Briefly, an appropriate amount of DOTAP (16.0 mg) was dissolved in 10 mL of a methanol-chloroform solution (1:1 vol/vol), and the organic solvent was subsequently removed by overnight vacuum desiccation. The resulting dried lipid film was rehydrated in a CsCl aqueous solution at the appropriate electrolyte concentration, at a temperature of 25°C (well above the phase transition temperature of DOTAP (44), T_f = 0°C) for 2 h. The resulting aqueous lipid mixture was sonicated (at T = 25°C for 1 h, pulsed power mode) until the solution appeared optically transparent in white light. A homogeneous liposomal suspension of approximately uniformly sized unilamellar vesicles with an average diameter (from dynamic light-scattering measurement, intensity-averaged size distribution; see Appendix) of 60 ± 8 nm was obtained. The final liposome concentration was 1.6 10¹⁶ particles/mL.

Two different CsCl concentrations (0.1 M and 0.01 M) were employed. In the polyion-induced complexation experiments, equal amounts of the two liposome suspensions prepared at the two different CsCl concentrations were mixed together immediately before the addition of the polyion to induce aggregation, to have, within the same cluster, heavily and lightly Cs-loaded liposomes. With this procedure, the electrolyte concentration in the suspending medium becomes 0.055 M. By adding to this mixed liposome suspension an equal amount of an aqueous solution with varying polyion content, the CsCl concentration in the medium is further halved, to the final concentration of 0.0275 M.

Aggregation was initiated by adding the NaPA aqueous solution (prepared at an appropriate concentration) by a single mixing step to a mixed suspension of liposomes including in their core an aqueous solution 0.1 M CsCl and liposomes including an aqueous solution 0.01 M CsCl, both the two species dispersed in an aqueous solution 0.0275 M CsCl. In all the experiments, the final concentration of liposomes was 0.8 10¹⁶ liposomes/mL. Differently CsCl-loaded liposomes maintain their integrity over a long period of time and liposome fusion or swelling induced by osmotic effects does not occur (20). The effective polyion-induced aggregation was checked by means of dynamic light-scattering measurements (the hydrodynamic radius of the aggregates) and by means of transmission electron microscopy measurements (the visual inspection of the aggregates). Charge inversion occurring at the isoelectric point was monitored by means of ζ-potential measurements. The pH values of the solutions were at pH ≈ 6.2. All experiments were carried out at a temperature of 25.0 ± 0.2°C and each series of measurements was repeated several times to check reproducibility.

Light-scattering measurements

Size and size-distribution of single liposomes and polyion-liposome aggregates were characterized by dynamic light-scattering measurements. For all dynamic light-scattering measurements, an optical fiber probe (model No. FOQELS, Brookhaven Instruments, Worcestershire, UK) has been employed, in conjunction with a Brookhaven 9000 AT logarithmic correlator. In this fiber-optic probe, the Gaussian laser beam transmitted by a mono-mode optical fiber illuminates the scattering volume, and a second fiber, positioned at a fixed angle of 137.5°, collects the scattered light. The main advantage of this apparatus, when compared to more traditional ones, consists in its inherent larger insensitiveness to multiple scattering effects (45).

Dynamic light scattering measures the normalized (second-order) time autocorrelation function g(2)(τ) of scattered-light intensity. For Brownian particles, this quantity is related to the normalized (first-order) autocorrelation function g(1)(τ) by the Siegert relationship

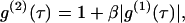(1)

where β is a spatial coherence factor depending on the geometry of the detection system. For a dilute suspension of monodispersed particles, g(1)(τ) decays exponentially with a decay rate Γ = q²D, where q is the magnitude of the scattering wavevector, and D is the translational diffusion coefficient, related to the hydrodynamic radius R of the suspended particles through the Stokes-Einstein relationship,

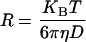(2)

with K_BT the thermal energy and η the viscosity of the suspending medium.

For a polydispersed system, g⁽¹⁾(τ) can be expressed as

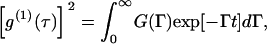(3)

where G(Γ) is the particle size distribution function.

To obtain G(Γ), the measured autocorrelation functions g⁽¹⁾(τ) were analyzed by means of the CONTIN algorithm (46,47). Since it is well known that the inversion of autocorrelation data in light-scattering experiments to obtain the size distribution is an “ill-conditioned problem,” in our analysis, we compared the G(Γ) distributions calculated using CONTIN with the distributions obtained by a different method, the Lawson's NNLS algorithm (48), and we have only considered those peaks in the particle distributions that do not depend on the algorithm employed.

The control parameters of both the two algorithms we have employed were set to obtain, in terms of the particle size, the intensity-weighted size distribution (49).

ζ-potential measurements

The electrophoretic measurements were carried out by means of the laser Doppler electrophoresis technique using a Malvern Zetamaster apparatus (Malvern Instruments, Worcestershire, UK) equipped with a 5 mW HeNe laser and a backscattering (173°) optical fiber probe. The mobility μ of the diffusing aggregates was converted into a ζ-potential using the Smoluchowski relation ζ = μη/ɛ, where ɛ and η are the permittivity and the viscosity, respectively, of the solution.

TEM measurements

TEM measurements were carried out by means of a Zeiss 902 microscope (Carl Zeiss, Jena, Germany) operating at 80 kV, equipped with an electron energy loss filter (EF-TEM). To enhance contrast and resolution, Electron spectroscopy imaging (ESI) mode was used. ESI is an evolution of electron energy loss spectroscopy, which measures the energy loss suffered by the high-energy incident electrons when transmitted across the sample. The main advantage of this technique is that, since only the electrons that show the energy loss characteristic of their interaction with a specified element contribute to the image formation, a topographic map of that particular element within the sample can be obtained. As a further advantage, energy filtering allows the suppression of the contribution of inelastic scattering that typically occurs when the sample is mainly made of light elements, as in the case of biological samples. Moreover, filtering reduces chromatic aberrations, which is usually the main factor in determining the maximum attainable resolution in a conventional TEM, working with biological samples (50).

In our case, thanks to the procedure employed for the preparation of liposome suspension, the presence of Cesium (with its relatively high atomic number) entrapped within the inner core of the liposomes allows us to visualize the vesicles with good resolution, without any need of a staining procedure. In addition, for some selected samples, a negative contrast staining has been used. In this case, before samples were completely dried, 10 μl of 2% aqueous phosphotungstic acid solution (pH-adjusted to 7.3 using 1 N NaOH) was employed as staining solution.

Sample preparation for EF-TEM observation consists simply in the deposition of a droplet of the suspension containing the polyion-coated Cs-liposome complexes onto a 300-mesh copper grid for electron microscopy covered by 20-nm thin amorphous carbon film.

Images were acquired by a digital charge-coupled device camera, model Proscan (Proscan Elektronische Systeme, Lagerlechfeld, Germany) HSC2 (1024 × 1024 pixels), thermostated by a Peltier cooler. Image analysis was carried out by a digital analyzer SIS 3.0, which allows us to obtain elemental (in our case, Cs) maps using the two-windows method (50), to enhance the contrast and sharpness of the acquired images and to perform statistics. The overall attainable resolution can be evaluated on the order of 2 nm.

A comparison between the size and size distribution of the aggregates obtained from light-scattering measurements and from the inspection of TEM images is presented in the Appendix.

RESULTS AND DISCUSSION

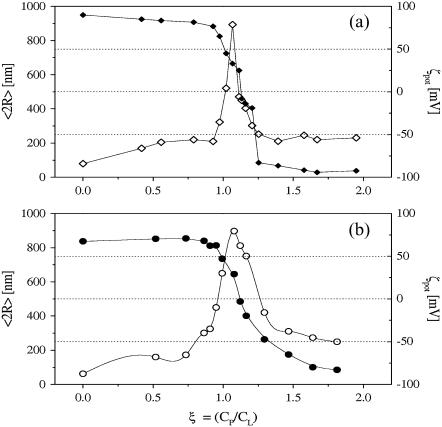
The evolution of the hydrodynamic radius R for the complexes of Cs-loaded DOTAP liposomes with NaPA polyelectrolyte, at a fixed lipid content (0.8 mg/mL) and for increasing polymer concentration, is shown in Fig. 1 for the two electrolyte concentrations employed (0.1 and 0.01 M CsCl, respectively). Polyion concentration is defined through the ratio ξ = N⁻/N⁺ (hereafter, charge ratio) of the stoichiometric charge of the polyion (N⁻) to the total number of the charged groups on the lipids (N⁺). For both the CsCl electrolyte concentrations, at low polyion content, the hydrodynamic diameter 2R of the complexes, measured by dynamic light scattering from intensity-averaged size distribution, is ∼60 nm, very close, within the experimental uncertainties, to the size of the original liposomes. With the increase of the polyion content, the size of the complexes increases up to a maximum of the order of 0.9 μm, which is attained close to the neutralization point, at ξ ≈ 1, as evidenced by the inversion of the measured ζ-potential (Fig. 1). Then, the size of the aggregates decreases until the one of the original liposomes is reached again (for a detailed analysis of this behavior see (25,51)).

FIGURE 1.

Average hydrodynamic diameter 〈2R〉 (open symbols), and ζ-potential (solid symbols), of NaPA-DOTAP complexes as a function of the polyion/DOTAP charge ratio parameter ξ, for the two different molar concentrations of CsCl employed in liposome preparation: (a) CsCl 0.1 M and (b) CsCl 0.01 M. Lines are to guide the eye only.

This phenomenology is the typical re-entrant condensation observed in similar systems also in the absence of Cs (10,17,24,25,52,53), thus evidencing that the basic mechanisms of aggregation of pd-liposomes remains unmodified by the presence of electrolytes at different concentrations, either inside or outside the liposome vesicles.

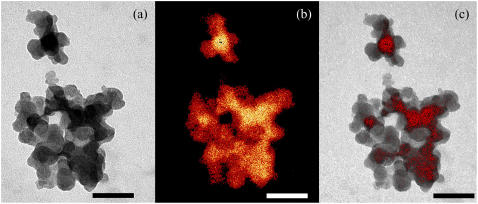
Fig. 2 shows an ESI-TEM image of a typical aggregate induced by adding an appropriate amount of NaPA polyions to a liposome suspension formed by a mixture of heavily and lightly Cs-loaded liposomes. Differently Cs-loaded liposomes refer to liposomes containing 0.1 M and 0.01 M CsCl aqueous core, respectively.

FIGURE 2.

ESI-TEM image of a typical aggregate of heavily (0.1 M) and lightly (0.01 M) Cs-loaded liposomes. In panel a, the aggregate appears built up by globular particles and darker and lighter individual globules are clearly recognized. In the absence of any staining, the contrast observed is to be ascribed to differences in the elastic scattering of electrons due to local changes in the Cs density. Panel b shows the Cs map of the same aggregate as in panel a, obtained applying the two-windows method (50) around the M_{4, 5}-Cs edge (see Fig. 3). In this image, red-gold levels correspond to variations in Cs concentration. Comparing this topographic map and the real image in panel a makes evident that Cs is contained within the aggregate, and that the liposomes in the aggregate, loaded with different Cs concentrations (0.1 M and 0.01 M) maintain their individuality. In panel c, the Cs map, but with a threshold set at 50% intensity, and the high-contrast reference image of panel a, are superimposed. Bars represent 100 nm.

The aggregate clearly appears as a cluster of small (∼30 nm in diameter) globular particles, and, within the aggregate, darker and lighter zones are plainly distinguished. Being as the sample is not stained, the strong contrast observed is only due to differences in the Cs concentration, which cause, in TEM measurements, differences in the elastic scattering of electrons in different areas of the sample.

Fig. 3 shows the electron energy-loss spectroscopy spectrum, obtained from a circular zone centered on the Cesium-loaded liposome aggregate. An elemental map of Cs can be created for the same frame (Fig. 2 b) by using the two-windows method. In this procedure, the topographic map of the element Cs is obtained using only the electrons characteristic of the Cs-M_4,5 edge, obtained by filtering the transmitted electrons in an energy window of ∼30 eV beyond the edge onset and subtracting the unspecific background (50).

FIGURE 3.

Electron energy-loss spectroscopy spectrum, collected from a zone containing lipoplexes, showing the characteristic M_{4, 5} edge of Cs.

From the map shown in Fig. 2 b, the correlation between CsCl concentration and contrast in the real image clearly appears. When, in Fig. 2 c, the same map, but with a threshold set at 50% intensity (to visualize only the high Cs concentration zones) and the high-contrast reference image of Fig. 2 a are superimposed, the coincidence is striking.

The clearcut edges of the different regions clearly evidence the presence of intact liposomes filled with the two Cs-concentrations employed, ruling out the occurrence of a rearrangement of the bilayers within the aggregate, with a fusion of the vesicles, which would be accompanied by a mixing-up of the contents of the different compartments, resulting in a blurring-out of the contours.

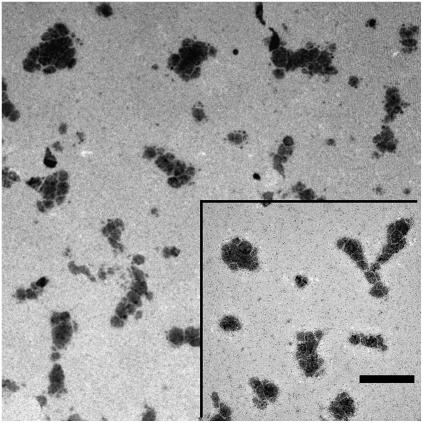
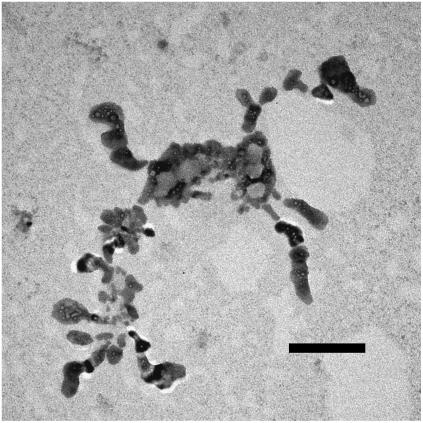
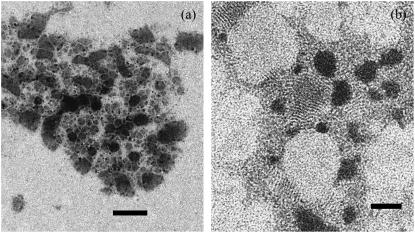
At a smaller magnification, the overall aspect and the shape of the aggregates can be better appreciated (Figs. 4 and 5). Whereas smaller aggregates appear to have a more compact and approximately roundish shape (Fig. 4), larger aggregates rapidly becomes elongated or even fractal-like (Fig. 5). Such a behavior is to be expected in colloidal systems, when aggregation results from the combination of a short-range attraction and a much longer-range repulsion (36,37).

FIGURE 4.

At a lower magnification, the smaller aggregates appear to have a more compact and approximately roundish shape, while larger aggregates are more elongated. Bar represents 400 nm.

FIGURE 5.

In some cases, large fractal-like aggregates appear. Darker and lighter liposomes (high Cs and low Cs concentration, respectively) are clearly distinguishable. Bar is 200 nm.

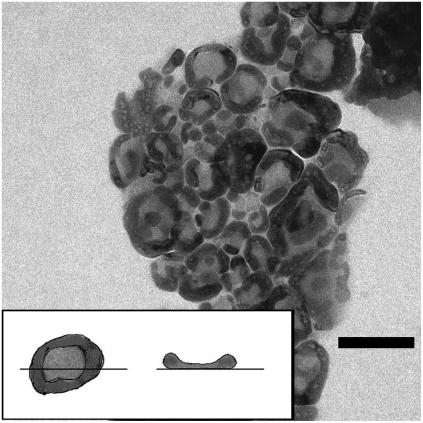
Larger liposomes, when deposited on the support for electron microscopy, tend to assume a doughnut shape (Fig. 6). The cartoon in the inset of the figure illustrates this effect. Since there is a minimum radius of curvature that the liposome double layer can bend, the larger liposomes within the aggregates (which in the dehydration process flatten on the copper grid support) appear with a thicker border and a thinner center. The surface tension of the liquid that is drying-up forces CsCl electrolyte to withdraw from the central region of the vesicles, when they collapse in the microscope vacuum chamber, so that larger amounts of CsCl settle and crystallize within an annular region around the perimeter inside the flattened vesicles. In fact, within a great majority of these characteristic doughnuts, small particles appear. Their contrast changes with defocusing, showing the typical behavior of crystalline materials (Fresnel fringes (54)). This effect further supports the hypothesis that the annular region is due to deposit of Cs, partially crystallizing in small crystals, and this finding enforces the evidence that liposomes maintain their integrity within the aggregates.

FIGURE 6.

Larger liposomes, when deposited on the support, tend to assume a doughnut shape (as the cartoon in the inset illustrates), probably due to the combined effects of the finite minimum radius of curvature that the vesicle double layer can bend, and of the surface tension of the filling aqueous medium, which forces the electrolyte to withdraw from the central region of the vesicles when they collapse in the microscope vacuum chamber. Bar is 100 nm.

In Fig. 7, we show a typical complex formed following the above stated procedure, using a double-stranded DNA polyion to induce aggregation, instead of NaPA polyion. In this case, a mixture of liposomes containing pure water and CsCl solution was employed. In the absence of Cs, liposomes are not visualized, because of the lack of contrast, appearing as an empty space between Cs-loaded vesicles. In addition, in Fig. 7 B, the effect of a negative contrast staining using phosphotungstic acid is shown. Now, among the darker Cs-loaded liposomes, the contour of water-filled liposomes is clearly visible.

FIGURE 7.

(a) A typical aggregate induced by DNA polyion in a mixture of water-filled and Cs-loaded liposomes. Water-filled liposomes are not visible and only appear as empty space between the Cs-loaded liposomes. Bar is 200 nm. (b) Negative staining allows the water-filled liposome contour to be recognizable. Bar is 50 nm.

CONCLUSIONS

There is increasing evidence in experiments (25,34,38) and simulations (36,37) that, in colloidal systems, a combination of a short-ranged attraction and a much longer-range repulsion lead to a highly nontrivial phase behavior. The existence of a fluid phase of finite-sized equilibrium aggregates has been demonstrated for different colloidal systems (34,38). With this work, we provide further evidence to support the results of our previous investigations (17,25) showing that, in the case of polyion-decorated charged liposomes as well, clusters form in which liposomes maintain their individuality.

It remains to be clarified whether or not this phase is a true equilibrium phase or a dynamically entrapped phase, due to an intrinsic instability of the component liposomes. The nonequilibrium nature of one-component liposomes is commonly accepted. However, some new evidences have been recently underlined that, in the case of charged phospholipids, vesicles, instead of multilamellar phases, could represent the thermodynamically stable structure in excess water (55), as it was already suggested (56).

We have provided further evidence for the existence of a new multicompartment phase in polyion-coated liposome complexes that has potential applications in drug delivery. The self-assembling of lipidic vesicles into mesoscopic aggregates appears as a hierarchical process where, at a lower level, clusters formed by intact vesicles stuck together by the oppositely charged polyions give rise to relatively large, equilibrium aggregates, which can be considered as a new class of colloids with a rich and not yet completely understood phenomenology. Some major questions remain open concerning the thermodynamic and kinetic nature of this state of the system, and further investigations should focus on this issue.

APPENDIX

In dynamic light scattering on polydisperse systems, in extracting the size-distribution of the suspended particles from the measured light-scattered autocorrelation functions, two different pathways can be followed (see, for example (57)). Assuming a distribution of decaying rates, the correlation function g(1)(τ) can be written according to Eq. 3. If an analytical form for the size distribution is hypothesized, in principle, using the appropriate Mie factors, the function G(Γ) can be calculated and the parameters of the distribution are obtained by a best-fitting procedure to the measured correlation function.

Without any assumption on the size distribution, the decay rates G(Γ) can be obtained numerically as the inverse Laplace transform of g(1)(τ). Several algorithms such as Provencher's CONTIN (46,47) or Lawson's NNLS algorithms (48) have been proposed for optimizing this procedure. Numerical Laplace inversion is a well-known “ill-conditioned” problem, i.e., even small experimental uncertainties in the data may lead to large differences in the particle-size distributions.

A criterion for a quantitative measure of the degree of ill-conditioning of the problem has been proposed (49). Following this criterion, the ill-conditioning of the inversion of g(1)(τ) for intensity-, volume-, and particle number-averaged size distribution increases in that order. This criterion gives a quantitative basis to the common empirical choice of using the intensity-weighted average to calculate a mean radius of the particles in the suspension. However, it must be kept in mind that, with this choice, the contribution of large particles (the scattering-center efficiency of a particle increases as a function of radius r as r⁶, up to radii of ≈100 nm) is strongly enhanced.

The values of the radius of the liposomes and of the radius of the aggregates shown in Fig. 1 are, as usual, intensity-averaged values.

The apparent inconsistency with TEM images (Figs. 2 and 4–6), where the whole aggregates and the liposomes appear systematically smaller, can be overcome if the intensity-weighted average diameter is compared with an analogous intensity-weighted average diameter, calculated weighting by a factor r⁶ the radii obtained from a careful visual analysis of several TEM images.

Within this procedure, an average diameter of (78 ± 16) nm is obtained for liposomes within the aggregates from TEM images, to be compared with the corresponding value of (60 ± 8) nm measured by light-scattering for single liposomes. The agreement appears reasonable. On the other hand, when a number-averaged diameter is calculated from the TEM images and is compared with a number-averaged diameter obtained from CONTIN analysis of the light-scattered correlation function, the agreement is poorer ((33 ± 13) nm from images against (13 ± 12) nm from light scattering), despite the fact that a qualitative agreement is maintained (intensity-average, emphasizing the contribution of the larger particles, is, in any case, larger than the number-average radius).

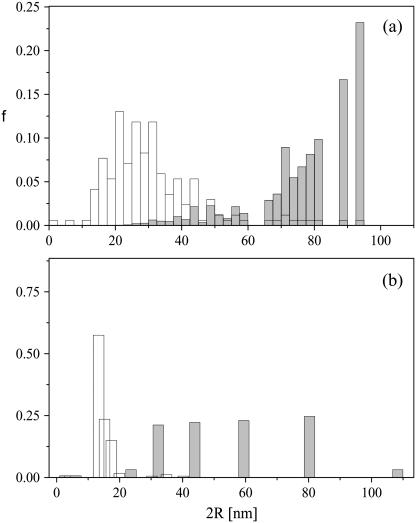
In Fig. 8, a number-weighted distribution for the liposomes within the aggregates, from visual analysis of several TEM images, is shown in Fig. 8 a (open bars), together with the corresponding intensity-weighted distribution, calculated by weighting the experimental counts by an r⁶ weight (shaded bars). In Fig. 8 b, the corresponding size distributions for the single liposomes obtained from LS are shown for comparison. Shaded bars represent the distribution calculated from the CONTIN algorithm in intensity-weighted mode, and open bars represent the distribution calculated in the number-weighted mode.

FIGURE 8.

Number-weighted and intensity-weighted size distribution. (a, open bar) Number-averaged distribution of the liposome size from the analysis of TEM images; (shaded bar) intensity-averaged distribution of liposomes considering an r⁶ weight. (b) The corresponding size distribution of liposome size from light-scattering measurements. (Open bar) Number-averaged distribution; (shaded bar) intensity-averaged distribution.

Although a quantitative comparison of the two distributions shown in Fig. 8, a and b, is not completely meaningful, it is plainly evident that the differences among intensity-weighted and number-weighted distribution are maintained in both cases, as well as the analogies between the distributions calculated by the same mode from the TEM images and from light-scattering measurements. A correlation exists, despite the fact that data in Fig. 8 a refer to the size of the liposomes inside the aggregates, while, in Fig. 8 b, the distribution of the single isolated liposomes (in the absence of the polyion) is considered.