Structure of Tightly Membrane-Bound Mastoparan-X, a G-Protein-Activating Peptide, Determined by Solid-State NMR

Abstract

The structure of mastoparan-X (MP-X), a G-protein activating peptide from wasp venom, in the state tightly bound to anionic phospholipid bilayers was determined by solid-state NMR spectroscopy. Carbon-13 and nitrogen-15 NMR signals of uniformly labeled MP-X were completely assigned by multidimensional intraresidue C–C, N–C^αC^β, and N–C^α–C′, and interresidue C^α–C^αC^β, N–C^αC^β, and N–C′–C^α correlation experiments. The backbone torsion angles were predicted from the chemical shifts of ¹³C′, ¹³C^α, ¹³C^β, and ¹⁵N signals with the aid of protein NMR database programs. In addition, two ¹³C–¹³C and three ¹³C–¹⁵N distances between backbone nuclei were precisely measured by rotational resonance and REDOR experiments, respectively. The backbone structure of MP-X was determined from the 26 dihedral angle restraints and five distances with an average root-mean-square deviation of 0.6 Å. Peptide MP-X in the bilayer-bound state formed an amphiphilic α-helix for residues Trp³−Leu¹⁴ and adopted an extended conformation for Asn². This membrane-bound conformation is discussed in relation to the peptide's activities to form pores in membranes and to activate G-proteins. This study demonstrates the power of multidimensional solid-state NMR of uniformly isotope-labeled molecules and distance measurements for determining the structures of peptides bound to lipid membranes.

INTRODUCTION

Mastoparan-X (MP-X), I-N-W-K-G-I-A-A-M-A-K-K-L-L-NH₂, is one of the mastoparans (MPs) that were isolated from wasp venoms as peptides that induce histamine release from mast cells (1). This activity was found to be mediated by the peptides′ ability to directly stimulate the guanosine diphosphate/guanosine triphosphate exchange of G_i/o-type G-proteins, an ability attributed also to liganded G-protein-coupled receptors (2,3). Since G-proteins are located within cells, MPs must penetrate into the cells to activate G-proteins. In fact, MPs perturb the bilayer structure and increase the cation permeability across membranes upon strong binding (4). Such an interaction with membranes facilitates the translocation of MPs across the lipid bilayer. The structures of membrane-bound MPs have also attracted much attention, because the activity of MPs to stimulate G-proteins is greatly enhanced when purified G-proteins are reconstituted in membranes (2). Further, the membrane binding is known to stabilize the active conformations of peptides in general (5). This binding to membranes is followed by binding to G-proteins for MPs.

Structures of MPs have been investigated under various conditions: Conformations of MP-X molecules loosely bound to G-protein G_i1α and lipid membranes have been studied by a transferred nuclear Overhauser effect (TRNOE) method of solution NMR (5,6). Mastoparan structures have also been analyzed by solution NMR in several model membrane and membrane-mimic systems (7–11). The structure of MP-X precipitated from a methanol solution has been investigated by solid-state NMR recently (12). These studies indicated that MPs adopt an amphiphilic helical conformation.

Some variations in the structures of MPs were also highlighted: a kink found in the helix of mastoparan-S is considered to be important for the peptide's selectivity to Gs rather than to G_i/o (13); the formation of an intramolecular hydrogen bond at the N-terminal amide affects the ability of MP-AF to perturb the cell membranes (11). It is thus essential to obtain high-resolution structures of the peptides bound to their targets to clarify the mechanisms and specificity of the actions.

The structure determination of membrane-bound peptides and proteins, however, remains difficult even with advanced methodologies. X-ray and electron diffraction analyses are hampered by the difficulty of preparing high-quality crystals. Solution NMR analysis of membrane-bound peptides/proteins is very difficult because of the severe resonance line broadening due to the slow tumbling motion of the large membrane complexes. Thus, solution NMR analyses of membrane proteins and peptides have been conducted under membrane-mimicking environments of micelles (14), bicelles (10), and less physiological organic solvents (15). The information obtained under these conditions, however, may not reflect the real structures in the membrane-bound states because the packing of detergent/lipid molecules in micelles/bicelles is not the same as that in membranes. The TRNOE method adapted to determine conformations of MP-X bound to lipid vesicles (5) also has inherent limitations: TRNOE does not give chemical shifts that allow the prediction of dihedral angles. TRNOE can be applied only to peptides that bind to membranes weakly enough to enable the transfer of NOE on a timescale shorter than a magnetic relaxation time T₁.

In contrast to the solution NMR, solid-state NMR has several advantages in determining the structure of membrane-bound and noncrystalline proteins. Application of solid-state NMR is not limited by slow molecular motions. Structures of uniaxially oriented membrane proteins have been determined by anisotropic nuclear magnetic interactions (16). Recently, multidimensional magic-angle spinning (MAS) NMR has been shown to provide constraints sufficient for the protein structure determination (17,18). This MAS solid-state NMR has been used for structural analysis of a small uniformly isotope-labeled membrane protein (19) and for signal assignments of semiselectively labeled membrane proteins (20,21). The solid-state NMR distance measurements have permitted the detailed structural analyses of membrane proteins (22) and amyloid proteins (23).

In this study, we determined the structure of MP-X tightly bound to anionic membranes by multidimensional MAS solid-state NMR. The ¹³C and ¹⁵N signals were assigned in a sequence-specific manner for uniformly isotope-labeled MP-X. In addition, conformation-dependent distances were measured precisely for selectively labeled peptides. A high-resolution structure was calculated from the distances and the dihedral angle constraints predicted from the chemical shifts. The successful determination of the structure of MP-X tightly bound to membranes illustrates the applicability of multidimensional solid-state NMR and the distance measurements to the structure determination of membrane-bound peptides and proteins.

MATERIALS AND METHODS

Preparation of isotope-labeled MP-X

Uniformly ¹³C, ¹⁵N-labeled MP-X was overexpressed in Escherichia coli BL21 Star (DE3) cells (Invitrogen, Carlsbad, CA) as a recombinant fusion protein with Saccharomyces cerevisiae ubiquitin under the T7 promoter according to the reported method (24). The fusion protein had a decahistidine tag at its N-terminus. The E. coli cells were grown in M9 minimum media containing ¹⁵NH₄Cl and [¹³C₆] glucose or ¹³C, ¹⁵N-labeled Chlorella media (Chlorella Industry, Tokyo, Japan) with 1.5 mg/L [¹³C₆] glucose. The protein was purified with a Ni²⁺-NTA agarose affinity column. The ubiquitin-MP-X-Gly was cleaved specifically at the C-terminus of ubiquitin with yeast ubiquitin hydrolase, which was separately overexpressed in E. coli and purified. The C-terminus of MP-X-Gly was amidated by peptidylglysine α-amidating enzyme (Wako Pure Chemicals Industries, Osaka, Japan). The obtained MP-X was purified by reverse-phase high-performance liquid chromatography (via 5C₁₈-AR-II column (COSMOSIL) (Nakarai Tesque, Kyoto, Japan)). Peptides MP-X selectively labeled at [¹³C′] G5 and [¹³C^β] A8 and that at [¹³C′] A7 and [¹³C^β] A10 were synthesized by solid-phase peptide synthesis using FMOC chemistry. The labeled amino acids for peptide synthesis had a ¹³C abundance of 99%. Natural-abundance MP-X and MP-X labeled at ([¹³C′] I1 and [¹⁵N] G5), ([¹³C′] A10 and [¹⁵N] L13), and ([¹³C′] A10 and [¹⁵N] L14) were purchased from AnyGen (Gwang-ju, Korea). These six peptides were purified by reverse-phase high-performance liquid chromatography and lyophilized.

Preparation of liposomes and NMR samples

A mixture (50 mg) of 80% dipalmitoylphosphatidylcholine (DPPC) and 20% dipalmitoylphosphatidylglycerol (DPPG) by weight was dissolved in chloroform and ethanol (1:1). The lipid solution was washed with an aqueous solution containing 0.5 M sodium sulfate and 2 mM EDTA at pH 7.4. The lipid mixture predried with a rotary evaporator was dried under a flow of nitrogen gas and finally in a vacuum overnight. The lipid was suspended in a 5 mM Tris-HCl (pH 7.4) solution at room temperature. The lipid suspension was subjected to 15 freeze-thaw cycles between −190°C and 60°C to make uniform liposomes.

MP-X dissolved in ultrapure water was added to the liposome suspension with a lipids/MP-X molar ratio of 20. The MP-X and lipid suspension was subjected to 15 freeze-thaw cycles. The suspension was dried under a reduced pressure for 2.5 days and was solvated under an atmosphere at relative humidity 32% equilibrating with a saturated CaCl₂ solution at 25°C. About 22 mg and 40 mg of the sample were packed in 3.2-mm and 4-mm rotors, respectively.

NMR measurements

Most NMR experiments were carried out with an InfinityPlus 500 NMR spectrometer (Varian, Palo Alto, CA) having broadband triple- and double-resonance probes for 4-mm and 3.2-mm rotors at a static field of 11.8 T. Only 2D ¹³C-¹³C correlation experiments with radio-frequency-driven recoupling (RFDR) and SPC^z5 sequences (25,26) were performed with an InfinityPlus 600 NMR spectrometer operating at 14.1 T equipped with a broadband double-resonance probe for a 4-mm rotor.

The initial magnetization for the experiments was prepared by ramped-amplitude cross-polarization (CP) from proton magnetization with a contact time of ∼2.0 ms. The RF field amplitudes for ¹³C and ¹⁵N, γ_XB_X, were swept linearly over the condition, γ_XB_X/2π = γ_HB_H/2π − ν_R, where γ_HB_H and ν_R are the ¹H radio-frequency (RF) field amplitude and the sample spinning frequency, respectively. The amplitude γ_HB_H/2π was 60 kHz and 50 kHz for ¹³C and ¹⁵N experiments, respectively. The ¹H, ¹³C, and ¹⁵N RF field amplitudes for π/2 pulses were typically 70 kHz, 50 kHz, and 40 kHz, respectively. Except for rotational-resonance (RR) experiments, ν_R was 12.5 kHz and 14.0 kHz, with a precision of ∼5 Hz at 11.8 T and 14.1 T, respectively. The dwell time was 20 μs, unless otherwise specified. The C-H dipolar interactions during the evolution and mixing periods were decoupled with two-pulse phase modulation sequences and continuous wave RF fields at amplitudes of 75 and 90 kHz, respectively, for a 3.2-mm φ rotor, and 63 and 80 kHz for a 4-mm φ rotor. The relaxation delay was 3 s. The time-domain data were Fourier-transformed with an exponential line-broadening factor of ∼50 Hz by Felix2000 (Accelrys, San Diego, CA). The ¹³C shift was referenced to the methyl signal of hexamethyl benzene resonating at 19.2 ppm, which gives chemical shift relative to DSS (2,2-dimethylsilapentane-5-sulfonic acid) (27). The ¹⁵N shift reference was computed from the ratios of resonance frequencies.

Signal assignments of uniformly labeled MP-X

Two-dimensional broadband ¹³C-¹³C correlation spectra were obtained with an RFDR pulse sequence at γ_CB_C/2π of 50 kHz and a mixing time of 2.3 ms (25). An experimental data matrix 512(t₁) × 512(t₂) obtained with the States method for the phase-sensitive detection was zero-filled to 1024 × 1024, unless otherwise specified. Experiment duration was 14 h.

A band-selective correlation experiment for the aliphatic ¹³C region was performed with a sequence having a double-quantum (DQ) ¹³C-¹³C dipolar mixing period under the SPC^z5 pulse sequence consisting of the composite 0° pulse 15°_x210°_−x195°_x with a γ_CB_C/2π of 47 kHz and a mixing time of 2.0 ms (26). Experiment duration was 21 h.

The pulse sequence for 2D N–(C^αC^β) correlation had a single ¹⁵N-¹³C^α and ¹³C^α–¹³C^β DQ dipolar mixing period for 2 ms under γ_NB_N/2π of ∼6 kHz and γ_CB_C/2π varying from 5 to 7 kHz at B_C and B_N frequencies of 47 and 80 ppm; the amplitudes simultaneously satisfied γ_CB_C/2π + γ_NB_N/2π ≈ ν_R ≈ 12.5 kHz and 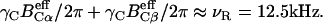The data matrix 256(t₁) × 512(t₂) was acquired with an experimental time of 46 h.

The magnetization was transferred from ¹⁵N to ¹³C with a 3.2-mm rotor under γ_NB_N/2π of ∼17 kHz and γ_CB_C/2π varying from 27 to 31 kHz, which satisfied γ_CB_C/2π ≈ γ_NB_N/2π + ν_R ≈ 30 kHz for 2D N_i+1–(C′C^α)_i and 2D (C^αC^β)_i+1–(C′C^α)_i experiments. The magnetization was transferred from ¹⁵N to ¹³C with a 4-mm rotor under γ_NB_N/2π of ∼5 kHz and γ_CB_C/2π varying from 6.8 to 9.2 kHz, which satisfied γ_CB_C/2π + γ_NB_N/2π ≈ ν_R ≈ 12.5 kHz for 3D N–C^α–C′, 2D N_i–(C^αC^β)_i+1, 2D C′_i–(C^αC^β)_i+1 and 3D N_i+1–C′_i–C_i^α experiments.

The sequence for 2D N_i+1–(C′C^α)_i correlation had a mixing period consisting of the CP from N_i+1 to C′_i with a 6-ms mixing time and RFDR magnetization transfer from C′_i to C_i^α with a 1.92-ms mixing time. The frequency of B_C was 190 ppm except for the RFDR pulses applied at 100 ppm. The data matrix 224(t₁) × 512(t₂) acquired with an experimental time of 18 h was zero-filled to 512 × 1024.

The pulse sequence for 2D N_i+1–(C′C^αC^β)_i correlation has a mixing period consisting of three mixing schemes as shown in Fig. 1 A. The γ_CB_C/2π amplitude for homonuclear rotary resonance (HORROR) was varied from 6.5 to 4 kHz under the effective fields for C^α and C^β spins, 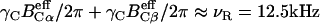. The B_C field was applied at 179, 100, and 66 ppm for the CP from N_i+1 to C′_i, RFDR and HORROR pulses, respectively. The data matrix 96(t₁) × 512(t₂) acquired with an experimental time of 52 h was zero-filled to 256 × 1024.

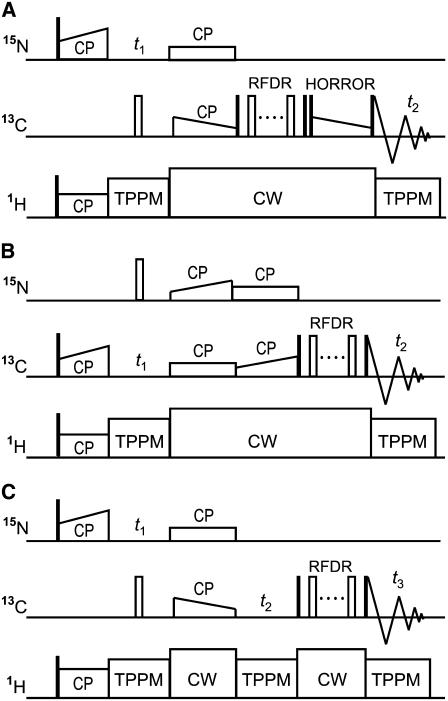
FIGURE 1.

Pulse sequences for 2D N_i+1–(C′C^αC^β)_i (A), 2D (C^αC^β)_i+1–(C′C^α)_i (B), and 3D 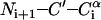(C) correlation experiments. The open and closed thin rectangles represent π and π/2 pulses, respectively. (A) The mixing period consists of the cross polarization from N_i+1 to C′_i with a mixing time of 2.0 ms, the magnetization transfer from C′_i to C^α_i under an RFDR sequence with a mixing time of 0.96 ms, and the DQ dipolar magnetization transfer from C^α_i to C^β_i under a ramped-amplitude HORROR sequence (49) with a mixing time of 1.5 ms. (B) The mixing period consists of cross-polarization from (C^αC^β)_i+1 to N_i+1, cross-polarization from N_i+1 to C′_i, and RFDR magnetization transfer from ¹³C′_i to C^α_i. The lengths for the first, second, and third mixing schemes were 6.0, 6.0, and 1.28 ms, respectively. (C) The N–C and C–C mixing times were 2.0 ms each.

The pulse sequence for 2D (C^αC^β)_i+1–(C′C^α)_i correlation has a mixing period consisting of three mixing schemes as shown in Fig. 1 B. The B_C field was applied at 38, 190, and 114 ppm for the first and second CP and RFDR, respectively, and the B_N field was at 119 ppm. Experiment duration was 55 h.

The pulse sequence for 3D N–C^α–C′ correlation is shown in Fig. 1 C. The B_C frequency was 58 and 118 ppm for the first and second mixing periods, respectively, and that of ¹⁵N was 114 ppm. The data matrix 14(t₁) × 36(t₂) × 512(t₃) acquired with an experimental time of 83 h was zero-filled to 128 × 512 × 2048. Dwell time was 400, 167, and 20 μs for t₁, t₂, and t₃, respectively.

The pulse sequence for 3D N_i+1–C′_i–C^α_i correlation was essentially the same as that for 3D N–C^α–C′ shown in Fig. 1 C, except for the B_C frequency. The frequency of B_C was 179 and 118 ppm for the first and second mixing periods, respectively. The experimental data matrix 15(t₁) × 22(t₂) × 512(t₃) acquired with an experimental time of 80 h was zero-filled to 128 × 128 × 2048. Dwell time was 400 (t₁), 250 (t₂), and 20 μs (t₃).

Rotational resonance

A constant-time RR pulse sequence (28) was used to suppress the evolution-time-dependent sample heating by the RF fields. The RR experiments for the A7 [¹³C′]–A10 [¹³C^β] and G5 [¹³C′]–A10 [¹³C^β] spin pairs were performed at ν_R of 20,200 and 19,730 kHz, respectively, at the n = 1 RR condition. We measured the intensities of signals in the difference spectra between the natural abundance and the labeled MP-X spectra at the same evolution time. The ¹³C–¹³C dipole couplings were obtained by fitting the simulated zero-quantum (ZQ) z-components 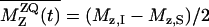to the experimental ones, where M_z,_i is the z-magnetization of spin i. The time-dependent was calculated in the ZQ subspace (29), where the zero-quantum relaxation, the dipole coupling, chemical shift anisotropies (30), and the distribution of isotropic shifts were taken into account. The relaxation time, 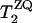, was estimated from 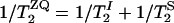, where 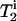is the single-quantum transverse relaxation time due to homogeneous broadening for spin i measured with spin-echo experiments off the rotational resonance condition (31,32). The 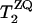relaxation times were 8.3 ms and 4.9 ms for the A7 [¹³C′]–A10 [¹³C^β] and G5 [¹³C′]–A10 [¹³C^β] pairs, respectively. Inhomogeneous broadening due to the chemical shift distribution at each site was considered (33) as

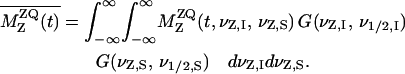(1)

Here, G(ν_z,i, ν_½,i) is the normalized Gaussian distribution as a function of resonance frequency offset ν_z,i for spin i and the linewidth at the half-height ν_½,i, where ν_½,i = ν_½,i,app – 1/πT₂ with the apparent linewidth, ν_½,i,app.

Rotational-echo double resonance

The normalized rotational-echo double resonance (REDOR) signal intensity was calculated from I_R/I₀ = (I – I_A)/(I_F – I_A), where I, I_F, and I_A are the REDOR and full-echo ¹³C signal intensities of the labeled sample, and the full-echo signal intensity of the natural-abundance sample, respectively. The number of scans was increased from 1000 to 5000 with the evolution time to compensate for the reduction in the signal/noise ratio. The dipolar couplings were obtained by fitting the simulated normalized REDOR signal intensities to the experimental ones. The dipolar dephasing was calculated by the numerical integration of a time-dependent Hamiltonian for the two-spin system including terms for the ¹³C–¹⁵N dipolar interaction, the isotropic chemical shifts and RF field amplitudes.

Measurements of chemical shift anisotropies

The apparent chemical shift anisotropies (CSAs) |σ₃₃−σ₁₁| were calculated from the spinning sideband intensities up to the eighth order at ν_R of 2 kHz by using program HBA provided by Dr. Klaus Eichele of the University of Tübingen (34). Simulation indicated that the effect of the ¹³C-¹⁴N dipolar coupling on the apparent carbonyl ¹³C CSA was <∼2 ppm at 11.8 T. Thus, we ignored this effect.

Structure calculation

The φ and ψ angles were predicted by TALOS for the primary structure MP-X-G where the C-terminal amide was replaced with Gly. The structure was calculated under the distance and dihedral angle constraints by the simulated annealing protocol in CYANA 1.0.6 (35). The 10 low-energy structures in the 100 optimized structures were analyzed using the software packages MOLMOL (36) and Swiss PDB viewer (37). The backbone root-mean-square deviation (RMSD) from the mean structure was calculated for N, C^α, C′, and O atoms. The obtained structures were deposited in the Protein Data Bank under ID code 2CZP.

RESULTS

Signal assignments of uniformly ¹³C,¹⁵N-labeled MP-X bound to lipid membrane

Solid-state NMR experiments were performed for MP-X tightly bound to lipid membrane composed of DPPC and DPPG. We optimized the sensitivity of the multidimensional MAS solid-state NMR by suppressing the large-amplitude motion of MP-X. The MP-X molecules were immobilized by gel-state lipid membranes at −20°C. The ¹³C and ¹⁵N signals were assigned with intraresidue 2D C-C, 2D N-(C^αC^β) and 3D N-C^α-C′ correlations and interresidue 2D N_i+1-(C′C^α)_i, 2D (C^αC^β)_i+1-(C′C^α)_i, 2D N_i+1-(C′C^αC^β)_i, and 3D N_i+1-C′_i-C^α_i correlations. The obtained chemical shifts were deposited in the BioMagResBank database under the accession number of 10001.

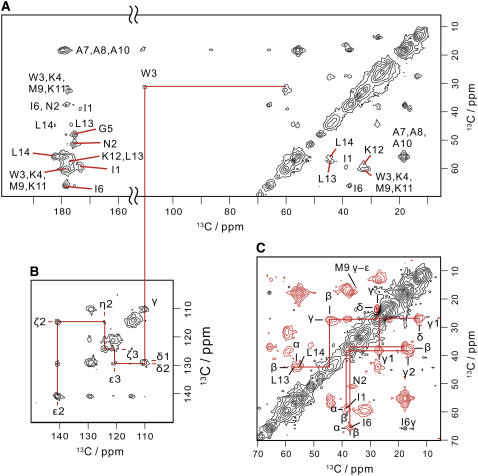
The 2D intraresidue ¹³C correlation spectra (Fig. 2) were obtained with the pulse sequences having the broadband ZQ and band-selective DQ dipolar mixing periods. In aliphatic regions, we assigned the peaks to amino acid ¹³C spin systems, (I1, I6), (N2), (W3, K4, M9, K11, K12), (A7, A8, A10), and (L13, L14) by their chemical shifts and spin connectivities. The signals for N2 were found in the correlation spectrum due to the DQ dipolar mixing. The C^α-C^β crosspeaks for W, K, and M are seen at ∼60 ppm (C^α) and 32 ppm (C^β) in the ZQ and DQ spectra. The chemical shift of W3^β was determined from the W3^β-W3^γ crosspeak in the ZQ spectrum.

FIGURE 2.

Two-dimensional ¹³C–¹³C spectra for intraresidue correlations of membrane-bound MP-X. (A) Two-dimensional broadband ¹³C correlation spectrum obtained with a pulse sequence having a ZQ dipolar mixing period under the RFDR pulse sequence. Assignments are given in the figure. (B) The tryptophan indole region of the 2D ¹³C correlation spectrum obtained with the same pulse sequence as used in A. (C) Two-dimensional band-selective ¹³C correlation spectrum for the aliphatic region. The pulse sequence for this spectrum has a DQ dipolar mixing period under the SPC^z5 sequence.

The intraresidue ¹⁵N–¹³C spectrum in Fig. 3 A provides ¹⁵N chemical shifts from crosspeaks corresponding to the ¹³C shifts determined above. The crosspeak between the amino ¹⁵N and ¹³C^α is due to I1. The peaks for N2, G5, and the rest of I, I6, can be found from their specific chemical shifts. The ¹⁵N chemical shifts of A and L are ∼121 and 115 ppm from the N–C^β and N–C^α signals. The N–C^β peaks have negative intensities because the ¹⁵N–¹³C dipolar couplings and ¹³C–¹³C DQ dipolar couplings were simultaneously recoupled in the mixing period.

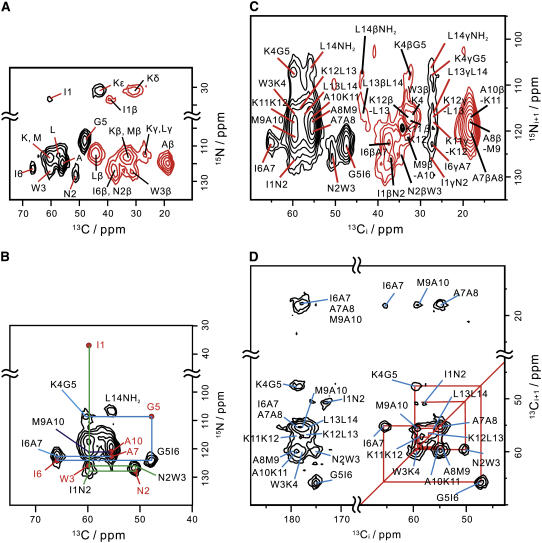
FIGURE 3.

Two-dimensional correlation spectra for the sequence-specific signal assignments of membrane-bound MP-X. (A) 2D N_i–(C^αC^β)_i correlation spectrum. (B) Two-dimensional N_i+1–(C′C^α)_i correlation spectrum for the ¹³C^α region. The signal peaks in the 2D N_i–(C^αC^β)_i spectra are represented by red solid circles. Crosspeaks used for the sequential assignments are connected by lines. (C) Aliphatic region of 2D N_i+1–(C′C^αC^β)_i spectrum. (D) Two-dimensional (C^αC^β)_i+1–(C′C^α)_i correlation spectrum. The pulse sequences for spectra C and D are given in Fig. 1, A and B, respectively.

The signal connectivities in 2D N_i–(C^αC^β)_i and 2D N_i+1–(C′C^α)_i spectra allow the sequential assignments as shown in Fig. 3 B. The intraresidue N_i–C^α_i crosspeak for I1 leads to the W3 peak along the green line sequentially. The blue line connects the crosspeaks from K4^N–G5^α to A7^N–A7^α. The connectivity between A10^N-M9^α and A10^N–A10^α peaks gives the ¹³C^α shifts of M9 and A10 as shown by the line. The ¹⁵NH₂–L14^α crosspeak for the C-terminal amide can be assigned from their chemical shifts. Since one of the two Leu C^α–C^β peaks in the ¹³C–¹³C correlation spectrum (Fig. 2 A) was assigned from the L14 C^α shift, the other peak is due to L13. Similarly, the C^α and C^β shifts for A8, K11, and K12 were specified with a precision of about ±1.0 ppm by decomposing the C^α–C^β signals under the restrictions of chemical shifts already determined. Thus, the correlations provided ¹³C^α and ¹³C^β shifts of all the residues and ¹⁵N shifts of I1, N2, W3, G5, I6, A7, A10, and the C-terminal amide. The ¹⁵N shifts of residues, K4, A8, M9, K11, K12, L13, and L14, can be specified with a precision of about ±1.5 ppm from N_i–(C^αC^β)_i (Fig. 3 A) and N_i+1–(C′C^αC^β)_i correlations (Fig. 3 C) at the ¹³C shifts determined previously.

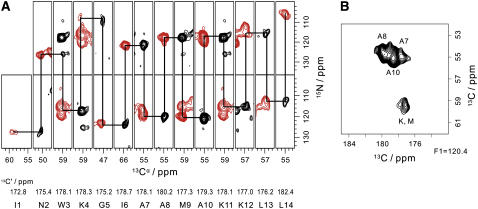
The 2D (C^αC^β)_i+1–(C′C^α)_i correlation confirms the sequential assignment as indicated in Fig. 3 D. In addition, it provides the C^α shift of A7 from the I6-A7 peak. Note that the three Ala C^β resonances were resolved by the C^α_i shifts of the preceding residues. The backbone signal assignments were reconfirmed with 3D N–C^α–C′ and 3D N_i+1–C′_i–C^α_i spectra. The two spectra permit the sequential assignment of all ¹⁵N, ¹³C′, and ¹³C^α signals by following the line in Fig. 4 A. All the carbonyl shifts were determined and the ¹⁵N shifts were refined from the 3D spectra. The three Ala C′ signals are partly resolved in the C^α–C′ cross section of the 3D N–C^α–C′ spectrum as seen in Fig. 4 B.

FIGURE 4.

Three-dimensional N_i–C^α_i–C′_i and N_i+1–C′_i–C^α_i spectra of membrane-bound MP-X. (A) Two-dimensional N-C^α cross sections selected from the 3D N_i–C^α_i–C′_i (black) and N_i+1–C′–C^α_i (red) correlation spectra at ¹³C′ frequencies. (B) Two-dimensional C^α_i–C′_i cross section selected from the 3D N_i–C^α_i–C′_i spectrum at F1 = 120.4 ppm in the ¹⁵N axis.

Here, the sequential backbone signal assignments were performed primarily using the 2D N_i–(C^αC^β)_i and 2D N_i+1–(C′C^α)_i spectra in Fig. 3 B. However, it is also possible to assign signals sequentially by mainly using the 2D (C^αC^β)_i+1–(C′C^α)_i spectrum in Fig. 3 D or 3D N_i–C^α_i–C′_i and N_i+1–C′_i–C^α_i spectra in Fig. 4 A. These three types of spectra in Figs. 3, B and D, and 4 A provide redundant information for the signal assignments and make them reliable. The C^α chemical shift often provides higher resolution than the ¹⁵N shifts, e.g., the three Ala C^β resonances are clearly resolved in the C^β_i+1–C^α_i spectrum (Fig. 3 D) but are not in the N_i+1–C^β_i spectrum (Fig. 3 C).

The ¹³C and ¹⁵N shifts of side chains other than C^β were also determined. The W3 ring signals were assigned from the crosspeaks in the 2D ¹³C correlation (Fig. 2 B) and 2D N_i+1–(C′C^α)_i correlation (data not shown). Side-chain crosspeaks for L and I were assigned along the lines in the 2D band-selective ¹³C correlation (Fig. 2 C). The signals for K were assigned from the N^α–C^γ and N^α–C^δ and N^ζ–C^ɛ signals in the 2D N–(C^αC^β) spectrum (Fig. 3 A). The ¹⁵N shift of N2 was obtained from the N^δ2-C^γ signal in the 3D N_i+1–C′_i–C^α_i spectrum (data not shown). The C^γ and C^ɛ shifts of M9 were determined from the A10^N–M9^γ signal in the 2D N_i+1–(C′C^αC^β)_i correlation (Fig. 3 C) and the C^γ–C^ɛ signal in the band-selective ¹³C correlation (Fig. 2 C).

Internuclear distance measurements

We measured ¹³C–¹³C and ¹³C–¹⁵N dipolar coupling constants in selectively isotope-labeled MP-X molecules to determine the distances for the backbone structural analysis. We prepared five peptides, each of which had an isotope-labeled spin pair as given in Table 1. The chemical shifts of the 10 labeled nuclei verified the signal assignments of uniformly labeled MP-X.

TABLE 1.

Experimental and calculated distances (Å) for MP-X

	Experimental*	Helix†	Sheet†
I1 [13C′]−G5 [15N]	6.0	4.0	11.0
G5 [13C′]–A8 [13Cβ]	4.2	4.1	9.2
A7 [13C′]–A10 [13Cβ]	4.2	4.1	9.2
A10 [13C′]–L13 [15N]	4.2	3.8	7.7
A10[13C′]–L14[15N]	4.4	4.0	11.0

^*Precision is ±0.1 Å for distances <4.5 Å and ±0.4 Å for a distance of 6.0 Å.

^†Distances were calculated with X-PLOR 3.1 (46) for an α-helix with (φ, ψ) = (−57°, −47°) and for a β-sheet with (−119°, 113°).

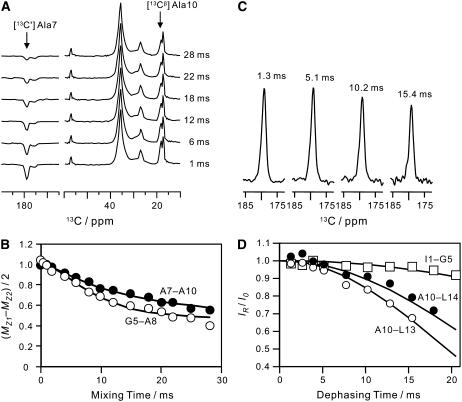
Dipolar couplings for ¹³C-¹³C spin pairs were measured by rotational resonance experiments (28). Fig. 5 A illustrates the spectra for RR on [¹³C′] A7, [¹³C^β] A10 MP-X. The positive and negative z-magnetization components at the labeled sites decreased with the mixing time τ_m, owing to the magnetization exchange by the dipolar coupling. The signal intensity differences for [¹³C′] A7, [¹³C^β] A10, and [¹³C′] G5, [¹³C^β] A8 MP-X are plotted as a function of τ_m in Fig. 5 B. The ZQ transverse relaxation time 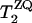was estimated from the single-quantum T₂ measured with spin-echo experiments (31,32). We obtained the dipolar coupling constants, D_i,j = K_i,j/r³, 91 and 89 Hz for A7 [¹³C′]–A10 [¹³C^β] and G5 [¹³C′]–A8 [¹³C^β] spin pairs, respectively, by fitting the simulated curves to experimental ones, where r is the distance and K_i,j = μ₀γ_iγ_j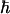/8π², with gyromagnetic ratio of spin i, γ_i.

FIGURE 5.

(A) ¹³C NMR spectra of [¹³C′] A7, [¹³C^β] A10 MP-X bound to the lipid bilayers as a function of the mixing time under the rotational resonance condition of n = 1 at ν_R = 20,200 kHz. (B) Magnetization exchange curves of ¹³C–¹³C spin pairs in selectively labeled MP-X under the n = 1 RR condition. Experimental ZQ z-magnetization for the A7 [¹³C′]–A10 [¹³C^β] pair and that for the G5 [¹³C′]–A8 [¹³C^β] pair are shown by solid and open circles, respectively. The solid lines give the simulated magnetization that minimized the RMSDs from the experimental magnetization curves at the distances in Table 1. (C) ¹³C NMR spectra of [¹³C′] A10, [¹⁵N] L13 MP-X as a function of dephasing time under the REDOR sequence. (D) Normalized REDOR curves obtained from ¹³C signal intensities for ¹³C–¹⁵N spin pairs in selectively labeled MP-X. The normalized REDOR signal intensities for A10 [¹³C′]–L13 [¹⁵N], A10 [¹³C′]–L14 [¹⁵N], and I1 [¹³C′]–G5 [¹⁵N] pairs are shown by open circles, solid circles, and squares, respectively.

Dipolar couplings for ¹³C-¹⁵N spin pairs were measured by REDOR experiments (22). The normalized ¹³C signal intensity, I_R/I₀, decreased by the dipolar dephasing as shown in Fig. 5, C and D, where I_R and I₀ are the intensities of REDOR and full-echo signals, respectively. The ¹³C-¹⁵N dipolar coupling constants were determined by minimizing the RMSD difference between the calculated and simulated dephasing curves. The dephasing curves for the A10 [¹³C′]–L13 [¹⁵N], A10 [¹³C′]–L14 [¹⁵N], and I1 [¹³C′]–G5 [¹⁵N] pairs provided the coupling constants of 38, 31, and 13 Hz, respectively.

The dipolar coupling constants were converted to the internuclear distances in Table 1 by following r = (S_D K_i,j/(D_i,j))^1/3 with the scaling factor for the dipolar couplings S_D ≈ 0.91. Internuclear distances in crystalline molecules determined by solid-state NMR are 1–2% longer than those by diffraction methods for spins separated by more than two bonds when S_D = 1 (38). This gives the scaling factor for crystals S_C ≈ 0.95 to correct NMR distances. We monitored the molecular motion from the CSAs, |σ₃₃–σ₁₁|, of the selectively labeled carbonyl ¹³C and amide ¹⁵N nuclei. The apparent CSAs measured from the spinning sideband intensities are ∼0.96 of those in crystal states on the average (Table 2), which gives the scaling factor S_M for the membrane-bound state relative to crystal states. Consequently, the distances were obtained with the scaling factor S_D = S_CS_M ≈ 0.91.

TABLE 2.

Chemical shift anisotropies (|σ₃₃−σ₁₁|/ppm) of MP-X and crystalline peptides

	MP-X*	Models
[13C′] I1	157	160†
[15N] G5	157	181‡
[13C′] G5	149	146‡
[13C′] A7	154	160§
[13C′] A8	160	160§
[13C′] A10	160	160§
[15N] L13	164	174‡
[15N] L14	156	174‡

Precision is ±2 ppm.

^†CSA for Ala residues is given since CSAs for amino acids Iso and Ala have almost the same values (47).

^‡Data taken from Brender et al. (48).

^§Data taken from Wei et al. (30).

Structure calculation of MP-X from chemical shifts and distances

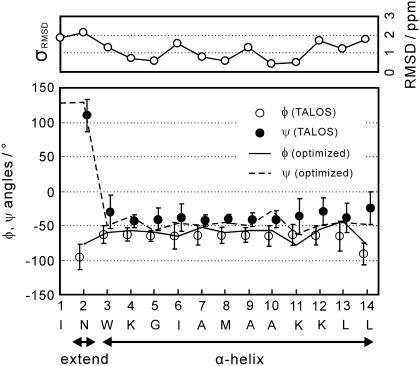
Conformation-dependent chemical shifts of proteins were used for secondary-structure analysis in solid states (12,17,19) as well as in solution (39). We predicted the backbone dihedral angles φ and ψ with a precision of ∼±15° from the C^α, C^β, C′, and N chemical shifts with the program TALOS based on a protein NMR database (40). The predicted dihedral angles in Fig. 6 indicate that membrane-bound MP-X adopts an extended conformation at residue 2 and an α-helix at residues 3−14. This structure is consistent with the experimental distances shown in Table 1, where the distances show that MP-X forms a helical structure except for the N-terminal region.

FIGURE 6.

Backbone dihedral angles, φ and ψ, of membrane-bound MP-X predicted from ¹³C^α, ¹³C^β, ¹³C′, and ¹⁵N chemical shifts using TALOS. RMSDs between experimental and predicted carbon-13 chemical shifts are also shown. The predicted ¹³C′, ¹³C^α, and ¹³C^β chemical shifts were calculated by SHIFTX from the atomic coordinates of the determined structure. The chemical shift of amidated C′ in L14 was not included in the computation of the RMSD. The error bars indicate twice the standard deviations, 2σ, of the angles selected from the database by TALOS for σ < 15°, and indicate σ for σ > 15°. This procedure makes the error bars nearly equal to the reported prediction errors of TALOS for MP-X.

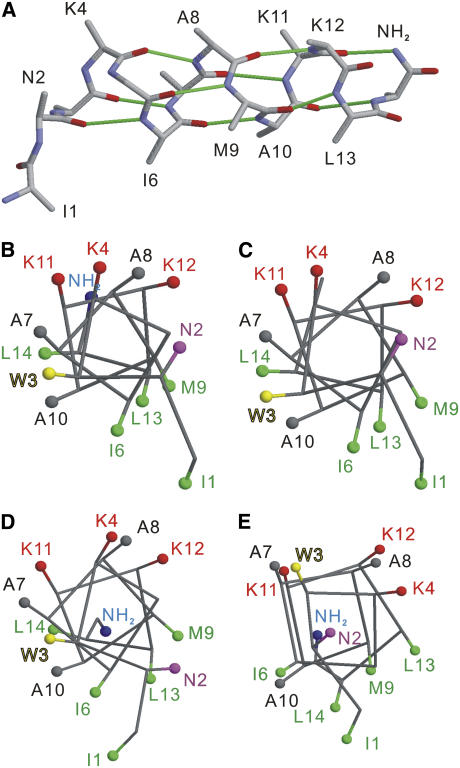
The structure of MP-X was determined by the simulated annealing in program CYANA under the five distance and 26 torsion angle restraints given in Table 1 and Fig. 6, respectively. Fig. 7 A shows an optimal structure that agrees with the dihedral angles and distances within the precisions. The backbone RMSD was <0.8 Å for every residue, and was 0.6 Å on the average. The hydrogen bonding pattern of the α-helix is seen for residues 2−14 as in Fig. 7 A, though the residue 11 has dihedral angles different from those for the typical α-helix (Fig. 6).

FIGURE 7.

(A) Backbone structure of membrane-bound MP-X calculated from distance and dihedral angle constraints. Hydrogen bonds in the backbone are represented by solid lines colored green. (B–E) Head-on view of the helical wheels for MP-X: (B) tightly membrane-bound structure determined by solid-state NMR; (C) solid-state structure precipitated from methanol solution; (D) weakly membrane-bound structure; and (E) G-protein bound structures by solution NMR. The C^β atoms and C-terminal amide are represented by balls. The structures shown were selected from the NMR-derived structures and have minimum backbone RMSDs from the average structures. Molecular graphics were prepared using RasMol (50).

To validate the dihedral angles obtained from chemical shifts by TALOS, we computed RMSD between the experimental chemical shifts and those predicted from the optimal structure that satisfies the angle and distance constraints. The ¹⁵N, ¹³C^α, ¹³C^β, and ¹³C′ chemical shifts were predicted semiempirically by the program SHIFTX, using a protein chemical shift database (41). The algorithm for the prediction is different from that used in TALOS. The chemical shift RMSD is shown as a function of the residue number in Fig. 6. The RMSD is <2.2 ppm, twice the RMS error in the prediction by SHIFTX, for all the residues. Thus, TALOS would not predict the dihedral angles erroneously.

The high-precision distances are important in restricting the peptide structure. Although the chemical shifts provide the information on local structures through the backbone dihedral angles, the distances correct accumulated errors in the structure built only with the angles. For example, the possibility of the 3₁₀-helix at the C-terminus can be eliminated from the distance measurements, because the experimental A10[¹³C′]–L14[¹⁵N] distance of 4.4 Å in Table 1 is much shorter than that for the 3₁₀-helix, 5.8 Å; it is closer to the distance for the α-helix, 4.0 Å. The difference between the two helices in ψ is only 20°, so that the distinction only by chemical shifts would not be possible without a careful statistical analysis with chemical shift databases.

DISCUSSION

Structural homogeneity and mobility of tightly membrane-bound MP-X

We completely assigned the ¹³C and ¹⁵N signals of membrane-bound MP-X. The linewidths reflect the distribution of the conformation through the chemical shifts. The apparent signal linewidths of the N, C′, C^α, and C^β resonances are ∼75 ± 14, 117 ± 18, 142 ± 24 and 134 ± 22 Hz on average at 11.8 T, respectively. The contribution of chemical shifts can be estimated by subtracting the effects of J couplings from the linewidths. The resultant linewidths are ∼1.0, 0.5, 0.5, and 0.7 ppm for the N, C′, C^α, and C^β resonances, respectively. These linewidths are much smaller than the full chemical shift variations due to the backbone conformations, ∼4 ppm and 8 ppm for ¹³C and ¹⁵N, respectively, and almost half of the linewidths reported for glycinated MP-X precipitated from methanol (12,42). Since MP-X is immobilized in the gel state at −20°C, the observed linewidths would indicate that the MP-X molecules adopt a well-defined structure.

We selected the lipid composition at which MP-X is tightly bound to the membrane. The increase in acidic phospholipid composition enhances the binding affinity and the cation permeability of the membrane by the pore formation with MPs (4,43). At the lipid composition DPPC/DPPG = 4:1 we used, however, MP-X does not perturb the membrane by forming the pores (4). This lipid composition also excludes random coil conformations of MP-X in aqueous solutions (5), as shown by the narrow signal linewidths and chemical shifts determined by a unique structure.

The CSAs of the selectively labeled ¹⁵N and carbonyl ¹³C of MP-X at the experimental temperature were presented in Table 2. They were constant within ±5% from −60°C up to the prephase transition temperature, 25°C (data not shown). We have also observed CSA of the ³¹P-NMR for the membrane-MP-X system. An asymmetric NMR powder pattern of ³¹P in the lipid headgroup exhibited a CSA of 187 ppm at −20°C, indicating the absence of rapid, axially symmetric rotational diffusion. The distance measurements for the A10-L14 spin pair at 10°C and −20°C gave the same dipolar coupling of 38 Hz. Therefore, MP-X did not undergo large-amplitude motions in the backbone for residues 1−14 on a timescale shorter than ∼10 ms. The consistency of the distances obtained from the dipolar couplings with the dihedral angles from the shifts in the determined structure also supports this notion. The membrane-MP-X system would not cause the problems in the NMR structural analysis up to the prephase transition temperature.

The dynamics of MP-X, however, has the effect of reducing the apparent C-C and C-N dipolar couplings by ∼9% as described in Results. This local motion was characterized by the order parameter S_D = 0.91. This parameter can be interpreted as a wobbling motion of internuclear vectors with an amplitude of ∼30° (44). This small-amplitude motion may be associated with the narrow signal linewidths mentioned previously.

Characteristics of the tightly membrane-bound MP-X structure

The membrane-bound structure determined by the solid-state NMR study is presented in Fig. 7 A. This structure has the hydrogen bonds for the α-helix between CO in residue i and NH in residue i + 4, for i = 2–10, and between CO in residue 11 and NH in the amide at the C-terminus. Since N2 has dihedral angles for an extended conformation, as shown in Fig. 6, CO in I1 does not form an intramolecular hydrogen bond. This backbone provides an amphiphilic helix; the side chains of K4, K11, and K12 located on one side form the hydrophilic face carrying net positive charges, and side chains of I1, W3, I6, M9, L13, and L14 on the other side form the hydrophobic face. This structure strongly suggests that the helix lies in the interface between the water layer and the hydrophobic domain of lipid bilayers with nonpolar residues facing the alkyl chains of the lipids. Details of the binding mode of MP-X to the lipid bilayers based on the determined structure will be dealt with in a subsequent paper.

The obtained structure is compared with other MP-X structures in Fig. 7, B–E. The helix formation of residues 3−14 is a common feature to the structures for tightly membrane-bound MP-X (B), glycinated MP-X precipitated from a methanol solution studied by solid-state NMR (12) (C), weakly membrane-bound MP-X structures (5) (D), and G-protein-bound structures (6) (E) studied by solution TRNOE NMR. The bicelle-bound MP-X was also reported to form the α-helix (10). The backbone RMSDs of structure B from C–E are 0.57, 0.95, and 1.89 Å, respectively. Thus the tightly membrane-bound MP-X structure (B) is almost the same as the precipitated MP-X structure (C) over the entire backbone. This high similarity in structure mainly results from the agreement in backbone chemical shifts. The RMSD between experimental ¹³C chemical shifts for structures B and C is 1.3 ppm, which is comparable to 1.2 ppm, the RMSD of the prediction error averaged for residues 1−14 shown in Fig. 6.

The tightly (B) and weakly membrane-bound structures (D) have a similar amphiphilic α-helix. This similarity indicates that the increase in the membrane affinity due to the lipid acidity is simply induced by electrostatic effects that do not cause major backbone structural changes. However, two differences between structures B and D should be noted. The C-terminal amides of the two structures point in almost opposite directions. This dissimilarity is primarily due to ψ of L14. The NH₂ orientation in B allows the formation of the hydrogen bond between NH₂ at the C-terminus and CO in K11, whereas that in D does not. This hydrogen bond in B would be important in stabilizing the helix structure up to the C-terminal region and thus enhancing the ability to disrupt lipid membranes, as shown by the molecular dynamics simulation for eumenine mastoparan AF (11). The C-terminal amide orientation in B also contributes to forming the hydrophilic surface of the helix with the NH₂ group. The other difference is the orientation of the N2 side chain, which is mainly due to the dihedral angle φ of W3. The tightly bound structure takes a φ angle for the α-helix, −60°, but the weakly bound structure takes a φ angle of −145°. The side-chain orientation of N2 toward the hydrophilic face would allow the side chain to contact the water layer. This feature is compatible with the secondary ¹H chemical shifts of MP-X bound to bicelles (10). The secondary shifts of H^α and H^N suggest that W3 takes a helical conformation and N2 is in a hydrophilic environment. Thus, one side of the helix surface determined in this work is perfectly hydrophobic.

The two membrane-bound MP-X structures (B and D) differ from the G-protein bound structure (E) in the number of repeating residues per helix turn. This difference places the W3 side chain on the hydrophilic face formed by the three Lys residues in the structure (E). Structure-activity relationship studies of MPs indicated that those positively charged residues are crucial for the activity on G-proteins (2). MP-X molecules would first bind to the membranes with the structural transition from the random coil to the helical structure, and bind to G-proteins after the lateral diffusion on the membrane surfaces (5). Thus, the membrane-bound structures would accelerate the G-protein binding, because the membrane-bound structures are analogs to the G-protein bound structure.

The MP-X structures are commonly characterized by the extended conformation of N2 and helical conformation of residues 3−14. This conformation of N2 makes the I1 side chain form a part of the hydrophobic surface as shown by structures B and D, which would be stabilized, especially in the interface region between the lipid and water layers. The residue N2 adopts the extended conformation also in the G-protein-bound and precipitated solid states where the formation of a hydrophilic surface may not be critically important. This suggests that the extended conformation is not due to the membrane environments but due to the intrinsic propensity of Asn that hinders the helix formation (45).

The oligomerization of MP-X would be relevant to the membrane-pore formation. However, the tightly membrane-bound MP-X molecules would not make oligomers for the membrane pores in this study because of the PC/PG composition used. Even if MP-X forms oligomers, the MP-X molecule would adopt a structure similar to that of the membrane-bound MP-X. This is because in the solid state, where an MP-X molecule is surrounded by other MP-X molecules, MP-X takes the structure (C) that is very similar to the membrane-bound one (B). Note that the oligomerization did not have direct effects on the present structure determination for the following reasons 1), the dihedral angles used for the determination were predicted from the chemical shifts governed by the intramolecular structure; and 2), the distances were also obtained by attributing the dipolar couplings to intramolecular spin pairs. The distances were consistent with the angles in the optimized structure: we do not need to consider a third spin coupled with an intermolecular dipolar interaction.

CONCLUSIONS

We have determined the backbone structure of tightly membrane-bound MP-X by MAS solid-state NMR. The ¹³C and ¹⁵N signals of uniformly labeled MP-X were completely assigned. The obtained chemical shifts provided constraints on the dihedral angles by using protein NMR database programs. The measurements of ¹³C–¹³C and ¹³C–¹⁵N dipolar couplings in the selectively labeled MP-X molecules gave the precise internuclear distances. These dihedral angles and distances enabled the determination of the membrane-bound structure at a backbone RMSD of 0.6 Å.

The determined MP-X structure revealed features that are key to understanding the interaction of the amphiphilic α-helix with the lipid bilayer membranes. The assigned signals can be used as probes for monitoring the interaction by chemical shift perturbation or observing dipolar couplings with spins in the membranes. The method in this study is also applicable to the structural studies of G-protein-bound and pore-forming peptides.

The solid-state NMR techniques employed form the foundation for application to the membrane proteins. The straightforward application would allow partial sequence-specific signal assignments of the uniformly isotope-labeled membrane proteins. The method described herein can be improved by combining with other techniques. Semiselective labeling would facilitate the signal assignments and distance measurements (20,21). Intensive use of the relationship between chemical shift and structure would accelerate signal assignments and structural analysis (39). Further signal narrowing and sensitivity enhancements would also make practical application to larger proteins (17–19).