Maximum Likelihood Estimation of Molecular Motor Kinetics from Staircase Dwell-Time Sequences

Abstract

Molecular motors, such as kinesin, myosin, or dynein, convert chemical energy into mechanical energy by hydrolyzing ATP. The mechanical energy is used for moving in discrete steps along the cytoskeleton and carrying a molecular load. High resolution single molecule recordings of motor steps appear as a stochastic sequence of dwells, resembling a staircase. Staircase data can also be obtained from other molecular machines such as F₁-ATPase, RNA polymerase, or topoisomerase. We developed a maximum likelihood algorithm that estimates the rate constants between different conformational states of the protein, including motor steps. We model the motor with a periodic Markov model that reflects the repetitive chemistry of the motor step. We estimated the kinetics from the idealized dwell-sequence by numerical maximization of the likelihood function for discrete-time Markov models. This approach eliminates the need for missed event correction. The algorithm can fit kinetic models of arbitrary complexity, such as uniform or alternating step chemistry, reversible or irreversible kinetics, ATP concentration and mechanical force-dependent rates, etc. The method allows global fitting across stationary and nonstationary experimental conditions, and user-defined a priori constraints on rate constants. The algorithm was tested with simulated data, and implemented in the free QuB software.

INTRODUCTION

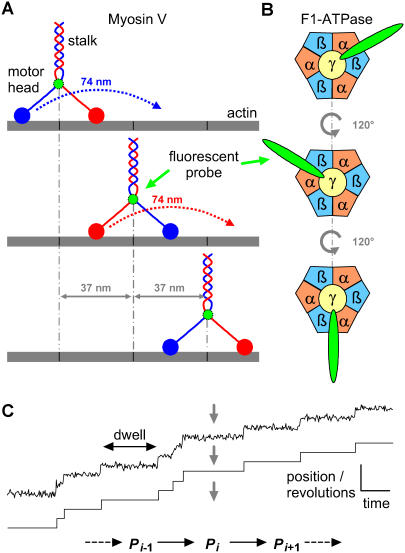
Processive motor proteins, such as kinesin, myosin, or dynein, convert chemical energy into mechanical energy by hydrolyzing ATP. The mechanical energy is used for moving in discrete steps along the cytoskeleton and carrying a molecular load (1). The mechano-chemistry of molecular motors is a repetitive chain of identical reaction units (2). Each unit corresponds to all the conformations—including ATP binding states—taken by the protein at each position. The reaction units in the chain are connected by motor step transitions, corresponding to forward or backward steps taken by the motor along its track. Myosin V, for example, is a dimeric motor protein walking with a hand-over-hand mechanism along actin filaments, taking a 37-nm step per ATP hydrolyzed. In the hand-over-hand motion, the motor alternately moves its heads to walk: first, the rear head moves 74 nm and becomes the leading head; next, the other head moves 74 nm and takes the lead position, and so on (3,4) (Fig. 1 A).

FIGURE 1.

Myosin V and F₁-ATPase are typical molecular motors that convert chemical energy into mechanical energy by hydrolyzing ATP. (A) Myosin V is a dimeric motor protein, walking with a hand-over-hand mechanism along the actin filament, with the stalk taking 37-nm steps per ATP hydrolyzed (3). (B) F₁-ATPase is a rotary motor that unidirectionally turns a rotor (γ-subunit) inside a stator (α₃β₃-complex). The rotor turns in 120° steps, one for each ATP hydrolyzed. Each 120° step consists of an 80° ATP-driven substep, followed by a 40° substep (8,9). (C) By attaching a probe to the motor protein, staircase data are constructed from single-molecule measurements. For a linear motor (myosin V), each dwell in the staircase data represents the location of the protein at a given position along its tracks, whereas for a rotary motor (F₁-ATPase), each dwell corresponds to a given number of revolutions taken by the rotor. The duration of each dwell is random, with exponential distribution determined by kinetics and by experimental conditions, such as ATP concentration or applied mechanical force. Due to finite sampling time, more than one step may occur within the sampling interval, resulting in missed events. At each position, the motor undergoes transitions between two or more conformations. One of these transitions is ATP binding.

The motor movement can be visualized by attaching a fluorescent probe to the molecule. Single-molecule recordings of motor steps appear as a stochastic sequence of dwells (3,5,6) resembling a staircase (Fig. 1 C). Each dwell corresponds to a defined position of a single motor. The duration of each dwell is random, with an exponential distribution determined by the kinetics. Generally, two consecutive dwells correspond to a step between two consecutive positions. However, due to the finite time resolution, the motor protein may take more than one step within the sampling interval, resulting in missed events. We developed a maximum likelihood idealization algorithm to provide the dwell-sequence for kinetic analysis (7). This procedure finds the motor's most likely position for each data point (implicitly detecting jump points), and estimates the step-size distribution and transition probabilities. The idealization was tested successfully with different types of staircase data: uniform or alternating small and large steps, constant or variable step size, and reversible or irreversible kinetics.

Staircase data can be obtained from other molecular machines at the single-molecule level. A typical example is the F₁-ATPase, which is a rotary molecular motor (Fig. 1 B). Unidirectional rotation of the central γ-subunit is powered by ATP hydrolysis at three catalytic sites arranged 120° apart. At high resolution, each 120° step can be resolved into an 80° substep, driven by ATP binding, and another 40° substep (8,9). Tracking the RNA polymerase position on the DNA template (10), or tracking the topoisomerase activity (11) also generates staircase data. What all these experiments have in common is the observation of a process with periodic chemistry through an increasing stochastic variable (i.e., position or rotational angle). In contrast, other single molecule data, such as the patch-clamp recording of the current flowing through a single ion channel (12), observe a nonperiodic stochastic variable with only a few states.

Stochastic data cannot be analyzed by fitting the mean. Instead, one must fit probability distributions, or maximize the likelihood. The simplest way to analyze dwell-sequences is to construct a dwell-time histogram (13) and fit it with a sum of exponentials, or directly with the probability density function (PDF). However, there are a few critical disadvantages to histogram fitting. Most importantly, the information provided by the correlation between dwell-times is not utilized. For a model with N_S states, at equilibrium, a maximum number of 2N_S–1 parameters can be extracted by histogram fitting: the time constant and the weight for each exponential component, minus one for the constraint that weights sum to one.

For example, the model shown in Fig. 2 A has four rate constants but, since N_S = 2, only three parameters can be uniquely identified by histogram fitting. Thus, while the time constants of the underlying process can be estimated by histogram fitting, a detailed kinetic mechanism may be impossible to derive due to missing information. Furthermore, histogram fitting does not account for missed events, and requires a large amount of data to avoid counting errors. This can be a problem for single molecule fluorescence experiments, where photobleaching is limiting. Some of these problems are solved by maximizing the likelihood function. The maximum likelihood method utilizes all the information contained in the data and its estimates are asymptotically unbiased (14).

FIGURE 2.

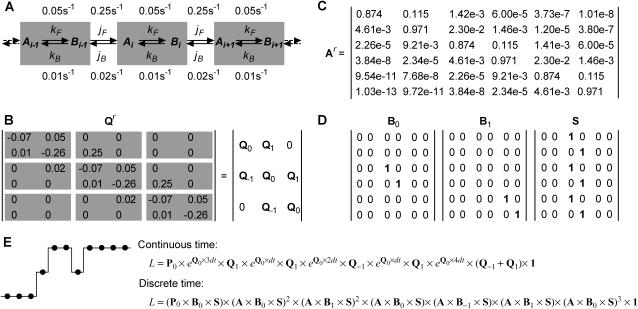
Molecular motors can be represented with reduced Markov models. (A) The mechano-chemistry of molecular motors is a repetitive chain of identical reaction units. Each unit includes the conformations assumed by the protein while located at a given position along the cytoskeleton. The example shown is for a model with two states per reaction unit. Only transitions between states within different units can be detected experimentally. (B) The rate matrix Q of the Markov model is block tridiagonal and periodic. Shown is a submatrix Q^r copied from the theoretically infinite Q, and its block representation. Note that the first and last rows are not zero-sum. (C) A truncated transition probability matrix A^r is calculated as 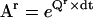. The example is shown for a sampling interval dt = 0.5 s. Note that A^r is also periodic. (D) Auxiliary matrices (B_i and S) used in the calculation of the discrete-time likelihood function. (E) An example of likelihood calculation, for either the continuous-time or the discrete-time Markov model (see text for details).

We present a maximum likelihood algorithm (the maximum idealized point likelihood, or MIP) that estimates the rate constants of conformation and step transitions, from dwell-time sequences. We model the molecular motor with an aggregated periodic Markov model. Each molecular conformation is assigned to a state in the model, and transitions between states are quantified by rate constants. The states of the Markov model must include not only the finite set of allosteric conformations, but also the position along the substrate, which may be large. However, we take advantage of the periodic chemistry, and reduce the Markov model to those core states and transitions that fully describe the kinetic mechanism. To reflect periodicity, certain constraints are imposed on these core transitions. In the calculation of the likelihood function, this reduced model is, in effect, recycled at each data point. Although computation with the truncated model is only asymptotically exact, the precision can be improved by increasing the size of the core model. For small data sets, optimization with the full model is possible (15), but it becomes too slow and numerically unstable for larger data sets that may require hundreds of states.

Stochastic single molecule data can be represented either with discrete-time or with continuous-time Markov models. A discrete-time algorithm maximizes the likelihood of a sequence of data points (16,17), while a continuous-time algorithm maximizes the likelihood of a sequence of intervals (18,19). Both algorithm types fully utilize the information contained in the data, and should give statistically equal estimates. For convenience, the likelihood function to be maximized by our MIP program is formulated for a discrete-time Markov model, with the added benefit that a correction for missed events (20) is no longer necessary.

The algorithm described here has advanced features (as described in (21)), such as global fitting across experimental conditions of arbitrary time course, linear constraints on rate constants (in addition to those reflecting the periodic step chemistry), etc. The algorithm can handle models with arbitrary kinetic complexity, including external driving forces, such as concentration, force, voltage, etc. The likelihood function and its derivatives are calculated analytically, permitting robust and fast (seconds to minutes) maximization. We tested the algorithm with a variety of kinetic models and simulated staircase data. Optimization with MIP was similar to the output from other maximum likelihood algorithms designed to estimate the rate constants of nonperiodic Markov models (17,19).

MATERIALS AND METHODS

All the computer work was done with the QuB program (www.qub.buffalo.edu; SUNY at Buffalo, Buffalo, NY) running MS Windows XP on a 3.0 GHz Intel PC. Staircase and non-staircase noisy data and idealized dwell-time sequences (subject to finite temporal resolution) were generated with the SIM routine. The simulator also provides the actual number of transitions for any pair of states, n_ij, and the actual time spent in each state, t_i. From these values, the true rate constants are calculated as k_ij = n_ij/t_i. Staircase data were generated with periodic Markov models, as utilized for processive molecular motors, while non-staircase data were generated with nonperiodic Markov models, as utilized for ion channels. For estimation of rate constants, we used the MIP, MPL, and MIL routines. MIP works by optimizing the discrete-time likelihood of either a staircase or a non-staircase dwell-time sequence. MPL maximizes the discrete-time likelihood of a data sequence generated by a nonperiodic Markov model (17). MIL maximizes the continuous-time likelihood of a dwell-time sequence, and provides first-order correction of missed events (19). All three algorithms calculate analytically the gradients of the likelihood function, and maximize the likelihood function using the same fast variable metric optimizer (dfpmin), implemented as in Press et al. (22) with modifications.

MODEL AND ALGORITHMS

Markov model

The behavior of a single molecule is well described with Markov models. At any position p along the substrate, the motor molecule is assumed to exist in one of N_S aggregated (i.e., experimentally undistinguishable) states. Thus, a staircase data set where the motor randomly walks across N_P positions requires a model with N_S × N_P states. Note that, due to missed events and reversible chemistry, the number of observed dwells may be different than N_P. In general, the rate constants of a Markov model are expressed as a rate matrix Q (23). For staircase data, the resulting rate matrix Q has a dimension (N_S × N_P) × (N_S × N_P). The Q matrix has each off-diagonal element q_ij equal to the rate constant between states i→j, and each diagonal element q_ii equal to the negative sum of the off-diagonal elements of row i, so that the sum of each row is zero (this reflects the fact that the probability of being somewhere is unity). Hence, −1/q_ij is equal to the mean lifetime of state i. Each rate constant q_ij has the Eyring expression (24)

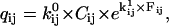(1)

where 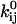is a preexponential factor, C_ij is the concentration of some ligand (such as ATP), and 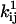is an exponential factor (Arrhenius), multiplied by the magnitude of the driving force F_ij (e.g., mechanical force). If the rate is not concentration-dependent, then by definition C_ij = 1. Note that including C_ij in Eq. 1 relies on the assumption that C_ij is constant, in which case the kinetics are (pseudo) first-order. The units of the exponential factor 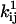depend of the units of the driving force F_ij.

The occupancy of the N_S × N_P states is represented with a state probability vector P, of dimension (N_S × N_P). The Kolmogorov equation describes the dynamics of P,

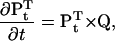(2)

where P_t is the state probability vector at time t, and the superscript T denotes vector transposition. The Chapman-Kolmogorov solution allows calculation of P_t, given some initial value P₀:

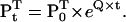(3)

In the same way, the solution of P_t can be advanced over the sampling interval dt,

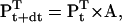(4)

where A is the transition probability matrix, of dimension (N_S × N_P) × (N_S × N_P). Each element a_ij is equal to the conditional probability that the process is in state j at time t+dt, given that it was in state i at time t. The A matrix is

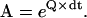(5)

By definition, the molecule cannot take more than one step at a time. Thus, the kinetic states at position p are directly connected only to the kinetic states at position p + 1 (forward step), and to the kinetic states at position p − 1 (backward step) (Fig. 2 A). Therefore, Q is block-tridiagonal (Fig. 2 B). Due to the periodicity of the kinetic model, the Q and A matrices have the following additional properties:

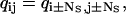(6)

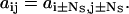(7)

These two properties, together with the band-tridiagonal structure of the Q matrix, make the calculation of any q_ij element trivial. However, as further shown, the A matrix is also required to calculate the likelihood function in the discrete-time case. Even though the length of the reaction chain is practically limited by experimental conditions, the size of the corresponding Markov model could be very large, with possibly hundreds of states. How does one calculate the A matrix when Q is large?

Within a sampling interval dt, the motor can maintain position or can take any number of steps, back and forth. However, if the position at time t is known, the position at t + dt is expected to be in the neighborhood, and the probability of finding the motor at a further-away position decreases exponentially with the distance. If the sampling interval is short relative to the kinetics, the probability of the motor having taken more than a small number of steps approaches zero: a_ij → 0, for j sufficiently far from i. While Q is band-tridiagonal, A is periodically banded. The size of any band of A is equal to N_S rows, and any two adjacent bands are identical but shifted horizontally by N_S columns (Fig. 2 C). For a full representation of A, it is therefore enough to calculate the elements a_ij within a band, such that j is within a certain distance from i, small enough to permit computation, yet large enough for precision. The other elements a_ij, where j is farther from i, can be approximated as zero. Any other band of A can be constructed simply by shifting left or right by a multiple of N_S columns.

A practical way of calculating the transition probabilities a_ij with minimal error is the following: first, a truncated rate matrix Q^r is constructed as if it were copied as a submatrix from an infinite Q. The size of Q^r is (2r + 1) × (2r + 1) reaction units, where each unit has N_S states. The truncation order r is chosen to be greater than the highest-order step detected in the staircase data. A truncated A^r matrix is subsequently obtained from Q^r using Eq. 5. We have chosen the spectral decomposition technique (25,26), which obtains the A^r matrix as

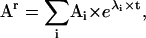(8)

where A_i values are the spectral matrices obtained from the eigenvectors of Q^r, and λ_i are the eigenvalues of Q^r. A submatrix copied from the theoretically infinite A should be approximately equal to the corresponding submatrix copied from A^r, if r is sufficiently large. For the example shown in Fig. 2 C, we found that the approximation error becomes negligible for r ≥ 3. Note that since the first and last rows of Q^r do not have zero sum, the A^r matrix is no longer row-stochastic, i.e., the sum of each row is not one. In conclusion, all calculations can be done with a truncated model of small size.

Dwell-time probability density function

The probability density function for the lifetime of an aggregated Markov model in a given class is a sum of exponentials, with as many components as states in that class (27). To calculate the PDF, Q is partitioned into submatrices Q_ab of dimension (N_a × N_b), where N_a and N_b are the numbers of states in aggregation classes a and b, respectively. The PDF of the transitions between classes a and b is given by the matrix G_ab(t), as

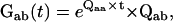(9)

where Q_aa is the submatrix of Q that contains only transitions within class a, and Q_ab is the submatrix containing transitions between classes a and b. The matrix 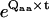represents the probabilities of transition within class a. The expression G_ab(t)_ij is the conditional PDF that the process stays for time t in class a, given that it entered class a through state i and that it exited into class b through state j. To calculate the unconditional PDF, one must take into account the probabilities of entering through each state of class a, and all possible exit classes b ≠ a. Thus, the PDF of dwelling for time t in class a, denoted f_a(t), has the expression (27,28)

(10)

where the vector P_a (of dimension N_a) represents the entry probabilities in class a, and 1 is a vector of ones, of dimension matching Q_ab. With the assumption that the process is at equilibrium, P_a can be calculated as (27)

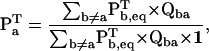(11)

where P_b,eq is a vector of dimension N_b, containing the equilibrium probabilities for the states in class b. Essentially, the above expression calculates the entry probabilities into class a as the equilibrium probabilities in class b ≠ a multiplied by the rates between b→a. The role of the denominator is to normalize the resulting probabilities to one. For a simple two-state model, Eq. 10 reduces to .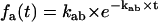

Likelihood function for the continuous-time model

The one-dimensional PDF (Eqs. 9 and 10) can be used to calculate the joint PDF of a sequence of dwells (t, a) as (29)

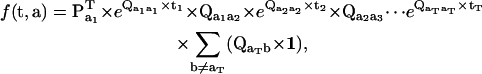(12)

where t is the dwell-time sequence t = [t₁, t₂, …, t_T], and a is the class sequence a = [a₁, a₂, …, a_T]. The value f(t, a) is in fact the likelihood of observing the dwell-sequence (t, a), given the model and its parameter values.

The likelihood function above is formulated for an ideal dwell-sequence, in which all transitions between different classes are observed. In practice, due to finite temporal resolution, some short dwells will always be missed. These missed events may result in observed steps between nonconsecutive positions. Notice that the submatrix for transitions between nonconsecutive positions is zero, which causes the likelihood to be zero too. Without a correction for missed events, dwell-times are overestimated, and model parameters are biased. The distortion caused by missed events can be corrected by an exact but slow solution (30,31), or by a fast approximation (19,32). For example, in the first-order correction (19), the PDF has exactly the same form, except it uses the matrices ^eQ_aa and ^eQ_ab, corrected for missed events, as

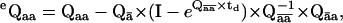(13)

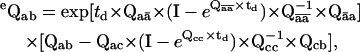(14)

where I is the identity matrix and t_d is the dead-time. The index value ā refers to those states that are not in class a, and c refers to those states that are neither a nor b.

In the case of processive molecular motors, there is generally only one aggregation class, and its dwell-time PDF has N_S exponentials. The Q matrix can be partitioned using three submatrices Q₀, Q₋₁, and Q₁, as shown in Fig. 2 B. Thus, Q₀ is the submatrix of transitions within the same reaction unit, while Q₋₁ and Q₁ are the submatrices of transitions between consecutive units, in the forward or backward direction, respectively. The dwell-time PDF has the expression

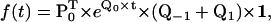(15)

where P₀ is the vector of entry probabilities into one unit. P₀ can be obtained as

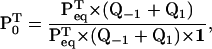(16)

where P_eq is the vector of equilibrium probabilities for the states in one reaction unit. The calculation of P_eq deserves some discussion: the equilibrium probability for any state i along the chain should be very small, theoretically zero for an infinite chain. However, since the process is periodic, dwells are indistinguishable: dwells corresponding to different positions have identical PDF. Therefore, the equilibrium probability for a state i inside a reaction unit, taken separately, is obtained by summing the probability of that state across all reaction units, which is a finite number. Furthermore, the same value is obtained whether the sum is over an open and infinite chain, or over a circular and finite chain. Thus, a practical way to calculate P_eq is by constructing a circular model that contains two reaction units connected in a loop. From the Q matrix of this circular model, equilibrium probabilities can be calculated with the method described in Colquhoun and Hawkes (23). From these, P_eq,i is obtained as twice the equilibrium probability of state i in one unit of the circular model.

The likelihood L of a staircase dwell-sequence can be written as

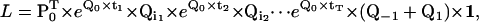(17)

where Q_i is equal to either Q₁ or Q₋₁, depending on whether the step between the two consecutive dwells is in the forward or in the backward direction. An example of how to calculate the likelihood function for a given dwell-time sequence is shown in Fig. 2 E. Application of the missed events correction to staircase data is possible, but for details we refer the reader to Colquhoun et al. (18) and Qin et al. (19). Note that, due to the missed events correction, the submatrix for transitions between nonconsecutive positions is no longer zero.

Likelihood function for the discrete-time model

For easier understanding and without loss of generality, we assume that the maximum step detected in the data is of order ±1, i.e., any two consecutive measurements are not separated by more than one position. To better illustrate the method, we also assume the kinetic model is reversible, with two states per reaction unit, such as shown in Fig. 2 A. We choose a truncation order r = 1, and thus the model has 2r+1 = 3 units (referred to as left, center, and right), and a total of six states. Hence, the Q^r and A^r matrices have a dimension of 3×3 units, or 6×6 elements. Similarly, the state probability vector P and all other vectors used in the computation have a dimension of three units. For increased numerical accuracy, A^r should be obtained from a larger Q^r before truncation.

The likelihood L of a sequence [0…T] of idealized staircase data points is given in matrix form by the expression

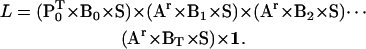(18)

The likelihood expression above is similar to that in Qin et al. (17). The value P₀ is the initial state probability vector. All its entries are zero, except those corresponding to the center unit, which are nonzero and sum to one. The value B_t is a diagonal matrix, with entries equal to either 0 or 1 (Fig. 2 D). For data points at the beginning of dwells, after a forward jump, the entries in the left block are one and all the others are zero. For points corresponding to a backward jump, the entries in the right block are one and all the others are zero. For all other points, the entries in the center block are one and all the others are zero. At each point t, the appropriate B_t matrix is plugged into the likelihood expression (Fig. 2 E).

In Qin et al. (17), B_t is also a diagonal matrix, but its diagonal entries are Gaussian conditional probability densities. There, these probability densities measure how likely it is that a noisy data point was obtained while the process was in a given state. Here, the probability densities are replaced with zero or one, since the signal is already separated from noise. Note that with data obtained from motors with high step variability (e.g., dynein), the step order may be ambiguous. In this case, B_t can be modified as to include all possible jump orders, each with a calculated weight. The value S is a permutation matrix (Fig. 2 D) that sums, blockwise, the state probabilities, moves the sum into the center block and clears the left and right blocks. The role of the S matrix is to map the likelihood computation from the theoretically infinite state space into the finite, small state space of the truncated A^r matrix. This is permitted by the periodic chemistry and by the periodic properties of the A matrix (Eq. 7).

In short, the likelihood function in Eq. 18 propagates the state probabilities through the time sequence, according to Eq. 4, but it also compares the theoretical prediction with the data. The calculation starts with the initial state probabilities P₀, which represent the a priori knowledge about the initial state occupancies. Then, for each time t, P_t+1 is first predicted by post-multiplying P_t with the A^r matrix (as in Eq. 4). The prediction is then corrected by the evidence contained in the data, i.e., by post-multiplication with the diagonal matrix B_t+1. This correction leaves unmodified the entries in the state probability vector corresponding to those states that match the actual data, while it zeroes all the others. The corrected P_t+1 is the a posteriori estimate. The corrected state probabilities are then reset by post-multiplication with the permutation matrix S, so that only the states in the center block are occupied and the others are zero. Although the same result can be achieved without explicitly using the S matrix, this formulation permits a consistent matrix form of the likelihood function and of its derivatives, as shown below. Consequently, only the relative difference in position between two consecutive data points is used. Note that the S matrix is strictly necessary only at the beginning of dwells and has no effect otherwise. Finally, the a posteriori state probabilities at the last data point are summed over all states, by post-multiplication with a column vector of ones. This sum is equal to the likelihood. The more the prediction matches the actual data, the higher the likelihood. An example of how to calculate the likelihood for a point sequence is shown in Fig. 2 E.

Maximization of the likelihood function

The objective is to find the parameter set θ^ML that maximizes the likelihood L, or, equivalently, the log-likelihood LL:

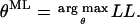(19)

Either the continuous-time or the discrete-time likelihood function can be maximized. Here, we have chosen the discrete-time case, for two main reasons: it is a simpler computation, and it does not require correction for missed events. The likelihood function is maximized numerically. For details of implementation, we refer the interested reader to Milescu et al. (21). The parameters to be estimated are the preexponential and the exponential factors 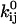and 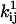, for each rate constant q_ij. A transformation of variable enforces the constraint of positive preexponential factors 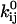(21). Other constraints are the model periodicity (Eq. 6), and those derived from a priori knowledge (21), such as fixed or scaled rates, or microscopic reversibility of cycles. We implemented an efficient mechanism for imposing these constraints using the singular value decomposition, as previously reported (17,21). The algorithm optimizes a set x of free parameters, from which the kinetic parameters 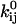and 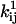are subsequently calculated. Each constraint reduces by one the number of free parameters.

The likelihood is computed using recursive forward and backward vector variables α and β, initialized and calculated as (17)

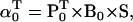(20)

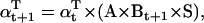(21)

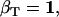(22)

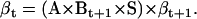(23)

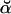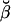Numerical underflow is avoided by using the scaling factors s_t to calculate the normalized probabilities and , as

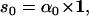(24)

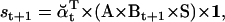(25)

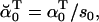(26)

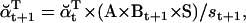(27)

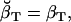(28)

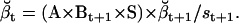(29)

Note that 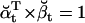, since the same scaling factors were used for both α and β. Hence, LL can be conveniently calculated using the scaling factors s_t, while its derivatives ∂LL/∂q_ij can be calculated using the chain rule of matrix differentiation, as

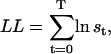(30)

(31)

The derivatives 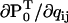, ∂A/∂q_ij, ∂Q/∂q_ij, and the A matrix itself are calculated as in Milescu et al. (21), with the mention that ∂Q/∂q_ij takes into account the periodic chemistry (Eq. 6). The derivative of LL with respect to a free parameter x_k is calculated with the chain rule, as

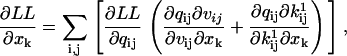(32)

where 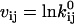, , 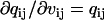and 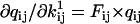are obtained as in Milescu et al. (21). In the above calculation, A and Q are the truncated matrices. The indexes i and j are for the off-diagonal entries in the Q matrix corresponding to nonzero rates in the kinetic model. Note that the likelihood function can be maximized without its analytical derivatives, but their availability allows for a significantly faster and more precise maximization. The optimization routine we used calculates the covariance matrix of the free parameters x. From this, we calculate the error estimates of the rates (21).

We accelerated the computation of the likelihood function and its derivatives by precomputing multiplications of identical terms in the likelihood function (Eq. 18). For example, a dwell of length 73 points can be represented in the likelihood calculation either as a product of 73 identical terms, or more efficiently as a smaller product of powers, such as the following:

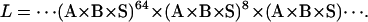(33)

Note that the sum of the exponents 64 + 8 + 1 = 73. These exponents can be conveniently chosen as powers of two, e.g., 1, 2, 4, 8…, etc. Thus, one can first calculate the power with exponent one, which by multiplication with itself gives the power with exponent two, and so on. It is therefore enough to calculate the term A × B × S and then its 2nd, 4th, 8th… powers. Thus, K terms in the series (A × B × S)^2k can be calculated in only K matrix multiplications, and only once for the whole data set. This treatment, applied to the likelihood function and its derivatives, results in a considerable speed improvement.

RESULTS

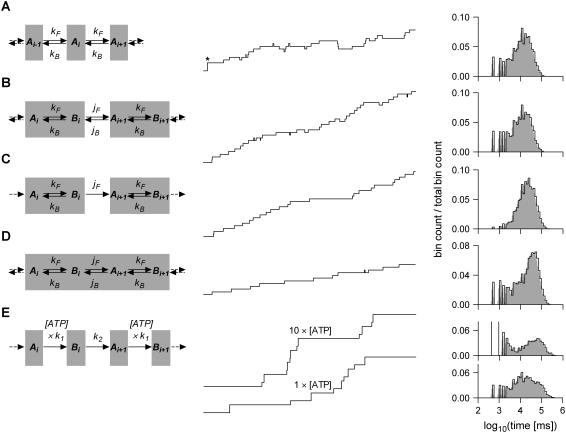
Fig. 3 shows a few examples of kinetic models that can be modeled by our algorithm. For each model, only motor steps can be observed (transitions between different units) but not transitions between states inside the same reaction unit. All models implicitly include ATP binding and mechanical force-dependent steps. In Fig. 3, only model E is formulated with explicit ATP binding, to emphasize its special characteristic of having alternating steps with different chemistry. This model describes the two substeps of the F₁-ATPase: an 80° ATP binding substep and a 40° substep (8,9). Alternating steps are handled by our method, with the simple modification that the permutation matrix S is applied only after a repeating pair of two alternating units. An illustration of the need for constraints on rate constants is model C, which describes a molecular motor, such as myosin V (3), with the fluorescent probe attached to the motor head. In this case, only every other motor step can be observed. Consequently, there are twice as many states per reaction unit but, due to constraints, the number of free parameters remains the same as for model B. Notice how dwell-time histograms are truncated, since dwells shorter than the sampling interval (as shown, dt = 500 ms) are missed.

FIGURE 3.

Molecular motor kinetics can be represented by a variety of models. Shown are a few examples of kinetic models and their simulated staircase data and dwell-time histograms. These models have one state per reaction unit (A and E), or two states (B and C), and have reversible (A, B, and D), or irreversible (C and E) kinetics. Even when not explicitly stated, all models include an ATP binding state, and mechanical force-dependent transitions. Model D corresponds to, e.g., myosin V experiments where the fluorescent probe is attached to the motor head, resulting in double steps of 74 nm. The apparent kinetics are slower, as a single dwell consists of two consecutive steps. Model E corresponds to F₁-ATPase experiments, with an 80° ATP binding substep, followed by a 40° substep. Notice how the lifetime of those dwells after a 40° substep becomes shorter at higher ATP concentration. Due to finite sampling, some unitary steps are missed (e.g., the double step in trace A, marked with a star). Missed events could, in principle, occur anywhere between two samples. Notice the effect of missed events on dwell-time histograms.

Solving models with one state per reaction unit (Fig. 3 A) is trivial: the two rates can be calculated by hand simply by dividing the number of forward and backward jumps (including missed events) by the length of the data. Although trivial, single-state models are informative about possible bias in the maximum likelihood estimates. We tested the algorithm with both reversible and irreversible data generated by single-state models. The rates obtained by the maximum likelihood algorithm were equal (within numerical precision) to the rates obtained by hand calculation. These results validate the algorithm, and show that the estimates are unbiased.

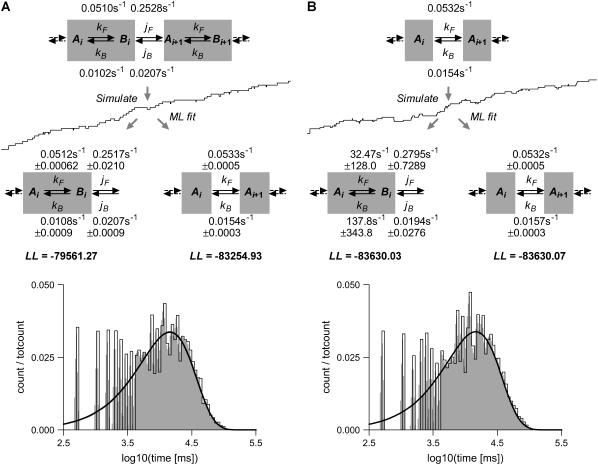
Next, we tested the algorithm with a nontrivial model with two states per reaction unit, as shown in Fig. 2 A. First, data simulated with the two-state model were fit with either the correct model, or with a single-state model (Fig. 4 A). The estimates obtained with the correct model are virtually identical to the true rates used by the simulator. Furthermore, the difference between the true and the estimated rates, however small, is well within the standard deviation of the estimates, as calculated by the optimizer. The two models have nearly identical PDFs (shown overlapped on the dwell-time histogram), but their log-likelihoods are very different: −79,561.27 (two-state model) versus −83,254.93 (one-state model). Clearly, the correct model is favored by the likelihood function. In contrast, the histogram fitting, which ignores correlations in time, is not capable of distinguishing the two models.

FIGURE 4.

Maximum likelihood can select the correct model. Staircase data were simulated with the two-state model shown in panel A, or with the single-state model shown in panel B, sampled at dt = 0.5 s. For each simulation model, the true rate constants are given, calculated as k_ij = n_ij/T_i, where n_ij is the actual number of transitions i→j, and T_i is the actual time spent in state i, as randomly chosen by the simulation routine. Each simulation was then maximum likelihood-fit with either model. The PDF curves for the ML estimates are shown overlapped on the dwell-time histograms, without correction for missed events. In panel A, the log-likelihood LL is significantly greater for the correct model, even considering the additional two free parameters, while the PDF lines overlap almost perfectly. In panel B, the two models have virtually identical LL and PDF. Notice that estimates obtained with the correct model are very accurate. In panel B, estimates obtained with the wrong model have a very large standard deviation. Notice how, due to missed events, the histogram appears to be slightly shifted to the right relative to the ideal PDF curve.

Is the increase in likelihood for larger models spurious, simply the result of having more fitting parameters? The correct model has four parameters while the single-state model has only two. To estimate the role of an increasing number of parameters on the increase in likelihood, we used the Akaike (AIC) (33) and the Bayesian (BIC) (34) information criteria, defined as

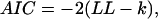(34)

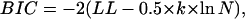(35)

where k is the number of free parameters and N is the number of data points. For our example, both AIC and BIC favor the correct model by a large margin. We also simulated data with the single-state model and fit them with both models (Fig. 4 B). In this case, the log-likelihoods are virtually identical, and likewise the PDF curves. This indicates that the larger model is overfitting. Also indicative of overfitting is the large standard deviation of the estimates.

Statistical distributions of kinetic estimates

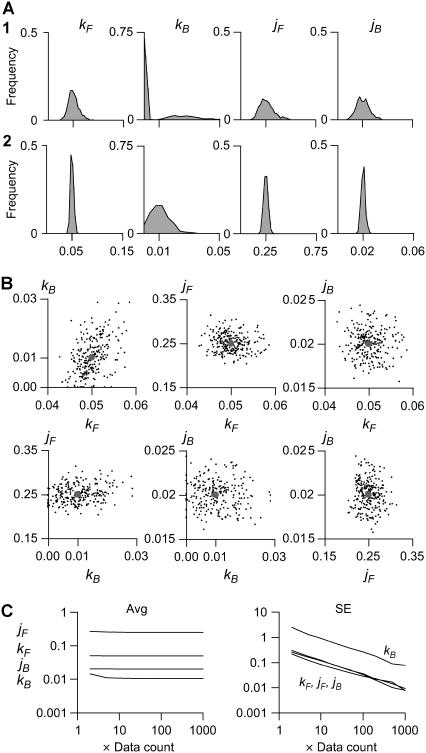
To determine the statistical properties of the estimates, we simulated staircase data with the two-state model shown in Fig. 3 A. We found that the estimates for all rates have Gaussian distributions (Fig. 5 A). However, obtaining a meaningful rate estimate requires that sufficient information about that transition is contained in the data. For example, k_B had a large variance and it was bimodal when only two data traces were globally fit (Fig. 5 A, upper graphs). A large fraction of the estimates consisted of zero values (in the optimization, we constrained k_B ≥ 1 × 10⁻⁵ s⁻¹), while the remaining fraction consisted of finite values, loosely centered on the true (simulated) value. The explanation is simple: in the simulated data file used for analysis, the following transitions were counted: B_i→A_i = 5315; A_i→B_i = 98,532; B_i→A_i+1 = 131,627; and A_i+1→B_i = 39,477. As the file had 1000 segments of 5000 points each, the B_i→A_i transition (quantified by k_B) occurred approximately once per trace. While some traces had one or a few B_i→A_i transitions, others had none. This shortage of information explains the poor quality of k_B estimates (Fig. 5 A, upper graphs). In comparison, the distribution of the k_B estimates improved considerably when 20 segments were globally fit (Fig. 5 A, lower graphs).

FIGURE 5.

Statistical distribution of maximum-likelihood kinetic estimates. Five-thousand dwell-sequences, each 5000 points long, sampled at dt = 0.5 s, were simulated with the model shown in Fig. 2 A and were globally fit in groups of 2…1000. (A) Rate constants are Gaussian-distributed with a width proportional to the number of data points globally fit (two traces in A1, and 20 traces in A2). The distribution of k_B has much higher variance, and is bimodal when only two traces were fit (A1). This is explained by the scarcity of k_B transitions: only ≈1 per segment, compared to >10 per segment for all other rates. (B) There is no apparent cross-correlation between the estimates of different parameters. The example shown is for the global fit of 20 traces. The implication is that if one parameter cannot be reliably estimated (i.e., k_B), it will not lower the precision of the other estimates. The solid circles mark the correct values. (C) All four rate constants were estimated without bias, when at least 10 traces were globally fit, i.e., at least 10…100 transitions for each rate. The standard error of all but k_B estimates was below 10%, when at least 10 traces were globally fit. Considering the actual number of simulated transitions, all parameters are estimated with similar precision.

We also observed a lack of cross-correlation between different pairs of estimates (Fig. 5 B), which implies that the parameters are rather orthogonal. All four rate constants were estimated without bias (Fig. 5 C, left graph) if at least 10 traces were globally fit. The standard error of all estimates was <10% (Fig. 5 C, right graph) if the analyzed data contained at least a few hundred events of each transition. We emphasize that the source of this variance is the stochastic nature of the dwell-sequence, and not the optimization program. One should regard these results as a measure of how much the estimates obtained from experimental data may depart from the true parameters of the generating process, under conditions of limited data.

We also tested the algorithm with irreversible data, generated with the same model but with either k_B = 0, or j_B = 0 (see Fig. 3 C). As before, we constrained the estimated rates to be ≥1 × 10⁻⁵ s⁻¹, to avoid numerical problems. The data were analyzed in groups of 20 segments, with the zero rate (k_B or j_B) as a free parameter, or constrained to 1 × 10⁻⁵. In both cases, we obtained statistically correct estimates (results not shown). Data simulated with j_B = 0 contain direct evidence for a zero j_B, i.e., they lack backward steps. Thus, the algorithm theoretically should have obtained all j_B estimates equal to 1 × 10⁻⁵. In practice, the optimizer estimated j_B as 2.01 × 10⁻⁵ ± 4.02 × 10⁻⁵ (max = 4.6 × 10⁻⁴), close to the expected value. In contrast, data simulated with k_B = 0 do not contain direct evidence for a zero k_B. Although ideally k_B should also have been estimated as 1 × 10⁻⁵, in practice j_B was estimated as 2.2 × 10⁻⁴ ± 8.6 × 10⁻⁴ (max = 1 × 10⁻²), a fairly good approximation.

Comparison between MIP and other kinetic algorithms

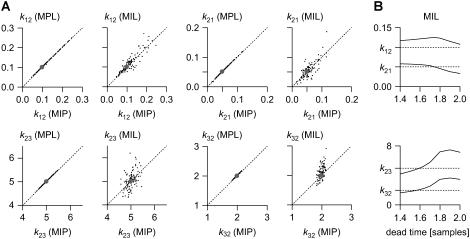
The MIP algorithm may be applied to data generated by nonperiodic Markov models, such as single-channel data, with the removal of the S matrix from Eq. 18. We compared MIP against the MIL (19) and MPL (17) maximum likelihood algorithms used for single channel analysis. We simulated data with a three-state, closed-open-closed model. To test the effect of missed events, we intentionally chose two of the four rate constants to be comparable to the sampling time (2 s⁻¹ and 5 s⁻¹, versus a sampling time dt = 0.1 s). Fig. 6 A shows that the three methods are equivalent, and their estimates are statistically equal. As expected, the cross-correlation is almost perfect between MIP and MPL, as they are both point methods designed for discrete-time Markov models, as opposed to MIL, which is interval-based and designed for continuous-time Markov models.

FIGURE 6.

Comparison between discrete-time and continuous-time maximum-likelihood algorithms. One-hundred data sets, each 100-s long, sampled at 10 Hz, were simulated with the nonperiodic model closed-open-closed (k₁₂ = 0.1 s⁻¹, k₂₁ = 0.05 s⁻¹, k₂₃ = 5.0 s⁻¹, and k₃₂ = 2.0 s⁻¹), and were maximum likelihood-fit individually. We tested the following algorithms: MIP (discrete-time, presented in this article), MPL (discrete-time) (17), and MIL (continuous-time, first-order missed events correction) (19). (A) Cross-correlation plots show that estimates obtained with MIP (x axis) match almost perfectly the estimates obtained from the same data set with MPL (y axis), and are well correlated with the estimates obtained with MIL (y axis). Notice that MIL's estimates have greater variance than those obtained with the other two algorithms. (B) Estimates obtained with MIL may depend critically on the choice of dead-time parameter for missed event correction. In the example shown, the best values were obtained with a dead-time ≈1.6 × dt, where dt is the sampling interval. MIP and MPL do not require missed event correction. The dotted lines mark the true parameter values.

The experiment also showed that it is legitimate to replace the Gaussian densities in the likelihood function with hard probabilities of zero and one, when the data are already idealized. MIL estimates seem to have greater variance than MIP or MPL estimates, which suggests that MIP requires less data to achieve the same precision. More importantly, the experiment demonstrates that a discrete-time method implicitly handles missed events as well as, or better than, the continuous-time method which explicitly requires correction for missed events. MIL estimates may depend critically on the choice of the dead-time parameter (19). For this experiment, we found the best value to be ≈1.6 times the sampling interval (Fig. 6 B), but the dead-time is a function of the model and data.

The convergence time of the three programs (using a MIP premultiplication order of 16) scaled approximately as 1 (MIL): 1.6 (MIP): 8 (MPL). MIL is clearly the fastest, as it operates with dwells and not points (there are fewer dwells than points), but MIP is close. Thus, the potentially slower computation of point-based methods is no longer a problem. For example, fitting a two-state model to a data set with ∼100 dwells converged in seconds. Fitting a model with four states to a few thousands of dwells takes minutes. All three programs converged in approximately the same number of iterations.

DISCUSSION

Molecular motors are mechano-chemical systems that in vivo may depart from simple (pseudo-) first-order kinetics. However, under the right in vitro experimental setup their intrinsic kinetics can be studied using Markov models, which can include dependence on external stimuli, such as ATP used to convert chemical into mechanical energy, or the generation of mechanical motion and force (2). The parameters thus obtained can be incorporated into more comprehensive in vivo models. In this article, we showed that:

1. The potentially very large but periodic Markov model can be reduced to a small, truncated version.

2. The likelihood function of the stochastic staircase dwell-sequence can be formulated in a compact form, for chemistry of arbitrary complexity.

3. Unbiased kinetic parameters can be estimated by numerical maximization of the likelihood function.

Continuous-time versus discrete-time models

The discrete-time likelihood function makes no assumption about what happens between sampling points, and therefore does not miss events. In contrast, in the continuous-time model, it is assumed that the process does not change class during a dwell. Since this is not actually the case, a correction for missed events is necessary (19,30–32). MIP does not require correction for missed events and thus has the potential of being more accurate than interval-based algorithms that have to deal with missed events (18,19). It does not mean, however, that a point method such as MIP will work at any temporal resolution. Thus, when the sampling is too slow relative to the kinetics, the process will reach equilibrium between samples, and information about transitions will simply be lost. Neither MIP nor any other method can extract useful estimates in this case.

The rate estimates are unbiased and Gaussian

The maximum likelihood rate estimates are intrinsically unbiased, but the confidence level depends on the amount of available data (Fig. 5). Thus, a rate cannot be properly estimated when the corresponding transition occurs rarely. In this case, the distribution of the estimate may appear biased, or bimodal (Fig. 5 A, upper graphs). While this is generally not a problem with single-channel data which usually contain a large number of events, it can be a serious factor with data limited by photobleaching or by short substrate filaments. We recommend testing algorithm performance using simulated data to explore the errors in particular cases. We emphasize that this variability is determined by the stochastic nature of single-molecule data and not due to the algorithm.

Parameter identifiability and model selection

Although the likelihood function (Eq. 18) fully utilizes the information contained in the data, any modeling study must answer two important questions: for a given model, how many kinetic parameters can be uniquely identified? Second, can two models be distinguished, according to some objective criterion? Regarding the first question, it is known that the maximum number of parameters that can be estimated from equilibrium single channel data is 2 × N_C × N_O (29,35), where N_C and N_O are the numbers of closed and open states, respectively. How do we define closed and open in the case of staircase data? In a sense, the molecular motor model has only one aggregation class; however, jump transitions can be observed. Therefore, a minimal representation of the periodic model presented in Fig. 2 A can be formulated with four state transitions (denoted by k_F, k_B, j_F, and j_B) connecting three states (e.g., A_i, B_i, and A_i+1) that can be partitioned in two conductance classes: states A_i and B_i are closed, and A_i+1 is open. From such a model, a maximum of four kinetic parameters should be uniquely identifiable. Our analysis (see Figs. 4 and 5) confirmed this prediction: all four rate constants were uniquely identified.

In practice, the maximum number of parameters that can be determined is a function of the kinetic model, the experimental protocol (stationary versus nonstationary, local versus global fitting, etc.), and the availability of an adequate amount of data (see Fig. 5). If more complex models are to be studied, the parameter identifiability may be improved by manipulation of experimental conditions, e.g., global fitting across different ATP concentrations or mechanical force values (21). The algorithm presented here was implemented with this need in mind, and can globally model data obtained under different experimental protocols, including nonstationary stimuli (21).

With respect to model identifiability, it is known that two Markov models that are related by a similarity transform give identical likelihood (36,37) and thus cannot be distinguished. In this case, global fitting across different conditions or using nonstationary stimuli will improve identifiability. Furthermore, due to the stochastic nature of the data, the likelihood estimator has an intrinsic variance proportional to the number of data points. When there are few data points, the likelihood distributions for two different models may overlap. In the example shown in Fig. 4, the two models were correctly selected because we used a relatively large amount of data. Again, we recommend using simulations to check the statistical separation between likelihood distributions. Note that when models of different size are compared, their likelihoods must be scaled for the number of free parameters and for the amount of data, as shown in Results.

Reversible models and truncated matrices do not pose numerical problems

Two kinds of numerical errors may in principle affect the kinetics algorithm. First, irreversible models may easily result in confluent (i.e., degenerate) Q matrix eigenvalues. In this case, the transition matrix A cannot be calculated using the convenient spectral decomposition (25,26). A simple yet effective solution is to set a lower limit on rates, for example constraining the rates to >1/data length. Although this could potentially introduce bias in estimates, we found this bias to be negligible in practice.

The second source of numerical error is computing the truncated transition probability matrix A^r. The error between the truncated and the theoretical A matrices decreases with the truncation order. However, since the computational speed scales quadratically with the size of the model, the truncation order is chosen as a compromise between accuracy and speed. We found that a model with 2r+1 = 7…9 units runs reasonably fast (seconds to minutes) and has an error that is negligible relative to the intrinsic variance of the estimates. Note that when the analyzed data lack backward steps (i.e., they are irreversible), the model can be simplified to only r+1 units, since the left block states will never be occupied in the likelihood chain.