Diffusion Rate Limitations in Actin-Based Propulsion of Hard and Deformable Particles

Abstract

The mechanism by which actin polymerization propels intracellular vesicles and invasive microorganisms remains an open question. Several recent quantitative studies have examined propulsion of biomimetic particles such as polystyrene microspheres, phospholipid vesicles, and oil droplets. In addition to allowing quantitative measurement of parameters such as the dependence of particle speed on its size, these systems have also revealed characteristic behaviors such a saltatory motion of hard particles and oscillatory deformation of soft particles. Such measurements and observations provide tests for proposed mechanisms of actin-based motility. In the actoclampin filament end-tracking motor model, particle-surface-bound filament end-tracking proteins are involved in load-insensitive processive insertion of actin subunits onto elongating filament plus-ends that are persistently tethered to the surface. In contrast, the tethered-ratchet model assumes working filaments are untethered and the free-ended filaments grow as thermal ratchets in a load-sensitive manner. This article presents a model for the diffusion and consumption of actin monomers during actin-based particle propulsion to predict the monomer concentration field around motile particles. The results suggest that the various behaviors of biomimetic particles, including dynamic saltatory motion of hard particles and oscillatory vesicle deformations, can be quantitatively and self-consistently explained by load-insensitive, diffusion-limited elongation of (+)-end-tethered actin filaments, consistent with predictions of the actoclampin filament-end tracking mechanism.

INTRODUCTION

Actin polymerization generates the forces that form protrusions during cell crawling as well as the propulsive force that drives intracellular transport of endosomes and some invasive microorganisms (1). Despite its broad relevance, the mechanism(s) for force generation by polymerization remains controversial. Several recent studies have examined the propulsion of particles (of diameter 0.25–10 μm), such as polystyrene microspheres, oil droplets, and vesicles, under relatively well-defined conditions in vitro. Propulsion requires particles to be coated with filament-nucleation protein factors such as Listeria ActA, neural Wiskott-Aldrich syndrome protein (N-WASP), or the N-WASP verprolin/cofilin homology/acidic (VCA) domain, which polymerize actin filaments from the particles surface to generate a dense F-actin “rocket tail,” similar to that formed by invasive intracellular microorganisms like Listeria monocytogenes. There is increasing evidence that these surface-bound factors also play a role in facilitating (+)-end assembly after filament nucleation (2–6) (ActA by its interaction with vasodilator-stimulated phosphoprotein, i.e., VASP).

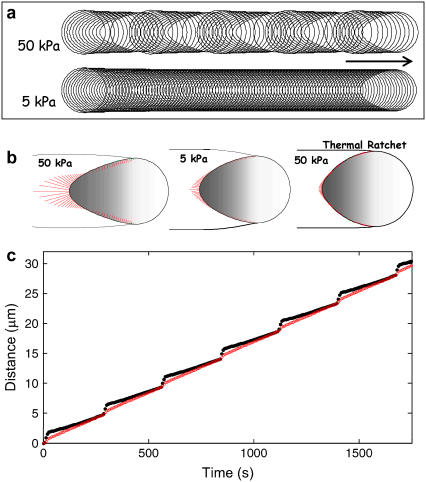
Analysis of particle motile behavior (e.g., speed, particle deformation, saltatory motion, etc.) under controlled conditions gives insight into the possible propulsion mechanisms and provides quantitative data to test propulsion models. For example, the speed of VCA-coated particles was found to be inversely proportional to particle radius (7), and particles exceeding ∼1.5-μm radius were found to exhibit saltatory motion (Fig. 1 a), with recursive phases of slowing during which the actin-rich tail became denser, to result in a sequence of phase-dense bands in the actin tail of width that was found to be independent of particle radius (8). Schwartz et al. (9) found that flat particles can move as effectively as spherical particles, which appears to rule out the requirement for surface curvature in a squeezing propulsion mechanism (10). Also, Wiesner et al. (11) found that increasing concentrations of methylcellulose, expected to greatly increase the drag on the propelled microspheres without hindering monomer access to filament ends, did not retard speed of N-WASP-coated particles. Moreover, the attachment of a motile particle to a surface did not hinder the rate of elongation of the actin rocket tail away from the bead (11), further demonstrating that hydrodynamic drag forces on the particle do not govern particle speed.

FIGURE 1.

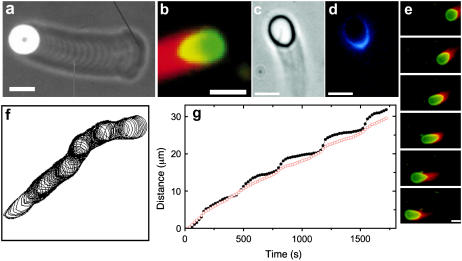
Micrographs from published studies on actin-based propulsion of hard and soft (deformable) particles. (a) A 9.1-μm diameter propelled hard particle displaying a succession of bands that resulted from saltatory motion (image from Bernheim-Groswasser et al. (8)). (b–g) Characteristic behaviors of deformation of phospholipid vesicles undergoing actin-based propulsion in cell extracts. (b) Fluorescence micrograph of a deformed of vesicle (image from Upadhyaya et al. (12); used by permission) showing actin in red and phospholipid in green (bar = 3 μm). (c,d) Phase-contrast and corresponding fluorescent image (from Upadhyaya et al. (12)) of the ActA distribution on the vesicle surface, showing colocalization of ActA with actin filaments (bar = 4 μm). (e) Sequence showing similar teardrop vesicle distension followed by a retraction phase (35-s intervals; bar = 2 μm) (images from Giardini et al. (13), used by permission). (f) Vesicle contours from Upadhyaya et al. (12) showing oscillations (at 20-s interval) of a ∼1.5-μm radius phospholipid vesicle. (g) Trajectories of front and rear vesicle surfaces reported by Upadhyaya et al. (12), with vesicle rear positions shown by solid black dots and the front positions by red circles. During the distension phase, the speed of the vesicle rear is nearly constant until it detaches and the vesicle quickly rounds-up to begin the cycle anew, with ∼5-μm distance between rounding phases.

Studies on deformable soft particles like vesicles and oil droplets have allowed estimation of the magnitude of the force generated by actin polymerization. Upadhyaya et al. (12) and Giardini et al. (13) both found that initially spherical ActA-coated vesicles evolved to teardrop shapes during actin-based propulsion in cell extracts (Fig. 1, b–e). By analyzing the shape and mechanical energy of the deformed vesicles, Upadhyaya et al. (12) estimated compressive stresses on the vesicle near the sides of the actin tail to be ∼3–4 nN/μm², with typical 6–8 nN/μm² tensile stress at the center of the actin tail, much higher than any expected viscous stresses on the vesicle surface. Some vesicles were also observed to distend periodically to a critical tensile stress on the vesicle at the tail center, at which point the vesicle detached from the tail and quickly rounded, whereupon the distension phase of the cycle began anew (Fig. 1, e and f). During the distension phase, the vesicle surface at the tail center advanced at a nearly constant speed that was less than the simultaneous speed of the leading edge of the vesicle. This difference in speeds between the vesicle front and rear persisted until the critical stress was reached (Fig. 1 g). Importantly, the increasing tensile stress at the tail center during the distension phase (before detachment) did not accelerate the advancement of the vesicle's rearward surface.

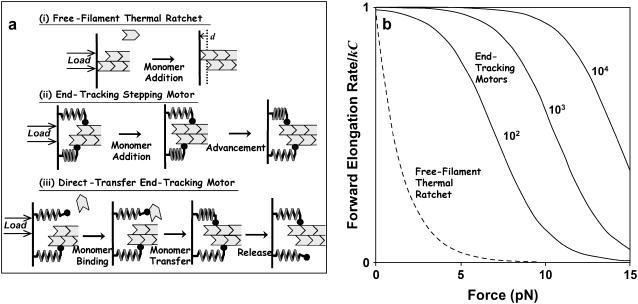
Such data on biomimetic particle motility may help discriminate between current models for the molecular mechanism of actin-based propulsion. Two fundamentally different models for force generation (Fig. 2) are (Fig. 2 a) the free-filament thermal ratchet (e.g., the elastic Brownian-ratchet model (14,15)), in which working filaments ends are not tethered and must make excursions from the motile surface to permit (+)-end monomer addition; and (Fig. 2 b) the filament end-tracking motor model (actoclampin) (2,16,17), in which elongating (+)-ends are persistently attached to particle-surface-bound filament-tracking proteins that processively add monomers onto the tethered filament (+)-end. In addition to the differences in the thermodynamic limit on the forces that can be generated (analyzed previously in Dickinson et al. (16)), these models make different predictions for the force-dependence kinetics of the forward filament elongation rate (Fig. 2 b). In the free-filament thermal ratchet, the forward elongation rate is kC, where C is the local monomer concentration near the filament end, and k is the (force-sensitive) bimolecular rate constant for monomer addition to the filament end (∼10 μM⁻¹ s⁻¹; (18)). Because thermal fluctuations at the filament end must work against a load to create the space needed to bind a new monomer, k decreases exponentially with the load force F (i.e., 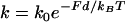, where k₀ is the rate constant for an unstressed filament, d is the added length per monomer (2.7 nm), and k_BT is the thermal energy (Boltzmann constant × temperature)). That is, the work Fd is the effective activation energy of the rate-limiting monomer-binding step. In contrast, in the filament end-tracking motor model (Fig. 2 a), filament end-tracking proteins hold the filament end to the surface, allowing monomers to bind from solution in a potentially force-insensitive manner, an event followed by one or more faster force-dependent steps (which may be facilitated by ATP hydrolysis) to complete the subunit-addition cycle. The monomer-binding step is typically expected to be slowest and rate-limiting, because it requires (local) diffusion of the monomer from the solution to encounter the end-tracking motor binding site (2), whereas the force-dependent advancement step(s) only require local molecular motions. If the steps are considered irreversible, then the forward rate (s⁻¹) of an end-tracking cycle is approximately

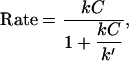(1)

where 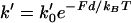is the rate (s⁻¹) of the force-dependent advancement step(s). (Here, the transition-state energy of the advancement is assumed to change by the work Fd required by the advancement step.) In this case, forward rate is unhindered by loads 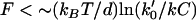(compared to the characteristic force k_BT/d for hindering a free-filament thermal ratchet). Whereas (kC)⁻¹ is typically ∼0.1 s in motility experiments, the time required for a protein to fluctuate the distance d = 2.7 nm by thermal motions is only ∼1 μs, implying k′ can theoretically be as much as 10⁵ times faster than kC, thus allowing the net rate of forward steps in the cycle to proceed unhindered by forces up to ∼10 pN per filament or more. This distinction between the end-tracking motors and the free-filament thermal ratchet kinetics leaves aside the potential thermodynamic advantages of capturing on-filament ATP hydrolysis in the end-tracking cycle for greater work, which we treated previously (16).

FIGURE 2.

Models for force-generation by actin filament elongation. (a) Cycles of force-dependent monomer addition: (i) A free filament end operating as a thermal ratchet requires thermal fluctuations to bring the filament end to a distance d = 2.7 nm from the surface with a frequency that decreases exponentially with load, F. In contrast, the filament end-tracking motors (such as (ii) end-tracking stepping motor and (iii) direct-transfer end-tracking motor (16)) can bind monomers from solution in a potentially load-insensitive manner, with the force only affecting the activation energies of the faster kinetic step(s) that complete the cycle (which are stepping of the tracking protein in (ii) and monomer transfer or release of the tracking protein in (iii)). Filament end-tracking motors also allow elongation under tension, whereas the free-filament models require other binding mechanisms to explain how tensile stresses are supported. (b) A comparison of the forward elongation rates (i.e., neglecting the reverse steps), scaled to binding rate kC (monomer binding rate constant × monomer concentration). Because the activation energy of monomer binding to a free-filament thermal ratchet is load-dependent, the elongation rate kC is kinetically hindered to its half-maximum at force F = ln(2)k_BT/d ∼ 1 pN. In contrast, filament end-tracking motors slow to half-maximum at force 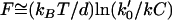, which can be ∼10 pN or more, depending on the of the rate k₀′ of the slowest remaining step of the end-tracking cycle. Here, curves for three values of k₀′/kC = 10², 10³, 10⁴ are shown, with corresponding values 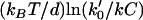at 7.1 pN, 10.6 pN, and 14.1 pN, respectively.

Another salient difference between the two models relates to how the filaments bear tension. The tethered-ratchet version of the elastic Brownian ratchet-model assumes all working filaments are unattached, but the actin network transiently binds to the surface through Arp2/3 complexes during the nucleation of nascent filaments (15). As the motile surface is pushed by free filaments, the resulting tensile force on the nascent filaments breaks these linkages, allowing the surface to advance. In contrast, the filament end-tracking motor model assumes the (+)-ends of working filaments are persistently tethered to the motile surface by the end-tracking proteins (e.g., ActA·VASP, N-WASP, or VCA peptide) and continue to elongate in a manner unaffected by tension, although mounting tensile forces may ultimately detach the tethered filaments from the surface. In this view, the stress on the surface due to polymerization is a force balance between “pushing” filaments that have elongated further (or are growing faster) and “pulling” tethered filaments that are also elongating, but under tension.

These considerations lead to a critical question in interpreting the measurements in terms of force-generation mechanisms: How does the load affect the filament elongation rate? This question cannot be answered without accounting for other rate limitations on filament elongation, such as local depletion of monomers, which may occur due to rapid consumption of monomers as they are incorporated into growing filament ends at a surface. Although potential diffusion-rate limitations on actin gel formation on a surface were recently addressed by Plastino et al. (19), the diffusion-rate limitations have not been previously accounted for in the interpretation of results from particle-propulsion experiments. The diffusion rate will limit the net elongation rate if the characteristic reaction velocity (kρ) is comparable to, or faster than, the diffusion velocity (D/R₀) (i.e., the diffusive mass transfer coefficient to a sphere), where R₀ is the particle radius (which is the characteristic diffusion length to a sphere), ρ is the surface density of filament ends consuming monomers, and D is the local monomer diffusion coefficient. (A list of parameter definitions is given in Table 1, and a list of variable definitions is given in Table 2). For actin tails and the cytoplasm, D is 2–6 μm²/s (19,20), and ρ ∼ 10³ μm⁻² (based on 25–30-nm filament spacing (12,21)), resulting in a reaction/diffusion velocity ratio kρR₀/D > 1 for particle radii >∼0.25 μm. Therefore, actin-based particle propulsion in most published studies is expected to be limited to some extent by long-range diffusion to the particle surface (not to be confused with short-range diffusion-rate limited binding of an actin monomer to a filament-end (22)).

TABLE 1.

Definitions and values of model parameters

Symbol	Definition	Range	References	Value used
C∞	Bulk concentration of polymerizable monomer	0.3–10 μM		varied
d	Added filament length per monomer	2.7 nm	(47)	2.7 nm
D	Monomer diffusivity within F-actin tail	2–6 μm2/s	(19,20,48)	5 μm2/s
De	Monomer diffusivity outside F-actin tail	5–50 μm2/s	(20,24,25,49)	15 μm2/s
Fb	Filament-surface bond strength	∼10–20 pN	(12)	10 pN
k	Bimolecular rate constant for actin binding to filament ends	3–20 μM−1 s−1	(18)	10 μM−1 s−1
R0	Particle radius (undeformed)	0.25–5 μm		varied
E	Young's Modulus of F-actin tail	1–15 kPa	(19,27)	varied
ρ0	Filament density at tail center	500–2000 μm−2	(12,21,50,51)	1100 μm−2

TABLE 2.

Definitions of model variables

Symbol	Definition
C	Monomer concentration (μM)
F	Force on filament end (pN)
Rs	Radius of spherical cap at vesicle front (not contact actin tail) (μm)
u	Dimensionless monomer concentration (= C/C∞)
v	Particle speed (μm/s)
X = (R,Z)	Position (μm)
x = (r,z)	Dimensionless position
κ	Reaction /diffusion velocity ratio (= kρ0R/D)
φ	Filament orientation relative to propulsion direction (rad)
ρ	Filament-end density on particle surface (μm−2)
σ	Stress on particle surface (μN/μm2)
θ	Angular on particle surface from tail center (rad)

Expressed another way, unless there exists another unknown mechanism for supplying monomer to the particle surface, the minimum flux of monomers, vρ/d, to achieve a speed v, cannot exceed the maximum diffusive flux of monomer to the surface, which, for a sphere, is ∼DC_∞/R₀, for bulk solution monomer concentration C_∞. Consequently, the diffusion-limited speed for a 1-μm radius particle in a solution of ∼1–2 μM profilin-actin is ∼1 μm/min, very close to what is typically observed in particle propulsion experiments in vitro (7,11).

In this article, we test our assertion that force-insensitive, diffusion-limited elongation of (+)-end-tethered actin filaments is sufficient to explain the essential properties of actin-based particle propulsion by solving the governing reaction-diffusion equations to estimate the monomer concentration profiles around biomimetic particles during propulsion. From these profiles, the model predicts the speed and the characteristic dynamics of hard particles and soft particles undergoing actin-based motility. Our analysis shows that the monomer concentration gradients and force-insensitive elongation of persistently tethered filament (+)-ends can quantitatively predict and explain key results reported for biomimetic particles, including the particle-size dependence on hard particle speed and saltatory motion, as well as the characteristic distended shape and oscillatory motion of soft particles.

MODEL AND ANALYSIS

Calculation of monomer concentration fields

In this section, we estimate the monomer concentration profile around a spherical biomimetic particle, as illustrated in Fig. 3. After symmetry breaking, particles typically have actin tails primarily covering the rear hemispherical surface (23), with filaments on the forward surface being sparse enough to neglect in our analysis. We assume the monomer concentration field is at a quasi-steady state, with negligible convection as justified by the low Pèclet number, Pe = vR₀/D ≪ 1, for a typical speed of v ∼1 μm/min. In calculating the monomer concentration field, we ignore the effects of any nearby surfaces in the motility chamber, noting their presence would only further decrease the net diffusive flux to the particle surface.

FIGURE 3.

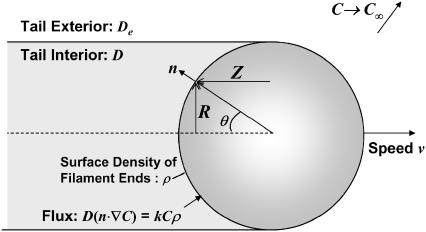
Model formulation. The particle surface contacting the tail consumes monomers by the first-order reaction rate kC for monomer-binding to filament-ends (at surface density ρ), where k is the bimolecular (association) rate constant and C is the local monomer concentration (μM). The net diffusive flux at the surface matches the consumption rate at the surface, such that Dn · ∇C = kρC, where n is the outward unit normal at the surface. Monomers may have different diffusivities inside and outside of the tail region (D and D_e, respectively). The monomer concentration C and its flux are continuous at the tail center and at the boundary between tail and surrounding medium, and the concentration far from the particle approaches the bulk concentration, C_∞.

The likelihood of different diffusivities inside versus outside the actin tail is treated by assigning different diffusion coefficients D and D_e, respectively, such that

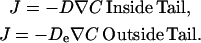(2)

The steady-state continuity equation (neglecting convection) results in the Laplace equation for both regions:

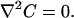(3)

Monomers are assumed to be consumed at the particle surface with a reaction flux kCρ, where k is bimolecular association rate constant (μM⁻¹ s⁻¹) for monomer binding to filament-ends (or to end-tracking proteins operating on the filament-ends, as in Fig. 2 c mechanism iii, assumed to be of similar value), and ρ is the filament-end surface density (#/μm²), which may depend on surface position (parameterized by angle θ) in the form ρ = ρ₀f(θ), where ρ₀ is the density at the center of the tail. The assumption of first-order consumption of monomers requires the monomer concentration to be sufficiently high for irreversible assembly, but sufficiently low to neglect potential saturation of the first step of the end-tracking motor cycles (16) (the implications of saturation are addressed in the Discussion). The boundary condition at the particle surface inside the tail is therefore

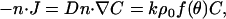(4)

and that outside the tail is

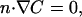(5)

where n is the outward unit normal vector on the particle surface. At the tail boundary, the fluxes and concentrations must match, hence

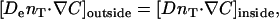(6)

where n_T is the outward-pointing unit normal vector on the tail boundary. This flux-matching condition implies the gradient in monomer concentration is discontinuous when D and D_e differ. Axial symmetry at the tail center requires ∂C/∂R = 0 at R = 0, and the C approaches the bulk monomer concentration C_∞ at large distances from the particle (C→ C_∞ for (R²+Z²)^1/2→ ∞).

To make the equations dimensionless, we define u ≡ C/C_∞, z ≡ Z/R_0, r ≡ R/R₀, which yields the dimensionless equations,

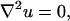(7)

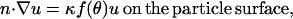(8)

(9)

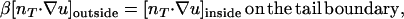(10)

where β = D_e/D, and κ ≡ kρ₀R₀/D is the key dimensionless group representing the ratio of the reaction velocity (kρ₀) to the diffusion velocity (D/R₀).

A useful reference solution is that for a uniformly reactive sphere (f=1) with D_e = D. In this case, the analytical solution is straightforward and given by

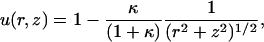(11)

such that u = (1+κ)⁻¹ on the particle surface. In the limit of small κ, the concentration profile becomes uniform (u = 1), and the elongation rate kC of filaments at the surface becomes simply kC_∞ . Conversely, in the limit of large κ, the surface becomes a perfect sink for monomer (u ∼ κ⁻¹), and the elongation rate approaches the diffusion-rate limit kC ≅ DC_∞/ρ₀R₀, hence independent of k. The reaction- and diffusion-rate limits for the more-general cases with nonuniform f and D ≠ D_e are similar but require numerical calculation.

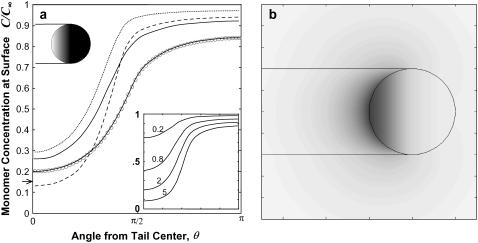
As described in the Appendix, the boundary element method was used to solve the boundary integrals corresponding to Eqs. 7–10. The calculated monomer concentration profiles are plotted in Fig. 4 for a sphere having uniform density of filaments on its half-sphere (f = 1 for 0 < θ < π/2, otherwise f = 0). The concentration of monomer at the center of the tail C(0) decreases with κ. While a larger diffusivity outside the tail does increase C(0) somewhat, the diffusivity within the tail is what primarily governs the profile; even the dilute aqueous-solution value of D_e = 50 μm²/s leads to tail-center concentration not differing greatly from the case with D_e = 5 μm²/s. Hereafter, we assume D_e = 15 μm²/s, a value accounting for the higher viscosity of cell extract (24,25), and we assume D_e is similar for methylcellulose-containing purified protein solutions, noting that the results and conclusions are not strongly sensitive to this parameter.

FIGURE 4.

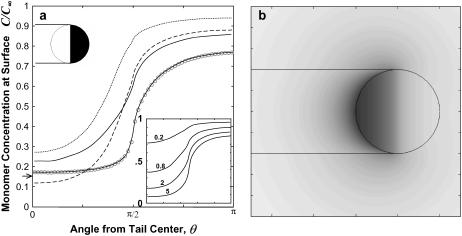
Predicted monomer concentration profiles for a particle with a uniform surface density of filament-ends (ρ₀ = (30 nm)⁻²) on the tail-contacting half-sphere (indicated in the inset by open region on the sphere). (a) The monomer concentration at the particle surface plotted versus angular distance from tail center (R₀ = 1.5 μm), with different combinations of the tail diffusivity (D) and surrounding medium diffusivity (D_e): D = 5 μm²/s, D_e = 15 μm²/s (solid line) D = 5 μm²/s, D_e = 50 μm²/s (dotted line); D = 2 μm²/s, D_e = 50 μm²/s (dashed line); and D = 5 μm²/s, D_e = 5 μm²/s (solid line with circles, with circles showing the node values from the boundary element calculation and the solid line showing the analytical solution). The arrow on the ordinate axis shows the surface concentration for a uniformly reaction sphere, u = (1+κ)⁻¹. The inset plot shows profiles for the different particle radii (in μm) indicated (D = 5 μm²/s, D_e = 15 μm²/s). (b) A contour plot showing monomer concentration field C(r,z), represented by the gray level (white, C = C_∞; black, C = 0) (R₀ = 1.5 μm, D = 5 μm²/s, D_e = 15 μm²/s).

Hard-particle dynamics

If the elongating filament (+)-ends are persistently tethered to a hard-particle surface by filament end-tracking proteins, the particle speed would be limited by the most-slowly elongating filaments, which are those at the tail center, where the monomer concentration is lowest. It is reasonable to assume these tense filaments would be oriented or pulled into alignment toward the propulsion direction, in which case, the particle speed is approximately

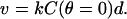(12)

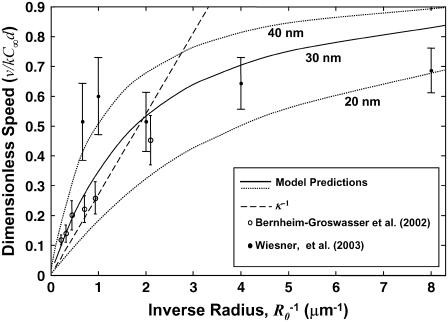
In Fig. 5, the dimensionless velocity (vd/kC_∞) is plotted as a function of 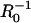and compared to experimental data reported by Bernheim-Groswasser et al. (7) and from Wiesner et al. (11) for the speed-dependence on size of VCA-coated and N-WASP-coated particles, respectively. The transition from reaction-limited to diffusion-limited speed is revealed by the transition from 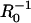-dependent to R₀-independent speed. Overall, the model agrees closely with experimental results for reasonable parameter values of D = 5 μm²/s, 30-nm filament spacing (ρ = (30 nm)⁻²), and k = 10 μM⁻¹ s⁻¹, noting the two outlying points have large uncertainties and still fall within a factor of two of the predictions. Also shown are predicted curves for 20-nm and 40-nm filament spacings to illustrate the sensitivity to this parameter (discussed below). Notably, this good agreement requires no freely fitted parameters and suggests that diffusion-rate limited elongation of tethered filaments is what primarily determines the velocity in these experiments. However, filament detachment or breakage during so-called saltatory motion (7,8) may allow transient increases in the velocity above this limit by temporarily reducing the filament density ρ or by temporarily breaking the mechanical connections between filament-ends at the surface and the rest of the actin tail.

FIGURE 5.

Predicted particle speed versus inverse particle radius, 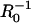. The solid line is the predicted dimensionless speed v/kC_∞d = C(0)/C_∞, obtained from the boundary element solution of the monomer concentration profile C(θ). The dashed line represents the diffusion-limited speed for a uniform sphere (v/kC_∞d = κ⁻¹). Also shown are experimental data for VCA-coated beads from Bernheim-Groswasser et al. (7) (open circles) and for N-WASP coated particles from Wiesner et al. (11) (solid circles). Experimental monomer concentrations for these studies were estimated at 1.5 and 1.4 μM, respectively, taken as the profilin-actin concentrations resulting from equilibrium binding (K_d = 0.1 μM, (18)) of profilin (at concentrations 2.5 μM and 2.4 μM, respectively) to actin-ATP (∼0.3 μM at steady-state treadmilling). Our estimate for ρ₀ = (30 nm)⁻² is based on 30-nm filament spacing, and curves for filament spacings of 20 nm and 40 nm are also shown. Other assumed parameters used for scaling the data are: k = 10 μM⁻¹ s⁻¹, D = 5 μm²/s, and D_e = 15 μm²/s.

The accumulation of stress leading to saltatory motion (7,8) can be explained directly by diffusion-limited filament elongation. Because the particle is rigid, the faster-growing outer filaments (those with higher C(θ), see Fig. 4) must accommodate their greater elongation rate by changing their average orientation φ with respect to the direction of motion, as to maintain the relation

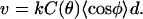(13)

A decrease in 〈cos φ〉 corresponds in an increase in F-actin concentration (∼ρ/d〈cos φ〉), which should increase the surface pressure at the outer tail region, in balance with the tensile stresses on filaments in the tail center. This increase in local F-actin concentration would explain the observed dense F-actin bands along rocket tails that form during the slow phase of saltatory motion (8). Dense-band formation continues until the stress on the filaments at the tail center builds up to a critical stress σ_c, whereupon the slower central filaments will detach, allowing the particle to temporarily move forward at a faster speed now only limited by the elongation rate of the outer filaments. This phase of increased speed would persist until new filaments reform at the tail center and rebind to the rest of the tail, thus beginning the cycle anew.

This qualitative explanation can be tested quantitatively with the following simple model that utilizes our calculation of C(θ). Let the rate of stress increase on the filaments in tail center (σ₀) be proportional to the difference in the inner versus outer filament elongation rates, such that

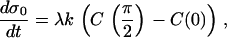(14)

where λ is a proportionality constant that relates surface stress to the local F-actin concentration. The time required to reach the critical stress for detachment t_D is then

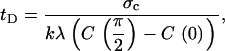(15)

and the length of the dense band generated before detachment w_b is

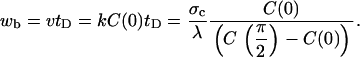(16)

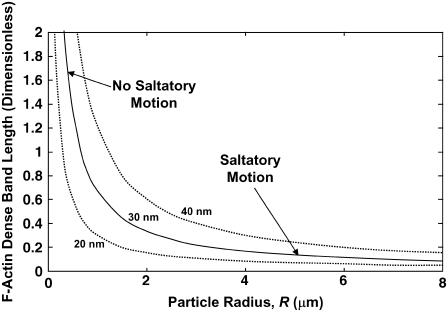
The dimensionless band length wλ/σ_c = C(0)/(C(π/2)–C(0)), which can be determined only from the monomer concentration profile on the particle surface C(θ), is plotted versus particle radius in Fig. 6. Notably, for particle radii >∼1.5 μm, the band length is predicted to become asymptotically independent of particle radius. Yet, for small radii (<∼1 μm), the band length increases without bound. In this regime, any increase in F-actin would be distributed over a very long band length, and thus would be too slight to observe. Alternatively, the slow buildup of stresses might be relieved by processes other than collective filament detachment at the tail center, such as slow spontaneous detachment of individual taut filaments or slow deformation of the actin network. The predicted transition between these two limits matches the experimental findings of Bernheim-Groswasser et al. (8), who reported two phases of motion: smaller particles <∼1.5-μm radius showed no saltatory motion, while the band thickness was size-independent for larger particles. The simple model presented here provides a quantitative explanation of the observed critical radius of saltatory motion, and is additional support for our assertion that diffusion-limited elongation of persistently tethered filament (+)-ends explains the propulsive properties of biomimetic hard particles. It also serves as a prelude for a more sophisticated model, as presented in the next section, for the differential stress accumulation on soft-particle surfaces similarly resulting from monomer concentration gradients.

FIGURE 6.

The predicted dimensionless length of dense tail bands appearing during particle saltatory motion is plotted versus inverse radius (D = 5 μm²/s) for the three different shown values of the filament spacing used in Fig. 5. For large radii, where the particle speed is diffusion-limited, the wavelength becomes asymptotically uniform; for small radii, speed is reaction-limited and the wavelength becomes unbounded, such that saltatory motion does not occur. The transition between smooth motion and saltatory motion occurs at radii of ∼1.5 μm, consistent with observations of Bernheim-Groswasser et al. (8).

Soft-particle dynamics

We now model the propulsion of soft particles, such as vesicles and oil drops, addressing specifically whether force-insensitive, diffusion-limited elongation of tethered filaments can account for their observed characteristic teardrop shape and oscillatory motions. By definition, soft particles differ from hard particles in that the surface may deform in response to stress. In addition, the tethered filaments (+)-ends (and their end-tracking proteins) cannot sustain a tangential stress and can move laterally on the soft particle surface in response to stresses.

Vesicles translating relative to their stationary F-actin tails cannot evolve into quasi-static distended shapes when the outer filaments are elongating more slowly in the propulsion direction than filaments under tension at the tail center, unless somehow new filament ends are continually nucleated on the vesicle surface at outer tail boundary in a way that compensates for the loss of F-actin there due to vesicle translation. The simulations of Upadhyaya et al. (12) to estimate actin-induced stresses from their observed vesicle shapes assumed the force-sensitive thermal ratchet kinetics, with filament elongation directed inwardly normal to the vesicle surface. Their treatment, which did not account for vesicle translation relative to its tail, led to the conclusion that filaments at the tail edge (which are growing radially inward, hence perpendicular to the propulsion direction) are kinetically stalled at their maximum compressive force. This result seems physically untenable when one takes into consideration vesicle translation relative to the stationary F-actin tail, as it would require the population of maximally compressed filaments, oriented perpendicular to the propulsion direction, to continually and immediately appear at the tail edge, where the radial thickness of the tail is experimentally observed to approach zero (see Fig. 1).

In our model, we assume filaments are oriented on average toward the direction of propulsion. Because the surface-tethered (+)-ends elongate on average in the same direction as the translation of the vesicle surface, this assumption implies a quasi-static surface-distribution of filament ends is possible. However, because the projection of any surface area element in the filament orientation direction (the z direction) decreases radially toward the outer tail, the density of filament ends on the vesicle surface is also expected to decrease toward the outer tail, depending on the density of F-actin. We take the simplest assumption of a uniform F-actin concentration in the tail at quasi-steady state, which would be expected when any stresses resulting from the generation a nonuniform F-actin concentration are dispersed by a slow radial rearrangement of the filament ends attached to the fluid membrane. In this case, the density of filament ends meeting the vesicle surface is simply proportional to the component of the unit normal vector in the z direction (i.e., f(θ) = n_z(θ)). This assumption therefore predicts a diminishing surface density of end-tracking proteins, very much like the experimentally observed surface densities of ActA or VCA on motile soft particles, where a continuous gradient was seen to fall from a maximum, at the tail center, to a nearly zero density at the tail edge (12,13,26) (see Fig. 1 d). As shown in Fig. 7, the monomer concentration field resulting from this assumed gradated filament-end density is not greatly different than the field resulting from assuming uniform ρ on the half-sphere, and either field would generate similar soft-particle distensions discussed below.

FIGURE 7.

Predicted monomer concentration profiles for a round vesicle (1.5-μm radius). Assuming a uniform F-actin concentration in the tail with filaments oriented on average toward velocity direction, the surface density of filament-ends on the tail-contacting surface is proportional to the unit normal vector component, n_z (i.e., ρ = ρ₀n_z with ρ₀ = (30 nm)⁻²). The surface density is indicted by the gray level on the inset sphere (white, ρ = ρ₀; black, ρ = 0). (a) The monomer concentration at the particle surface is plotted versus angular distance from tail center for the values of the tail diffusivity (D) and surrounding medium diffusivity (D_e) given in the Fig. 4 caption, with the arrow on the ordinate axis again showing the solution for a uniformly reaction sphere, u = (1+κ)⁻¹. (b) Contour plot showing monomer concentration field C(r,z) (white, C = C^∞; black, C = 0) for corresponding conditions in Fig. 4.

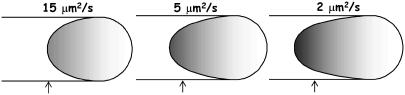
We first simulated the effect of diffusion limitations on vesicle shape without considering any mechanical limitations. Here, the vesicle was assumed completely compliant at its tail-contacting rearward surface, which was allowed to advance in the propulsion direction with local speed given by kC(θ)d. The front of the vesicle (not in contact with the tail) was assumed to maintain a hemispherical membrane cap of constant radius R_s = R₀. As shown in Fig. 8, the faster outer-filament elongation rate, resulting from the monomer concentration gradient, caused the vesicle to distend and assume a teardrop shape similar to those observed experimentally (Fig. 1). Importantly, the predicted evolution to a teardrop shape resulted entirely from diffusion-limited elongation of surface-tethered filaments and required no stresses on the vesicle or force-effects on filament elongation. Therefore, it is reasonable to surmise that the characteristic teardrop shapes observed in the experiments likewise resulted primarily from diffusion-limited filament elongation, not stress-dependent filament elongation. If so, this could explain why similar teardrop shapes were observed despite the occasional presence of a long membrane tube extending down the center of actin tail (13), a situation which should have much different vesicle stresses (i.e., different osmotic pressure and membrane tension). However, a more complete prediction of dynamic vesicle shape changes does require a treatment of the vesicle mechanics, as described below and detailed in the Appendix.

FIGURE 8.

Tear-drop-shaped soft particles evolving from diffusion-limited filament elongation. Shapes similar to those of experimentally observed phospholipid vesicles (12,13) (see Fig. 1) were obtained by simulating only the diffusion-limited filament growth in the direction of propulsion, without needing to account for force-dependence filament elongation or vesicle stresses (i.e., a completely compliant vesicle). Vesicle shapes are shown for different diffusivities after a displacement from an initially round shape centered at the arrows (k = 10 μM⁻¹ s⁻¹, ρ₀ = (30 nm)⁻², and D_e = 15 μm²/s) for the same expired dimensionless simulation time 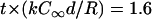. Gray level represents monomer concentration at the vesicle surfaces (white, C = C_∞; black, C = 0).

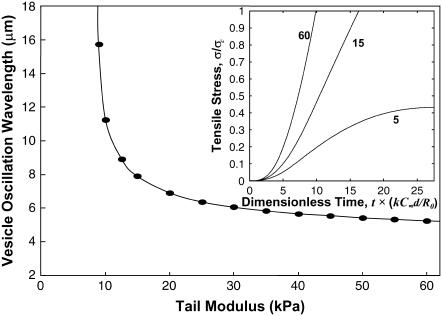
The dynamics of vesicle deformation was simulated using the same treatment of vesicle membrane tension and osmotic pressure applied by Upadhyaya et al. (12), while also accounting for membrane bending rigidity and the elastic deformation (10) of the F-actin tail (see the Appendix for details of the mechanical model and simulation methods). As shown in Fig. 9 (and Supplementary Material Movie 1), the simulations predict that vesicles with sufficiently rigid actin tails continue to deform and accumulate stress on the slowest filaments at the tail center until the center reaches a critical tensile stress σ_c = ρ₀F_b, where F_b ∼ 10 pN is the filament-vesicle bond strength (12) (see Fig. 1 f). The vesicle-tail interface then ruptures, creating a contact line that peels forward, thereby allowing the vesicle to become rounded again (see the first sequence of vesicle contours in Fig. 9 a). Though not central to our arguments, the rounding speed during the peeling phase should generally be rate-limited by the speed of bond rupture and/or the rate of water flux across the membrane needed to restore the initial volume (Appendix). Accounting for water flux only, our simulations recapitulated the experimental timescale for vesicle-rounding reasonably well. Vesicle oscillations required a sufficiently rigid actin network, characterized by the Young's Modulus E, and vesicles with a less compliant tail evolved to a static shape with no oscillations (second sequence of contours in Fig. 9 a and Supplementary Material Movie 2). Also shown in Fig. 9 b are the predicted stress distributions on the vesicle surfaces for the two cases in Fig. 9 a. Our simulations predict that compressive stresses are distributed fairly evenly on the vesicle sides and fall to zero at the tail boundary. This stress distribution contrasts that of Upadhyaya et al. (12), who predicted (based on assumptions described above) a compressive-stress distribution that increased to a maximum at the outer tail boundary, where the tail thickness decreased to zero, and then dropped precipitously to zero beyond the tail boundary (see Fig. 2 c from Upadhyaya et al. (12)), a situation which would require an infinitely-rigid actin tail at that location.

FIGURE 9.

Simulation of vesicle dynamics. (a) Contour sequences of the vesicle shapes (20-s intervals) are shown for two different values of the Young's modulus E of the actin tail, showing predicted cycles of distension/rounding for a higher modulus (E = 50 kPa), and a steady-state shape for a lower modulus (E = 5 kPa). Oscillations result from detachment of tethered filaments at the point of highest stress, which creates a contact line that “peels” (i.e., further filament-surface bond breakage at the translating contact line) toward the vesicle front, allowing it to round (D = 5 μm²/s, ρ₀ = (30 nm)⁻², C_∞ = 1.25 μM). (b) Predicted stress distribution from actin network on vesicles are shown in red (tensile stresses directed outward, compressive stresses inward), for simulations shown in panel a and for a vesicle under the same conditions (with E = 50 kPa), but with filament assembly obeying free-filament thermal ratchet kinetics. For the left vesicle (with E = 50 kPa), the stress distribution immediately before detachment is shown (with longest line thus corresponding to 11 nN/μm), and the stress distribution at steady-state is shown for the others. (c) Simulated trajectories of the vesicle front and rear positions (E = 40 kPa), showing predictions consistent with results reported by Upadhyaya et al. (12) (see Fig. 1). The distance between oscillations is ∼5 μm, and the speeds of the vesicle front and rear during distension phases were nearly constant with time.

As shown in Fig. 9 c, for tails with higher moduli (E = 40 kPa shown here), the simulated trajectories of the front and rear of the motile vesicles are remarkably similar to the vesicle oscillations reported by Upadhyaya et al. (see Fig. 1, f and g). Importantly, because the vesicle remains in a quasi-mechanical-equilibrium, the predicted oscillation wavelength (i.e., the distance traveled between consecutive detachment phases indicated on the ordinate axis in Fig. 9 c) is independent of the timescale and thus depends only the monomer-concentration profile (i.e., on dimensionless κ), the vesicle radius, the critical stress for filament detachment σ_c, and Young's Modulus E of the actin tail. However, the dimensional timescale of the simulation is determined by kC_∞, thus requiring a value for the bulk concentration C_∞, which was unreported for these experiments (12). We found that setting the timescale by assigning a value of 1.25 μM for C_∞ (a reasonable profilin-actin concentration for cell extracts) recapitulates the experimental time-axis.

As shown in Fig. 10, the predicted oscillation wavelength becomes asymptotically independent of E at higher moduli, but depends sharply on E for lower moduli. The transition from nonoscillatory behavior to oscillatory behavior occurs at E ∼ 9 kPa, a value falling within the range estimated for actin rocket tails (1–15 kPa) (19,27). For E < ∼9 kPa, the actin network is sufficiently compliant to disperse the stresses, allowing the vesicle to assume a steady state with no shape oscillations, as shown in Fig. 9 a. For larger moduli, oscillations occur with wavelengths approaching a constant value of ∼5 μm, which closely matches the value observed in the trajectories of Upadhyaya et al. (12) (see Fig. 1). This predicted biphasic behavior with tail modulus provides an attractive explanation for why oscillations occur in some, but not all, soft particle trajectories (13,26): slight variability in the mechanical rigidity of the actin tail can account for the different dynamics. The buildup of tensile stress at the tail center is also plotted in the Fig. 10 inset, for vesicles starting from an initially spherical shape. Consistent with experimental trajectories, the speed of the vesicle rear remained constant during the distension phase, despite the increasing tensile stresses ramping from zero to the critical stress (here, σ_c = 11 nN/μm², assuming F_b = 10 pN and ρ₀ = (30 nm)⁻²). The constant speed at the tail center with increasing tensile stress, is a consequence of the speed being limited by force-insensitive elongation of persistently tethered filaments under tension at the tail center, and is contrary to what would be expected by a propulsion mechanism resisted by friction or tension-induced bond breakage (as in, for example, the tethered-ratchet model (15)).

FIGURE 10.

The oscillation wavelength (i.e., the distance traveled between detachment/rounding phases) is plotted versus actin tail modulus. The simulations predict a sharp transition from nonoscillating behavior (infinite wavelength) for E < 9 kPa, to oscillations with wavelength asymptotically approaching a constant value ∼5 μm for higher moduli. The inset shows the increase in stress at the tail center over time, for E = 5, 15, and 60 kPa. During vesicle distension, the stress on the center filaments rises to reach the critical stress of detachment (assumed here to be 11 nN/μm²) for the higher moduli, but levels off to a steady state before the critical stress is reached for the lower modulus. In either case, the vesicle speed at the tail center did not accelerate with increasing tensile stress (see Fig. 9 c), a predicted property of force-insensitive elongation of tethered filaments.

Finally, we repeated our simulations under the same conditions as above (with the higher modulus E = 50 kPa), but thermal-ratchet kinetics instead (i.e., 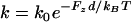) for compressed filaments, which are working against the component of the filament load in the propulsion direction (i.e., F_z = n_zσ /ρ = σ /ρ₀). We found that the kinetic retardation of outer filaments under compression prevented significant distensions of the vesicle (Fig. 9 b and Supplementary Material Movie 3), and tensile stresses at the tail center remained <1 nN/μm² up to the steady state. Therefore, the accumulation of large tensile stresses in our simulations required force-insensitive elongation as well as a sufficiently rigid actin tail.

DISCUSSION

Interpretation of experiments using biomimetic particles benefits from realistic models of the actin dynamics at the particle surface. In this article, we demonstrate that diffusion-limited, force-insensitive elongation of end-tracked filaments explains the signature properties of hard and soft particles undergoing actin-based motility. First, the particle-speed dependence on particle size arises from the greater characteristic diffusion length of larger particles, and our predicted speeds are in good agreement with published data (7,11). Second, the concentration gradient arising from monomer consumption should result in faster filament growth and compressive stress buildup on outer filaments of the rocket tail, in balance with tensile stresses on the slower filaments at the tail center. For rigid particles, the faster elongation rates must be accommodated by changes in filament orientation, resulting in a local increase in F-actin concentration. This stress differential between slower and faster filaments should rise until the stress on the tense filaments in the tail center causes their detachment from the particle surface, allowing the particle to proceed forward at a faster rate, thereby initiating a cycle of saltatory motion. We predict 1), that saltatory motion should occur only for particles >∼1.5-μm radius, consistent with the experimentally observed critical particle radius for the saltatory motion to appear; and 2), that the width of dense F-actin gel bands in the tail behind larger particles should be asymptotically independent particle-size, also consistent with experiments (7,11). Finally, our simulations of vesicle dynamics predict that a similar accumulation of stress due to the monomer concentration gradient causes the distension of vesicles into teardrop shapes and the characteristic oscillatory motion observed experimentally.

It is important to emphasize that the prediction of diffusion-limited velocity for particles >∼1 μm radius is robust over reasonable value ranges for the relatively few parameters needed to capture these behaviors. The parameter with most uncertainty is filament-end density, ρ. Our estimate of 30-nm filament spacing is somewhat larger that other estimates for biomimetic systems (e.g., Upadhyaya et al. (12) and Plastino et al. (19), where 25-nm and 10-nm filament spacings, respectively, were assumed), but these lower values would actually yield a greater diffusional resistance than predicted here and would only serve to strengthen our arguments. (A 10-nm filament spacing also seems physically unrealistic, since a 7-nm actin filament diameter would leave only a 3-nm gap through which the 5-nm-diameter monomers would be expected to diffuse.) We recognize that other factors than those treated in our model may influence diffusion-limited propulsion, such as: a likely effect of spatially-varying F-actin concentration on the monomer diffusivity in the tail during saltatory motion; a possible effect of monomer depletion on filament-end density at the tail center (creating, for example, a void at the tail center; see below); and possibly more complicated nonlinear actin network mechanics than in our treatment. We assumed all filament (+)-ends consuming monomers are tethered and share tensile forces, but a subpopulation of untethered filament ends could exist within in the tail and contribute to monomer consumption, especially under conditions that promote Arp2/3-mediated branching or filament severing (28). Despite these limitations, the fact that such good quantitative agreement is achieved with so few necessary assumptions for such a wide variety of hard- and soft-particle behaviors (e.g., speed versus radius, vesicle distension, transition to and constant band thickness in saltatory motion) using the same parameter set and no free parameters, supports our assertion that propulsion in these systems is governed primarily by diffusion-limited, force-insensitive elongation of surface-tethered filaments.

The results of this analysis are important to understanding the molecular mechanism of force generation by actin polymerization. The salient dynamics observed experimentally for hard- and soft-particle propulsion was predicted assuming no force-dependence of the filament elongation rate, even under compressive and tensile forces of several pN per filament. Such compressive forces should present no kinetic hindrance to filament end-tracking motors (see Fig. 2 b), but should slow elongation of free-filament thermal ratchets, thereby slowing the outer filaments in the tail and preventing the accumulation of compressive stress. As shown previously (2,16), the filament end-tracking motor hypothesis also provides an explanation of how filaments can efficiently harness ATP hydrolysis energy to generate forces of this magnitude. In other words, the analysis presented here shows that the key experimental observations from biomimetic systems are entirely consistent with the actoclampin filament end-tracking motor hypothesis, with force-insensitive elongation under tensile forces or compressive forces up to several pN per filament (2,16). In contrast, the tethered-ratchet model (15) requires working filaments to be unattached (bearing no tension) and predicts an exponentially decreasing elongation rate with load, decreasing to a half-maximum rate at only ∼1 pN/filament. Moreover, in the tethered-ratchet model, only those filaments undergoing nucleation are assumed to resist tensile forces, estimated up to ∼10 pN or more per filament (based on an average among all filaments) during vesicle distensions (12). Because only a small fraction of filaments (1–10%) are assumed to be nucleating at any time in the tethered-ratchet model, these nascent attached filaments would therefore have to sustain enormous forces of 100–1000 pN per attached filament to balance the experimentally estimated vesicle tensile stress. For these reasons, the experimental observation of tensile-stress-independent speed of the vesicle rear appears to favor the actoclampin model over the tethered-ratchet model, especially in light of our simulations.

Force generation by filament end-tracking motors requires processive filament assembly by the surface-bound components, specifically by surface-bound ActA·VASP, N-WASP, and the VCA peptide on the biomimetic particles considered here. We have previously published extensive arguments for Act·VASP as the likely processive end-tracking complex for Listeria and ActA-coated particles (2,16,29). For the other components, it is important to note that VASP, WASP, N-WASP, and the VCA peptide all share repeats of the WASP Homology Domain 2 (WH2) sequence, which has been recently argued based on structural considerations, to be involved directly in (+)-end assembly (3,6,30). Supporting the idea that WH2 domains are critical in filament assembly during particle propulsion is the fact that effective propulsion of Listeria, Shigella, Rickettsia, and Burkholderia pseudomallei all require WH2-like domains, which are present in Listeria ActA-bound Ena/VASP proteins, Shigella IscA-bound N-WASP, or directly by the WH2-like domains in the bacterial surface proteins RickA and BimA on Rickettsia and Burkholderia, respectively (31). In actin-rich tails behind these organisms, branching by Arp2/3 is either only minimally present or nonexistent as in the case of Rickettsia motility, suggesting that Arp2/3-mediated branching is not critical to the propulsion mechanism(s), consistent with the finding of continued effective propulsion of Listeria in vitro after the removal of Arp2/3 from the motility medium (32).

In the cases of N-WASP and VASP, polyproline regions neighboring the WH2 domains likely facilitate plus-end assembly by binding and supplying profilin-actin by direct-transfer, in a mechanism first proposed by Dickinson et. al. (29) and now believed to be similarly involved in actin filament (+)-end assembly by formins (16,33–35). In the end-tracking motor hypothesis, a multivalent interaction is required for processivity, but this property can be effectively imparted by juxtaposed end-tracking proteins immobilized to a surface. Such a condition would be favored by random surface coverage at sufficiently high density.

When the propulsion speed is diffusion-limited, any experimental conditions that reduce the filament-end density at the surface should increase the monomer concentration at the surface and thereby enhance particle speed. This prediction provides an alternative explanation of observations of Samarin et al. (28), who found that VASP's enhancement of particle speed correlated with a decrease in filament density in the tail. VASP's inhibition of the formation of new filaments ends by Arp2/3-mediated branching, as reported by Skoble et al. (36), should be sufficient to enhance particle speed by our model. In another study, Plastino et al. (37) found that motile VASP-coated particles generated a void in the tail center, which also correlated with increased particle speeds, findings that are likewise consistent with our predictions. Though not modeled here, such a center void would be anticipated if (+)-end-tethered central filaments elongate too slowly or are too few to stably integrate into the hollow tail without first detaching quickly under high tensile forces.

At first glance, force-insensitive filament elongation may appear to be at odds with the force-velocity measurements of Marcy et al. (38), who found a ∼50% increase in speed of N-WASP-coated beads with increasing tensile force, with particles detaching from their tails at higher tensile forces. They also found a decrease in velocity with increasing compressive load, up to a ∼60% decrease at loads >2–3 nN, above which no further decrease was observed. These moderate effects on particle speed could be explained by changes in filament orientation within the tail or in filament-end density, without invoking a force-dependence on filament elongation. That is, the tensile force in these experiments may have simply pulled the slower filaments into alignment (i.e., increasing 〈cos φ〉) and/or detached the taut-most slower filaments, thereby increasing the supply of monomer to the remaining tethered filaments. Similarly, rather than slowing filament elongation, compressive forces may have slowed velocity by simply orienting filaments at angles away from the velocity direction (reducing 〈cos φ〉, see Eq. 13), an explanation which is consistent with the observed increase in F-actin concentration during the slowing phase of the saltatory motion of larger beads. In other words, the measured particle speeds are not necessarily proportional to the elongation rates of filaments that are capable of reorienting. The recent force-velocity measurements of Parekh et al. (39) are likewise consistent with particle speed being limited by force-insensitive elongation of persistently tethered filament (+)-ends in that they observed no force-dependence on velocity over a wide range of loads. They also made the seemingly puzzling observation that, after a large load capable of slowing speed was subsequently reduced to smaller load, the speed increased to a value that was greater than previously observed at the same smaller load. This behavior would be expected if the imposed load-reduction shifted the force balance onto the tethered filaments, thereby placing a fraction of them under high tension and detaching them from the surface. The resulting reduction in filament-end density should then increase the local monomer concentration at the particle surface with a resultant increase in speed. Our results point to the importance of examining filament density and/or orientation in such force-velocity measurements to discriminate between force effects on elongation versus those effects arising from actin-filament compliance.

The viewpoint that actin-based propulsion is rate-limited primarily by the rate of long-range monomer diffusion and binding to tethered elongating filaments ends may help explain many puzzling observations of Listeria propulsion. Because Listeria have radii of ∼0.5 μm, and should thus have a κ-value > 1, it is anticipated that the rate of long-range (∼1-μm) monomer diffusion will at least partially limit motility and may completely determine propulsion speeds under conditions where diffusion is slowed or the filament density is large. This prediction is consistent with the observed inverse correlation between Listeria speed and tail density (40,41). Moreover, the decrease in velocities observed by McGrath et al. (41) with increasing concentrations of methyl cellulose may be explained by a reduction in long-range diffusion to the bacterial surface caused by the thickening agent added to the cell extract, rather than an increase in viscous drag on the particle itself. Also arguing against the relevance of viscous drag is the observation of surface-bound particles that have a similar rate of tail formation similar to that of unbound particles (11).

Though not taken into account here, it is also important to note that the first step in the filament end-tracking motor cycles is predicted to become saturated with bound monomer at sufficiently high monomer concentrations, which would asymptotically result in concentration-independent motility rates, consistent with some experimental studies (16). In this limit, the effective reaction velocity (i.e., the maximum reaction flux divided by the monomer concentration), and thus κ, would decrease with increasing concentration, presenting the possibility of a transition from diffusion-limited to reaction-limited particle speeds with increasing monomer concentrations. Consequently, the observation of monomer-concentration-independent, reaction-limited speeds at high monomer concentrations does not necessarily contradict diffusion-limited speeds at lower concentrations.

Because both diffusivity and actin-binding to filament ends have Arrhenius-type temperature-dependencies (22), the Arrhenius temperature dependence for Listeria speed, as reported by Soo et al. (40), is to be anticipated if motility is rate-limited by monomer binding, by diffusion, or both. The effective activation energy of diffusion in the tail may also depend strongly on the actin tail density. Therefore, the observed population-variability in activation energies of bacterial speed could be explained by population-variability in ActA density and tail density. The observations of Soo et al. (40) are thus consistent with arguments presented here and with the actoclampin model.

In summary, important observations of actin-based propulsion of biomimetic particles and beads can be explained in a quantitatively self-consistent manner as the consequence of diffusion-limited elongation of (+)-end tethered actin filaments, unhindered by compressive or tensile forces up to several pN per filament. These properties, as well as the observed colocalization of putative end-tracking components ActA and N-WASP's VCA domain with the filament ends on soft particles, are consistent with the filament end-tracking motor (actoclampin) hypothesis. Together with its ability to explain other characteristics of Listeria trajectories (2,17), the energy source for several-pN force generation (16), and the likely role for the key structural domains of VASP, N-WASP, and formins (3,16,29), the actoclampin model continues to provide an attractive unifying hypothesis for force production in actin-based motility.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

APPENDIX

Analytical solution of monomer concentration field

To validate subsequent boundary element calculations, the dimensionless monomer concentration u was first solved analytically for the case of equal diffusivities, D_e = D. Letting w(r,z) ≡ 1 − u(r,z), the boundary condition for w on the particle surface becomes

(A-1)

Applying Green's second identity to w and the axisymmetric spherical harmonics on the domain outside the unit sphere, which, together with Eq. A-1, yields the boundary integral equation:

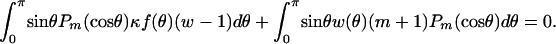(A-2)

Upon introducing the series 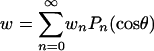, Eq. A-2 becomes

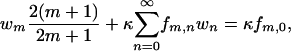(A-3)

where 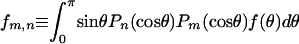. For a uniform sphere, f_m,n = 2δ_m,n, thus 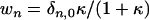, making 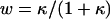everywhere on the surface. For a uniform half-sphere,

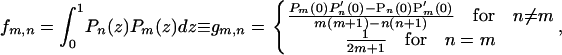(A-4)

and for f(z) = n_z = z, we have

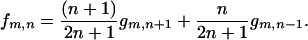(A-5)

Upon applying either Eqs. A-4 or A-5 depending on the filament-density assumption, {w_m}can be found to desired precision by truncating the series in Eq. A-3 and solving the resulting linear system.

Boundary element solution of the monomer concentration field

For the more general cases of axisymmetric deformation or D_e ≠ D, the field w(r,z) = 1 − u(r,z) was solved using the boundary element method in which the surface boundary integrals are approximated by discretizing the surface into constant-valued surface elements, yielding a system of algebraic equations that can be solved for the unknown boundary values and fluxes on the surface elements (42). Then w(r,z) in the three-dimensional domain can be calculated from the solved surface boundary values and fluxes. Here, the flux-matching boundary condition for w at the tail surface is

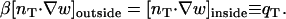(A-6)

Let {w_v,i}, {w_o,m}, and {w_T,k} be the constant-element values of w on the particle-tail boundary (N_v elements), front particle-surrounding medium boundary (N_o elements), and tail-surrounding medium boundary (N_T elements), respectively. Accounting for the conjoined domains of the tail and surrounding medium (42), the discretization of the boundary integrals on the surfaces of the two domains yields the following set of four algebraic equations:

Rear particle-tail boundary, i = 1 to N_v

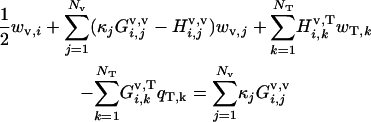(A-7)

Front particle-medium boundary, m = 1 to N_o

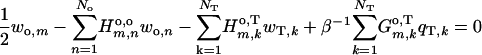(A-8)

Inside tail-surrounding medium boundary, k = 1 to N_T

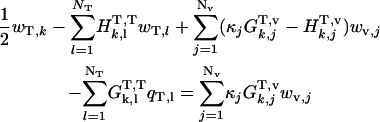(A-9)

Outside tail-surrounding medium boundary, k = 1 to N_T

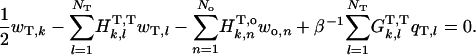(A-10)

The various matrix components are integrals over the line elements, {S_n}, given by

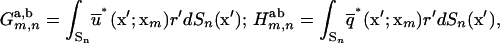(A-11)

where superscripts a and b indicate the surfaces upon which x and x′, respectively, are locate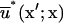d, and 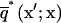are the fundamental solution, 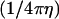and its normal derivative, 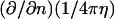integrated over the azimuthal coordinate, respectively, with η ≡ |x′–x|. These functions can be written in terms of elliptic integrals (42):

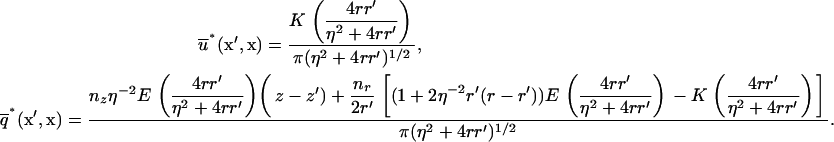(A-12)

The integrals in Eq. A-11 were calculated numerically using Gaussian quadratures, except for the singular integrals arising in the diagonal matrix entries (,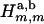), which were solved analytically in the vicinity of the singularity point where η = 0, by exploiting the following asymptotic approximations for small ɛ (42):

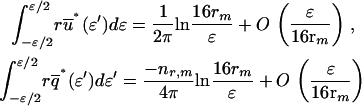(A-13)

The results in Figs. 4 and 7 were obtained using N_v = N_o = 30 front and rear vesicle-surface elements, N_T = 40 actin tail elements, and ɛ = 10⁻⁴r_m. The vesicle rear and front surface node positions were spaced by equal increments in θ from 0 to π/2, and from π/2 to π, respectively. In the vesicle simulations, a higher node density was used near the tail center to account for the higher curvature there, with 20 elements covering the range 0 < θ < π/8, 20 covering π/8 < θ < π/2 (hence N_v = 40), and 20 covering π/2 < θ < π (N_o = 20). The first 10 tail nodes were placed at the same z positions as the 10 vesicle-tail nodes closest to the tail boundary, and the rest were spaced at logarithmically increasing intervals with the last tail element capping the tail at a distance of 10 radii from the vesicle. (Because the concentration varies as z⁻¹, solutions assuming any tail length >∼6 radii were indistinguishable.) The accuracy of the solution method was confirmed by comparison to the analytical solution for β = 1 (see Figs. 4 and 7).

Simulation of vesicle dynamics

The simulation procedure involved the following steps for each time increment, δt:

1. Updating of the z-node positions {z_i} on the rearward vesicle surface based on the local polymerization rates (i.e., δz_i = −(kC_∞d/R₀)u_v,iδt);

2. Calculation of the new stress σ distributions at the node positions arising from the incremental change in vesicle shape; and

3. Updating the r-node positions accounting for the change in σ and the resultant deformation of the actin tail surrounding the vesicle.

Since shape changes occurred slowly relative to vesicle translation, the step size δt was set at 10⁻³R₀/kC_∞d (typically ∼0.03 s), which was sufficiently small to ensure dynamics were independent of δt. We also found that the concentrations {u_v,i} could be recalculated once every 20 time steps with no significant reduction in accuracy, again because of the slowly evolving vesicle shape.

We approximated the region of the actin tail cupping the vesicle as an elastic material with Young's modulus E (10) and accounted for its radial expansion, while neglecting deformations in the z direction. Volume of F-actin was assumed conserved during the radial expansions, requiring the incremental radial expansion δr at the vesicle surface to correspond to an expansion of at any radial position across the actin tail, and to an incremental change in the azimuthal strain by the amount 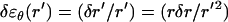. The relationship between δr and the incremental change δσr of the radial component of the stress acting on the tail can then be found by integrating the differential in the incremental radial stress, 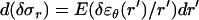over the tail width (i.e., from r to r_T,),

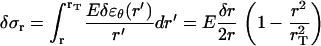(A-14)

Note that for small tail thickness, 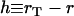, this formula recovers the well-known thin-shell approximation 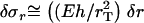. Application of Eq. A-14 required the tail boundary position at each node position, which were also tracked in the simulation. Because the node positions on the vesicle surface move relative to the stationary tail, the tail radius at each vesicle node r_T(z_i) was first translated due to the change in z_i by the amount 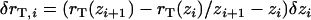, then updated after the expansion δr_i using δr_T(z_i) = (r_i/r_T(z_i)) δr_i.

The normal stress σ at the vesicle surface creates the stress on the actin tail and its value at each node is necessary to calculate the radial expansions from Eq. A-14. The stress was determined from the membrane tension τ_d, the osmotic pressure Π, and the bending rigidity (bending modulus k_c) (43),

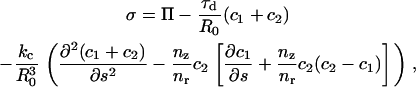(A-15)

where c₁ =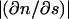 and c₂ = 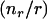are the minimum and maximum principal curvatures on the axisymmetric surface (dimensionless, scaled to 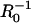), respectively, and s is the arc (dimensionless, scaled to R₀) tracing the vesicle boundary toward the positive z direction (i.e., toward the tail center). Curvatures and derivatives with respect to s were estimated by second-order finite-difference approximations using the constant-boundary-element values. Because changes in σ (thus, in δσ_r = δ(n_rσ) depend on shape (i.e., on {r_i} and {δr_i}), solving Eq. A-14 for all tail-contacting nodes required simultaneous solution (using the Newton-Raphson method) of a set nonlinear algebraic equations for {δr_i}, the tension τ_d, and the center position z_s of the frontal half-sphere. The new radius R_s of the frontal half-sphere depends on z_s and the position {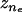,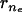} of the tail-contacting node closest to the tail boundary, 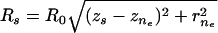. The remaining equations for the simultaneous solution are the constitutive equation for tension (12,44),

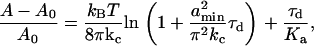(A-16)

and the stress balance on the vesicle front accounting for the osmotic pressure,

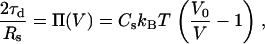(A-17)

where A and V are the volume and area (obtained from {r_i},{z_i}, z_s, and R_s), A₀ and V₀ are the initial values of A and V of the spherical (unstressed) vesicle, K_a is the membrane stretch modulus, a_min is the shortest membrane undulation wavelength, and C_s is the initial concentration of solute in the undeformed vesicle. Conveniently, the various parameters appearing in Eqs. A-15–A17 were estimated by Upadhyaya et al. (12) (k_c = 9 k_BT, C_s = 240 mM, K_a = 100 nN/μm, a_min = 50 nm), allowing comparison of our simulations to their experiments.

Vesicle detachment and rounding

Once σ exceeds σ_crit = ρ₀F_b at the tail center, a new contact line is assumed to form there and propagate (“peel”) toward the vesicle front, rupturing filament-vesicle bonds assumed to have characteristic bond strength F_b and maximum stretch length, L_b (assumed ∼1 nm) at the point of rupture. The work to break a springlike bond is 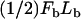(45), such that the effective surface tension that resists peeling is 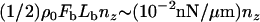. Filament-surface bonds therefore continue to rupture and the contact line advances toward the vesicle front until either the vesicle rounds entirely, or until mechanical equilibrium is reestablished. The actin-tail was assumed to be rigid on this faster timescale of rounding, and the influence of vesicle bending rigidity was neglected in determining shape during the rounding phase, justified by the small characteristic bending length 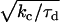and small width of the zone of stretched bonds near the contact line, (2k_cL_b/F_bρ)^1/4 (<10–30 nm) (45) compared to the radii of the unattached vesicle regions. The force condition for continued propagation of the contact line is (45)

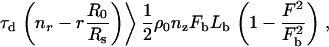(A-18)

where the left-hand side is the force per unit length on the contact line due to membrane tension, and the right-hand side is the work per area required to break the bonds under initial load F = σ/ρ near the contact line. However, for any reasonable values of F_b and L_b, the equilibrium condition was never approached in our simulations; therefore, the rounding phase was assumed to be completed once the speed of the advancing detached vesicle rear became less than the prior tail-center speed caused by polymerization, at which time the polymerization speed was assumed to again govern the forward motion. To simulate rounding, the contact boundary was incremented along the s-arc toward the vesicle front, the resulting volume change δV was calculated, and the time δt required for the volume change was added to the simulation time. Assuming water flux across the membrane is rate-limiting during rounding, δt was estimated from

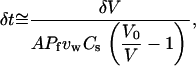(A-19)

where P_f is the permeability coefficient of water (∼30 μm/s for phospholipid vesicles (46)), and v_w is the molar volume of water (∼18 ml/mol). The value δV was determined from new quasi-equilibrium vesicle shape using Eqs. A-16 and A-17, now with spherical caps of radius R_s existing on both the vesicle front and the detached membrane region. Upon completion of the rounding phase, a new tail was assumed to have reformed at the rear-facing surfaces (n_z > 0) by the resumption of the distension phase, with initial thickness set to be zero (i.e., r_T = r) for the newly rear-facing surface outside the previous tail-contacting zone (i.e., on the small region of the surface having n_z > 0 on the spherical frontal bulge created during rounding).