The effect of antibody-dependent enhancement on the transmission dynamics and persistence of multiple-strain pathogens

Abstract

Cross-reactive antibodies produced by a mammalian host during infection by a particular microparasitic strain usually have the effect of reducing the probability of the host being infected by a different, but closely related, pathogen strain. Such cross-reactive immunological responses thereby induce between-strain competition within the pathogen population. However, in some cases such as dengue virus, evidence suggests that cross-reactive antibodies act to enhance rather than restrict the severity of a subsequent infection by another strain. This cooperative mechanism is thought to explain why pre-existing immunity to dengue virus is an important risk factor for the development of severe disease (i.e., dengue shock syndrome and dengue hemorrhagic fever). In this paper, we explore the effect of antibody-dependent enhancement on the transmission dynamics of multistrain pathogen populations. We show that enhancement frequently may generate complex and persistent cyclical or chaotic epidemic behavior. Furthermore, enhancement acts to permit the coexistence of all strains where in its absence only one or a subset would persist.

Many important pathogens of humans and other animals exist as sets of discrete strains. In previous studies of the transmission dynamics and population genetics of such multistrain pathogen systems, the focus of attention has been on the effects of cross-immunity, generated by recovery from infection with one strain, which acts to inhibit infection with another strain (mediated by immunological responses to antigens or epitopes shared by all strains) (1–5). It has been shown that antigens eliciting strongly inhibitory immune responses will act to organize pathogen populations into discrete strains with minimal overlap between them in the important variable epitopes (3). At intermediate levels of inhibition, discrete strain structure still forms, but may be unstable with cyclical or chaotic temporal changes in strain abundance (5). No discrete strain structure forms under weak immune selection.

Other pathogens, however, are believed to induce enhancement rather than inhibition of infection with strains of the same infectious agent. One such example is antibody-dependent enhancement (ADE) of viral infections, where cross-reactive antibodies generated by a previous exposure to a heterologous strain are believed to facilitate the within-host replication of a second invading strain. Enhancement of viral replication has been observed in vitro for dengue (6–8) and a variety of flaviviruses and other viruses (9, 10), including HIV (11, 12).

In this paper the epidemiological consequences of this form of antibody-mediated between-strain interaction are explored, where previous exposure may increase rather than decrease the probability of transmission of a second strain. Analyses focus on exploring the range of transmission dynamics and epidemic behavior that may be exhibited by such interactions, and the consequences of this phenomenon for the persistence of multistrain pathogens within human populations.

In the case of dengue, ADE is thought to be responsible for the observation that pre-existing immunity (detected via serology) to one of the four strains of the viral etiological agent is an important risk factor for the development of severe disease such as dengue shock syndrome and dengue hemorrhagic fever (13–19). An enhanced risk of serious disease is observed even when the initial immunity is maternally acquired (6). Because of the complexity of the relationship between dengue disease and infection, we restrict ourselves to modeling the dynamics of infection, rather than symptomatic case incidence.

Model Structure

We consider the simplest case of two strains circulating within a human community. We assume that infection with a given strain i (where i = 1 or 2) confers lifelong strain-specific immunity, such that the fraction of the population already exposed to strain i, x_i, cannot be infected again by the same strain. The deterministic dynamics of x_i are defined by:

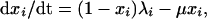1

where λ_i is the force or per capita rate of infection of strain i, and μ is the mortality rate of the host (1/μ = host life expectancy). Host population size is assumed to be constant. The population is structured into a proportion susceptible to both strains, s, a proportion infectious with a primary infection with strain i, y_i, and a proportion with a secondary infection with strain i having previously been exposed to the other strain j, y_ji. The dynamics of these infectious fractions are described by the following equations:

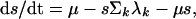2

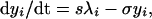3

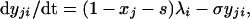4

where 1/σ is the average duration of infectiousness. Note that σ also is taken to incorporate host mortality, μ (where μ ≪ σ), and that the model uses overlapping compartments, so that individuals in the y_i or y_ji categories are also in the x_i category. Eq. 4 is obtained by noting that 1 − x_j − s, the fraction of the population that is neither susceptible nor previously exposed to strain j, is simply the proportion of the population that has been exposed to strain i only. This simplification is clearly only valid when considering a two-strain system. Similarly, z, the proportion exposed to both strains, is just given by z = x₁ + x₂ − (1 − s).

It is assumed that the cross-reactive antibodies generated by previous exposure to a heterologous strain will result in either an increase or decrease in the transmission probability of the virus (another possibility is that susceptibility to the second strain is modified; the dynamics of the resulting model are very similar to those of the model described here). The force of infection of strain i, λ_i, is thus a linear combination of y_i and y_ji:

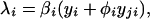5

where φ_i represents the degree of enhancement (φ_i > 1) or neutralization (φ_i < 1) induced by the circulating cross-reactive antibodies in the host. Combining Eqs. 3–5 then gives a single equation for the λ_i:

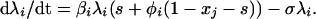6

Epidemiology of Dengue

There is good evidence to suggest that serotype (= strain) 2 of the dengue virus (DEN-2) is responsible for most severe symptomatic infections and that the vast majority of such symptomatic cases are secondary infections (18–21). Some evidence exists to suggest that primary DEN-1 infection followed by secondary DEN-2 infection is the most likely infection sequence to produce severe disease (18). There is also limited data indicating that although severe disease is much less common for non-DEN-2 strains it is again restricted to those with secondary infections (19). As such, while accepting the hypothesis that increased virulence on second infection is a marker for ADE (17), it is difficult to argue from epidemiological data alone that enhancement is greater for DEN-2 than other strains. In the absence of detailed longitudinal cohort studies, tracking the severity of disease after primary and secondary infections for all combinations of strains, it could be argued that DEN-2 is intrinsically more pathogenic whether in a primary or secondary setting. Also, although many experimental in vitro studies in human mononuclear phagocytic cells and various animal models have concentrated on DEN-2 because of its clinical importance, ADE has been demonstrated for all dengue strains and a spectrum of other flaviviruses (9, 10, 15). However, very few studies of ADE have been comparative in nature with quantitative measures of the severity of disease made for each strain and each sequence of infection by different strains. At present, therefore, there is only very limited experimental data on the degree of enhancement for the different strains (22). In the case of in vitro studies it is difficult to translate observations into epidemiological measures. We therefore explore a wide range of parameter assignments for the degree of enhancement.

While strain-specific forces of infection theoretically can be estimated from age-stratified serological data, this exercise is complicated by interactions between strains and the inability to discriminate between multitypic infections. Some studies suggest that DEN-2 is generally more prevalent but in general strain dominance hierarchies appear to vary geographically and temporally. In our analyses we therefore make the assumption that the reproductive ratios (numbers of secondary infections generated by single primary infections in entirely susceptible populations), R_oi (23), of the two strains are identical. As seen below, this assumption implies the transmission coefficients of both strains are the same (β₁ = β₂). However, the results are robust to significant strain asymmetry in transmission success.

Transmission Dynamics of Dengue

In the absence of antibody-mediated enhancement or inhibition (i.e., φ_i = φ_j =1) each strain will settle to an equilibrium prevalence independent of the other strain, with x_i = 1 − R_oi (where R_oi = β_i/σ is the basic reproductive ratio of strain i). In contrast, if the cross-reactive antibodies from a previous infection are capable of rapidly neutralizing a second infection (φ_i = φ_j = 0), then the strain with the higher R_o will competitively displace the other. More generally, for invasion of strain i into a population with strain j alone to be possible, we require:

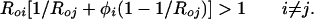7

In other words the primary invading infective needs to generate more than one secondary infection for the invasion to succeed.

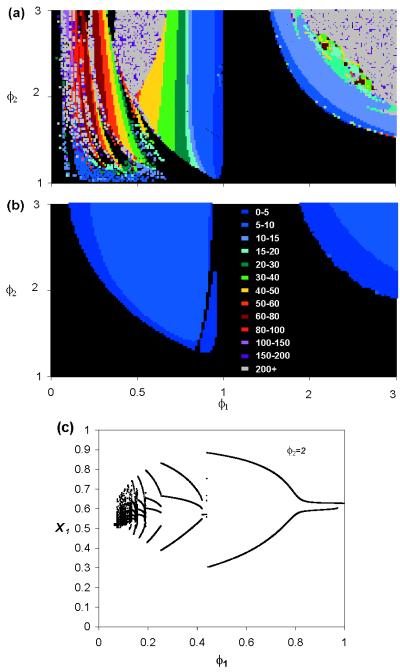
Because all four dengue serotypes (= strains) are known to be able to coexist in some human communities, Eq. 7 often must be satisfied for both i = 1 and i = 2 in the dengue system. However, of greatest importance is the observation that the coexistence equilibrium point is unstable for large regions of the parameter space, resulting in the system exhibiting complex cyclical or chaotic behavior. The remarkable range and complexity of the nonlinear dynamics exhibited is illustrated in Fig. 1a for a range of possible values of φ₁ and φ₂. Note that no cycles are seen for the case of entirely neutralizing cross-reactive antibodies (i.e., no enhancement) for a two-strain system. In contrast, cyclical and chaotic dynamics are common if one or both strains experience ADE. Further insight into the complex nature of these epidemic dynamics generated by antibody-dependent enhancement can be gained from Fig. 1c, which shows the dynamical bifurcation structure along a line through the parameter space of Fig. 1a. Qualitatively, enhancement generates oscillations by causing epidemics of the enhanced strain to “overshoot” in the presence of the other strain (compared with the behavior seen when only one strain is present), until the unexposed population is temporarily exhausted and incidence falls dramatically. The magnitude of this overshoot is sufficient to destabilize the endemic equilibrium.

Figure 1.

(a) Isoperiodic diagram of deterministic model, indicating nature of model dynamics, as a function of degree, φ_i, of ADE for each of two strains. Color designates period of epidemic cycle (in years), with black indicating equilibrium coexistence (no cycles). Note that because the system is symmetrical between the strains, φ₁ is varied between 0 and 3, and φ₂ only between 1 and 3. No cycles are seen for the case when both φ₁ and φ₂ are negative. Parameters: R₀₁ = R₀₂ = 2, the recovery rate is σ = 100/yr, and host life span 1/μ = 50 yr. No background force of infection (λ₀ = 0). For most points where the period is plotted as over 200 yr, the dynamics are chaotic. (b) As in a, but with λ₀ = 10⁻⁵ (5 infectives/million per yr). (c) Bifurcation diagram plotting the local maxima of x₁ against φ₁ (for values of φ₁ where limit cycles exist), with φ₁ being varied between 0 and 1. φ₂ = 2 and other parameters as in a. This diagram represents a horizontal slice through the left-hand half of a showing a complex cascade of bifurcations, with limit cycle regions interspersed by chaotic regimes. Integration of the deterministic model used the Bulirsch-Stoer method for maximum numerical accuracy, with randomly chosen (nonsymmetrical) initial conditions. Convergence to any equilibrium point or limit cycle was ensured by discarding the first 10,000 yr of each resulting time series.

Our model system ignores many complexities inherent in natural host-infectious disease systems, such as the discrete structure of real populations, spatial structure, and chance effects (= stochasticity), that may effect the long-period cycles or large amplitude chaos predicted by the basic model (24). An obvious problem is that stochastic effects may cause disease extinction in the deep inter-epidemic troughs. Indeed, in this way, the generation of epidemic cycles can be seen to reduce the probability of disease persistence, or, equivalently, increase the critical community size required for the disease to persist. To examine these factors we take account of the known infection reservoir in mosquito vectors and other primate species via the inclusion of a small background force of infection, λ_0i, to represent a constant trickle of new infections entering the population. For simplicity, we assume that the background force of infection is the same for each strain (λ₀₁ = λ₀₂ = λ₀). As shown in Fig. 1b, the effects of this modification on the behavior of the deterministic model is to replace the long-period cycles with cycles of shorter period in the range of 3 to 10 yr. However, unlike the case with no background force of infection (Fig. 1a), here the cycles are preserved in the stochastic version of the model, even in populations of moderate size (1–10 million). This persistence occurs because the reservoir acts to reduce the likelihood of extinction. Simulations (which used a 0.5-day time step, discrete time approximation to the continuous time Markov process) based on the stochastic version of the epidemic model reveal variability both in the inter-epidemic period and in the order in which epidemics of the different serotypes occur.

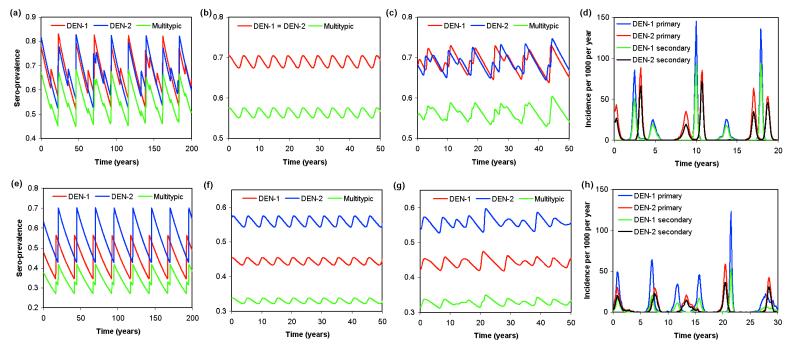
Fig. 2 a–c records changes over time in seroprevalence for a defined set of parameters where both strains experience ADE, for three different model variants (the simple deterministic model, the deterministic model with immigration of infection from a reservoir, and the stochastic framework with immigration). Fig. 2d displays a time series of the incidence of infection corresponding to Fig. 2c. The corresponding time series for the case where only one strain experiences ADE are shown in Fig. 2 e–h.

Figure 2.

(a–c) Sero-prevalence time series for system with R₀₁ = R₀₂ = 2, σ = 100/yr, 1/μ = 50 yr, φ₁ = φ₂ = 2.5. (a) Deterministic model, with λ₀ = 0. Note that the dynamics are chaotic with a quasi-period of about 25 yr. A symmetry-breaking bifurcation has given rise to partially nonsynchronized oscillations of the two strains. (b) Deterministic model with λ₀ = 10⁻⁶. The background force of infection eliminates large-amplitude limit cycle or chaotic attractors, simplifying the dynamics and restoring exact synchronization of the oscillations of both strains. (c) Stochastic model with λ₀ = 10⁻⁶. The dynamics show the “ghost” of the deterministic chaotic attractor from a modifying the simple limit cycles dynamics of b. (d) As in c but showing infection incidence. (e–h) As in a–d, but with φ₁ = 0.75 and φ₂ = 1.5. Dynamical trends are similar to the pure ADE case, but average prevalences now differ and the limit cycles of the two strains are never now in phase.

The analyses so far have not been based on the assumption that ADE is antibody titer dependent as suggested by some experimental and observational studies (7, 8). However, extending the model framework to include this subtlety via the inclusion of a latent stage immediately after the infection event during which cross-reactive antibodies are always neutralizing does not significantly affect dynamical behavior (even if the latent period is as long as 6 months). The time delay introduced by this modification induces cycles throughout the parameter space recorded in Fig. 1 as long as relative enhancement (where any cross-neutralization has to decrease after the latent period) occurs.

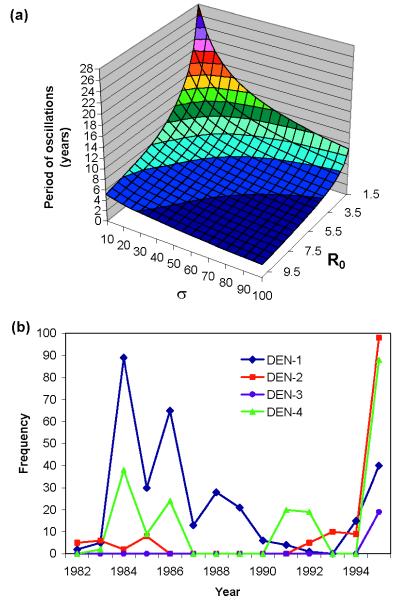
Finally, Fig. 3a shows the sensitivity of the period of the oscillations generated in the deterministic model without infection reservoir to R₀ and the rate of loss of infectiousness, σ, demonstrating that the results presented here do not depend on assumptions made regarding the duration of infectiousness of dengue.

Figure 3.

(a) Dependence of epidemic period (in yr) on R₀ of strains and recovery rate, σ, for deterministic model with 1/μ = 50 yr, R₀₁ = R₀₂, φ₁ = 0.8, φ₂ = 2, and λ₀ = 10⁻⁶. (b) Numbers of cases associated with the four serotypes as reported by Briseno-Garcia et al. (21) for the period 1982–1995 in Mexico.

Discussion

Our analyses have shown that ADE acts to induce cyclical epidemics of cocirculating strains for a wide range of biologically realistic parameter assignments. The focus has been on DEN infection because of the relative depth of information available for this infectious disease, but the results apply more broadly to a wide variety of other infections. Where longitudinal epidemiological data permits comparison, the prediction of oscillatory behavior in the incidence of dengue and unpredictable ordering of epidemics of the different strains is supported (21, 25). For example, longitudinal data from Mexico recording changes in the abundance of the four major serotypes reveal dramatically fluctuating incidences suggestive of oscillations with a period of around 5 yr (21). More detailed comparisons between prediction and observation require long-time series of the incidences of the different strains, which, unfortunately, are not available at present.

The complex dynamical properties of the infectious diseases system influenced by ADE have important implications for the collection and interpretation of epidemiological data. For example, analysis of the age-stratified incidence of symptomatic infections is problematic in the absence of longitudinal data from patients to determine their past history of experience of different strains. Similarly, inferring incidence from cross-sectional serological surveys of prevalence is difficult because a time-independent force of infection cannot be assumed because of the large-scale cycles in infectious disease abundance. Instead it is necessary to use strain-specific sero-prevalence data to reconstruct past force-of-infection history. Such epidemiological methods currently are being developed, but require multiple, temporally separated data sets that are finely stratified by age. Even if cocirculating strains were in a stable equilibrium, analysis of serological data is problematic at present because of an inability to distinguish strain-specific antibodies after secondary infection and the fact that the occurrence of ADE invalidates assumptions about strain independence that often is (implicitly) imbedded in statistical methodology.

The major result of our analyses concerns the ability of ADE to induce sustained large-amplitude oscillations in disease incidence, with inter-epidemic periods of a few to many years. Also of importance is the observation that despite such complex cyclical dynamics the different strains of the infectious agent are easily able to coexist. Indeed, it would even be possible for one strain of low-transmission potential, able to induce significant ADE, to persist by piggybacking on another strain where in the absence of the latter the strain would go extinct (i.e., R_oi < 1).

Although the model described here has been specifically applied to dengue, consideration of the epidemiological effects of enhancement may be important for a much wider range of pathogens that exhibit between-strain, immune system-mediated cooperative interactions. As mentioned earlier, as well as flaviviruses (9, 10), in vitro ADE of HIV replication also has been demonstrated (11, 12) with potentially serious implications for evaluating monotypic vaccination programs. Low-titer antibodies to the sexual stages of Plasmodium vivax also are believed to enhance transmission (26) in a nonspecific manner. Moreover, mechanisms other than direct ADE also may generate cooperative interactions; blocking antibodies, as opposed to cellular responses, have been reported in P. falciparum (27) and in bacterial infections that exhibit many strain types such as Neisseria gonorrhoeae (28). More recently, studies of HIV (27) and hepatitis B virus (29) have shown that the simultaneous presence of a variant antagonist epitope can induce nonresponsiveness, or limited responsiveness of cytotoxic T cells to its target antagonistic epitope (30). The down-regulation of cellular immune responses in this manner (altered peptide ligand antagonism) also has been demonstrated in P. falciparum (31) and has been linked to the unusual distribution of parasite variants in some human communities.

Given the potential importance of cooperative mechanisms in determining the transmission dynamics of a wide variety of infectious agents it is clearly important for future epidemiological research to focus on the collection of strain-stratified longitudinal data to help identify oscillatory fluctuations in incidence and other key signatures of cooperation. Interventions, such as immunization targeted at some subset of the total number of strains, may induce unexpected consequences, which will be correctly interpreted only given a precise understanding of the underlying dynamical properties of these complex systems.

ABBREVIATIONS

ADE

antibody-dependent enhancement

DEN

dengue virus