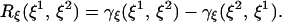Extending the definition of entropy to nonequilibrium steady states

Abstract

We study the nonequilibrium statistical mechanics of a finite classical system subjected to nongradient forces ξ and maintained at fixed kinetic energy (Hoover–Evans isokinetic thermostat). We assume that the microscopic dynamics is sufficiently chaotic (Gallavotti–Cohen chaotic hypothesis) and that there is a natural nonequilibrium steady-state ρ_ξ. When ξ is replaced by ξ + δξ, one can compute the change δρ of ρ_ξ (linear response) and define an entropy change δS based on energy considerations. When ξ is varied around a loop, the total change of S need not vanish: Outside of equilibrium the entropy has curvature. However, at equilibrium (i.e., if ξ is a gradient) we show that the curvature is zero, and that the entropy S(ξ + δξ) near equilibrium is well defined to second order in δξ.

The purpose of this article is to discuss the statistical mechanics of a finite physical system maintained in a nonequilibrium steady state at a constant temperature. In such a system, entropy is produced at some constant rate ≥ 0. Here we investigate the possibility of also associating a finite entropy S with our nonequilibrium system, extending the definition of equilibrium entropy. We restrict our discussion to the case of a classical system with an isokinetic thermostat [as defined by Hoover (1) and Evans and Morriss (2), see below].

If ρ(dx) = g(x)dx is the probability measure in phase space corresponding to an equilibrium state, the corresponding Gibbs entropy is

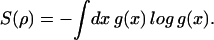The probability measure ρ(dx) describing a nonequilibrium steady state is in general singular with respect to dx, and the corresponding Gibbs entropy thus is −∞. To extend the definition of entropy outside of equilibrium we shall use another idea, based on the thermodynamic relation δS = δQ/T, where δQ is energy-exchanged, and T is the absolute temperature.

We consider a finite mechanical system in a nonequilibrium (in general) steady-state ρ_ξ under the effect of a nongradient (in general) force ξ and an isokinetic thermostat at temperature β⁻¹. We give below a definition of the entropy increment S(ξ → ξ + δξ) corresponding to a small increment δξ of ξ. Our definition is based on energy exchanged, uses the microscopic dynamics of the system, and agrees with the equilibrium statistical mechanics definition when ξ and δξ are gradient forces, i.e., for equilibrium situations. Outside of equilibrium, for a loop ξ → ⋯ → ξ, the sum S(loop) of the entropy increments in not expected to vanish in general. This means that the “entropy connection” has a curvature. Because S(loop) is of second order in the size of the loop, the increment S(ξ → ξ + δξ) is well defined to first order in δξ. If ξ is a gradient the curvature vanishes, and therefore the entropy close to equilibrium

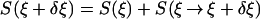is well defined to second order in δξ.

Systems outside of equilibrium exhibit a variety of phenomena such as metastability and hysteresis, which we want to exclude here. We assume that a nonequilibrium steady state is naturally defined, and we study its variations under parameter changes by using the techniques of the ergodic theory of differentiable dynamical systems. Basically we assume that the microscopic dynamics is sufficiently chaotic [this is the content of the chaotic hypothesis of Gallavotti and Cohen (3)]. Our nonequilibrium steady-state ρ_ξ is then a natural or Sinai–Ruelle–Bowen (SRB) measure, and we apply linear response theory (4) to determine changes of ρ_ξ for variations ξ → ξ + δξ. The linear response is given by integrals over time which generalize those appearing in the fluctuation–dissipation theorem.

Mathematical proofs of the linear response formulas are within reach under suitable assumptions of uniform hyperbolicity. (A hyperbolic system with singularities and isokinetic thermostat close to equilibrium has been rigorously studied in ref. 5). But in general, uniform hyperbolicity assumptions are unrealistically strong from a physical point of view. This article is thus meant as theoretical physics rather than mathematical physics. There is a leap of faith in believing that our linear response formulas apply to any given physical setup, but the situation is not worse than for applications of the fluctuation–dissipation theorem.

In ref. 6 another approach to the definition of entropy outside of equilibrium was proposed (Lyapunov entropy) replacing phase space volume by volume in a suitable (Kaplan–Yorke) reduced dimension. This idea was taken up in ref. 7, where an attempt is made at defining the entropy in the large system limit. We do not investigate here this limit. Physically, the entropy is defined best in the large system limit as the Boltzmann entropy, a concept based on the phase space volume associated with a given macrostate and vigorously defended by Lebowitz (8). It remains to be verified whether the definition of entropy given in this article can be related to the Boltzmann entropy. One would also like to check that our results are not tied to the use of the isokinetic thermostat but extend to more general situations. (The isokinetic thermostat is very convenient for calculations but does not quite reproduce the Hamiltonian time evolution at equilibrium.)

Isokinetic Time Evolution

We consider the classical time evolution

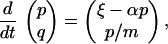where p, q ∈ R^N. We shall also use the notation x = (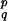) ∈ R^2N and rewrite Eq. 1 as

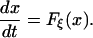The Euclidean scalar product of vectors a, b in R^N or R^2N will be denoted by a⋅b. The force ξ = ξ(q) is not necessarily a gradient, and we take

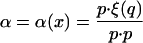so that

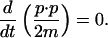The term −αp in Eq. 1 corresponds to the much-discussed isokinetic thermostat (a special case of the Gaussian thermostat of refs. 1, 2, and 9). We shall denote by (f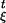)_t∈R the flow defined by Eq. 2, i.e. f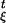x is the solution at time t corresponding to the initial condition x.

Entropy Changes

The local rate e_ξ(x) of volume contraction corresponding to the vector field F_ξ is minus its divergence and easily computed to be Φ(x) = (N − 1)α(x). This is identified with the local rate of entropy production (see refs. 10 and 11). When integrated over a nonequilibrium steady-state ρ_ξ(dx), it gives the corresponding global rate of entropy production. It is natural to define the change of entropy S(ξ → ξ + δξ) to be the entropy released in the time interval [0, +∞) when the force ξ + δξ acting during the interval (−∞, 0) is replaced by ξ in the interval [0, +∞). At time t ≥ 0 our system is in a state ρ_ξ + δ_tρ, which reduces to ρ_ξ+δξ at t = 0 and tends to ρ_ξ when t → ∞ (an expression for δ_tρ will be given below). We have thus to first order in δξ

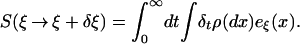Dynamical Assumptions

In order to proceed we need now to make some assumptions on the dynamics defined by Eq. 1 and on the measure ρ_ξ. As we have said, we want the time evolution to be sufficiently chaotic, i.e., the flow (f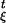) to be hyperbolic in some mathematical sense and the nonequilibrium steady-state ρ_ξ to be an SRB measure. For our purposes we can define an SRB measure as a limit lim_t→+∞ (f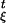)*σ where σ is absolutely continuous with respect to dp dq conditioned to {(p, q) : p⋅p/2m = K}. An SRB measure is usually singular, but “smooth along unstable directions.” For a physical discussion of the present setup see ref. 6. We shall also assume exponential decay of correlations (see refs. 12 and 13). As a consequence of these assumptions we have the following linear response formula (see ref. 4):

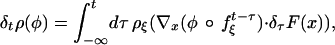where δ_tF is a time-dependent small perturbation of the right-hand side F_ξ of Eq. 2, and δ_tρ is the corresponding perturbation of ρ_ξ at time t. The integral over τ converges exponentially. The test function φ is assumed to be differentiable, because δ_tρ is in general a distribution rather than a measure. We have written ρ_ξ(φ) = ∫ ρ_ξ(dx)φ(x) and similarly for δρ. Note that for time-independent δF the time-independent δρ is given by

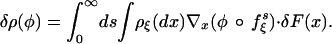Notation

We have defined

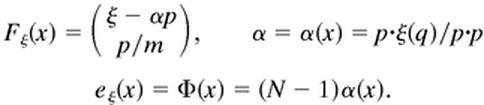We shall use infinitesimal perturbations δξ = ξⁱ, δF = Fⁱ (no time dependence, i = 1, 2) and let

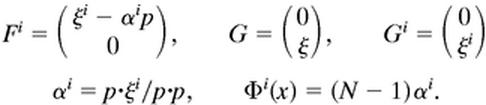We also denote by K the kinetic energy (conserved by Eq. 1), and let β⁻¹ be the corresponding temperature:

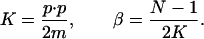We shall from now on write f = f^t and ρ_ξ = ρ.

Proposition.

With the above notation let

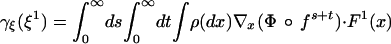define a linear form in ξ¹. Then, to first order in ξ¹,

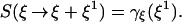Using Eqs. 3–6 we have indeed

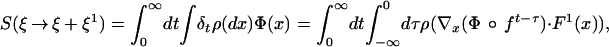and replacing t by s, τ by −t gives Eq. 8.

Curvature

To second order in ξ¹ we have

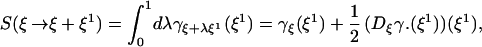where D_ξγ.(ξ¹) is the functional derivative of γ_ξ(ξ¹) with respect to ξ. And an easy second order calculation gives

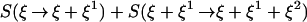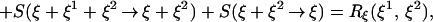where the curvature form R_ξ is defined by

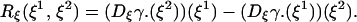If C is a closed curve in the space of force fields ξ, the change of entropy corresponding to turning around the curve is

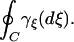It is of second order in the size of the curve if R_ξ ≠ 0 and of higher order if the curvature vanishes.

Proposition.

Define a bilinear form in ξ¹, ξ² by

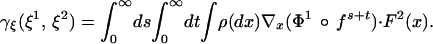Assume now that ξ̃ is locally gradient and write G̃ = (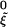). Then

1. (i)  γ_ξ(ξ¹) = γ_ξ(ξ, ξ¹);

2. (ii)  γ_ξ(ξ̃, ξ¹) = −β ∫ 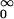ds ∫ ρ(dx)G̃(f^sx)⋅(T_xf^s)F¹ (x);

3. (iii)  (D_ξγ.(ξ̃, ξ¹))(ξ²) = −β ∫ 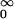ds ∫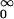 dt ∫ ρ(dx)

   

   whereΨ̃^is(x) = G̃(f^sx) ⋅ (T_xf^s)Fⁱ(x);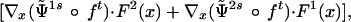

4. (iv)  (D_ξγ_η(⋅, ξ¹))(ξ²) = γ_η(ξ², ξ¹)

5. (v)  If ξ is locally gradient, then

   

   i follows directly from Eqs. 7 and 10.
6. The assumption that ξ̃ is locally gradient means that we have a configuration space D ⊂ R^N which is not simply connected and that ξ̃(q) = −∇_qṼ, where Ṽ is a “multivalued function” on D. Writing f^tx = (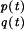), Φ̃ = (N − 1)p⋅ξ̃/p⋅p, we have

   

   and hence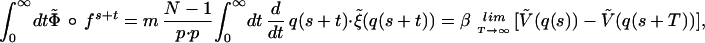

   

   which proves ii.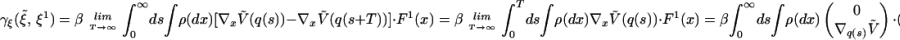
7. We thus have

   

   

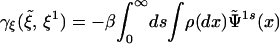
   Therefore, because ρ and f^s both depend on ξ,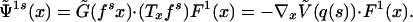

   

   

   

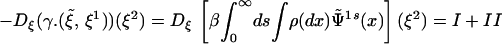
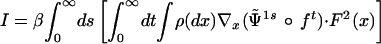
   where we have renamed s the variable s − t in the last line. This proves iii.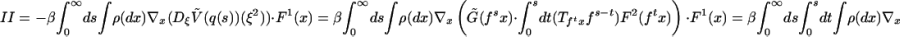

8. iv follows from Eq. 10.

9. v follows from Eq. 9, iii, and iv, where we take ξ̃ = η = ξ.

The Gradient Case

The situation where ξ is a global gradient, i.e., there is a potential function V = V(q) such that ξ(q) = −∇_qV, is called equilibrium in the present context. Let then

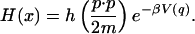The divergence of HF_ξ is

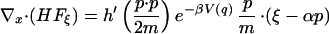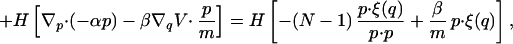which vanishes if h(p⋅p/2m) = δ(p⋅p/2m − K) and β = (N − 1)/2K. Therefore the probability measure

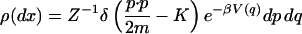(with normalizing factor Z⁻¹) is invariant under (f^t) (see ref. 2) and is the SRB measure ρ in the present case.

Note that, using Eq. 11 and integrating by parts, we obtain

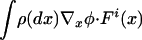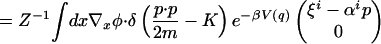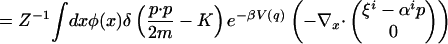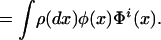Define

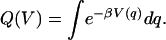Then the (configurational) Gibbs entropy associated with ρ is

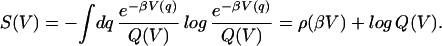If V¹ is a small perturbation of V, we find to first order in V¹

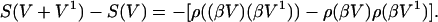Using Eq. 8, i, and ii of the above proposition and Eq. 12, we obtain

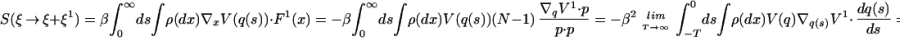Therefore the standard estimate (Eq. 13) from equilibrium statistical mechanics agrees with the “nonequilibrium” prediction based on Eq. 8.

Proposition.

Assume that ξ is a global gradient, then

1. (i)  γ_ξ(ξ¹, ξ²) = ∫ 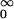ds ∫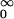 dt ∫ ρ(dx)(Φ¹ ∘ f^s+t)Φ²(x), and

2. (ii)  R_ξ(ξ¹, ξ²) = 0.

From Eqs. 10 and 12, i directly follows. We use now the involution I: (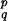) ↦ ()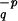, under which Φⁱ is odd, time is reversed, and ρ is invariant (“microscopic reversibility”). Thus

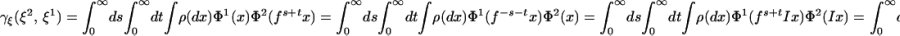and therefore R_ξ = 0 by (V) of the previous proposition, proving ii.

Second-Order Formula

From the above considerations it follows that if ξ is a gradient (ξ = −∇V), the entropy at temperature β⁻¹ can be written consistently to second order with respect to a (nongradient) perturbation ξ¹ of ξ as

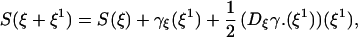where S(ξ) is the equilibrium entropy for ξ, and

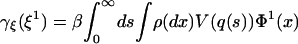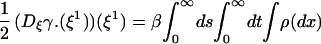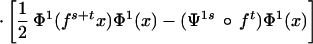with Ψ^1s = −∇_xV(q(s))⋅F¹(x) and other notations explained earlier. We have not studied S(ξ + ξ¹) from the point of view of convexity.

Conclusion

In this article we have considered a classical system with isokinetic time evolution defined by Eq. 1 corresponding to a time-independent force ξ and temperature β⁻¹. For such a system we have defined an entropy increment S(ξ → ξ + δξ) corresponding to an increment δξ of the force (see Eqs. 7 and 8). Our definition agrees with the equilibrium statistical mechanics formula (for the Gibbs entropy) if ξ, δξ are gradient forces. If ξ is a gradient, but not necessarily δξ, we can write

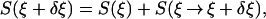where S(ξ) is the equilibrium entropy, and S(ξ → ξ + δξ) is well defined by Eq. 14 to second order in δξ.

Abbreviations

• SRB, Sinai–Ruelle–Bowen