Cost minimization by helpers in cooperative vertebrates

Abstract

When parents invest heavily in reproduction they commonly suffer significant energetic costs. Parents reduce the long-term fitness implications of these costs through increased foraging and reduced reproductive investment in the future. Similar behavioral modifications might be expected among helpers in societies of cooperative vertebrates, in which helping is associated with energetic costs. By using multivariate analyses and experiments, we show that in cooperative meerkats, Suricata suricatta, helping is associated with substantial short-term growth costs but limited long-term fitness costs. This association forms because individual contributions to cooperation are initially condition dependent, and, because when helpers invest heavily in cooperation, they increase their foraging rate during the subsequent nonbreeding period and reduce their level of cooperative investment in the subsequent reproductive period. These results provide a unique demonstration that despite significant short-term costs, helpers, like breeders, are able to reduce the fitness consequences of these costs through behavioral modifications.

Because the theory of natural selection predicts that individuals maximize their fitness by maximizing their own breeding success, cooperative breeding, wherein individuals act altruistically by helping to raise the offspring of others, represents an enigma (1–4). Adaptive hypotheses of cooperative breeding propose that helpers gain indirect fitness benefits if rb > c (where r is the relatedness between altruist and beneficiary, b is the benefit to the beneficiary, and c is the cost to the altruist), or direct fitness benefits if personal benefits (b) exceed personal costs (c; refs. 3–5). Knowledge of both the costs and benefits of helping is thus critical to understanding and quantifying selection on cooperative breeding.

Investigations into the adaptive nature of helping in societies of cooperative vertebrates have concentrated almost exclusively on the benefits of cooperation, and such benefits are now well documented (6–9). By contrast, the costs of cooperation have largely been ignored (7, 10); five studies have examined the short-term energetic costs of helping, and five have examined the long-term fitness costs. In the short term, helping is associated with significant reductions in growth among cichlid fish (Lamprologus brichardi; ref. 11) and significant weight loss among gray-crowned babblers (Pomatostomus temporalis; ref. 12), alpine marmots (Marmota marmota; ref. 13), white-winged choughs (Corcorax melanorhamphos; ref. 14), and meerkats (Suricata suricatta; ref. 15). By contrast, there is little firm evidence to suggest that helpers necessarily incur fitness costs in the long term. Although significant associations between levels of helper investment and helper survival have been demonstrated in pied kingfisher (Ceryle rudis; ref. 16) and stripe-backed wren (Campylorhynchus nuchalis; ref. 17), no such associations have been found in alpine marmot (13), banded mongoose (Mungos mungo; ref. 18), or Florida scrub-jay (Aphelocoma coerulescens; ref. 19). However, it should be noted that all investigations into long-term fitness costs of cooperation have considered the effects of contributing to one breeding season on one fitness cost only (i.e., survival), have generally failed to control for helper age and condition, and may have been unable to dissociate mortality from dispersal.

Nevertheless, the long-term fitness costs of helping may be less than is generally assumed, because studies in noncooperatively breeding vertebrates show that parents may adopt three tactics to reduce the long-term costs of investment in parental care (20–22). Parents frequently invest with respect to their condition (20), and supplemental feeding experiments in cooperative breeders suggest that contributions to cooperation by helpers may also be condition dependent (23–25). In addition, when parents invest heavily in parental care, they may increase their foraging effort between subsequent reproductive events and reduce their level of investment in the following event (21, 22). It is not currently known whether helpers employ either of these latter two behavioral tactics, but, if they do, they may be able to compensate for any condition lost during helping in the short term, and hence reduce the fitness costs of helping in the long term. The aim of this study is to use multivariate statistical approaches and experiments in the cooperative meerkat to: (i) document the short-term growth costs involved with contributing to two different cooperative activities (babysitting and pupfeeding); (ii) examine whether costs accumulate in the short term to result in significant long-term reductions in weight, as well as reduced probabilities of survival, dispersal, and breeding; and (iii) investigate whether helpers show behavioral modifications, similar to those reported for noncooperative vertebrates, that potentially mediate the costs of cooperation for the long term.

Meerkats are small (<1 kg) desert mongooses of southern Africa that live in extended family groups of 2–40 individuals. Dominant females, the principal breeders in groups, produce up to four litters per year of around four pups per litter, although subordinate females may breed in the natal group from their first year (26, 27). Litters remain in the natal burrow during the first month, and pups follow the group on foraging trips thereafter. Pups become independent at 3 months of age and soon after begin to contribute to cooperation, although investment by those under 6 months of age is typically low (25). Helpers improve breeding success in two main ways, through guarding pups at the natal burrow (babysitting; ref. 27) and through provisioning pups with invertebrates and small vertebrates while they follow the group (pupfeeding; refs. 28 and 29). Contributions to babysitting and pupfeeding by helpers over 6 months old vary dramatically (range = 0–73%, median = 10%), but those that contribute heavily to babysitting also contribute heavily to pup feeding within the same breeding attempt (30). Finally, both male and female helpers typically disperse in single-sex parties between the ages of 1 and 3 years (25), and, through the behavior of individuals before dispersing, we are able to dissociate dispersal from death.

Materials and Methods

Study Site.

The study was carried out on ≈300 individual meerkats from 14 groups: 3 groups were studied between January 1995 and May 1998 in the Kalahari Gemsbok National Park (25°17′S, 20°32′E), and 10 groups were studied between June 1996 and January 2001 in farmland 200 km to the east, near Vanzylsrus, South Africa (26°58′S, 21°49′E). Details of climate and habitat are provided elsewhere (15, 29). Groups were generally visited daily during the babysitting period and every one to five mornings for 3–4 h during the pupfeeding period. During these visits, the identity of babysitters and pupfeeders was recorded. All animals within these 14 groups were habituated, could be observed at extremely close range (<1 m), and most could be weighed repeatedly (±1 g) each day by using electronic balances and crumbs of hard-boiled egg. Pups ranged in number from 1 to 13 (mean = 5.3) and were defined as individuals under 3 months old. Helpers were defined as subordinate, nonbreeding individuals over 6 months of age; helper number (hereafter referred to as group size) ranged from 3 to 27 (mean = 14) between groups and from 0 to 23 within groups (between different breeding events). Nonbreeding periods refer to times when there were no pups present in the group, whereas babysitting and pupfeeding periods refer to times when pups were less than 1 month old and were kept at the natal burrow and when they were between 1 and 3 months old and were being fed by helpers, respectively.

Short-Term Costs.

First, we investigate whether helper growth rates vary between periods of nonbreeding, babysitting, and pupfeeding. We obtained 22,082 morning, preforaging weights during nonbreeding periods, 14,128 during babysitting periods, and 24,060 during pupfeeding periods for 399 individuals. Growth rates were estimated by regressing time (in days) against the morning weights collected for each individual during each period, and by using the gradient of the resulting slopes as a measure of growth over the relevant period in grams per day (g/d). Overall, we obtained 2,455 growth estimates for 356 individuals over 68 nonbreeding periods, 100 babysitting periods, and 106 pupfeeding periods. Second, we investigate whether helper growth rates are related to individual levels of investment in babysitting and pupfeeding. During each litter, individual contributions to babysitting were expressed as the number of days that individuals were observed to babysit out of the number of days that individuals were observed, whereas individual contributions to pupfeeding were expressed as the number of food items delivered to pups per minute of observation. Contributions to both babysitting and pup feeding were then categorized as being low (bottom third), medium (middle third), or high (top third). Effects on growth of both period and individual contributions to babysitting and pupfeeding are analyzed by using general linear mixed models, a procedure of general linear model in which both fixed and random terms can be fitted (ref. 31; see Statistical Analyses). In each analysis, growth is fitted as the response term, and period (for first analysis) or helper investment/period (for second analysis) are fitted as the main fixed terms. Individual, litter, and group identities are fitted as random terms to control for repeated measures. In addition, our analyses control for potentially confounding influences of group size, helper age, weight, and sex by fitting each as additional fixed effects.

To confirm a causal basis for any negative relationship found between helper contributions and their growth, we experimentally manipulated the helper/pup ratios of groups by temporarily adding two to five pups to 11 groups for 3–4 h (which already had similarly aged pups). This experiment caused helper:pup ratios of groups to be temporarily decreased from 4:1 to 2.5:1. We compare the mean rate at which the same helpers in the same groups gained weight (g/h) in the 2 days before and the 2 days after the experiment with their mean rate of weight gain during the day of the experiment. Finally, to ensure that changes in the number of pups in a litter are associated with changes in the level at which helpers feed pups, we use multivariate analyses to investigate the effects of litter size on: (i) the proportion of food items found by helpers that they provide to pups; and (ii) helper contributions to the other two main cooperative activities conducted during pupfeeding periods, social digging, and raised guarding. The first analysis is based on an average of 200 min of focal observations on each helper during each pupfeeding period, whereas the second two analyses are based on an average of 20 h of ad lib data collected on each group over the same time periods. These analyses are conducted by using general linear mixed models, controlling for group size, helper age, and sex, as well as repeated measures within individuals, litters, and groups.

Long-Term Costs.

The few studies to have previously investigated the fitness costs of helping in cooperative vertebrates have all compared the survival of hard-working and lazy helpers from one breeding attempt to the next (13, 16–19). This approach does not consider the possibility that short-term costs accumulate over several attempts to influence fitness costs or that factors other than survival are affected. Therefore, we investigate the effects of a helper's cumulative contribution to cooperation in all previous breeding attempts on several correlates of fitness (see below), while controlling for its contribution in the previous attempt. We restrict our data set to include only those individuals for which we know complete helping history from independence. The importance of individual contributions to cooperation for long-term costs is based on cumulative contributions to babysitting at the farm site. However, individual contributions to babysitting and pupfeeding are highly correlated within breeding events (30), and so an individual's contributions to babysitting will reflect its contributions to cooperation generally.

First, we investigate whether the weight of individuals over 6 months old is associated with their cumulative contribution to babysitting over all previous attempts (n = 113 females, 129 males). Weight is known to correlate with three fitness traits in social mammals and may therefore represent one route through which a cost of helping may arise, although costs could also arise independently of weight. In meerkats, heavy individuals are more likely to survive their first year of life than lighter individuals (28), and weight is a significant predictor of survival in other social mammals (32). In addition, in naked mole-rats (Heterocephalus glaber; ref. 33), dispersing individuals contribute little to cooperation and are heavier than similarly aged nondispersing individuals. Finally, in meerkats, weight significantly influences the probability that subordinate and dominant females conceive within any 3-month period (26), their litter sizes at birth (27), and the weight of their pups at weaning (27). Second, we investigate whether cumulative contributions to babysitting are related to the probability that males and females will die or disperse by the time the dominant female next gives birth (n = 69 females, 88 males) and the probability that subordinate females will breed within the next event (n = 69). Analyses are conducted by using a general linear mixed model (weight analysis) or generalized linear mixed models (dispersal, survival, breeding analyses with binomial error structure). In each analysis, we fit as fixed effects an individual's cumulative contribution to cooperation, its contribution in the previous attempt, as well its group size, age, sex, and weight at independence (3–4 months old). Individual, litter, and group identities are fitted as random terms to control for repeated measure within each. Weight at independence is fitted to control for differences in individual quality, because weight at this age predicts foraging success (28) and contribution to specific cooperative activities (25) in the first year of life. It is important to note that (i) fitness traits are investigated independently of current helper weight, and (ii) cumulative contributions to cooperation are both a consequence of investment level in each breeding attempt and the number of breeding attempts in which it has been involved.

Behavioral Modifications.

We investigate whether helpers adjust their behavior to potentially reduce the long-term costs of cooperation, as has been shown for parents in noncooperatively breeding vertebrates (20–22). First, we investigate whether individual levels of investment in the previous breeding attempt are correlated with their daily weight gain (g/h) and rates of growth (g/day) during subsequent periods of nonbreeding. Daily weight gain reflects short-term changes in foraging effort and success (28), whereas growth reflects more long-term changes in body mass. The relationship between contributions to cooperation and subsequent rates of both daily weight gain and growth are investigated by using two general linear mixed models in which helper daily weight gain or growth during the nonbreeding season (n = 562) is fitted as the response term, and contributions to cooperation during the previous event is fitted as the main fixed effect. Only contributions to babysitting are used in this analysis because individual contributions to babysitting and pupfeeding are highly correlated within events (30). In each analysis, we control for potential confounding influences of group size, helper age, weight, daily weight gain over the previous nonbreeding period, and sex, as well as repeated measures within individuals, periods, and groups. Second, by calculating the change in contribution to babysitting (n = 471) and pupfeeding (n = 536) by each individual helper between successive events, we investigate whether helpers adjust their contributions to cooperation between successive breeding events. Thus, in two general linear models (one for babysitting and one for pupfeeding), we fit the change in contribution between successive events as the response variable and helper contribution to cooperation in the previous event (low, medium, high), group size, age, sex, weight, and the number of days between successive events as fixed effects. General linear models are used instead of mixed models because repeated measures within individuals, litters, and groups all constitute negative components of variance, and the results obtained are qualitatively very similar.

We conducted a supplemental feeding experiment to test whether changes in contributions to cooperation between successive events are dependent on condition. We fed 25 helpers (aged 6–18 months) with 24 g of hard-boiled egg for 26 ± 4 days during babysitting and 33 ± 12 days during pupfeeding. Changes in contributions to cooperation are measured for the same helpers when fed and not fed. Again, we use two general linear models (one for babysitting and one for pupfeeding) to investigate whether feeding helpers influences their change in contribution between successive events. In each analysis, change in contribution is fitted as the response term, whereas the previous contribution to cooperation (low/high), feeding treatment (fed/unfed), group size, helper age, and sex are all fitted as fixed effects. Individual identity represents a negative component of variance in a mixed model.

Statistical Analyses.

General linear mixed models with normal error structures and generalized linear mixed models with binomial error structures and logit link functions were conducted in GENSTAT 5 V.4.1 (Rothamstead Experimental Station, Harpenden, U.K.). Mixed models allow both fixed and random components to be fitted to a model; random components take into consideration repeated sampling within the same individuals, litters, or groups (31). The significance of explanatory terms in mixed models is assessed by their Wald statistics, which are distributed as χ² for each term fitted in the model last. Mixed models were not conducted when all random terms represented negative components of variance. All two-way and three-way interactions were assessed, but only those that reached statistical significance (P < 0.05) are presented. All means are presented ±1 SD in the text and ±1 SE in the graphs.

Results

Short-Term Costs.

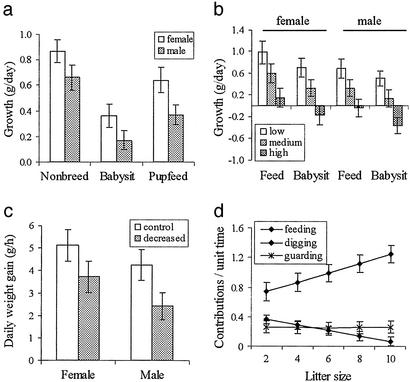
Helper growth rates vary significantly with helper sex and the reproductive status of the group. Females have faster rates of growth than males, but helpers of both sexes grow fastest during periods of nonbreeding and slowest during periods of babysitting, whereas growth rates are intermediate during pupfeeding (Fig. 1a). In addition, individual differences in growth rates are associated with their levels of investment (Fig. 1b). When individuals contribute little to either babysitting or pupfeeding, they have similar rates of growth to those during periods of nonbreeding. By contrast, when individuals contribute medium amounts, they have significantly reduced rates of growth, and this reduction is even more pronounced when they contribute heavily (Fig. 1b). Reductions in growth rates with increases in contributions to cooperation are significantly more pronounced among males than females.

Figure 1.

Effects of breeding period and contribution to cooperation on helper growth rates (g/day). (a) Breeding period (χ² = 39.57, df = 2, P < 0.001) and helper sex (χ² = 21.56, df = 1, P < 0.001) significantly influenced growth rates, and there was a nonsignificant tendency for males to grow more slowly than females during periods of cooperation (χ² = 4.80, df = 2, P = 0.091). (b) Helpers that contributed more to cooperation had slower growth rates (χ² = 37.72, df = 5, P < 0.001), and this tended to be especially true of males (χ² = 14.69, df = 5, P < 0.012; “Feed” refers to periods of pupfeeding). (c) Experimental decreases in helper:pup ratios caused helpers to have reduced rates of weight gain (g/h; paired t test, t₉ = 3.41, P = 0.009). (d) Increases in litter size were positively associated with increases in the proportion of food items found, which helpers gave away (χ² = 9.45, df = 1, P = 0.002); negatively associated with contributions to social digging (F_1,87 = 8.60, P = 0.004); and not associated with contributions to raised guarding (F_1,73 = 0.25, P = 0.62). Contributions to pupfeeding are shown on a per-hour basis, whereas contributions to social digging and raised guarding are shown on a 3-h basis.

These relationships between investment in cooperation and growth are likely to have a causal basis. Experimental decreases in the helper:pup ratios of groups are associated with significant reductions in the rates of helper weight gain (Fig. 1c), a close correlate of growth (28). The causality of this negative relationship between contribution to pupfeeding and helper weight gain is further emphasized by the fact that increases in litter sizes are associated with significant increases in the ratio of food items found by helpers and provided to pups but are not associated with increases in individual contributions to either social digging or raised guarding (Fig. 1d).

Long-Term Costs.

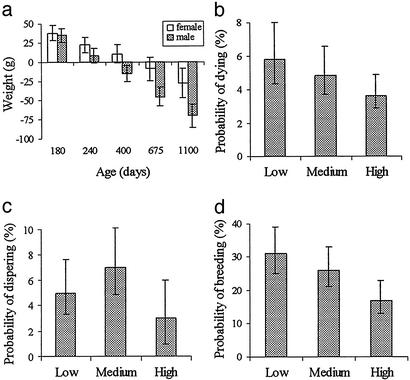
We found no evidence to suggest that an individual's contribution to cooperation in a previous event significantly influences its weight or its probability of survival, dispersal, or reproduction before the next breeding event (all P values >0.5). In addition, evidence that cumulative contributions to cooperation are associated with long-term costs is variable. Helper investment is initially condition dependent in both males and females, but high investors are significantly lighter than low investors by the age of 12 months in males and 18 months in females (Fig. 2a), and weight differences between high and low investors continue to increase after this age. However, we found no relationship between helper investment and probability of mortality (Fig. 2b) or dispersal (Fig. 2c), although subordinate females breed less in their natal group if they have invested heavily in cooperation (Fig. 2d).

Figure 2.

Association between cumulative contribution to cooperation and (a) weight (interaction term: sex * log age * cumulative contribution, χ² = 5.06, df = 1, P = 0.025); (b) probability of mortality (χ² = 1.04, df = 2, P = 0.59); (c) probability of dispersal (χ² = 1.45, df = 2, P = 0.48); and (d) probability of breeding (χ² = 8.39, df = 2, P = 0.015). (a) Relative differences in weight between top- and bottom-investing males and females over time. (b and c) Sexes are combined because there was no differences between the two (P = 0.8).

Behavioral Modifications.

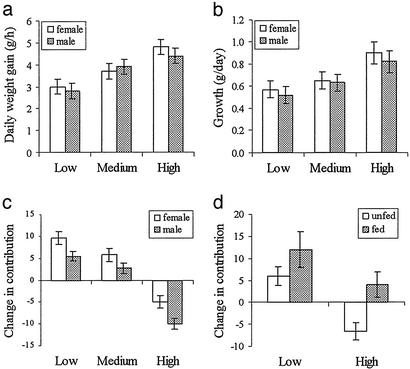
Helpers use three behavioral tactics to reduce the potential of incurring long-term costs of helping. First, initial levels of helper investment are conditional on weight (Fig. 2a), and we have previously demonstrated experimentally a causal relationship between helper weight and contribution to cooperation (25). Second, individuals that invest heavily during a breeding attempt subsequently raise their foraging effort, because high investors have faster rates of daily weight gain (Fig. 3a) and faster rates of growth (Fig. 3b) during the subsequent nonbreeding period than low investors. However, this compensatory behavior may not be sufficient to replace lost condition. Assuming a babysitting period of 30 days (15) and a peak pupfeeding period of 40 days (29), we calculate that, after each breeding event, medium and top investment carers will lose 28 g and 56 g more than bottom investors, respectively. Given the differences in rates of weight gain between helpers during periods of nonbreeding (Fig. 3a), we estimate that medium and top investors need 93 and 112 days of nonbreeding, respectively, to make up for their costs incurred. However, helpers only have a median of 25 days of nonbreeding before the next litter is born, suggesting that they are unlikely to be able to regain all weight lost.

Figure 3.

Effect of contribution to cooperation on (a) rates of daily weight gain (g/h; χ² = 6.28, df = 2, P = 0.043) and (b) growth rates (g/day; χ² = 7.67, df = 2, P = 0.022) during subsequent periods of nonbreeding. (c) Changes in contributions to cooperation between successive events were significantly influenced by levels of investment in the previous event (babysitting, GLM, F_2,464 = 95.08, P < 0.001; pupfeeding, F_2,530 = 101.72, P < 0.001). (d) Supplemental feeding increased contributions to babysitting (F_1,81 = 10.32, P = 0.002) and pupfeeding (F_1,97 = 21.87, P < 0.001) irrespective of previous contributions (interactions between fed/unfed and previous contribution P > 0.6 for babysitting, P > 0.4 for pupfeeding). (c and d) Percentage increases or decrease in contributions for babysitting only.

Helpers therefore have a third tactic that they may use to reduce the potential for long-term costs. Individuals investing heavily in one breeding event significantly reduce their contribution in the following event, whereas those previously investing little significantly increase their contribution (Fig. 3c). This effect could result from the fact that helpers that invest heavily in a breeding attempt would be expected to show a decrease in their subsequent investment by chance (and vice versa for low investing helpers; ref. 34). However, the extent to which individuals decrease contributions between consecutive events is significantly influenced by the interbirth interval of the dominant female and, hence, by the amount of time that top investors have to recover from the costs incurred during the previous event (babysitting, F_1,530 = 4.69, P = 0.031; pupfeeding, F_1,530 = 15.82, P < 0.001). In addition, supplemental feeding a sample of helpers that have either invested little or heavily in the previous attempt shows that both low and high investors significantly increase their contributions in the subsequent event (Fig. 3d).

Discussion

Our results show that the short-term energetic costs of cooperation vary substantially with the type of cooperative activity conducted, as well as with the amount invested. Despite substantial short-term costs, we found no evidence to suggest that the costs incurred in one event translate into fitness costs before the next event and only limited evidence that short-term costs accumulate to significantly influence fitness costs in the future. This is because when helpers invest highly in cooperation, they (i) are initially heavy, (ii) increase their foraging effort and growth during subsequent periods of nonbreeding, and (iii) reduce their investment in cooperation in the subsequent breeding event.

Previous studies have shown convincingly that levels of helper investment may be associated with short-term energetic costs (11–15). Such findings have led to the suggestion that, contrary to a recent proposition (35), helping is unlikely to be a selectively neutral trait arising simply because helpers are stimulated to provide care to begging offspring (15, 36). Evidence that cooperation is associated with short-term energetic costs does not provide satisfactory verification that helping is costly in the long-term and therefore neither negates the idea that helping is selectively neutral nor supports the idea that helping is adaptive. This point is potentially an important one because there seems to be no clear evidence to suggest that helping is universally associated with costs to personal fitness in the long term. Of the five studies (13, 17–20) that have investigated whether individual contributions to cooperation in one breeding event influence the probability of surviving to the next, only two provide evidence of a cost (17, 18). However, none of these studies investigated whether helpers may show behavioral tactics that could reduce the long-term costs of helping and, hence, whether helpers may show an adaptive response to cooperation.

These five studies could be criticized in two ways. Strictly speaking, none controlled for helper age and condition, two factors that are likely to be associated with survival probability. In addition, all five studies investigated the effects of helping in one season on a single fitness correlate (i.e., survival) and may not have been able to dissociate between death and dispersal. By using a multivariate statistical approach that controlled for group size, helper age, and helper weight at independence, we found no evidence to suggest that levels of investment in one breeding event reduce the probability of individual survival or dispersal to the next event, or the probability that females will breed in the next event. Furthermore, we provide mixed evidence to suggest that short-term costs accumulate over many breeding events to influence costs in the long term. In both males and females, helpers that invest heavily in cooperation are generally lighter in adulthood than those that only invest little. Despite these differences in weight, high-investing helpers do not have significantly higher rates of mortality, or lower rates of dispersal, than more low-investing helpers. We do not rule out the possibility that survival and dispersal costs are evident under certain circumstances or that we were unable to control satisfactorily for individual quality. However, high-investing females do have a reduced probability of conceiving in their natal group, probably resulting from their lower weight, because weight is an important predictor of subordinate female conception in meerkats (26). Unfortunately, we were not able to investigate the long-term breeding costs to males. Thus, six of six studies (including this one) provide good evidence that helpers incur substantial short-term costs, but only two of six (including this one) have found helping to be associated with long-term survival costs, although we do find that costs may accumulate to affect the fecundity of subordinate females.

There are four likely reasons why short-term energetic costs may not lead to substantial long-term fitness costs for helpers in cooperative vertebrates. First, individual contributions to cooperation may be condition dependent. We show here that helpers of both sexes initially invest more in cooperation if they are relatively heavy. In addition, we have previously shown that supplemental feeding raises individual contributions to specific cooperative activities in meerkats (25), and similar findings have been reported for two avian species (23, 24). Therefore, although hard-working helpers may lose more weight than more lazy helpers, this need not lead to an overall reduction of relative condition, especially in those species in which helpers typically remain only for a short period before dispersing. Second, when helpers invest heavily in cooperation, they may be able to compensate for their increased energetic investment by foraging more intensively during the subsequent period of nonbreeding. Although this behavioral tactic is insufficient to fully compensate for lost growth in meerkats, it is because of the short interbirth intervals found in this species (27). Helpers of more seasonal species, with longer interbirth intervals, may be better able to compensate more fully for any short-term energetic costs incurred during helping. Third, when helpers invest heavily in one breeding attempt, they may reduce their investment in the subsequent attempt. This result is found independently of helper weight, although supplemental feeding caused helpers to increase levels of investment irrespective of how much they had invested in the previous attempt.

Finally, helpers may reduce their investment in cooperation before critical life-history phases. Previously, we have shown that, from their second year, meerkat males reduce their investment in babysitting and pupfeeding, and that reductions by all males are particularly prominent in the breeding events immediately before dispersal (25). Surprisingly, although females decrease their investment in pupfeeding from their second year, they continue to increase their contributions to more costly babysitting (25). This paradox may be explained by younger individuals being unwilling to compensate for any reductions in contributions to babysitting by older females because they are less efficient at foraging (25). Alternatively, it may be a result of dominant females evicting old subordinate females from their group in the weeks before giving birth (37), because on their return, evicted females conduct more babysitting than nonevicted females (generalized linear mixed model controlling for female age and helper number, χ² = 9.69, df = 1, P = 0.006). Therefore, old subordinates may be constrained from adopting an optimal strategy because of their need to compensate for low levels of investment by younger individuals or because of their desire to get back into their group (whilst avoiding the dominant female) after being evicted (37). These alternatives could explain why subordinate females incur a fecundity cost as a result of their level of contribution to babysitting and may provide a mechanism for female evictions in this species, because the presence of subordinate pups causes decreases in helper:pup ratios and, hence, reduced growth rates for pups of the dominant female (28, 29).

Our study has at least two important implications. First, substantial short-term costs need not be manifest in the long term, as helpers may adopt several behavioral tactics aimed at reducing the long-term implications of such costs. These tactics may be particularly successful among those species with long interbirth intervals in which individuals commonly disperse after one or two breeding events. Second, behavioral tactics used to reduce the long-term fitness costs of helping supports the idea that helping is a transitory behavior by which helpers improve their inclusive fitness indirectly (38) and their survival chances directly (7, 9) while waiting for an opportunity to breed. Consequently, among cooperative vertebrates, contributions to cooperation may be best understood as part of a life-history strategy (10), with helpers, like breeders, deciding how much to invest in each breeding event depending on the costs and benefits in both the short and long term. Further long-term studies of both the costs and benefits of cooperation will play a critical role in improving our understanding of individual investment rules and the maintenance of cooperative breeding systems. Finally, only by investigating the costs of cooperation in the long term, and the mechanisms of such costs, can selection for cooperation be quantified and the evolutionary dynamics of helping fully understood in societies of cooperative vertebrates.