Abstract
Anti-malaria vaccines and drugs could be greatly improved if we knew which phases of Plasmodium falciparum development in red blood cells are major inducers and which are major targets of natural immune responses. This information should focus attention on relevant immunogens and prove useful in developing immune-based therapies. Here we explore the hypothesis that innate immune responses mediate synchronization between the replication cycles of parasites in different red blood cells which is reflected in periodic fevers. Based on a recently developed, rather general mathematical model, we find that periodicity is highly sensitive to the position of both the inducing phase interval and the target phase interval in the parasite replication cycle. In addition, the degree of variability in the length of the replication cycle also strongly affects periodicity. To produce synchronization, the inducing and the target phase intervals must be developmentally distant from each other. We developed a computer program which prompts for information based on measurements of the numbers of erythrocytes in two replication cycle intervals chosen by the researcher, tests our model, and predicts the two phase intervals most critical to the synchronizing immune response. The program can be obtained from the authors.
Human malaria is caused by protozoan parasites of the genus Plasmodium. Plasmodium initially infects the liver, but then moves into the blood, where it multiplies and persists through an asexual replication cycle in red blood cells. After invasion of a red blood cell, Plasmodium falciparum undergoes continuous phenotypic change and several rounds of mitotic division. After ≈48 h, the infected cell bursts and releases free parasites, which either invade another red blood cell or are quickly (<0.5 h) removed from the bloodstream by a variety of mechanisms. The cycle is then repeated. P. falciparum produces the least persistent (and most pathogenic) malaria infections, but even these typically last for months unless treated or fatal. Many other intracellular parasites and viruses can be cleared within days or weeks by the adaptive cytotoxic immune response that involves expansion of CD8 T cells. These cells both kill infected cells and impede virus replication with soluble cytokines. Because red blood cells do not express the critical molecule MHC-1 on their surface, the blood-stage malaria parasites cannot induce the CD8 T cell response and, even though the response is induced by other infected tissues, such as liver, are probably not vulnerable to its cytotoxic action. Fortunately, Plasmodium-infected red blood cells seem to induce innate immune responses that slow the growth of early blood-stage infections; so far, the best known of these involve inflammatory cytokines (1, 2), but additional candidates are emerging as well (3, 4). It is not yet known which of the many types of innate and acquired responses are most critical for controlling Plasmodium blood-stage replication, and which Plasmodium proteins are the most critical immunogens.
The aim of this work is to expedite the identification of immunogens critical for controlling blood-stage malaria infection. The input information required by this approach is derived from the quasi-periodic behavior of the density of infected cells in the blood of an infected individual. Periodic spikes of fever have been the hallmark of malaria infection since the dawn of medical science (5) and, for the past century, the period of oscillation has been identified with the length of the replication cycle (6). Because high fever (a defense mechanism) is associated in time with release of free parasites, the existence of periodicity indicates that parasite replication in many different red blood cells is synchronized: parasites enter and are released from these cells at approximately the same times.
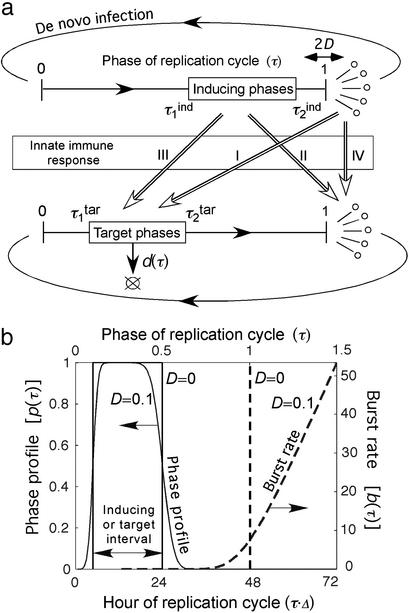
The most consistent explanation of synchrony offered to date (7) postulates that the critical components of the innate response are stimulated by and act upon two distinct phase intervals of the P. falciparum replication cycle: an inducing interval and a target interval (Fig. 1a). If this is the case, it stands to reason that synchronization allows most of the parasite population to evade most of the immune response. The idea is based on the observation that the level of an inflammatory cytokine tracks the level of its immunogen with only a small delay, much less than the replication cycle length, which is ≈48 h. If parasites are synchronized at the time when they induce the response, none of them are vulnerable to it, and when they arrive at the phase interval in which they are vulnerable, the response has already faded. Once the innate immune response is active, a parasite population, initially randomized in phase, will automatically progress to and remain in synchrony. Note that an acquired (antibody) response alone does not predict such an effect, because, unlike an innate response, it is associated with time delays larger than the period of oscillations: in a naïve host, antibody response takes days to weeks to develop. Synchronization in P. falciparum is only partial: parasitemia often shows chaotic fluctuations on top of periodic behavior. According to the above scenario, one reason for partial synchrony is that the inducing and the target intervals have a finite length in time, and these lengths are not expected to be commensurate with the replication cycle length (i.e., these time periods are not integer multiples of a smaller length). Another factor is that the precise length of the replication cycle (on average, 48 h) may vary between individual infected cells.
Figure 1.
Model of immune response and age-structured population kinetics in a blood-stage malaria infection. (a) A schematic of the model. Arrows with open heads (I–IV) show the four possible cases of interaction between phase intervals of intracellular or free parasites, which can either induce or be a target of an innate response. (b) Dashed line represents the cell burst rate vs. the phase (Mathematical Formalism, Eq. 5). The solid line represents the phase profile (Eq. 8) determining, for the target interval, the relative death rate for different phases (Eq. 9), and for the inducing interval, the relative contribution of different phases into the innate response (Eq. 7). The values of D and the interval boundaries chosen for this example are shown on the figure.
In the present work, rather than postulate or guess particular inducing and target-phase intervals and predict the existence of oscillations, as has been done previously (8, 9), we reverse the problem and show how to determine the corresponding phase intervals from observed oscillations. We emphasize that the entire approach is rather general, because it does not require knowledge of the details of Plasmodium replication in red blood cells or of specific mechanisms of innate response.
Our method may have clinical applications. In principle, by observing which proteins are expressed only during the predicted intervals of the parasite cycle, it is possible to identify critical immunogens and target proteins as well as the crucial parts of the innate response. For instance, malaria patients might be treated with viral vectors expressing both the critical immunogens to boost the relevant innate response and the peptides to bind the critical target proteins. Other drugs could be used to suppress the unwanted parts of innate response irrelevant to parasite control and harmful to patients.
Model of Malaria Population
All possibilities for the innate immune response can be classified in four major groups (Fig. 1a I–IV). Innate response can be induced by either free parasites or intracellular parasites in a specific phase interval [e.g., all parasites between fractions 0.3 (14.4 h) and 0.5 (24 h) of the intracellular cycle length, Δ = 48 h] and can act, also, on either free or intracellular parasites in a phase interval. The level of response is assumed to be proportional to the number of cells within the inducing-phase interval. When the host response acts on free parasites, it is described by the decrease of the effective number of free parasites per bursting cell (replication ratio, r); when the host response acts on intracellular parasites, it is assumed to increase the death rate of infected cells in the phase interval [d (τ, t), Eq. 9 in Mathematical Formalism]. Regarding the detailed kinetics of the host response, we consider two cases in parallel. The response level increases either gradually as the number of response-inducing cells grows (“gradual response”), or abruptly, when that number crosses a threshold (“threshold response”). See Eqs. 6 and 9 in Mathematical Formalism.
Correspondence between a given biological phase of an infected cell when parasites express a particular set of antigenic proteins and the time elapsed since invasion of a cell is not precise. We assume that the time elapsed between invasion and any subsequent developmental phase is normally distributed, with a relative standard deviation (SD) given by the product of a fixed parameter, D, and the square root of the average elapsed time in units of Δ. The time dependence assumes that the variation of the elapsed time for a given biological phase is accumulated linearly over the elapsed time. In particular, the bursting time has a relative SD equal to D. Fig. 1b shows the corresponding cell bursting rate and a “phase profile” describing the participation of different phases in host response for a particular inducing phase interval. To complete the model, we made several additional assumptions (see Assumptions and Simplifications).
Population kinetics in the model can be calculated from Eqs. 1–10 (see Mathematical Formalism), which postulate that infected cells, in each phase of the Plasmodium cycle, either (i) burst, at a rate depending on their proximity to the average bursting time (Δ) and on D; (ii) die, at a rate depending on the number of response-inducing cells and on the type of response, i.e., gradual or threshold; or (iii) progress to the next phase. Model parameters are defined in Table 1. Essentially, the model has five continuous parameters (D and the boundaries of the inducing and the target phase interval, τ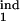 , τ
, τ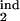 , τ
, τ , τ
, τ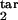 ) and one discrete parameter (a gradual or a threshold immune response) which are used as free-fitting parameters. The particular choice of other parameters within a broad range of values is not important.
) and one discrete parameter (a gradual or a threshold immune response) which are used as free-fitting parameters. The particular choice of other parameters within a broad range of values is not important.
Table 1.
Parameters of the model of malaria population (see Fig. 1)
| Symbol | Meaning |
|---|---|
| Δ | Replication cycle length |
| t0 | Time interval during which free parasites induce the response |
| Nc | Characteristic number of infected cells inducing the response |
| r0 | Maximum value of replication ratio |
| rlow | Replication ratio when the number of cells inducing the threshold response exceeds Nc |
τ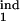 , τ , τ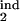
|
The lower and upper boundaries of the inducing phase interval in units of Δ |
τ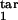 , τ , τ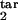
|
The lower and upper boundaries of the target phase interval in units of Δ |
| D | Relative standard deviation of the burst time |
| d | Death rate of infected cells |
| b | Burst rate of infected cells |
| tol | The relative tolerance |
Δ is set in the present work at 48 h but can be adjusted to fit other replication cycle lengths; t0, Nc determine the scale in parasite density and are set at 1. We have taken the values r0 = 10, r low = 0.01 from in vitro studies (7), but have found that changing r0 above 3, or r low below 0.1, does not significantly alter the results. The remaining five parameters are free-fitting parameters.
Different Types of Malaria Kinetics
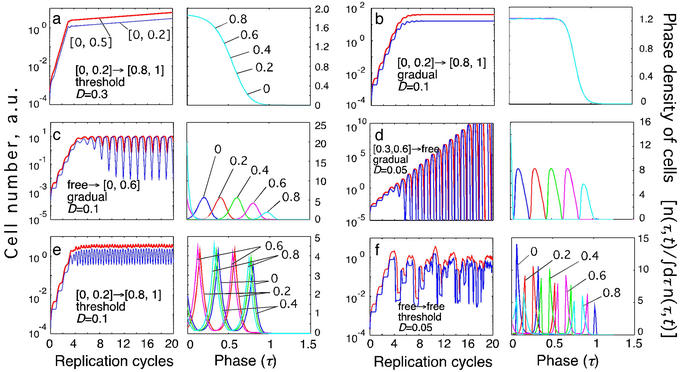
We performed numeric simulations of a primary blood-phase infection by using the model described above. Depending on the values of the five model parameters, several different behaviors emerged (Fig. 2). We can classify different types of behavior based on the existence of steady infection, the degree of periodicity, and the oscillation period. In some cases, immune response cannot control infection, and a steady infection is never established (Fig. 2 a and d). In some cases, synchrony and oscillations are absent (Fig. 2 a and b). The cases in which different infected cells are partially synchronized can be detected in oscillations of the number of cells in an interval of the replication cycle (Fig. 2 c–f Left) and in the accumulation of cells near a phase of the cycle that shifts with time (Figs. 2 c–f Right). Note that the number of cells in a narrow interval (blue line in Fig. 2 Left) oscillates at a larger amplitude than the number of cells in a broader interval (red line in Fig. 2 Left). Throughout this paper, we use intervals [0, 0.2] and [0, 0.5] as examples of the narrow interval and the broad interval, respectively. Such choices are particularly appropriate for P. falciparum infections because of its sequestration in capillaries during later stages of the replication cycle. Depending on the parameter set, the predicted period of oscillations is either close to the replication cycle length, Δ (Fig. 2 c and d) or to Δ/2 (Fig. 2e). This dual prediction of the model may explain why some malaria patients experience fever peaks every other day (tertian) and some have them daily (quotidian).
Figure 2.
Examples of different types of kinetics of an infected cell population in a primary infection. Initially, cells are assumed to be distributed uniformly over the parasite replication cycle phase. (Left) The dependence of the infected cell numbers in the interval [0, 0.5] (thick red lines) and in the interval [0, 0.2] (thin blue lines; Mathematical Formalism, Eq. 11) on time (in units of Δ). (Right) The phase density of infected cells vs. the phase of replication cycle, τ, at five equally spaced times within the 10th cycle of infection (shown at curves in units of Δ). The phase density at each time is normalized, so that its total integral is equal to 1. (Left) Model parameters for different cases: inducing interval [τ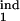 , τ
, τ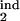 ] → target interval [τ
] → target interval [τ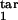 , τ
, τ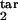 ], the type of immune response (threshold or gradual), and D (Table 1 and Fig. 1a). (a) Unlimited expansion of infected cells. (b) Steady state in the absence of oscillations. (c) Steady state with periodic oscillations caused by parasite synchronization (period close to Δ, tertian). (d) Unlimited expansion with oscillations. (e) Oscillations with half-period (close to Δ/2, quotidian). (f) Chaotic oscillations.
], the type of immune response (threshold or gradual), and D (Table 1 and Fig. 1a). (a) Unlimited expansion of infected cells. (b) Steady state in the absence of oscillations. (c) Steady state with periodic oscillations caused by parasite synchronization (period close to Δ, tertian). (d) Unlimited expansion with oscillations. (e) Oscillations with half-period (close to Δ/2, quotidian). (f) Chaotic oscillations.
Periodicity Region
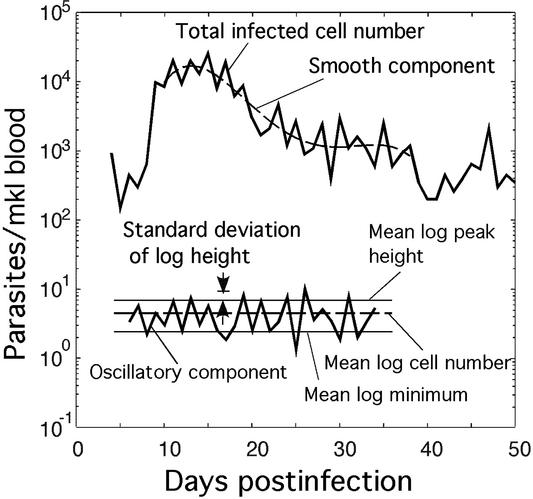
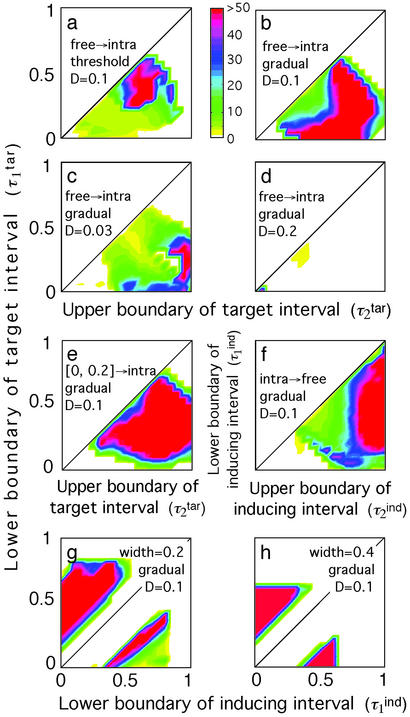
Most patients show either steady periodic oscillations or steady oscillations with a strong chaotic component, i.e., the types of behavior shown in Fig. 2 c, e, and f, respectively. To quantitate the degree of chaos, we introduce a “periodicity parameter” for the number of cells in the broad interval, [0, 0.5], which is defined as the ratio of the difference between mean decimal logs of the peak heights and minima to the SD of log peak heights (Fig. 3). To eliminate cases in which oscillations have zero or a very small magnitude, we set the periodicity parameter to 0 (white color in Fig. 4) when the ratio of the log-averaged peak heights to minima is smaller than a cut-off value of 2. The examples of “topographic map” diagrams in Fig. 4 show the periodicity parameter as a function of two of the four phase-interval boundaries. High values of the parameter (green, blue, and red colors in Fig. 4) indicate steady periodic behavior (examples in Fig. 2 c and e) with a small chaotic component. Low values (yellow color) indicate either the lack of steady state (Fig. 2d) or a large chaotic component (Fig. 2f). At smaller D, the area of steady periodicity shifts toward older parasites and shrinks for parasites of intermediate age (yellow region in the middle of Fig. 4c).
Figure 3.
Periodic oscillations of parasitemia in a P. falciparum infection (25). (Upper) Fitting of the monotonic component of the log parasite number (solid line) with a fourth-order polynomial (dashed line). Orders five to seven give very similar results. (Lower) The oscillatory component of the log parasite number (solid line). Experimental quantities that can be used for fitting data to the model (Fig. 5) are shown.
Figure 4.
Topographic maps for the “periodicity parameter” characterizing the degree of periodicity caused by synchronization of parasites. Colors show the value of the periodicity parameter (a, color bar) defined as in the text. Plot axes are two of the four boundaries of the target- and inducing-phase intervals shown as fractions of Δ = 48 h (τ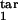 , τ
, τ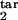 , τ
, τ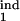 , and τ
, and τ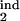 ). The value of D, the host response type (gradual or threshold), and the other two interval boundaries are fixed and shown on the panels. (a–d) Free parasites induce a response against intracellular parasites. (e) Intracellular parasites induce a response against intracellular parasites. (f) Intracellular parasites induce a response against free parasites. (g and h) Intracellular parasites induce a response against intracellular parasites in another interval of the same width.
). The value of D, the host response type (gradual or threshold), and the other two interval boundaries are fixed and shown on the panels. (a–d) Free parasites induce a response against intracellular parasites. (e) Intracellular parasites induce a response against intracellular parasites. (f) Intracellular parasites induce a response against free parasites. (g and h) Intracellular parasites induce a response against intracellular parasites in another interval of the same width.
Altogether, we obtained almost 500 such topographic plots for different values of D (0.05, 0.07, 0.1, 0.15), a gradual or threshold response, and under different restrictions on two of the four interval boundaries τ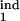 , τ
, τ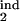 , τ
, τ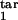 , τ
, τ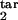 , each changing from 0 to 1 in steps of 0.1. In general, the existence of periodicity is sensitive to the location of the inducing and target-phase intervals within the cycle, the type of response (gradual or threshold; compare Fig. 4 a and b), and the value of D (e.g., Fig. 4 b–d); it vanishes altogether between D = 0.2 and D = 0.3, for all of the values of the other parameters (Fig. 4d). When the inducing and target-phase intervals are of similar width, the result depends primarily on the relative position of the two intervals and less on their absolute position in the replication cycle (Fig. 4 g and h).
, each changing from 0 to 1 in steps of 0.1. In general, the existence of periodicity is sensitive to the location of the inducing and target-phase intervals within the cycle, the type of response (gradual or threshold; compare Fig. 4 a and b), and the value of D (e.g., Fig. 4 b–d); it vanishes altogether between D = 0.2 and D = 0.3, for all of the values of the other parameters (Fig. 4d). When the inducing and target-phase intervals are of similar width, the result depends primarily on the relative position of the two intervals and less on their absolute position in the replication cycle (Fig. 4 g and h).
Our results differ from those reported for another model, which can be viewed approximately as a particular case of our model with a threshold type of host response (8). It postulates the existence of five discrete stages of the intracellular parasite replication cycle and that most of the host response is stimulated by the earliest stage, [0, 0.2] “young rings” phenotype, and directed against the oldest stage, [0.8, 1] “segmenters.” The length of each stage is assumed to obey a Poisson distribution with approximately the same mean value, implying D = 1/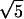 ≈ 0.4. The authors predict synchronization and strong oscillations, with a period close to Δ = 48 h, figure 5 in ref. 8. Based on our results, synchronization cannot occur at such high values of D (Figs. 4d and 2a). At much smaller D, oscillations can occur, but their period, for this choice of participating intervals, is close to Δ/2 = 24 h (Fig. 2e). Independently of these findings, we carefully repeated the numeric calculations described in the paper (8) and did not obtain the oscillations shown in its figure 5. We do not understand the discrepancy.
≈ 0.4. The authors predict synchronization and strong oscillations, with a period close to Δ = 48 h, figure 5 in ref. 8. Based on our results, synchronization cannot occur at such high values of D (Figs. 4d and 2a). At much smaller D, oscillations can occur, but their period, for this choice of participating intervals, is close to Δ/2 = 24 h (Fig. 2e). Independently of these findings, we carefully repeated the numeric calculations described in the paper (8) and did not obtain the oscillations shown in its figure 5. We do not understand the discrepancy.
How to Derive Participating Phase Intervals from Parasitological Data
In real life, the model parameters are unknown, although infected cells can be quantitated at multiple time points. Sensitivity of results to the model parameters demonstrated above allows accurate determination of the inducing- and the target-phase intervals from the results of parasitological assays. To infer five continuous parameters (τ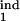 , τ
, τ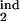 , τ
, τ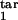 , τ
, τ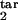 , D), we need five or, better, six experimentally determined quantities. To obtain them, a researcher would have to measure three quantities defined in the legend to Fig. 5 and illustrated in Fig. 3 for the numbers of infected cells in two different (in width or location) intervals of the replication cycle which can be chosen by the researcher (in our example, [0, 0.2] and [0, 0.5]). The sampling frequency should not be less than four times a day, over the time period including 10–15 oscillation peaks.
, D), we need five or, better, six experimentally determined quantities. To obtain them, a researcher would have to measure three quantities defined in the legend to Fig. 5 and illustrated in Fig. 3 for the numbers of infected cells in two different (in width or location) intervals of the replication cycle which can be chosen by the researcher (in our example, [0, 0.2] and [0, 0.5]). The sampling frequency should not be less than four times a day, over the time period including 10–15 oscillation peaks.
Figure 5.
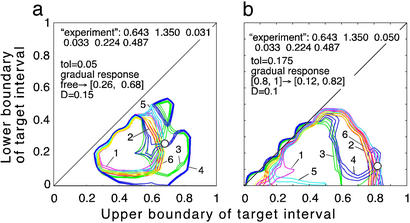
Prediction of the inducing and the target intervals from six mock experimental quantities. (a and b) Fitting model parameters to two sets of mock experimental values are shown at the top. Three contour lines (tolerance strips) of each color correspond to a mock experimental value and to the same value decreased and increased by the relative tolerance, tol. White circles show the areas where the tolerance strips for all of the six quantities overlap. Relative tolerance, tol, and best-fit model parameters (the innate response type, inducing interval [τ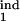 , τ
, τ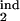 ], target interval [τ
], target interval [τ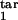 , τ
, τ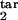 ], and D) are shown. Axes show the target interval boundaries [τ
], and D) are shown. Axes show the target interval boundaries [τ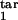 , τ
, τ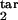 ]. Experimental quantities 1 (magenta), 3 (green), and 5 (cyan) are defined based on the time dependence of the infected cell number in the cycle interval [0, 0.5] as follows: 1, mean [log10 (local maximum of cell number)] − mean [log10 (local minimum)]; 3, std [log10 (local maximum)]; 5, mean [log10 (local maximum)] − mean [log10 (cell number at any time)]. Quantities 2 (red), 4 (blue), and 6 (yellow) are defined in the same way, except the interval [0, 0.2] is used.
]. Experimental quantities 1 (magenta), 3 (green), and 5 (cyan) are defined based on the time dependence of the infected cell number in the cycle interval [0, 0.5] as follows: 1, mean [log10 (local maximum of cell number)] − mean [log10 (local minimum)]; 3, std [log10 (local maximum)]; 5, mean [log10 (local maximum)] − mean [log10 (cell number at any time)]. Quantities 2 (red), 4 (blue), and 6 (yellow) are defined in the same way, except the interval [0, 0.2] is used.
To illustrate how our method works, we consider a mock experiment in which we invent the numbers for the six quantities (Fig. 5a). First, we choose a value of the relative tolerance (tol = 0.05), which shows how accurately we wish to match six mock experimental values to their theoretical predictions, the inducing interval (free parasites), the value of D (D = 0.15), and the type of response (gradual). For each mock experimental value, we draw the tolerance strip, centered at the contour of constant height corresponding to this value and bound between the two contours corresponding to the same experimental value decreased and increased relatively by the tolerance (six colors in Fig. 5a). To find whether we have a positive match of theory to experiment, we check whether there is an area where all of the strips overlap. The center of the overlap area yields the predicted target interval boundaries. In our example in Fig. 5a, the strips overlap at [τ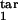 , τ
, τ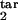 ] = [0.26, 0.68] (circle in Fig. 5a). If we change the inducing interval to, say, [0.1, 0.2], the overlap area disappears (case not shown). We repeat this procedure for different sets of parameters (τ
] = [0.26, 0.68] (circle in Fig. 5a). If we change the inducing interval to, say, [0.1, 0.2], the overlap area disappears (case not shown). We repeat this procedure for different sets of parameters (τ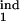 , τ
, τ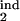 , D), with a step for each value, and for the other (threshold) type of the response, to find other positive matches. In this mock experiment, we obtained the single matching set of parameters shown in Fig. 5a. We developed a program package which carries out the described procedure automatically. If the total number of positive matches is more than one or is zero (no matches), the program decreases or increases tol, respectively, and repeats the search, until it obtains one positive match. This case represents the most probable set of model parameters.
, D), with a step for each value, and for the other (threshold) type of the response, to find other positive matches. In this mock experiment, we obtained the single matching set of parameters shown in Fig. 5a. We developed a program package which carries out the described procedure automatically. If the total number of positive matches is more than one or is zero (no matches), the program decreases or increases tol, respectively, and repeats the search, until it obtains one positive match. This case represents the most probable set of model parameters.
The resulting value of tol provides a direct test for the applicability of the model. The small value of tol = 0.05 in the above example (Fig. 5a) shows a good fit of theory to the mock experiment. In fact, we have artificially selected the set of mock experimental values shown in Fig. 5a to illustrate such a case. Most other sets of mock experimental values require much higher values of tol to obtain a single positive match. For instance, changing the value of the third mock experimental quantity from 0.031 to 0.05 requires tol = 0.175, to have a single positive match (Fig. 5b). If this were a real experiment, such a high value of tol could mean that the present model applies poorly to the system under study. (Another possibility would be that the experiment requires more frequent sampling.) Another test of the model is to compare the predicted period of oscillations with the actual period, which will be, in most cases, close to either 24 or 48 h. To find the predicted period, and for visual assessment, the program draws, for the matching set of parameters, the time-dependencies analogous to those shown in Fig. 2.
Assumptions and Simplifications
We based our model on several assumptions, some of which we have already stated. Here, we briefly discuss those that remain. (i) We assumed that the effect of any intrinsic cycle in the host, such as a daily (diurnal) cycle, is small compared with the mechanism that mediates synchronization between infected cells. Supporting evidence is that parasitemia classically shows peaks every other day (tertian) and that, in some individuals, the period of oscillations differs somewhat from 48 h. Our analysis predicts periods of oscillation that are not necessarily equal to the replication cycle length, which may explain the existence of periodicities other than tertian (Fig. 3). (ii) We assumed that a single-phase interval induces and a single interval receives the host response. In fact, several such pairs of intervals might act in parallel. The many possible differences in parameter values between individuals make it unlikely that several such processes would be tuned so as to be approximately similar in all individuals; one is likely to dominate over the others. (iii) We assumed that the onset and the end of immunogenicity occur rather abruptly in a developmental phase. This assumption is difficult to assess in the existing literature; direct experimental tests of the sort described above are needed. (iv) We neglected the depletion of susceptible red blood cells because, in most cases, it is observed to be relatively small. (v) We assumed that each cell is infected only once. Superinfection of already-infected cells, although it exists, is expected to be a small correction because the fraction of red blood cells infected is itself small (<20%) in most cases (10, 11). (vi) We considered only the asexual blood phases of the parasite. A (small) fraction of the parasites released by bursting cells become gametocytes (sexual, transmissible forms) and are removed from the asexual replication cycle. This effect might be taken into account by modifying the replication ratio, r0; however, particular values of r0 are shown to be unimportant in this context, provided that they are large in the absence of an immune response (Table 1, legend). (vii) Degrees of synchrony seem to reflect hosts' previous exposure to malaria (12, 13), which implies a role for antibody response not considered explicitly in this work. Antibody-dependent and other acquired responses may play a role in increasing synchronization as an initial infection progresses, or in subsequent infections (14, 15). Because antibody response is relatively slow, it can be taken into account within our model by simply modifying fixed parameters, which are in any case determined by fitting.
Multiple “broods” of parasite may coexist within an individual infection, such that different periodic sequences alternate or superimpose in peaks of parasitemia. One can anticipate two cases, as follows: (i) if the broods are immunologically similar, the above single-brood procedure can be applied to the numbers of infected cells added over broods; (ii) if different broods have rather different target- or inducing-phase intervals, a more complex multi-brood model would be required. Because different broods interact through innate responses, the set of critical immunogens might differ from a simple combination of single-brood immunogens. Which one is the case can be determined from the tolerance parameter value, as described above. At this stage, to identify the critical immunogens of separate broods, we recommend that data from single-brood infections be selected. Once a good match with theory is reported, the model could be generalized to the multi-brood case. Other hidden factors cause separate peaks to disappear or shift, presenting irregular features that defy ready categorization (10, 16, 17). This variability is the background from which the periodic cycles analyzed here may arise (18, 19).
Our analysis reinforces the conclusion that sampling intervals of less than 1 day provide critical information about within-host parasite dynamics (20). The sampling frequency required for our method is at least four times a day. Another condition is that infected cells have to be sampled in, at least, two distinct intervals of the malaria replication cycle. We are not aware of any such data in the literature (compare daily sampling in the example shown in Fig. 3). The ability to predict the phases of Plasmodium development most critical to host response should help to improve clinical, pharmacological, and vaccine-based interventions in malaria (21–24).
Mathematical Formalism
We use the formalism of an age-structured population. The density of infected cells n(τ, t) in time phase τ of parasite replication cycle at current time t (Fig. 2 Right) satisfies the kinetic equation
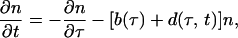 |
1 |
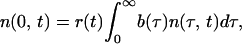 |
2 |
where t and τ are in units of replication cycle length Δ, parameters b(τ) and d(τ, t) are the burst and the death rate of infected cells in phase τ, respectively, and r(t) is the replication ratio, i.e., the number of new cells infected by free parasites released from a bursting cell. The latter three functions are defined below. The death rate d(τ, t) depends on t explicitly, because it depends on the number of cells in the inducing-phase interval. Expression for b(t) can be obtained from the assumption in the main text that the time at which a cell bursts obeys a normal distribution centered at τ = 1, with the SD denoted D. At d ≡ 0, this assumption can be written as
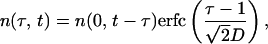 |
3 |
where erfc(x) is the complementary error function, defined as
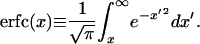 |
4 |
Eq. 3 satisfies Eq. 1, if d ≡ 0 and b(τ) is given by
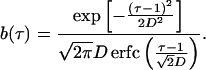 |
5 |
The replication ratio, r(t), in Eq. 2 depends on whether the inducing and the target parasites are free or intracellular (Fig. 1a), and whether the response is threshold or gradual, as given by
 |
6 |
where arrows point from the inducing parasite type to the target parasite type, Nind(t) is the number of inducing infected cells, given by
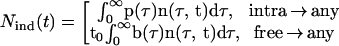 |
7 |
and Nc and t0 are arbitrarily set to 1 (Table 1). Other choices of these two parameters affect only the absolute level of infected cell number, which, everywhere in the present work, is given in arbitrary units. The function p(τ) in the upper portion of Eq. 7 determines the contribution of each phase to the response. Its form can be obtained, assuming that the onset and the end of immunogenicity are abrupt in biological replication phase, and that different biological phases are statistically uniform and, hence, contribute equally to the variation in the value of τ corresponding to a biological phase. Under these assumptions, we have
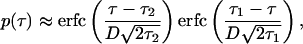 |
8 |
where τ1 = τ , τ2 = τ
, τ2 = τ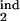 are the boundaries of the inducing-phase interval (Table 1) and D
are the boundaries of the inducing-phase interval (Table 1) and D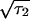 ≪ τ2, τ1.
≪ τ2, τ1.
Finally, the death rate in Eq. 1 is given by
 |
9 |
where Nind(t) is given by Eq. 7 and p(τ) is given by Eq. 8, in which τ1 = τ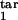 , τ2 = τ
, τ2 = τ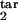 . The constant d0 in Eq. 9 is given by
. The constant d0 in Eq. 9 is given by
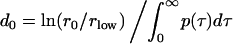 |
10 |
to ensure the same net effect of host response on the number of released free parasites, as in the case when it acts directly on free parasites (compare Eq. 6).
For numerical simulation, the results of which are shown in Figs. 2, 4, and 5, we use discrete versions of the equations above by dividing the average replication time Δ (which includes the brief intercellular period) into K phase intervals. Results change only by a few percent between K = 80 and K = 160 for the gradual response and K = 160 and K = 320 for the threshold response. We use K = 80 as the base value. In particular, the discrete version of Eq. 1 has a form
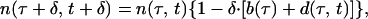 |
11 |
where δ = Δ/K. We have found that the results are not sensitive to particular values of rlow and r0, provided the first is much smaller and the second is much larger than 1. This leaves us with five continuous parameters: D, τ , τ
, τ , τ
, τ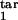 , and τ
, and τ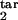 . The separate case of free parasites as an inducing or target interval is denoted as [τ1, τ2] = [1, 1]. To find out how the program works, a user has to install MATLAB software, obtain the program package from the authors, and enter “StartHere” in the command line.
. The separate case of free parasites as an inducing or target interval is denoted as [τ1, τ2] = [1, 1]. To find out how the program works, a user has to install MATLAB software, obtain the program package from the authors, and enter “StartHere” in the command line.
The procedure described in the main text and Fig. 5 proposes separate measurements of the cell number, Mexp(t), for two different intervals [τ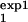 , τ
, τ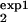 ] and [τ
] and [τ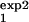 , τ
, τ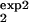 ]. It is important that the two intervals differ as much as possible either in the width or in the location. The value predicted for Mexp(t) in one interval, [τ
]. It is important that the two intervals differ as much as possible either in the width or in the location. The value predicted for Mexp(t) in one interval, [τ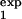 , τ
, τ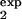 ], is given by
], is given by
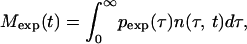 |
12 |
where pexp(t) is determined by Eq. 8, in which τ1 = τ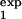 , τ2 = τ
, τ2 = τ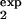 . Eq. 12 reflects the fact that infected cells in vivo are sorted by biological markers that may be expressed by infected cells slightly earlier or later in time of an individual infection.
. Eq. 12 reflects the fact that infected cells in vivo are sorted by biological markers that may be expressed by infected cells slightly earlier or later in time of an individual infection.
Acknowledgments
We thank Edward Goldberg and Barbara Sorkin for help with presentation, and William Bossert and Steven Rich for critical comments. The work was supported by National Institutes of Health Grant K25AI01811 (to I.M.R.) and a National Institutes of Health National Research Service Award (to F.E.M.).
References
- 1.Kwiatkowski D, Cannon J G, Maigue K R, Cerami A, Dinarello C A. Clin Exp Immunol. 1989;77:361–366. [PMC free article] [PubMed] [Google Scholar]
- 2.Richards A L. Int J Parasitol. 1997;27:1251–1263. doi: 10.1016/s0020-7519(97)00122-7. [DOI] [PubMed] [Google Scholar]
- 3.Troye-Blomberg M, Perlmann P, Nilsson L M, Perlmann H. Parassitologia (Rome) 1999;41:131–138. [PubMed] [Google Scholar]
- 4.Good M F, Doolan D. Curr Opin Immunol. 1999;11:412–419. doi: 10.1016/S0952-7915(99)80069-7. [DOI] [PubMed] [Google Scholar]
- 5.Hippocrates . Works. Cambridge, MA: Harvard Univ. Press; 1959. [Google Scholar]
- 6.Golgi C. In: Tropical Medicine and Parasitology. Kean B H, Mott K E, Russell A J, editors. Vol. 1. Ithaca, NY: Cornell Univ. Press; 1978. pp. 27–35. [Google Scholar]
- 7.Kwiatkowski D, Nowak M. Proc Natl Acad Sci USA. 1991;88:5111–5113. doi: 10.1073/pnas.88.12.5111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Gravenor M B, Kwiatkowski D. Parasitology. 1998;117:97–105. doi: 10.1017/s0031182098002893. [DOI] [PubMed] [Google Scholar]
- 9.Hoshen M B, Heinrich R, Stein W D, Ginsburg H. Parasitology. 2000;121:227–235. doi: 10.1017/s0031182099006368. [DOI] [PubMed] [Google Scholar]
- 10.Wernsdorfer W H, McGregor I. Malaria. Edinburgh: Churchill Livingstone; 1988. [Google Scholar]
- 11.Jakeman G N, Saul A, Hogarth W L, Collins W E. Parasitology. 1999;199:127–133. doi: 10.1017/s0031182099004564. [DOI] [PubMed] [Google Scholar]
- 12.Boyd M F. Malariology. Philadelphia: Saunders; 1949. [Google Scholar]
- 13.Shute P G. J Trop Med Hyg. 1958;61:57–61. [PubMed] [Google Scholar]
- 14.Silamut K, White N J. Trans R Soc Trop Med Hyg. 1993;87:436–443. doi: 10.1016/0035-9203(93)90028-o. [DOI] [PubMed] [Google Scholar]
- 15.Bouharoun-Tayoun H, Oeuvray C, Lunel F, Druilhe P. J Exp Med. 1995;182:409–418. doi: 10.1084/jem.182.2.409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Coatney G R, Collins W E, Warren M, Contacos P G. The Primate Malarias. Bethesda, MD: U.S. Department of Health, Education, and Welfare; 1971. [Google Scholar]
- 17.Farnert A, Snounou G, Rooth I, Bjorkman A. Am J Trop Med Hyg. 1997;56:538–547. doi: 10.4269/ajtmh.1997.56.538. [DOI] [PubMed] [Google Scholar]
- 18.McKenzie F E, Jeffery G M, Collins W E. J Parasitol. 2001;87:626–637. doi: 10.1645/0022-3395(2001)087[0626:PMBSD]2.0.CO;2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.McKenzie F E, Jeffery G M, Collins W E. J Parasitol. 2002;88:521–535. doi: 10.1645/0022-3395(2002)088[0521:PVBSD]2.0.CO;2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Delley V, Bouvier P, Breslow N, Doumbo O, Sagara I. Trop Med Int Health. 2000;5:404–412. doi: 10.1046/j.1365-3156.2000.00566.x. [DOI] [PubMed] [Google Scholar]
- 21.Chotivanich K, Udomsangpetch R, Simpson J A, Newton P, Pukrittayakamee S. J Infect Dis. 2000;181:1206–1209. doi: 10.1086/315353. [DOI] [PubMed] [Google Scholar]
- 22.White N J, Chapman D, Watt G. Trans R Soc Trop Med Hyg. 1992;86:590–597. doi: 10.1016/0035-9203(92)90141-x. [DOI] [PubMed] [Google Scholar]
- 23.Landau I, Caillard V, Beaute-Lafitte A, Chabaud A. Parassitologia (Rome) 1993;35:s55–s57. [PubMed] [Google Scholar]
- 24.Austin D J, White N J, Anderson R M. J Theor Biol. 1998;194:313–339. doi: 10.1006/jtbi.1997.0438. [DOI] [PubMed] [Google Scholar]
- 25.Collins W E, Jeffery G M. Am J Trop Med Hyg. 1999;61:s4–s48. doi: 10.4269/tropmed.1999.61-036. [DOI] [PubMed] [Google Scholar]