The evolution of altruistic punishment

Abstract

Both laboratory and field data suggest that people punish noncooperators even in one-shot interactions. Although such “altruistic punishment” may explain the high levels of cooperation in human societies, it creates an evolutionary puzzle: existing models suggest that altruistic cooperation among nonrelatives is evolutionarily stable only in small groups. Thus, applying such models to the evolution of altruistic punishment leads to the prediction that people will not incur costs to punish others to provide benefits to large groups of nonrelatives. However, here we show that an important asymmetry between altruistic cooperation and altruistic punishment allows altruistic punishment to evolve in populations engaged in one-time, anonymous interactions. This process allows both altruistic punishment and altruistic cooperation to be maintained even when groups are large and other parameter values approximate conditions that characterize cultural evolution in the small-scale societies in which humans lived for most of our prehistory.

Unlike any other species, humans cooperate with non-kin in large groups. This behavior is puzzling from an evolutionary perspective because cooperating individuals incur individual costs to confer benefits on unrelated group members. None of the mechanisms commonly used to explain such behavior allows the evolution of altruistic cooperation in large groups. Repeated interactions may support cooperation in dyadic relations (1–3), but this mechanism is unsustainable if the number of individuals interacting strategically is larger than a handful (4). Interdemic group selection can lead to the evolution of altruism only when groups are small and migration is infrequent (5–8). A third recently proposed mechanism (9) requires that asocial, solitary types out-compete individuals living in uncooperative social groups, an implausible assumption for humans.

Altruistic punishment provides one solution to this puzzle. In laboratory experiments, people punish noncooperators at a cost to themselves even in one-shot interactions (10, 11) and ethnographic data suggest that such altruistic punishment helps to sustain cooperation in human societies (12). It might seem that invoking altruistic punishment simply creates a new evolutionary puzzle: why do people incur costs to punish others and provide benefits to nonrelatives? However, here we show that group selection can lead to the evolution of altruistic punishment in larger groups because the problem of deterring free riders in the case of altruistic cooperation is fundamentally different from the problem of deterring free riders in the case of altruistic punishment. This asymmetry arises because the payoff disadvantage of altruistic cooperators relative to defectors is independent of the frequency of defectors in the population, whereas the cost disadvantage for those engaged in altruistic punishment declines as defectors become rare because acts of punishment become very infrequent (13). Thus, when altruistic punishers are common, individual level selection operating against them is weak.

To see why, consider a model in which a large population is divided into groups of size n. There are two behavioral types, contributors and defectors. Contributors incur a cost c to produce a total benefit b that is shared equally among group members. Defectors incur no costs and produce no benefits. If the fraction of contributors in the group is x, the expected payoff for contributors is bx − c and the expected payoff for defectors is bx, so the payoff disadvantage of the contributors is a constant c independent of the distribution of types in the population. Now add a third type, “punishers” who cooperate and then punish each defector in their group, reducing each defector's payoff by p/n at a cost k/n to the punisher. If the frequency of punishers is y, the expected payoffs become b(x + y) − c to contributors, b(x + y) − py to defectors, and b(x + y) − c − k(1 − x − y) to punishers. Contributors have higher fitness than defectors if punishers are sufficiently common that the cost of being punished exceeds the cost of cooperating (py > c). Punishers suffer a fitness disadvantage of k(1 − x − y) compared with nonpunishing contributors. Thus, punishment is altruistic and mere contributors are “second-order free riders.” Note, however, that the payoff disadvantage of punishers relative to contributors approaches zero as defectors become rare because there is no need for punishment. In a more realistic model (like the one below) the costs of monitoring or punishing occasional mistaken defections would mean that punishers have slightly lower fitness than contributors, and that defection is the only one of these three strategies that is an evolutionarily stable strategy in a single isolated population. However, the fact that punishers experience only a small disadvantage when defectors are rare means that weak within-group evolutionary forces, such as mutation (13) or a conformist tendency (14), can stabilize punishment and allow cooperation to persist. But neither produces a systematic tendency to evolve toward a cooperative outcome. Here we explore the possibility that selection among groups leads to the evolution of altruistic punishment when it could not maintain altruistic cooperation.

Suppose that more cooperative groups are less prone to extinction. Humans always live in social groups in which cooperative activities play a crucial role. In small-scale societies, such groups frequently become extinct (15). It is plausible that more cooperative groups are less subject to extinction because they are more effective in warfare, more successful in coinsuring, more adept at managing commons resources, or for similar reasons. This means that, all other things being equal, group selection will tend to increase the frequency of cooperation in the population. Because groups with more punishers will tend to exhibit a greater frequency of cooperative behaviors (by both contributors and punishers), the frequency of punishers and cooperative behaviors will be positively correlated across groups. As a result, punishment will increase as a “correlated response” to group selection that favors more cooperative groups. Because selection within groups against punishment is weak when punishment is common, this process might support the evolution of substantial levels of punishment and maintain punishment once it is common.

To evaluate this intuitive argument we studied the following model using simulation methods. There are N groups. Local density-dependent competition maintains each group at a constant population size n. Individuals interact in a two-stage “game.” During the first stage, contributors and punishers cooperate with probability 1 − e and defect with probability e. Cooperation reduces the payoff of cooperators by an amount c, and increases the ability of the group to compete with other groups. For simplicity, we begin by assuming that cooperation has no effect on the individual payoffs of others, but does reduce the probability of group extinction. Defectors always defect. During the second stage, punishers punish each individual who defected during the first stage. After the second stage, individuals encounter another individual from their own group with probability 1 − m and an individual from another randomly chosen group with probability m. An individual i who encounters an individual j imitates j with probability W_j/(W_j + W_i), where W_x is the payoff of individual x in the game, including the costs of any punishment received or delivered. Thus, imitation has two distinct effects: first, it creates a selection-like process that causes higher payoff behaviors to spread within groups. Second, it creates a migration-like process that causes behaviors to diffuse from one group to another at a rate proportional to m. Because cooperation has no individual level benefits, defectors spread between groups more rapidly than do contributors or punishers. Group selection occurs through intergroup conflict (16). In each time period, groups are paired at random, and with probability ɛ, intergroup conflict results in one group defeating and replacing the other group. The probability that group i defeats group j is 1/2(1 + (d_j − d_i)), where d_q is the frequency of defectors in group q. This means that the group with more defectors is more likely to lose a conflict. Note that cooperation is the sole target of the resulting group selection process; punishment increases only to the extent that the frequency of punishers is correlated with that of cooperation across groups. Finally, with probability μ individuals of each type spontaneously switch into one of the two other types. The presence of mutation and erroneous defection ensure that punishers will incur some punishment costs, even when they are common, thus placing them at a disadvantage with respect to the contributors.

Methods

Two simulation programs implementing the model were independently written, one by R.B. in Visual Basic, and a second by H.G. in Delphi. Code is available on request. Results from the two programs are highly similar. In all simulations there were 128 groups. Initially one group consisted of all altruistic punishers and the other 127 groups were all defectors. Various random processes could cause such an initial shift. Sampling variation in who is imitated (17) could increase the frequency of punishers. Randomly varying environments can lead to similar shifts (18) in populations. Finally, individual learning can be conceptualized as a process in which individuals use data from the environment to infer the best behavior. Learning experiences of individuals within a population may often be correlated because they are using the same data. Thus, random variation in such correlated learning experiences could also cause equilibrium shifts in large populations. We do not model these processes here. Simulations were run for 2,000 time periods. The long run average results plotted in Figs. 1–4 represent the average of frequencies over the last 1,000 time periods of 10 simulations.

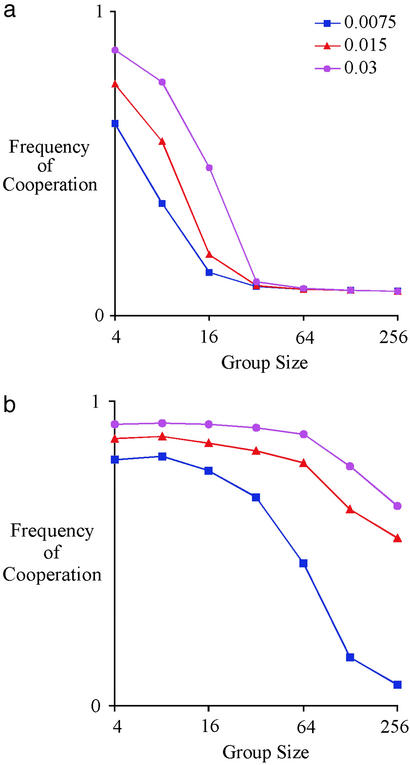
Figure 1.

The evolution of cooperation is strongly affected by the presence of punishment. (a) The long run average frequency of cooperation (i.e., the sum of the frequencies of contributors and punishers) as a function of group size when there is no punishment (p = k = 0) for three different conflict rates, 0.075, 0.015, and 0.003. Group selection is ineffective unless groups are quite small. (b) When there is punishment (p = 0.8, k = 0.2), group selection can maintain cooperation in substantially larger groups.

Figure 4.

Punishment does not aid in the evolution of cooperation when the costs born by punishers are fixed, independent of the number of defectors in the group. Here we plot the long run average frequency of cooperation when the costs of punishing are proportional to the frequency of defectors (variable cost), fixed at a constant cost equal to the cost of cooperating (c), and when there is no punishment.

Base case parameters were chosen to represent cultural evolution in small-scale societies. We set the time period to be 1 year. Because individually beneficial cultural traits, such as technical innovations, diffuse through populations in 10–100 years (19, 20), we set the cost of cooperation, c, and punishing, k, so that traits with this cost advantage would spread in 50 time periods (c = k = 0.2). To capture the intuition that in human societies punishment is more costly to the punishee than to the punisher we set the cost of being punished to four times the cost of punishing (p = 0.8). We assume that erroneous defection is relatively rare (e = 0.02). The migration rate, m, was set so that in the absence of any other evolutionary forces (i.e., c = p = k = e = ɛ = 0), passive diffusion will cause two neighboring groups that are initially as different as possible to achieve the same trait frequencies in ≈50 time periods (m = 0.01), a value that approximates the migration rates in a number of small-scale societies (21). We set the value of the mutation rate so that the long run average frequency of an ordinary adaptive trait with payoff advantage c is ≈0.9 (μ = 0.01). This means that mutation maintains considerable variation, but not so much as to overwhelm adaptive forces. We assume that the average group extinction rate is consistent with a recent estimate of cultural extinction rates in small-scale societies, ≈0.0075 (15). Because only one of the two groups entering into a conflict becomes extinct this implies that ɛ = 0.015.

Results

Simulations using this model indicate that group selection can maintain altruistic punishment and altruistic cooperation over a wider range of parameter values than group selection will sustain altruistic cooperation alone. Fig. 1 compares the long run average levels of cooperation with and without punishment for a range of group sizes and extinction rates. If there is no punishment, our simulations replicate the standard result: group selection can support high frequencies of cooperative behavior only if groups are quite small. However, adding punishment sustains substantial amounts of cooperation in much larger groups. As one would expect, increasing the rate of extinction increases the long run average amount of cooperation.

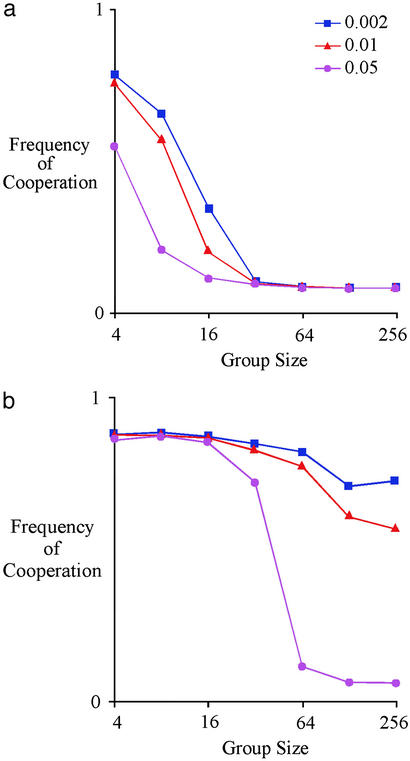
In this model, group selection leads to the evolution of cooperation only if migration is sufficiently limited to sustain substantial between-group differences in the frequency of defectors. Fig. 2 shows that when the migration rate increases, levels of cooperation fall precipitously. When punishers are common defectors do badly, but when punishers are rare defectors do well. Thus, the imitation of high payoff individuals creates a selection-like adaptive force that acts to maintain variation between groups in the frequency of defectors. However, if there is too much migration, this process cannot maintain enough variation between groups for group selection to be effective.

Figure 2.

The evolution of cooperation is strongly affected by rate of mixing between groups. (a) The long run average frequency of cooperation (i.e., the sum of the frequencies of contributors and punishers) as a function of group size when there is no punishment (p = k = 0) for three mixing rates, 0.002, 0.01, and 0.05. Group selection is ineffective unless groups are quite small. (b) When there is punishment (p = 0.8, k = 0.2), group selection can maintain cooperation in larger groups for all rates of mixing. However, at higher rates of mixing, cooperation does not persist in the largest groups.

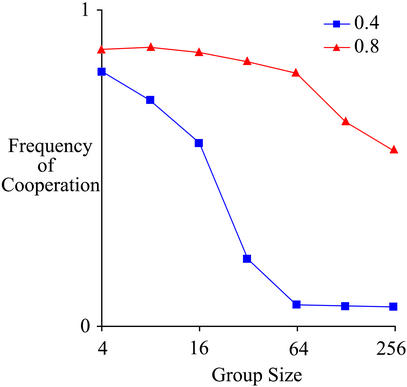
The long run average amount of cooperation is also sensitive to the cost of being punished (Fig. 3). When the cost of being punished is at base case value (p = 4k), even a modest frequency of punishers will cause defectors to be selected against, and, as a result, there is a substantial correlation between the frequency of cooperation and punishment across groups. When the cost of being punished is twice the cost of cooperation (p = 2k), punishment does not sufficiently reduce the relative payoff of defectors, and the correlation between the frequency of cooperators and punishers declines. Lower correlations mean that selection among groups cannot compensate for the decline of punishers within groups, and eventually both punishers and contributors decline.

Figure 3.

The evolution of cooperation is sensitive to the cost of being punished (p). Here we plot the long run average frequency of cooperation with the base case cost of being punished (p = 0.8) and with a lower value of p. Lower values of p result in much lower levels of cooperation.

It is important to see that punishment leads to increased cooperation only to the extent that the costs associated with being a punisher decline as defectors become rare. Monitoring costs, for example, must be paid whether or not there are any defectors. When such costs are substantial, or when the probability of mistaken defection is high enough that punishers bear significant costs even when defectors are rare, group selection does not lead to the evolution of altruistic punishment (Fig. 4). However, because people live in long-lasting social groups and language allows the spread of information about who did what, it is plausible that monitoring costs may often be small compared with enforcement costs. This result also leads to an empirical prediction: people should be less inclined to pay fixed than variable punishment costs if the mechanism outlined here is responsible for the psychology of altruistic punishment.

Further sensitivity analyses suggest that these results are robust. In addition to the results described above we have studied the sensitivity of the model to variations in the remaining parameter values. Decreasing the mutation rate substantially increases the long run average levels of cooperation. Random drift-like processes have an important effect on trait frequencies in this model. Standard models of genetic drift suggest that lower mutation rates will cause groups to stay nearer the boundaries of the state space, (22) and our simulations confirm this prediction. Increasing mutation rate, on average, increases the amount of punishment that must be administered and therefore increases the payoff advantage of second order free riders compared with altruistic punishers. Increasing e, the error rate, reduces the long run average amount of cooperation. Reducing the number of groups, N, adds random noise to the results. We also tested the sensitivity of the model to three structural changes. We modified the payoffs so that each cooperative act produces a per capita benefit of b/n for each other group member, and modified the extinction model so that the probability of group extinction is proportional to the difference between warring groups in average payoffs including the costs of punishment, rather than simply the difference in frequency of cooperators. The dynamics of this model are more complicated because now group selection acts against punishers because punishment reduces mean group payoffs. However, the correlated effect of group selection on cooperation still tends to increase punishment as in the original model. The relative magnitude of these two effects depends on the magnitude of the per capita benefit to group members of each cooperative act, b/n. For reasonable values of b (2c, 4c, and 8c), the results of this model are qualitatively similar to those shown above. We also investigated a model in which cooperation and punishment are characters that vary continuously from zero to one. An individual with cooperation value x behaves like a cooperator with probability x and like a defector with probability 1 − x. Similarly, an individual with a punishment value y behaves like a punisher with probability y and like a nonpunisher with probability 1 − y. New mutants are uniformly distributed. The steady-state mean levels of cooperation in this model are similar to the base model. Finally, we studied a model without extinction analogous to a recent model of selection among stable equilibria because of biased imitation (23). Populations are arranged in a ring, and individuals imitate only individuals drawn from the neighboring two groups. Cooperative acts produce a per capita benefit b/n so that groups with more cooperators have higher average payoff, and thus cooperation will, all other things being equal, tend to spread because individuals are prone to imitate successful neighbors. We could find no reasonable parameter combination that led to significant long run average levels of cooperation in this last model.

Discussion

We have shown that although the logic underlying altruistic cooperation and altruistic punishment is similar, their evolutionary dynamics are not. In the absence of punishment, within-group adaptation acts to decrease the frequency of altruistic cooperation, and as a consequence weak drift-like forces are insufficient to maintain substantial variation between groups. In groups in which altruistic punishers are common, defectors are excluded, and this maintains variation in the amount of cooperation between groups. Moreover, in such groups punishers bear few costs, and punishers decrease only very slowly in competition with contributors. As a result, group selection is more effective at maintaining altruistic punishment than altruistic cooperation.

These results suggest that group selection can play an important role in the cultural evolution of cooperative behavior and moralistic punishment in humans. The importance of group selection is always a quantitative issue. There is no doubt that selection among groups acts to favor individually costly, group beneficial behaviors. The question is always, is group selection important under plausible conditions? With parameter values chosen to represent cultural evolution in small-scale societies, cooperation is sustained in groups on the order of 100 individuals. If the “individuals” in the model represent family groups (on grounds that they migrate together and adopt common practices), altruistic punishment could be sustained in groups of 600 people, a size much larger than typical foraging bands and about the size of many ethno-linguistic units in nonagricultural societies. Group selection is more effective in this model than in standard models for two reasons: first, in groups in which defectors are rare, punishers suffer only a small payoff disadvantage compared with contributors, and as a result, variation in the frequency of punishers is eroded slowly. Second, payoff biased imitation maintains variation among groups in the frequency of cooperation, because in groups in which punishers are common, defectors achieve a low payoff and are unlikely to be imitated.

It would be possible to construct an otherwise similar genetic model in which natural selection played the same role that payoff biased imitation plays in the present model, and there is little doubt that for analogous parameter values the results for such a genetic model would be very similar to the results presented here. However, such a choice of parameters would not be reasonable for a genetic model because natural selection is typically much weaker than migration for small, neighboring social groups of humans. Our results (Fig. 2) suggest that for parameters appropriate for a genetic model, the group selection process modeled here will not be effective. It should be noted, however, that the genetic evolution of moral emotions might be favored by ordinary natural selection in social environments shaped by cultural group selection (24, 25).