Abstract
Major experimental and computational efforts are targeted at the characterization of transcriptional networks on a genomic scale. The ultimate goal of many of these studies is to construct networks associating transcription factors with genes via well-defined binding sites. Weaker regulatory interactions other than those occurring at high-affinity binding sites are largely ignored and are not well understood. Here I show that low-affinity interactions are abundant in vivo and quantifiable from current high-throughput ChIP experiments. I develop algorithms that predict DNA-binding energies from sequences and ChIP data across a wide dynamic range of affinities and use them to reveal widespread functionality of low-affinity transcription factor binding. Evolutionary analysis suggests that binding energies of many transcription factors are conserved even in promoters lacking classical binding sites. Gene expression analysis shows that such promoters can generate significant expression. I estimate that while only a small percentage of the genome is strongly regulated by a typical transcription factor, up to an order of magnitude more may be involved in weaker interactions. Low-affinity transcription factor–DNA interaction may therefore be important both evolutionarily and functionally.
Transcriptional programs are commonly described via the identification of cis-elements in gene regulatory regions and their association with sequence-specific transcription factors (TFs). The highly prevalent working hypothesis, here denoted the “digital” model for transcriptional networks (Fig. 1A), is that TFs either bind perfectly to a sequence motif, or cannot bind it at all. The complexity of transcriptional regulation is therefore implicitly assumed to be originating from a combinatorial code associating several well-defined binding sites, and not from a more loose integrated contribution of many potential binding sites and many candidate TFs. It is clear that the reactions underlying transcriptional regulation are much more complicated than the simple logic used to describe it. For example, characterization of mechanisms that control stochastic and noisy gene expression (Elowitz et al. 2002; Paulsson 2004; Raser and O’Shea 2005) or accurate quantitative analysis of transcriptional switches (Ronen et al. 2002; Bintu et al. 2005) requires an “analog” framework. Still, in most genome-wide studies it is assumed that the digital model is a reasonable compromise, in particular given the quality of the data. With the advent of genomic technology, we may revisit this basic assumption of our approach to describing large-scale transcriptional regulation.
Figure 1.
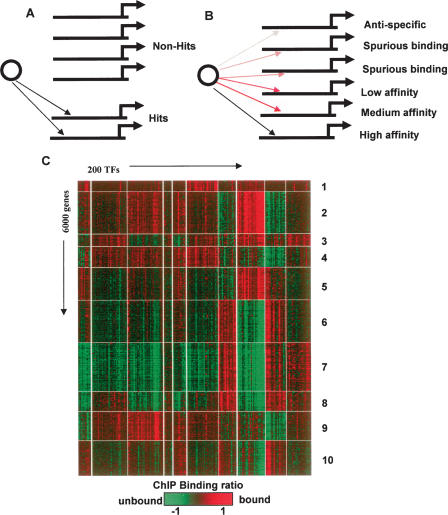
The transcriptional program in yeast: digital or analog? According to the prevalent “digital” hypothesis for transcriptional regulation (A), complex regulatory programs are described using wiring diagrams that associate TFs to genes deterministically. In the alternative “analog” model (B), many TFs may affect each gene at drastically different levels of specificity. Two-way clustering of 200 ChIP binding profiles and 6000 yeast genes (C) reveals groups of genes with remarkably similar binding ratios in all 200 ChIP experiments. Few of the entries in the homogeneous submatrices represent high-specificity TF–gene associations. The clusters and their association with biological functions (Supplemental Table 1) suggest that ChIP experiments may reflect complex and functionally meaningful organization of low-affinity TF–gene interactions.
Recently, the combination of Chromatin Immunoprecipitation (ChIP) and microarray technologies (ChIP on chip) opened the way for genome-wide localization of transcription factor binding (Ren et al. 2000; Iyer et al. 2001). In an extensive set of experiments, a comprehensive repertoire of 200 budding yeast TFs were profiled for binding in standard growth conditions and several additional environments (Lee et al. 2002; Harbison et al. 2004). A similar approach is now being applied to human systems, with hopes for deeper understanding of transcriptional regulation and mis-regulation in disease (Li et al. 2003; Cawley et al. 2004; Odom et al. 2004). Although the ChIP-on-chip technology generates quantitative readouts, the current analysis protocols (Harbison et al. 2004) conform to the digital paradigm: The data are analyzed such that a P-value threshold transforms the measurements into a set of binary TF–gene interactions. The current scheme is therefore assuming that ChIP experiments cannot be interpreted quantitatively, and that the functional essence of the interaction between TFs and genes can be described by means of a parameter-less network.
Here I show that an analog model for transcriptional switches (Fig. 1B) is a practical and advantageous alternative to the digital model, particularly when analyzing complex regulatory networks using ChIP experiments. Instead of focusing on a set of a few dozens of high-specificity hits for each TF, ChIP experiments are analyzed quantitatively, using (possibly noisy) estimates on TF-binding affinities for thousands of promoters. It is shown that the quantitative approach greatly enhances the characterization of binding preferences for many TFs and outperforms current analysis methods. Importantly, the results suggest that binding of TFs to low-affinity promoters occurs abundantly in vivo, is determined by promoter sequences, and constitutes a substantial fraction of the interaction between TFs and DNA (thereby making it widely detectable in ChIP experiments). Furthermore, the analysis indicates that low-affinity TF binding may be functionally important: The predicted TF binding energies of orthologous promoters from different yeast species are shown to be more conserved than expected by neutrality. Conservation analysis suggests that selection due to a single TF may affect significant parts of the genome (10%–20%), much more than expected by purifying selection on strict binding sites. This finding is supported by analysis of gene expression. In conditions that activate a TF, one may associate the TF-binding affinity with a measurable change in gene expression for a large part of the genome (10% and more). According to these results, low-affinity TF–gene interactions are important features of genomic regulatory programs, with possible roles in fine-tuning the transcriptional phenotype and in providing abundant evolutionary raw material for its continuous modification.
Results
ChIP binding ratios are informative over the entire specificity range
The yeast transcriptional network was mapped extensively using ChIP-on-chip experiments quantifying the genome-wide binding profiles of 200 TFs in rich media and several other conditions (Harbison et al. 2004). To roughly determine how much information exists in low-affinity TF–gene interactions, and to visualize possible global patterns in this extensive data set, two-way clustering of the intergenic regions and TFs was performed given the ChIP TF-binding ratios (Methods). Clusters represent groups of genes with similar ChIP binding ratios across dozens of TFs. Only a tiny fraction of the genes are considered as high-specificity targets (hits) for each TF, thus the cluster pattern is a result of similarities over ChIP values that refer to nonspecific binding. Functional enrichment strongly associates specific biological functions with some of the clusters (Methods; Suppplemental Table 1). For example, genes in cluster 7 consist mainly of ribosomal proteins (P < 10−66) and exhibit remarkably similar binding ratios across all of the 200 TFs, although only a few TFs (e.g., Fhl1, Ifh1, Rap1, Sfp1) (Schawalder et al. 2004; Wade et al. 2004) are associated with high-affinity ribosomal protein regulation. The similarity holds even when TFs have negative binding ratios for genes from the cluster. Such high information content in nonspecific binding profiles could be a result of experimental or normalization artifacts, or it may indicate that TF–DNA interactions are functionally organized even when not reflecting highly specific interaction over well-defined binding sites.
ChIP data and PWM predictions correlate over a wide dynamic range
By comparing sequence-based prediction of TF affinities to ChIP binding ratios, we can test if low-specificity binding detected by ChIP provides quantitative indication to variability in in vivo binding strengths or is by and large a noisy indication to biological cases of high-specificity targets. The common method for predicting TF–DNA interaction from sequences is based on Position Weight Matrices (PWMs) (Stormo and Hartzell III 1989), which are known to provide reasonable energetic approximation for the binding interaction in vitro (Liu and Clarke 2002). According to our results (see Supplemental Table 2), PWM predictions and ChIP binding ratios are highly correlated. The analysis first used PWMs that were taken from the Harbison et al. (2004) study and were generated using only qualitative partition of the genes into hits (P < 0.001) and non-hits (P > 0.001). Although no quantitative information was used to infer the PWMs, the ChIP-to-PWM correlation is strong even when restricting to the set of promoters with ChIP P-values higher than the common 0.001 threshold or even a more permissive 0.01 threshold. Figure 2A shows that, in fact, no threshold can induce a partitioning of the genes into two groups in which sequences do not predict ChIP, and that typically, correlation exists for both genes above and below the threshold. For example, for MBP1, a highly significant dependency between ChIP values and the sequence is observed even for the genes with ChIP binding P-values exceeding 0.2, a value that is currently not considered to indicate any binding is occurring.
Figure 2.
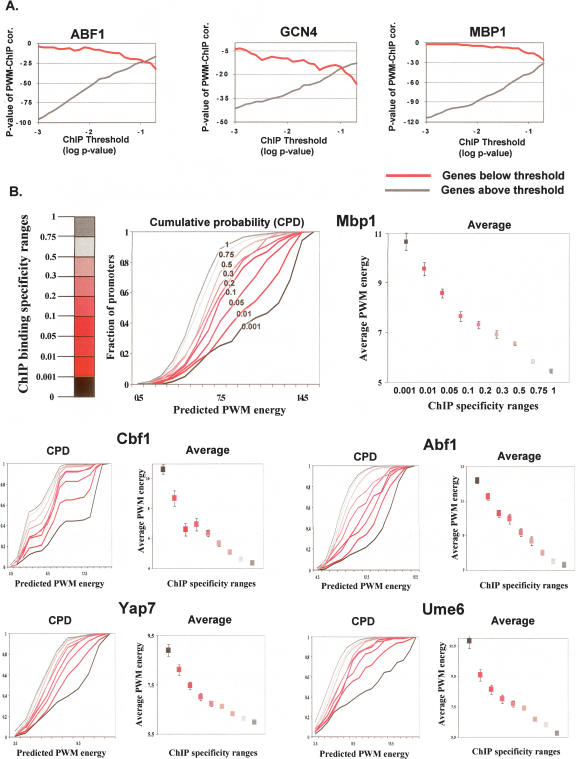
Quantitative ChIP to sequence correlation. (A) ChIP and PWM correlation above and below a P-value threshold. Shown are log P-values of the Spearman correlation between ChIP binding ratios and PWM energy predictions (y-axis). Using a range of possible thresholds (x-axis), correlations were computed separately for genes with ChIP values below (red) and above (black) the threshold. In all cases, a significant correlation is observed in both sets of genes, and for all selections of thresholds. (B) Sequence–ChIP correlation reveals in vivo low-specificity binding. Shown are averages and cumulative probability distributions (CPDs) of PWM binding energies for groups of genes with ChIP values within certain intervals. Remarkable monotonicity is observed in all cases, with predicted energies of groups with higher-significance P-values (left) consistently higher than those of groups with less-significant P-values (right). The monotonicity is holding for very low specificity ranges, suggesting ChIP profiles are informative over a wide dynamic range of specificities.
Figure 3, B and C, further exemplifies broad ChIP-to-sequence correlation. It is shown how the PWM predictions are monotonically decreasing as the ChIP values decrease, even for ChIP ranges way below the high-significance levels. The distribution for the Mbp1 profile shows, for example, that PWM predictions for genes with ChIP P-values in the 0.3–0.5 range are significantly higher than those of genes with ChIP P-values in the 0.5–0.75 range (P < 10−10; KS test).
Figure 3.
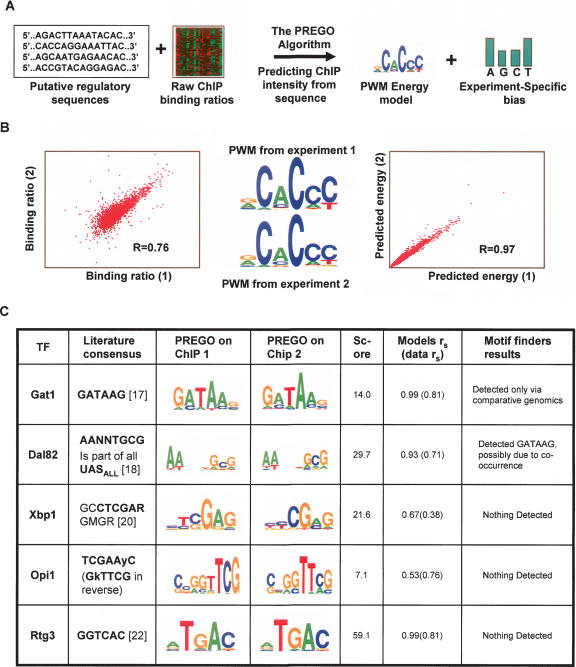
Motif regression reveals known and novel binding sites. (A) The PREGO algorithm. The PREGO algorithm was developed to fit PWM models to raw ChIP-on-chip profiles. The algorithm combines ChIP and sequence data and builds PWM models with optimal prediction accuracy over the entire affinity spectrum. (B) Robustness of PWM energy predictions. Applying the PREGO algorithm independently to individual experiments demonstrates the robustness of the derived energy models. Shown here is the correlation between two Aft2 experiments (left), the two PWM models derived from them (middle), and the correlation of the energy predictions for these two PWMs. The remarkable reproducibility suggests that PREGO-derived PWMs may be used quantitatively. (C) Using low-affinity promoters improves motif-finding sensitivity. Shown are examples of PWMs inferred by the PREGO algorithm from ChIP profiles in which the motif-finding approach failed to find motifs. All the cases shown are confirmed by additional evidence from the literature. See Methods for definition of the PWMs score. “Models rs” represents the Spearman correlation of energy predictions from PWMs generated using two different arrays. “Data rs” represents the Spearman correlation of the two raw ChIP profiles used to construct the two PWMs.
Using quantitative ChIP profiles for PWM regression
Motivated by the above results on the magnitude of correlation between PWM predictions and ChIP measurements, an algorithm to perform regression of a PWM model to an entire ChIP binding profile was developed. The PREGO algorithm exploits information from the full spectrum of binding energies, and differs substantially from extant motif-finding algorithms that search for a PWM model that discriminate “hits” from “non-hits.” In order to use ChIP data as a quantitative proxy to TF-binding energy, extensive low-level analysis of 775 raw ChIP profiles was performed (Supplemental note 1). Significant experimental biases that were previously not taken into account were eliminated. These included mainly effects related to variable probes’ GC content (Supplemental Fig. 1), but also systematic effects of low-complexity sequences [like poly(A/T) tracts]. The PREGO algorithm inherently controls for such effects: It reports PWM models that are significant given a normalized profile lacking correlation to nucleotide composition or low-complexity sequence motifs (Methods). The entire algorithmic pipeline (Fig. 3A; Supplemental Fig. 2) is applied separately to individual arrays, to allow comparison of the results on raw data from triplicate experiments and to ensure the quality of the inferred models (Fig. 3B).
The PREGO algorithm was applied to the 775 available raw ChIP profiles from the Harbison et al. (2004) study. All known PWMs that were detected in these data before using the motif-finding approach were also detected using PREGO, and in many cases the algorithm detected PWMs that match literature evidence but could not be detected in the ChIP data before. Figure 4C provides several examples to demonstrate the potency of the approach (additional information is available on my Web site, http://uqbar.rockefeller.edu/~atanay/prego).
Figure 4.
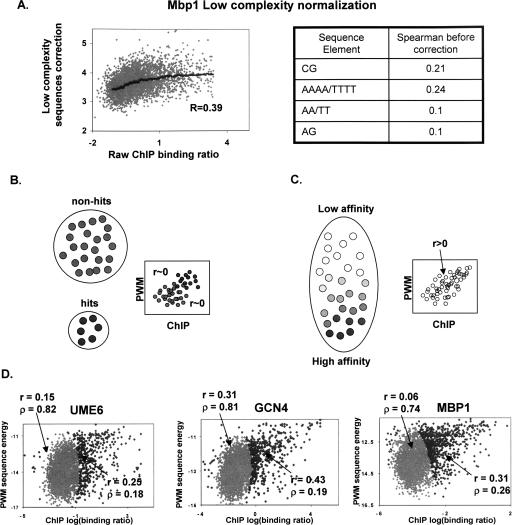
Testing the digital model. (A) Normalizing ChIP data. PREGO performs internal normalization of the ChIP data to eliminate any correlation of the binding ratios to single or dinucleotide composition or to low complexity sequences [typically poly(A) or poly(T) tracts]. Shown are the scatter and trend of the raw Mbp1 ChIP binding ratio versus the inferred correction, involving contribution from several dinucleotides and an AAAA/TTTT motif. The Spearman correlation of each of the sequence features used in the normalization and the ChIP data is also shown (right). (B,C) Discrete versus analog models. If TF–gene interactions can be reasonably approximated as either occurring or not occurring (hits or non-hits), then the joint distribution of ChIP and PWM predictions should reflect zero covariance inside such two ideal subsets of the genome (left). If ChIP and PWM provide quantitative estimations on in vivo binding affinity, then no partition of the genome can eliminate their correlation (right). It is therefore possible to test the validity of the digital assumption by fitting two distributions to the data and analyzing their parameters. (D) ChIP-sequence correlation reflects an analog behavior. Analysis of the ChIP/PWM joint distributions for three TFs reveals that their quantitative correlation cannot be explained as a consequence of the mixture of two distributions (Methods). Shown are inferred maximum likelihood distributions for hits (darker) and non-hits (brighter). The mixture coefficients (ρ) and correlation coefficients (r) are indicated. The analysis suggests that about one-fifth of the genome is influenced by each of the TFs, and that for at least one-fifth of the genome, ChIP- and sequence-based estimations of affinity are correlated in a quantitative fashion.
Discovery of known and novel PWMs using motif regression
Gat1 is a GATA factor with known function in the regulation of nitrogen catabolism (Kuruvilla et al. 2001). The known binding motif of this factor (GATAAG) could not be found using any of the motif-finding algorithms used by Harbison et al. (2004). The motif was detected successfully only using comparative analysis of Saccharomyces species. PREGO was applied to three raw Gat1 ChIP profiles (measured after treatment with Rapamycin) and successfully recovered the known motif in all cases, without using additional data and with excellent reproducibility (rs of the binding energy predictions from two different arrays = 0.99). Analysis of three Dal82 binding profiles under Rapamycin illustrates a different important advantage of PREGO. Dal82 is known to be involved in the regulation of DAL genes, and was associated with UISALL elements using standard reporter analysis (Dorrington and Cooper 1993). Since the UISALL elements are quite long, Dal82 exact binding preferences are not known in detail. Previously, applying motif finding to the set of 62 Dal82 ChIP hits yielded the GATAAG motif (Harbison et al. 2004). However, PREGO analysis indicates that GATAAG is not correlated with Dal82 binding and suggests AANNTGCG as the functional motif. Interestingly, the known UISALL sequences do not include GATA elements, but all of them contain a copy of AANNTGCG, suggesting that the identification of GATAAG as a Dal82-associated motif was a consequence of the co-occurrence of GATA boxes and UISALL in DAL promoters and that Dal82 binding preferences may be modeled more accurately using the motif reported here. PREGO is therefore shown to be effective in controlling for co-occurrence artifacts that can bias the results of standard motif finders.
Frequently in the yeast data set, ChIP analysis generated few or no high-specificity hits for a certain TF. Using the entire range of specificities, PREGO could characterize TFs’ binding preferences even in such circumstances. The Opi1 factor is known to be involved in phospholipid genes regulation. Its ChIP profile yielded only three high significance hits, preventing motif finders from detecting any PWM. PREGO analysis revealed the motif CCGGTTCG in two of the triplicates and a shorter version of it (GGTTC) in the third one. This motif is similar to a previously identified Opi1-bound element (in reverse complement, TCGAAyC). Xbp1 is a known stress regulator, with possible roles in the regulation of cell cycle and cell size (Mai and Breeden 1997; Miled et al. 2001). Although 76 significant Xbp1 targets were identified in ChIP profiling under mild H2O2 treatment, no motif could be found in them before, even when using comparative genomics. The PREGO algorithm was able to very strongly associate the motif CTCGAG with each of the three available Xbp1 profiles, confirming a previous report on Xbp1’s binding consensus GCCTCGARGMGR (Mai and Breeden 1997). Interestingly, in a previous work (Tanay et al. 2004a), we have identified CTCGAG as a possible motif using evolutionary analysis, but could not associate it with a TF. The Rtg3 factor was shown before to bind a GGTCAC motif, using mutational analysis of CIT2 UASr (Jia et al. 1997). PREGO analysis reveals the motif GTCAT as remarkably correlative to the Rtg3 affinity profiles under both Rapamycin and H2O2. The motif GTCACG, which is more similar to UASr, is also associated with the Rapamycin profile, but more weakly than GTCAT. As in the previous cases, motif-finding algorithms fail to find any significant motif enriched in the set of 52 genes associated with Rtg3.
Quantifying the magnitude of low-specificity TF–DNA binding
Using the entire range of ChIP values to infer PWMs was demonstrated above to be of considerable utility. The nature of correlation between low-specificity ChIP values and the sequence remained unclear, however. Importantly, such correlation is unlikely to be an experimental artifact resulting from systematic bias toward certain nucleotides, dinucleotides, or any other low-complexity sequence feature, since these features are normalized by the PREGO algorithm (see Fig. 4A for an example).
One possible reason for the puzzling ChIP-to-sequence correlation over low-specificity targets may be the imperfect nature of ChIP experiments. It could be argued that the targets of a TF are essentially “digital” (hits or non-hits), but that owing to experimental noise, as ChIP values decrease they reflect a smaller probability of observing a hit, therefore correlating positively with the (also imperfect) sequence-based predictions. If this is the case (Fig. 4B), then some (unknown) partition of the genes to hits and non-hits would eliminate the ChIP-to-sequence correlation: If, for example, we could know exactly the set of non-hits, we should observe zero correlation between ChIP and PWM predictions inside it. Based on this intuition, we can estimate the extent of quantitative information in the ChIP data by fitting the ChIP–PWM two-dimensional distribution as a mixture of two distributions: one representing the typical ChIP and PWM values of “hits” and the other representing these for “non-hits” (Methods). We can then test the relative weights of these distributions (indicating how many genes may be classified as “hits”) and the distributions’ covariances (indicating how much quantitative information exists in the data).
Figure 4D shows the results of such analysis for three TFs, making it clear that the data is strikingly non-“digital”—it is impossible to explain the correlation of ChIP and PWMs using two distributions with zero covariance, and in fact, in each of the three cases, ∼20% of the promoters are inferred to be interacting with the TF, and a highly significant ChIP–sequence correlation is observed. Binding to very weak sites may therefore occur sufficiently often to allow detection in ChIP experiments. Individual low-affinity promoters cannot be identified as deterministic TF targets, because binding occurs probabilistically in vivo, but we can still roughly predict the level of such binding from the sequence.
Binding energies are evolutionarily conserved even when strong binding sites are lacking
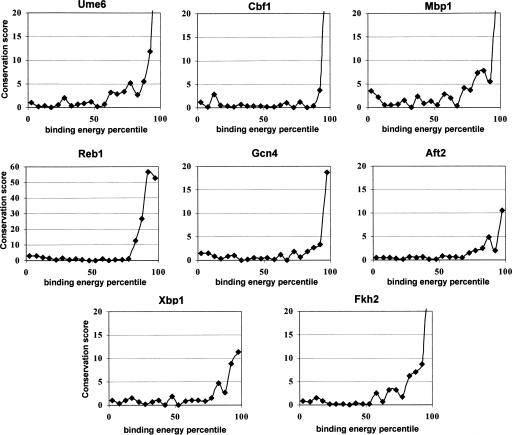
The remarkable correlation between promoter sequences and low-affinity ChIP values, and the success of the regression approach in detecting PWM models that could not be detected in the ChIP data before, suggest that (1) probabilistic or transient binding of TFs to low-affinity binding sites occurs sufficiently often to be quantified in ChIP experiments and (2) the magnitude of such binding is determined by the promoter sequence (and is therefore predictable by PWMs). One way to test whether these abundant weak TF–gene interactions carry functional relevance is to estimate their level of evolutionary conservation. Comparative genomics is used extensively to characterize TF-binding sites as conserved loci (Cliften et al. 2003; Kellis et al. 2003), and several models were suggested to describe the selective pressures affecting them (Moses et al. 2003; Tanay et al. 2004a). If binding of a TF to low-affinity promoters is functionally important, one would expect to observe selection operating not only on individual binding sites, but also on the total affinity of each promoter to that TF. A gene weakly regulated by a TF may be pushed to remain so in the course of evolution, but the pressure would not be focused on a specific locus but would be dispersed over the entire promoter, selecting for the integrated binding energy over many possible weak loci. To test if such selection exists, I used orthologous yeast promoters and developed a conservation score that compares the observed evolutionary changes in the total predicted promoter binding energy to those expected under a neutral model (Methods). The analysis therefore tested if the integrated interaction energy of a TF and an entire promoter is more conserved than expected by chance. Conservation analysis was performed on groups of promoters with similar Saccharomyces cerevisiae binding energies, allowing the characterization of the relations between affinity and conservation. The analysis shown in Figure 5 indicates that energy conservation goes beyond the well-documented conservation of binding sites.
Figure 5.
Evolutionary conservation of predicted binding energies. Plotted are the conservation scores of genes with low (left) to high (right) TF-binding energies. (x-axis) S. cerevisiae binding energy percentile. (y-axis) Conservation score (Methods). In all cases, the binding energies of higher-affinity promoters are conserved. For several of the TFs, conservation is observed on a significant fraction of the genome (10%–20%), reflecting widespread selection on the binding energy of promoters lacking high-affinity binding sites.
According to the results, conservation of energy is detectable in a large number of promoters, greatly exceeding the top few affinity percentiles predicted to have significant binding sites. For example, Gcn4 and Cbf1 are estimated to affect roughly 10% of the genome (Gcn4 may affect more weakly an additional 10%). The conservation of energies predicted for other TFs may be even broader. Mbp1 and Ume6 conservation peak at the top 5%, but remain significant on up to half of the affinity spectrum. Mbp1 binds the cell cycle box ACGCGT (with additional factors) (Simon et al. 2001). It is possible that its role in regulating the cell cycle is dependent on the exact quantitative properties of the binding interaction, therefore increasing the selective pressure. For Ume6, a key regulator of meiosis (Strich et al. 1994) and additional processes, the broad conservation of binding energies may be related to the role of this factor in widespread Rpd3–Sin3-based chromatin modification (Kadosh and Struhl 1997).
The analysis of Figure 5 is based on many simplifying assumptions (e.g., summing PWM probabilities to estimate binding energies, simulating a neutral model, ignoring combinatorial interaction between TFs). Still there is evidence that the observed conservation of weak interaction energies reflects genuine selection. The neutral model used in the simulations is based on the evolutionary dynamics at the exact regions analyzed, modeling context-dependent mutations and using parameters estimated directly from the data (Methods). The observed conservation is therefore unlikely to be a consequence of GC content conservation or other simple background effects. Similar results were obtained when analyzing sequences from several yeast species (see the supporting Web site, http://uqbar.rockefeller.edu/~atanay/prego, for details). As an additional control, the conservation analysis was repeated on parts of the promoters that are less likely to be active (−600 to −350) and parts of the promoter that are usually highly active (−350 to −100). Indeed, significantly less conservation of binding energy is observed for sequences in the less active ranges (see the supporting Web site, http://uqbar.rockefeller.edu/~atanay/prego). One should note that in some of the cases, the conservation observed when analyzing weak binding energies for one TF could be a byproduct of the selection on optimal binding sites of another TF. Since the observed conservation is consistently biased to the upper affinity percentiles, such indirect effects are likely to hold mostly for TFs that bind very similar PWMs. An additional support for the surprising estimates on the breadth of selective pressure on weak binding energies comes from analysis of gene expression (see below).
Low-affinity promoters may generate weak gene expression
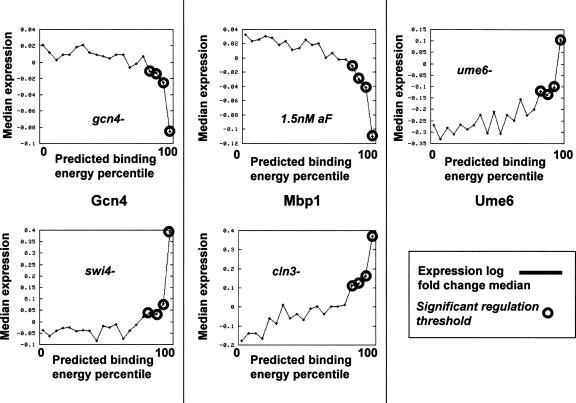
One possible explanation for the broad conservation of TF-binding energies may be the ability of low-affinity promoters to generate gene expression. Weak TF–gene interactions are unlikely to drive a major effect at the expression level. Still, it is possible that subtle TF binding preferences can modulate the level of expression noise or have other mild effects on transcriptional switches. One may observe small changes in expression by grouping together genes with similar predicted binding energies and analyzing their behavior at appropriate conditions. Figure 6 shows the results of such analysis for three TFs. For Gcn4, the expression measurements were taken from two mutants (data from Hughes et al. 2000). Since Gcn4 is a positive regulator of many genes, the gcn4− strain is showing repressed gene expression for Gcn4-associated genes in general. The effect is strongest for genes in the top five affinity percentiles, but significance repression is observed for genes in the 90–95 percentiles and even the 85–90 percentiles (compare to Gcn4 evolutionary conservation profile, Fig. 5). The reciprocal effect is observed in the swi4− strain, in which Gcn4 genes are induced. Analysis of Mbp1 targets in cells induced by α-factor (data from Roberts et al. 2000) or in the cln3− strain (data from Spellman et al. 1998) similarly confirms the ability of promoters not at the top five affinity percentiles to generate observable expression. A similar effect is observed for Ume6 (expression in a ume6 strain) (data from Williams et al. 2002). Analysis of a large collection of gene expression profiles (see the supporting Web site, http://uqbar.rockefeller.edu/~atanay/prego) reveals many more cases of significant correlation between expression profiles and weak predicted binding energies, thereby showing that the examples in Figure 6 are probably not anecdotal.
Figure 6.
Low-affinity promoters generate gene expression. Shown is the gene expression generated by promoters with low (left) to high (right) predicted TF-binding energies. (x-axis) Percentile of predicted TF-binding energy. (y-axis) Median of log fold expression changes in bins of 5 affinity percentiles. The experimental condition is different for each plot and is noted on the graph. Bins that represent significant up- or down-regulation (Methods) are labeled in circles. The plots suggest that some TFs (e.g., Gcn4, Mbp1) may weakly affect the expression of a substantial number of genes even when clear binding sites are lacking.
Discussion
Low-affinity TF–DNA interactions are shown here to be surprisingly widespread in vivo, with possible functional and evolutionary implications. Transcription factors bind DNA stochastically, and it is therefore expected that they would be interacting with promoters at different levels of specificity, depending on an affinity that is determined (at least partially) by the DNA sequence. Several models were developed before to describe the interaction between TFs and DNA at variable affinities (Gerland et al. 2002; Rajewsky et al. 2002; Brown and Callan Jr. 2004; Mustonen and Lassig 2005). It is still not understood, however, to what extant various cellular mechanisms modulate the levels of specific versus nonspecific TF binding, and how accurate and deterministic are different parts of the transcriptional network in vivo. The present study demonstrates that we can use ChIP experiments, so far considered to indicate only high-affinity TF targets, to quantify weak transcriptional interactions and combine them with promoter sequence analysis. One can therefore exploit comprehensive ChIP experiments to outline an “analog” model for transcriptional networks, and to explore the role of low-specificity, probabilistic TF–DNA interactions in genomic regulatory programs. The present work should motivate further adaptation of mechanistic models for TF–DNA interaction to the analysis of genome-wide data sets going beyond the simple PWMs used here.
Low-specificity TF–DNA interactions may be functional or nonfunctional. Nonfunctional interactions are unlikely to affect gene expression, and would be occurring transiently with marginal effects on the transcriptional program. Functional interactions may spuriously affect gene expression, either adding up with other mechanisms to form a significant effect on the transcriptional program, or modulating the level of gene expression stochasticity by increasing or decreasing the level of sporadic binding to the promoter (Raser and O’Shea 2005). According to the evolutionary and gene expression analysis reported here, it is likely that many of the low-specificity transcriptional interactions in yeast are weakly functional. It is shown that for substantial parts of the genome, the total binding energy (and not just the existence of a binding site) is conserved and that on average, promoters with low predicted binding affinities can still generate gene expression. The discrete deterministic view on transcriptional networks may still be a reasonable compromise when studying major regulatory effects using limited experimental resources, but regulatory programs may actually feature a more complex combination of stochastic interactions at different levels of specificity. Evolutionarily, transcriptional programs in which a discrete logic is softened by a combination of low-affinity interactions may be more flexible. Such programs can allow changes to be gradually accumulated, therefore alleviating selective pressure on specific loci (e.g., classical binding sites) and increasing their ability to evolve.
At the technical level, this work suggests a new framework for the analysis ChIP experiments. The approach presented here is relatively direct, attempting the inference of standard models for TF binding energy and ignoring important aspects of the binding process (e.g., competition, saturation) (Nachman et al. 2004; Tanay and Shamir 2004; Bintu et al. 2005; Granek and Clarke 2005). Still, the application of the new techniques on a genomic scale is proven to be more effective than the combined results of several mature and fine-tuned algorithms that were used before (Harbison et al. 2004). The new PREGO algorithm outperforms extant methods simply because it uses much more information in a biologically justifiable way. Extensive mapping of regulatory networks is well under way in several model systems other than yeast, with high hopes for revolutionizing the study of transcriptional regulation in mammals and disease. Many of these efforts are based on the ChIP-on-chip technology, using increasingly better coverage of complex genomes (Cawley et al. 2004; Odom et al. 2004; Ren and Dynlacht 2004). Applying a quantitative approach to the analysis of these studies and carefully evaluating the role of TF–DNA interactions beyond well-characterized binding sites may be highly beneficial for these studies. The results on yeast here (and see Supplemental Fig. 3 for analysis of a small human ChIP data set) suggest that such a quantitative approach may be practical sooner than expected.
Methods
Data processing
Raw ChIP GenePix files were downloaded from the ArrayExpress site (accession W-MIT-10). Annotations of several array types were changed to assign the probes correctly (these were updated in ArrayExpress). When referring to binding P-values, the P-values reported in Harbison et al. (2004) are used (taken from the paper’s supporting Web site). When referring to raw values, the binding ratios originally computed by the GenePix software were used. Yeast promoters sequences were downloaded from SGD (http://www.yeastgenome.org), with corrected Saccharomyces mikatae gene start annotation as in Tanay et al. (2005). SGD GO annotations were downloaded from (http://www.geneontology.org). A yeast gene expression compendium collected from more than 60 publications was used as in Tanay et al. (2004b; references are available in the supporting Web site). Clustering was performed using standard two-way k-means. Functional enrichment was performed using the TANGO program (available from the supporting Web site).
ChIP normalization
All ChIP profiles were normalized as part of the PREGO preprocess (Supplemental Fig. 2). The normalization ensures that single and dinucleotide probe frequencies, as well as sequences longer than 5 of the form Poly-X or Poly-XY, are not correlated with the normalized ChIP profiles.
Testing quantitative ChIP–sequence correlation
ChIP data and PWM predictions for each TF were combined to generate a two-dimensional joint distribution. An EM algorithm was implemented to detect the maximum likelihood mixture of two binormal distributions given the data. The mixture model is parameterized by the means and covariance matrices of two distributions (one representing “hits” and the other “non-hits”), and by a mixture coefficient that determines the relative weights of the two distributions. EM was performed from multiple starting points with perfect convergence coherence suggesting that the global optimum was discovered. Performing EM on a model that assumes the covariance in each of the two distributions was zero (as suggested by the digital hypothesis) generated significantly lower likelihood. Moreover, re-estimating the posterior distributions from such null-covariance models yielded significant covariance in all cases, reconfirming that the correlation between ChIP and sequence is, indeed, quantitative and cannot be explained by a noisy approximation of a digital phenomenon.
Predicting binding energies
A PWM P of length l is defining a probability distribution over l-mer sequences by setting Pr(s1. . .sl) to Πip(i, si). Given a promoter sequence s, we define the PWM predicted binding energy to s as E(P, s) = ∑jΠip(i, si + j) (summing up contributions from all possible positions). The results in this study were derived using promoter positions −600 to 0, unless otherwise stated.
Energy regression algorithm
Given a chip profile Rg, specifying the binding ratio for each promoter g ∈ G, and a set of promoter sequences sg, we wish to search for a PWM model P such that E(P, sg) optimally predicts Rg. Prediction accuracy is quantified using the Spearman correlation of E(P, sg) and Rg. Fitting a PWM to a raw ChIP profile was performed using the newly developed PREGO program. The PREGO algorithm consists of two phases. In the first phase (analogously to the REDUCE algorithm [Bussemaker et al. 2001], but using nonparametric rank correlation statistics), PREGO screens a very large repertoire of combinatorial motifs (all k-mers with one gap, here k < 9). For each combinatorial motif, the algorithm rapidly approximates the Spearman correlation between the number of k-mer appearances in the promoter and the ChIP binding ratio. The algorithm computes the P-value of the independence hypothesis based on the correlation coefficient and corrects it for multiple testing using Bonferroni’s factor. Whenever it finds a k-mer with P-value exceeding the significance threshold (P < 0.01), it continues to the second phase. In its second phase, PREGO uses correlative k-mers to initiate a PWM regression algorithm. PWMs are nonlinear, thus exact linear regression is not possible. Instead, an efficient local optimization procedure that maximizes the correlation of the model was developed. The algorithm pseudo-code is given in Supplemental Figure 1.
Evolutionary analysis
The simulation of neutral evolution on the yeast promoter regions under study was performed using a model that takes into account the context of mutations (Siepel and Haussler 2004). The model was used to simulate the promoter sequence of, for example, S. mikatae, given the sequence of an orthologous S. cerevisiae promoter. To simulate the S. mikatae nucleotide at position i, the model looks up a probability table using the cerevisiae dinucleotide at position i − 1, i and the simulated mikatae nucleotide at position i − 1. The model parameters were estimated by counting dinucleotide alignments in multiple alignments of sensu stricto promoters (Cliften et al. 2003). Denote the number of aligned cerevisiae–mikatae dinucleotides ab and cd by nabcd. Then define Pr(d | abc) = nabcd/∑x(nabcx). To test the conservation of the binding affinities predicted by a PWM p, 2500 genes for which the orthologous S. mikatae promoter contained at least 400 bp were identified. The promoters were then divided into 20 groups, each with a specific range of PWM energies in S. cerevisiae (so that each group consists of five energy percentiles). Using the neutral model, 10 simulated genome-wide collections of orthologous promoters were then generated (10 were enough for obtaining statistically significant results, since pooling of the genes in each group was used). The binding energy changes between each S. cerevisiae promoter and its true and randomized S. mikatae orthologs were computed, and the absolute values of energy changes for each of the 20 groups were collected. Using Kolmogorov-Smirnov statistics, the distributions of real and randomized energy changes were compared and a P-value was computed to reject the neutrality assumption in each bin. The conservation score of each group of genes was defined as −log10(P), where P is the KS P-value.
Gene expression analysis
To test the effect of binding affinities on gene expression, experiments in which the TF of interest is active were selected from a large compendium. Using the TF’s PWM, the genes were partitioned into 20 groups of increasing predicted binding energies. The distribution of gene expressions in each group and its median were then computed. In addition, the distribution of gene expression in each group was compared to the combined distribution of all sets with smaller affinities (thus, e.g., the expression of genes with affinities in the 85–90 percentiles was compared to expression of genes with affinities in the 0–85 percentiles). The P-values reported in Figure 6 were generated using KS tests on these two sets.
Acknowledgments
I thank R. Shamir, I. Gat Viks, M. Kupiec, D. Pe’er, and E. Siggia for discussions and critical reading of the manuscript; three anonymous referees for comments; and the Rothschild foundation for support.
Footnotes
[Supplemental material is available online at www.genome.org and at http://uqbar.rockefeller.edu/~atanay/prego.]
Article published online before print. Article and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.5113606
References
- Bintu L., Buchler N.E., Garcia H.G., Gerland U., Hwa T., Kondev J., Phillips R., Buchler N.E., Garcia H.G., Gerland U., Hwa T., Kondev J., Phillips R., Garcia H.G., Gerland U., Hwa T., Kondev J., Phillips R., Gerland U., Hwa T., Kondev J., Phillips R., Hwa T., Kondev J., Phillips R., Kondev J., Phillips R., Phillips R. Transcriptional regulation by the numbers: Models. Curr. Opin. Genet. Dev. 2005;15:116–124. doi: 10.1016/j.gde.2005.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown C.T., Callan C.G., Jr., Callan C.G., Jr. Evolutionary comparisons suggest many novel cAMP response protein binding sites in Escherichia coli. Proc. Natl. Acad. Sci. 2004;101:2404–2409. doi: 10.1073/pnas.0308628100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bussemaker H.J., Li H., Siggia E.D., Li H., Siggia E.D., Siggia E.D. Regulatory element detection using correlation with expression. Nat. Genet. 2001;27:167–171. doi: 10.1038/84792. [DOI] [PubMed] [Google Scholar]
- Cawley S., Bekiranov S., Ng H.H., Kapranov P., Sekinger E.A., Kampa D., Piccolboni A., Sementchenko V., Cheng J., Williams A.J., Bekiranov S., Ng H.H., Kapranov P., Sekinger E.A., Kampa D., Piccolboni A., Sementchenko V., Cheng J., Williams A.J., Ng H.H., Kapranov P., Sekinger E.A., Kampa D., Piccolboni A., Sementchenko V., Cheng J., Williams A.J., Kapranov P., Sekinger E.A., Kampa D., Piccolboni A., Sementchenko V., Cheng J., Williams A.J., Sekinger E.A., Kampa D., Piccolboni A., Sementchenko V., Cheng J., Williams A.J., Kampa D., Piccolboni A., Sementchenko V., Cheng J., Williams A.J., Piccolboni A., Sementchenko V., Cheng J., Williams A.J., Sementchenko V., Cheng J., Williams A.J., Cheng J., Williams A.J., Williams A.J., et al. Unbiased mapping of transcription factor binding sites along human chromosomes 21 and 22 points to widespread regulation of noncoding RNAs. Cell. 2004;116:499–509. doi: 10.1016/s0092-8674(04)00127-8. [DOI] [PubMed] [Google Scholar]
- Cliften P., Sudarsanam P., Desikan A., Fulton L., Fulton B., Majors J., Waterston R., Cohen B.A., Johnston M., Sudarsanam P., Desikan A., Fulton L., Fulton B., Majors J., Waterston R., Cohen B.A., Johnston M., Desikan A., Fulton L., Fulton B., Majors J., Waterston R., Cohen B.A., Johnston M., Fulton L., Fulton B., Majors J., Waterston R., Cohen B.A., Johnston M., Fulton B., Majors J., Waterston R., Cohen B.A., Johnston M., Majors J., Waterston R., Cohen B.A., Johnston M., Waterston R., Cohen B.A., Johnston M., Cohen B.A., Johnston M., Johnston M. Finding functional features in Saccharomyces genomes by phylogenetic footprinting. Science. 2003;301:71–76. doi: 10.1126/science.1084337. [DOI] [PubMed] [Google Scholar]
- Dorrington R.A., Cooper T.G., Cooper T.G. The DAL82 protein of Saccharomyces cerevisiae binds to the DAL upstream induction sequence (UIS). Nucleic Acids Res. 1993;21:3777–3784. doi: 10.1093/nar/21.16.3777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elowitz M.B., Levine A.J., Siggia E.D., Swain P.S., Levine A.J., Siggia E.D., Swain P.S., Siggia E.D., Swain P.S., Swain P.S. Stochastic gene expression in a single cell. Science. 2002;297:1183–1186. doi: 10.1126/science.1070919. [DOI] [PubMed] [Google Scholar]
- Gerland U., Moroz J.D., Hwa T., Moroz J.D., Hwa T., Hwa T. Physical constraints and functional characteristics of transcription factor–DNA interaction. Proc. Natl. Acad. Sci. 2002;99:12015–12020. doi: 10.1073/pnas.192693599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Granek J.A., Clarke N.D., Clarke N.D. Explicit equilibrium modeling of transcription-factor binding and gene regulation. Genome Biol. 2005;6:R87. doi: 10.1186/gb-2005-6-10-r87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harbison C.T., Gordon D.B., Lee T.I., Rinaldi N.J., Macisaac K.D., Danford T.W., Hannett N.M., Tagne J.B., Reynolds D.B., Yoo J., Gordon D.B., Lee T.I., Rinaldi N.J., Macisaac K.D., Danford T.W., Hannett N.M., Tagne J.B., Reynolds D.B., Yoo J., Lee T.I., Rinaldi N.J., Macisaac K.D., Danford T.W., Hannett N.M., Tagne J.B., Reynolds D.B., Yoo J., Rinaldi N.J., Macisaac K.D., Danford T.W., Hannett N.M., Tagne J.B., Reynolds D.B., Yoo J., Macisaac K.D., Danford T.W., Hannett N.M., Tagne J.B., Reynolds D.B., Yoo J., Danford T.W., Hannett N.M., Tagne J.B., Reynolds D.B., Yoo J., Hannett N.M., Tagne J.B., Reynolds D.B., Yoo J., Tagne J.B., Reynolds D.B., Yoo J., Reynolds D.B., Yoo J., Yoo J., et al. Transcriptional regulatory code of a eukaryotic genome. Nature. 2004;431:99–104. doi: 10.1038/nature02800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hughes T.R., Marton M.J., Jones A.R., Roberts C.J., Stoughton R., Armour C.D., Bennett H.A., Coffey E., Dai H., He Y.D., Marton M.J., Jones A.R., Roberts C.J., Stoughton R., Armour C.D., Bennett H.A., Coffey E., Dai H., He Y.D., Jones A.R., Roberts C.J., Stoughton R., Armour C.D., Bennett H.A., Coffey E., Dai H., He Y.D., Roberts C.J., Stoughton R., Armour C.D., Bennett H.A., Coffey E., Dai H., He Y.D., Stoughton R., Armour C.D., Bennett H.A., Coffey E., Dai H., He Y.D., Armour C.D., Bennett H.A., Coffey E., Dai H., He Y.D., Bennett H.A., Coffey E., Dai H., He Y.D., Coffey E., Dai H., He Y.D., Dai H., He Y.D., He Y.D., et al. Functional discovery via a compendium of expression profiles. Cell. 2000;102:109–126. doi: 10.1016/s0092-8674(00)00015-5. [DOI] [PubMed] [Google Scholar]
- Iyer V.R., Horak C.E., Scafe C.S., Botstein D., Snyder M., Brown P.O., Horak C.E., Scafe C.S., Botstein D., Snyder M., Brown P.O., Scafe C.S., Botstein D., Snyder M., Brown P.O., Botstein D., Snyder M., Brown P.O., Snyder M., Brown P.O., Brown P.O. Genomic binding sites of the yeast cell-cycle transcription factors SBF and MBF. Nature. 2001;409:533–538. doi: 10.1038/35054095. [DOI] [PubMed] [Google Scholar]
- Jia Y., Rothermel B., Thornton J., Butow R.A., Rothermel B., Thornton J., Butow R.A., Thornton J., Butow R.A., Butow R.A. A basic helix–loop–helix-leucine zipper transcription complex in yeast functions in a signaling pathway from mitochondria to the nucleus. Mol. Cell. Biol. 1997;17:1110–1117. doi: 10.1128/mcb.17.3.1110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kadosh D., Struhl K., Struhl K. Repression by Ume6 involves recruitment of a complex containing Sin3 corepressor and Rpd3 histone deacetylase to target promoters. Cell. 1997;89:365–371. doi: 10.1016/s0092-8674(00)80217-2. [DOI] [PubMed] [Google Scholar]
- Kellis M., Patterson N., Endrizzi M., Birren B., Lander E.S., Patterson N., Endrizzi M., Birren B., Lander E.S., Endrizzi M., Birren B., Lander E.S., Birren B., Lander E.S., Lander E.S. Sequencing and comparison of yeast species to identify genes and regulatory elements. Nature. 2003;423:241–254. doi: 10.1038/nature01644. [DOI] [PubMed] [Google Scholar]
- Kuruvilla F.G., Shamji A.F., Schreiber S.L., Shamji A.F., Schreiber S.L., Schreiber S.L. Carbon- and nitrogen-quality signaling to translation are mediated by distinct GATA-type transcription factors. Proc. Natl. Acad. Sci. 2001;98:7283–7288. doi: 10.1073/pnas.121186898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee T.I., Rinaldi N.J., Robert F., Odom D.T., Bar-Joseph Z., Gerber G.K., Hannett N.M., Harbison C.T., Thompson C.M., Simon I., Rinaldi N.J., Robert F., Odom D.T., Bar-Joseph Z., Gerber G.K., Hannett N.M., Harbison C.T., Thompson C.M., Simon I., Robert F., Odom D.T., Bar-Joseph Z., Gerber G.K., Hannett N.M., Harbison C.T., Thompson C.M., Simon I., Odom D.T., Bar-Joseph Z., Gerber G.K., Hannett N.M., Harbison C.T., Thompson C.M., Simon I., Bar-Joseph Z., Gerber G.K., Hannett N.M., Harbison C.T., Thompson C.M., Simon I., Gerber G.K., Hannett N.M., Harbison C.T., Thompson C.M., Simon I., Hannett N.M., Harbison C.T., Thompson C.M., Simon I., Harbison C.T., Thompson C.M., Simon I., Thompson C.M., Simon I., Simon I., et al. Transcriptional regulatory networks in Saccharomyces cerevisiae. Science. 2002;298:799–804. doi: 10.1126/science.1075090. [DOI] [PubMed] [Google Scholar]
- Li Z., Van Calcar S., Qu C., Cavenee W.K., Zhang M.Q., Ren B., Van Calcar S., Qu C., Cavenee W.K., Zhang M.Q., Ren B., Qu C., Cavenee W.K., Zhang M.Q., Ren B., Cavenee W.K., Zhang M.Q., Ren B., Zhang M.Q., Ren B., Ren B. A global transcriptional regulatory role for c-Myc in Burkitt’s lymphoma cells. Proc. Natl. Acad. Sci. 2003;100:8164–8169. doi: 10.1073/pnas.1332764100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X., Clarke N.D., Clarke N.D. Rationalization of gene regulation by a eukaryotic transcription factor: Calculation of regulatory region occupancy from predicted binding affinities. J. Mol. Biol. 2002;323:1–8. doi: 10.1016/s0022-2836(02)00894-x. [DOI] [PubMed] [Google Scholar]
- Mai B., Breeden L., Breeden L. Xbp1, a stress-induced transcriptional repressor of the Saccharomyces cerevisiae Swi4/Mbp1 family. Mol. Cell. Biol. 1997;17:6491–6501. doi: 10.1128/mcb.17.11.6491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miled C., Mann C., Faye G., Mann C., Faye G., Faye G. Xbp1-mediated repression of CLB gene expression contributes to the modifications of yeast cell morphology and cell cycle seen during nitrogen-limited growth. Mol. Cell. Biol. 2001;21:3714–3724. doi: 10.1128/MCB.21.11.3714-3724.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moses A.M., Chiang D.Y., Kellis M., Lander E.S., Eisen M.B., Chiang D.Y., Kellis M., Lander E.S., Eisen M.B., Kellis M., Lander E.S., Eisen M.B., Lander E.S., Eisen M.B., Eisen M.B. Position specific variation in the rate of evolution in transcription factor binding sites. BMC Evol. Biol. 2003;3:19. doi: 10.1186/1471-2148-3-19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mustonen V., Lassig M., Lassig M. Evolutionary population genetics of promoters: Predicting binding sites and functional phylogenies. Proc. Natl. Acad. Sci. 2005;102:15936–15941. doi: 10.1073/pnas.0505537102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nachman I., Regev A., Friedman N., Regev A., Friedman N., Friedman N. Inferring quantitative models of regulatory networks from expression data. Bioinformatics. 2004;20(Suppl 1):I248–I256. doi: 10.1093/bioinformatics/bth941. [DOI] [PubMed] [Google Scholar]
- Odom D.T., Zizlsperger N., Gordon D.B., Bell G.W., Rinaldi N.J., Murray H.L., Volkert T.L., Schreiber J., Rolfe P.A., Gifford D.K., Zizlsperger N., Gordon D.B., Bell G.W., Rinaldi N.J., Murray H.L., Volkert T.L., Schreiber J., Rolfe P.A., Gifford D.K., Gordon D.B., Bell G.W., Rinaldi N.J., Murray H.L., Volkert T.L., Schreiber J., Rolfe P.A., Gifford D.K., Bell G.W., Rinaldi N.J., Murray H.L., Volkert T.L., Schreiber J., Rolfe P.A., Gifford D.K., Rinaldi N.J., Murray H.L., Volkert T.L., Schreiber J., Rolfe P.A., Gifford D.K., Murray H.L., Volkert T.L., Schreiber J., Rolfe P.A., Gifford D.K., Volkert T.L., Schreiber J., Rolfe P.A., Gifford D.K., Schreiber J., Rolfe P.A., Gifford D.K., Rolfe P.A., Gifford D.K., Gifford D.K., et al. Control of pancreas and liver gene expression by HNF transcription factors. Science. 2004;303:1378–1381. doi: 10.1126/science.1089769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paulsson J. Summing up the noise in gene networks. Nature. 2004;427:415–418. doi: 10.1038/nature02257. [DOI] [PubMed] [Google Scholar]
- Rajewsky N., Vergassola M., Gaul U., Siggia E.D., Vergassola M., Gaul U., Siggia E.D., Gaul U., Siggia E.D., Siggia E.D. Computational detection of genomic cis-regulatory modules applied to body patterning in the early Drosophila embryo. BMC Bioinformatics. 2002;3:30. doi: 10.1186/1471-2105-3-30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raser J.M., O’Shea E.K., O’Shea E.K. Noise in gene expression: Origins, consequences, and control. Science. 2005;309:2010–2013. doi: 10.1126/science.1105891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ren B., Dynlacht B.D., Dynlacht B.D. Use of chromatin immunoprecipitationassays in genome-wide location analysis of mammalian transcription factors. Methods Enzymol. 2004;376:304–315. doi: 10.1016/S0076-6879(03)76020-0. [DOI] [PubMed] [Google Scholar]
- Ren B., Robert F., Wyrick J.J., Aparicio O., Jennings E.G., Simon I., Zeitlinger J., Schreiber J., Hannett N., Kanin E., Robert F., Wyrick J.J., Aparicio O., Jennings E.G., Simon I., Zeitlinger J., Schreiber J., Hannett N., Kanin E., Wyrick J.J., Aparicio O., Jennings E.G., Simon I., Zeitlinger J., Schreiber J., Hannett N., Kanin E., Aparicio O., Jennings E.G., Simon I., Zeitlinger J., Schreiber J., Hannett N., Kanin E., Jennings E.G., Simon I., Zeitlinger J., Schreiber J., Hannett N., Kanin E., Simon I., Zeitlinger J., Schreiber J., Hannett N., Kanin E., Zeitlinger J., Schreiber J., Hannett N., Kanin E., Schreiber J., Hannett N., Kanin E., Hannett N., Kanin E., Kanin E., et al. Genome-wide location and function of DNA binding proteins. Science. 2000;290:2306–2309. doi: 10.1126/science.290.5500.2306. [DOI] [PubMed] [Google Scholar]
- Roberts C.J., Nelson B., Marton M.J., Stoughton R., Meyer M.R., Bennett H.A., He Y.D., Dai H., Walker W.L., Hughes T.R., Nelson B., Marton M.J., Stoughton R., Meyer M.R., Bennett H.A., He Y.D., Dai H., Walker W.L., Hughes T.R., Marton M.J., Stoughton R., Meyer M.R., Bennett H.A., He Y.D., Dai H., Walker W.L., Hughes T.R., Stoughton R., Meyer M.R., Bennett H.A., He Y.D., Dai H., Walker W.L., Hughes T.R., Meyer M.R., Bennett H.A., He Y.D., Dai H., Walker W.L., Hughes T.R., Bennett H.A., He Y.D., Dai H., Walker W.L., Hughes T.R., He Y.D., Dai H., Walker W.L., Hughes T.R., Dai H., Walker W.L., Hughes T.R., Walker W.L., Hughes T.R., Hughes T.R., et al. Signaling and circuitry of multiple MAPK pathways revealed by a matrix of global gene expression profiles. Science. 2000;287:873–880. doi: 10.1126/science.287.5454.873. [DOI] [PubMed] [Google Scholar]
- Ronen M., Rosenberg R., Shraiman B.I., Alon U., Rosenberg R., Shraiman B.I., Alon U., Shraiman B.I., Alon U., Alon U. Assigning numbers to the arrows: Parameterizing a gene regulation network by using accurate expression kinetics. Proc. Natl. Acad. Sci. 2002;99:10555–10560. doi: 10.1073/pnas.152046799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schawalder S.B., Kabani M., Howald I., Choudhury U., Werner M., Shore D., Kabani M., Howald I., Choudhury U., Werner M., Shore D., Howald I., Choudhury U., Werner M., Shore D., Choudhury U., Werner M., Shore D., Werner M., Shore D., Shore D. Growth-regulated recruitment of the essential yeast ribosomal protein gene activator Ifh1. Nature. 2004;432:1058–1061. doi: 10.1038/nature03200. [DOI] [PubMed] [Google Scholar]
- Siepel A., Haussler D., Haussler D. Phylogenetic estimation of context-dependent substitution rates by maximum likelihood. Mol. Biol. Evol. 2004;21:468–488. doi: 10.1093/molbev/msh039. [DOI] [PubMed] [Google Scholar]
- Simon I., Barnett J., Hannett N., Harbison C.T., Rinaldi N.J., Volkert T.L., Wyrick J.J., Zeitlinger J., Gifford D.K., Jaakkola T.S., Barnett J., Hannett N., Harbison C.T., Rinaldi N.J., Volkert T.L., Wyrick J.J., Zeitlinger J., Gifford D.K., Jaakkola T.S., Hannett N., Harbison C.T., Rinaldi N.J., Volkert T.L., Wyrick J.J., Zeitlinger J., Gifford D.K., Jaakkola T.S., Harbison C.T., Rinaldi N.J., Volkert T.L., Wyrick J.J., Zeitlinger J., Gifford D.K., Jaakkola T.S., Rinaldi N.J., Volkert T.L., Wyrick J.J., Zeitlinger J., Gifford D.K., Jaakkola T.S., Volkert T.L., Wyrick J.J., Zeitlinger J., Gifford D.K., Jaakkola T.S., Wyrick J.J., Zeitlinger J., Gifford D.K., Jaakkola T.S., Zeitlinger J., Gifford D.K., Jaakkola T.S., Gifford D.K., Jaakkola T.S., Jaakkola T.S., et al. Serial regulation of transcriptional regulators in the yeast cell cycle. Cell. 2001;106:697–708. doi: 10.1016/s0092-8674(01)00494-9. [DOI] [PubMed] [Google Scholar]
- Spellman P.T., Sherlock G., Zhang M.Q., Iyer V.R., Anders K., Eisen M.B., Brown P.O., Botstein D., Futcher B., Sherlock G., Zhang M.Q., Iyer V.R., Anders K., Eisen M.B., Brown P.O., Botstein D., Futcher B., Zhang M.Q., Iyer V.R., Anders K., Eisen M.B., Brown P.O., Botstein D., Futcher B., Iyer V.R., Anders K., Eisen M.B., Brown P.O., Botstein D., Futcher B., Anders K., Eisen M.B., Brown P.O., Botstein D., Futcher B., Eisen M.B., Brown P.O., Botstein D., Futcher B., Brown P.O., Botstein D., Futcher B., Botstein D., Futcher B., Futcher B. Comprehensive identification of cell cycle-regulated genes of the yeast Saccharomyces cerevisiae by microarray hybridization. Mol. Biol. Cell. 1998;9:3273–3297. doi: 10.1091/mbc.9.12.3273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stormo G.D., Hartzell G.W., III, Hartzell G.W., III Identifying protein-binding sites from unaligned DNA fragments. Proc. Natl. Acad. Sci. 1989;86:1183–1187. doi: 10.1073/pnas.86.4.1183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strich R., Surosky R.T., Steber C., Dubois E., Messenguy F., Esposito R.E., Surosky R.T., Steber C., Dubois E., Messenguy F., Esposito R.E., Steber C., Dubois E., Messenguy F., Esposito R.E., Dubois E., Messenguy F., Esposito R.E., Messenguy F., Esposito R.E., Esposito R.E. UME6 is a key regulator of nitrogen repression and meiotic development. Genes & Dev. 1994;8:796–810. doi: 10.1101/gad.8.7.796. [DOI] [PubMed] [Google Scholar]
- Tanay A., Shamir R., Shamir R. Multilevel modeling and inference of transcription regulation. J. Comput. Biol. 2004;11:357–375. doi: 10.1089/1066527041410364. [DOI] [PubMed] [Google Scholar]
- Tanay A., Gat-Viks I., Shamir R., Gat-Viks I., Shamir R., Shamir R. A global view of the selection forces in the evolution of yeast cis-regulation. Genome Res. 2004a;14:829–834. doi: 10.1101/gr.2064404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanay A., Sharan R., Kupiec M., Shamir R., Sharan R., Kupiec M., Shamir R., Kupiec M., Shamir R., Shamir R. Revealing modularity and organization in the yeast molecular network by integrated analysis of highly heterogeneous genome-wide data. Proc. Natl. Acad. Sci. 2004b;101:2981–2986. doi: 10.1073/pnas.0308661100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanay A., Regev A., Shamir R., Regev A., Shamir R., Shamir R. Conservation and evolvability in regulatory networks: The evolution of ribosomal regulation in yeast. Proc. Natl. Acad. Sci. 2005;102:7203–7208. doi: 10.1073/pnas.0502521102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wade J.T., Hall D.B., Struhl K., Hall D.B., Struhl K., Struhl K. The transcription factor Ifh1 is a key regulator of yeast ribosomal protein genes. Nature. 2004;432:1054–1058. doi: 10.1038/nature03175. [DOI] [PubMed] [Google Scholar]
- Williams R.M., Primig M., Washburn B.K., Winzeler E.A., Bellis M., de Sarrauste Menthiere C., Davis R.W., Esposito R.E., Primig M., Washburn B.K., Winzeler E.A., Bellis M., de Sarrauste Menthiere C., Davis R.W., Esposito R.E., Washburn B.K., Winzeler E.A., Bellis M., de Sarrauste Menthiere C., Davis R.W., Esposito R.E., Winzeler E.A., Bellis M., de Sarrauste Menthiere C., Davis R.W., Esposito R.E., Bellis M., de Sarrauste Menthiere C., Davis R.W., Esposito R.E., de Sarrauste Menthiere C., Davis R.W., Esposito R.E., Davis R.W., Esposito R.E., Esposito R.E. The Ume6 regulon coordinates metabolic and meiotic gene expression in yeast. Proc. Natl. Acad. Sci. 2002;99:13431–13436. doi: 10.1073/pnas.202495299. [DOI] [PMC free article] [PubMed] [Google Scholar]