Vibrational spectroscopy and normal mode analysis of Fe(II) octaethylporphyrin

Abstract

The normal mode spectrum for the four-coordinated heme compound Fe(II) octaethylporphyrin, Fe(OEP), has been determined by refining force constants to the experimental Fe vibrational density of states measured with nuclear resonance vibrational spectroscopy (NRVS). Convergence of the calculated spectrum to the data was achieved by first imposing D₄ symmetry on the model structure as well as the force constants, progressively including different internal coordinates of motion, then allowing the true C_i (or S₂) point group symmetry of the C_i¹ Fe(OEP) crystal structure. The NRVS-refined normal modes are in good agreement with Raman and IR spectra at high frequencies. Prior density functional theory predictions for a model porphyrin are similar to the core modes computed with the best-fit force field, but significant differences between D₄ and C_i modes underline the sensitivity of porphyrin Fe normal modes to structural details. Some differences between the C_i best fit and the NRVS data can be attributed to intermolecular contacts not included in the normal mode analysis.

1.Introduction

Normal modes are long-lived characteristic vibrations of any system of coupled atomic oscillators, from diatomic molecules to complex proteins. Peaks observed with vibrational spectroscopies, e.g infrared, Raman, and inelastic neutron scattering, are experimental manifestations of normal modes. Normal mode analysis relies on interatomic force constants that couple each atom to every other atom, because they determine the mode frequencies and amplitudes. These same force constants also constrain the time-evolution of a molecule’s conformation, and hence are essential inputs for molecular dynamics simulations using all-atom empirical potentials^1-4.

For heme proteins in particular, their complexity suggests a conceptual framework for investigating heme dynamics: Begin with the core porphyrin molecule, then the simplest 4-coordinated Fe porphyrin compounds, followed by more complex 5 and 6-coordinated hemes that mimic binding in proteins, and finally the complete protein incorporating the protoporphyrin-IX heme molecule^5–7. It will be useful to compare normal modes from porphyrin compounds to those in heme proteins, to determine how the coupling of the protein to the heme may selectively enhance or suppress various modes important for ligand binding and other biochemical functions⁸. While the various parts of this framework have long been pursued using both vibrational spectroscopies and computational approaches^6,9–13, new opportunities for progress are now possible with nuclear resonance vibrational spectroscopy (NRVS) due to its unique capability of measuring Fe-specific vibrational frequencies and amplitudes¹⁴.

In this report we present experimental NRVS results and a normal mode analysis for Fe(II) octaethylporphyrin, Fe(OEP), one of the simplest 4-coordinated Fe porphyrins. The skeletal iron porphyrin structure is a planar complex of D_4h point group symmetry, with one iron, four nitrogen and twenty carbon atoms and with eight pyrrole and four meso binding sites; Fe(OEP) binds ethyl groups at the pyrrole sites (Figure 1). Empirical force constants for Fe(OEP) are adjusted to have the output of normal mode calculations fit the Fe vibrational density of states (VDOS) obtained from NRVS data, and also to fit the frequencies of Raman and infrared (IR) lines. This unique technique offers a significant advance in characterizing the low frequency dynamics of Fe porphyrins, which are critical for understanding the chemistry that can occur at the active site.

Figure 1.

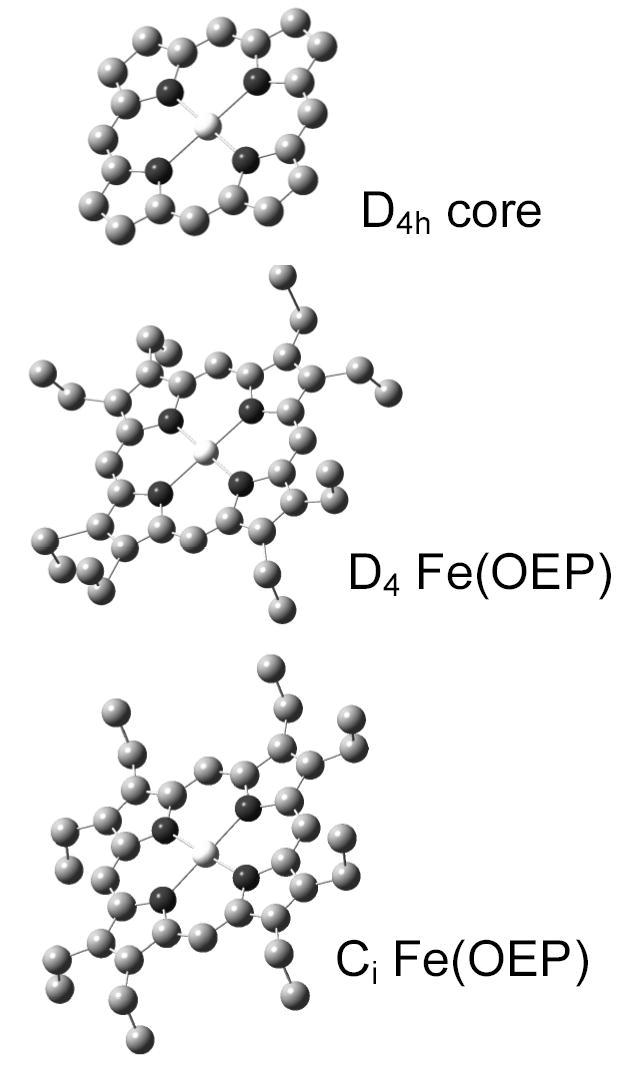
Top – structure of the 25-atom porphyrin core, a planar arrangement of Fe, four N, and 20 C atoms with four-fold (point group D_4h) symmetry. Center – a model for Fe(II) octaethylporphyrin with D₄ symmetry for the eight ethyl groups bound to the pyrrole carbons, a useful intermediate for normal mode refinements. Bottom – the structure of Fe(II) octaethylporphyrin with the true S₂ point group symmetry (space group C_i¹).

Normal modes for metalloporphyrins have been calculated before using empirical force constants as well as ab initio density functional theory (DFT)^11,15–18. Predicted normal mode frequencies are most often compared to Raman and infrared absorption spectra to assess the validity of the calculation. Raman and IR data reveal relatively little, however, about important low frequency Fe modes involving delocalized motions of multiple atoms. This problem is partially remedied by NRVS, an x-ray synchrotron-based technique that can determine the complete VDOS of the ⁵⁷Fe atoms in a suitable specimen. NRVS has been extensively described elswhere^14,19–26. We note here two especially relevant properties: only the motion of Fe atoms is detected, and all modes with significant Fe motion (in the direction of the x-ray beam) are observed. Unlike Raman scattering, for example, there is no question that each peak is due to Fe motion. There also are no optical selection rules to obscure Fe modes. This makes the deduced VDOS an ideal data set for guiding normal mode calculations whenever Fe is the primary focus^27–30.

A difficulty with normal mode analysis is the large number of parameters in the problem. The number of non-zero normal modes is 3n-6, where n is the number of atoms in the molecule. Each atom is subject to a force field that is typically described in terms of stretch, bend, torsion, and out-of-plane force constants (or internal coordinates)³¹. Furthermore it is often the case that phenomenological “off-diagonal” force constants connecting different parts of a molecule are needed. A calculation also requires the equilibrium position of each atom. The number of parameters thus far exceeds the number of terms needed to describe any given data set, indicating that the problem is manifestly underdetermined. This somewhat overstates the difficulty, however, because these parameters are not all independent. In the normal mode calculations described below, the number of parameters is significantly reduced by imposing the molecular symmetry on the set of force constants. We employed a step-by-step procedure that allowed efficient refinement of the normal mode spectrum to the NRVS results, described below.

2. Sample preparation and NRVS measurement

The preparation of ⁵⁷Fe(OEP) began with the metallation reaction using 95% ⁵⁷Fe enriched iron based on the method of Landergren and Baltzer³². 33 mg (0.20 mmol) of 95% ⁵⁷Fe enriched Fe₂O₃ was weighed into a Schlenk flask along with a stir bar, and 5 mL of concentrated HCl was added via pipette. The solution was stirred while heated in an oil bath at 60° C, whereupon the solid material dissolved giving a greenish yellow solution. The solution volume was reduced to near dryness under vacuum. 100 mL of chlorobenzene, distilled over P₂O₅, was added and the solution refluxed at 130° C for 2 hours. The solvent was distilled off and the solvent volume was reduced to about 40 mL. The traces of H₂O form an azeotrope with the C₆H₅Cl and is distilled off. As the solution volume is reduced, the solution changes color to a dark sandy brown.

1.2 mmol of the free-base porphyrin [H₂(OEP)] was weighed into a separate Schlenk equipped with a stir bar and 10 mL of C₆H₅Cl, distilled over P₂O₅, and 0.5 mL of 2,4,6-trimethylpyridine was added. The solution was stirred to ensure complete dissolution before being subjected to three freeze/pump/thaw cycles. Care was taken to ensure the resulting solution was kept under an anaerobic atmosphere at all times since the presence of trace amounts of O₂ are known to reduce the efficiency of the metallation reaction. The solution was then transferred via cannula to the Schlenk containing the ⁵⁷FeCl₂ solution in C₆H₅Cl.

The resulting solution was stirred overnight while being heated in an oil bath at 80° C. Complete metallation was confirmed by UV-vis spectroscopy and the absence of any traces of fluorescence. The solution was then transferred to a 100-mL round-bottomed flask and rotavapped to dryness. The resulting solid was redissolved in about 50 mL of CH₂Cl₂ and washed with several portions of H₂O to remove any excess ⁵⁷Fe. The solution was then shaken with a dilute solution of HCl to ensure complete conversion to [⁵⁷Fe(OEP)(Cl)] prior to being dried over MgSO₄. The solution volume was reduced on a rotary evaporator and the solid product was obtained by recrystallization from CH₂Cl₂/methanol. [⁵⁷Fe(OEP)]₂O was obtained by shaking the ferric chloride with aqueous NaOH solution prior to drying over MgSO₄ and recrystallization from CH₂Cl₂/hexanes.

[⁵⁷Fe(OEP)] is extremely susceptible to oxidation even in the solid state; the resulting product is the mu-oxo dimer [⁵⁷Fe(OEP)]₂O. Extreme care must be taken in the preparation and handling of this material to prevent exposure to even trace amounts of O₂. The reduction to yield the four-coordinate species was carried out using a local modification of the method reported by Stolzenberg³³. 150 mg of [⁵⁷Fe(OEP)]₂O was dissolved in 15 mL of benzene distilled over Na/benzophenone. The solution was stirred to ensure complete dissolution and then subjected to three freeze/pump/thaw cycles. 1.5 mL of ethanethiol was added via pipette and the solution was stirred overnight. A color change from a greenish-brown to a vivid red color was observed, the latter color is characteristic of the reduced species. The solution of [⁵⁷Fe(OEP)] was reduced to dryness under vacuum. The solid material, still sealed inside the Schlenk was transferred to the drybox and the Schlenk opened once inside. The resulting powder was found to be extremely staticky and proved difficult to handle. To combat this problem, a small amount of Apiezon M grease was applied to the end of a long spatula and this was scraped around the inside of the Schlenk whereupon the solid material was found to adhere to the grease. The spatula was removed and the powder/grease mixture smeared on a glass slide before being mixed thoroughly to form a homogeneous mull that was transferred to the NRVS sample holder. A small portion of this mull was transferred to a Mössbauer cup and the identity and purity of the sample confirmed by Mössbauer spectroscopy. At 4.2 K, the values of the isomer shift (0.68 mm/sec) and the quadrupole splitting (1.64 mm/sec) agree with those values reported previously³⁴.

NRVS measurements were conducted at the XOR-CAT sector 3-ID-D station of the Advanced Photon Source, Argonne National Laboratory. Specimens were placed in machined sapphire sample holders and cooled to about 20 K. The resonant absorption of incident x-rays was monitored by Fe K fluorescence observed with a time-resolving Si avalanche photo-diode detector. Iron dynamics are probed by measuring the x-ray absorption spectrum over a typical energy range of +/- 700 cm⁻¹ about the Mössbauer resonance. By scanning the x-ray energy both below and above the resonance energy, the Stokes and anti-Stokes components of the absorption spectrum are obtained. This provides a direct measure of the sample temperature, and allows for the extraction of the Fe partial vibrational density of states (VDOS) using the PHOENIX program^23,28,35.

Figures 2 and 3 both show the Fe VDOS plotted against various normal mode simulations, as discussed in detail below. Regarding the question of possible perturbation of these results by the host Apiezon M grease, we point out first of all that there was no visual evidence that the crystalline particles dissolved into this grease. If one conservatively assumes a typical particle size of only one micron in diameter, the fraction of porphyrin molecules on the surface is no more than 0.1% of the total, making direct surface interactions essentially unobservable. We also point out that four-coordinate FeOEP is highly reactive. If a significant fraction of these molecules increased the Fe coordination via some type of intermolecular interaction with the grease, one might expect features similar to the ligand modes observed at higher frequencies in other 5 and 6-coordinated Fe porphyrins^27–30. No such features are seen, with nearly all spectral weight ending near 360 cm⁻¹, below that of any of the higher coordinated compounds (which also employed grease for sample mounting).

Figure 2.

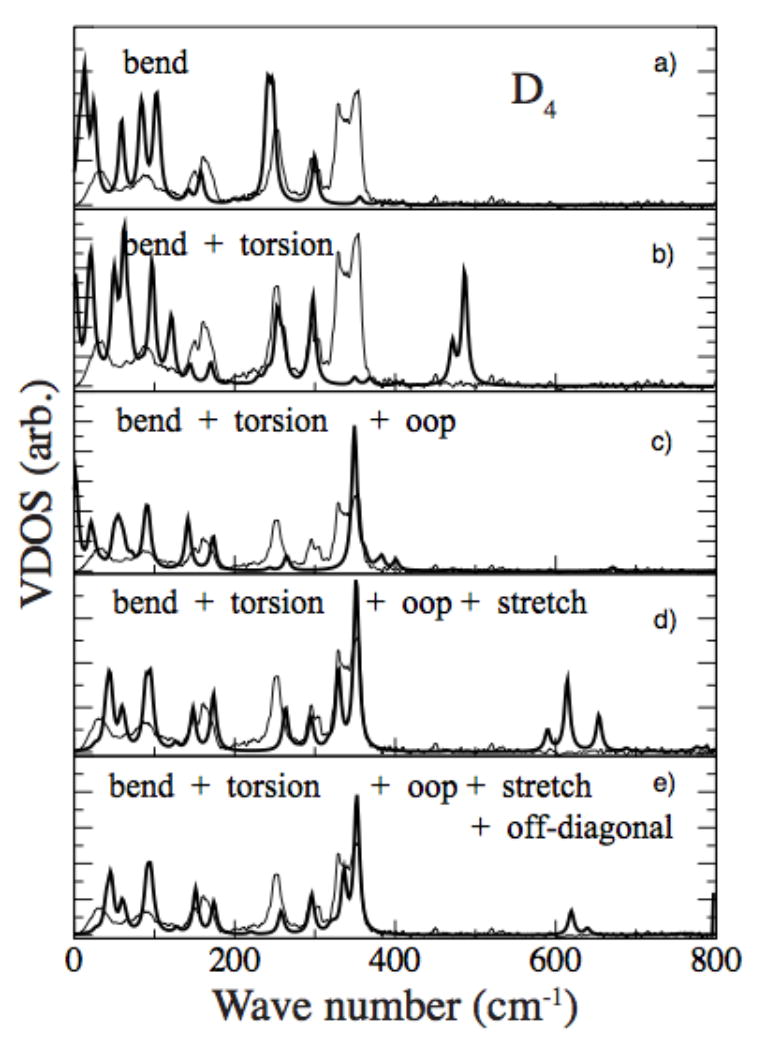
Comparison of intermediate fits to the NRVS Fe vibrational density of states (thin line). Top panel (a) shows best fit when only bend force constants are non-zero, followed successively with the addition of torsions (b), then out-of-plane (c), stretch force constants (d), and finally the effect of off-diagonal interactions (e). The force field and structure are constrained to have D₄ symmetry.

Figure 3.

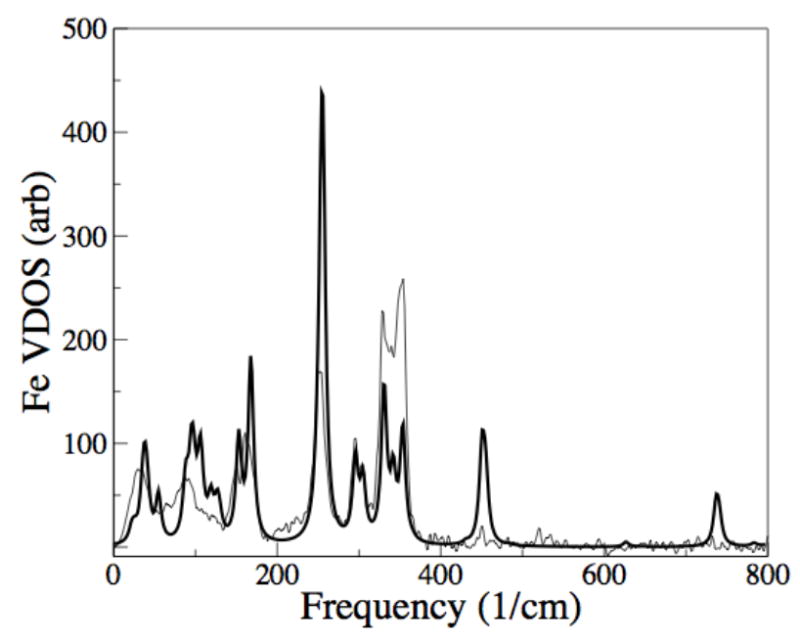
Best-fit Fe(OEP) vibrational density of states (heavy line) using a refined force field with C_i symmetry, compared with NRVS measurement (light line).

3. Normal Mode Calculations

The molecular structure of Fe(OEP) has been determined by x-ray crystallography³⁶. Force fields for similar metalloporphyrins are available from previous efforts to fit resonance Raman data or infrared absorption data, sometimes in conjunction with isotopic substitution to help assess mode character^16–18. As was the case in all prior NRVS studies of porphyrins, however, these force fields did not reproduce the salient features in the measured Fe VDOS^27–30. With a single molecule in the unit cell, the point group symmetry of the molecule is C_i (or S₂), which contains the inversion symmetry element. We found it computationally more effective to first assume a higher symmetry D₄ structure for the Fe(OEP) molecule, with ethyl group displacements alternating between above and below the porphyrin plane (Fig. 1). After getting a good fit, that force field was then used as the starting point for the C_i¹ structure.

Fe(OEP) consists of one iron, 4 nitrogen and 36 carbon atoms, leading to 117 modes (=3n-6) of finite frequency. (Hydrogen atoms are treated by adding their mass to an adjacent carbon atom.) We follow standard computational procedures for solving the eigenvalue equations for the normal modes and representing the solution in terms of the Fe vibrational density of states²⁷ for direct comparison with the NRVS output, including convolution with the 8 cm⁻¹ instrumental resolution. The diagonal elements of the force constant matrix include 48 stretch, 78 bend, 136 torsion, and 78 out-of-plane force constants; interaction force constants are represented by off-diagonal terms. The matrix has a dimension of 334 x 334, illustrating the underdetermined nature of normal mode analysis in molecules of this size.

To simplify the problem, we first impose D₄ symmetry on both the structure and the force field. (There are four two-fold rotation axes in the porphyrin plane, giving the molecule a four-fold perpendicular rotation axis.) This reduces the force field to only 7 stretch group force constants, 12 bend group force constants, and 17 torsion group force constants. For simplicity the 78 out-of-plane bend force constants are assigned the same nominal value; the final best fit was fairly insensitive to variations in these. This yields 37 parameters to make a best fit refinement to VDOS data consisting of about ten peaks of different heights, widths and frequencies.

We use the force field from a closely related molecule, chloro iron octaethylporphyrin, Fe(III)OEP-Cl²⁹, as the starting point for the Fe(OEP) calculations. To remove some of the randomness in varying force constants while refining the normal mode spectrum to the measured VDOS, we developed a systematic protocol that proved to efficiently converge to a good fit. Typical porphyrin force constants have stretch constants with the largest values (usually 1-10 mdyn/Å). Next are bending force constants (0.1-1 mdyn/Å), then torsion and out-of-plane constants (0.001-0.5 mdyn/Å). Examining the effects of these groups separately, we found that the bends had the largest role in the vibrations. Hence, we begin the normal mode analysis by considering only the groups of bend forces, setting all others to zero, that converged to the fit shown in Figure 2a. The next step was introducing torsion force constants one at a time, keeping bends untouched, then adding the out-of-plane force constants (Fig. 2c), and the stretch force constants (Fig 2d). Next, interaction force constants (off-diagonal terms) were introduced; this best-fit normal mode spectrum for D₄ symmetry is shown in Figure 2e. The final step was to use this best-fit force field as the starting point for the C_i structure, which quickly led to the final best-fit normal mode spectrum shown in Figure 3.

To compare the character of Fe(OEP) modes with core porphyrin modes, we use the final best-fit force constants from the C_i Fe(OEP) structure to calculate the normal modes of the D_4h 25-atom core porphyrin (Fig 1). We then calculate the overlap (inner product) between the eigenvectors of each Fe(OEP) mode and the set of core modes. Inspection of the core eigenvectors, as well as the potential energy distributions (PEDs) among the various bonds involved, allowed specific modes to be identified with the conventional labeling scheme, e.g. ν₅₀, ν₅₃, γ₉, etc^15,37-39.

The overlap with the core for Fe(OEP) modes with the largest Fe displacements is given in Table 1, along with PEDs and an “assignment” of the calculated normal mode in terms of the core modes with largest overlap. Because the dimensionality of the Fe(OEP) eigenvectors is greater than the core’s, the elements corresponding to the extra ethyl components were dropped to make them equal. These truncated eigenvectors no longer comprise a complete orthonormal basis set, but still reflect the general composition of each Fe(OEP) mode in terms of core modes.

Table 1.

Overlap of certain best-fit Fe(OEP) normal modes (with true C_i point group symmetry) with core porphyrin modes. The second column lists the bonds that have most of the potential energy associated with the calculated normal mode, which is useful for comparing these modes with the results of other calculations. The third column gives an approximate assignment in terms of core porphyrin modes. Core modes for the remaining columns were calculated using the same C_i force field, applied to the 25-atom porphyrin core structure (1 Fe, 4 N, & 20 C atoms with planar D_4h symmetry). The C_i normal modes were truncated to match the dimensionality of the core modes (dropping the outermost ethyl components); this eliminates the orthonormality of the eigenvectors, accounting for overlap totals in excess of unity for many modes. Although assignments are made (third column), in every case there is significant overlap with multiple core modes, illustrating the limited usefulness of using core modes.

			Overlap with core modes
Ci mode Freq (cm−1)	Potential Energy Distribution (%)	Core mode Assignment	γ7	γ9	ν50a	ν50b	ν51a	ν51b	ν52a	ν52b	ν53
54	δ BC-XC-YC3,7 (5)	γ9	1	46	19	2	13	23	11	9	1
95	δ BC-XC-YC4,6,8 (45)	γ7	20	13	5	8	-	8	2	3	1
106	δ BC-XC-YC2,3 (21)	ν52	7	-	2	3	3	9	6	11	4
153	δ N-AC-BC1,3 (22)	ν52+γ7	19	1	18	4	14	16	45	37	19
168	δ N-AC-BC2 (28)+ν FeN4 (10)	ν52+γ7	30	8	4	7	3	15	19	6	9
254	δ AC-N-AC3,7 (18)+ν FeN2,4 (37)	ν51,52	-	1	7	11	41	8	3	25	2
256	δ AC-N-AC1,5,8 (22)+ν FeN1,3 (47)	ν51,52+γ7	30	13	1	1	27	9	27	26	13
	ν FeN1,3 (10)+δ AC-BC-XC7,8 (12)
296	+δ AC-BC-BC3,4,7,8 (41)	ν51,52,53	14	9	19	11	39	26	39	38	41
305	δ AC-BC-XC5,6 (16)+δ AC-BC-BC1,2,5,6 (40)	ν51,53+γ7	35	24	1	9	16	31	19	12	4
331	τ N-N-N-Fe1,2,3,4 (64)	ν50,51+γ7	26	3	22	4	12	22	17	12	8
354	δ N-AC-MC (25)+ν FeN2,4 (12)	ν50,53	4	10	9	48	5	7	2	3	4
450	ν AC-N-AC3,7 (12)+δ AC-BC-XC3,7 (20)	ν50+γ7	20	3	6	21	14	2	12	3	13
757	ν AC-BC7,8 (10)+ν BC-XC7,8 (10)	γ9	8	28	7	3	9	1	14	10	10

4. Results

Refining the force constants to the NRVS data is a particularly stringent constraint on modes that have large Fe atomic displacements, which because of the large Fe mass tend to be at lower frequencies and delocalized among multiple atoms. The best fit normal modes can also be checked against Raman and IR spectra, however. These include optically-allowed modes at higher frequencies that tend to be more localized, with little if any Fe participation. Table 2 lists the 22 normal modes with the highest frequencies, as well as the PEDs for certain bonds and an assignment based on those PEDs, and compares them to the nearest line in either a published Raman spectrum⁴⁰ or an IR spectrum⁴¹. Good agreement is seen, with only a few of the 22 deviating by more than 1% from the Raman or IR value.

Table 2.

Comparison with Raman and IR spectroscopies. The best-fit normal modes at high frequencies (first column) are listed with those bonds that have the highest percentage of potential energy for that mode (second column). This allows these calculated modes to be compared to standard characterizations of porphyrin normal modes and to assign them a mode label (third column). The difference of the calculated frequencies with the nearest Raman line from the data of Kitegawa et al.³⁹ are shown in the fourth column, and with the nearest line in the infrared spectrum from Kincaid et al.⁴¹ in the final column.

Normal Mode frequency (cm−1)	Potential Energy Distribution, %	Mode Assignment	Shift from Raman (cm−1)	Shift from IR (cm−1)
1643	ν AC-MC (8)+ ν AC-BC (37)	ν10	3
1609	ν AC-MC (46)+ ν AC-BC (13)	ν19	-1
1539	ν AC-BC (16)+ ν BC-XC (12)	ν11	-8	-12
1507	ν AC-MC (14)+ ν AC-BC (25)	ν3	3
1414	ν BC-XC (10)+ ν XC-YC (21)	ν29	6
1371	ν BC-XC (5)+ ν XC-YC (27)	ν20	-6
1367	ν BC-BC (7)+ ν XC-YC (28)	ν12	3
1317	ν BC-BC (9)+ ν XC-YC (27)	ν17	2
1259	τ Fe-AC-AC-N (18)	ν13		-17
1217	ν AC-N (6)+ ν XC-YC (23)	ν43	1
1156	ν AC-BC (6)+ ν XC-YC (11)	ν22		2
1129	ν BC-XC (9)+ ν BC-BC (13)	ν5		12
982	ν AC-N (12)+ ν AC-MC (31)	ν45		-9
821	τ AC-BC-XC-BC (29)	ν32		-9
757	ν AC-BC (5)+ ν BC-XC (5)	ν24		5
741	ν AC-BC (24)+ ν BC-XC (16)	ν47		-3

The overlap results (Table 1) clearly show that all Fe(OEP) normal modes exhibit considerable mixing of in-plane and out-of-plane core porphyrin modes. Fe(OEP) modes are conveniently separated into three groups, however: in-plane vibrations of the porphyrin core, out-of-plane vibrations of the porphyrin core, and out-of-plane ethyl vibrations. We can compare Fe(OEP) results with trends seen in several other heme model compounds: chloro iron octaethylporphyrin, Fe(III)(OEP)Cl, which has a monatomic chloride ligand²⁹; nitrosyl iron tetraphenylporphyrin, Fe(II)(TPP)NO, having a diatomic ligand and four meso-bound phenyl groups instead of the eight ethyls²⁸; 2-methylimidazole iron tetraphenylporphyrin, Fe(II)(TPP)(2MeIm), where an imidazole complex is the sole ligand²⁷; and carbonmonoxy 1-methylimidazole iron tetraphenylporphyrin, Fe(II)(TPP)(1MeIm)CO, with both a diatomic ligand and an imidazole complex³⁰. Note that the iron atom in Fe(OEP) is four-coordinated, while the other model compounds are either 5 or 6-coordinated.

Twelve different modes between 106 and 450 cm⁻¹ have large overlap with ν₅₀, ν₅₁, ν₅₂, and ν₅₃ porphyrin core in-plane modes (and sometimes also with the γ₇ out-of-plane mode). For comparison, the range for similar in-plane modes is 135-284 cm⁻¹ for Fe(OEP)-Cl, 237-406 cm⁻¹ for Fe(TPP)NO, 244-471 cm⁻¹ for Fe(TPP)(2MeIm), and 222-406 cm⁻¹ for Fe(TPP)(1MeIm)CO. In general terms, it appears that these more complex compounds have in-plane modes weighted towards somewhat higher frequencies than found in the simpler, 4-coordinated Fe(OEP).

The out-of-plane motions in Fe(OEP) are clearly seen in modes at 54 and 95 cm⁻¹, and with substantial in-plane mixing at 153, 168, and 305 cm⁻¹. A comparison with the more complex model compounds reveals several trends: 1) all have a prominent γ₉ mode in the range 70-80 cm⁻¹, with the 54 cm⁻¹ Fe(OEP) mode the exception; 2) out-of-plane modes hybridize with motions of the ethyls and phenyls to produce low frequency modes in the 20-60 cm⁻¹ range; and 3) where unligated Fe(OEP) has many modes of mixed in-plane and out-of-plane character, the presence of ligands stimulates multiple distinct modes where out-of-plane porphyrin motion couples with Fe-ligand motions in the 200-600 cm⁻¹ range.

The ethyl and phenyl groups contribute most significantly to the lowest frequency modes in each of the model compounds, and typically this is also the region with the poorest fit to the data. NRVS measurements were made on bulk, polycrystalline powder specimens, but the normal mode calculations describe a single, isolated molecule. All inter-molecular couplings are ignored, yet these are certainly important for some modes that involve components of the heme in direct contact with adjacent molecules. Prominent ethyl modes are predicted for 33 cm⁻¹ and 67- cm⁻¹ in Fe(OEP), where the data however show a continuum. We suggest that the role of the ethyls in intermolecular contacts make them less accurately modeled by the single-molecule normal mode calculations. As a test, we repeated the calculations with the same set of the force constants and structure after artificially doubling the mass of carbon at the end of each ethyl group. Since this was found to cause large shifts in peaks below 100 cm⁻¹ but not in the region 100 cm⁻¹ – 600 cm⁻¹, we conclude that intermolecular contacts at the ethyls are likely to cause disagreement between single-molecule normal mode analysis and NRVS data below 100 cm⁻¹. We also call attention to the normal mode predicted at 757 cm⁻¹, but not seen in the data (Figure 3). Modes similar to this were observed throughout much of the refinement process, and physically reasonable adjustments to the force constants failed to suppress them. Analyses of the other model compounds discussed above did not lead to Fe VDOS peaks at such high frequencies, suggesting this may be associated with the unligated condition of Fe(OEP). Examination of the associated eigenvector reveals substantial participation of the ethyl groups. Furthermore the calculation with doubled mass of the terminal ethyl carbon atom that shifted the ethyl modes below 100 cm⁻¹ also caused a large shift in this mode, while leaving the modes in the 100-600 cm⁻¹ range largely unperturbed. We conclude, therefore, that this predicted mode is not seen in NRVS due to damping by the (neglected) intermolecular contact forces that also affect the ethyl modes below 100 cm⁻¹.

Density functional theory (DFT) provides an ab initio approach to calculating vibrational dynamics in systems of increasing size and complexity^11,42–46. Recent work has also utilized NRVS measurements to validate DFT predictions of the Fe VDOS for Fe(II)(TPP)NO, with good success for many of the porphyrin modes. (Standard functionals proved to be inadequate for accurately representing the Fe-NO interaction, however, causing several ligand modes to disagree with the NRVS data.) DFT calculations were also performed by Kozlowski et al.¹⁰ on a model Fe porphyrin compound with eight methyl substituents arranged in a planar D_4h conformation. As shown in Table 3, these results are in fairly good agreement with normal modes of the D_4h 25 atom porphyrin core, using the force field from the NRVS-refined best fit on the D₄ Fe(OEP) structure. (The overall consistency between DFT and the normal mode refinement to NRVS data is strong evidence that both approaches can describe the overall Fe dynamics of this molecule with reasonable accuracy.) While both the NRVS-refined modes and the DFT modes give similar results for the core, comparison with the full C_i¹ spectrum shows that having non-planar ethyl substituents in the true molecular symmetry leads to single core modes overlapping with multiple Fe(OEP) modes over wide frequency ranges. That is, the additional degrees of freedom arising from the ethyls is enough to cause the character of a core mode to be hybridized among several modes of the actual molecule.

Table 3.

Calculated normal mode dependence on peripheral substituent configuration. Mode labels in the first column refer to porphyrin core modes with large Fe amplitudes. The porphyrin core normal mode analysis (second column) lists the wave number (cm⁻¹) calculated for these modes for the D_4h 25-atom skeletal structure (1 Fe, 4 N, 20 C; hydrogen masses are added to the 8 pyrrole carbons), using the force field derived from the C_i best fit to the NRVS data on Fe(OEP). The next column reprints a published DFT calculation on the porphyrin core plus eight methyl substituents in a planar D_4h conformation¹⁰. These are in generally good agreement with the porphyrin core NMA results. The final column summarizes results from Table 1 for the C_i point group (C_i¹ space group) structure. Including the true symmetry and non-planar structure of the ethyl substituents eliminates any direct correspondence with core modes for several normal modes, including the absence of any mode with significant ν₈ symmetry.

Mode	Porphyrin core (D4h) (NMA)	Core + methyls (D4h) (DFT)	FeOEP (Ci) (NMA)
γ9	70	65	54
γ8	245	234	-
γ7	345	380	168,256,305
ν53	282	290	296
ν52	188	178	153,256
ν51	240	233	254
ν50	368	343	354

5. Conclusions

NRVS measurements of the Fe vibrational density of states for one of the simplest porphyrins, Fe(II) octaethylporphyrin, were used to refine the force field for a normal mode analysis that yielded good agreement with NRVS, Raman, and IR spectroscopies, and also with density functional theory predictions. This experimental validation of the normal mode spectrum puts the understanding of core porphyrin dynamics on firmer ground, providing a reference for comparison with more complex heme compounds and heme proteins. It will be especially useful to use this force field as well as those for the 5 and 6-coordinated Fe porphyrins whose normal mode spectra have been refined to NRVS data, to explore the underlying physical causes of the dependence of porphyrin dynamics on the Fe coordination state. Because the normal mode analysis assumes only an isolated molecule as opposed to a periodic crystalline array, certain calculated modes especially at low frequencies are not in good agreement with the NRVS data. Better fits to the NRVS data will likely require explicit treatment of intermolecular forces, and NRVS measurements on single crystals of Fe(OEP) would further constrain the best-fit force field.