Reinforcement and the Genetics of Hybrid Incompatibilities

Abstract

Recent empirical studies suggest that genes involved in speciation are often sex-linked. We derive a general analytic model of reinforcement to study the effects of sex linkage on reinforcement under three forms of selection against hybrids: one-locus, two-locus, and ecological incompatibilities. We show that the pattern of sex linkage can have a large effect on the amount of reinforcement due to hybrid incompatibility. Sex linkage of genes involved in postzygotic isolation generally increases the strength of reinforcement, but only if genes involved in prezygotic isolation are also sex linked. We use exact simulations to test the accuracy of the approximation and find that qualitative predictions made assuming weak selection can hold when selection is strong. Our simulations also show that incompatibilities that evolve in allopatry by drift or weak selection are likely to be lost by swamping during secondary contact, even when selection against hybrids is strong.

A growing body of empirical work suggests that many genes involved in speciation are sex linked (Grula and Taylor 1980; Heisler 1984; Reinhold 1998; Ritchie 2000; Iyengar et al. 2002; Lindholm and Breden 2002; SÆtre et al. 2003). We have also learned that intrinsic hybrid incompatibilities are often the result of epistatic interactions between two or more loci (Coyne and Orr 2004), typically involving both autosomal and sex-linked genes (Schartl 1995; Presgraves 2003; Barbash et al. 2004). Does sex linkage of genes involved in pre- and postzygotic isolation promote speciation?

Postzygotic isolation is thought to evolve through the accumulation of genetic incompatibilities during allopatric separation. Prezygotic isolation can evolve through reinforcement, which is the evolution of increased prezygotic isolation as a result of selection against hybrids (Dobzhansky 1940; Blair 1955; Howard 1993). Empirical evidence for reinforcement comes from studies of insects, birds, fish, amphibians, and other taxa (Howard 1993; Coyne and Orr 2004).

Theoretical studies of reinforcement have explored several genetic and geographic situations, demonstrating that reinforcement is expected under general conditions (Kirkpatrick and Servedio 1999; Kirkpatrick 2000, 2001; Kirkpatrick and Ravigné 2002; Lemmon et al. 2004). Kirkpatrick (2001) studied reinforcement due to ecological incompatibilities in haploids, finding that the amount of reinforcement increases rapidly (quadratically) with increasing divergence in the ecological trait. Theoretical studies have also demonstrated that increased linkage between incompatibility loci generally decreases the amount of reinforcement (Kirkpatrick and Servedio 1999; Servedio and SÆtre 2003). The only study considering the effects of sex linkage is a simulation study by Servedio and SÆtre (2003), who compared the amount of reinforcement expected when all loci are autosomal to the amount expected when all loci are Z-linked. They concluded that sex linkage enhances reinforcement. Servedio and Sætre did not, however, consider incompatibilities between autosomal and sex-linked genes, which are quite common in nature (Schartl 1995; Presgraves 2003; Barbash et al. 2004). What is missing from the theoretical literature is an analytic model of reinforcement that can accommodate any pattern of sex linkage and any number of incompatibility genes.

In this article, we derive a general analytic model of reinforcement that allows for any form of pre- and postzygotic isolation. We study the effects of sex linkage by applying the general model to three specific types of postzygotic isolation (hybrid incompatibility): selection at a single locus, selection on two incompatible loci, and selection on an ecological intermediate. We focus on the evolution of prezygotic isolation (female preference) on an island population that hybridizes with migrants arriving from a continental population. There are several reasons why this situation is of interest. First, islands are a prolific source of new species (Mayr 1963). Second, the assumption is not as restrictive as it first appears. This model will, for example, apply to cases where migration is two-way but selection or some other force constrains the evolution of speciation genes in one population. Third and most importantly, the measure of reinforcement is clear. Reinforcement is simply the amount of divergence in the preference between the island and the continent. When selection does not act against hybridization, the preference on the island will match that of the continent because migration will reduce any initial divergence in the preference to zero. Any divergence in the preference that remains, then, is a result of reinforcement.

Our model suggests that sex linkage of hybrid incompatibility genes enhances reinforcement, but only when the female preference genes are also sex-linked. We also show that autosome–X (or autosome–Z) incompatibilities are favorable to reinforcement regardless of whether the preference genes are autosomal or X-linked (or Z-linked). We test the accuracy of the approximations using exact four-locus simulations.

ANALYTIC MODEL

Notation and assumptions:

Our model describes the evolution of biallelic loci in a diploid, sexually reproducing population. The notation, which follows Kirkpatrick et al. (2002), is described in detail below and summarized in the appendix. We say that genes carried by an individual occupy positions. A position is defined to be the locus at which a gene resides, the sex of the individual carrying it, and the sex of the individual from which it was inherited. Four positions exist for an autosomal locus, three exist for an X-linked (Z-linked) locus, and one exists for a Y-linked (W-linked) locus. At an autosomal locus i, for example, the gene carried by a female and inherited from a female (the individual's mother) is denoted i_ff, while the gene she inherited from a male (her father) is written i_fm. Segregating at each locus are two alleles, denoted 0 and 1. On the island, the frequency of allele 1 at position i (where i could represent i_ff, i_fm, i_mf, or i_mm) is denoted p_i, with q_i = 1 − p_i. Loci may be linked or unlinked.

We divide the loci into three nonoverlapping sets: one containing the female preference loci, one containing the male trait loci, and one containing the hybrid incompatibility loci. These sets are denoted P, T, and H, respectively. The set of all positions in females that affect the preference is written P_f. With n autosomal loci, for example, there are 2n positions in this set. Each set may contain any number of loci. We make no assumptions about the type of natural and sexual selection on the male trait, which means that any type of mating system is applicable.

A female's mating preference phenotype P and a male's display trait phenotype T are allowed to be any aspect of their phenotypes that affects who they are likely to mate. For simplicity, we assume that the genes affecting the preference and trait have additive effects and that there is no imprinting (that is, alleles inherited from mothers and fathers are expressed equally). The female preference loci are assumed to be free of direct selection. This allows us to isolate the effects of reinforcement that results from selection acting on the male trait and hybrid incompatibility loci. We make no assumptions about how the preference loci are inherited (autosomally or sex-linked). For simplicity, however, we do assume that they all share the same mode of inheritance. The trait loci are autosomal. The effects of sex linkage of the male trait and female preference are studied in Hall and Kirkpatrick (2006).

All loci that affect the hybrids but not the preference or the male trait are designated as the hybrid incompatibility loci. These loci can have any pattern of additive or nonadditive gene action (that is, dominance and/or epistasis) involving any combination of the loci. We make no assumptions about the mode of inheritance of these loci: they may be autosomal, sex-linked, or cytoplasmic.

We study the evolution of female preference on an island that receives migrants from a continent that is at equilibrium. Migration occurs at a rate m, which is defined to be the proportion of newly arrived migrants on the island just after migration. The model applies equally to a pair of sympatric species between which there is one-way introgression. In that case, m represents the rate of hybridization between the focal species and the other species, and all descendants of hybrid matings are considered to belong to the focal population.

We assume a life cycle that begins with zygotes, followed by selection on the hybrid incompatibility loci, followed by migration, followed by natural and/or sexual selection on the male trait loci, followed by mating. The cycle ends with transmission and the generation of new zygotes. We also assume nonoverlapping generations and that the effects of genetic drift and mutation are negligible.

The female preference on the island will evolve as an indirect response to direct selection on other loci, namely the male trait and hybrid incompatibility loci. Indirect selection depends on two things. The first is the strength of direct selection. We denote the strength of direct selection acting on a set of positions U by a_U. Kirkpatrick et al. (2002) explain how a_U can be calculated for any pattern of selection, including arbitrary forms of epistasis and dominance. This means that results for reinforcement that are derived in terms of the a_U can be applied to any kind of hybrid incompatibility, as we will see shortly. The second thing on which indirect selection depends is the strength of associations (linkage disequilibria) among positions. We denote the associations among positions in the set U as D_U. The algebraic definition for D_U is given in Kirkpatrick et al. (2002), which can be consulted for more details.

General results:

We begin by deriving a model of reinforcement that is general with regard to the form of selection against hybrids. We then apply the general model to specific types of hybrid incompatibility to determine the effects of sex linkage on the potential for reinforcement. For purposes of clarity, only the main results are presented below; the detailed derivation of each result is given in the supplemental material at http://www.genetics.org/supplemental/.

Under our assumption that the preference genes have additive effects, the preference phenotype of a particular female can be written

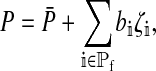(1)

where 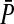is the mean preference among female zygotes on the island, b_i is the difference in the preference caused by carrying allele 1 rather than allele 0 at position i, and ζ_i = q_i if the female carries allele 1 at position i and −p_i otherwise. The summation includes one term for each of the positions affecting the preference in females.

Reinforcement of the preference on the island will result in divergence between the mean values of the preference on the continent (denoted P^C) and the island. The change in the mean preference in females from the start of one generation to the next is

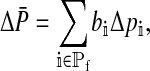(2)

where Δp_i is the per-generation change in the allele frequency at position i.

In the supplemental material (http://www.genetics.org/supplemental/), we show that the per-generation change, Δp_i, can be written as a function of the change caused by selection and migration within a generation, which is

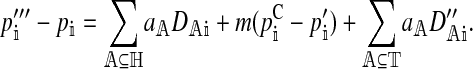(3)

We use primes to denote variables at different stages in the life cycle, with no primes denoting a value in zygotes, one prime denoting a value after selection on hybrid incompatibility, two primes denoting a value after migration, and three primes denoting a value after natural and sexual selection on the male trait. A superscript C denotes a value in the continental population.

To make further progress, we need expressions for the associations (the D) that appear in (3), which change under the forces of selection, migration, nonrandom mating, and recombination. Here we use the “quasi-linkage equilibrium” (QLE) approximation (Barton and Turelli 1991; Kirkpatrick et al. 2002). The key assumptions are that the selection coefficients (the a) and associations (the D) are ≪1, which allows us to neglect terms where they appear as higher powers. The assumption regarding the associations will be met when the forces that generate associations (selection and migration) are weak relative to the forces breaking them down (recombination), so we require that recombination rates be not too small. We also assume that migration is weak relative to selection, such that m is of O(a²). The supplemental material (http://www.genetics.org/supplemental/) shows how we can then derive O(a) approximations for the associations.

To simplify the analysis, we assume that the preference loci are unlinked to the incompatibility loci. We find the amount of reinforcement at equilibrium by combining (2) and (3) and setting the change in (2) to zero. In the supplemental material (http://www.genetics.org/supplemental/) we find that the difference between the mean preference on the island and continent is

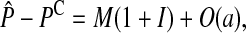(4)

where a hat denotes a value at equilibrium and O(a) indicates that terms proportional to the a have been neglected. M represents the effect of selection acting on the male trait loci,

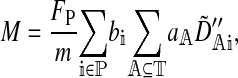(5)

where the tilde represents a QLE approximation and F_P is the proportion of preference genes found in females (for example, F_P = when the preference loci are all autosomally inherited and when they are all X-linked). Hall and Kirkpatrick (2006) use (5) to study in detail how sex linkage of the female preference and male display trait affect reinforcement.

The value of I quantifies the strength of hybrid incompatibility in terms of its effect on the reinforcement of the female preference. I is defined as

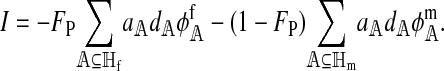(6)

The left and right terms represent the effect of selection against hybrid incompatibilities in females and males, respectively. Here, 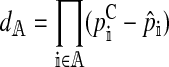. Expressions for 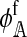and 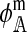are derived in the supplemental material (http://www.genetics.org/supplemental/). Their values depend on three things: (1) the type of hybrid incompatibility, (2) how the preference and incompatibility loci are inherited, and (3) the recombination rates between hybrid incompatibility loci.

Equations 4–6 are our primary results. By specifying how the hybrid incompatibility genes are selected and inherited, we can use (6) to make quantitative predictions. Before doing that, however, we can draw three general conclusions. The first conclusion is that the amount of reinforcement depends on how the female preference and hybrid incompatibility genes are inherited. That follows from the fact that the F_P (the fraction of preference positions in females) and the φ_A depend on the mode of inheritance.

The second conclusion is that the amount of reinforcement will increase with increasing strengths of selection against hybrids (reflected in larger values of a_A) and increasing amounts of divergence at the hybrid incompatibility loci (reflected in larger absolute values of d_A). Note, however, that reinforcement can occur when I = 0, implying that selection on the male trait alone can produce reinforcement (Kirkpatrick and Servedio 1999). Selection on genes other than the male trait genes may enhance reinforcement, but only if M > 0 (implying that there is natural or sexual selection on the male trait favoring it to diverge from the continent).

The third conclusion is that the total effect of selection against hybrids on reinforcement can be separated into an effect due to selection on females [the first summation in (6)] and an effect due to selection on males [the second summation in (6)]. These effects are weighted by F_P and (1 − F_P), which are the proportions of time the preference genes spend in females and males, respectively. If all preference loci are autosomal, for example, then 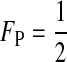and effects from the two sexes are weighted equally. If all preference genes are X-linked, however, then 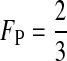and the female effect is given more weight. The mode of inheritance of the female preference genes, therefore, influences the relative effects of selection against male and female hybrids on reinforcement (see also Hall and Kirkpatrick 2006).

To simplify the analyses, we now make three additional assumptions. The first assumption is that the island and continent are nearly fixed for alternative alleles (alleles 1 and 0, respectively) at the hybrid incompatibility loci. When this is true, d_A ≈ (−1)ⁿ, where n is the number of positions in A. The assumption is good as long as the strength of migration is weak relative to the strength of selection against hybrids and migrants.

The second assumption is that males are the heterogametic sex. We make this assumption only for clarity of presentation. For taxa in which females are the heterogametic sex, an expression for I can be obtained from (6) by simply interchanging the notation for males and females. This means that an autosome–X incompatibility, for example, has the same effect as an autosome–Z incompatibility.

Third, we assume that the quantity M defined in (5) is independent of how the preference loci are inherited. This approximation is based on the results of Hall and Kirkpatrick (2006), who find that changing the mode of inheritance of the preference from autosomal to X-linked alters M by <10% when the trait is autosomal. This simplification allows us to isolate the consequences of sex linkage on reinforcement through its effects on I, which represents the force of selection on hybrid incompatibility.

We now use (6) to derive equations for I considering three types of incompatibilities: those due to selection on a single locus, those due to interactions between two loci, and those due to selection against an ecological intermediate. For one- and two-locus incompatibilities, we consider all possible combinations of three modes of inheritance (autosomal, X-linked, and Y-linked) for the female preference and hybrid incompatibility loci. We then compare the cases and determine the combinations that are expected to produce the most reinforcement.

One-locus incompatibilities:

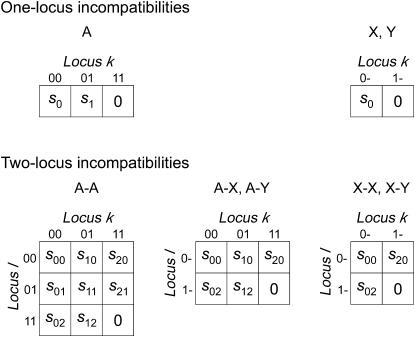
In the previous section, we derived a general equation describing the effect of any form of selection against hybrids on reinforcement. Here we use that equation to study incompatibilities resulting from selection on a single locus, k. This type of incompatibility can evolve when the fitness effects of the locus are environment dependent, for example, when one allele is favored on the continent and another on the island. For generality we allow females and males to have different fitnesses. Our notation for the strengths of selection against different genotypes is given in the top half of Figure 1, where s₀ is the strength of selection against an individual homozygous/hemizygous for the continental allele, and s₁ is the strength of selection against a heterozygote. The preference loci may be autosomal or X-linked and the incompatibility locus may be autosomal, X-linked, or Y-linked.

Figure 1.

Notation denoting the strengths of selection against genotypes of the heterogametic sex. The homogametic sex maintains the genotypes (and notation) seen in the leftmost column, regardless of sex linkage. Fitnesses are defined to be relative to the island genotype, which is fixed for the 1 allele at all incompatibility loci. Hybrid incompatibilities are a result of selection on either one or two loci, where each locus may be autosomal (A), X-linked (X), or Y-linked (Y). For two-locus incompatibilities, the pattern of sex linkage is denoted using two letters joined by a dash. A–X, for example, indicates that the k locus is autosomal and the l locus is X-linked.

In the supplemental material (http://www.genetics.org/supplemental/), we derive expressions for 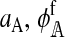, and 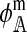. Plugging those results into (6) and simplifying, we obtain the expressions for the effect on reinforcement, I. Those expressions are summarized in Table 1, where f and m denote coefficients for females and males, respectively. The effect of two or more independent one-locus incompatibilities can be studied by simply summing up the appropriate values from Table 1.

TABLE 1.

Effect of one-locus incompatibilities on reinforcement (I)

Incompatibility	Autosomal preference	X-linked preference
Autosomal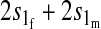
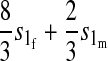X-linked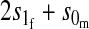
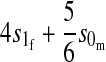Y-linked		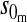0

Results in Table 1 show that under general conditions, reinforcement is expected to be strongest when the preference and the incompatibility have the same mode of inheritance (autosomal, X-linked, or Z-linked). Other combinations are expected to produce smaller amounts of reinforcement. This conclusion is robust so long as males and females with the same genotype have equal fitness, the island allele is not recessive, and there is no overdominance (i.e., s₁ > s₀/2).

We can also see from Table 1 that the amount of reinforcement generally increases with the strength of selection against hybrids. The one exception is when the preference and incompatibility loci reside on different sex chromosomes. No reinforcement is possible in this case because the two loci cannot be inherited together.

Two-locus incompatibilities:

Two-locus hybrid incompatibilities, first discussed by Bateson (1909), Dobzhansky (1934, 1937), and Muller (1939, 1940, 1942), are thought to be common in nature and have been the focus of extensive empirical and theoretical studies (Coyne and Orr 2004). Here we apply the general result (6) to two-locus hybrid incompatibilities.

We denote the loci involved as k and l and the rate of recombination between them as r_kl. Again, we allow females and males to have different fitnesses. Our notation for the strengths of selection against different genotypes is given in the bottom half of Figure 1. Five combinations of modes of inheritance for the two incompatibility loci exist: autosome–autosome (A–A), autosome–X (A–X), autosome–Y (A–Y), X–X, and X–Y. Since the preference may be autosomal or X-linked, there are a total of 10 combinations when all three loci are considered.

In the supplemental material (http://www.genetics.org/supplemental/), we derive expressions for 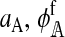, and 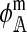for each of the 10 combinations of modes of inheritance. Plugging these expressions into (6) yields the expressions for I given in Table 2. For simplicity of presentation, Table 2 presents the expressions for I assuming that males and females with the same genotype have the same fitness and that dosage compensation exists. More general expressions for I are given in the supplemental material.

TABLE 2.

Effect of two-locus incompatibilities on reinforcement (I)

Incompatibility	Autosomal preference	X-linked preference
A–A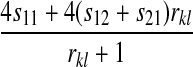
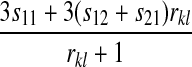A–X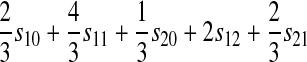
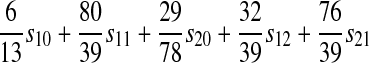A–Y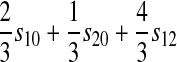
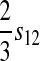X–X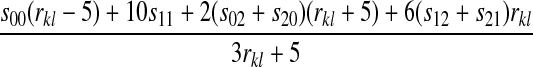
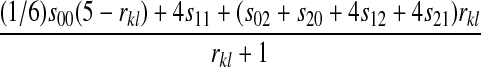X–Y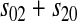

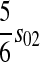Table 2 can be used to show that increased linkage between the incompatibility loci decreases the amount of reinforcement for commonly observed types of incompatibilities. These results are consistent with previous theory (Kirkpatrick and Servedio 1999; Servedio and SÆtre 2003).

The general model derived above can accommodate any pattern of dominance and epistasis, as well as any pattern of sex linkage. Here we compare different types of incompatibilities to determine how sex linkage affects reinforcement. To make the analysis tractable, we reduce the number of parameters by making the following biologically realistic assumptions: (1) free recombination between hybrid incompatibility, (2) dosage compensation, and (3) males and females with the same genotype have equal fitness. Note that the third assumption does not imply that males and females of the same hybrid class have equal fitness.

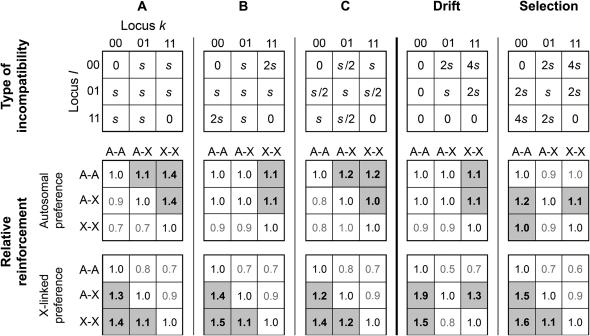
To determine the effect of sex linkage on reinforcement, we computed I for A–A, A–X, A–Y, X–X, and X–Y incompatibilities using Table 2 and then compared the values in a pairwise fashion. We studied the five patterns of hybrid incompatibility presented in the top row of Figure 2. Type A reflects an incompatibility in which all individuals with a mixture of the two alleles (0 and 1) have equal fitness. Type B is similar to A, except that individuals homozygous for different alleles at the two loci have even lower fitness. For type C, studied by Servedio and SÆtre (2003), individuals with more intermediate genotypes have lower fitness. The type labeled Drift, which was studied by Turelli and Orr (2000), implies that the ancestral genotype (bottom left) and derived genotypes (top left and bottom right) have equal fitness. Selection is similar to Drift, except that the derived genotypes have higher fitness than the ancestral genotype. By comparing the results from the five patterns, we can identify how our conclusions may be affected by particular assumptions about the type of two-locus incompatibility.

Figure 2.

The effect of sex linkage on reinforcement for five types of hybrid incompatibility. The five matrices in the top row denote five types of hybrid incompatibility at two loci, k and l. The types labeled Drift and Selection correspond to empirically observed patterns (Turelli and Orr 2000) and type C corresponds to that studied by Servedio and SÆtre (2003). Values in the center and bottom rows indicate the relative amounts of reinforcement due to A–A, A–X, and X–X incompatibilities. The amount of reinforcement for the pattern of sex linkage indicated to the left of the value is divided by that for the pattern indicated above the value. For example, the value 1.4 found in the bottom leftmost square indicates that an X–X incompatibility is expected to produce 1.4 times more reinforcement than an A–A incompatibility. Values >1 before rounding are shaded. For comparisons involving A–Y and X–Y incompatibilities, see the supplemental material at http://www.genetics.org/supplemental/.

Two conclusions can be drawn from Figure 2. First, it is clear that the type of incompatibility that is expected to contribute the most to reinforcement depends on whether or not the female preference is sex linked. This result holds for all five patterns of hybrid incompatibility studied (also see supplemental material at http://www.genetics.org/supplemental/ for a more detailed analysis). When the preference is autosomally inherited (Figure 2, center row), A–A and A–X incompatibilities are expected to contribute the most. When the preference is X-linked (Figure 2, bottom row), however, X–X and A–X incompatibilities are expected to be more important. This result is consistent with our results for one-locus incompatibilities.

The second conclusion is that the mode of inheritance of the hybrid incompatibility has only a moderate effect when A–Y and X–Y incompatibilities are ignored. When A–Y and X–Y incompatibilities are considered, however, sex linkage can have a very large effect (see supplemental material at http://www.genetics.org/supplemental/), in some cases exceeding a 10-fold effect. The reason is that very little reinforcement is expected when one or more incompatibility loci are Y-linked and the preference locus is X-linked. Analogous results apply to taxa with Z–W sex determination.

Ecological incompatibilities:

How does selection against ecologically inferior hybrids favor reinforcement of prezygotic isolation? Here we apply the general model derived above to the situation in which genes contribute additively to a quantitative trait, such as body size or bill length. In this model, hybrids are selected against because they have intermediate phenotypes that are selected against. We assume that in the absence of migration, the island and continent populations would be fixed for alternative alleles at a set of loci. Below we present an equation for the amount of reinforcement, assuming that all incompatibility loci are autosomal, X-linked, or Y-linked. More general equations allowing for any combination of loci are given in the supplemental material (http://www.genetics.org/supplemental/).

For simplicity, we assume that the n loci influencing the ecological trait have equal allele frequencies and equal effects on the trait. We also assume that the ecological trait is determined by a large number of loci, each with a small effect. The mean values of the ecological trait on the continent and island are given by Z^C and Z, respectively. Selection against the hybrids is a function of the directional selection gradient β and the stabilizing selection gradient Γ acting on the ecological trait. (Negative values of Γ correspond to stabilizing selection and positive values to disruptive selection.) The values of the selection gradients depend on the fitness function for the ecological trait and also on the distribution of that trait in the island population. That distribution evolves in response to selection and migration, which causes the values of the selection gradients to change. The β and Γ in the expressions that follow refer to the equilibrium values for the gradients. See Lande and Arnold (1983) and Kirkpatrick (2001) for more details.

In the supplemental material (http://www.genetics.org/supplemental/) we show that the effect on reinforcement from selection on the ecological trait is

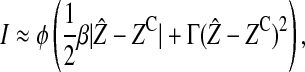(7)

where 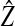is the equilibrium value of the ecological trait on the island and the value of φ depends on how the preference and ecological trait are inherited (see Table 3).

TABLE 3.

Effect of ecological incompatibilities on reinforcement (φ)

Incompatibility	Autosomal preference	X-linked preference
Autosomal	8	6
X-linked	6	8.5
Y-linked	2	0

Table 3 shows that the type of incompatibility that is expected to contribute most to reinforcement depends on how the female preference is inherited. Autosomal incompatibilities contribute more when the preference is also autosomal, whereas X-linked incompatibilities contribute more when the preference is X-linked. Y-linked incompatibilities are expected to contribute relatively little, regardless of how the female preference is inherited. Equation 7 also shows that the amount of reinforcement due to selection acting on an ecological trait increases linearly with the strength of directional selection acting on the island, linearly with the strength of disruptive selection acting on the island, and faster than linearly (quadratically) with the equilibrium amount of divergence in the ecological trait between the continent and the island.

SIMULATIONS

The analytic model developed above utilizes a QLE approximation that is accurate when selection and migration are sufficiently weak. Here we use exact simulations to answer three questions: (1) How does the accuracy of the analytic approximation decrease with an increasing strength of selection?, (2) Do qualitative results obtained from the weak selection approximation hold when selection is strong?, and (3) Is the outcome of secondary contact the same for incompatibilities that evolve by selection as opposed to drift? We find that the analytic approximation is quite good when selection is weak, that qualitative conclusions hold when selection is strong, and that the outcome of secondary contact can be very different for incompatibilities that evolve by selection as opposed to drift.

Notation and assumptions:

The analytic model allows any number of loci to contribute to the female preference, male trait, and hybrid incompatibility. Here we consider a special case of that model: When one locus contributes to the female preference, one locus contributes to the male trait, and two loci contribute to the hybrid incompatibility. We assume that females have a preference of 1 + α for males with a trait genotype that matches their preference genotype, relative to males with other genotypes. Mating probabilities are calculated using preference values and genotype frequencies taken just before mating (Kirkpatrick 1982). We also assume natural selection disfavoring continental male trait alleles on the island, with heterozygotes taking a fitness of 1 − s_T/2, and homozygotes/hemizygotes taking a fitness of 1 − s_T. To maximize the potential for reinforcement, we assume that the continental allele frequencies at the preference and trait loci are 0.5. Initial allele frequencies on the island were 1.0 for the male trait and 0.5 for the female preference (initial frequencies on the island had a negligible effect on equilibrium values). The continent and island were initially fixed for alternate alleles at the hybrid incompatibility loci. We assumed a heritability of 1 and that all loci are unlinked. Without loss of generality, we choose the following phenotypic values for the preference and trait: 0 for individuals homozygous/hemizygous for the continental allele, 1 for heterozygous individuals, and 2 for individuals homozygous/hemizygous for the island allele. Simulations were run until the change in each allele frequency between generations was <10⁻¹².

Accuracy of the approximation:

How does the accuracy of the analytic approximation decrease as the strength of selection is increased? We answered this question by comparing exact values for the amount of reinforcement (obtained from the simulations at equilibrium) with the corresponding approximate values (obtained from the analytic model given in Equation 4). To calculate the analytic approximation, we used the expression for (5) derived by Hall and Kirkpatrick (2006) in terms of measurable quantities (see their Equation 5). Error of the analytic approximation was calculated as 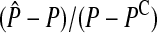, where 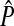and P are the approximate and exact values of the preference on the island, respectively. This is a measure of the accuracy of the entire model, which is a function of the accuracy of (5) (the male trait component) and of (6) (the hybrid incompatibility component).

We varied the strength of reinforcement by varying the values of the parameters describing migration and selection, while holding the relationship among those parameters constant. More specifically, we denoted the strength of selection as s and set m = s/80, s_T = s, α = 2s, s₀₀ = 0, s₁₁ = s/4, s₀₁ = s₁₀ = s₁₂ = s₂₁ = s/2, s₀₂ = s₂₀ = s. These assumptions correspond to the incompatibility type labeled Selection in Figure 2.

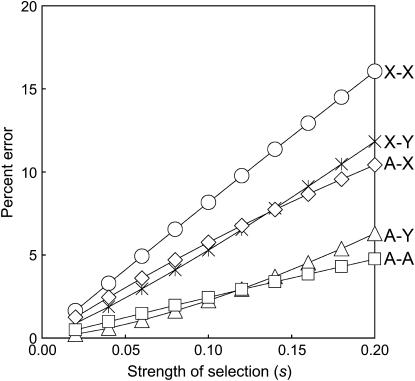
Figure 3 shows how the error in the analytic approximation increases with the strength of selection for five different types of sex linkage (preference and trait are autosomal). Figure 3 suggests that when selection is weak the accuracy of the analytic approximation is quite good (the percentage of error is on the order of the strength of selection).

Figure 3.

Accuracy of the analytic approximation for weak to moderate selection. Percentage of error, calculated as (P_approx − P_exact)/(P_exact − P^C), is plotted as a function of the strength of selection (s) for five types of hybrid incompatibility: autosome–autosome (A–A), autosome–X (A–X), autosome–Y (A–Y), X–X, and X–Y. Exact values were obtained from four-locus simulations. The strengths of migration (m), natural selection on the male trait (s_T), and sexual selection (α) were varied as a function of s, where m = s/80, s_T = s, α = 2s. The strength of selection on hybrid incompatibility also varied as a function of s, where s₀₀ = 0, s₁₁ = s/4, s₀₁ = s₁₀ = s₁₂ = s₂₁ = s/2, s₀₂ = s₂₀ = s.

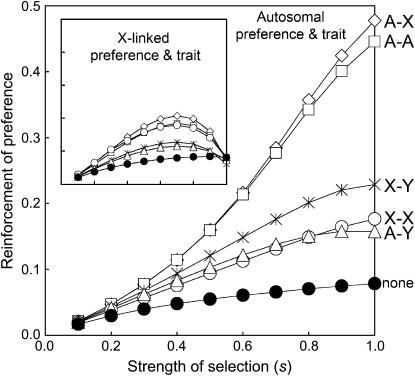
Servedio (2004) criticizes the QLE approximation, suggesting that conclusions drawn from models assuming weak selection cannot be applied to situations involving strong selection. To test this claim, we extended the simulations to include conditions of very strong selection. Results from these simulations are presented in Figure 4. The main figure presents the results obtained when the preference and trait are autosomal and the inset presents results obtained when they are X-linked.

Figure 4.

Reinforcement of female preference when selection against hybrids is strong. The amount of reinforcement (P_exact − P^C) is plotted as a function of the strength of selection. Exact values were obtained from four-locus simulations. The strengths of migration, natural selection on the male trait, sexual selection, and selection on the hybrid incompatibility were varied as a function of s (see Figure 3 legend). The main figure presents results obtained when the preference and trait are autosomal, whereas the inset presents results obtained when the preference and trait are X-linked. The curve labeled none corresponds to the situation in which there is no selection against hybrid incompatibility.

We can conclude from Figure 4 that qualitative patterns observed when selection is weak can hold when selection is very strong. These simulations present two patterns that Servedio found problematic. First, the simulations involving an autosomal preference and trait show a rank-order change in the relative amounts of reinforcement as selection becomes strong, indicated by the fact that the lines corresponding to A–Y and X–X incompatibilities cross when s ≈ 0.8. This rank-order change, however, does not change the qualitative conclusions: Incompatibilities that are especially favorable to reinforcement remain so. Second, the simulations involving an X-linked preference and trait show a highly nonlinear relationship between the strength of selection and the amount of reinforcement. Note that despite this nonlinear relationship, the qualitative patterns observed when selection is weak are also observed when selection is strong. For example, the observation that when the preference and trait are X-linked, A–Y and X–Y incompatibilities are weaker than other types is consistent across the entire range of s.

Selection vs. drift:

Recent empirical studies suggest that hybrid incompatibilities evolve by selection instead of drift (Presgraves et al. 2003; Barbash et al. 2004; Wu and Ting 2004). Authors of some recent theoretical studies of hybrid incompatibilities, however, have assumed that incompatibilities evolve by drift (Turelli and Orr 2000; Gavrilets 2003). Is the outcome of secondary contact the same for incompatibilities that evolve by selection as opposed to drift? To answer this question we focused on the types denoted Drift and Selection in Figure 2. The type labeled Drift is consistent with the assumption that the incompatibility evolved by drift, whereas the type labeled Selection is consistent with the assumption that the incompatibility evolved by selection. For each of these two types, we conducted a series of simulations in which we independently varied the relative strength of selection and migration and recorded the amount of reinforcement at equilibrium. Simulation procedures were the same as those described in Notation and assumptions above, with autosomal inheritance of all four loci, α = 2, and s_T = 1.

The simulations revealed a phenomenon that is not currently appreciated. Postzygotic isolation can be lost through genetic swamping despite strong selection against hybrids, if selection against the ancestral genotype is weak. The reason for this result is that individuals of a particular hybrid class may have different genotypes. If one or more of these genotypes (such as the ancestral genotype) have high fitness, then individuals with those genotypes will survive, allowing introgression of alleles from one species to the other. This will occur even if selection against the hybrid class as a whole is strong. Our simulations demonstrated the result of this pattern. When the incompatibility type labeled Drift was assumed in the simulations, the incompatibility could be maintained only if all F₁ hybrids died (s = 1) or there was no migration (m = 0). This implies that for the incompatibility that evolved by drift, swamping could occur despite strong selection against the hybrid classes. When the incompatibility type labeled Selection was assumed in the simulations, in contrast, the incompatibility was maintained whenever m < s/12.

The simple conclusion that we can draw from these simulations is that the strength of selection against the hybrid classes may not be the best indicator of whether or not postzygotic isolation is likely to be maintained (or whether or not reinforcement will occur). Other factors, such as whether the postzygotic isolation evolved by selection or drift, may also determine the fate of incompatibilities in hybridizing populations. This result has important implications for the relative importance of selection and drift in the evolution of hybrid incompatibility.

DISCUSSION

We have shown that sex linkage influences how hybrid incompatibility contributes to reinforcement. In general, sex-linked incompatibilities are expected to produce more reinforcement than autosomal incompatibilities when female preference is also sex-linked. When the preference is not sex-linked, however, autosomal (and autosome–X) incompatibilities produce more reinforcement. (autosome–X incompatibilities are favorable to reinforcement regardless of how the preference is inherited.) These results hold for many types of hybrid incompatibility, including selection against heterozygotes at a single locus, selection against incompatible alleles at two loci, and selection against ecological intermediates. The strength of the effect, which depends on the genetic details, can be quite large but is typically less than twofold when Y-linkage is ignored.

The weak selection approximation we utilized has recently been criticized by Servedio (2004), who suggested that results from models assuming weak selection cannot apply to situations involving strong selection. Our simulations suggest otherwise. We found that even when reinforcement changes nonlinearly with increasing selection, qualitative patterns hold regardless of the strength of selection. Simulations have also shown the approximation to be more accurate when strong selection is a function of many genes each with small effect rather than a function of a few genes with large effect (data not shown). This suggests that the accuracy we report is a conservative estimate since we considered the worst case (a few genes with large effect). We conclude, therefore, that our qualitative conclusions may hold even when selection against hybrids is strong.

Our simulations also show that incompatibilities that evolve in allopatry by drift or weak selection are likely to be lost by swamping during secondary contact, even when the strength of selection against hybrids is strong. This observation suggests that the rate of hybridization during secondary contact may determine the types of incompatibilities that can persist. With very infrequent hybridization, incompatibilities that evolved by weak selection can be maintained, but with moderate to strong hybridization, only incompatibilities that evolved by very strong selection can be maintained. Incompatibilities that evolved by drift will be lost in the face of any degree of hybridization, assuming some introgression.

Secondary contact should act as a sieve, therefore, removing incompatibilities that evolved by drift or weak selection but retaining those that evolved by strong selection. This incompatibility sieve should produce at least two empirical patterns. First, taxa that have not come into secondary contact since their divergence should have a greater proportion of incompatibilities that evolved by drift and weak selection than taxa that hybridize. The second pattern is that if incompatibilities sometimes evolve by drift in allopatry, then upon secondary contact the amount of intrinsic postzygotic isolation should decline until only incompatibilities that evolved by strong selection remain. If a sufficient amount of postzygotic isolation remains, the populations may remain distinct; otherwise, the populations will fuse into one.

The incompatibility sieve is also expected to produce the striking pattern that is observed in hybridizing taxa: Incompatibilities between hybridizing taxa evolved by selection. The OdsH locus in Drosophila, for example, has been shown to be a result of gene duplication followed by positive selection (Ting et al. 1998, 2000, 2004; Sun et al. 2004; Wu and Ting 2004). Both the Nup96 gene and the candidate factor Nup153 appear to be products of recent positive selection (Presgraves et al. 2003; D. Presgraves, personal communication). Barbash et al. (2004) have shown that Hmr, a factor causing incompatibility between D. melanogaster and its sibling species, has also been under recent positive selection. While there may be other factors contributing to this pattern, such as observational or publication bias, the incompatibility sieve provides a plausible hypothesis for why we may be observing so many incompatibilities that evolved by selection rather than by drift.

Appendix

Summary of notation

Loci, contexts, positions, and sets of positions
i	A single locus i
i	A single position at locus i
ifm	The position at the i locus that is found in a female and inherited from her father
A	A set of positions
Af	A set of positions in females
U	A set of loci
P	The set of positions that affect the female preference
T	The set of positions that affect the male trait
H	The set of positions that affect hybrid fitness but not the male trait or female preference
Summations and products
∑i∈A	A sum over all positions i in the set A
∑U⊆A	A sum over all subsets U of the set A, including the set A itself and the empty set Ø
∏i∈A	A product over all positions i in the set A
Allele frequencies
pi	The frequency of the 1 allele at the position i on the island
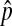	The equilibrium frequency of the 1 allele on the island
pC	The equilibrium frequency of the 1 allele on the continent
Δp	The change in the allele frequency during one generation
dA	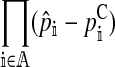, the allele frequency divergence between the continent and island
Phenotypes, fitnesses, and selection
P	The preference of a particular female on the island
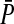	The average preference in females on the island
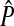	The equilibrium value of the preference in females on the island
PC	The average preference in females on the continent at equilibrium
Z	The value of the ecological trait on the island
ZC	The value of the ecological trait on the continent
	The equilibrium value of the ecological trait on the island
bi	The difference in the preference of carrying allele 1 rather than allele 0 at position i
ζi	Equals qi if the female carries allele 1 at position i and −pi otherwise
aA	The selection coefficient for the set of positions A
s	A traditional selection coefficient
β	The strength of directional selection on the island
Γ	The strength of disruptive selection on the island
Associations
DAi	The association among the positions in the set Ai at the start of the generation
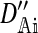	The association among the positions in the set Ai after migration
Miscellaneous
rkl	The probability that recombination will break up the loci k and l
m	The proportion of newly arrived migrants on the island, just after migration
I	The effect on reinforcement due to selection on the hybrid incompatibility loci
M	The effect on reinforcement due to selection on the male trait loci
FP	The proportion of female preference genes found in females