Building of an Experimental Cline With Arabidopsis thaliana to Estimate Herbicide Fitness Cost

Abstract

Various management strategies aim at maintaining pesticide resistance frequency under a threshold value by taking advantage of the benefit of the fitness penalty (the cost) expressed by the resistance allele outside the treated area or during the pesticide selection “off years.” One method to estimate a fitness cost is to analyze the resistance allele frequency along transects across treated and untreated areas. On the basis of the shape of the cline, this method gives the relative contributions of both gene flow and the fitness difference between genotypes in the treated and untreated areas. Taking advantage of the properties of such migration–selection balance, an artificial cline was built up to optimize the conditions where the fitness cost of two herbicide-resistant mutants (acetolactate synthase and auxin-induced target genes) in the model species Arabidopsis thaliana could be more accurately measured. The analysis of the microevolutionary dynamics in these experimental populations indicated mean fitness costs of ∼15 and 92% for the csr1-1 and axr2-1 resistances, respectively. In addition, negative frequency dependence for the fitness cost was also detected for the axr2-1 resistance. The advantages and disadvantages of the cline approach are discussed in regard to other methods of cost estimation. This comparison highlights the powerful ability of an experimental cline to measure low fitness costs and detect sensibility to frequency-dependent variations.

PREDICTING the evolution of resistance to both pesticides and pathogens shares the central assumption that resistance is associated with a fitness cost (Coustau et al. 2000). Fitness costs play a central role in models describing the maintenance of polymorphisms in disease resistance genes, as they allow the persistence of alternative alleles (reviewed in Burdon and Thrall 1999). The estimate of a fitness cost conferred by a resistance gene is also of primary importance when dealing with the pesticide resistance management strategies designed to keep resistance frequency under a threshold acceptable value (Maxwell and Mortimer 1994; Lenormand and Raymond 1998). Associating fitness costs to pesticide resistance genes is a logical and in many cases valid assumption that is based on both theory and observations. First, genetic changes conferring adaptation to a new “environment” may involve a large modification of the previous phenotype and may therefore induce a fitness penalty in the previous environment (Fisher 1958; Fry 2003). Second, resistance polymorphisms seem to persist in populations (Purrington 2000). This maintenance of polymorphism is thought to result from the occurrence of a selection pressure against resistance in the absence of the corresponding pesticide, which acts to decrease the frequency of the resistance gene in untreated areas.

Obtaining a precise estimate of a fitness cost associated with pesticide resistance alleles is often difficult. A potentially powerful method is to study the geographic gradients of allele frequency (“clines”) in natural populations located along a variable environment, i.e., across treated and untreated areas in the case of pesticide resistance (Lenormand et al. 1999; Lenormand and Raymond 2000). The shape of the cline step depends on the fitness difference between the genotypes in the treated and untreated regions, the fitness of any intermediate genotypes (such as heterozygotes), and the amount of gene flow (Nagylaki 1975). Migration–selection models have been developed to estimate both migration rates and selection coefficients in clines (Haldane 1948; May et al. 1975). Studying a cline reveals the respective forces of selection that tend to sort the genotypes and migration that tends to homogenize the allele frequency along the cline. The idea developed in this article is that a migration–selection balance can be turned into an advantageous and straightforward experimental system if one of the forces is fixed: if migration is experimentally controlled, then there can be only one single stable equilibrium cline of allele frequency depending on the sole fitness differences between genotypes, i.e., the fitness cost of resistance.

An experimental transect between treated and untreated areas was thus built up here to assess the fitness cost of two herbicide-resistant mutants in the selfing species Arabidopsis thaliana: the well-characterized chlorsulfuron resistance (Bergelson et al. 1996; Purrington and Bergelson 1997, 1999) and one resistance mutant to the herbicide 2,4-D (Wilson et al. 1990). The chlorsulfuron herbicide (sulfonylurea group) inhibits the branched-chain amino acid biosynthetic enzyme acetolactate synthase (ALS) (LaRossa and Falco 1984). The 2,4-D herbicide (phenoxy-carboxylic acids group) disrupts very diverse aspects of plant development (stem cell elongation, cell division during lateral root formation, and vascular strand differentiation; Nagpal et al. 2000).

Migration is controlled in this experiment, allowing for the fitness cost (designed as the selection coefficient in the absence of herbicide spray) for each resistance to be directly inferred from the modification of the allele frequencies along the cline. These microevolutionary patterns have been analyzed over three and four generations for the axr2-1 and csr1-1 resistance genes, respectively.

MATERIALS AND METHODS

Genetics of resistance:

The chlorsulfuron-resistance (csr1-1) and the 2,4-D-resistance (axr2-1) lines of A. thaliana were isolated by Haughn and Somerville (1986) and Estelle and Somerville (1987), respectively, from ethyl methanesulfonate (EMS) mutagenized populations of the wild-type Columbia (Col) ecotype. The csr1-1 mutant is resistant due to a point mutation resulting in a Pro-to-Ser substitution at the 197th amino acid (Haughn et al. 1988), while the axr2-1 mutant is resistant due to a point mutation resulting in a Pro-to-Ser substitution at the 87th amino acid (Nagpal et al. 2000). The two resistance mutant lines were provided to us via the Nottingham Stock Centre.

As previously described in Roux et al. (2004), a process of “genetic background randomization” was performed for each resistance line by generating a segregating F₂ population from a cross between each mutant line (Col genetic background) and the male-sterile sensitive line NW77 (Ler genetic background). Each cross was replicated (designated as families) by using two different plants from the same mutant line. The strategy of crossing inbred lines allows the estimation of a cost due nearly exclusively to a difference in resistance traits (reviewed in Strauss et al. 2002). Moreover, crosses between Ler and Col genetic backgrounds increase the genetic variance at the F₂ generation and thus provide a measure of the mean cost of each resistance gene under an enlarged diversity of genetic backgrounds mixing the Ler and Col origins.

In a previous study, the total seed production differential between SS and RR plants from an F₂ segregating family was used to measure the fitness cost of several herbicide-resistant mutant lines in A. thaliana (Roux et al. 2004). This direct method provided estimates of 37 and 92% costs for the csr1-1 and axr2-1 resistant mutants, respectively. However, a more precise determination of the total fitness penalties would take into account all stages of the plant life cycle, i.e., a measure from seed to seed over generations. Analyzing resistance allele frequency evolution in isolated populations (with an initial resistance allele frequency of 50%) over seven successive generations resulted in fitness cost estimates of 0 and 89% for the csr1-1 and axr2-1 resistant mutants, respectively (Roux et al. 2005). In the present study, 15 RR and 15 SS plants from each F₂ segregating population were randomly selected for each family and resistance gene to build up the parental gene pool of an experimental cline. Experimental populations were then initiated with RR and SS F₃ seeds only. Assuming an outcrossing rate of 2% in A. thaliana (Bergelson et al. 1998), heterozygosity was expected to be extremely low in the experimental populations.

Experimental design:

The choice of the experimental cline designed here is illustrated in Figure 1. It involved one resistant “source” population and nine “sink” populations. For each generation, each experimental population consisted of 100 sown seeds. At the first generation, the resistance allele frequency was 1 in the source population (q_s) and decreased with an increment of 0.1 from 0.9 to 0.1 in sink populations 1–9 (q₁–q₉), respectively. Although these initial resistance allele frequencies are rather specific, it permitted us first to focus on situations where the fitness cost associated with resistance is in a position to greatly affect the resistance gene frequencies and second to test to what degree the fitness costs may vary with resistance gene frequency in the population (a parameter rarely described). An asymmetric pattern of migration was created to construct the next generations (see Figure 1). Sink populations received RR migrant seeds from the source population while, for simplicity, the RR source received no immigration and was grown separately to be maintained free from any contamination. In the RR source population, the frequency of the resistance allele was therefore artificially maintained at 1. For each generation, the migration rate m_s→x from the population source decreased with an increment of 0.01 from 0.09 to 0.01 in sink population 1 to sink population 9, respectively (as if they were ranked from the nearest to the farthest distance from the source). To buffer the influence of genetic drift along the cline, a small amount of migration was also introduced between adjacent neighbor sink populations. In this study, sink populations therefore also received migrant seeds from their two adjacent neighbor populations (except for sink population 9 receiving no following sink population emigrants). The migration rates from the preceding sink population m_x−1→x and the following sink population m_x+1→x were fixed here at 0.05. Sink populations received the remaining proportion m_x→x of seeds from their own populations. Five replicates of this experimental design were performed for each resistance gene.

Figure 1.

Experimental design to estimate the fitness cost associated with the csr1-1 and axr2-1 resistances. The artificial cline buildup here has one resistant “source” population and nine “sink” populations with an asymmetric seed migration m_s→x from the source to the sinks. Sink populations receive migrant seeds (m_x+1→x and m_x−1→x) from adjacent populations, and the remaining proportion m_x→x of seeds comes from their own populations (see materials and methods for description of values of migration).

For each of the nine experimental sink populations representing a cline, plants were grown in 17 × 27 × 7-cm plastic trays. Throughout four generations (G₁–G₄) for the csr1-1 resistance and three generations (G₁–G₃) for the axr2-1 resistance, the populations were allowed to freely self-fertilize. At the end of each generation, seeds were carefully harvested and bulked separately for each population. Throughout the experiment, generations were discrete, nonoverlapping, and kept as isolated gene pools (except for the controlled migration events). Each generation was conducted under natural light supplemented by artificial light to provide a 16-hr photoperiod. The temperature was maintained between 20° and 25°. To avoid microenvironmental heterogeneities, the trays were regularly rotated throughout the growing period.

Data collection:

To assess the evolution of resistance allele frequencies along the cline for each generation, a sample of 100 seeds was randomly selected from the bulk seeds of each population. The seeds produced at generations 1, 2, and 3 could be used to determine the resistance allele frequencies of generations 2, 3, and 4, respectively. DNA was extracted from 10-day-old germinated seedlings grown on agar medium complemented with micro- and macronutriments to optimize germination rates. For each population and generation, 48 seedlings were randomly selected and each seedling was then placed in a microcentrifuge tube containing 50 μl of the extraction buffer described by Saini et al. (1999). The seedlings were crushed using a mixer mill. Tubes were placed in a water bath at 95° for 6 min, transferred onto ice for 5 min, and vortexed for 15 sec. DNA extracts were kept at −20° prior to genotyping.

For the axr2-1 resistance, an allele-specific PCR method was used to discriminate between the three genotypes (SS, RR, and RS) for each mutation as described in Roux et al. (2004). For the csr1-1 resistance allele, genetic frequencies in sink populations were obtained more quickly with newly available single-nucleotide polymorphism (SNP) genotyping techniques: the Amplifluor technology. This technology is based on allele-specific PCR amplification combined with the use of universal energy-transfer-labeled Amplifluor primers (Myakishev et al. 2001).

Estimating fitness cost:

As A. thaliana is an annual plant with very low heterozygosity (Bergelson et al. 1998), we assumed that the microevolution of herbicide resistance over a few generations could be accurately described by a haploid model. Referring to Figure 1, the value of the fitness cost necessary to produce allele frequency changes of a given magnitude in sink populations 2–8 can be determined from the general equation

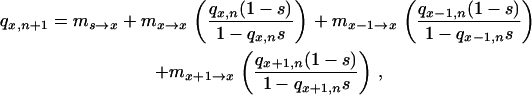(1)

where q_x,n and q_x,n+1 are the resistance allele frequencies of the sink population “x” at generations n and n + 1, respectively; q_x−1,n and q_x+1,n are the frequencies of the previous and following sink population of the sink population x, respectively, at generation n; s is the selection coefficient—positive or negative selection coefficient s indicates a fitness cost or a fitness advantage of the resistance allele, respectively; and m_s→x, m_x−1→x, m_x+1→x, and m_x→x are migrations rates as described above. To maintain stable plant densities, the values of the parameters m_s→x, m_x−1→x, and m_x+1→x were fixed in our experiment:

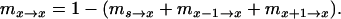(2)

Appropriate modified versions of Equations 1 and 2 were applied to sink populations 1 and 9, as these populations receive immigrants from only one neighbor and the source population.

Iterations of Equation 1 were then performed simultaneously for four generations over the range from 1 to −1 for the selection coefficient s (in 0.005 increments), to generate a set of all expected resistance allele frequencies in each sink population for each potential value of selection coefficient s. The observed resistance allele frequencies in the experiment were then checked against all expected values to determine the best-fitting selection coefficient s estimates for each resistance gene, sink population, and generation. For each population, generation, and resistance, the five replicates permitted us to calculate a mean fitness cost and its associated standard error (see Table 1).

TABLE 1.

Estimated coefficients of selection (s) for the csr1-1 and axr2-1 resistances based on Equation 1 (see materialsandmethods)

		Coefficient of selection (±SE)a
Sink population	csr1-1 resistance			axr2-1 resistance
		Generation:	2	3	4	2	3
1	−0.44 ± 0.34 (a)	−0.30 ± 0.29 (a)	0.18 ± 0.08 (a)	0.99 ± 0.003 (a)	0.94 ± 0.015 (b)
2	−0.19 ± 0.27 (a)	−0.16 ± 0.13 (a)	0.16 ± 0.15 (a)	0.99 ± 0.003 (a)	0.94 ± 0.013 (b)
3	0.11 ± 0.11 (a)	0.15 ± 0.15 (a)	0.34 ± 0.04 (a)	0.97 ± 0.006 (ac)	0.91 ± 0.020 (b)
4	−0.01 ± 0.29 (a)	0.16 ± 0.17 (a)	0.20 ± 0.07 (a)	0.95 ± 0.023 (abc)	0.93 ± 0.024 (ab)
5	0.18 ± 0.17 (a)	0.18 ± 0.10 (a)	0.27 ± 0.05 (a)	0.91 ± 0.017 (b)	0.98 ± 0.005 (a)
6	0.09 ± 0.24 (a)	0.12 ± 0.19 (a)	0.22 ± 0.14 (a)	0.95 ± 0.012 (c)	0.98 ± 0.006 (a)
7	0.02 ± 0.23 (a)	0.29 ± 0.15 (a)	0.29 ± 0.11 (a)	0.92 ± 0.038 (abc)	0.86 ± 0.045 (bc)
8	0.07 ± 0.17 (a)	0.33 ± 0.19 (a)	0.19 ± 0.04 (a)	0.86 ± 0.065 (abcd)	0.85 ± 0.065 (bc)
9	0.08 ± 0.30 (a)	0.44 ± 0.13 (a)	0.04 ± 0.19 (a)	0.66 ± 0.056 (d)	0.82 ± 0.005 (c)
Overall meanb:		−0.01 ± 0.08	0.14 ± 0.06	0.21 ± 0.04	0.92 ± 0.017	0.92 ± 0.012

For each generation, different letters within parentheses indicate different groups according to sink population, after pairwise comparisons using the Mann–Whitney U-test (without application of any post hoc test).

^aSelection coefficients are based on the mean frequency deviations of the resistance alleles. Positive or negative coefficient selection indicates a fitness cost or a fitness advantage of the resistance allele, respectively.

^bOverall mean indicates mean selection coefficient over sink populations and replicates.

Testing frequency dependence of the cost:

For each resistance gene, the equality of the fitness cost estimates found over the nine sink populations can be tested. Rejecting equality would indicate that the fitness cost is not a constant parameter but a frequency-dependent value. At generation 4 for the csr1-1 resistance and at generations 2 and 3 for the axr2-1 resistance, no simple transformation succeeded in restoring homogeneity of variance between sink populations, as confirmed by significant Levene's test results (data not shown). For each generation and each resistance allele, the Kruskall–Wallis nonparametric test was thus applied to detect the equality of the fitness cost estimates found over the nine sink populations, i.e., any effect of the initial resistance allele frequency on the estimates of fitness cost. Analyses were performed with Systat 10 software (SPSS).

Partitioning dynamics between migration–selection balance and random genetic drift:

Figure 2 illustrates for generations 2, 3, and 4 the expected evolution of the shape of the cline as a function of selection coefficient s. The parameter of migration has been purposely fixed in our experimental populations so that the shape of the cline would remain at equilibrium, i.e., remain linear over time, if the fitness cost equals 10% (s = 0.1) in absence of any genetic drift effect. From Equation 1 it is easy to show (as in Figure 2) that a resistance allele with a higher fitness cost than the 10% arbitrary reference will induce a greater deviation from the initial resistance allele frequency in sink population 1, where the resistant individuals are the most frequent, than in sink population 9, where the resistant individuals are the rarest. Contrarily, for resistance alleles that confer an advantage compared to the susceptible allele (or at least express a cost <10%), the deviation from the initial resistance allele frequency will be much greater for sink population 9 than for sink population 1, i.e., when the initial resistance allele frequency is low and there is a greater potential to increase. So, covering the whole range of allele frequencies increases the capacity for an accurate fitness cost measure under optimal conditions. Once migration rates are fixed, the higher the departure from an arbitrary cost is (here fixed to 10%), the higher the divergence from a stable (here linear) cline.

Figure 2.

Expected evolution of the shape of the cline as a function of selection coefficient s. At generations 2, 3, and 4, the expected resistance allele frequencies after migration are plotted against the sink populations for seven selection coefficients, from s = −0.3 to s = 0.9 with an increment of 0.2. The initial frequencies remain stable over generations for a fitness cost of 10% (s = 0.1); i.e., the shape of the cline remains linear and stable over time (dashed line).

For a given sink population, an observed resistance allele frequency that differs from the initial resistance allele frequency would thus indicate that the selection coefficient s attached to the resistance allele differs from 0.1. However, in clines under migration and natural selection, genetic drift can also induce allele frequency fluctuations (Felsenstein 1975; Slatkin and Maruyama 1975). To determine that the change in resistance allele frequencies from the initial frequencies in the experimental populations is not attributable to the effect of genetic drift alone, 95% confidence limits around initial frequencies were derived from simulations of drift variance with the Metapop software (Le Corre et al. 1997; Le Corre and Kremer 2003), a population genetics program designed to study the genetic evolution of a subdivided population of a diploid species under natural selection. In Metapop, if q_x is the resistance allele frequency in sink population x after selection, then the generation is completed by genetic drift, which occurs by having only N adults survive density-dependent population size regulation in each sink population. The effects of this population size regulation on the genetic composition are equivalent to drawing N seeds, sampling with replacement from a population with gene frequency q_x. The experimental cline design was thus simulated over four generations with the parameters (migration, number of sown seeds, and breeding system) described above. As the initial frequencies in each sink population remain stable without genetic drift for a selection coefficient of 0.1, this latter value was used for the simulation. Five hundreds replicates of the simulation were performed to build up the 95% confidence intervals under genetic drift alone. Empirical results were then compared to the 95% confidence intervals (illustrated by the dashed lines in Figure 3) to unambiguously identify the deviations of the resistance allele frequencies at generations 2, 3, and 4 from the initial frequencies that cannot be attributed to genetic drift alone.

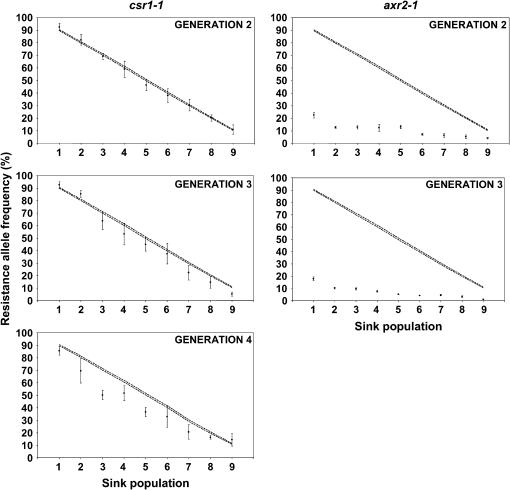
Figure 3.

Observed frequencies over time of the csr1-1 and axr2-1 resistance genes as a function of distance to the resistant source population. Symbols represent mean allele frequencies (with associated standard errors) of five replicates (48 seedlings genotyped for each population). Where errors bars are not indicated, they are less than the height of the symbol. Dashed lines represent the 95% confidence intervals around the expected mean frequency in the presence of fitness cost of 10% (s = 0.1), on the basis of simulations of drift variance (Metapop software). Resistance allele frequencies are expressed in percentages.

RESULTS

A total of 10,800 seedlings were genotyped to obtain 225 resistance allele frequency measures. For the csr1-1 resistance gene, 6480 seedlings were genotyped: 48 seedlings × 9 sink populations × 5 replicates × 3 generations (G₂, G₃, and G₄). For the axr2-1 resistance gene, 4320 seedlings were genotyped: 48 seedlings × 9 sink populations × 5 replicates × 2 generations (G₂ and G₃). Irrespective of the genotyping technique used, 100% of controls gave accurate results. We are thus highly confident in the quality of the measure of genotypic frequencies.

At generation 2, 0.9 and 0.7% of seedlings were found to be heterozygous for the csr1-1 and axr2-1 resistance alleles, indicating outcrossing rates of 1.8 and 1.4%, respectively. These values are close to those found in previous studies (Snape and Lawrence 1971; Bergelson et al. 1998) and were considered small enough to not significantly affect the haploid model used in Equations 1 and 2.

The evolution of the csr1-1 and axr2-1 resistance allele frequencies as a function of distance (migration rate) to the resistant source population is illustrated in Figure 3. A significant deviation from initial resistance allele frequency occurs whenever the average resistance allele frequency (and associated error bars) was outside the 95% confidence interval simulated from the effects of genetic drift alone. Here, the observed fluctuations of the resistance allele frequency between replicates are of magnitude greater than the 95% confidence intervals (Figure 3), especially for the csr1-1 resistance. This suggests an experimental population size N_e smaller than the theoretical one calculated in the Metapop software (see discussion).

Allele frequency deviations from the cline for each population indicate that s deviates from 0.1 in that population, while significant differences between populations in the magnitude of their deviation from the cline indicate the fitness cost is frequency dependent. The axr2-1 resistance allele exhibited a significantly strong shift from the initial frequency in all sink populations and generations (Figure 3), indicating a much higher fitness cost than 10% (Table 1). Over replicates, sink populations, and generations, the axr2-1 resistance conferred a mean fitness cost of 92% (Table 1). The fitness cost estimates were also found to be unequal over the nine sink populations at both generations 2 and 3 (generation 2, Kruskall–Wallis test statistic = 24.12, P = 0.002; generation 3, Kruskall–Wallis test statistic = 23.37, P = 0.003). The fitness cost conferred by axr2-1 was thus found to depend on its initial frequency in the sink populations: the fitness cost in sink population 9 was significantly lower than fitness costs in sink populations 1 and 2 at both generations 2 and 3 (Table 1). The fitness cost conferred by the axr2-1 resistance would therefore express a negative frequency dependence under our experimental conditions.

The results for the csr1-1 resistance are complex as the deviations depended on sink populations and generations. First, three generations were necessary for the csr1-1 resistance allele to significantly deviate from its initial frequency in most sink populations (Figure 3). At generation 2, none of the nine sink populations showed a significant departure from a fitness cost of 10% (Table 1). At generation 3, the csr1-1 resistance allele exhibited a significant decrease from the initial frequencies in only two sink populations (7 and 9) while at generation 4, six sink populations (2–5, 7, and 8) were significantly affected. Over replicates and sink populations, the csr1-1 resistance conferred a mean advantage of 1% and a mean fitness cost of 14% at generations 2 and 3, respectively (Table 1). These values do not significantly deviate from a fitness cost of 10% (one-sample two-tailed t-test: generation 2, t = 1.400, P = 0.168; generation 3, t = −0.573, P = 0.569). By contrast, the csr1-1 resistance conferred a fitness cost of 21% at generation 4, a value that significantly deviates from a fitness cost of 10% (one-sample two-tailed t-test, t = −3.134, P = 0.003). Overall, the mean cost for csr1-1 was ∼15%. With a cost of 10% the frequencies along our experimental cline would have been at equilibrium since the first generation. With a cost of ∼15% the csr1-1 resistance allele frequencies in the sink populations progressively departed from the initial frequencies only over generations (as in Figure 2). Second, in contrast to the axr2-1 resistance, no frequency dependence was found for the fitness cost estimates of the csr1-1 resistance in any generation (generation 2, Kruskall–Wallis test statistic = 2.99, P = 0.935; generation 3, Kruskall–Wallis test statistic = 11.17, P = 0.192; generation 4, Kruskall–Wallis test statistic = 4.82, P = 0.777).

DISCUSSION

In clines under migration and selection, allele frequency fluctuations can also arise from genetic drift (Felsenstein 1975; Slatkin and Maruyama 1975). To determine that the change in resistance allele frequencies in our experimental populations is not attributable to the effect of genetic drift alone, 95% confidence limits around initial frequencies were derived from simulations of drift variance with the Metapop software (Le Corre et al. 1997; Le Corre and Kremer 2003). The observed fluctuations of the resistance allele frequency between replicates are of magnitude greater than the 95% confidence intervals, suggesting an experimental population size N_e smaller than the theoretical one calculated in the Metapop software. The discrepancy cannot result from the 98.5% selfing reproductive system that is already taken into account in Metapop (reducing N_e from 100 to 51). Two explanations could be advanced for this observed discrepancy. First, the number of reproductive adults is equal to the number of sown seeds in the Metapop software. In our experimental populations, after self-thinning, the mean number of reproductive adults was measured as 83.9 plants per population, contributing to slightly reducing experimental population size N_e. The incorporation of the experimental value of 83.9 reproductive adults in a new run of simulations with the Metapop software does marginally affect our results: only the csr1-1 resistance allele frequency in sink population 2 at generation 4 was found not to differ from its initial frequency with a number of 83.9 reproductive adults; while it exhibited a significant decrease with a number of 100 reproductive adults. Second, the discrepancy can also come from the difference between the simulations and the experiment in the probability for a reproductive plant to contribute to population reproduction. The probability to reproduce in Metapop is equal among individuals and is assumed to fit a Poisson distribution for the number of offspring produced. Skewed distributions of the fitness sets within the experimental RR or SS class are probably contributing to reducing the effective size. Unfortunately, there is no way to directly assess the distribution of fitness within a sink population as seeds were harvested in bulk and not on a plant-by-plant basis. Still, in a similar experiment regarding greenhouse conditions and plant densities but not genetic background (see Lavigne et al. 2001 for details), variance in silique number was found to be 11.9 times greater than the mean (N = 92, mean = 44.9, variance = 537). This overspread distribution of a fitness-related trait in our competitive conditions would support the expectation for a further reduced N_e.

Fitness cost:

Determination of a fitness cost associated with pesticide resistance alleles can be achieved using two general groups of methods (e.g., Bourguet et al. 2004). The first group contains the direct measures of fitness based on comparing fitness components among resistant and susceptible individuals (method 1). It has the advantage of revealing which specific traits may underlie a fitness cost, although one can rarely ascertain that the total fitness has been correctly decomposed into a full set of relevant and analyzable traits. For instance, most experimental work estimates plant fitness from total seed production while the seed quality is seldom tested (Bergelson and Purrington 1996). The second group of methods refers to the definition of fitness, i.e., the average per capita lifetime contribution of individuals of a genotype to future generations in this population (Futuyma 1997). It involves the measure of changes in the frequencies of resistance alleles either in isolated populations that are not treated with pesticides over several generations (method 2; Cochran 1993; Boivin et al. 2003; Gustafsson et al. 2003) or in several connected populations located along a transect between treated and untreated areas (method 3; Lenormand et al. 1999). Methods 2 and 3 are the only ones that estimate complete fitness costs. Surprisingly, these have seldom been used in plants to assess a fitness penalty of a gene conferring resistance to either an abiotic or a biotic stress. However, new efficient throughput techniques in genotyping will facilitate the direct measurement of resistance allele frequency evolution.

For the two csr1-1 and axr2-1 resistance mutations analyzed here, the different methods to measure fitness cost were initiated with sister seeds originating from the same seed bulk. The comparison of the fitness cost found in each method can therefore be unambiguously assessed: (1) method 1, comparison of total seed productions between SS and RR plants (Roux et al. 2004); (2) method 2, evolution of resistance allele frequency in 12 herbicide-free isolated populations (each of 120 individuals) over time (Roux et al. 2005); and (3) method 3, evolution of a cline over time (this study).

The csr1-1 resistance mutation illustrates a case where direct and indirect methods to measure fitness cost result in different estimates. One explanation for an apparent discrepancy between the ∼15% cost detected in this experimental cline and the 36–37% found by Roux et al. (2004) with method 1 and Bergelson et al. (1996) could be that only a “seed-to-seed”-based method will integrate the characteristics of the seeds produced by the resistant and susceptible plants, respectively. When compared to susceptible references a higher and faster germination rate was found in some chlorsulfuron-resistant weed populations (Tranel and Wright 2002). Thus, a slight decrease in seed production conferred by the csr1-1 resistance allele at the homozygous state would be compensated for by a higher germination rate or a faster germination. Second, in isolated herbicide-free populations, the dynamics of the resistance allele frequency over time are expected to be correlated to the cost of the resistance; i.e., the more costly the resistance genes are, the more rapidly they will tend to be eliminated from the population. Wright (1948) showed, however, that both random genetic drift and selection pressures influence the frequencies of alleles in populations. In our isolated herbicide-free A. thaliana populations (method 2), any fitness cost <15% would be hardly detected over time with the population size used in this work (experiment total size: 12 replicates of 120 sown seeds) as the selection would roughly equal the general stochastic fluctuations governed by the genetic drift. In our experimental cline (experiment total size: 5 replicates of 1000 sown seeds), the influence of genetic drift on the evolution of the resistance allele frequency may have been buffered by gene flow among neighbor populations. Numerous replicates and huge populations are thus necessary in method 2 to overcome the effect of genetic drift to evaluate low fitness cost conferred by a resistance allele, while gene flow between populations in method 3 would contribute to buffer the effects of genetic drift along the cline. When studying theoretically the probability of fixation of slightly advantageous or deleterious mutations when selection and genetic drift interact, Whitlock (2000) came to a similar conclusion.

The estimated cost of 92% found here for the axr2-1 resistance allele is very close to the 89% cost that was previously estimated in the direct comparison of the total seed number produced by homozygous susceptible SS and resistant RR plants at the F₂ generation (Roux et al. 2004). It was even equal to the other indirect estimate of 92% (method 2). A strong fitness penalty therefore overcomes any other source of fluctuation such as genetic drift or unchecked trait variation. The potential for discrepancy between the methods is alleviated by such a high cost associated with the axr2-1 resistance allele.

In natural weed populations, the very high survival of csr1-1 RR plants under chlorsulfuron spray is not expected to be counterbalanced by a fitness penalty of 15%, which would explain the great occurrence of sulfonylurea resistance in fields (Tranel and Wright 2002). By contrast, the cost–benefit balance associated with the axr2-1 2,4-D resistance is much less favorable to the evolution of resistance in the field as the survival of axr2-1 R plants under 2,4-D spray would be largely counterbalanced by such a high fitness cost. This balance seems verified in fields as axr2-1 resistance has not yet been described in natural weed populations submitted to 2,4-D treatment.

Frequency dependence:

Excluding the models studying selection of cost modifiers, most models of pesticide and disease resistance management consider the fitness of a resistant genotype as a constant parameter, regardless of whether the resistant genotype is rare or common. An interesting complication is to consider the possibility that the fitness cost of a resistance changes as the resistant genotype frequency changes in the population. Such a frequency dependence of the fitness cost has two consequences on pesticide resistance evolution. First, compared to a frequency-independent resistance cost, the initial frequencies of a resistance prior to pesticide exposure in a population are expected to be much lower or higher if the fitness cost is positively or negatively frequency dependent, respectively (Jasieniuk et al. 1996). Second, it is predicted that resistance should decline quickly in a population after pesticide application ceases, provided that the resistance phenotype is ecologically costly compared to the susceptible phenotype (Bourdôt et al. 1996). The rate of decline of a resistance allele would thus fluctuate greatly in the presence of positive or negative frequency dependence.

Along our experimental cline, the resistance allele frequencies cover the whole range from 0 to 1 at the first generation. The fitness cost of resistance can therefore be estimated under all resistance allele frequencies in a single step. In isolated polymorphic populations, there would also be several resistance allele frequencies as the resistance gene tends to be eliminated over time. It could, however, take several generations to observe a shift of the fitness cost due to frequency dependence. In contrast to some other resistant weed species that exhibited positive frequency dependence of fitness cost (Amaranthus hybridus, Chenopodium album; Gressel and Segel 1990), the axr2-1 resistance allele showed a negative frequency-dependent fitness cost in our experimental cline. A hypothesis fitting this observation could come from a differential sensitivity of the absolute fitness of the resistant and susceptible plants toward their respective frequency in the population. Timpte et al. (1994) found that the morphological variance of the axr2-1 RR plants was less than that of the axr2-1 SS plants so that the relative fitness of the resistant plants would indeed increase as the frequency of the susceptible plants increased. Analysis of absolute fitness among SS and RR plants over different frequencies of the axr2-1 resistance allele could confirm this hypothesis.

We investigated the use of an artificial cline approach for the measure of a fitness cost. Once the migration rates are fixed, the stability of the resistance allele frequency along the cline depends on the fitness cost expressed. This method seems to be a powerful approach to quantify the fitness cost associated with an herbicide resistance gene as the gene flow between populations lessens the potential fluctuations introduced by genetic drift. Thus, smaller fitness differences between genotypes should be experimentally more tractable under an artificial cline approach. Moreover, the potential for frequency dependence of a fitness cost can be tested in few generations provided that the initial frequencies cover some range of frequencies. To better model the population genetics trajectories, fitness should be measured at various ratios of susceptible to resistant individuals, especially those that closely approximate the initial low frequencies of resistant individuals in the field.