The Evolution of Mobile DNAs: When Will Transposons Create Phylogenies That Look As If There Is a Master Gene?

Abstract

Some families of mammalian interspersed repetitive DNA, such as the Alu SINE sequence, appear to have evolved by the serial replacement of one active sequence with another, consistent with there being a single source of transposition: the “master gene.” Alternative models, in which multiple source sequences are simultaneously active, have been called “transposon models.” Transposon models differ in the proportion of elements that are active and in whether inactivation occurs at the moment of transposition or later. Here we examine the predictions of various types of transposon model regarding the patterns of sequence variation expected at an equilibrium between transposition, inactivation, and deletion. Under the master gene model, all bifurcations in the true tree of elements occur in a single lineage. We show that this property will also hold approximately for transposon models in which most elements are inactive and where at least some of the inactivation events occur after transposition. Such tree shapes are therefore not conclusive evidence for a single source of transposition.

A family of interspersed repetitive DNAs shows sequence similarity as a result of shared descent. Sequence diversity of mobile DNAs can give insight into the mechanisms through which these elements have spread through the genome. The diversity includes variation between “host” individuals in the presence or absence of an element at a particular location and the sequence diversity between copies at differing genomic locations. In Drosophila, variation between individuals in mobile DNA positions is high, and few euchromosomal sites of transposable elements are fixed in populations (Charlesworth et al. 1994). However, in humans, most interspersed repeats are fixed. While polymorphisms of the Alu short interspersed nuclear element (SINE), in particular, are useful in the creation of trees of human chromosomes and populations (Stoneking et al. 1997; Watkins et al. 2001), such polymorphic sites form a tiny fraction of the ∼1 million Alu sequences in the genome (International Human Genome Sequencing Consortium 2001).

The Alu SINE sequence is ∼290 bp in length. It is moved to new genomic locations by reverse transcriptase and endonuclease functions supplied by the abundant LINE-1 (L-1) long interspersed nuclear element (LINE) sequence. Alu element copies belong to a few sequence subfamilies (reviewed by Batzer and Deininger 2002), which differ by characteristic base substitutions. One can assess how long ago individual copies of a subfamily were inserted into the genome, by seeing how different they are from the subfamily consensus (Shen et al. 1991). For older subfamilies, copies differ greatly not only from the subfamily consensus, but from all other copies. This was noted by Britten (1994) and implies that the subfamily is no longer transposing, since recent transpositions would create similar pairs of copies. The simplest interpretation for this serial replacement of Alu subfamilies is that a single active Alu locus, or “master gene,” is the source of all transpositions. Differences between subfamilies represent changes in the DNA sequence of the master gene. There are now ∼850,000 copies of the Sx and J subfamilies, apparently active consecutively ∼50 million years ago. These were followed by the Sg subfamily, currently represented by 40,000 copies, and the Y subfamily, now with 200,000 copies, which includes elements active more recently.

However, this master gene model cannot be exactly correct for Alu sequences. At least three sub-subfamilies, Ya, Yb, and Yc, are currently active—seen through their insertions creating de novo mutations and their insertion sites being polymorphic in humans. Having multiple active templates is referred to by Deininger et al. (1992) as a “transposon” model. There is evidence that the total rate of Alu insertion has been variable in time (International Human Genome Sequencing Consortium 2001), with the current rate estimated to be only one two-hundredth of what it was >40 million years ago (Deininger and Batzer 1999).

A similar pattern is seen for the L-1 element in humans. Again, there has been a pattern of serial replacement, with a series of subfamilies called L1PA5, L1PA4, L1PA3B, L1PA2, and L1PA1 being successively active over the past 25 million years (Boissinot et al. 2000; Boissinot and Furano 2001). However, again like Alu, more than one L1PA1 sub-subfamily is currently active. The mouse L-1 sequences also have multiple sources presently active (Mears and Hutchinson 2001).

What are the likely patterns of similarity between members of an interspersed repetitive sequence family? One of us (Brookfield 1986) considered the phylogeny predicted by the model for transposable element frequency spectra produced by Langley et al. (1983), with the added assumption that all copies of a transposable element family had equal transposition rates. The main prediction was the expected time in generations to common ancestry at equilibrium for two randomly sampled members of the family. This (using the terminology in this article) is n(1 + 4N_eν)/(2ν), where ν is the effective rate of transposition per genome, n is the element copy number per haploid genome, and N_e is the effective size of the host population. This gives unrealistically high values for the times to common ancestry for human repetitive sequences, of billions of generations. This model was developed further by Kaplan and Hudson (1989).

The model assumes that all members of a family have equal transposition rates. This is not true of the human repeats. For the L-1 element, the majority of copies are inactivated at their moment of insertion, by truncations at their 5′ ends (Voliva et al. 1983). One of us (Brookfield 2001a) showed that, if only a proportion β of transposable element insertions are subsequently active, the expected time in generations to common ancestry for elements sampled at randomly chosen sites will be (2(1 − β) + nβ(1 + 4N_eν))/(2ν) generations. However, this is incomplete. Since inactivating mutations are neutral at any given site, in addition to insertional inactivation, active elements are inactivated by random mutation, a phenomenon called the “pseudogene effect” by McAllister and Werren (1997).

Models of the master gene model include Clough et al.'s (1996) model of transposable elements in a single haploid host. Transposition can either follow the master gene model, with the same sequence always used as the source of the transpositions, or the “random template” model, in which all copies of the sequence are equally likely to transpose. These authors have no copy number equilibrium in their model, but an expanding element family. The random template model corresponds to that of Ohta (1986), who showed that one would not expect the subfamilies seen in the Alu family under such a model. Tachida's (1996) model of the master gene hypothesis included a narrow time window in the past when a family expanded using a single master gene as a transposition template. When applied to the Alu data, the model underestimated the number of shared differences from the consensus sequence, a result consistent with multiple simultaneously active templates.

Here we model the expected phylogeny of a transposable element family at copy number equilibrium when there are multiple templates for transposition. The model applies to elements that replicate in transposition, either directly or indirectly. We assume a nonrecombining tree, although recombination and gene conversion between Alu sequences, for example, is probable and has been detected (Roy et al. 2000; Salem et al. 2003).

The main finding is that the most distinctive property of the phylogeny expected under the master gene model—all the bifurcations in the phylogeny leading to the sampled sequences occurring on the same branch—will be approximately duplicated in many models with multiple simultaneously active source loci. In particular, this is the expected result of models in which inactivation of elements occurs by the pseudogene effect.

METHODS AND ANALYTICAL RESULTS

We assume (initially) that the population size is small—elements at given genomic locations are rapidly lost or fixed by genetic drift—and we treat the population as a single haploid genome. Insertions are never advantageous to the hosts, while disadvantageous insertions are eliminated by selection before they give any transpositions. Thus, the rate of creation of new fixed sites is the neutral transposition rate per gamete, of ν transpositions per genome. Transposition is replicative and all “active” elements can be donors in transposition events. However, not all transpositions into neutral sites create active elements. Of the total transposition rate of ν, the rate of transposition to create active elements is ν_a and the rate creating inactive elements is ν_i. In addition, active elements are inactivated by mutation through the pseudogene effect. κ is the rate of inactivation of elements and d the rate of deletion of elements. We assume equilibrium between transposition, inactivation, and deletion.

The rate of increase in active elements is ν_a and the rate of loss is n₁(κ + d), where n₁ is the number of active elements per genome. Thus, at equilibrium, n₁ is ν_a /(κ + d). The equilibrium number of inactive elements, n₂, is (ν_i + n₁κ)/d, or ((ν_i + ν_a)κ + ν_id)/(d(κ + d)), with n = n₁ + n₂ = (ν_i + ν_a)/d elements in total.

The expected phylogeny of transposable elements when some are inactive:

Imagine a sample containing i inactive and a active elements, where i ≪ n₂ and a ≪ n₁. If we consider a coalescence process for our elements, four different types of events are possible. These define three probabilities.

The first is the probability of an activation event without coalescence, which can occur through two different events. An inactive element could be created at transposition from an active element that is not ancestral to any other elements present in the sample. Alternatively, an inactivation could occur in situ as governed by the parameter κ. Either one results in i dropping by 1 and a increasing by 1. The summed probability per generation is symbolized here by P(i → i − 1, a → a + 1).

Another event is an inactive element being created at transposition, from an active element that is ancestral to element(s) in the sample. This creates a coalescence between an active and an inactive element, and i will drop by 1 and a will be unchanged. The probability is symbolized by P(i → i − 1, a → a).

The other type of event is two active elements coalescing. a will drop by 1, and i will be unchanged. The probability is symbolized here by P(i → i, a → a − 1).

The relative likelihoods depend on P(i → i − 1, a → a + 1), P(i → i − 1, a → a), and P(i → i, a → a − 1). P(event), the probability of some change in the distribution per generation, is given by

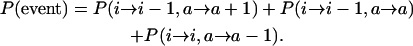We now define the probabilities that the first event will be an activation, defined as P(Act), that the first event will be a coalescence between active and inactive elements, or P(Cai), and that the first event will be a coalescence between two active elements, or P(Ca), i.e.,

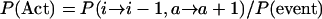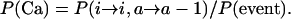For P(i → i, a → a − 1), what is the probability that a pair of active elements shares descent in the last generation? The expected number of active elements created per generation is ν_a, and so the probability that one of the two elements being considered is derived by transposition in the last generation is 2ν_a/n₁ (given that this is ≪1). The probability that the other copy represents the donor element of this transposition is 1/(n₁ − 1). So the probability of coalescence of any two active elements per generation is 2ν_a/(n₁(n₁ − 1)). This is, at equilibrium, 2(κ + d)²/(ν_a − κ − d). Call this T. Given a active elements in the sample, and thus a(a − 1)/2 pairs of elements, P(i → i, a → a − 1) is a(a − 1)T/2.

For P(i → i − 1, a → a), consider an active and an inactive element. The expected number of inactive elements created by transposition in the last generation is ν_i, and so the probability that the inactive element has transposed in the last generation is ν_i/n₂. The probability that the other, active, copy represents the donor element of this transposition is 1/n₁. So the probability of coalescence of any pair of an active and an inactive element per generation is ν_i/(n₁ · n₂). This is, at equilibrium, ν_i(d(κ +d)²)/(ν_a((ν_i + ν_a)κ + ν_id)). Call this F. P(i → i − 1, a → a) is thus iaF.

The rate at which inactive elements are lost is n₂d, and the rate at which inactive elements are created from active elements (by transposition or mutation) must, at equilibrium, also be n₂d. Thus, the probability that any given one of the i inactive elements in the sample either fuses with an active element or is activated must be d. The probability of it coalescing with an active element is aF, so the probability of activation without coalescence must be d − aF. P(i → i − 1, a → a + 1) is thus i(d − aF).

Table 1 shows, for one set of parameters, for sample sizes up to five, and for all combinations of active and inactive elements, the relative probabilities of each type of change. The columns represent different total numbers of elements in a sample, and the rows differ in the number of inactives. Shown are probabilities, for a coalescence process starting in a given section, that the first event would be an activation (a move to the section above), or an active–inactive coalescence (up and diagonally left), or a coalescence between actives (to the left).

TABLE 1.

Probabilities of activation and coalescence events for differing sample constitutions

i\i + a	2	3	4	5
0	P(Act) = 0	P(Act) = 0	P(Act) = 0	P(Act) = 0
P(Ca) = 1	P(Ca) = 1	P(Ca) = 1	P(Ca) = 1
P(Cai) = 0	P(Cai) = 0	P(Cai) = 0	P(Cai) = 0
1	P(Act) = 0.9	P(Act) = 0.2667	P(Act) = 0.1000	P(Act) = 0.0461
P(Ca) = 0	P(Ca) = 0.6667	P(Ca) = 0.8571	P(Ca) = 0.9231
P(Cai) = 0.1	P(Cai) = 0.0667	P(Cai) = 0.0429	P(Cai) = 0.0308
2	P(Act) = 1	P(Act) = 0.9000	P(Act) = 0.4000	P(Act) = 0.1750
P(Ca) = 0	P(Ca) = 0	P(Ca) = 0.5	P(Ca) = 0.75
P(Cai) = 0	P(Cai) = 0.1000	P(Cai) = 0.1000	P(Cai) = 0.0750
3	P(Act) = 1	P(Act) = 0.9	P(Act) = 0.48
P(Ca) = 0	P(Ca) = 0	P(Ca) = 0.4
P(Cai) = 0	P(Cai) = 0.100	P(Cai) = 0.12
4	P(Act) = 1	P(Act) = 0.9
P(Ca) = 0	P(Ca) = 0
P(Cai) = 0	P(Cai) = 0.1
5	P(Act) = 1
P(Ca) = 0
				P(Cai) = 0

F = 0.00001, T = 0.0002, d = 0.0001.

The master gene property—all bifurcations are in a single lineage:

With a master gene, all bifurcations in the true tree occur on a single branch. How likely is this master gene property for a transposable element family? One way of describing such a phylogeny is that, at any time, only one lineage can be ancestral to more than one element in the sample.

We calculate the probability of this property if all elements are active. Sample five active elements (Figure 1) and classify lineages into two types. D, or derived, lineages have a single descendant in the sample, while M lineages are ancestors of more than one element in the sample. Under the master gene property, at no time can there have been more than one M lineage.

Figure 1.

Loss of the master gene property during the coalescence of five elements. The lineages marked M, shown as double lines, are ancestors of more than one element in the sample. In the second and third coalescences, the master gene property—no more than one M lineage—can be lost.

Starting with five D elements (leftmost in Figure 1), the first coalescence creates three D lineages and one M lineage. The next coalescence might fuse the M lineage to one of the D lineages (with probability 0.5) or might fuse two D lineages (with probability 0.5). Thus, after two coalescences, there is a 50% probability of two D lineages and one M lineage and a 50% probability of one D lineage and two M lineages. For the latter (below the line in Figure 2), the master gene property does not hold. In the third coalescence, given a two D, one M arrangement, there is a one in three chance of the two D elements fusing, again destroying the master gene property. Thus, with sample size five, there is a one in three chance of the master gene property. In general, the probability of this property, given i lineages in the sample, is

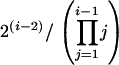However, if some sequences are inactive, the probability of the master gene property is increased. Assuming ν_i = 0, at each coalescence, two active elements fuse. An ancestral sequence (of type M) will inevitably be active, but few others might be, and so the probability of successive fusions including M elements will be increased.

Figure 2.

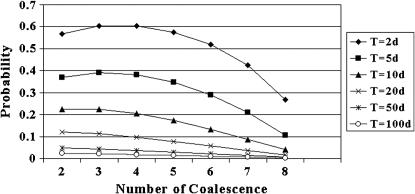
The probabilities that individual coalescences in a transposon phylogeny (sample size 10) fail to show the master gene property. This is when F = 0, and the T/d ratio varies from 2 to 100.

Table 2 shows a set of probabilities when ν_i = 0. Table 3 uses Table 2's values and calculates the probability of the master gene property (i.e., M = 1 at all times) for any possible sample of i inactive and a active sequences. With five inactive elements (the bottom right-hand section) the probability of the master gene property is 0.6947, which is more than twice that for five active elements.

TABLE 2.

Probabilities of activation and coalescence events for differing sample constitutions, without inactivation at transposition

i\i + a	2	3	4	5
0	P(Act) = 0	P(Act) = 0	P(Act) = 0	P(Act) = 0
P(Ca) = 1	P(Ca) = 1	P(Ca) = 1	P(Ca) = 1
1	P(Act) = 1	P(Act) = 0.3333	P(Act) = 0.1429	P(Act) = 0.0769
P(Ca) = 0	P(Ca) = 0.6667	P(Ca) = 0.8571	P(Ca) = 0.9231
2	P(Act) = 1	P(Act) = 1	P(Act) = 0.5	P(Act) = 0.25
P(Ca) = 0	P(Ca) = 0	P(Ca) = 0.5	P(Ca) = 0.75
3	P(Act) = 1	P(Act) = 1	P(Act) = 0.6
P(Ca) = 0	P(Ca) = 0	P(Ca) = 0.4
4	P(Act) = 1	P(Act) = 1
P(Ca) = 0	P(Ca) = 0
5	P(Act) = 1
				P(Ca) = 0

F = 0.000, T = 0.0002, d = 0.0001.

TABLE 3.

Probabilities that the master gene property will hold (i.e., M = 1) for different sample constitutions

i\i + a	2	3	4	5
0	P(M = 1) = 1	P(M = 1) = 1	P(M = 1) = 0.6667	P(M = 1) = 0.3333
1	P(M = 1) = 1	P(M = 1) = 1	P(M = 1) = 0.8571	P(M = 1) = 0.5384
2	P(M = 1) = 1	P(M = 1) = 1	P(M = 1) = 0.8730	P(M = 1) = 0.6763
3	P(M = 1) = 1	P(M = 1) = 0.8730	P(M = 1) = 0.6947
4	P(M = 1) = 0.8730	P(M = 1) = 0.6947
5				P(M = 1) = 0.6947

T = 0.0002, F = 0, d = 0.0001.

The effect of T/d:

Whether the master gene property is likely to hold depends on the relative sizes of T and d. When d is large relative to T, inactive elements rapidly turn into active elements, while coalescence of active elements is slow. Since many active ancestors exist when coalescences occur, the master gene property is unlikely. If T ≫ d then, as soon as two active elements exist, they are likely to coalesce, and thus the same lineage is involved in each coalescence event, and the master gene property is more likely. Figure 2 shows the probability of the master gene property being lost, at each opportunity, in a sample of 10 inactive elements. The lines represent differing T/d ratios, with the lowest representing T = 100d. It is the more recent coalescences (although not the most recent) that are least likely to show the master gene property.

RESULTS OF SIMULATIONS

We have an abundant sequence family at equilibrium with 100,000 copies in the genome, with a rate of deletion, d, of 10⁻⁶. Suppose, for now, that inactivation occurs by the pseudogene effect; i.e., ν_i = 0. Since n₁ + n₂ = 100,000, and this is ν_a/d, ν_a = 100,000d or 0.1. The proportion of elements that are active is determined by the rate of inactivation, κ. For 1000 active elements, since κ + d = ν_a/n₁, κ = 0.000099. For 100 active elements, κ = 0.000999. These differing values for κ have interesting consequences for T. For n₁ = 1000, T = 2.02 × 10⁻⁷, 5 times smaller than d. However, if n₁ = 100, T = 2.02 × 10⁻⁵, 20 times bigger than d. A 10-fold difference in n₁ makes a 100-fold difference in T. The master gene property depends on the relative sizes of T and d, and there are very different probabilities of a master gene-like phylogeny with 100 and with 1000 active elements.

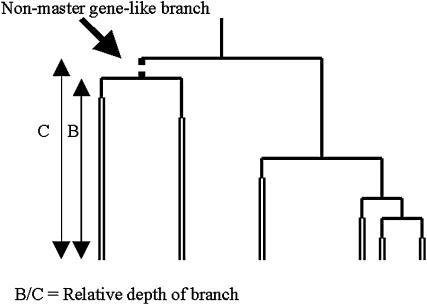
Even with n₁ = 100, it is unlikely that the master gene property will hold perfectly. But short internal branches not supporting the master gene property are unlikely to have many mutations and will be hard to detect. Figure 3 quantifies the length of a branch that fails to show the master gene property, one connecting two sequences to the master gene. The time to the coalescence not showing the master gene property is B, while the time to when this lineage coalesces with that of the master gene is C. Any coalescence failing to show the master gene property will have a B/C ratio associated with it. B/C ratios near one will make it hard to detect departures from a master gene tree using sequence information.

Figure 3.

An example of a coalescence that fails to show the master gene property and the way in which the length of a branch failing to show this property can be described. B is the time back to a nonmaster gene coalescence, and C is the time to when the lineage created coalesces with the master gene lineage. Our ability to detect the existence of the branch from sequence information relies on B/C being considerably less than one.

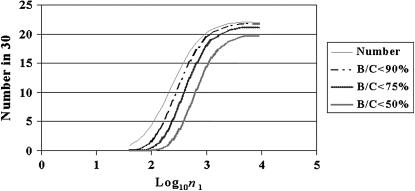
We simulate phylogenies with d = 0.000001, ν_i = 0, and ν_a = 0.1. n₁ + n₂ = 100,000 elements. For each tree, we total the number of coalescence events not involving the master gene (defined as the ancestor of the two sequences first coalescing). We vary n₁ by changing κ and see the effect of κ on T and on the expected shape of the tree. The sample is 30 inactive elements. The time taken for any given event in the phylogeny is exponentially distributed with a mean of 1/P(event) generations. Each coalescent yields a number of nonmaster gene coalescences and the numbers with a B/C ratio <90%, <75%, and <50%, respectively. For each n₁ value, we average over 1000 simulations. We see a sharp change in the outcome (Figures 4 and 5). When n₁ = 1000 (i.e., log₁₀n₁ = 3) or larger, there are many long internal branches—we do not see the master gene property. Then, sharply, as n₁ drops to 100 (i.e., log₁₀n₁ = 2), the number of coalescences failing to show the master gene property drops from ∼20 to ∼4, and these create very short branches. For a large family (100,000 copies), even with 100 elements active, the phylogeny produced may be indistinguishable from that expected from a master gene model.

Figure 4.

The impact of the inactivation rate, κ, and the resulting number of active elements at equilibrium (n₁, shown on a log₁₀ scale) on the extent to which phylogenies of elements resemble master gene phylogenies. Four lines show, from top to bottom, the average numbers of coalescences that fail to show the master gene property and the average numbers for which B/C <0.9, <0.75, and <0.5, respectively. d = 10⁻⁶, ν_a = 0.1, and ν_i = 0.

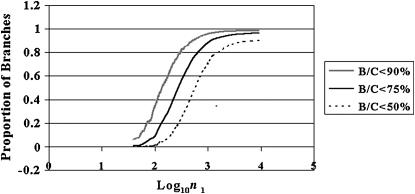
Figure 5.

Figure 4 replotted, showing the proportions of coalescences failing to show the master gene property that have B/C values <90, <75, and <50%, respectively.

What determines the number of active elements at which this sudden change in tree shape is seen? Since the probability of an activation is id, and the probability of a fusion is a(a − 1)T/2, what number of active elements corresponds to d = T/2? This arises when d = (κ + d)²/(ν_a − κ − d). But, if ν_a ≫ κ ≫ d, this implies dν_a ≈ κ². However, since, if ν_i = 0, n₁ ≈ ν_a/κ, and n₁ + n₂ ≈ ν_a/d, and this implies that n₁ ≈ 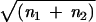. A master gene-like phylogeny is seen when the number of active elements is less than the square root of the total number.

Inactivation at transposition:

Above we assumed that ν_i = 0. What happens when there is inactivation at the moment of transposition (ν_i > 0)? Consider the case when all inactivation occurs at transposition (κ = 0). d is still 10⁻⁶, n₁ = 30 (so the phylogeny would look very like the master gene if there was no inactivation at transposition), and n₁ + n₂ = 100,000. This implies that ν_a = 3 × 10⁻⁵ and ν_i = 0.09997. The values for T and F are, respectively, 6.9 × 10⁻⁸ and 3.33 × 10⁻⁸. This model corresponds to that of Brookfield (2001a). Simulations (not shown here) show phylogenies very different from a master gene, since d is ∼14 times greater than either T or F. Active elements are both being created and being lost slowly.

So, the finding that ≤100 active elements of 100,000 create phylogenies similar to the master gene depends on inactivation occurring through the pseudogene effect and not at the moment of transposition. But the pseudogene effect must act to some degree—κ cannot, in reality, be zero. We assume now that some inactivations occur at the moment of transposition and some by the pseudogene effect. Suppose the rates of generation of inactive elements by each route are equal (i.e., ν_i = n₁κ). We make n₁ = 30, and n₁ + n₂ = 100,000, as before, with d = 10⁻⁶. This implies that ν_a = 0.050025, ν_i = 0.049975, and κ = 0.0016658. Now T = 1.15 × 10⁻⁴ and F = 1.67 × 10⁻⁸. Thus, with half of the inactivations occurring at transposition, T is 115 times bigger than d, and simulated phylogenies look like master gene phylogenies. If 90% of inactivations are by transposition and 10% by the pseudogene effect, T = 2.31 × 10⁻⁵ and F = 3.0 × 10⁻⁸. T is >23 times larger than d, and so a master gene-like phylogeny arises if even a small proportion of inactivations occur in situ.

Host population size:

We have above assumed a single haploid genome. In reality, transposable element insertions will have frequencies in a diploid population of effective size N_e, and at the moment of insertion a transposed element will have a population frequency of 1/2N_e. What effect does host population size have? First, consider the probability of activation. Since inactivation is created by an inactivating mutation in a single copy of the element, the probability of activation remains d in a model in which element sites have frequencies, given that inactivation is through the pseudogene effect.

Active elements are involved in transposition, and their times to coalescence are affected by the effective population size. We use an argument of Brookfield (1986). Active elements, at neutral sites throughout the genome, are subject to random drift and inactivation at rate κ. The much smaller effect of deletion is ignored. At equilibrium, their frequency distribution follows an infinite-alleles distribution with neutral parameter 4N_eκ. Define the frequency of active elements at a given site as f/2N_e, where f is the number of chromosomes of 2N_e that have active elements at that site. Let p(f/2N_e) be the expected frequency of sites with frequency f/2N_e, such that

Now consider two random active elements. The probability that exactly one of the elements is derived by transposition in the last generation is ∼2ν_a/n₁. If so, we need to consider the probability that it has been derived from an element at a site with frequency f/2N_e. The probability that it is derived from such a site is (f/2N_e)p(f/2N_e). What is the probability that the other element sampled is at the site that is the source of this transposition? If the site has frequency f/2N_e, then the proportion of all active elements that are at this site is f/2n₁N_e. Thus the probability that the two sampled elements are a new insertion derived from a site with frequency f/2N_e and an element from the site that was the source of this insertion is 2ν_a(f/2N_e)²p(f/2N_e)/n₁². Summed over all f, this gives a probability that we sample a new insertion and an element from the site that was the source of the insertion, which is

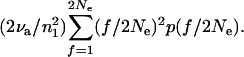(1)

Now make the approximation that the time of occupancy of an individual transposable element site is short relative to the time between successive coalescences (which will be true if n₁ ≫ a). This allows us to treat the sampling of a newly transposed element from a new site and an element from the donor site as being a coalescence of two lineages (the extra time to common ancestry of two elements at the same site is ignored). So (1) is also the probability that two random active elements coalesce in a given generation. However,

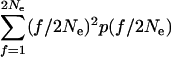is the expected homozygosity in the infinite-alleles distribution, which, in this case, is 1/(1 + 4N_eκ). Thus the probability of a fusion between two lineages is 2ν_a/(n₁²(1 + 4N_eκ)), and the total probability of a coalescence in a given generation is a(a − 1)ν_a/(n₁²(1 + 4N_eκ)).

But, given that n₁ ≈ ν_a/κ, we substitute for n₁, giving a probability of a coalescence in a given generation of a(a − 1)κ²/(ν_a(1 + 4N_eκ)).

The effect of host population size is thus simply to decrease T ∼(1 + 4N_eκ)-fold, making the tree much less master gene like if 4N_eκ ≫ 1. In humans, heterozygosity at the base pair level is ∼10⁻³, even in unconstrained genomic regions where μ ≈ μ_N, and so 4N_eμ is only ∼10⁻³. Since κ is the mutation rate per base, μ, multiplied by the number of bases in the sequence whose mutation will inactivate the sequence, which must be <300 for Alu sequences, we can be confident that 4N_eκ < 1. This leaves the phylogeny almost unaffected by the inclusion of the effective size. [It is, however, possible that inactivation of the Alu sequence is brought about by mutation of CpG doublets, which will occur at a higher rate than other mutational processes (Batzer et al. 1990)].

Why does 4N_eκ make a difference? Master gene-like trees arise because the n₁ active elements all share ancestry that is recent compared to intervals between activation events in the ancestry of the inactive elements in the sample. An active element will fuse quickly with the lineage designated the master gene branch, prior to the creation of a further active element. But, given neutrality, two active elements cannot be expected to have common ancestry any more recently than 2n₁N_e generations ago, this being the total number of active elements in the population.

The parameter F is also reduced by a factor (1 + 4N_eκ).

DISCUSSION

We show that a model, at equilibrium, with a small proportion of elements active, and at least a reasonable proportion of element inactivations being at their chromosome location, will almost inevitably lead to phylogenies suggesting a master gene. While inspired by human LINE and SINE sequences, this applies to any heterogeneous sequence family in any species. It assumes that subfamilies are not independently regulated—the overall transposition rates υ_a and υ_i are fixed, and all active elements from all subfamilies have equal transposition probabilities.

There are two strong reasons why the transposon model is more satisfactory than the master gene model. The first is that selection operating on any master gene is mysterious since the master gene's function is mysterious. Even if a master gene is selectively maintained as a result of its unknown function, selection would not necessarily maintain its being a source of transposition. But selective maintenance of transposability in a transposon family follows from transposition itself—the sequences required persist since copies that have, by chance, retained them increase their genomic copy numbers by replicative transposition. Indeed, Britten (1994) noted purifying selection maintaining DNA sequence blocks in the Alu element. These include the protein-binding sequences involved in RNA polymerase III transcription (which is required for these retroposons to transpose).

The other argument for the transposon model, at least for Alu and L-1 sequences, is that, given that multiple source elements are now active, why should this not have held earlier? Indeed, even “old” sequence families are still active at a low level (Johanning et al. 2003). Why, then, should the master gene model seem to have applied more in the past than now? Part of the answer can be discerned from Figure 3. When T ≫ d, and thus the master gene property is most likely to hold, it is the recent coalescences that have the highest chance of departing from this property, while earlier coalescence events follow it more closely.

However, while numerous features of the data are reproduced in this simplistic model, processes of transposition are complex. The model assumes that all active elements transpose at equal rates. More probable is that activity is lost gradually by mutations that sequentially diminish the ability of an element to transpose. Inactivation of Alu sequences may occur particularly rapidly through mutation of CpG sequences, present at high frequency in active elements but underrepresented in their inactive descendants (Batzer and Deininger 2002). Variation in transposability between active elements may be inherited in the act of transposition. In addition to the gradual deterioration of elements, mutations might increase transposition rate, creating subfamilies that increase rapidly, as a result of a deterministic advantage. In the L-1 sequence's recent evolution, part of the coiled-coil domain of the protein encoded by ORF1 shows evidence (in the form of an elevated amino acid replacement rate relative to the synonymous rate) of adaptive evolution (Boissinot and Furano 2001). This domain is involved in protein–protein interactions, and the evolution could involve adaptation to a changing host protein. Selectively driven turnover will increase the phylogeny's resemblance to a master gene, since advantageous variants will create selective sweeps through the population of active sequences. Jordan and McDonald (1998) studied variation between the LTRs of copia retrotransposons in Drosophila melanogaster and found evidence for selection operating between different subfamilies of these elements, which differ in their binding sites for transcription factors—which may affect copia transcription and therefore transposition.

In addition, the model used here is unrealistic in its assumption that the copy numbers of elements are at equilibrium. The constant genomic rate of transpositional gain of elements, coupled with a rate of loss of elements that varies with copy number, creates an unrealistically strong stabilization of copy number. Even with regulation of element numbers, there will be random fluctuations with time in the number of elements, particularly active elements, which would tend to lower the time depth of the trees.

The model also assumes that all elements are at neutral sites. Numerous examples are accumulating of element insertions apparently creating benefits for hosts, especially in humans (Batzer and Deininger 2002). In the human genome, older Alu elements are found preferentially in gene-rich regions, a result interpreted as due to selection favoring insertions in this region (International Human Genome Sequencing Consortium 2001). However, selection could not, in itself, create changes over this very slow timescale, since younger elements that do not show this enrichment are already fixed (Brookfield 2001b).

We have here studied the expected phylogenies of transposable genetic element families in which the vast majority of copies are inactive. These may lead to an interpretation that only a single source locus (a master gene) is active. However, it appears that there is no compelling evidence that the master gene model has ever applied to any transposable element family.