Abstract
A variety of estimators have been developed to use genetic marker information in inferring the admixture proportions (parental contributions) of a hybrid population. The majority of these estimators used allele frequency data, ignored molecular information that is available in markers such as microsatellites and DNA sequences, and assumed that mutations are absent since the admixture event. As a result, these estimators may fail to deliver an estimate or give rather poor estimates when admixture is ancient and thus mutations are not negligible. A previous molecular estimator based its inference of admixture proportions on the average coalescent times between pairs of genes taken from within and between populations. In this article I propose an estimator that considers the entire genealogy of all of the sampled genes and infers admixture proportions from the numbers of segregating sites in DNA sequence samples. By considering the genealogy of all sequences rather than pairs of sequences, this new estimator also allows the joint estimation of other interesting parameters in the admixture model, such as admixture time, divergence time, population size, and mutation rate. Comparative analyses of simulated data indicate that the new coalescent estimator generally yields better estimates of admixture proportions than the previous molecular estimator, especially when the parental populations are not highly differentiated. It also gives reasonably accurate estimates of other admixture parameters. A human mtDNA sequence data set was analyzed to demonstrate the method, and the analysis results are discussed and compared with those from previous studies.
OVER the past 70 years, many statistical methods have been developed and applied to estimating the genetic compositions of admixed/hybrid populations, using genetic marker data (for recent reviews see Beaumont 2003; Choisy et al. 2004; Excoffier et al. 2005). The primary interest is to infer, from the amount and pattern of genetic variation revealed by markers, the proportional contributions of two or more potential parental populations to the gene pool of an admixed population (Chakraborty 1986). Estimating such admixture proportions helps in understanding the evolutionary history of populations (e.g., Chikhi et al. 2002; Wen et al. 2004), in genetic epidemiological investigations (Chakraborty and Weiss 1986, 1988), and in assessing the risk of diseases in human populations. In conservation biology, knowledge of admixture proportions helps in making informed management of endangered species in the wild.
Most methods available use allele frequency data to estimate admixture proportions, exploiting the genetic characteristic of an admixed population that its allele frequencies should be intermediate between those of the parental populations (Cavalli-Sforza and Bodmer 1971; Bertorelle and Excoffier 1998). The main differences among these methods are whether or not to take genetic drift into account and how to select (e.g., Chakraborty et al. 1992) and treat allele frequency data statistically. Traditional methods are usually moment estimators that ignore the genetic drift that occurred to the parental and hybrid populations since the admixture event (e.g., Glass and Li 1953; Roberts and Hiorns 1965; Elston 1971; Long 1991; Chakraborty et al. 1992), while recent ones are usually likelihood or Baysian estimators (e.g., Thompson 1973; Chikhi et al. 2001; Wang 2003), allowing the joint estimation of admixture proportions and genetic drift. A flexible method based on some summary statistics and approximate Bayesian computation (Beaumont et al. 2002; Marjoram et al. 2003) has been proposed recently, which estimates admixture proportion, genetic drift, and mutation parameters simultaneously from linked or unlinked microsatellite markers (Excoffier et al. 2005).
Molecular markers, such as DNA sequences and microsatellites that are now used widely, provide us not only allele frequency information, but also deep genealogical information revealed by the molecular diversity of sampled genes. Most of the above methods do not use such molecular information and assume that mutations are absent since the admixture event, causing two potential problems. One is that discarding molecular information may result in a loss of estimation precision, especially when the mutation rate is high for markers such as large DNA sequences. The other is that when admixture is ancient and thus mutations are not negligible, these methods may fail to deliver an estimate or give rather poor estimates. Realizing these problems, Bertorelle and Excoffier (1998) developed a novel estimator that uses both allele frequency and molecular information and explicitly takes mutations into account in estimating admixture proportions. The estimator was shown to be less biased and, in some situations, to yield more precise estimates of admixture proportions (Bertorelle and Excoffier 1998; Wang 2003). Later on, the estimator was extended by Dupanloup and Bertorelle (2001) to allow three or more parental populations contributing to the admixture.
In this article I develop a new molecular estimator under a well-defined admixture model (Bertorelle and Excoffier 1998; Wang 2003; Excoffier et al. 2005) and compare it with the previous molecular estimator by using both simulated and real data. While the previous molecular estimator bases its inference on the average coalescent times between two genes taken from within and between populations, the current one considers the entire genealogy of the sampled genes and infers admixture from the numbers of segregating sites in DNA sequence samples. By considering the genealogy of all sequences rather than pairs of sequences, this new estimator also allows the joint estimation of other interesting parameters such as admixture time, divergence time, population size, and mutation rate as well as admixture proportions.
METHODS
The admixture model:
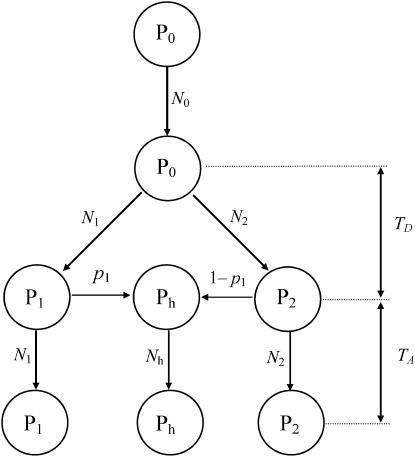
Several recent studies adopt the admixture model proposed by Bertorelle and Excoffier (1998), with slight modifications (Chikhi et al. 2001; Wang 2003; Choisy et al. 2004; Excoffier et al. 2005). In this study, I use the admixture model of Excoffier et al. (2005), as illustrated in Figure 1. I assume an ancestral population, P0, splits into two parental populations, P1 and P2, which evolve separately for TD generations. At that point of time, a hybrid population, Ph, is instantaneously created by combining genes of proportions p1 and p2 = 1 − p1 taken at random from parental populations P1 and P2, respectively. After the admixture event, the three populations evolve in isolation for a period of TA generations, when a sample of individuals is taken from each population for examining some markers. I also assume, as is implicit in all previous admixture models, that neither direct nor indirect selection is associated with the markers surveyed, and the markers are from diploid and autosomal loci. With 2N (N, the effective population size) replaced by N, however, the method applies to haploid markers (such as mtDNA) as well.
Figure 1.—
The admixture model. It is assumed that an ancestral population, P0, is split into two parental populations P1 and P2, which evolve independently for TD generations before they contribute genes of proportions p1 and 1 − p1 to form the hybrid population, Ph. After the admixture event, P1, P2, and Ph evolve independently for TA generations before a sample of individuals is taken from each of them to assay some markers. The effective sizes of populations P0, P1, P2, and Ph are N0, N1, N2, and Nh, respectively.
The above admixture model is characterized by seven parameters, which are the effective sizes of the ancestral (N0), parental (N1 and N2), and admixed (Nh) populations; the times (in the unit of generations) of divergence (TD) and admixture (TA); and the admixture proportion p1. The seven parameters are denoted by set ω = {N0, N1, N2, Nh, TA, TD, p1}. Without an external standard, however, it is impossible to estimate the absolute values of population size and time. They are therefore rescaled by the mutation rate (μ) of markers as θk = 4Nkμ (k = 0, 1, 2, h), τk = Tkμ (k = A, D), and the estimable parameters are denoted by Ω = {θ0, θ1, θ2, θh, τA, τD, p1}.
The mutation model:
To utilize molecular information and account for mutations explicitly in estimating admixture, a suitable mutation model must be specified to describe the mutational process of markers. Herein I use DNA sequences as markers, which are assumed to follow the infinite-site model of mutations (Kimura 1969). Under this model, a locus is composed of so many sites that no more than one mutation occurs at any site in the genealogy of the sampled sequences. I also assume a constant-rate neutral mutation process, in which each offspring sequence differs from its parental one by an average of μ mutations. Under these assumptions, the number of mutations in a sample of DNA sequences is identical to the number of nucleotides that are polymorphic (segregating) in the sample. Therefore, the expected number of segregating sites in a sample is simply the product of μ and the expected total branch length of the genealogy of the sample (see, e.g., Tajima 1983; Hudson 1990).
Expected numbers of segregating sites:
In this section, I derive the expected total branch length of the genealogy (ETBLG) (denoted by Δ) of a sample of DNA sequences given parameter set ω. The expected number of segregating sites in a sample is simply the product of Δ and mutation rate μ under the infinite-site model. In the next section, the observed numbers of segregating sites are fitted to these expected values to obtain least-squares estimates of Ω.
Suppose n1, n2, and nh sequences of a given locus are sampled at random from the current P1, P2, and Ph populations, respectively. The n = n1 + n2 + nh sequences can be arranged to constitute seven composite (artificial) samples. Samples 1, 2, and 3 contain sequences solely from populations P1, P2, and Ph, respectively. Samples 4, 5, and 6 are obtained by merging samples 1 and 2, 1 and 3, and 2 and 3, respectively. Sample 7 contains all of the n sequences. The sample sizes (number of sequences) for samples 1, 2, … , 7 are therefore n1, n2, nh, n1 + n2, n1 + nh, n2 + nh, and n1 + n2 + nh, respectively.
Expected total branch length of a genealogy:
For convenience in deriving the ETBLG of a sample of sequences, time is measured backward hereafter. The current time when the sample was taken is designated as generation zero and the time T generations ago is referred to as generation T. Consider the ETBLG of sample 1, Δ1, conditional on parameters ω. The genealogy can be partitioned into two segments, the first being formed by the coalescent process in population P1 during time interval [0, TA + TD], while the second is formed by the coalescent process in population P0 during time interval [TA + TD, ∞]. The expected total branch length of segment one can be derived, as shown in appendix a, as
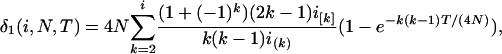 |
(1) |
where i = n1 is the initial number of sequences, N = N1 is the effective population size, T = TA + TD is the time interval, and 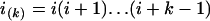 and
and 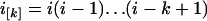 are the rising and falling factorial functions, respectively.
are the rising and falling factorial functions, respectively.
For the second segment, the initial number of sequences, j (n1 ≥ j ≥ 2), at time TA + TD is a random variable. The probability of an initial i sequences at time zero coalescing into j sequences at time T in a population with effective size N is
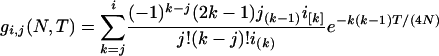 |
(2) |
(Tavaré 1984). Inserting i = n1, T = TA + TD, and N = N1 into (2) gives the probability that j (n1 ≥ j ≥ 2) sequences are left extant at time TA + TD in population 1. Given j at time TA + TD and the effective size of the ancestral population N0, the expected total branch length of the second segment of genealogy (e.g., Hudson 1990) is 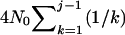 . Summing over all possible values of j gives the expected total branch length of the second segment of genealogy
. Summing over all possible values of j gives the expected total branch length of the second segment of genealogy
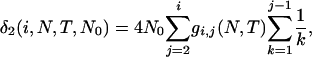 |
(3) |
where i = n1, N = N1, T = TA + TD. The ETBLG is the sum of (1) and (3),
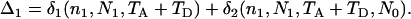 |
(4) |
When 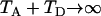 ,
, 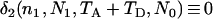 irrespective of the parameter values of
irrespective of the parameter values of 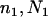 , and N0, as is expected because the most recent common ancestor (MRCA) must be found in the first segment of genealogy. In such a case, (4) reduces to
, and N0, as is expected because the most recent common ancestor (MRCA) must be found in the first segment of genealogy. In such a case, (4) reduces to 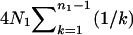 , the expected total branch length of the genealogy of n1 sequences from a population of a constant size N1 (e.g., Hudson 1990). It can be shown that when N0 = N1, (4) also reduces to
, the expected total branch length of the genealogy of n1 sequences from a population of a constant size N1 (e.g., Hudson 1990). It can be shown that when N0 = N1, (4) also reduces to 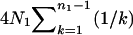 irrespective of TA and TD, as expected.
irrespective of TA and TD, as expected.
Similarly, the ETBLG of sample 2 conditional on parameter set ω, Δ2, is calculated by the right side of (4), replacing N1 by N2 and n1 by n2, respectively.
The derivation for the ETBLG of sample 3 is much more complicated. The genealogy is again partitioned into two segments. The first segment is formed by the coalescent process of an initial nh sequences in population Ph during interval [0, TA]. The expected total branch length of this segment is calculated by (1) with i = nh, N = Nh, and T = TA. The second segment is formed by the coalescent processes in populations P1 and/or P2 during time interval [TA, TA + TD] and then in ancestral population P0 during time interval [TA + TD, ∞]. The probability of i = nh sequences coalescing into j = m sequences at time T = TA in population Ph with effective size N = Nh is calculated by (2). According to the sources of the m extant sequences at time TA, three cases are distinguishable.
Case 1: The m extant sequences at time TA come exclusively from population P1. When this case occurs, with probability
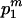 , the expected total branch length of the second segment of genealogy given m can be calculated by the sum of (1) and (3), replacing i, N, and T by m, N1, and TD, respectively.
, the expected total branch length of the second segment of genealogy given m can be calculated by the sum of (1) and (3), replacing i, N, and T by m, N1, and TD, respectively.Case 2: The m extant sequences at time TA come exclusively from population P2. When this case occurs, with probability
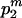 where
where 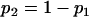 , the expected total length of the second segment of genealogy given m can be calculated by the sum of (1) and (3), replacing i, N, and T by m, N2, and TD, respectively.
, the expected total length of the second segment of genealogy given m can be calculated by the sum of (1) and (3), replacing i, N, and T by m, N2, and TD, respectively.Case 3: Among the m extant sequences at time TA, m1 (0 < m1 < m) sequences come from population P1 and m2 = m − m1 from P2. When this case occurs, with the binomial probability of
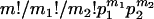 , the second segment of genealogy can be further partitioned into three subsegments. Subsegment 1 is formed by the coalescent process of the initial m1 sequences at time TA in population P1 during interval [TA, TA + TD]. The expected total branch length of this subsegment can be derived, shown in appendix a, as
, the second segment of genealogy can be further partitioned into three subsegments. Subsegment 1 is formed by the coalescent process of the initial m1 sequences at time TA in population P1 during interval [TA, TA + TD]. The expected total branch length of this subsegment can be derived, shown in appendix a, as
 |
(5) |
where i = m1 is the initial number of sequences, N = N1 is the effective size, and T = TD is the length of time. Subsegment 2 is formed by the coalescent process of the initial m2 sequences at time TA in population P2 during interval [TA, TA + TD]. The expected total branch length of this subsegment can be calculated similarly by (5) replacing i, N, and T by m2, N2, and TD, respectively. The third subsegment is formed by the coalescent process in ancestral population P0 during the time interval [TA + TD, ∞]. Suppose m3 and m4 sequences are extant at time TA + TD in populations P1 and P2, respectively, with probabilities 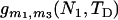 and
and 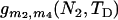 , respectively, calculated by (2). The expected total branch length of the segment of genealogy for the given initial m3 + m4 sequences in population P0 during the time interval [TA + TD, ∞] is (e.g., Hudson 1990)
, respectively, calculated by (2). The expected total branch length of the segment of genealogy for the given initial m3 + m4 sequences in population P0 during the time interval [TA + TD, ∞] is (e.g., Hudson 1990) 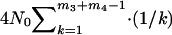 . Considering all possible values of m3 and m4 leads to the expected total branch length of the third subsegment of genealogy,
. Considering all possible values of m3 and m4 leads to the expected total branch length of the third subsegment of genealogy, 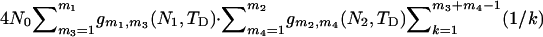 . Summing over the three subsegments gives the expected total branch length of the second segment of genealogy in case 3.
. Summing over the three subsegments gives the expected total branch length of the second segment of genealogy in case 3.
Summing over the three cases yields the expected total branch length of genealogy for segment 2. Adding the expected total branch lengths of segments 1 and 2 gives the ETBLG of sample 3,
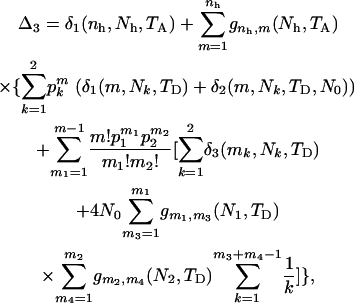 |
(6) |
where 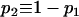 and
and 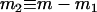 . It can be shown that, when Nk =
. It can be shown that, when Nk = 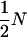 (k = 0, 1, 2, h) and nh = 2, (6) reduces to
(k = 0, 1, 2, h) and nh = 2, (6) reduces to 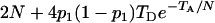 , which is twice the expected coalescent time between a pair of sequences from the admixed haploid population derived by Bertorelle and Excoffier (1998).
, which is twice the expected coalescent time between a pair of sequences from the admixed haploid population derived by Bertorelle and Excoffier (1998).
Using an approach similar to the derivation of (6), I also obtained, as shown in appendix a, the equations for the ETBLGs of samples 4–7.
Expected number of segregating sites:
Under the infinite-site model assumed above, the expected number of segregating sites (ES) in a sample is simply the product of mutation rate μ and ETBLG of the sample. The expected number of segregating sites of the kth sample conditional on parameter set Ω, ESk, can then be calculated by the equation for Δk by replacing Nj, TA, and TD with θj/4, τA, and τB, respectively, where k = 1, 2, … , 7 and j = 0, 1, 2, h.
Estimation of parameters:
Suppose, for a single locus with (unknown) mutation rate μ, the number of segregating sites in sample k (k = 1, 2, … , 7) is observed to be OSk. Estimates of the parameters Ω = {θ0, θ1, θ2, θh, τA, τD, p1} can be obtained by fitting these observed to the expected numbers of segregating sites by a least-squares approach,
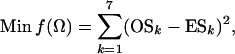 |
(7) |
where ESk is calculated as shown above. Since f(Ω) is a complicated function of the seven parameters and no closed form of solution is possible, some numerical methods have to be adopted for the estimation. The first derivatives of f(Ω) with respect to each of the seven parameters can be obtained and used in the multidimensional Newton–Raphson algorithm for the estimates of Ω from (7). However, the computation is intensive, especially when sample sizes are large, because both function (7) and its derivatives are not trivial to compute. Further, such an algorithm is sometimes fooled by a local rather than a global minimum of f(Ω). Having tried several methods, I finally choose to use Powell's quadratically convergent method (Press et al. 1996) with slight modifications. This algorithm does not require the computation of derivatives, and with the modification it updates only one of the parameters in most iterations so that only part of (7) needs to be recalculated. For example, updating θ1 does not alter ES2 but changes only parts of the calculations of ESj for j = 3, 4, … , 7. Therefore, the algorithm coupled with storing/reusing the computational results for different parts of ESj could reduce computational burden tremendously. To speed up computation, this algorithm occasionally updates multiple parameters simultaneously along an optimal direction determined by collecting and using information of previous iterations. Some comparative analyses of simulated data indicated that Powell's algorithm is less often stuck on a local minimum than the Newton–Raphson algorithm. In the results shown below, each simulated data set is analyzed in five independent replicates, each with a randomly chosen set of starting parameter values. The final estimates are those from the replicate with the minimum value of f(Ω). To analyze an empirical data set, more starting points can be used to obtain more reliable estimates.
The computational load of (7) increases rapidly with the numbers of sequences from the three populations. Furthermore, it is difficult to calculate (2) quickly and accurately because it is a series having terms of large values and alternating signs. To avoid large numerical errors in calculating (2) and thus (7) for large genealogies (a sample of ≥100 sequences), I conduct computations using high precision of hundreds of significant digits (depending on sample size). An alternative option is to adopt a Markov chain Monte Carlo method proposed by Griffiths and Tavaré (1994) as in O'Ryan et al. (1998).
Multiple loci:
For multiple independent loci, it is inappropriate to use simply the average numbers of segregating sites over loci as data in the estimation. Distinctive loci may have different mutation rates because of the differences in mutation rate per base pair and/or in the sequence length. Different loci may also have different sample sizes, resulting in different ETBLGs and thus different expected numbers of segregating sites. The above methodology can be extended to use multilocus data jointly in estimating the parameters Ω = {θ0, θ1, θ2, θh, τA, τD, p1}. In addition, the relative mutation rate of each locus can be estimated simultaneously.
Suppose a number of L unlinked loci have been surveyed, with locus l (l = 1, 2, … , L) having a mutation rate μl and a sample size of nj,l sequences from population Pj (j = 1, 2, h). Without loss of generality, I scale parameters Nj (j = 0, 1, 2, h), TA, TD, and μl (l = 2, 3, … , L) by μ1, the mutation rate of the first locus. The set of parameters to be estimated now becomes Ω = {θ0, θ1, θ2, θh, τA, τD, p1, λ2, λ3, … , λL}, where θj = 4Njμ1 (j = 0, 1, 2, h), τA =TAμ1, τD =TDμ1, and λl = μl/μ1 (l = 2, 3, … , L). The least-squares function for multiple loci becomes
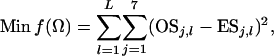 |
(8) |
where OSj,l and ESj,l are observed and expected numbers of segregating sites for locus l in composite sample j (j = 1, 2, … , 7). ESj,1 is calculated as before, while ESj,l for locus l with l ≥ 2 is calculated using parameters {θ0, θ1, θ2, θh, τA, τD, p1} and then multiplied by λl.
The value of p1 and the relative values of θj (j = 0, 1, 2, h), τA, and τD obtained from (8) are independent of the locus chosen to scale the parameters. This is because mutation rate does not affect the genealogies and acts only as a multiplier with ETBLGs in determining the expected numbers of segregating sites. Using a locus with a smaller (larger) mutation rate to scale the parameters causes just a proportional decrease (increase) in the estimates of θj (j = 0, 1, 2, h), τA, and τD and has no affect on the estimates of p1. This can be checked easily by simulations.
Simulations:
Monte Carlo simulations were run to generate data sets with known parameters. These data were then analyzed by the newly developed estimator to check its quality of estimates, to investigate its statistical properties, and to compare it with a previous molecular estimator. Although quite a few admixture estimators are available, only the one of Bertorelle and Excoffier (1998) is a molecular estimator designed to use molecular information and take mutations into account. Therefore I confine my comparison to this molecular estimator in this study.
Following the coalescence approach (Hudson 1990) and the admixture model (Figure 1), the genealogies of the n1 + n2 + nh DNA sequences from the current three populations were reconstructed until the MRCA was found. Poisson-distributed mutations were then imposed on the reconstructed gene tree. Recombination was assumed to be absent and mutations were assumed to follow the infinite-site model. Data for different loci were generated independently, and monomorphic loci with no segregating sites were discarded. The sequence data were then processed to extract information for different estimators. For the current estimator, the number of segregating sites in each of the seven composite samples was obtained. For Bertorelle and Excoffier's molecular estimator, the mean coalescence time (scaled by mutation rate) was estimated by the mean number of site differences between pairs of sequences.
Several statistics are adopted to measure the quality of estimates from simulated data. First, the applicability (denoted as Appl%) of an estimator is calculated as the percentage of replicates in which admixture proportion estimates can be made successfully and the estimates are in the legitimate range of [0, 1] (Choisy et al. 2004). Second, the mean and root mean square errors (the square root of mean squared errors, denoted by RMSE) of estimates across replicates are calculated. Third, “factor 2” is calculated as the proportion of replicates in which the estimated value is within the interval bounded by values equal to 50 and 200% that of the true value (Excoffier et al. 2005). This measurement overlaps with RMSE in telling how close the estimates are to the true parameter value, but it is less affected by extreme outliers of the distribution of estimates. For most combinations of parameters, 1000 replicates were conducted.
Analysis of an empirical data set:
For demonstration, the estimator proposed herein was applied to the analysis of a published data set from McLean et al. (2003). They sequenced the hypervariable segments I (HVSI, 364 bp in length) and II (HVSII, 343 bp in length) of the mtDNA from 47 Sierra Leoneans, 12 European–Americans, 12 rural Gullah-speaking African–Americans, 12 urban African–Americans living in Charleston, South Carolina, and 12 Jamaicans. Assuming that African–American populations are admixtures by Europeans and Africans (e.g., Parra et al. 1998), the mtDNA data can be analyzed by the coalescent estimator to infer the European genetic contributions to the gene pool of each of the three African–American populations and the admixture time, divergence time, and genetic drift (population size) of each parental and admixed population involved. Sites in HVSI and HVSII sequences with missing or ambiguous information were eliminated, resulting in 295 and 275 unambiguous sites for HVSI and HVSII, respectively, utilized in the analysis. Due to the absence of recombination in human mtDNA, HVSI and HVSII are effectively a single locus. Sequences for the two loci are thus combined to form single-locus data before being analyzed by the two molecular estimators of admixture.
RESULTS
Simulations:
Many factors are important in determining the quality of admixture estimates, including the true parameters (defined by the genetic model in Figure 1) being estimated and the marker information content influenced by the number of loci, the number of individuals genotyped, and the polymorphism of each locus (e.g., Wang 2003; Choisy et al. 2004; Excoffier et al. 2005). The factor combinations are prohibitively too numerous to consider in a simulation study. Here I choose to present the estimation results in some hopefully typical scenarios.
The performances of the current and previous molecular estimators in estimating admixture proportions for the scenarios of a short or long divergence time (TD = 2500 or 10,000 generations); short, intermediate, or long admixture time (TA = 50, 500, or 5000 generations); and small or moderate admixture (p1 = 0.05 or 0.20) are summarized in Table 1. Sample size for each population is assumed to be either 20 or 40, and the number of loci is assumed to be 1, 5, or 10 with the same mutation rate of 0.001 per DNA sequence per generation. When the divergence time is short (TD = 2500) so that parental populations are not highly differentiated (TD/N = 0.5) when admixture occurs, the Appl% of the mY estimator is only ∼70–90% for the case of a single locus, and 10–30% of p1 estimates from this estimator are either smaller than zero or greater than one. Although the Appl% of the mY estimator improves with an increasing amount of marker information (mainly number of loci), it is still <90% for slight admixture even if 5 loci are used. Note that the increase in Appl% of the mY estimator with an increasing TA is an artifact, because a large TA results in the estimates of p1 biased toward 0.5 and thus in fewer negative estimates. In contrast, the new estimator gives the estimates of p1 that are always in the legitimate range of [0, 1]. Compared with the mY estimator, the new estimator is generally much less biased and has much smaller RMSE.
TABLE 1.
Estimates of admixture proportions from simulations
|
TD = 2,500
|
TD = 10,000
|
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| New estimator
|
mY
|
New estimator
|
mY
|
|||||||||
| S/L | p1 | TA | Mean | RMSE | Mean | RMSE | Appl% | Mean | RMSE | Mean | RMSE | Appl% |
| 20/1 | 0.05 | 50 | 0.075 | 0.138 | 0.126 | 0.343 | 71.5 | 0.081 | 0.128 | 0.071 | 0.085 | 86.6 |
| 500 | 0.102 | 0.186 | 0.178 | 0.387 | 76.5 | 0.088 | 0.146 | 0.087 | 0.125 | 86.8 | ||
| 5000 | 0.260 | 0.478 | 0.347 | 0.523 | 83.1 | 0.102 | 0.213 | 0.199 | 0.247 | 95.7 | ||
| 0.20 | 50 | 0.236 | 0.220 | 0.269 | 0.309 | 85.7 | 0.251 | 0.207 | 0.221 | 0.114 | 98.7 | |
| 500 | 0.249 | 0.259 | 0.278 | 0.375 | 83.6 | 0.265 | 0.225 | 0.230 | 0.151 | 97.8 | ||
| 5000 | 0.336 | 0.415 | 0.379 | 0.470 | 84.0 | 0.257 | 0.293 | 0.295 | 0.261 | 96.8 | ||
| 20/5 | 0.05 | 50 | 0.054 | 0.065 | 0.129 | 0.150 | 88.4 | 0.059 | 0.047 | 0.068 | 0.042 | 97.6 |
| 500 | 0.067 | 0.097 | 0.167 | 0.189 | 90.6 | 0.064 | 0.056 | 0.080 | 0.058 | 97.3 | ||
| 5000 | 0.186 | 0.302 | 0.346 | 0.353 | 97.1 | 0.063 | 0.088 | 0.188 | 0.165 | 99.8 | ||
| 0.20 | 50 | 0.212 | 0.126 | 0.260 | 0.138 | 97.6 | 0.215 | 0.104 | 0.211 | 0.054 | 100 | |
| 500 | 0.232 | 0.163 | 0.286 | 0.177 | 97.0 | 0.227 | 0.118 | 0.221 | 0.075 | 99.9 | ||
| 5000 | 0.285 | 0.324 | 0.389 | 0.268 | 98.2 | 0.215 | 0.160 | 0.292 | 0.153 | 99.9 | ||
| 20/10 | 0.05 | 50 | 0.051 | 0.048 | 0.127 | 0.117 | 93.4 | 0.054 | 0.031 | 0.067 | 0.033 | 99.2 |
| 500 | 0.063 | 0.076 | 0.172 | 0.160 | 95.5 | 0.059 | 0.037 | 0.080 | 0.047 | 99.2 | ||
| 5000 | 0.158 | 0.251 | 0.352 | 0.328 | 99.6 | 0.055 | 0.062 | 0.184 | 0.148 | 100 | ||
| 0.20 | 50 | 0.209 | 0.097 | 0.258 | 0.100 | 99.9 | 0.209 | 0.076 | 0.212 | 0.041 | 100 | |
| 500 | 0.224 | 0.126 | 0.281 | 0.136 | 98.9 | 0.219 | 0.087 | 0.222 | 0.056 | 100 | ||
| 5000 | 0.258 | 0.275 | 0.400 | 0.236 | 99.8 | 0.204 | 0.116 | 0.289 | 0.124 | 100 | ||
| 40/1 | 0.05 | 50 | 0.064 | 0.101 | 0.100 | 0.258 | 72.5 | 0.073 | 0.099 | 0.061 | 0.072 | 88.4 |
| 500 | 0.096 | 0.167 | 0.139 | 0.365 | 74.3 | 0.089 | 0.133 | 0.076 | 0.103 | 84.9 | ||
| 5000 | 0.238 | 0.405 | 0.356 | 0.533 | 82.2 | 0.088 | 0.190 | 0.191 | 0.232 | 94.7 | ||
| 0.20 | 50 | 0.216 | 0.171 | 0.234 | 0.237 | 89.8 | 0.231 | 0.187 | 0.205 | 0.083 | 99.0 | |
| 500 | 0.255 | 0.229 | 0.249 | 0.341 | 83.6 | 0.271 | 0.226 | 0.215 | 0.129 | 97.6 | ||
| 5000 | 0.324 | 0.410 | 0.408 | 0.482 | 84.9 | 0.254 | 0.291 | 0.298 | 0.267 | 95.7 | ||
| 40/5 | 0.05 | 50 | 0.054 | 0.048 | 0.098 | 0.108 | 86.8 | 0.055 | 0.038 | 0.059 | 0.030 | 98.0 |
| 500 | 0.070 | 0.086 | 0.145 | 0.174 | 86.6 | 0.064 | 0.055 | 0.075 | 0.051 | 97.2 | ||
| 5000 | 0.173 | 0.286 | 0.348 | 0.354 | 97.3 | 0.066 | 0.090 | 0.182 | 0.160 | 99.8 | ||
| 0.20 | 50 | 0.206 | 0.097 | 0.229 | 0.101 | 97.9 | 0.205 | 0.099 | 0.204 | 0.040 | 100 | |
| 500 | 0.229 | 0.135 | 0.260 | 0.151 | 96.9 | 0.230 | 0.116 | 0.216 | 0.064 | 100 | ||
| 5000 | 0.277 | 0.308 | 0.396 | 0.269 | 97.8 | 0.222 | 0.160 | 0.289 | 0.152 | 99.8 | ||
| 40/10 | 0.05 | 50 | 0.052 | 0.034 | 0.099 | 0.083 | 94.0 | 0.053 | 0.025 | 0.059 | 0.022 | 99.6 |
| 500 | 0.066 | 0.064 | 0.146 | 0.136 | 93.1 | 0.059 | 0.035 | 0.074 | 0.039 | 99.5 | ||
| 5000 | 0.134 | 0.215 | 0.349 | 0.325 | 99.7 | 0.059 | 0.064 | 0.179 | 0.145 | 100 | ||
| 0.20 | 50 | 0.205 | 0.071 | 0.230 | 0.072 | 100 | 0.198 | 0.067 | 0.205 | 0.029 | 100 | |
| 500 | 0.229 | 0.101 | 0.267 | 0.117 | 99.3 | 0.217 | 0.085 | 0.215 | 0.047 | 100 | ||
| 5000 | 0.256 | 0.264 | 0.399 | 0.236 | 99.9 | 0.210 | 0.120 | 0.283 | 0.121 | 100 | ||
For each parameter combination, estimates of admixture proportion are obtained from 1000 replicates using the new estimator and Bertorelle and Excoffier's (1998) estimator mY. The parameters are TD = 2500 or 10,000 generations; TA = 50, 500, or 5000 generations; Nj = 5000 (j = 0, 1, 2, h); the sample size S = 20 or 40 for all three populations; the number of loci L = 1, 5, or 10; and the admixture proportion p1 = 0.05 or 0.20. The applicability of the new estimator is always 100% irrespective the parameter combinations and is thus not listed.
When the divergence time is long (TD = 10,000 generations) so that parental populations are highly differentiated (TD/N = 2) before they contribute to the admixture, the performances of the two estimators become similar. The mY estimator has an Appl% close to 100%, except when a single locus is used in estimating small admixture proportions. The new estimator is less biased than the mY estimator, especially when admixture is small and TA is large. The main merit of molecular estimators in comparison with traditional estimators is that mutations after the admixture events can be accounted for so that ancient admixture can be inferred accurately. The current estimator allows almost unbiased estimation of admixture proportions even if TA = 5000 (TA/N = 1) when the divergence time is long and multilocus data are available. In contrast, the mY estimator gives estimates of p1 biased toward 0.5 when admixture is ancient.
In addition to admixture proportions, the new estimator can also provide estimates of other interesting parameters. Table 2 summarizes the properties of the estimates of θ0, θ1, θ2, θh, τA, τD, and relative mutation rates (λl). It can be seen that θ1, θ2, and μl are very well estimated with small biases and RMSEs, while θh is the most difficult parameter to estimate. This is understandable because information about θh comes from the coalescent events in the hybrid population during time interval [0, TA] only, and these events are too few when nh and TA/Nh are small to allow accurate estimates of θh. Indeed, the quality of θh-estimates increases with an increasing sample size and admixture time, as shown in Table 2. Similarly, the quality of τA estimates is dependent on the number of coalescent events in the three populations during interval [0, TA] and thus increases with an increasing admixture time (TA) and a decreasing population size (N1, N2, Nh). In contrast, τD is more accurately estimated with a decreasing admixture time (TA). Small TA means fewer coalescent events during interval [0, TA] and more coalescent events during time interval [TA, TA + TD] and thus more information about τD. For similar reasons, θ0 is better estimated with a smaller value of TA + TD. The estimates of all parameters are improved substantially by increasing the number of loci and sample sizes.
TABLE 2.
Estimates of divergence and admixture times and population sizes from simulations
| One locus
|
Five loci
|
||||||
|---|---|---|---|---|---|---|---|
| Parameters | True value | Mean | RMSE | Factor2 | Mean | RMSE | Factor2 |
| TD = 10,000, TA = 500, S = 40 | |||||||
| θ1 | 20 | 24.2 | 13.6 | 0.87 | 21.2 | 5.5 | 0.99 |
| θ2 | 20 | 23.1 | 10.7 | 0.91 | 21.1 | 5.4 | 0.99 |
| θh | 20 | 42.1 | 105.1 | 0.44 | 26.2 | 28.9 | 0.86 |
| θ0 | 20 | 12.1 | 19.1 | 0.31 | 15.4 | 12.9 | 0.60 |
| τA | 0.5 | 0.41 | 0.38 | 0.53 | 0.46 | 0.21 | 0.85 |
| τD | 10 | 15.6 | 11.2 | 0.71 | 15.4 | 8.0 | 0.78 |
| λl | 1 | 1.02 | 0.26 | 0.99 | |||
| TD = 2,500, TA = 50, S = 40 | |||||||
| θ1 | 20 | 17.9 | 11.8 | 0.75 | 18.4 | 6.0 | 0.95 |
| θ2 | 20 | 17.1 | 9.1 | 0.80 | 18.2 | 5.3 | 0.97 |
| θh | 20 | 79.0 | 183.1 | 0.05 | 49.4 | 132.3 | 0.22 |
| θ0 | 20 | 24.4 | 14.2 | 0.75 | 23.1 | 7.5 | 0.97 |
| τA | 0.05 | 0.09 | 0.14 | 0.17 | 0.08 | 0.10 | 0.33 |
| τD | 2.5 | 2.7 | 1.5 | 0.78 | 2.6 | 0.86 | 0.96 |
| λl | 1 | 1.05 | 0.31 | 0.99 | |||
| TD = 10,000, TA = 500, S = 100 | |||||||
| θ1 | 20 | 22.6 | 9.0 | 0.94 | 21.7 | 7.6 | 0.95 |
| θ2 | 20 | 22.8 | 9.1 | 0.95 | 22.1 | 7.7 | 0.96 |
| θh | 20 | 39.6 | 28.9 | 0.74 | 28.1 | 27.9 | 0.90 |
| θ0 | 20 | 12.0 | 17.3 | 0.33 | 18.3 | 13.7 | 0.61 |
| τA | 0.5 | 0.49 | 0.37 | 0.68 | 0.48 | 0.23 | 0.85 |
| τD | 10 | 17.2 | 14.0 | 0.63 | 13.6 | 7.5 | 0.76 |
| λl | 1 | 1.02 | 0.21 | 1.00 | |||
| TD = 2,500, TA = 50, S = 100 | |||||||
| θ1 | 20 | 19.2 | 7.0 | 0.93 | 19.2 | 4.7 | 0.98 |
| θ2 | 20 | 18.5 | 5.9 | 0.94 | 19.2 | 4.9 | 0.99 |
| θh | 20 | 39.8 | 85.0 | 0.24 | 35.3 | 72.5 | 0.50 |
| θ0 | 20 | 23.5 | 11.7 | 0.83 | 22.2 | 7.1 | 0.99 |
| τA | 0.05 | 0.06 | 0.09 | 0.45 | 0.06 | 0.04 | 0.63 |
| τD | 2.5 | 2.8 | 1.6 | 0.78 | 2.8 | 1.0 | 0.94 |
| λl | 1 | 0.99 | 0.22 | 1.00 | |||
The parameters being estimated are θi = 4μ1Ni (i = 0, 1, 2, h), τA = μ1TA, τD = μ1TD, and λl = μl/μ1 (l = 2, 3, 4, 5). A total of 1000 simulated data sets are generated and analyzed, assuming Ni = 5000 (i = 0, 1, 2, h), p1 = 0.2, μl = 0.001 (l = 1, … , 5), and TD = 10,000 and TA = 500 or TD = 2500 and TA = 50. The sample size S = 40 or 100 for all three populations, and the number of loci L = 1 or 5.
I adopt the parametric bootstrapping technique to assess the uncertainties of admixture estimates from the new estimator. This is rendered possible because all the parameters fully defining the admixture model in Figure 1 can be estimated by the new estimator. Parametric bootstrapping is more appropriate than nonparametric bootstrapping (Bertorelle and Excoffier 1998) because the latter tends to yield too conservative estimates of uncertainties when the number of resampling units (loci, sequences) is small. Due to the heavy computational burden of the current estimator, however, it is difficult to evaluate the performance of the parametric bootstrapping procedure using extensive simulations. Table 3 lists the uncertainty estimates, which are average upper and lower limits of 95% confidence intervals (C.I.95%) and coverage (frequency of the true parameter value being covered by the estimated C.I.95%), for the cases of a single locus and five loci. In each case, 100 replicate data sets are simulated, and each data set is analyzed for point and C.I.95% estimates using 500 bootstrapping samples. The parameter values used in generating the simulated data sets are θk = 20 (k = 0, 1, 2, h), τA = 0.5, τD = 10, μ = 0.001, and 20 sequences for each locus from each population. As can be seen, the true parameter value is included in the estimated 95% confidence intervals in ∼95% of the replicates for both the single-locus and the five-loci cases. The confidence intervals for five loci are much narrower than those for a single locus, as is expected. In accordance with the results listed in Table 2, θh is the most difficult parameter to estimate, as indicated by the extremely large confidence intervals.
TABLE 3.
Estimates of confidence intervals by parametric bootstrapping
| One locus
|
Five loci
|
||||||
|---|---|---|---|---|---|---|---|
| Parameters | True value | Coverage | C.I.95L | C.I.95U | Coverage | C.I.95L | C.I.95U |
| θ1 | 20 | 0.91 | 6.23 | 74.44 | 0.91 | 7.18 | 30.71 |
| θ2 | 20 | 0.93 | 5.68 | 42.87 | 0.92 | 8.07 | 30.07 |
| θh | 20 | 0.99 | 1.08 | ∞ | 0.98 | 2.71 | ∞ |
| θ0 | 20 | 0.99 | 0.41 | 94.17 | 0.99 | 0.55 | 78.12 |
| τA | 0.5 | 0.95 | 0.05 | 1.95 | 0.96 | 0.06 | 1.20 |
| τD | 10 | 0.93 | 3.62 | 36.62 | 0.94 | 4.43 | 34.75 |
| p1 | 0.2 | 0.92 | 0.03 | 0.75 | 0.95 | 0.07 | 0.49 |
A total of 100 data sets were simulated, assuming the parameter values listed in column 2, μl = 0.001 (l = 1, … , 5), and a sample size S = 20 for each population and locus. Each data set was analyzed by the coalescent estimator with 500 bootstrapping samples. C.I.95L (C.I.95U) is the average lower (upper) limit of the estimated 95% confidence intervals, and coverage gives the frequency that the true parameter value is included in the estimated 95% confidence intervals.
Admixture analysis of human populations:
The mtDNA sequence data from McLean et al. (2003) are analyzed by Bertorelle and Excoffier's (1998) mY estimator and the new estimator. Parametric bootstrapping and nonparametric bootstrapping are adopted for the new and mY estimators, respectively, to ascertain the uncertainties of the estimates using 1000 samples of size identical to the original samples. The estimates of the European contributions to each of the three admixed African–American and Jamaican populations are listed in Table 4.
TABLE 4.
Admixture analysis results of three human admixed populations
| Gullah
|
Charleston
|
Jamaican
|
||||
|---|---|---|---|---|---|---|
| Admixture parameters | Estimate | 95% C.I. | Estimate | 95% C.I. | Estimate | 95% C.I. |
| τD | 2.053 | 0.113, 5.844 | 1.883 | 0.003, 6.242 | 1.868 | 0.001, 6.057 |
| τA | 0.001 | 0.000, 0.848 | 0.114 | 0.000, 0.820 | 0.196 | 0.000, 1.050 |
| θ1 | 5.006 | 0.565, 22.931 | 4.175 | 0.034, 18.860 | 3.972 | 0.020, 18.992 |
| θ2 | 45.146 | 8.662, 106.283 | 32.207 | 0.152, 143.713 | 34.083 | 0.129, 137.628 |
| θh | 0.001 | 0.000, ∞ | 0.848 | 0.000, ∞ | 2.142 | 0.000, ∞ |
| θ0 | 16.492 | 1.927, 47.619 | 19.933 | 1.728, 49.476 | 21.787 | 0.847, 53.180 |
| p1 | 0.001 | 0.000, 0.546 | 0.064 | 0.000, 0.752 | 0.048 | 0.000, 0.870 |
| p1* | 0.090 | −0.343, 0.356 | 0.500 | −0.008, 0.681 | −0.063 | −0.490, 0.330 |
The 95% confidence intervals are obtained from 1000 bootstrapping samples. The estimated parameters are θi = 4μNi, τA = μTA, τD = μTD, where Ni is the female effective size of population i (i = 0, 1, 2, h for ancestral, European, African, and admixed populations, respectively). The European contribution to an admixed population was obtained from the new estimator (line headed by p1) and the mY estimator (line headed by p1*). The other seven parameters were estimated by the new estimator only.
The European contributions to the three admixed populations are estimated to be <7% from the new coalescent estimator and are in close agreement with previous estimates (Parra et al. 2001; McLean et al. 2003). McLean et al. (2003) calculated admixture proportions from the frequencies of haplotypes composed of three HVS restriction site polymorphisms (RSPs). These RSPs are chosen because they are substantially differentiated between African and European populations and are thus highly informative for admixture analysis. Furthermore, a large number of 1396 individuals from the same five populations as the mtDNA sequence data analyzed herein are assayed for the RSPs. The estimated European contributions from their analyses are 0.030, 0.069, and −0.027 for the Gullahs, Charleston African–Americans, and the Jamaicans, respectively. From large samples (∼100 sequences per population) of HVSI data, the European contributions to the three admixed populations were estimated to be ∼0% using the highly informative haplogroup H frequencies (Parra et al. 2001) and were estimated to be 0.065 and 0.129 for the Charleston and Jamaican populations, respectively, from both haplogroup H and L frequencies (Parra et al. 1998). In general, these estimates are much lower than those inferred from many informative nuclear markers (Parra et al. 1998), indicating that European females contributed little to the admixtures. The sex-biased admixtures, with European males contributing substantially greater than European females, were confirmed by analyzing the Y Alu polymorphic (YAP) informative markers (Parra et al. 1998). It is encouraging that with a sample size as small as 12 sequences, the new coalescent estimator yields similar results.
The mY estimator yields estimates of European contributions to the Gullah or Jamaican population that are low and roughly compatible with estimates from the other estimators and data, but estimates of European contribution to the Charleston population (0.5) that is much larger than other estimates and is even larger than the estimate from nuclear markers (0.12, Parra et al. 1998). The estimated European contribution to the Jamaican population was −0.063, which is not surprising given the simulation result that the mY estimator often yields negative estimates when admixture proportion is low (Table 1).
For both molecular estimators and all of the three admixed populations, the 95% confidence intervals for the admixture estimates determined by parametric and nonparametric bootstrapping are quite broad. This is perhaps not surprising because the data set is small with effectively a single locus and only 12 sequences from a population. More loci and larger sample sizes are required to obtain more precise admixture estimates.
In addition to admixture proportions, the new estimator also gives the estimates of divergence times, admixture times, population sizes, and relative mutation rates. These estimates are listed in Table 4. Because human mtDNA does not recombine (Pakendorf and Stoneking 2005), HVSI and -II sequences were obtained from the same individuals (McLean et al. 2003), and the sample sizes are very small, the genealogical information that can be extracted from the data set is quite limited and the analysis results need to be interpreted with caution. Divergence time between the Africans and Europeans is estimated to be 1.9 on average. In the literature, the estimates of mutation rate for HVSs are quite diverse, the median value being ∼0.1/site/million years (MY) (Pakendorf and Stoneking 2005; Santos et al. 2005). The total mutation rate for HVSI and -II is therefore ∼70/MY or 0.0021/generation if the generation interval is taken to be 30 years. The absolute divergence time is thus estimated to be 1.9/(70/MY) = 27,143 years, which is roughly in agreement with the estimate of <60,000 years from phylogenetic analysis of mtDNA control regions (e.g., Watson et al. 1997; Quintana-Murci et al. 1999). Subsequent migration after the split of Eurasian from African population could reduce the divergence and thus lead to an underestimation of divergence time (Wang 2003).
The point estimates of admixture time are quite variable from the three admixture analyses. Using the mutation rate estimate of 70/MY, the admixture time is estimated to be 6, 1628, and 2801 years ago for the Gullah, Charleston, and Jamaican populations, respectively. The first estimate is too small while the last two estimates are too high compared with the historical evidence that the American–African populations were formed 150 years ago (Parra et al. 1998). For all of the three admixed populations, however, the 95%C.I.'s are fairly consistent and well include the admixture time of 150 years.
The parental and ancestral population sizes (θ1, θ2, θ0) are well estimated while the admixed population size (θh) is poorly estimated, as indicated by the corresponding widths of 95%C.I.'s. On average, the African population size is estimated to be 8 and 37 times larger than that of European and admixed populations, respectively, and the European population is 4 times larger than admixed populations. The results seem to be plausible and are at least qualitatively in agreement with previous studies.
DISCUSSION
In this article, I show that DNA sequence data can be utilized more efficiently in admixture inferences by considering the entire genealogy of all sampled sequences rather than the genealogy of pairs of sequences. In comparison with a previous molecular estimator (Bertorelle and Excoffier 1998), the new estimator provides better estimates of admixture proportions, which are always in the legitimate range of [0, 1] and have usually higher accuracy and precision, especially when divergence time is short and/or admixture time is long (Table 1). In addition, it allows reasonably good estimation of other important parameters of the admixture model, such as the divergence time, admixture time, and population sizes (Table 2). These parameters are scaled by the mutation rate of the markers, but their relative values are still meaningful in understanding the admixture events. When marker mutation rates are known, the absolute values of divergence and admixture times and population sizes can be easily calculated from the estimates. Other advantages of the new estimator are that it can use information from multiple loci with different mutation rates in estimating admixture and relative mutation rates jointly and that it automatically accounts for variable sample sizes both among and within loci because its inferences are based on the genealogy of an entire sample rather than pairs of sequences. The simulation results shown in Tables 1 and 2 assumed equal sample sizes among populations and loci and equal mutation rates among loci. When either or both of these two quantities vary, the new estimator is expected to perform even better than the previous molecular estimator (Bertorelle and Excoffier 1998). Furthermore, the previous molecular estimator assumes an equal size of all populations involved in the admixture. The assumption is now redundant in the new estimator and all population sizes can be estimated jointly with admixture proportions.
The differences between the current and previous molecular estimators of admixture are in close analogy with those between Watterson's and Tajima's estimators of 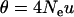 from DNA sequence data. Watterson (1975) showed that, under the infinite-site mutation model, the product of mutation rate and expected total branch length of the genealogy of a sample of sequences gives the expected number of segregating sites of the sample. From this relationship, he derived the estimator
from DNA sequence data. Watterson (1975) showed that, under the infinite-site mutation model, the product of mutation rate and expected total branch length of the genealogy of a sample of sequences gives the expected number of segregating sites of the sample. From this relationship, he derived the estimator 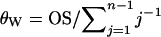 , where OS is the observed number of segregating sites in a sample of n sequences. Tajima's estimator, θT, is given by the average number of nucleotide differences between two sequences (Tajima 1983). It is well known that both estimators are unbiased, but θW is generally more efficient than θT because it has a smaller variance, and the difference increases with sample size (Li 1997; Wang 2005). In the special case of a single Wright–Fisher population (say, parental population 1), the admixture model has just one parameter (θ) and my admixture estimator (7) reduces to θW, as is expected. The previous molecular estimator of admixture (Bertorelle and Excoffier 1998) uses the mean number of nucleotide differences between pairs of sequences as information and is thus quite similar in this respect to θT.
, where OS is the observed number of segregating sites in a sample of n sequences. Tajima's estimator, θT, is given by the average number of nucleotide differences between two sequences (Tajima 1983). It is well known that both estimators are unbiased, but θW is generally more efficient than θT because it has a smaller variance, and the difference increases with sample size (Li 1997; Wang 2005). In the special case of a single Wright–Fisher population (say, parental population 1), the admixture model has just one parameter (θ) and my admixture estimator (7) reduces to θW, as is expected. The previous molecular estimator of admixture (Bertorelle and Excoffier 1998) uses the mean number of nucleotide differences between pairs of sequences as information and is thus quite similar in this respect to θT.
Some assumptions made in deriving the current estimator can be relaxed without affecting much of the validity of the estimator. Although the current estimator assumes diploid nuclear markers, it applies to maternally (mtDNA) or paternally (Y chromosome) inherited markers as well. The only difference is in the explanation of the parameter θ that corresponds to different effective sizes. It is assumed that there is no recombination at a locus. However, I use means rather than variances of the number of segregating sites as data in the estimator, and therefore it should apply to loci with recombination. Like Watterson's estimator, the current admixture estimator should actually give better estimates when there is recombination, although the estimated uncertainties might become too exaggerative. The current estimator also assumes two parental populations contributing to the admixture. It is straightforward to extend the method to the case of three or more parental populations. However, the computational burden increases very rapidly with the number of parental populations. Even with two parental populations as assumed in this study, the estimator's computational load increases so rapidly with sample sizes that it can cope only with samples of a few hundred sequences on an ordinary PC. Further refinements of the computational algorithms are necessary before the estimator is extended to more complicated situations such as three or more parental populations.
There is also room for methodological improvements of the current estimator. In (7), the expected numbers of segregating sites of the seven composite samples are obviously nonindependent, because each original sample of sequences appears in four of the seven composite samples. Ideally, their variance and covariance structure should be incorporated into a general least-squares framework to obtain estimates of the seven parameters. However, it is extremely difficult to derive this variance and covariance matrix analytically, and computation of the matrix numerically by simulations is too CPU demanding to be realistic. Although (7) ignored this variance and covariance structure, it should provide unbiased estimates as verified by simulations. The estimator's precision may be improved by the proper weighting based on the variance and covariance matrix.
A software package, Molecular Estimator of Admixture (MEAdmix), computing the admixture estimator and finding the confidence intervals by parametric bootstrapping, is available for free download from http://www.zoo.cam.ac.uk/ioz/software.htm.
Acknowledgments
I thank David C. McLean for sending me the human mtDNA sequence data that were analyzed by my new admixture estimator and Laurent Excoffier, Brigitte Pakendorf, Bruce Walsh, and two anonymous referees for critical reading and constructive comments on earlier versions of this manuscript.
APPENDIX A: THE EXPECTED TOTAL BRANCH LENGTH OF A GENEALOGY
Suppose i genes at a locus are sampled randomly from a Wright–Fisher population of N diploid individuals. Looking backward in time, the current time when the sample was taken is designated as generation zero and the time T generations ago is referred to as generation T. As T → ∞, these i genes will coalesce into their MRCA, and the ETBLG is 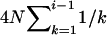 generations (e.g., Hudson 1990). When T is a fixed definite number, however, the MRCA may or may not be found in the interval of [0, T] and j (1 ≤ j ≤ i) lineages may be left extant at generation T. The probability of j distinct lineages extant at time T,
generations (e.g., Hudson 1990). When T is a fixed definite number, however, the MRCA may or may not be found in the interval of [0, T] and j (1 ≤ j ≤ i) lineages may be left extant at generation T. The probability of j distinct lineages extant at time T, 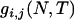 , is given by (2) (Tavaré 1984). Given i, j, N, and T, the expected time, ETm, during which there are m (j ≤ m ≤ i) distinct lineages in a genealogy is derived as follows:
, is given by (2) (Tavaré 1984). Given i, j, N, and T, the expected time, ETm, during which there are m (j ≤ m ≤ i) distinct lineages in a genealogy is derived as follows:
- ETm for m = i: Conditional on i, j < i, N, and T, the probability of the time interval (in generations), Ti, during which there are i distinct lineages is
ETi is thus obtained by the integration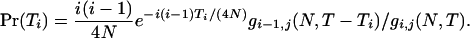
which, after some algebra, simplifies to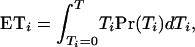
where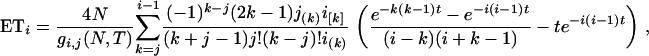
(A1) 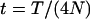 .
. - ETm for j < m < i: Similarly, the expected time (in generations) during which there are m distinct lineages (j < m < i), given i, j < i − 1, N, and T, is obtained by integration:
It can be simplified to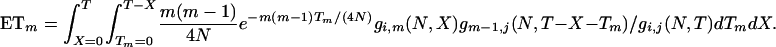
where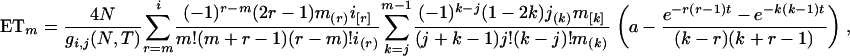
(A2) 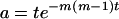 when r = m and
when r = m and 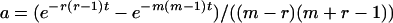 otherwise, and
otherwise, and 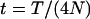 .
. - ETm for m = j: The expected time during which there are m = j distinct lineages, given i, j ≤ i, N, and T, is obtained by integration,
which leads to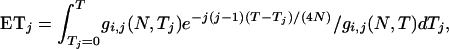
where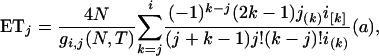
(A3) 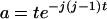 when k = j and
when k = j and 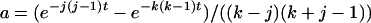 otherwise, and
otherwise, and 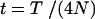 . When no coalescent events occur in the interval of [0, T] (i.e., j = i), (A3) reduces to
. When no coalescent events occur in the interval of [0, T] (i.e., j = i), (A3) reduces to 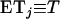 , as is expected.
, as is expected.
The ETBLG in the interval [0, T] can be calculated using (A1–A3), in two separate cases. In the first case, the part of the genealogy after the MRCA is found, branch length T1, is irrelevant and excluded. In the second case, T1 is included in the ETBLG. Cases 2 and 1 apply when the MRCA lineage is and is not to be included in another genealogy involving other genes formed after T. The ETBLG conditional on i, j, N, T is
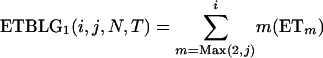 |
(A4) |
if T1 is excluded and is
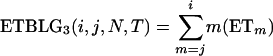 |
(A5) |
if T1 is included.
Considering all possible values of j given i, N, and T, the ETBLG in case 1 is
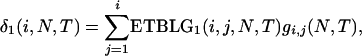 |
which, after some algebra, reduces to (1) in the text. As T → ∞, (1) further reduces to 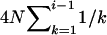 (e.g., Hudson 1990), as is expected. Similarly, the ETBLG in case 2 is
(e.g., Hudson 1990), as is expected. Similarly, the ETBLG in case 2 is
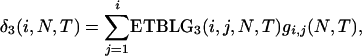 |
which reduces to (5) in the text.
APPENDIX B: THE ETBLG OF SAMPLES 4–7
The expected total branch length of the genealogy (ETBLG) for sample 4 can be derived, using the approach adopted in deriving (6) in the text, as
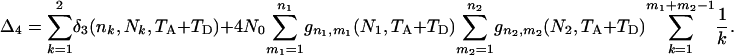 |
(B1) |
When n1 = n2 = 1 and Nk = N (k = 0, 1, 2), (B1) reduces to 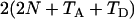 , which is twice the expected coalescent time between a sequence from parental population 1 and a sequence from parental population 2.
, which is twice the expected coalescent time between a sequence from parental population 1 and a sequence from parental population 2.
The ETBLG for sample 5 is
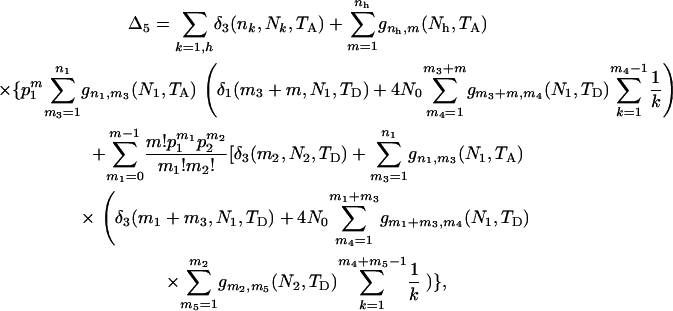 |
(B2) |
where 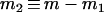 and
and 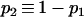 . As is expected, (B2) reduces to
. As is expected, (B2) reduces to 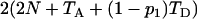 , twice the average coalescent time between a sequence from parental population 1 and a sequence from the admixed population, when n1 = nh = 1 and Nk = N (k = 0, 1, 2, h). For sample 6, Δ6 is calculated by the right side of (B2) by exchanging
, twice the average coalescent time between a sequence from parental population 1 and a sequence from the admixed population, when n1 = nh = 1 and Nk = N (k = 0, 1, 2, h). For sample 6, Δ6 is calculated by the right side of (B2) by exchanging 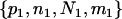 and
and 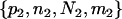 .
.
The ETBLG of sample 7 is
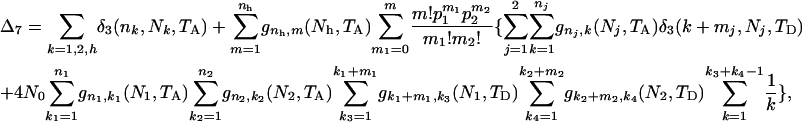 |
(B3) |
where 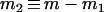 and
and 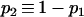 .
.
References
- Beaumont, M. A., 2003. Conservation genetics, pp. 775–780 in Handbook of Statistical Genetics, Ed. 2, edited by D. J. Balding, M. Bishop and C. Cannings. John Wiley & Sons, Chichester, England.
- Beaumont, M. A., W. Zhang and D. J. Balding, 2002. Approximate Bayesian computation in population genetics. Genetics 162: 2025–2035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertorelle, G., and L. Excoffier, 1998. Inferring admixture proportions from molecular data. Mol. Biol. Evol. 15: 1298–1311. [DOI] [PubMed] [Google Scholar]
- Cavalli-Sforza, L. L., and W. F. Bodmer, 1971. The Genetics of Human Populations. W. H. Freeman, San Francisco.
- Chakraborty, R., 1986. Gene admixture in human populations: models and predictions. Yearb. Phys. Anthropol. 29: 1–43. [Google Scholar]
- Chakraborty, R., and K. M. Weiss, 1986. Frequencies of complex diseases in hybrid populations. Am. J. Phys. Anthropol. 70: 489–503. [DOI] [PubMed] [Google Scholar]
- Chakraborty, R., and K. M. Weiss, 1988. Admixture as a toll for finding linked genes and detecting that difference from allelic association between loci. Proc. Natl. Acad. Sci. USA 85: 9119–9123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chakraborty, R., M. I. Kamboh, M. Nwankwo and R. E. Ferrell, 1992. Caucasian genes in American blacks: new data. Am. J. Hum. Genet. 50: 145–155. [PMC free article] [PubMed] [Google Scholar]
- Chikhi, L., M. W. Bruford and M. A. Beaumont, 2001. Estimation of admixture proportions: a likelihood-based approach using Markov chain Monte Carlo. Genetics 158: 1347–1362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chikhi, L., R. A. Nichols, G. Barbujani and M. A. Beaumont, 2002. Y genetic data support the Neolithic demic diffusion model. Proc. Natl. Acad. Sci. USA 99: 11008–11013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choisy, M., P. Franck and J. M. Cornuet, 2004. Estimating admixture proportions with microsatellites: comparison of methods based on simulated data. Mol. Ecol. 13: 955–968. [DOI] [PubMed] [Google Scholar]
- Dupanloup, I., and G. Bertorelle, 2001. Inferring admixture proportions from molecular data: extension to any number of parental populations. Mol. Biol. Evol. 18: 672–675. [DOI] [PubMed] [Google Scholar]
- Elston, R. C., 1971. The estimation of admixture in racial hybrids. Ann. Hum. Genet. 35: 9–17. [DOI] [PubMed] [Google Scholar]
- Excoffier, L., A. Estoup and J. M. Cornuet, 2005. Bayesian analysis of an admixture model with mutations and arbitrarily linked markers. Genetics 169: 1727–1738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glass, B., and C. C. Li, 1953. The dynamics of racial intermixture—an analysis based on the American Negro. Am. J. Hum. Genet. 5: 1–19. [PMC free article] [PubMed] [Google Scholar]
- Griffiths, R. C., and S. Tavaré, 1994. Simulating probability distributions in the coalescent. Theor. Popul. Biol. 46: 131–159. [Google Scholar]
- Hudson, R. R., 1990. Gene genealogies and the coalescent process, pp. 1–44 in Oxford Surveys in Evolutionary Biology, edited by D. J. Futuyma and J. D. Antonovics. Oxford University Press, New York.
- Kimura, M., 1969. The number of heterozygous nucleotide sites maintained in a finite population due to steady flux of mutations. Genetics 61: 893–903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li, W. H., 1997. Molecular Evolution. Sinauer Associates, Sunderland, MA.
- Long, J. C., 1991. The genetic structure of admixed populations. Genetics 127: 417–428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marjoram, P., J. Molitor, V. Plagnol and S. Tavare, 2003. Markov chain Monte Carlo without likelihoods. Proc. Natl. Acad. Sci. USA 100: 15324–15328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McLean, D. C., I. Spruill, S. Gevao, E. Y. S. Morrison, O. S. Bernard et al., 2003. Three novel mtDNA restriction site polymorphisms allow exploration of population affinities of African Americans. Hum. Biol. 75: 147–161. [DOI] [PubMed] [Google Scholar]
- O'Ryan, C., E. H. Harley, M. W. Bruford, M. A. Beaumont, R. K. Wayne et al., 1998. Microsatellite analysis of genetic diversity in fragmented South African buffalo populations. Anim. Conserv. 1: 85–94. [Google Scholar]
- Pakendorf, B., and M. Stoneking, 2005. Mitochondrial DNA and human evolution. Annu. Rev. Genomics Hum. Genet. 6: 165–183. [DOI] [PubMed] [Google Scholar]
- Parra, E. J., A. Marcini, J. Akey, J. Martinson, M. A. Batzer et al., 1998. Estimating African American admixture proportions by use of population-specific alleles. Am. J. Hum. Genet. 63: 1839–1851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parra, E. J., R. A. Kittles, G. Argyropoulos, C. L. Pfaff, K. Hiester et al., 2001. Ancestral proportions and admixture dynamics in geographically defined African Americans living in South Carolina. Am. J. Phys. Anthropol. 114: 18–29. [DOI] [PubMed] [Google Scholar]
- Press, W. H., S. A. Teukolsky, W. T. Vetterling and B. P. Flannery, 1996. Numerical Recipes in Fortran 77, Ed. 2. Cambridge University Press, Cambridge, UK.
- Quintana-Murci, L., O. Semino, H. J. Bandelt, G. Passarino, K. McElreavey et al., 1999. Genetic evidence of an early exit of Homo sapiens sapiens from Africa through eastern Africa. Nat. Genet. 23: 437–441. [DOI] [PubMed] [Google Scholar]
- Roberts, D. F., and R. W. Hiorns, 1965. Methods of analysis of the genetic composition of a hybrid population. Hum. Biol. 37: 38–43. [PubMed] [Google Scholar]
- Santos, C., R. Montiel, B. Sierra, C. Bettencourt, E. Fernandez et al., 2005. Understanding differences between phylogenetic and pedigree-derived mtDNA mutation rate: a model using families from the Azores Islands (Portugal). Mol. Biol. Evol. 22: 1490–1505. [DOI] [PubMed] [Google Scholar]
- Tajima, F., 1983. Evolutionary relationship of DNA sequences in finite populations. Genetics 105: 437–460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tavaré, S., 1984. Lines of descent and genealogical processes, and their applications in population genetics models. Theor. Popul. Biol. 26: 119–164. [DOI] [PubMed] [Google Scholar]
- Thompson, E. A., 1973. The Icelandic admixture problem. Ann. Hum. Genet. 37: 69–80. [DOI] [PubMed] [Google Scholar]
- Wang, J., 2003. Maximum-likelihood estimation of admixture proportions from genetic data. Genetics 164: 747–765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, J., 2005. Estimation of effective population sizes from data on genetic markers. Philos. Trans. R. Soc. B 360: 1395–1409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watson, E., P. Forster, M. Richards and H. J. Bandelt, 1997. Mitochondrial footprints of human expansions in Africa. Am. J. Hum. Genet. 61: 691–704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watterson, G. A., 1975. On the number of segregating sites in genetical models without recombination. Theor. Popul. Biol. 7: 256–276. [DOI] [PubMed] [Google Scholar]
- Wen, B., H. Li, D. R. Lu, X. F. Song, F. Zhang et al., 2004. Genetic evidence supports demic diffusion of Han culture. Nature 431: 302–305. [DOI] [PubMed] [Google Scholar]