Abstract
Objective To investigate the accuracy of interpretation of probabilistic screening information by different stakeholder groups and whether presentation as frequencies improves accuracy.
Design Between participants experimental design; participants responded to screening information embedded in a scenario.
Setting Regional maternity service and national conferences and training days.
Participants 43 pregnant women attending their first antenatal appointment in a regional maternity service; 40 companions accompanying the women to their appointments; 42 midwives; 41 obstetricians. Participation rates were 56%, 48%, 89%, and 71% respectively.
Measures Participants estimated the probability that a positive screening test result meant that a baby actually had Down's syndrome on the basis of all the relevant information, which was presented in a scenario. They were randomly assigned to scenarios that presented the information in percentage (n = 86) or frequency (n = 83) format. They also gave basic demographic information and rated their confidence in their estimate.
Results Most responses (86%) were incorrect. Obstetricians gave significantly more correct answers (although still only 43%) than either midwives (0%) or pregnant women (9%). Overall, the proportion of correct answers was higher for presentation as frequencies (24%) than for presentation as percentages (6%), but further analysis showed that this difference occurred only in responses from obstetricians. Many health professionals were confident in their incorrect responses.
Conclusions Most stakeholders in pregnancy screening draw incorrect inferences from probabilistic information, and health professionals need to be aware of the difficulties that both they and their patients have with such information. Moreover, they should be aware that different people make different mistakes and that ways of conveying information that help some people will not help others.
Introduction
Medicine is making increasing use of biochemical, imaging, and genetic screening tests that provide probabilistic information. Extensive psychological research has shown that most people, including health professionals, incorrectly interpret such information.1 The usual method for laboratory research has been to present probabilistic information in a scenario relating to medical screening or other hypothetical situations and ask respondents to draw a conclusion. Such research has extensively investigated the incorrect answers given in order to understand the reasoning processes that lead to them and suggests that respondents typically ignore information essential to a mathematically correct answer.
Early laboratory research suggested extreme overestimation or underestimation when respondents estimated the probability that a positive screening result indicated that the relevant condition was present. Furthermore, scenarios describing medical screening produced more overestimation than did ones describing screening of machine parts.2 More recent applied research with patients has also shown frequent misinterpretation of screening results.3
The suggestion that evolution and experience equip people better to understand probabilistic information expressed as frequencies in a population, rather than as probabilities for an individual,4 led to the practical recommendation that medical practitioners should present screening information as frequencies, perhaps pictorially.5,6 We therefore tested the effect of a change from presentation as percentages to presentation as frequencies on the level of correct estimates and the types of error made in response to a scenario based on screening of maternal blood serum for Down's syndrome, which is now routinely offered to all pregnant women. Previous research has neglected the potential differences between different stakeholder groups in their interpretation of screening information that has current personal or professional relevance to them. We therefore compared responses of obstetricians, midwives, pregnant women, and their companions at an antenatal appointment.
Clinically, the impact of inaccurate estimates would be magnified if those making them were confident in them.7 Therefore, we also examined respondents' confidence in their ratings.
Methods
Participants
The data presented here are part of a larger study in which participants were randomised to one of four scenarios that presented information on either health (prenatal) screening or machine parts screening using presentation either as percentages or as frequencies. This paper presents the prenatal screening scenarios only, comparing responses from the frequency and percentage scenarios. We recruited participants from four stakeholder groups: pregnant women, the people accompanying them to antenatal appointments, midwives, and obstetricians. Within each group, we randomised consenting participants (see below) to one of the four scenarios.
Effect sizes for presentation as frequencies versus percentages in previous studies with student samples have been large.4 Allowing for a separate analysis in each stakeholder group, 40 cases per group presented with a prenatal screening scenario gave 89% power to detect an effect size of W = 0.50 (which is large but smaller than those reported4) at α = 0.05.8 Target recruitment was therefore 80 from each participant group.
Numbers who were approached and participated in each group for the whole study were as follows: 151 pregnant women approached, 82 (54%) responded, of whom 43 received the health scenario; 166 companions approached, 80 (48%) responded, of whom 40 received the health scenario; 92 midwives approached, 82 (89%) responded, of whom 42 received the health scenario; 116 obstetricians approached, 82 (71%) responded, of whom 41 received the health scenario. We excluded from the respondent numbers above and from the analysis three pregnant women and two companions who agreed to participate and were randomised but were called in to their appointment before completing the questionnaire and three women who completed only the demographic section of the questionnaire. The analysis presented here is of responses to the health context scenarios only.
Companions included 33 partners (all men) and seven female relatives (one unknown relationship). All midwives and 25 obstetricians were women. Table 1 shows the number in each group who responded to a frequency or percentage scenario.
Table 1.
Percentage (number) of respondents from each stakeholder group who provided answers that were correct, overestimates, or underestimates
| Pregnant women | Companions | Midwives | Obstetricians | Total | |
|---|---|---|---|---|---|
| Presentation as percentages | |||||
| Correct | 5 (1) | 15 (3) | 0 | 5 (1) | 6 (5) |
| Overestimate | 68 (15) | 50 (10) | 46 (10) | 76 (16) | 60 (51) |
| Underestimate | 27 (6) | 35 (7) | 55 (12) | 19 (4) | 34 (29) |
| Total | 100 (22) | 100 (20) | 100 (22) | 100 (21) | 100 (85) |
| Presentation as frequencies | |||||
| Correct | 14 (3) | 15 (3) | 0 | 65 (13) | 24 (19) |
| Overestimate | 38 (8) | 40 (8) | 35 (7) | 15 (3) | 32 (26) |
| Underestimate | 48 (10) | 45 (9) | 65 (13) | 20 (4) | 44 (36) |
| Total | 100 (21) | 100 (20) | 100 (20) | 100 (20) | 100 (81) |
| All | |||||
| Correct | 9 (4) | 15 (6) | 0 | 34 (14) | 15 (24) |
| Overestimate | 54 (23) | 45 (18) | 41 (17) | 46 (19) | 46 (77) |
| Underestimate | 37 (16) | 40 (16) | 60 (25) | 20 (8) | 39 (65) |
| Total | 100 (43) | 100 (40) | 100 (42) | 100 (41) | 100 (166) |
Procedure
The researcher (HW) recruited all participants in person, and they completed questionnaires in her presence. She recruited pregnant women and the people accompanying them while they were waiting for the first antenatal appointment at a regional maternity service. She recruited health professionals at national training events or through a regional maternity service, and they completed the questionnaire during breaks from work or training.
In order to randomly assign scenarios to participants, the questionnaires were placed in sealed plain A5 envelopes, which were hand shuffled by the researcher so that the sequence was completely concealed. As respondents were recruited, the researcher took the next envelope from the stack.
Questionnaires sought basic demographic information and then presented a screening scenario (box 1) that described a positive screening result and contained mathematically equivalent information (sensitivity of test, false positive rate, and population incidence of the outcome), presented in percentage format (n = 86) or frequency format (n = 83). We asked respondents to estimate the probability that a positive test result meant that the baby had Down's syndrome (that is, the positive predictive value for the test). They also rated their confidence in their answer from 1 (not at all confident) to 6 (very confident).
Analysis
We converted responses to percentages for presentation and analysis. The correct response was 47.6% (box 2). We categorised estimates from 45.0% to 50.0% as correct. We regarded all other responses as incorrect and categorised them into overestimates and underestimates.
Box 1: Screening scenario
Version 1: percentages
The serum test screens pregnant women for babies with Down's syndrome. The test is a very good one, but not perfect. Roughly 1% of babies have Down's syndrome. If the baby has Down's syndrome, there is a 90% chance that the result will be positive. If the baby is unaffected, there is still a 1% chance that the result will be positive. A pregnant woman has been tested and the result is positive. What is the chance that her baby actually has Down's syndrome? -...........%
Version 2: frequencies
The serum test screens pregnant women for babies with Down's syndrome. The test is a very good one, but not perfect. Roughly 100 babies out of 10 000 have Down's syndrome. Of these 100 babies with Down's syndrome, 90 will have a positive test result. Of the remaining 9900 unaffected babies, 99 will still have a positive test result. How many pregnant women who have a positive result to the test actually have a baby with Down's syndrome?........... out of............
Box 2: An explanation of how to derive the correct answer2
If 10 000 pregnant women were tested, we would expect 100 (1% of 10 000) to have babies with Down's syndrome
Of these 100 babies with Down's syndrome, the test result would be positive for 90 (90% of 100) and negative for 10
Of the 9900 unaffected babies, 99 (1% of 9900) will also test positive, and 9801 will have a negative test result
So, out of the 10 000 pregnant women tested, we would expect to see 189 (90+99) positive test results. Only 90 of these actually have babies with Down's syndrome, which is 47.6%
Therefore, 47.6% of pregnant women who have a positive result to the test would actually have a baby with Down's syndrome
We compared the participant groups on the proportion of correct responses and then on the proportion of incorrect responses that were overestimates versus underestimates. We followed significant effects by pairwise comparisons. We next compared presentation as frequencies with presentation as percentages for the proportion of correct responses in the total sample and then in each respondent group. We used Pearson χ2 to make comparisons except when, for pairwise comparisons, the low proportion of correct responses led to expected cell frequencies under five, when we used Fisher's exact test (two tailed).9 Finally, we report the confidence in incorrect responses for different groups.
Results
As expected, most (n = 142; 86%) responses were incorrect. Whereas the correct answer was 47.6%, most responses were close to 0% or 100%. Popular answers clustered around specific values. The two most frequent answers were 1.0% (n = 32; 19% of the sample) and 90.0% (n = 46; 27% of the sample), and these were produced by all groups and in response to both presentations.
Between group differences
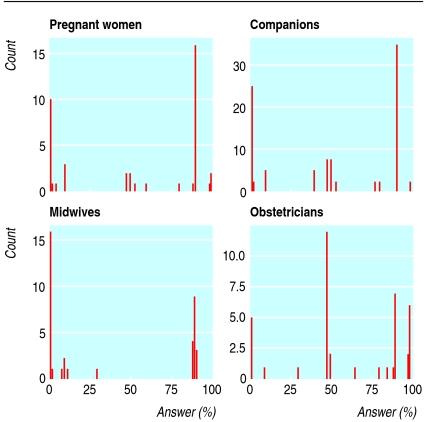
Figure 1 shows the distribution of responses in each group. The groups differed in the proportion of correct answers (table 1; χ2 = 20.9, df = 3; P < 0.001). Pairwise comparison showed that obstetricians were more often correct than either pregnant women (P = 0.007) or midwives (P < 0.001), and companions were more often correct than midwives (P = 0.011). The groups did not differ in the proportion of overestimates versus underestimates (χ2 = 6.4, df = 3; P = 0.093).
Fig 1.
Distribution of responses from the four participant groups. X axis is response to scenario expressed as percentage (width interval=0.5%); y axis is number of responses
Frequency presentation versus percentage presentation
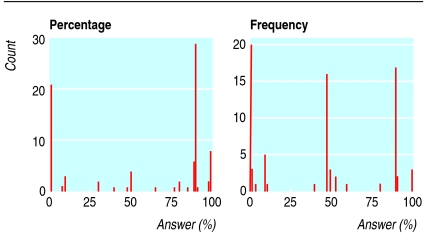
Figure 2 shows the distribution of responses to the percentage and frequency scenarios. The proportion of correct answers was much higher to presentation as frequencies than to presentation as percentages (table 1; χ2 = 10.4, df = 1; P = 0.001). However, this overall effect concealed an important between group difference. In pregnant women, companions, and midwives, the proportion of correct answers remained low whether presentation was as frequencies or percentages, with no difference (companions and midwives) or no significant difference (pregnant women: P = 0.35, Fisher's exact test) between the two (table 1). In obstetricians, by contrast, presentation as frequencies produced many more correct answers than did presentation as percentages (χ2 = 16.5, df = 1; P < 0.01).
Fig 2.
Distribution of responses to presentation as percentages versus frequencies. X axis is response to scenario expressed as percentage (width interval=0.5%); y axis is number of responses
Presentation also influenced the types of error made (χ2 = 6.7, df = 1; P = 0.010); percentages produced more overestimates, and frequencies produced more underestimates. However, when we investigated the effect within each group separately, no differences were significant.
Confidence in responses
Table 2 shows that, even among respondents who answered incorrectly, many were confident in their responses. Whereas most of the pregnant women who gave incorrect answers scored in the lower range of the confidence rating, people who were in a position to advise them were more confident. In particular, obstetricians who gave incorrect responses were generally highly confident, with a modal rating of 4 on the scale from 1 to 6. Midwives showed a bimodal distribution—although many also scored 4, a similar proportion were not at all confident.
Table 2.
Confidence ratings for participants who gave an incorrect response to the scenario, shown as percentage (number) of those responding incorrectly in each group who chose that rating
| Group
|
Confidence rating |
No response
|
|||||
|---|---|---|---|---|---|---|---|
| 1: Not at all confident | 2 | 3 | 4 | 5 | 6: Very confident | ||
| Pregnant women | 21 (9) | 23 (10) | 23 (10) | 9 (4) | 14 (6) | 7 (3) | 2 (1) |
| Companions | 13 (5) | 13 (5) | 18 (7) | 25 (10) | 13 (5) | 18 (7) | 3 (1) |
| Midwives | 26 (11) | 17 (7) | 14 (6) | 26 (11) | 10 (4) | 5 (2) | 2 (1) |
| Obstetricians | 5 (2) | 10 (4) | 12 (5) | 24 (10) | 20 (8) | 29 (12) | 0 |
Discussion
Probabilistic reasoning has consistently been shown to be poor, and previous research has indicated that presentation of frequencies improves understanding. In this study, a simple change from presentation as percentages to presentation as frequencies did indeed improve the accuracy of interpretation of information about screening for Down's syndrome, but only obstetricians benefited and only 65% of these were correct. Almost all the potential users of the test—that is, pregnant women, their companions, and midwives—were still incorrect. The benefits of presentation as frequencies therefore depended on the characteristics of the respondents. Basic cognitive psychology research in this area has generally used undergraduate students, and applied research has concentrated on professionals; that is, populations have been preselected for academic ability and experience of formal education. This study sounds a warning that research on undergraduates and professionals may not generalise to the much more heterogeneous groups of service users.
The correct interpretation of the information presented in this scenario was that a woman with a positive screening result had about a 50% probability that the baby did, in fact, have Down's syndrome. As has been found in other studies,2 respondents' incorrect answers were mostly very high or very low. In other words, most respondents judged that the genetic anomaly was almost certainly present or almost certainly absent. Of the two most common responses, 90.0% corresponds to a reasoning error, well described in the literature, in which reasoning relies only on the sensitivity of the test,10 whereas 1.0% corresponds to an error of using only the base rate, which, although previously recognised, has received little attention from research.
Although presentation as frequencies did not increase accuracy overall, it did significantly change the balance of overestimates versus underestimates. On the basis of previous literature,10 this suggests a trend for presentation as percentages to increase neglect of the population base rate whereas presentation as frequencies increased overuse of the base rate. Given that the errors are so extreme—that is, most respondents thought the anomaly was almost certainly present or almost certainly absent—a minor change in presentation can have a major impact on the interpretation of results of screening tests.
One of the main criticisms of previous probabilistic reasoning research is that it lacks ecological validity.11 Respondents in this study were responding to an experimental task rather than being observed in their actual practice. However, the screening test was one in which each respondent group was potentially involved, and the elements of information in the scenario match those covered (in a more discursive form) in the standard NHS leaflet prepared by the UK National Screening Committee.12
Readers might be reassured by the finding that more obstetricians were correct, but midwives are the main source of information for pregnant women about this test,13 and, furthermore, nearly two thirds of obstetricians were incorrect. Moreover, many obstetricians and midwives were confident in their incorrect answers, indicating a disturbing lack of insight into their poor understanding of information directly relevant to their clinical practice.
Limitations of the study
The theoretical justification for using presentation as frequencies is that it facilitates a more “natural” style of reasoning,4 and, in changing from presentation as percentages to presentation as frequencies, previous researchers have manipulated several aspects of the presented information in an attempt to facilitate such reasoning. Indeed, some people have suggested that truly effective communication of probabilistic information will need to use decision aids such as visual presentations of risk.6 These might have increased the correct responses in pregnant women, companions, and midwives in our study. We chose to make the minimum changes necessary to convey information in a frequency format consistent with previous research. Nevertheless, this needed minor rewording of the scenario, and different changes might have led to different results. Clearly, further research is needed to identify the methods of presentation as frequencies that might facilitate understanding.
This study used manipulations of only one scenario, to which the correct answer was close to 50%. Both accuracy and the proportion of overestimates and underestimates may respond to changes in the base rate, sensitivity, and specificity used in the scenario. Furthermore, presentation of information in frequency format for some combinations of these key screening test parameters would require the use of larger numbers than the 10 000 denominator used here. Future research will need to examine whether users' difficulty in thinking about large numbers might counteract the benefits of presentation as frequencies. Finally, participation was voluntary, and clearly the study may be biased towards those who felt more comfortable with probabilistic data.
Implications for practice
Comparisons between stakeholders in screening highlight the importance of future research with user groups and non-medical professionals. Health professionals need to be aware that screening information presents difficulties to professionals and service users alike and that the erroneous conclusions being drawn by different groups may differ. Screening technologies are becoming increasingly available across many health settings, although the assumption that they are always beneficial has been disputed.14 The inability of the people actually using probabilistic screening information, both professionals and service users, to draw correct conclusions from it seriously challenges the usefulness of such screening in practice.
What is already known on this topic
Most people, including health professionals, do not draw mathematically correct inferences from probabilistic screening information
Some studies suggest that presentation as frequencies aids interpretation
What this study adds
Presentation as frequencies does not help everyone: a simple change from percentages to frequencies increased correct responses in obstetricians but not in midwives or service users
The change in presentation did change the type of errors that people made
Many respondents were very confident about their incorrect answers
Contributors: RB had the original idea for this research, and all three authors contributed to the research design. HW collected the data. RB did the analysis and drafted the manuscript in collaboration with PS and HW. RB is the guarantor.
Funding: Economic and Social Research Council, award reference RES-000-22-0352. The funders were not involved in the study design; in the collection, analysis, and interpretation of data; in the writing of the report; or in the decision to submit the paper for publication.
Competing interests: None declared.
Ethical approval: Liverpool (Adult) Research Ethics Committee 9/1/04, reference 02/05/063A.
References
- 1.Steurer J, Fischer JE, Bachmann LM, Koller M, ter Riet G. Communicating accuracy of tests to general practitioners: a controlled study. BMJ 2002;324: 824-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hammerton M. A case of radical probability estimation. J Exp Psychol 1973;101: 252-4. [Google Scholar]
- 3.Marteau TM, Senior V, Sasieni, P. Women's understanding of a “normal smear test result”: experimental questionnaire based study. BMJ 2001;322: 526-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Gigerenzer G, Hoffrage U. How to improve bayesian reasoning without instruction: frequency formats. Psychol Rev 1995;102: 684-704. [Google Scholar]
- 5.Gigerenzer G, Edwards E. Simple tools for understanding risks: from innumeracy to insight. BMJ 2003;327: 741-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Edwards A, Elwyn G, Mulley A. Explaining risks: turning numerical data into meaningful pictures. BMJ 2002;324: 827-30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Klein JG. Five pitfalls in decisions about diagnosis and prescribing. BMJ 2005;330: 781-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Cohen J. Statistical power analysis for the behavioural sciences. 2nd ed. Hillsdale: Lawrence Erlbaum Associates, 1988.
- 9.Fleiss JL. Statistical methods for rates and proportions. 2nd ed. Chichester: John Wiley & Sons, 1981.
- 10.Villejoubert G, Mandel D. The inverse fallacy: an account of deviations from Bayes's theorem and the additivity principle. Mem Cognit 2002;30: 171-8. [DOI] [PubMed] [Google Scholar]
- 11.Koehler J. The base rate fallacy reconsidered: descriptive, normative, and methodological challenges. Behav Brain Sci 1996;19: 1-53. [Google Scholar]
- 12.UK National Screening Committee. Testing for Down's syndrome in pregnancy. Oxford: UK National Screening Committee, 2004.
- 13.Bramwell R, Wade S. Down's syndrome screening: how do they know? In: Thompson AK, Chadwick RF, eds. Genetic information: acquisition, access and control. New York: Kluwer Academic/Plenum Publishers, 1999: 183-90.
- 14.Taylor P. Making decisions about mammography. BMJ 2005;330: 915-6. [DOI] [PMC free article] [PubMed] [Google Scholar]