Analyzing partially randomized nucleic acid pools: straight dope on doping

Abstract

Partially randomized (doped) pools are important for optimizing activities initially isolated by selection-amplification or SELEX, and for locating nucleotides critical for function. Here we present a method for calculating the number of unique sequences in a pool, and the expected copy number of each unique sequence with a specified number of changes from the original sequence. Surprisingly, small differences in doping can have large consequences for the number of copies of sequences with certain numbers of changes from the original sequence. We demonstrate the effects of pool size, percentage doping, length of the random region and taking aliquots from the original pool on the exploration of sequence space in a doped reselection experiment. A web form is provided for customized calculations.

INTRODUCTION

SELEX (1–3), selection of novel activities from randomized sequence pools of 10¹²–10¹⁵ unique nucleic acid molecules (∼2–2000 pmol), is remarkably successful at finding new nucleic acid ligands and catalysts. However, even the 10¹⁵ molecules in a large experiment cover only a tiny fraction of the possible sequences, e.g. a random region of just 20 nt has 4²⁰ or 1.1 × 10¹² possible sequences, and a random region of 100 has 4¹⁰⁰ or 1.6 × 10⁶⁰ possible sequences. Consequently, although the initial sequences recovered from SELEX are highly optimized, they frequently are not the best possible solutions.

One fruitful method for increasing the activity of selected sequences is doping, in which an original, successful sequence is partially randomized at some or all positions and reselected (4). Whereas the initial selection samples all of sequence space, albeit sparsely, the doped reselection can provide a dense exploration of the region surrounding the original active sequence. If the fitness landscape is relatively smooth (in other words, if acceptable ligands or catalysts tend to have similar sequences), doping and reselection can find molecules with much higher activity than the original. Additionally, the positions that remain constant after reselection are probably required for activity (as long as sequences that varied in those positions really were generated and selected against).

Here we review the statistical methods for estimating the fraction of the pool sequences that have a specified number of changes from the original sequence (5), and the number of possible sequences at each distance (6). We extend these methods to calculate explicitly the fraction and number of sequences found and missed at each number of changes and, in particular, the range over which every possible variant sequence is found (given a fixed pool size, number of randomized nucleotides and percentage doping).

METHODS

Calculating the probability of finding a sequence in a pool of sequences requires two pieces of information: the probability of finding the sequence in a single attempt, and the number of attempts to find it. The following calculations assume that the pattern of change is truly random: a change at one position does not affect the probability that its neighbors will also change, and there is an equal probability of changing to each of the three alternative nucleotides. Though not always precisely true, this is the obvious first approximation. Since the coupling frequencies of the different phosphoramidites used for synthesizing the pools are not identical, ratios can be adjusted to ensure equality [e.g. 0.26 dA:0.25 dC:0.29 dG:0.20 dT in Unrau and Bartel (7)].

Within a pool synthesized with a specified random length and percentage doping, the only factor that systematically affects the abundance of a particular sequence is what we will term its mutational distance, the number of positions at which it differs from the original sequence. The probability of finding a particular sequence depends on its mutational distance for two reasons. First, the probability of making different numbers of changes in a molecule is not constant, and depends on the doping. A lightly doped pool will have more molecules that are close to the original sequence, while a heavily doped pool will have more molecules that are dissimilar from it. Secondly, the number of possible sequences at each mutational distance increases rapidly as the mutational distance itself increases.

These approximations allow us to idealize the situation as the binomial distribution, first described by Jakob Bernoulli in 1713 and today familiar from introductory statistics textbooks [see, for example, Pfeiffer (8)]. For a sequence of length n with a specified number of changes k, there are n positions that could be chosen to make the first change. This leaves n – 1 positions where the second change could occur, n – 2 positions where the third change could occur, and so on until the last change, which could occur at any of n – k positions. Since each change is assumed to be independent, there are thus n × (n – 1) × (n – 2)… × (n – k) numbers of ways to pick a list of positions that will be mutated. This expression can be simplified as follows.

There are n! ways to arrange the n positions in order from the position that would be chosen first to the position that would be chosen last, where n! is the factorial function (1 × 2 × 3 × … × n). However, the kth position is the last position that changes: all positions after k will stay the same. There are thus k! ways to arrange the k positions that will change, and (n – k)! ways to arrange the remaining n – k positions that will remain constant. These rearrangements within each class (change or constant) have no effect on which positions are in each class. Dividing the total number of arrangements by the number of arrangements that give the same divisions into classes, we get the following equation for the number of unique combinations C, which is the binomial coefficient:

C = n!/[k!(n – k)!]1

Each of the k positions that changes could become any of the three alternative nucleotides. As shown in Cadwell and Joyce (6), the total number of possible sequences S at a specified mutational distance k is therefore given by:

S = 3^k × C2

The appropriate model for finding the fraction of the pool that lies at each mutational distance is the binomial distribution (5,6), which specifies how often a sequence of length n is expected to have exactly k changes. The expected number of changes depends on the amount of doping d, which is the probability of changing each position. For example, d of 0.15, or 15%, implies that at each position there is an 85% chance of retaining the original sequence and a 5% chance of changing to each of the three other nucleotides. For a particular sequence, the probability of changing at a position is d, and these changes have occurred k times, so the contribution from the changed positions to the overall probability of getting the sequence is d^k. Conversely, the probability of remaining constant at a position is (1 – d), and (n – k) positions have remained constant, so the contribution from these positions is (1 – d)^{(n – k)}.

However, many sequences are the same mutational distance from the original, both because there are three possible ways to change at each position and because different sequences do not necessarily change at the same positions. Weighting the combinations of sequence changes C given in equation 1 by the relative probabilities of each number of changes from the paragraph above, the formula for the fraction of the pool that lies at each mutational distance k is the binomial equation:

Pr (k changes) = C × d^k (1 – d)^{(n – k)}3

To obtain the number of molecules at each mutational distance, multiply the result from equation 3 by N, the total number of molecules in the pool.

Combining the number of possible sequences at each distance with the number of molecules actually found at each distance, it is possible to calculate the probability of finding a particular sequence (and hence the number of unique sequences found in the pool). For example, in a pool of length 50 with 25% doping and 10¹³ molecules, there are 2.59 × 10¹¹ molecules that are seven changes away from the original sequence. However, since there are only 3⁷ × 50!/ (7! × 43!) = 2.18 × 10¹¹ possible sequences that are seven changes away, there must be multiple copies of at least some of the sequences. Although on average there are about 1.18 copies of each of the possible seven-change variants, not every sequence will actually be present. (We will revisit this specific example in more detail later in the paper.) In order to find the number of unique sequences that are actually present, and hence the true copy number of those sequences (rather than the copy number averaged across all possible sequences), we need to find out how many sequences were missed by chance.

If there are S different sequences at a given mutational distance (as given by equation 2), the probability of finding a particular sequence when examining a randomly chosen molecule at this mutational distance is S^–1. Conversely, the probability that the sequence was not found is the complement of this probability, 1 – S^–1. Since the changes are random and independent, the probability that the sequence was not found in either of two molecules is (1 – S^–1)², and the probability that it was not found in any of M molecules is (1 – S^–1)^M. The probability that the sequence was found at least once is the complement of this probability, or 1 – (1 – S^–1)^M. Since there are S different sequences that could be found at a given mutational distance, the total number of unique sequences U found at each distance k is:

U = S × [1 – (1 – S^–1)^M]4

where M is the number of molecules at that distance that were found in the pool, using equation 3. Dividing M by U gives the average copy number of each of the sequences that was found at a distance k, and subtracting M from S gives the number of sequences that were absent.

However, using the formula directly on longer random regions (>40) causes numerical errors unless specialized software such as Mathematica or Maple is used. Since most biologists are unfamiliar with these programs, we have included as an Appendix approximations that work around the imprecision in more familiar software such as Excel. Using these approximations, the revised equation for the binomial becomes:

ln Pr (k) = ln (n) – {ln (k!) + ln [(n – k)!]} + k ln (d) + (n – k) ln (1 – d)5

The revised equation for the number of unique sequences, using the approximation (1 – x)^N = e^{N × ln (1 – x)} ≈e^{–N × x}, becomes:

U = S × (1 – e^–M/S)6

Returning to our example above (a pool of 10¹³ molecules, with a region of 50 nt doped at 25%), we can calculate the number of unique sequences that are exactly seven changes away from the original, and the copy number of each sequence present, as follows.

Step 1. Calculate the number of ways of choosing exactly seven positions out of 50 to change (this will be used both to calculate the number of possible sequences and to calculate the fraction of the pool at this mutational distance). The formula is 50!/(7! × 43!). 50! is about 3.04 × 10⁶⁴, which is small enough to calculate by typing the formula directly into a spreadsheet (although it would be necessary to calculate the log of the factorial, or to use the log of the gamma function, for longer sequences). The number of possible combinations is 9.99 × 10⁷, and the natural log of this number is 18.4.

Step 2. Calculate the number of different sequences that have exactly seven changes. The formula for this, as given in equation 2, is 3^k times the result from step 1. As 3⁷ is 2187, the natural log of which is 7.69, then the total number of possible sequences is e^{(7.69 + 18.4)}, or 2.18 × 10¹¹.

Step 3. Calculate the fraction of the pool molecules that have exactly seven changes. The formula for this, as given in equation 3, is the result from step 1 multiplied by the probability that 7 nt changed. This probability is 0.25⁷ × 0.75⁴³, reflecting the fact that seven positions changed (with probability 0.25 per position), and 43 positions remained the same (with probability 1 – 0.25 = 0.75 per position). Raising a small number to a high power often results in an underflow error (i.e. the number is rounded to zero), so calculate the natural logs of the probabilities directly: 7 × ln (0.25) + 43 × ln (0.75), giving –22.1. Adding this to the natural log of the result from step 1, the total is (18.4 – 22.0) = –3.65. Since e^–3.65 = 0.0259, ∼2.6% of the pool molecules have exactly seven changes.

Step 4. Calculate the number of molecules in the pool that have seven changes. This is the product of the result from step 3 and the pool size, giving 0.0259 × 10¹⁴ = 2.59 × 10¹¹ molecules.

Step 5. Calculate the average number of copies of each sequence at this mutational distance. This is the number of molecules divided by the number of possible sequences (i.e. the result from step 4 divided by the result from step 2: in this case (2.59 × 10¹¹)/(2.18 × 10¹¹), or 1.18. This figure might suggest that every sequence will be present at least once, but in fact some sequences are found many times while others are missed entirely. In the last step, we will see that the sequences that were found are actually more abundant.

Step 6. Calculate the probability that a particular sequence with seven changes is not present in the pool. This is (1 – {3⁷ × [50!/(7! × 43!)]}^–1)^{2.59 × 1011}. In this case, the number can be calculated directly by typing in the formula (giving 0.306), but if the number of changes had been as few as 14, the rounding error would make direct calculation impossible. Instead, calculate the natural log: 2.59 × 10¹¹ × ln (1 – S^–1), where S is the number of possible sequences from step 2 (which is 2.18 × 10¹¹). Since S^–1 is a very small number, we can use the approximation ln (1 – x) ≈ –x, so the calculation simplifies to (2.59 × 10¹¹)/(–2.18 × 10¹¹), which is –1.18. Exponentiating, we get a probability of 0.306 that any particular sequence was not found; in other words, despite the fact that there was more than one copy of each sequence on average, nearly a third of the possible sequences at this distance were not actually present.

Step 7. Calculate the probability that a sequence was found. This is 1 – Pr (not found) from step 6, = (1 – 0.306) = 0.694.

Step 8. Calculate the number of unique sequences that were found. This is the product of the number of possible sequences S from step 2 and the fraction that were found from step 7: 0.694 × 2.18 × 10¹¹ = 1.52 × 10¹¹.

Step 9. Calculate the copy number of the sequences that were found. This is the number of molecules at that mutational distance from step 4 divided by the number of unique sequences from step 8: 2.59 × 10¹¹/1.52 × 10¹¹ = 1.71. Compare with the estimate of 1.18 copies per sequence calculated at step 5: the difference is ∼45%.

Thus, for any combination of pool size, random length and doping, we can calculate the number of unique sequences at each mutational distance, and also the fraction of possible sequences that are present or absent at each distance. An Excel spreadsheet and a Perl program implementing the method are available at http://bayes.colorado.edu/doped_pools/.

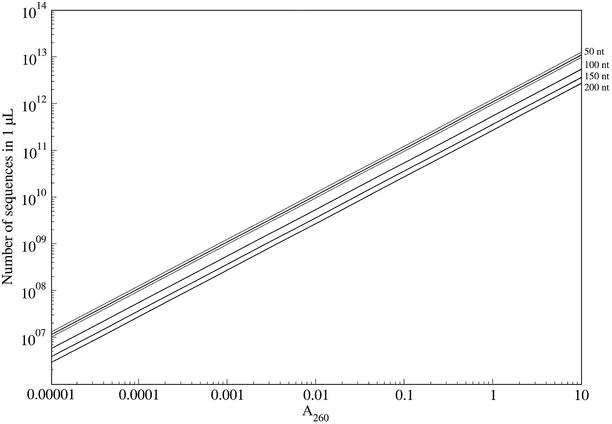
All the calculations presented here are in terms of numbers of sequences, but what is typically measured is the A₂₆₀ of the ssDNA pool produced in the synthesis. Figure 1 shows this conversion for molecules of total length (not just the length of the randomized region) 50, 100, 150 and 200 nt. These figures assume average molar extinction coefficients of 15 400 for dA, 7400 for dC, 11 500 for dG, and 8700 for dT in the context of a DNA strand, as reported on the Sigma-Genosys web page: http://www.sigmaaldrich.com.au/tec_qua.htm. Our web page calculates more accurate extinction coefficients based on the dinucleotide extinction coefficients reported on the same site, extending the technique to take into account the differences in dinucleotide frequencies with doping at specified positions in the sequence. Variation in base composition can have almost a 2-fold effect on the apparent number of sequences: the gray lines flanking the 50 nt line are for 75% pyrimidines (high) and for 75% purines (low). The ratio of the number of biased sequences to the number of unbiased sequences at a given A₂₆₀ is constant, so the potential error due to composition is not shown for the other lengths.

Figure 1.

Relationship between A₂₆₀ (x-axis) and number of sequences (y-axis) for single-stranded DNA of total length 50, 100, 150 and 200. Black lines assume equal base composition. Gray lines flanking the length 50 line indicate 75% pyrimidines (high) and 75% purines (low).

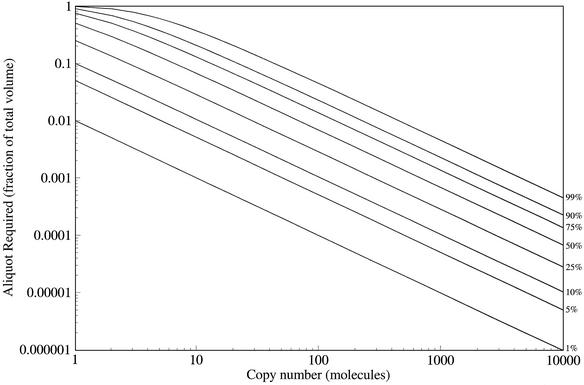
Pool DNA is seldom used directly: instead, the pool is amplified by PCR and/or each template DNA is transcribed into many copies of RNA. Although these techniques increase the number of copies of those sequences that survive the procedure, rare sequences can be lost due to sampling. Even having multiple copies of a sequence does not guarantee that it will be present in the final pool. Assuming that all sequences amplify and transcribe equally well (an assumption that is almost certainly false most of the time), let the aliquot that is carried forward in the experiment be some fraction f of the total pool. If every sequence were unique, the aliquot would contain f of the total sequences. However, a sequence with c copies has more than one chance to find itself in the aliquot. If the number of copies of the sequence is much smaller than the number of molecules in the aliquot (a factor of 1000 or more), then the probability that all of the copies were left behind is (1 – f)^c. Consequently, the fraction of the sequences that are present in the aliquot is 1 – (1 – f)^c. This is useful in conjunction with the calculations for the copy number and the number of unique sequences at each mutational distance, since the fraction of sequences at each distance that are carried over (or lost) can be calculated directly (Fig. 2). Therefore, experimental design that divides the pool should accommodate the disproportionate effect of this division on unique sequences and, therefore, on the total diversity of the pool.

Figure 2.

Aliquot required (y-axis) to contain at least one copy of the desired percentage (different lines) of molecules that are present in the original pool in a specified copy number (x-axis). For example, to obtain 99% of the single-copy molecules in a pool (top line, left-hand side), it is necessary to take an ‘aliquot’ that is 99% of the pool, but to obtain 99% of the molecules in the pool that are each present in 10 000 copies (top line, right-hand side), it is only necessary to take an aliquot of ∼0.06% of the pool.

Using this method, it can be seen that an aliquot of 1% of the total pool (e.g. 0.5 µl of a 50 µl pool) will contain ∼1% of the single-copy molecules, but at least 99% of all the molecules that are present in at least 500 copies. However, to get 99% of the molecules that are only present in five copies would take an aliquot of 60%, or 30 µl from the same pool (Fig. 2).

RESULTS

Here we take as a starting point a typical doped selection (random region 30 nt, 25% doping, 10¹⁴ sequences or ∼150 pmol) and investigate the effects of systematically varying each of these parameters (Fig. 3).

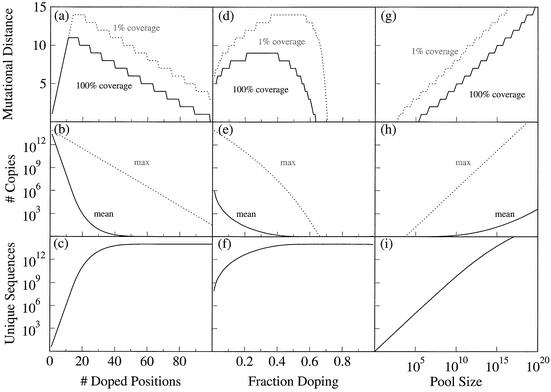
Figure 3.

Properties of doped sequence pools for different randomized region lengths, doping and number of sequences (first, second and third column, respectively), showing regions of 100% (solid line) and 1% (dotted line) sequence coverage (top row), average (solid line) and maximum (dotted line) copy number (center row), and total number of unique sequences (bottom row). Apart from the variable parameter in each column, the pool is assumed to be 30 nt with 25% doping and 10¹⁴ sequences. Often, the most abundant sequence in the pool [‘max’ in graphs (b), (e) and (h)] is the original sequence.

Varying the randomized length from 0 to 100, while keeping the doping constant at 25% and the number of sequences at 10¹⁴, every possible variant was found until the randomized region reached ∼11 nt (Fig. 3a). Thereafter, the distance at which all sequences (or at least 1% of sequences) were still found slowly decreased, until for a sequence with 100 random nt there was no mutational distance (except for the original sequence with no changes) where all possibilities were recovered. However, even at 100 nt, at least 1% of the 4.3 million possible sequences with up to three changes from the original were still found (Fig. 3).

As the number of doped positions increased, the maximum number of copies of a sequence decreased exponentially, while the average number of copies decreased exponentially at first and then leveled off (Fig. 3b, dotted and solid lines, respectively). However, even with a randomized region of 100 nt, there were still more than 30 copies of the original sequence and more than three copies of each one-change variant (although, on average, nearly every sequence was unique). When the number of doped positions was 30, there were 1.7 × 10¹⁰ copies of the original sequence, 2.0 × 10⁹ copies of each of the one-change variants and five copies of each of the 12-change variants (99% of which were found). However, when the number of doped positions increased to 50, the number of copies of the original sequence dropped to 5.6 × 10⁷, and only 0.02% of the possible 12-change variants were found (each a unique sequence).

The number of unique sequences (Fig. 3g) increased very rapidly between 0 and 18 nt, reaching 10⁶ sequences by 10 nt and 2.2 × 10¹⁰ sequences at 18, but the rate of change continually decreases as the number of positions increases. At 100 nt, every sequence with more than three changes from the original was almost certainly unique, and the number of different sequences was only about 5000 less than the total pool size of 10¹⁴.

Varying the amount of doping from 0 to 100% (note that 75% doping is complete randomization; further doping artificially depletes the pool in sequences that resemble the original sequence), while keeping the random region at 30 nt and the pool size at 10¹⁴, gave a somewhat more complex pattern. The region of complete coverage increased to a maximum of nine changes from 21–40% doping, and then rapidly declined again; above 63% doping, there was no number of changes that was completely covered (Fig. 3d, solid line). The pattern was similar for the region of 1% coverage (dotted line), although the maximum was somewhat greater (14 nt, from 36–57% doping). The maximum copy number started at 7.4 × 10¹³ at 1% doping and declined rapidly as doping increased, although even at 57% doping some sequences were present in thousands of copies (Fig. 3e, dotted line). In general, the average copy number (solid line) decreased much faster than did the maximum. The number of unique sequences started at about 82 million (for 1% doping). About 1% of the sequences were unique at 15% doping, 10% at 25% doping, 90% at 48% doping, and 99% at 55% doping. After 75% doping (complete sequence randomization), the number of sequences actually declines slightly (not readily visible on log scale), down to 8.8 × 10¹³ at 99% doping (Fig. 3f).

Varying the pool size from one to 10²⁰ molecules while holding the doping constant at 25% and the random region at 30 nt, we see that the mutational distance covered, the mean and average copy number and the total number of unique sequences all increase as the pool size increases (Fig. 3g–i). However, the maximum copy number increases much faster than the average copy number (compare dotted and solid lines in Fig. 3h), and increasing the pool size provides an ever-decreasing advantage in finding new unique sequences (Fig. 3i: slope starts to decrease above about 10⁷ sequences).

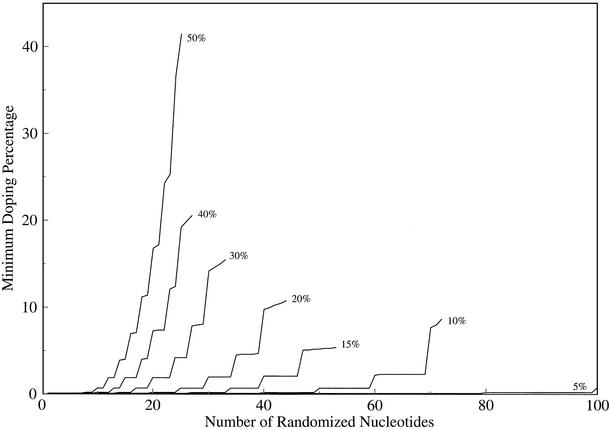
The minimum doping required in order to find a specified percentage of the sequences within a given mutational distance of the original sequence is shown in Figure 4. This is useful for designing experiments that are intended to explore the space close to the original sequence without finding alternative catalysts or ligands that are many point mutations distant. Figure 4 shows the minimum doping required to find sequences that are <5, 10, 15, 20, 30, 40 and 50% changed from the original sequence.

Figure 4.

Minimum percentage doping (y-axis) required to find, in a pool of 10¹⁴ molecules, 99% of the sequences with more than a specified similarity (lines, annotated, similarities ranging from 5 to 50%) to an original sequence with a particular number of partially randomized nucleotides (x-axis). Lines terminate at the length where the number of possible sequences is so large that it is impossible to find 99% of them in this size pool.

In general, considerably less than x% doping is required in order to find 99% of the sequences up to length x. For example, only 7% doping is required to find 99% of the sequences that are up to 50% different from a sequence with a randomized region of 16 nt (i.e. sequences that have fewer than eight changes), and only 2% doping is required to find 99% of the sequences that are up to 20% different from a sequence of length 30 (i.e. that have fewer than six changes). In all cases, the minimum amount of doping required begins very low, but rises increasingly rapidly with sequence length. The graph has a stepped appearance because there can only be a whole number of changes in a sequence, so the sequence lengths that are not divided evenly by a particular percentage behave in about the same way (e.g. from 60 to 69 nt, being within 10% of the original sequence means having fewer than seven changes).

DISCUSSION

The most important factors for the usual purposes of a doped selection are the coverage of sequences (i.e. the range of mutational distances where all the possible sequences are found or the range where at least some sequences are found) and the copy number (i.e. the average number of copies of each sequence that is present in the pool).

The region of the mutational space where every single sequence is expected to be found (top row of Fig. 3, area under the solid line), and the region where at least 1% of the possible sequences are expected to be found (area under the dotted line) increase as the length of the random region increases, but rapidly start to level off (Fig. 3a). This is because the number of possible sequences rapidly increases when each additional random position is added, in part because there are more ways to pick out a certain number of positions to change, and in part because each position that changes can produce three different sequences.

The variation with the fraction of doping is somewhat more complex (Fig. 3d). At low levels of doping, every sequence close to the original sequence is found and, as the doping increases, it is also possible to find all the sequences at progressively greater distances. As the doping increases above ∼40%, the sequences with few changes start to become rare and eventually vanish. The rare sequences could be restored by using very large sequence pools, but this might sometimes require kilograms of RNA.

As the doping gets to high levels, there are so many possible sequences that there is no region in which most of them are found. At the limit, consider 75% doping: at this level, the sequence has been completely randomized. A pool at that level is the same as a completely random pool, which samples all of sequence space but covers each region only sparsely. Thus, all plausible experiments employ <75% doping (unless the purpose is specifically to find sequences that differ from the original sequence more than would be expected by chance, perhaps to eliminate a known type of catalyst or ligand from an otherwise random pool).

One interesting observation is that, for reasonably long sequences, relatively small differences in doping make large differences in both the average and maximum copy number. For example, changing the doping from 15 to 20% reduced the average copy number from 85 to 23, nearly a 4-fold decrease. Similarly, changing from 25 to 35% reduced the average copy number 3.8-fold (8.8 to 2.4). Most of this contribution comes from large changes in the amount of the most abundant sequence classes (those closest to the original sequence), but small changes in doping can lead to unexpectedly large changes in pool complexity. For instance, the change from 15 to 20% doping increased the number of unique sequences from 1.17 × 10¹² to 4.29 × 10¹², and the change from 25 to 35% increased the number of unique sequences from 1.13 × 10¹³ to 4.23 × 10¹³. For finding rare activities, a 4-fold change in the number of unique sequences in the pool could make a significant difference.

The variation with pool size (Fig. 3g) is much more straightforward. Below some threshold pool size, there are so few sequences that many are missed by chance. As sequences are added, the coverage increases in approximately log- linear fashion. Since 10⁶ sequences allow all the one-change variants to be found, and 10²⁰ sequences allow allow all the 15-change variants to be found, the increase in the accessible mutational distance is about 1 additional nt with each order of magnitude increase in pool size. This is considerably less than the 1/log (3) or 2.1 additional nt that would be expected just from considering the increase in the number of randomized sequence positions: the additional difficulty in finding all possible sequences comes from the fact that there are also many ways to choose the particular positions that vary.

The difference between the mean copy number and the maximum copy number (solid and dotted lines, respectively, in Fig. 3b, e and h) is usually very large (orders of magnitude). In general, it is impossible to ensure both full coverage of a range of mutational distances while at the same time equalizing copy number: the reason is that in order that all of a large number of sequences can be found, others must be sampled many times. The discrepancy between mean and maximum copy number increases dramatically with pool size, and is more than 10 orders of magnitude for our ‘typical’ case (30 random positions, 25% doping, 10¹⁴ sequences). Only at very high levels of doping does the variance in copy number decrease, and then only because every sequence found is a unique sequence.

As expected, the number of unique sequences increases with the number of doped positions, the amount of doping and the pool size (Fig. 3c, f and i). If the mutational distance is not critical, relatively small changes in the number of doped positions and the amount of doping can achieve an effect that would otherwise require a large increase in pool size. However, the effect of doping levels off rapidly once every sequence is likely to be unique.

Because the number of possible sequences rises extremely rapidly as the mutational distance from the original sequence increases, the minimum percentage doping required to find most of the sequences up to a specified distance (Fig. 4) begins low and then increases roughly exponentially as the number of randomized nucleotides increases. Very little doping (<0.3%) is required to find all five-change variants of a 100 nt sequence, and <2% doping is required to find all the variants that are <10% distant from a 59 nt sequence. This suggests that if it is important to minimize the amount of sequence change, it is possible to explore quite a large region around the original sequence almost completely while keeping the average mutational distance very low. However, these pools will be dominated by the original sequence, which may be a problem for some applications.

The 5 and 10% lines in Figure 4 suggest that, unexpectedly, even the natural level of mutation in PCR may be sufficient to generate considerable sequence diversity. Returning to our example of a pool of 10¹⁴ molecules, a mutagenic PCR with an error rate over 20–25 rounds of 7 × 10^–3 per position (6) would generate all the four-error mutants for random regions up to 100 nt, and would generate at least 1% of the six-error mutants for randomized regions of up to 73 nt and 1% of the five-error mutants for randomized regions from 74 to 100 nt. In contrast, normal non-mutagenic PCR with an error rate of 10^–4 would only produce all the two-error mutants, and <1% of the possible four-error mutants, over this range. The number of mutants close to the original sequence can be quite large, e.g. there are over 128 million four-error mutants of an 80 nt sequence, and more than 4 × 10¹¹ six-error mutants. Thus mutagenic PCR alone can be an effective strategy for covering the region close to the original sequence, although it should be noted that the copy number of variant sequences will be low (generally, each sequence will be unique). Although it might take 5–15 rounds of selection to amplify any variant sequences with higher activity from such a pool, because the overall number of variant sequences is low, any noticeable enrichment of a variant over the original sequence under these conditions would be extremely likely to indicate a functional advantage.

Conclusions

These methods should be useful both for investigating the properties of doped pools in general and for investigators seeking to characterize the complexity of and distribution of sequences within their own pools for selections. Knowing not just the fraction of the pool that is found at each mutational distance, but also the actual number of unique sequences and their copy number, should assist in interpreting the results of selections. In particular, the relationship between the copy number, the mutational distance and the pool size is somewhat complex, which previously has made it difficult to assess whether a particular pattern of changes in the recovered sequences differs from the chance expectation.

Surprisingly, small changes in the level of doping have significant consequences for the copy number of individual sequences, the difference in frequency between the most abundant sequences in the pool and the average sequences, and the overall pool complexity. Since the extent of doping is sometimes chosen on an ad hoc basis, we hope that these methods will prove useful in adapting the properties of doped pools to particular goals.

To define a local region of sequence space, i.e. to find variants that are similar to the original, we recommend a low level of doping of about half the percentage sequence similarity that it would be desirable to cover at the 99% level (in other words, to find most of the sequences out to 10% similarity, dope at 5%) (Fig. 4). It should be possible to cover all the sequences out to four changes, and an appreciable number (1%) of the sequences out to five or six changes, through mutagenic PCR alone, although amplifying the variant sequences might take many rounds of selection.

To broaden a search, i.e. where the goal is to maximize the distance at which almost all sequences are still covered, we recommend a high level of doping between 30 and 50% (for 100% coverage), or between 40 and 60% (if 1% coverage is acceptable). Although this high level of doping will also produce sequences that are very distant from the original, it will also cover every sequence up to about 10 changes (for 100% coverage) or 15 changes (for 1% coverage). This application would also benefit from increasing the pool size (Fig. 3).

To equalize a search, where the goal is to ensure that all sequences are present in the same number of copies, we recommend a small pool and a high level of doping (40% to drive the mean copy number below 1; 60% for the maximum copy number). Unfortunately, the only way to ensure that no sequence is over-represented is to produce sequences that are very dissimilar to the original and that are only slightly different from completely random sequences. A small pool can help here by reducing the distance at which all molecules would be expected to occur only once (Fig. 3).

One area that invites further investigation is the effect of PCR and transcription on the abundance of different sequences. Although the techniques presented here give quantitative estimates if every sequence behaves the same way, anecdotal evidence suggests that even clones from the same sequence family but with slight sequence variations give very different transcription or PCR yields. Defining these effects may allow even more precise tracking of the number of unique molecules through each step of a selection.

APPENDIX

Avoiding numerical imprecision

Calculating the fraction of possible molecules that are absent from a pool necessitates raising a number that is very close to 1 to a very high power. A 32-bit computer stores floating-point numbers internally in a format resembling scientific notation, with a limited number of bits representing each part of the number. When two numbers that are very different in size are added or subtracted, the smaller number is rounded to zero. Consequently, it is not possible to represent a number closer to 1 than about 1 – 10^–17, and accuracy is generally poor above about 1 – 10^–14. This makes it difficult to calculate the results when k > 15, and impossible when k > 30.

These difficulties can be circumvented by using the approximation that e^x ≈ 1 + x when x is small (Fig. 5). The reason for this is that, at x = 0, the value of e^x is 1, and the slope is also 1 (by definition). Consequently, a small change in x causes a small but equal change in ln (x). Table 1 gives some useful applications of this rule.

Figure 5.

Approximations of e^x and ln (x) (black lines) by x + 1 and x – 1 (gray lines), respectively. Insets show the high quality of the approximation when x is small (for e^x) or close to 1 [for ln (x)].

Table 1. Approximations for exponentials and logs of probabilities close to 1 or 0.

Expression	Approximation
ex	1 + x
e–x	1 – x
ln (1 + x)	x
ln (1 – x)	–x
ln (x)	x – 1
1 – ex	–x

Similarly, the factorials required for calculating the binomial coefficient rapidly become too large to calculate. This can be avoided either by calculating the log of the factorial directly (by taking the sum of the logs of the numbers from 1 to n), by calculating the log of the gamma function ln [gamma(x + 1)] = ln (x!), or by using the approximation that ln (n!) ≈ nln (n) – n. The log of the gamma function can be calculated using Excel’s GAMMALN worksheet function. In practice, for the range of randomized pools in SELEX (up to 200 nt), calculating the sums of the logs is both accurate and reasonably efficient.

Consequently, these approximations make it possible to use standard programs to calculate pool parameters, avoiding the need to learn how to use specialized numerical software.