The structural basis for biphasic kinetics in the folding of the WW domain from a formin-binding protein: Lessons for protein design?

Abstract

The mechanism of formation of β-sheets is of great importance because of the significant role of such structures in the initiation and propagation of amyloid diseases. In this study we examine the folding of a series of three-stranded antiparallel β-sheets known as WW domains. Whereas other WW domains have been shown to fold with single-exponential kinetics, the WW domain from murine formin-binding protein 28 has recently been shown to fold with biphasic kinetics. By using a combination of kinetics and thermodynamics to characterize a simple model for this protein, the origins of the biphasic kinetics is found to lie in the fact that most of the protein is able to fold without requiring one of the β-hairpins to be correctly registered. The correct register of this hairpin is enforced by a surface-exposed hydrophobic contact, which is not present in other WW domains. This finding suggests the use of judiciously chosen surface-exposed hydrophobic pairs as a protein design strategy for enforcing the desired strand registry.

An understanding of the mechanism by which proteins reach their particular native state from the vast number of unfolded conformations will have broad-reaching implications, ranging from the prediction of protein structure from sequence to understanding diseases that originate from protein misfolding. Small model peptides and proteins have lent invaluable insight into the protein-folding process, as they afford simple systems in which the general features of folding may be elucidated (1, 2).

Because of the local nature of the interactions, the formation of helices has proven considerably easier to understand using simple models (3–5) than has the formation of β-sheets. Accordingly, the principles that govern the formation of β-sheets are not well understood, despite the fact that the formation of intermolecular β-sheets is thought to be the crucial event in the initiation and propagation of amyloid diseases such as Alzheimer's disease (6) and spongiform encephalopathy (7).

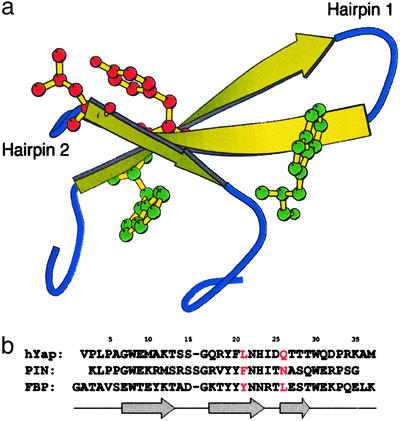
To further an understanding of the elements responsible for stability in β-sheets, de novo design methods have, in two cases, been used to construct three-stranded antiparallel β-sheets (8, 9), which have subsequently become the subject of both theoretical (10–12) and experimental (13, 14) folding studies. To ensure the generality of results toward natural proteins, however, we opt to study a series of three-stranded antiparallel β-sheet domains found in a variety of proteins: the WW domains (Fig. 1a).

Figure 1.

(a) The formin-binding protein (FBP) WW domain (PDB ID code 1E0L, model 2). Residues shown explicitly are Trp-8 (green), Tyr-21 (red), Leu-26 (red), and Trp-30 (green). (b) Sequence alignment of the hYAP, Pin, and FBP WW domains. Residue numbering corresponds to that of FBP, which will be used throughout this study. Residues at the 21 and 26 positions are red, to indicate those discussed in detail in this study. Arrows indicate locations of strands in the sequence.

WW domains, which bind proline-rich peptide sequences, have been identified in >200 nonredundant proteins to date (15). Because of the attractiveness of WW domains as a model for β-sheet formation, they have been the focus of several previous folding studies. The initial study of these systems examined the thermodynamics and kinetics of folding of the human Yes-associated protein (hYAP) WW domain (16). A subsequent study made use of the more stable Pin WW domain, to characterize in detail the dependence of folding on temperature and denaturant (17). Later, the thermodynamics and kinetics of folding were compared between the following three WW domains (18): one from hYAP, one from murine formin-binding protein (FBP) 28, and a de novo-designed WW domain. All three of the aforementioned studies (16–18) reported single-exponential kinetics for folding, corresponding to an apparent two-state mechanism.

A recent study (19), however, reports the observation of biphasic kinetics for the folding of the FBP WW domain. Biphasic kinetics is indicative of a more complex folding mechanism, and is typically taken as evidence for a folding intermediate. Protein-folding intermediates can compete with the native state when they have comparable free energies, which may occur under certain conditions. Folding through an intermediate may also lead to lower kinetic barriers, resulting in partially folded or misfolded states with free energies similar to the free energy of the native state. An increasing body of evidence suggests that amyloid fibrils, which are responsible for a number of human diseases, develop not from the native state of the responsible proteins, but rather, from partly folded precursors (20), and that modulation of the relative population of such conformations may lead to control over the rate of fibril formation (21).

In this study, we aim to distinguish between various kinetic models for the folding of proteins in the WW domain family, and to provide understanding at the structural level of the origins of these differing observations. We therefore require a representation of the protein that folds on time scales that are computationally accessible. The representation we employ is an off-lattice minimalist model, in which each amino acid residue is represented by one bead located at the α-carbon position. Because it has been observed that the use of generic pairwise potentials leads to energy landscapes considerably more rugged than those of real proteins (22, 23), we use a set of potential functions that contain terms that preferentially stabilize interactions present in the native state. Such potentials are typically referred to as Gō potentials.

These proteins share an identical topology, and thus it is expected that sequence effects will play a role in the origins of their differing folding kinetics. For this reason, the model includes modulation of the strength of the interactions and a pseudo-dihedral term, which are both sequence dependent, so that properties depending on details of sequence may emerge.

Such models were used in an earlier study (24) directed toward exploring the reasons for the differing folding mechanism of another pair of topologically analogous proteins, segment B1 of peptostreptococcal protein L and segment B1 of streptococcal protein G. Though both proteins share a topology consisting of two hairpins connected by a single helix and fold by an apparent two-state mechanism, the nature of the transition state in the two proteins differs. In protein L, the N-terminal hairpin is predominantly formed, whereas the C-terminal hairpin is unformed (25, 26); however, in protein G, the C-terminal hairpin has been shown to form ahead of the N-terminal hairpin (27–30). These differences emerged in the same simple model used here, which subsequently led to an explanation in terms of the enthalpy and entropy differences associated with the formation of each hairpin (24).

Methods

Procedure for Building Simplified Models.

The procedure used to build the simplified models described here has been developed for application to all proteins, independent of factors such as size and topology. Because of this development criterion, it is identical to that described in the characterization of the folding transition states of proteins L and G (24), in which reference complete details of the model-building procedure are available. The procedure is summarized below.

Each amino acid in the protein is represented in an off-lattice manner by a bead located at the α-carbon position. Interactions present in the all-atom representation are encoded by means of a series of potentials designed to distill the relevant features of the all-atom system down to this simple skeleton. The native state is built into these potentials by the use of favorable interactions between pairs of residues in contact in the native state and unfavorable interactions between all other pairs (Gō-like model).

To build such a potential, a list of contacts present in the native state must first be defined. A native contact is assigned to any pair of residues containing a backbone hydrogen bond (31) or with nonhydrogen side-chain atoms within 4.5 Å. Additional orientational native contacts are assigned to the residues adjacent to a hydrogen-bonded pair, to represent the cooperativity of the formation of hydrogen-bonding networks (32). All native contacts interact by means of a modified Lennard–Jones interaction featuring steeper walls and a small barrier, which is physically rationalized as a desolvation barrier that must be overcome before the favorable interaction energy may be realized (33–36). The potential is most favorable at the distance corresponding to the native state distance, where it has a value reflective of the identity of the amino acid pair (37).

All bonds and angles between adjacent residues are subject to a harmonic potential that is minimized at the value corresponding to the native geometry. A sequence-dependent potential is also applied to each dihedral, defined by four residues in sequence, which reflects the propensity of the involved residues toward formation of secondary structure.

All terms in the potential may be subsequently renormalized to set the temperature at which the folding transition occurs.

The model based on the Pin WW domain was built from a crystal structure (PDB ID code 1PIN), whereas the models based on the FBP WW domain were built from an ensemble of NMR structures (PDB ID code 1E0L). To best capture the available information in this ensemble of structures, the procedure described here was applied to each member of the ensemble, and the potentials were subsequently averaged.

Molecular Dynamics.

Molecular dynamics simulations were carried out by using the charmm macromolecular mechanics package (38) (charmm parameter files describing the Hamiltonian of each of the proteins used in this study are available on request). The time scale was defined by τ = (m/ɛ_res)^1/2r₀, where m is the mass of the average residue (119 atomic mass units), ɛ_res, is the average native contact energy per residue and r₀ is the average distance between adjacent (bonded) beads in the native state (3.8 Å). The model was evolved through high-friction Langevin dynamics, by using a friction coefficient β = 0.2/τ and time step Δτ = 0.0075τ. The virtual bond lengths were kept fixed by using shake (39).

A short simulation (1 × 10⁵ time steps) under strongly native promoting conditions (300 K) was used to generate the distribution of distances for each native contact. A distance cutoff was defined for each contact such that the contact was formed with a probability of 0.8 within the native-state basin. In all subsequent analyses, a particular native contact was deemed to be formed if the distance between the α-carbons involved in the contact was less than this distance cutoff.

Thermodynamic Characterization of Models.

To combine a series of molecular dynamics simulations under various conditions, thermodynamic analysis was carried out by using the weighted histogram analysis method (40). To improve the efficiency of sampling, a two-dimensional extension (41) of the replica exchange algorithm (42) was used. Each replica was assigned one of four temperatures (350, 385, 425, or 470 K) and one of four harmonic potentials applied to the radius of gyration (each of which had a force constant of 0.5 kcal/mol⋅Ų and a minimum at 1.0 R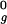, 1.5 R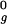, 2.0 R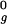, or 2.5 R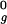, where R 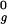represents the radius of gyration in the native state). After an initial equilibration period, each replica was simulated for 1.6 × 10⁸ Δτ. During this time, testing for exchanges took place every 2 × 10⁴ Δτ. Data were collected only every 500 Δτ, which is beyond the conformational correlation time of these model proteins.

Kinetic Characterization of Models.

Ensemble kinetic analysis was performed by averaging the value of a structural probe, typically the number of native contacts formed, over numerous (500) independent simulations as a function of time. Each simulation consisted of equilibration at high temperature (4 × 10⁷ steps of molecular dynamics well above the transition temperature determined from the thermodynamic analysis) followed by an instantaneous “T-jump” to refolding conditions (1.2 × 10⁸ steps of molecular dynamics slightly below the transition temperature determined from the thermodynamic analysis).

The average value of the structural property across all conformations at a given time was plotted as a function of time, leading to a kinetic trace analogous to those obtained experimentally. This trace was then alternatively fit to either a single-exponential function of the form

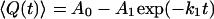1

or a double-exponential function of the form

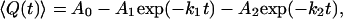2

where 〈Q(t)〉 is the mean value of the structural property of interest as a function of time, and A₀, A₁, A₂, k₁, and k₂ are free parameters in the fitting, corresponding to the relative amplitudes and the rate constants of the phases, respectively. This fitting allowed for the determination of the number of steps in the kinetic mechanism, as well as the relative amplitudes and the rate constants of the phases.

It should be noted that previous simulation studies of folding kinetics often carry out each folding simulation only until the folded state is reached in that particular simulation, by using some a priori definition of the folded state (43–45). The time required to reach the folded state is then averaged over the simulations, to compute the mean first-passage time for folding. The use of such an approach assumes that back-crossing from the folded state to the unfolded state is negligible, which is applicable only under conditions that strongly favor the native state. Furthermore, whereas the values of the times are highly sensitive to the definition of the folded state, the effects of perturbations or changing conditions are assumed not to depend on this definition. Finally, and most important in the context of this study, it is not clear as to how the distribution of first-passage times can clearly distinguish the kinetic complexity of the process under study. For this reason, we elect to use the ensemble kinetic analysis described above. We note that this method of ensemble kinetic analysis has also been used in several other theoretical studies of folding kinetics (46–50).

Results and Discussion

Initial Kinetic Characterization.

To determine the structural basis for the observed biphasic kinetics, it is first important to verify that this behavior is reproduced in the models used here. To this end, kinetic characterization was carried out by monitoring the ensemble mean number of native contacts formed as a function of time. This analysis was carried out by using models derived from the Pin WW domain and the FBP WW domain.

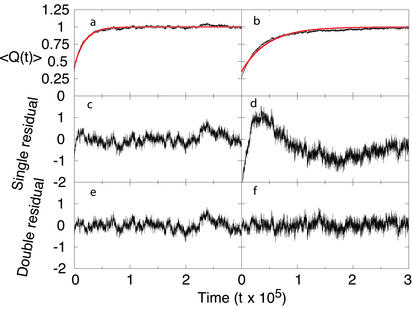
The kinetics of folding for the Pin WW domain was described well by a single-exponential function (Fig. 2 a, c, and e). Although the deviation from a single exponential for the FBP WW domain does not appear dramatic in the kinetic trace (Fig. 2b), the residual from a fit to a single exponential shows the characteristic shape of a curve that will be fit by an additional exponential (Fig. 2d). Accordingly, fitting to a double-exponential function leads to a residual that is centered about 0 at all times (Fig. 2f).

Figure 2.

Results from kinetic characterization of Pin (a, c, and e) and FBP (b, d, and f) folding. (a and b) The ensemble fraction of native contacts is shown as a function of time, along with the best-fit single exponential in red [〈Q(t)〉 is scaled by the fitting parameter A₀]. (c and d) The residual to this single exponential. (e and f) The residual to the best-fit double exponential. Pin WW domain is found to fit to a single exponential (Eq. 1) with parameters A₀ = 0.39, A₁ = 0.23, and k₁ = 5.5 × 10⁻⁵ τ⁻¹, whereas FBP WW domain is found to fit to a double exponential (Eq. 2) with parameters A₀ = 0.64, A₁ = 0.37, k₁ = 3.9 × 10⁻⁵ τ⁻¹, A₂ = 0.10, and k₂ = 5.8 × 10⁻⁶ τ⁻¹, where τ is the fundamental time scale (see Methods).

It is important to stress that the observed biphasic kinetics for the FBP WW domain are not simply because of fast relaxation associated with nonspecific reequilibration within a single basin after the T-jump: if this were the case, the kinetics for the Pin WW domain would be expected to show the same behavior. Even though such relaxation must undoubtedly be present, its time scale is sufficiently fast that it is masked by the slower phase or phases associated with folding.

These models capture the essential features of the differing kinetics for folding of the Pin and FBP WW domains. We therefore proceeded to examine the origins of the biphasic kinetics in FBP at the level of individual native contacts.

Detailed Kinetic Characterization.

To determine the contribution of each contact to the observed phases in the FBP kinetic trace, a modified kinetic trace was generated that included all native contacts except the contact of interest. This modified kinetic trace was then refit to Eq. 2, holding both rate constants fixed. The loss in amplitude of each phase on removal of any contact was indicative of the involvement of that contact to the corresponding kinetic process.

The first striking observation stemming from this analysis is that relatively few of the native contacts contribute to the observed slow phase. Almost all of the native contacts, by contrast, contribute to the observed fast phase. Of the few contacts that do not contribute to the observed fast phase, some do not contribute to the slow phase, either; the probability of formation these contacts changes only slightly on the folding of the remainder of the molecule. Not surprisingly, these contacts are generally found to be local contacts located near the termini of the molecule whose formation is not related to the folding of the remainder of the molecule. One exception is the Thr-13–Gly-16 contact, which is predominantly formed in the unfolded state.

All of the native contacts that contribute to the slow phase are found to be clustered in one region of the native state structure: the innermost portion of loop 2. Native contacts connecting this region of the protein to strand 1 (Glu-7–Thr-25, Trp-8–Glu-27, and Thr-9–Asn-23) are found to contribute to both observed phases, and native contacts connecting residues within loop 2 are found to contribute only to the slow phase. The strong clustering of these contacts in relation to the native state structure suggests an interpretation of the observed biphasic kinetics: the folding of loop 2 independently from the remainder of the protein. Surprisingly, contacts between the N-terminal part of strand 2 and the C-terminal part of strand 3, as well as contacts between the termini, contribute to the fast phase only, indicating that these contacts may form without the intervening loop.

The fact that contacts within either portion do not display biphasic kinetics, as well as the observation of both phases in the contacts connecting them, suggests that either piece of structure may form first (parallel pathways). In a sequential mechanism [unfolded (U) → intermediate (I) → native (N)], one would expect an exponential lag-phase to be incorporated into the rate of formation of contacts associated with the I → N step: the absence of such mixing rules out folding by means of a sequential mechanism.

To verify the (somewhat counterintuitive) conclusion that the formation of these innermost loop 2 contacts alone is responsible for the observed biphasic kinetics, as well as to validate the proposed mechanism, the collection of refolding trajectories was culled for trajectories in which the loop 2 contacts were fully formed on initiation of refolding (this condition was met in 23 of the 500 trajectories). The kinetic trace arising from these selected trajectories was found to fit to a single-exponential function. Furthermore, the rate constant observed in these selected trajectories (3.5 × 10⁻⁵ τ⁻¹) was commensurate with the rate constant of the previously observed fast phase (3.9 × 10⁻⁵ τ⁻¹), confirming the assertion that these contacts are indeed responsible for the observed slow phase.

As a further validation, each hairpin was subjected to the same refolding experiment in isolation. Hairpin 1 was found to demonstrate monophasic kinetics, whereas hairpin 2 was found to demonstrate biphasic kinetics, providing further support for our structural interpretation.

Having determined the structural features associated with each of the observed kinetic phases, we then turned to a thermodynamic analysis to rationalize the observation that loop 2 formation accounts for the slow phase of folding.

Thermodynamic Characterization.

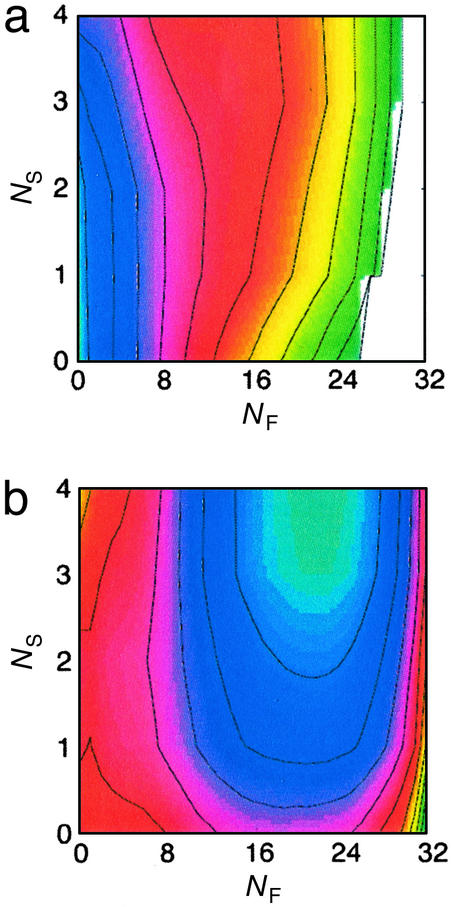
By using the weighted histogram analysis method (see Methods), it is possible to project the free energy onto any set of progress variables at any temperature. Having determined the structurally relevant contacts from the kinetic analysis, we define two progress variables: the number of native contacts formed within the innermost portion of loop 2 (N_S: Tyr-21–Leu-26, Asn-22–Thr-25, Asn-22–Leu-26, and Asn-22–Glu-27), and the number of native contacts formed in the remainder of the protein (N_F: native contacts associated with the observed fast phase). Native contacts connecting these two regions are not included in either progress variable, so that the reaction coordinates are independent.

The free energy is first simultaneously projected onto these two progress variables at 450 K, the temperature at which conformations were equilibrated before initiation of folding (Fig. 3a). A single minimum is apparent on this surface, located at the origin (N_F = 0, N_S = 0). The free energy increases sharply with increasing N_F, indicating that little residual structure is present in this part of the protein. By contrast, the minimum is very broad with respect to N_S, suggesting that loop 2 generally occupies collapsed conformations under these conditions.

Figure 3.

Results from thermodynamic characterization. A simultaneous projection of the FBP free-energy surface onto the number of native contacts formed in loop 2 (N_S) and the number of native contacts formed in the remainder of the protein (N_F), at the temperature of equilibration before refolding (a) and the temperature at which refolding was carried out (b). The free-energy difference between adjacent contour lines corresponds to k_BT.

The free energy is also projected onto these progress variables at 370 K, the temperature at which refolding was carried out (Fig. 3b). As expected, the minimum shifts to a location consistent with the folded protein (N_F = 22, N_S = 4). An additional saddle point is apparent (N_F = 1, N_S = 2), corresponding to conformations in which loop 2 is collapsed, yet the remainder of the protein is unformed. Several interesting features emerge on further inspection of this surface. First, the slope of this surface near the free energy minimum is steeper in the direction of N_F, when compared with N_S. This difference in the driving force, in the context of purely downhill folding, may explain the basis for the (relatively) slow formation of the loop 2 contacts. The independence of these progress variables (despite the inclusion in N_F of contacts between the N-terminal part of strand 2 and the C-terminal part of strand 3, as well as contacts between the termini) further emphasizes the lesson learned from the kinetic analysis: that the remainder of the protein can form in the absence of the loop 2 contacts.

The free-energy surfaces at these two temperatures contain only two minima. This observation supports the assertion that the biphasic kinetics derive from decoupled formation of these two pieces of structure: if the biphasic kinetics occurred because of a distinct kinetic trap, this trap would be manifest as an additional minimum on these free-energy surfaces.

As a final experiment, the refolding trajectories used in the kinetic analysis were again culled on the basis of their initial conditions, this time for trajectories in which no native contacts were formed in loop 2. The formation of loop 2 contacts was monitored as a function of time in these trajectories (159 of 500), and it was found to fit to a double-exponential function. The slower of the two rate constants matched that of the previously described slow phase, whereas the faster was a very fast phase (rate constant 1.7 × 10⁻⁴ τ⁻¹) not previously resolved. This very fast phase, which corresponds to the collapse of loop 2 from extended states, was not previously resolved because of its small amplitude, which, in turn, arose from the fact that this phase involves only a limited number of contacts and is present only in a fraction of the individual trajectories.

Examination of several conformations containing only one or two loop 2 contacts in an otherwise fully formed molecule reveals a common theme: a slight shift of the two strands, which prevents formation of some contacts while maintaining others. The free energy of such misregistered conformations is not considerably greater than the native state, which explains the slow relaxation to the native state from these conformations. The slow formation of the native state appears in our model because of the absence of a strong driving force, and possibly because of restrictions on the available degrees of freedom in this environment; additional factors may further support such a phenomenon. Inclusion of favorable energetic terms for nonnative hydrogen bonds would result in stabilization of misregistered conformations. Also, we note that earlier studies have suggested that the kinetic barrier associated with breaking hydrogen bonds in a β-sheet geometry is sizeable (51), offering further support for the conclusion that the correction of misregistered conformations accounts for the observed slow phase.

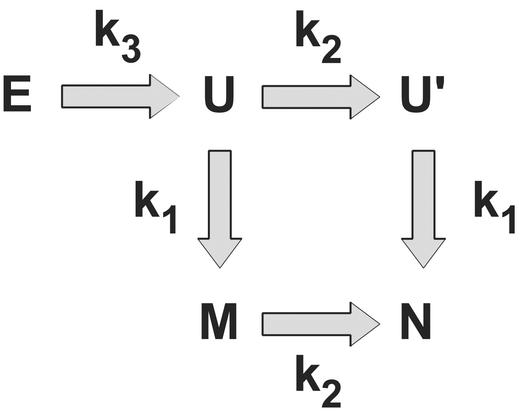
In summary, then, the folding of the FBP WW domain observed from this simple model may be described as follows: The loop 2 portion of the protein is often collapsed in the unfolded state, containing some, but not all, of the native contacts. Collapse of loop 2, in the members of the unfolded ensemble in which no loop 2 contacts are present, is the first step on initiation of refolding, and occurs on a very fast time scale. Folding then proceeds by the independent formation of the correct loop 2 contacts (in the slow phase) and the remainder of the protein (in the fast phase). The fact that loop 2 is collapsed in the unfolded state allows for the formation of contacts flanking it in sequence (e.g., contacts connecting the termini) without loop 2 reaching a fully native-like conformation. Loop 2 is observed to reach native-like conformations slowly (if at all) when the remainder of the protein is unfolded, because the free energy for this transition is uphill (Fig. 3b). This mechanism, complete with rate constants, is described in Fig. 4.

Figure 4.

The kinetic mechanism describing the folding of the FBP WW domain. E represents unfolded states in which loop 2 is extended, U represents the state in which loop 2 is collapsed but not native-like, and the remainder of the protein is unformed. U′ represents the state in which loop 2 is fully native-like, and the remainder of the protein is unformed. M represents the state in which loop 2 is misregistered, and the remainder of the protein is fully native-like. N represents the native state, in which the complete protein is formed. The observed rate constants (k_obs = k_for + k_rev) are k₁ = 3.9 × 10⁻⁵ τ⁻¹, k₂ = 5.8 × 10⁻⁶ τ⁻¹, and k₃ = 1.7 × 10⁻⁴ τ⁻¹, where τ is the fundamental time scale.

Rationalization of Experimental Observations.

Given the structural insight of the observed kinetics afforded by this simple model, it is now possible to understand several experimental observations of the folding of this protein. Starting with the observation that Pin folds with monophasic kinetics (17), we reexamined the positioning of loop 2 in both Pin and FBP. The Pin β-sheet is found to be more curved than the β-sheet in FBP. Formation of the hydrophobic cluster involving the chain termini (located on the convex side of the sheet) requires more stretching of the backbone in Pin than FBP, which in turn reduces the opportunity for misregistered conformations in loop 2.

Experimental observations from FBP also support this interpretation of the origins of the biphasic kinetics. We first note that the slow phase disappears when refolding takes place at elevated temperatures (19). This finding is consistent with the attribution of the slow phase to misregistered loop 2 conformations, because increasing temperature allows incorrect hydrogen bonds to be broken more quickly. This experimental observation further suggests that hydrophobic interactions are not involved in stabilizing these misregistered states because the hydrophobic effect is known to increase with temperature (52).

We then consider the observation that mutation of Trp-30 to either phenylalanine or alanine results in loss of the slow phase (19). This finding is also expected from the structural description above, because Trp-30 acts as the reporter for loop 2 rearrangements. Without Trp-30, the fluorescence signal arises only from the environment of Trp-8, and is therefore insensitive to minor rearrangements in loop 2.

More direct evidence for the involvement of loop 2 in the slow phase derives from the L26A mutant, designed to probe the importance of the Tyr-21–Leu-26 contact. It was suggested that these hydrophobic side chains, which interact in the native state, may approach more closely than their native-state distance in misregistered loop 2 conformations, providing additional stabilization for such states. Surprisingly, the opposite holds: whereas the fast phase is unaffected by this mutation, the slow phase is found to become even slower (19). As well as confirming the importance of loop 2 for the slow phase, but not the fast phase, these results suggest that mutation to alanine at this position actually stabilizes misregistered loop 2 conformations relative to the wild type. This characteristic in turn leads to a putative role for Leu-26 in the wild type: the surface-exposed Tyr-21–Leu-26 contact may be responsible for tying down loop 2 with the correctly formed hairpin. This feature is not needed in Pin, because formation of the correctly oriented hairpin is induced by formation of the hydrophobic cluster.

A survey of 200 WW domains identified by SMART V. 3.1 (53, 54), a tool that identifies and aligns domains from sequence databases, shows that FBP is the only WW domain that contains leucine at this position. Even more compelling, this position is almost always occupied by a charged residue or glycine (the amino acid frequencies at this position are as follows: 70 Lys, 59 Arg, 24 Gly, 21 Gln, 12 Asn, 5 Glu, 3 His, 2 Asp, 2 Ala, 1 Pro, and 1 Leu). Furthermore, residues 23–26, which constitute loop 2, confer specificity for ligand binding in many WW domains (ref. 55; affinity derives from a hydrophobic patch on the sheet). We therefore propose that functional requirements dictate the use of a particular series of amino acids in loop 2 of the FBP WW domain, which encode a preference for a loop geometry other than that required for binding (the latter corresponds to the native state). Evolution has designed against slipping of this hairpin by using Leu-26: the Tyr-21–Leu-26 contact imposes rigidity on this hairpin and locks it into a strand register consistent with the native state.

A recent study assayed the binding affinity of all possible single-point mutants of the hYAP WW domain (56). The mutant with a leucine at the position analogous to 26 in FBP (occupied by glutamine in wild-type hYAP) was found to maintain weak binding to its ligand, a polyproline helix. This finding is consistent with the role we ascribe to this leucine in FBP: binding affinity derives from the interaction of nearby hydrophobic groups (positions 19 and 21) with proline residues in the ligand, whereas many WW domains use polar residues at positions 23–26 to confer specificity for the correct ligand. Mutation to leucine at position 26 does not result in an inability to bind ligand in hYAP (56); rather, we expect this construct to demonstrate less selectivity in its choice of ligands. The fact that leucine is uncommon at this position is not a reflection of negative design by evolution, but, rather, a result of pressure to maximize specificity through the use of polar residues. Leucine at this position in FBP represents an indirect form of specificity, through enforcement of the desired strand registry.

Finally, we note that truncation of the five N-terminal residues of FBP leads to monophasic kinetics consistent with the fast phase (19). This observation is not predicted by the Gō-like model that we described. Nevertheless, it is not inconsistent with the structural model described here: the N terminus is close to loop 2 in the native state, and, hence, may participate in nonnative (stabilizing) interactions with loop 2 in the collapsed state. Alternatively, loop 2 may exist in the misregistered state at equilibrium under native promoting conditions in the truncated form (because of destabilization of the hydrophobic core), which explains the disappearance of the slow kinetic phase.

Conclusions

In summary, we have shown that a simple Gō model may be used to account for experimentally observed differences in folding kinetics among WW domains. We find that the FBP WW domain folds with biphasic kinetics because of independence in the formation of loop 2 contacts with respect to the remainder of the protein. A key surface-exposed hydrophobic contact has been identified (Tyr-21–Leu-26), which is not present in other WW domains. We propose that requirements for ligand specificity have led to a local sequence with a strong propensity for a misregistered loop. This propensity derives in part from functional constraints that do not allow the use of a strong turn-promoting sequence. To combat slippage in this functionally important region, Nature has used two strategies: fast folding in the remainder of the protein, and a surface-exposed hydrophobic pair. The kinetic phase corresponding to the folding of the remainder of the protein was reported to be the fastest known folding protein to date (18), which suggests evolutionary pressure to form the scaffold for loop 2 quickly, which in turn helps promote correct formation of this loop. The surface-exposed hydrophobic pair, meanwhile, provides a reward for correctly registering the strands, reducing slippage.

How, then, may we use this insight in the context of protein design? An incomplete understanding of the mapping from sequence to structure leads to designed sequences that are not fully optimized for the desired structure. These may be considered analogous to sequences in Nature that are not fully optimized for the desired structure, because of functional requirements. Whereas short strong turn-promoting sequences containing glycine may be used to design correctly registered β-hairpins, the design of more complex β-sheets may benefit from additional effort in designing cross-strand solvent-exposed side-chain interactions to ensure correctly registered strands (57, 58). Whereas attempts to include solvent-exposed hydrophobic groups are inherently dangerous because of the risk of stabilizing radically different folds, careful use of this structural motif in late stages of design may offer a method for enforcing the desired strand registry.

Abbreviations

FBP

formin-binding protein

hYAP

human Yes-associated protein