Why the kidney glomerulus does not clog: A gel permeation/diffusion hypothesis of renal function

Abstract

Current interpretations of kidney function in terms of a coarse filter followed by a fine filter have difficulty explaining why the glomerulus does not clog. I propose, as an alternative, a semiquantitative hypothesis that assumes that the size-selective property of the glomerulus is a consequence of the limited fraction of space in the glomerular basement membrane (a concentrated gel) into which macromolecules can permeate. The glomerular epithelial cell slits and slit diaphragms are assumed to impose substantial resistance to liquid flow across the glomerulus without acting as a molecular sieve. Calculations based on gel behavior show that proteins cross the glomerular basement membrane mainly by diffusion rather than by liquid flow, whereas water crosses entirely by flow. Thus, diffusion provides most of the protein, whereas flow provides the diluent. As a result, the single-nephron glomerular filtration rate (GFR) becomes a prime factor in (inversely) determining the concentration of proteins in early proximal tubular fluid. Because the reabsorption of proteins from the tubules is a saturable process, the gel permeation/diffusion hypothesis readily accounts for the albuminuria observed when single-nephron GFR is substantially reduced by severe pathological decreases in slit diaphragm length, such as occur in minimal-change nephrotic syndrome in humans, in animals treated with puromycin aminonucleoside, or in humans or animals with mutations in the gene coding for nephrin. My hypothesis predicts that albuminuria will ensue, even with a normal kidney, if the single-nephron GFR falls below ≈50% of normal.

How kidney glomeruli separate the macromolecular components of blood from small solutes has been debated for over 150 years (1, 2). The predominant current view, proposed in the 1960s by Karnovsky and Ainsworth (3), is that the glomerular basement membrane (GBM in Fig. 1) is a relatively coarse first stage filter and the slit diaphragm (SD in Fig. 1) is a second-stage molecular sieve with most pores being smaller than albumin. This view raises the question: Why doesn't it clog? In the following I provide an answer in the form of a semiquantitative gel permeation/diffusion hypothesis of renal function. Although many of the ideas that I discuss have been considered individually by others, their integration in this manner has not, to my knowledge, been described.

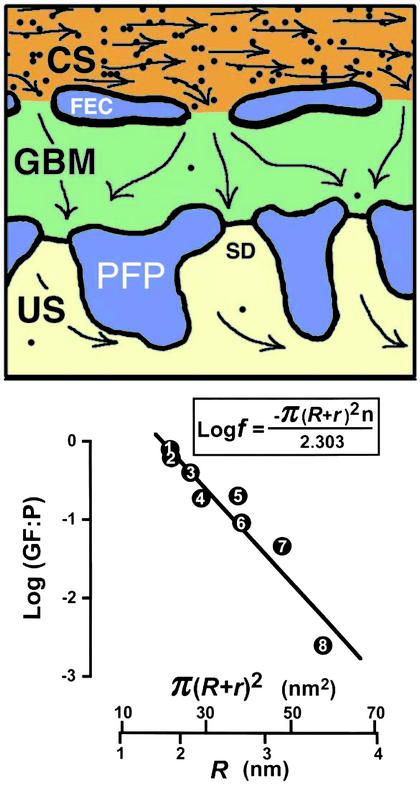
Figure 1.

Gel permeation as a factor in renal glomerular function. (Upper) The distribution of albumin molecules (black dots; number and size are approximately to scale) in an imaginary 7-nm (the diameter of albumin) ultrathin section of a glomerulus as predicted by gel permeation with an illustrative f value (see text) of 0.02. CS, capillary space; FEC, fenestrated endothelial cell; PFP, podocyte foot process; SD, slit diaphragm; US, urinary space. (Lower) The relationship between the Stokes radii, R, of eight proteins and the ratios (GF:P) of their concentrations in glomerular fluid and plasma observed experimentally in the dog (12). The graph, in the form predicted by Ogston's equation (boxed), plots the logarithm to the base 10 of GF:P (equivalent to f) against π(R + r)²⋅r. The radius of the gel fibers, r, was set at 0.75 nm. The plotted straight line accounts for 92% of the observed variance of GF:P (R² = 0.92; P = 0.0002); 1, myoglobin; 2, lysozyme; 3, β-lactoglobulin; 4, ovomucoid; 5, ovalbumin; 6, Bence Jones protein; 7, hemoglobin; and 8, serum albumin.

My permeation/diffusion hypothesis depends on two main assumptions: (i) that the GBM is a gel (4) having size-selective properties determined by permeation (5) and diffusion (6), not by filtration; and (ii) that the slit diaphragm is essential for normal glomerular structure but does not act as a molecular sieve, even though it introduces considerable resistance to hydrodynamic flow (7). No special assumptions are then required to explain either the absence of clogging or the behavior of albumin. I present calculations showing that diffusion plays a greater role in the transport of macromolecules across the GBM gel than does liquid flow. This conclusion leads to the important corollary that changes in the single-nephron glomerular filtration rate (GFR) do not greatly affect the amount of albumin transported across the GBM, but do affect (in inverse proportion to the GFR) the concentration of albumin in the early proximal tubular fluid. Because tubular absorption of albumin is a saturable process (8), albuminuria then becomes an expected outcome of marked reductions in single-nephron GFR induced by means that do not damage the GBM. The albuminuria that occurs under these circumstances does not imply any abnormality in the size-selectivity property of the glomerulus or in tubular function. On the other hand, my hypothesis does not exclude the occurrence of albuminuria with a near-normal GFR, if the basement membrane or the tubules are damaged.

GBM Size Selectivity

As indicated above, the most widely accepted explanation of glomerular size selectivity is that the GBM and the slit diaphragm act together as a filter with properties ascribed, in part, to sieving through pores. The thesis I develop here is that the size selectivity of the glomerulus resides solely in the GBM, which is a relatively concentrated gel. It therefore has the property, common to all gels, that large molecules permeate into a lesser fraction of its aqueous phase than do small molecules (5).

Fig. 1 Upper illustrates how gel permeation and the concept of fractional available volume can be applied to the glomerulus. This figure, drawn approximately to scale, shows the distribution of albumin molecules (black dots) predicted by gel permeation in an imaginary ultrathin section of a glomerulus at a thickness of 7 nm (the diameter of albumin). The plasma is assumed to be in complete equilibrium with the GBM, and for illustrative purposes I have set f, the fraction of gel space available to albumin (see below), at 0.02. Two comments on this illustration are appropriate. First, the diameters of glomerular capillaries are comparable to the diameter of red blood cells so that any local increase in the concentration of albumin (“concentration polarization”) that develops as fluid passes out of the capillaries into the GBM will be continuously obliterated by stirring due to the red cells. Second, the sparsity of albumin molecules in the GBM and their size relative to the dimensions of the slit diaphragm suggest that clogging is unlikely at this point in the glomerulus.

Ogston in 1958 (5) formalized the gel permeation principle in an elegantly simple equation, f = e^−π(R+r)2n, which describes how the fraction, f, of total gel space available to molecules of different radii, R, varies with the concentration, n, and radial thickness, r, of the gel fibers. Ogston's derivation of this equation is easily visualized. Thus, he pointed out that the center of a molecule of radius R cannot get closer to the center of a gel fiber of radius r than the sum of the two radii. Accordingly, in a 1-cm² cross section of a gel having n fibers per cm², the area excluded in this manner is π(R + r)²n. The fractional available area is therefore 1 − π(R + r)²n. This relationship is true for dilute gels but must be corrected for more concentrated gels, because some excluded areas are counted two or more times. The corrected equation is

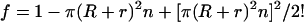1

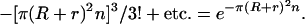Ogston's equation for the fractional available volume in gels has survived many experimental tests of its validity (9, 10) and has been rederived in other ways and has been somewhat modified (10, 11). It still remains the simplest equation that predicts reasonably well the relationship between the sizes of macromolecules and the space available to them in gels of differing concentration and composition.

Fig. 1 Lower explores the relationship between the Stokes radii, R, of eight proteins and the ratios (GF:P), of their concentrations in postglomerular fluid and plasma observed experimentally in the dog [compiled by Renkin and Gilmore (12) in their table 2]. The graph, in the form predicted by Ogston's equation (ref. 5; boxed in Fig. 1 Lower), plots the logarithm of GF:P (equivalent to the logarithm of f) against π(R + r)². The radius of the gel fibers, r, was set at 0.75 nm, but the fit is insensitive to this number. Least-squares regression analysis demonstrates that the plotted straight line accounts for 92% of the observed variance of GF:P (R² = 0.92; P = 0.0002) without the need for special assumptions regarding the behavior of albumin. These data are, therefore, generally consistent with the thesis that permeation of molecules into the GBM plays a very important role in the size-selectivity property of the glomerulus. This thesis does not exclude the possibility that charge, in addition to size, influences the selectivity of the GBM by further decreasing the fraction of gel space available, although current evidence indicates that the effects of charge are less than previously suggested (13).

Macromolecules Cross the GBM by Diffusion and by Liquid Flow

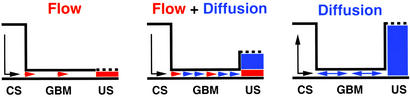
The fitted line in Fig. 1 is not, however, in complete agreement with Ogston's equation (5) because it extrapolates to GF:P = 1 before π(R + r)² = 0. This deviation suggests that other factors in addition to fractional gel exclusion affect the transport of macromolecules across the GBM. Accordingly, I set out three situations in Fig. 2 regarding this transport. Left illustrates the steady state expected if, as usually assumed to be the case, transport by liquid flow, J_F, (alternatively termed hydrodynamic flow or convection) is the only factor of significance, and transport by diffusion, J_D, can be neglected. Under these conditions, fluid flowing out of the GBM and into the urinary space has the same composition as it has in the membrane, namely P⋅f, where P is the plasma concentration of the molecule of interest and f is, as defined above, the fractional gel space available to the molecule.

Figure 2.

Steady-state concentrations and transport of albumin across the glomerulus. (Left) Transport by liquid flow only. (Right) Transport by diffusion only. (Center) Transport by flow and diffusion. The vertical dimension represents concentrations, and the arrows indicate transport. Effects of diffusion are blue and effects of flow are red. CS, capillary space; US, urinary space.

Fig. 2 Right illustrates the equilibrium situation if no liquid flow occurs. Under these circumstances the concentrations of the macromolecular solute in the capillary space and in the urinary space will equalize, even though the concentration of the macromolecule within the GBM can never exceed P⋅f. A unique set of experiments performed in 1976 by Ryan and Karnovsky (14) are readily understood in these terms. These investigators observed that when renal blood flow was normal, plasma albumin could not be detected in the urinary space. Very large amounts of albumin could, however, be detected in the urinary space if the renal artery and vein were temporarily ligated. Yet, when the blood flow was restored, the distribution of albumin promptly returned to normal. The authors interpreted their observations in terms of an increase in the porosity of the GBM and changes in the normal ultrafiltration flux. My interpretation is that in the absence of flow, the difference in the concentration of albumin on the two sides of the GBM rapidly disappears because diffusion across the GBM is no longer accompanied by the wash out of Bowman's space that normally occurs as a result of the flow of liquid.

This interpretation leads to the conclusion that in a normally functioning kidney the amount of albumin and of other macromolecules in postglomerular fluid is determined by the joint occurrence of transport across the GBM by flow and by diffusion, as illustrated in Fig. 2 Center and as discussed in the next section.

Transport of Albumin Across the GBM Is Mainly by Diffusion

Two factors are important in considering the transport of albumin and other macromolecules across the GBM. First, although the GBM is relatively concentrated (≈10% solid content), it is very thin (≈0.3 μm in humans). Second, diffusion through gels (6) is very much less affected by molecular size than is the fractional available volume (5). When these two factors are entered into suitable equations (summarized by Sten-Knudsen in 1978; ref. 15, and more recently by Deen et al. in 2001; ref.7) the conclusion appears inescapable that the transport of albumin across the GBM is mainly by diffusion rather than by liquid flow, as the following calculations illustrate.

The transport of albumin across the normal GBM by diffusion, J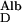, in the absence of flow, and when the concentration of albumin in the postglomerular fluid is small in comparison to its concentration in plasma, is given by

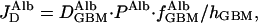2

where D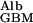 is the diffusion coefficient of albumin in the GBM, P^Alb is the concentration of albumin in plasma, f 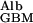is the fraction of GBM space available to albumin, and h_GBM is the thickness of the GBM. This relationship is intuitively reasonable because diffusional transport is obviously greater for molecules with larger diffusion coefficients, is driven by and is proportional to their upstream concentration, but is less when the fractional space available to them in the gel is small, and decreases as the membrane gets thicker. These four factors appear simply in Eq. 2.

The transport of albumin across the normal GBM by liquid flow, J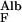, in the absence of diffusion, is given by

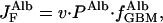3

where v is the velocity of the fluid crossing the GBM in cm/sec. This equation is equivalent to the statement made above, in relation to the Fig. 2 Left, that fluid flowing out of the GBM in the absence of diffusion has the same composition as it has in the GBM itself.

It is important to note that the transport of albumin mediated by diffusion and by flow both have f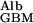, the fraction of GBM space available to albumin, as a multiplier (7). Consequently, as illustrated in Fig. 1, the transport of albumin (and of other macromolecules) across the GBM by any means is dominated by this fraction, which can be very small.

The relative contributions to the transport of albumin across the GBM because of diffusion and to flow can be determined by combining Eqs. 2 and 3 above to give

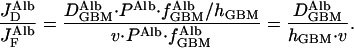4

I cannot find any published experimental estimates of D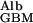, the diffusion coefficient of albumin in the GBM, although Edwards et al. (16) have measured the permeability, f_GBM⋅D_GBM/D_Water (their Φ⋅K_d), of bare glomerular capillaries using a Ficoll (Pharmacia) slightly larger than albumin. The two components of this permeability, f_GBM and D_GBM/D_Water, can be separated approximately by combining Ogston's equation for gel exclusion (Eq. 1) with his later equation for gel diffusion (6), which is

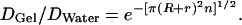5

Applying Eqs. 1 and 5 to the experimental data of Edwards et al. (16) gives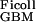 D/D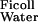 = 0.16 and f 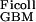= 0.038, corresponding to their experimental estimate of Φ⋅K_d = 0.0063. However, there are indications (10) that Ogston's diffusion equation does not always accurately predict D_Gel/D_Water. Some confirmation of this estimate is, therefore, desirable, and can be obtained from studies of D 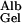in gels of known composition. Of the synthetic gels for which comparative data are available, polyacrylamide appears to offer the greatest hindrance to the diffusion of proteins (10). The ratio of 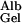D to D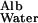 measured by Tong and Anderson (17) in an 8% polyacrylamide gel is ≈0.1 with an extrapolated value of 0.09 in a 10% gel. Because the solid content of the GBM is generally estimated to be of the order of 10%, I propose to use 0.1 as a conservatively low estimate of 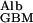D/D.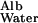

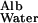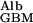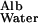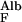From table 8 of Renkin and Gilmore (12), v in humans is ≈3 × 10⁻⁴ cm/sec and h_GBM is ≈3 × 10⁻⁵ cm; D is ≈6 × 10⁻⁷ cm²/sec and D/D is ≈0.1. Therefore J/J = D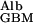/h_GBM⋅v = 6 × 10⁻⁷ × 0.1/3 × 10⁻⁵ × 3 × 10⁻⁴ = ≈7, which means that the transport of albumin across the GBM by diffusion is several times greater than its transport by flow.

The significance of this ratio becomes apparent when we consider what happens when GFR changes. Suppose that the single-nephron GFR, for physiological or pathological reasons, decreases by 50% without changing the composition or thickness of the GBM. This decrease in liquid flow will change the transport of albumin by flow from 1/8 to 1/16 of the normal total. But the transport of albumin by diffusion will remain unchanged at 7/8 of the normal total. Thus, the total transport of albumin will decrease slightly, to 15/16 normal, but its concentration in the postglomerular fluid will nearly double (15/16 ÷ 0.5 = 1.9). I show below that the tubular reabsorption of albumin becomes saturated as its concentration in the proximal tubule increases. This result means that, although a large decrease in GFR causes a slight decrease in the total amount of albumin crossing the glomerulus, it leads to a large increase in the fraction of the transglomerular albumin that reaches the urine.

The most important conclusion from this part of my analysis is that the concentration of albumin in the postglomerular fluid varies inversely with the single-nephron GFR because diffusion provides most of the protein, whereas flow provides the diluent.

Geometric Considerations

The calculations I have made to this point have been based on the tacit assumptions that the GBM is a gel of uniform composition and that all of its surface is available for diffusion, flow, or both. The first of these assumptions is certainly an oversimplification, because most transmission electron micrographs show a less dense layer (the lamina rara interna) between the capillary endothelial cells and the more dense main body of the GBM (the lamina densa), with a second less dense layer (the lamina rara externa) before the epithelial cells. The second assumption is also somewhat of an oversimplification because the endothelial cells block ≈80% of the capillary surface and the foot processes of the podocytes block ≈90% of the epithelial surface (7). However, this second complicating factor is likely to be partly abrogated by the first, because the two less dense layers facilitate diffusion and flow radially out of the fenestral openings and laterally back into the epithelial slits. The transport of albumin across the glomerulus by liquid flow is not affected by either of these complications, because it is determined by the volume of liquid traversing the glomerulus (the GFR) multiplied by the concentration of albumin in this liquid (P^Alb⋅f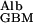); channeling or waisting of the flow does not affect this number. The transport of albumin across the GBM by diffusion could be affected. However, even under the very unlikely situation that the effective diffusional area of the GBM is reduced to 15% (the mean of the endothelial and epithelial openings), a 50% decrease in single-nephron GFR would still increase the concentration of albumin in postglomerular fluid to 1.5× normal.

Transport of Water Across the Glomerulus

The transport of water across the glomerulus is clearly because liquid flow is induced by hydraulic pressure; it cannot be by diffusion because the concentration of water in plasma is less than in postglomerular fluid as a consequence of the very much greater concentration of proteins in plasma. Approximately half of glomerular resistance to liquid flow is because of the GBM and half because of endothelial and epithelial cells, which, as indicated above, block roughly 80% and 90% of the total glomerular surface, respectively. The epithelial slits with their slit diaphragms impose more hydraulic resistance than the endothelial fenestrae (7, 12). Consequently, GFR, a measure of total liquid flow, is markedly affected by changes in the total length of the epithelial slits (18).

Tubular Reabsorption of Proteins Is Saturable

Determination of the concentration of proteins in the kidney glomerular and proximal tubular fluids has challenged investigators for many years. Indirect estimates are possible by measuring the renal clearance of the protein of interest and correcting for tubular reabsorption. The GF:P data used for the graph in Fig. 1 above were compiled by Renkin and Gilmore (12) from clearance measurements corrected in this manner.

Direct estimates of glomerular fluid concentrations of proteins by micropuncture assays face additional problems, which Tojo and Endou (19) have addressed systematically in anesthetized rats. Their estimate of the glomerular fluid concentration of albumin is 23 μg/ml, equivalent to a GF:P of 0.00062, the lowest well-documented value for this ratio that I can find. They also showed that the reabsorption of albumin is distributed almost uniformly along the proximal convoluted tubule, with only 3 ± 1% of the tubular albumin reaching the urine. If these very low values apply to normal humans, with a GFR of 120 ml/min and a plasma albumin concentration of 0.04 g/ml, the total transglomerular albumin passage would be ≈4 g/day (0.00062 × 0.04 × 120 × 60 × 24). Urinary excretion of albumin would be ≈120 mg/day (4,000 × 0.03), a value reasonably close to the normal daily excretion of albumin, which is generally considered to be <30 mg/day.

Various pathways for the tubular reabsorption of albumin and other proteins have been recognized and partially characterized (reviewed by Russo et al.; ref. 13). Park and Maack (8), for example, have measured the in vitro transport of albumin across isolated perfused proximal convoluted tubules of the rabbit. They describe two kinetically distinct systems: a low-capacity high-affinity system and a high-capacity low-affinity system. The former half-saturates at 31 μg/ml, close to the concentration (23 μg/ml) found by Tojo and Endou in rats (19), and has a maximum rate of transport of 0.064 ng per min per mm; the latter half-saturates at an albumin concentration of 1,200 μg/ml and has a maximum rate of transport of 3.7 ng of albumin per min per mm of tubule. Although Park and Maack (8) designated their high-affinity system as of low capacity, a comparable system in humans with the same characteristics (taking the number of nephrons in humans as 2 × 10⁶ and the average length of a human proximal tubule as 14 mm) could recover ≈2.6 g of albumin per day: a capacity comparable to the ≈4 g/day calculated above.

More than 90% of albumin-derived material recovered in the extratubular bathing solution in Park and Maack's (8) experiments was not precipitable with trichloracetic acid when the tubular albumin concentration was 30 μg/ml, implying that the high-affinity system is largely degradative. However, a substantial body of evidence has recently been accumulated demonstrating that the kidney can also retrieve albumin from tubular fluid and return it to the circulation without degradation (see for example Eppel et al.; ref. 20). In what follows, I assume, therefore, that albumin can be removed from the proximal tubules by two systems: one that returns it undegraded to the circulation, and the other that degrades it. I also assume, for reasons that I justify below, that the nondegradative pathway saturates at a lower proximal tubule concentration of albumin than the degradative pathway.

A Computer Simulation of Nephron Function

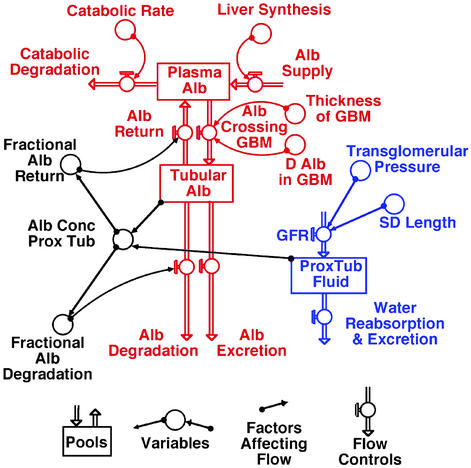
An informative way of testing the logical consistency of a hypothesis is to construct a computer simulation that incorporates its assumptions and then to compare the ability of the simulation to replicate a suitable set of in vivo observations. Fig. 3 outlines the elements of such a simulation of my gel permeation/diffusion hypothesis of renal function implemented with the help of a generally applicable set of programs for investigating the behavior of complex interacting systems (stella; Hanover High Performance Systems, Hanover, NH). Details are appended in Figs. 5 and 6, which are published as supporting information on the PNAS web site, www.pnas.org.

Figure 3.

The simplest representation of glomerular and tubular function that was informative in computer simulations with STELLA. Red and blue emphasize the transport of albumin (Alb) and water, respectively, and black emphasizes factors controlling the tubular reabsorption of albumin and its eventual fate.

In making this simulation, I assume that the amount of albumin in the plasma pool is determined by the balance between its daily synthesis in the liver, its catabolism by extrarenal tissues, and its removal and recovery by the kidney. There are three known fates for albumin traversing the GBM: a fraction of the total albumin entering the proximal tubule can be reabsorbed and returned undegraded to the plasma; a fraction can be reabsorbed in a degradative manner; and a fraction can be excreted undegraded in the urine. The concentration of albumin in the early proximal tubule is determined by (the total amount of albumin entering the proximal tubule)/(the amount of water entering the proximal tubule), with the amount of water being proportional to the GFR, which Bohman et al. (18) show varies with the total slit-diaphragm length. Finally, I assume that the fractional reabsorption of albumin decreases in a roughly sigmoidal fashion as the concentration of albumin in the proximal tubule increases and saturates the recovery systems, with the fractional recovery ranging from ≈1 at near normal tubular concentrations to <0.1 when tubular concentrations increase 6-fold. The simulation is not sensitive to the detailed shape of the fractional recovery curves, but it replicates the in vivo data considered below only if the nondegradative recovery of albumin saturates at lower concentrations than the degradative recovery.

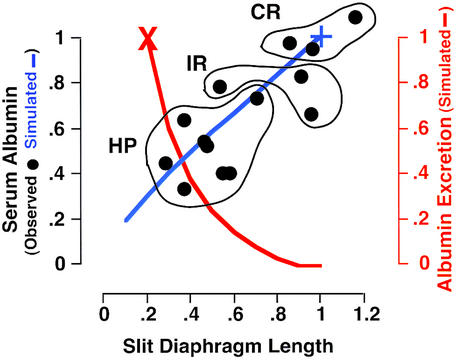
Minimal-change nephrotic syndrome provides a suitable test of the simulation and its assumptions. This condition is encountered quite frequently in children and is characterized by edema, heavy proteinuria, and hypoalbuminemia. Bohman et al. (18) have studied 14 children with clinical histories of the condition but in various degrees of remission at the time of study. Determinations for each patient were made of the GFR (inulin clearance), of effective renal plasma flow (para-aminohippuric acid clearance), of serum albumin concentrations, and of renal pathology (by electron microscopy of biopsied material). Mean foot process widths and the length density of slit diaphragms were calculated from measurements of the distance between and the number of glomerular epithelial cell slits per μm² of micrograph.

In Fig. 4 the individual points show the serum albumin concentrations in each of the 14 patients studied by Bohman et al. (18) plotted against the relative lengths of their slit diaphragms. The data points for three patients in complete remission (normal serum albumin and no proteinuria) are outlined and labeled CR, the data for three patients in incomplete remission (decreased serum albumin but no proteinuria) are labeled IR, and the data for eight patients with heavy proteinuria are labeled HP. The blue line shows the simulated serum albumin concentrations when the slit-diaphragm length changes from 1 to 0.1× normal, and the red line shows the simulated urinary excretion of albumin. Clearly, the simulated serum albumin concentration and albumin excretion are in good agreement with the observations on the patients. I conclude from this agreement that the assumptions made in the simulation regarding the effects of changes in GFR on the serum albumin concentration, the recovery of protein from proximal tubular fluid and the appearance of albuminuria, are sufficient to account for the main symptoms of minimal-change nephrotic syndrome without the need to assume any changes in the size-selectivity property of the glomerulus

Figure 4.

Effects of slit-diaphragm length on serum albumin concentration and urinary albumin excretion in 14 patients with minimal-change nephrotic syndrome. The data points are from Bohman et al. (18). CR, patients in complete remission with normal serum albumin and no proteinuria; IR, patients in incomplete remission with low serum albumin but no proteinuria; HP, patients with low serum albumin and heavy proteinuria. The blue and red lines show the simulated serum albumin concentrations and the simulated albumin excretion, respectively. Serum albumin and slit-diaphragm lengths are relative to the means of the three patients in complete remission (+). The albumin excretion is relative to that predicted by the simulation when the slit-diaphragm length is 20% normal (X).

Other Conditions and Predictions

Gel permeation and diffusion appear to have relevance in a variety of other pathological and physiological conditions that have been puzzling in the past. Thus, a decrease in slit-diaphragm length has been described in rats treated with puromycin aminonucleoside (21), most likely as a result of a substantial drug-induced decrease in the production of nephrin mRNA (22). The observed proteinuria in these animals, like that in the children with minimal-change nephrotic syndrome, is readily interpreted in terms of the gel permeation/diffusion hypothesis as a consequence of a marked decrease in GFR that results from the increase in glomerular hydraulic resistance caused by the decrease in slit-diaphragm length. No changes need be assumed in the size selectivity of the glomerulus.

Massive albuminuria and neonatal death have been described in mice completely lacking nephrin (23). Foot-process effacement is also very extensive in these animals and they have no normal slit diaphragms. I interpret their nephrotic phenotype likewise to be a consequence of a gross decrease in GFR because of the abnormalities in their epithelial slits. Again no changes in the normal size selectivity of the glomerulus need be assumed.

Other situations suggesting that reversible albuminuria is a direct consequence of a marked decrease in GFR include maximally strenuous exercise (24, 25) and severe congestive heart failure (26, 27). In both these situations, the albuminuria disappears promptly when the primary cause is removed. No renal abnormalities need be postulated.

These several examples highlight the simplest testable prediction of my gel permeation/diffusion interpretation of renal function: that albuminuria will rapidly develop in normal animals when the single-nephron GFR is reduced, by means that do not damage the GBM, to less than ≈50% of normal and that the albuminuria will promptly disappear when the GFR is returned to normal.

Conclusion

In the foregoing text I have reviewed experimental data relevant to the behavior of the kidney with respect to its ability to retain proteins in the circulation. I have developed a testable semiquantitative gel permeation/diffusion hypothesis that accounts for this ability in terms of a limited fraction of the GBM space into which macromolecules can permeate. I have also calculated that the transport of macromolecules across the membrane is predominantly by diffusion rather than by flow. Molecular sieving of macromolecules by the slit diaphragm is not a part of this hypothesis, but the diaphragm is assumed to impose substantial resistance to the flow of liquid (mainly water and small solutes) across the glomerulus. As a result of these relationships I show that the single-nephron GFR is a prime factor in (inversely) determining the concentration in the proximal tubules of macromolecules such as albumin. Because, under normal circumstances, the tubular concentration of albumin is below the level that saturates its retrieval systems, very little albumin reaches the urine. However, under various physiological and pathological circumstances in which single-nephron GFR is substantially less than normal, the tubular concentration of albumin can increase sufficiently to exceed this saturation level. The albuminuria which then occurs is reversible and does not imply any abnormalities in either the GBM or in the proximal tubules.

In closing I emphasize that I do not suggest that the gel permeation/diffusion hypothesis explains all situations in which proteinuria occurs, nor do I exclude the occurrence of proteinuria in association with a near-normal GFR when there is general or focal damage to the GBM or to the tubular protein reabsorption systems. I do suggest, however, that a reappraisal of current interpretations of kidney function in health and disease is worthwhile, bearing in mind the relationships that I have discussed.

Abbreviations

GBM

glomerular basement membrane

GFR

glomerular filtration rate

GF:P

ratio of protein concentrations in glomerular fluid and plasma