Cell and tumor classification using gene expression data: Construction of forests

Abstract

The advent of gene chips has led to a promising technology for cell, tumor, and cancer classification. We exploit and expand the methodology of recursive partitioning trees for tumor and cell classification from microarray gene expression data. To improve classification and prediction accuracy, we introduce a deterministic procedure to form forests of classification trees and compare their performance with extant alternatives. When two published and commonly used data sets are used, we find that the deterministic forests perform similarly to the random forests in terms of the error rate obtained from the leave-one-out procedure, and all of the forests are far better than the single trees. In addition, we provide graphical presentations to facilitate interpretation of complex forests and compare our findings with the current biological literature. In addition to numerical improvement, the main advantage of deterministic forests is reproducibility and scientific interpretability of all steps in tree construction.

Microarray chips represent a promising technology for tumor and cancer-type classification. Classical approaches to this problem do not discriminate among tumors with similar histopathologic features, despite the fact that they can vary with clinical course and in response to treatment. Classification and diagnosis based on gene expression profiles may provide more information than standard morphologies and, thereby, identify pathologically different tumor types. Many investigators have exploited a variety of analytical methods (1–5) to derive classification criteria for tumor- and cancer-type by using microarray data. In this regard, we introduced a methodology (6) based on classification trees and demonstrated that they were significantly more accurate for discriminating among distinct colon cancer tissues than other statistical approaches previously used.

The analyses in refs. 6 and 7 indicated that several equivalent (from the vantage point of minimizing classification error) trees were compatible with the same microarray data. This feature led to identification of several sets of candidate genes as the primary contributors to colon and breast cancer classification. Multiple equivalent trees are generic to classification problems where the number of variables (genes in the context of microarrays, frequency bands in the context of NMR spectroscopy) is substantially larger than the number of samples. However, the phenomenon of multiple equivalent trees raises the question of whether there are strategies for identifying a forest of such trees and where the forest could provide more precise and biologically interpretable classification rules than any individual tree. The purpose of this paper is to describe a new forest construction strategy and illustrate its use for cancer classification based on gene expression levels in microarrays. We use two published data sets for this purpose. Our methodology differs in both philosophy and algorithmic implementation from the production of random forests (12) in the machine learning literature. The essential limitation of random forest algorithms for our purposes is that one loses scientific interpretability in the structure of the trees as the result of random selections of variables in the original tree constructions.

Methods

Data Structure and the Classification Problem.

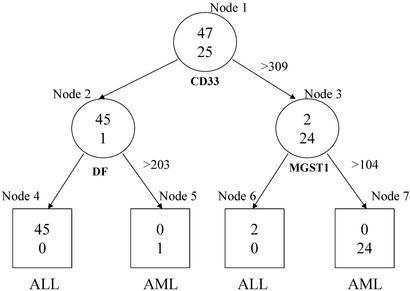
Let {(x_i, y_i)}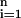, be a collection of n observations, where x_i is a vector consisting of the expression levels of m genes for the i-th observation (or sample), and y_i is the label or class (e.g., tumor type) of the ith observation, i = 1, … , n. Linear discriminant analysis, support vector machines and neural networks are common approaches for developing classification rules based on this general data structure. However, they do not have a built-in feature (variable) selection procedure. This is particularly important for extracting genes and associated expression levels that will be essential for classification rules from a large number of candidate genes (e.g., several thousand genes). As discussed in detail in refs. 6 and 7, tree-based methods become more desirable than their alternatives because they simultaneously integrate feature selection and classification, and produce simple and precise classification rules. This will become evident in the context of the specific examples discussed below. Another important feature of the tree-based methods is that classification rules can be represented by a simple string of Boolean statements, read directly from a tree. For example, in Fig. 1, a cell is classified as an acute myeloid leukemia cell when the expression levels for three genes, CD33, DF, and MGST1, satisfy ((CD33 ≤ 309) ∩ (DF > 203) ∪ (CD33 > 309) ∩ (MGST1 > 104)).

Figure 1.

A top tree produced by rtree program for the leukemia two-level data set. The circles represent internal nodes that are split further. The boxes are terminal nodes without a split. Inside each node are the counts of ALL (upper) and AML (lower) cells. Under each internal node is the gene whose expression is used to split the node with the splitting value on its right. Under each terminal node is the class label that dominates the classes of the cells in that node.

Growing a Single Tree.

Recursive partitioning (8, 9) is the basis for tree construction. It is a technique that builds a classification rule to predict class membership based on the feature information, and does so by extracting homogeneous strata from the sample. For example, in Fig. 1, the entire sample (the circle on the top, also called the root node) of 72 cells is split into two subgroups, which are called daughter nodes. The choice of the selected predictor (a gene) and its corresponding cutoff value (an expression level) are designed to provide maximum discrimination between a pair of tissue types. The quality of discrimination, referred to as node impurity, can be measured by the Gini index, defined as ∑_i≠j p_ip_j where p_i is the probability of a sample within the node have tissue (e.g., tumor) label i. The goodness of split is measured by a weighted sum of the within-node impurities. Another common measure of impurity is the entropy, ∑_i p_ilog(p_i). More formally, to split the root node by expression levels of gene k, namely, x_1k, … , x_nk, we ask for each value, c, between the minimum and maximum of these expression levels, whether subject i should be in the left or right daughter node according to whether x_ik ≤ c or x_ik > c, respectively. We select the cut-off value c_k so that the resulting goodness of split is optimized. We repeat this process for every gene and select a best candidate, based on minimum node impurity, among the set of m candidates as the final choice to split the root node.

Once the root node is split into two daughters, the daughter nodes, themselves, can be further split by repeating the above procedure. This partitioning process continues recursively. In general, one has to be concerned with the issue as to when the process should be terminated to avoid overfitting. Stopping rules or pruning procedures can be used to eliminate redundant nodes (8, 10, 11). This is less of an issue in microarray applications, because there tend to be an ample number of trees that have two, or at most three layers, with high resubstitution classification precision. Furthermore, trees where all terminal nodes have only one nonzero category (i.e., perfect classification) are the rule, rather than the exception. In the present context, we focus on trees that have at most three layers.

Deterministic Forest.

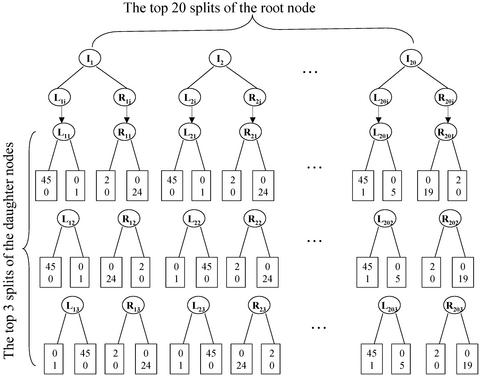
An important consequence of the fact that we have a small number of samples and a large number of gene expressions is that there are typically many splits that are indistinguishable or close by either the Gini- or entropy-based goodness-of-split criterion. This frequently leaves us with numerous trees all of which perfectly (or nearly) classify the initial sample. This population of trees is the basis for forming a forest; but it is, at this stage, too complex to be useful. An alternative preliminary screening of trees, which we adopt in the present study, consists of selecting a prespecified number, say 20, of the top splits of the root node and a prespecified number, say 3, of the top splits of the two daughter nodes of the root node. This use of top nodes gives rise to a total of 180 possible (20 by 3 by 3) trees, for example, as displayed in Fig. 2. Of particular interest among these 180 trees are those with perfect or near perfect classification precision. When a left or right daughter node of the root node is pure, further splits are not warranted. Thus, we usually do not have all of the 180 trees. To be consistent, we collect a fixed number of 100 available trees to form a deterministic forest. In addition, as revealed by Fig. 2, many splits of the daughter nodes lead to pure offspring nodes and hence are mathematically equivalent. For example, there are 424 splits of the left daughter node that lead to pure nodes. Instead of arbitrarily choosing three splits, we identify the underlying genes of the equivalent splits and reexamine the ranks of those genes when they produced the splits for the root node. For example, among the 424 splits of left daughter nodes, the splits based on following three genes, DF, CSTA, and SPTAN1, are ranked at top three when these three genes are used to split the root node. Thus, the bottom-left column of three splits are based on DF, CSTA, and SPTAN1.

Figure 2.

A schematic deterministic forest for the 2-class leukemia data. I₁, … , I₂₀ are the top 20 splits of the root node. For example, I₁ = (CD33 > 309). Each of these splits leads to a left (L) and a right (R) daughter node. The daughter nodes have their own splits (L_ij and R_ij, j = 1,2,3, i = 1, … , 20) and offspring. Three top splits are drawn underneath them. For example, L₁₁ = (DF > 203) and R₁₁ = (MGST1 > 104). Depending on the combinations of the splits of the root node (I's) and the daughter nodes (L's and R's), we end up with trees with different terminal nodes (rectangulars). Inside the terminal nodes are the counts of ALL (upper) and AML (lower) cells. For example, the combination of {I₁, L₁₁, R₁₁} corresponds to the top tree as depicted in Fig. 1.

Error Estimation.

To assess a tree or forest, we leave one sample out as a test sample and reconstruct a tree or forest using the same procedure as the one used to construct the tree or forest of interest, based on the remaining n − 1 cases. Then we classify the omitted sample based on the new tree or forest. Repeating this process n times, i.e., omitting each sample once, we count up the number of errors made in classifying the omitted sample with the modified tree or forest. We then tabulate the proportion of errors made across all n samples, (1/n)∑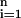 ɛ_i, where ɛ_i is the number of errors made in classifying the ith omitted sample.

The above leave-one-out cross validation procedure is a particular form of the jackknife. Because of the small number of samples in most current microarray experiments, this jackknifing procedure is preferable to the routine cross validation where a greater portion (usually ranging from one tenth to one half) of the full samples is left out as test samples. In the present application, the learning sample would become much smaller and the classification criteria would have far greater uncertainty.

In contrast to the above strategy, the random forest constructions from the machine learning literature are based on a perturb-and-combine strategy (sometimes referred to as arcing, ref. 12). Two of these methods are closely related to our approach. One is bagging (boostrapping and aggregating) that generates a random forest of trees by repeatedly drawing bootstrap samples from the original sample and by constructing trees for the bootstrap samples. The other strategy is random selection. Instead of choosing the best overall split of a node as described above, a random split among a prespecified number of top splits is chosen. Repeating this process also results in a random forest. The final classification is then based on the majority vote of all trees in the forest. Our data analysis presented below also confirms that such random forests improve the predication of class membership. Our key concern with regard to random forests lies in their lack of exact reproducibility. This is consequential when identification of a list of key genes useful for tumor classification is a fundamental objective of an investigation.

Data.

To compare the performance of our forest constructions with random forests, individual trees, and other commonly used methods of classification and discrimination, we use two published and frequently used data sets.

The first data set (1) is on leukemia and can be downloaded at http://www-genome.wi.mit.edu/cancer. It includes 25 mRNA samples with acute myeloid leukemia (AML), 38 samples with B cell acute lymphoblastic leukemia, and 9 samples with T cell acute lymphoblastic leukemia. Expression profiles were assessed for 7,129 genes for each sample. The question is whether the microarray data are useful in classifying the three types (or two types, AML and ALL) of leukemia.

The lymphoma data set by Alizadeh et al. (13) is our second example. Data are available on the three most prevalent adult lymphoma malignancies: B cell chronic lymphocytic leukemia (B-CLL), follicular lymphoma (FL), and diffuse large B cell lymphoma (DLBCL). There are a total of 84 samples (29 B-CLL, 9 FL, and 46 DLBCL) with expressions from 4,026 genes. We analyzed the data with 3,198 genes by removing the genes with at least eight missing values among all 84 samples. This lymphoma data set is available at http://llmpp.nih.gov/lymphoma.

Results

Comparisons.

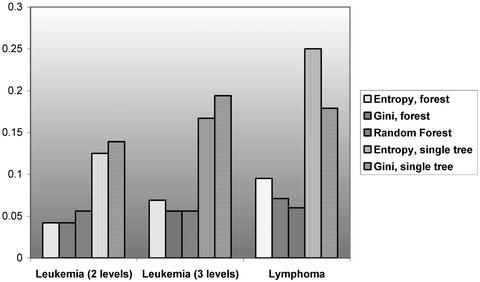
We analyzed the leukemia data set by treating the two “ALL” classes both together and separately. Thus, we have three operational data sets. Fig. 3 compares the misclassification rates among different classification methods. For each data set and each forest or tree, we used the leave-one-out cross validation to estimate the error rate. The sizes of both random and deterministic forests are 100.

Figure 3.

Error rate of classification trees and forests based on leave-one-out cross validation.

As displayed in Fig. 3, both deterministic and random forests have much reduced error rates (between half and one third) as opposed to a single tree. For the leukemia two-level data set, deterministic trees have a slight advantage over the random forests. For the leukemia three-level data set, the Gini-based deterministic forest has a similar performance with the random forest. For the lymphoma data set, the random forest is slightly better than the deterministic forests. Overall, the performances of the random and deterministic forests are similar and impressive for the three data sets.

Identifying Key Genes in the Deterministic Forest.

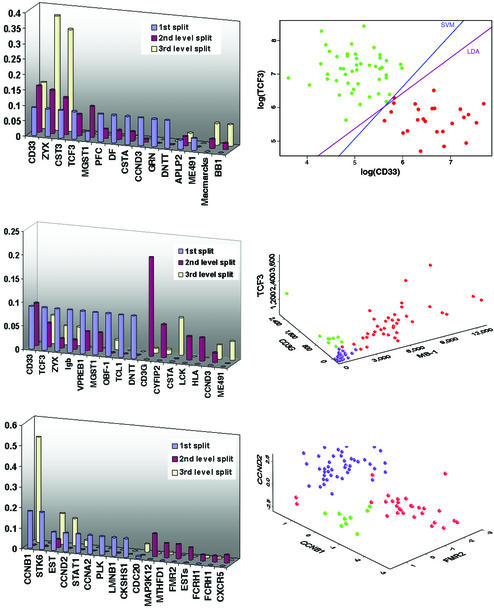
Reducing the misclassification rate is one objective, but our second objective is to understand the genes that participate in the forest formation. To this end, we assess the number of different genes appearing in the deterministic trees using the entropy and Gini index as impurities, and the frequencies of the genes used. This scrutiny should reveal the importance of the genes in classifying tumor tissues in the respective data sets. For the leukemia data set, when the two “ALL” were merged, 27 different genes appeared in the forest of 100 trees. When those two classes are treated distinctly, 35 different genes appeared in the forest of 100 trees. For the lymphoma data set, 49 different genes appeared in the forest of 100 trees. Fig. 4 Left presents the frequencies of the genes that are used relatively frequently among the three data sets. A high frequency is indicative of the importance of a gene in the respective classification.

Figure 4.

(Top) The analysis of leukemia two-level data set. (Left) Frequencies of genes used in the deterministic forest are presented. The 1st split, 2nd level split, and 3rd level split refer to the split of the root node, the split of the daughter nodes of the root node, and the split of the grand-daughter nodes of the root node, respectively. Genes used with low frequencies (<10%) are not shown. (Right) A 2D representation of a tree based on two “very important” genes. Two colors show a separation of ALL (green) and AML (red). In fact, we performed a post hoc linear discriminant analysis (LDA) and also used support vector machine (SVM) to classify leukemia cells by using this frequently occurring pair of genes. (Middle) The analysis of leukemia three-level data set. (Right) A 3D representation of a tree based on three “very important” genes. Three colors show a separation of B cell acute lymphoblastic leukemia (red), T cell acute lymphoblastic leukemia (green), and AML (purple). (Bottom) The analysis of lymphoma data set. (Right) A 3D representation of a tree based on three “very important” genes. Three colors show a separation of B cell chronic lymphocytic leukemia (red), FL (green), and diffuse large B cell lymphoma (purple).

Fig. 4 Right displays the expression levels of the “most important” genes in the designated data sets. Such frequency plots also provide a useful basis for variable selection. Once the important genes are identified, we can use the pairs or triples of genes to construct trees or forests and to form decision boundaries by using linear or quadratic discriminant analysis or support vector machines. Fig. 4 Right is based on the frequently occurring genes. For example, Fig. 4 Top Right illustrates how linear discriminant analysis or support vector machine can also be applied to classify tumor and cancer type by using the identified frequently occurring genes.

Discussion

To understand the scientific and clinical relevance of our results as displayed in Fig. 4, we conducted a MEDLINE search afterward and discovered that most of the genes that we found important have also been examined in the related contents. It is important to note that those key genes were identified from among several thousands of genes. Thus, the chance of selecting a gene with scientific relevance is very small.

In relation to Fig. 4 (Top and Middle), Parisi et al. (14) explored new therapeutic approaches to AML that focus on immune-based therapy through monoclonal antibodies that target and destroy malignant cells via specific cell receptors. One such agent is gemtuzumab (CMA-676), an agent that targets the CD33 antigen on malignant myeloid cells. Initial studies have shown significant anticancer activity. In another study (15), it is reported that CD33 is expressed by AML cells in >80% of patients but not by normal hematopoietic stem cells, suggesting that elimination of CD33(+) cells may be therapeutically beneficial. Furthermore, Privitera et al. identified the TFPT (FB1) gene as a molecular partner of TCF3 (E2A) in childhood pre-B cell ALL,§ and Yu and Chang (16) observed that human MB-1 was expressed by B cell lines.

For the genes in the last row of Fig. 4, Delmer et al. (17) reported overexpression of cyclin D2 (CCND2) in chronic B cell malignancies. Sonoki et al. (18) found that cyclin D3 (CCND3) is a target gene of mature B cell malignancies. Another study (19) concluded that glucocorticoids cause G₀/G₁ arrest of lymphoid cells. This is due, at least in part, to a decrease in the abundance of the G₁ progression factor, cyclin D3. The mRNA encoding cyclin D3 (CcnD3 mRNA) is rapidly down-regulated when dexamethasone is added to P1798 murine T lymphoma cells.

Nilson et al. (20) found that the AF-4 gene on human chromosome 4q21, a member of the AF-4, LAF-4 and FMR-2 gene family, was involved in reciprocal translocations to the ALL-1 gene on chromosome 11q23, which were associated with acute lymphoblastic leukemias. Hol et al. (21) suggests that the methylenetetrahydrofolate-dehydrogenase gene can act as a risk factor for human neural tube defects.

Clustering algorithms are commonly used in gene expression analyses (22). As a by-product of examining the trees in forests and genes frequently appearing the forests, we obtain gene clusters in a broad sense. Normally, a cluster consists of individual genes. Here, we can view the set of genes (pairs or triplets) that determine a tree (e.g., Fig. 4) as an object. Because some trees in the forest are similar (hence close to each other), they form clusters (hills) in the forest. Thus, the nature of the object (a gene versus a small set of genes) distinguishes our clusters from the standard clusters.

Finding the smallest number of genes that can accurately classify samples is useful because not only can it facilitate the search of new diagnostic procedures, but also enables us to find genes that are coregulated with this small set of genes (5). Although our initial intent was not exactly to look for the smallest number of genes that can accurately classify samples, we nonetheless achieved this desirable goal because most of our trees are based on pairs or triplets of genes and it is unlikely to reduce the number of used genes further. For example, for the same leukemia data (1), a shrunken centroids method of gene expression leads to a smallest set of 21 genes (5) to yield an accurate classification precision. In fact, the original analysis (1) requires a set of 50 genes to achieve a compatible precision. Our results indicate that using trees and forests as the classification method reduces the required number of genes substantially.

In summary, we introduced a strategy for construction of deterministic forests of sturdy trees that are accurate on classification, relative to comparable random forests, and facilitate identification of key genes for discriminating among tumor and cancer types. When three published and commonly used data sets were used, we found that the deterministic forest with two impurities outperforms other forests and single trees. In addition, we provided graphical presentations to understand our results and to identify important genes. The frequently occurring pairs or triples of genes can be further scrutinized by using trees or other classification methods. This provides a very useful data reduction and variable selection strategy. Finally, we justified our findings with a literature search and found that many of the frequently occurring genes are already known to be associated with the respective cancer or cell types.

Abbreviation

AML

acute myeloid leukemia