Context sensitivity of activity-dependent increases in cerebral blood flow

Abstract

Functional neuroimaging in humans is used widely to study brain function in relation to human disease and cognition. The neural basis of neuroimaging signals is probably synaptic activity, but the effect of context, defined as the interaction between synaptic inhibition, excitation, and the electroresponsive properties of the targeted neurons, is not well understood. We examined here the effect of interaction of synaptic excitation and net inhibition on the relationship between electrical activity and vascular signals in the cerebellar cortex. We show that stimulation of the net inhibitory parallel fibers simultaneously with stimulation of the excitatory climbing fibers leads to a further rise in total local field potentials (LFP) and cerebral blood flow (CBF) amplitudes, not a decrease, as predicted from theoretical studies. However, the combined stimulation of the parallel and climbing fiber systems produced changes in CBF and LFP that were smaller than their algebraic sum evoked by separate stimulation of either system. This finding was independent of the starting condition, i.e., whether inhibition was superimposed on a state of excitation or vice versa. The attenuation of the increases in LFP and CBF amplitudes was similar, suggesting that synaptic activity and CBF were coupled under these conditions. The result might be explained by a relative neuronal refractoriness that relates to the intrinsic membrane properties of Purkinje cells, which determine the recovery time of these cells. Our work implies that neuronal and vascular signals are context-sensitive and that their amplitudes are modulated by the electroresponsive properties of the targeted neurons.

Over the last 30 years, the development of new and exciting techniques has enabled us to observe the localization of function in the human brain and to discover how the working brain supports mental activity (1–4). The most commonly applied brain imaging techniques, positron-emission tomography and functional MRI, use signals that are derived from local changes in cerebral blood flow (CBF) or the blood oxygen level-dependent (BOLD) signal that, in a complex way, is related to oxygen metabolism and CBF (5). There is a robust empirical relationship between the stimulus-evoked CBF or BOLD signals and the changes in activity of the underlying neuronal networks. One of the topics that is being studied intensively at the moment is how we translate the neuroimaging signals to classical neurophysiology (6–10). The results from such work suggest that CBF and BOLD signals are better correlated with the input to a given cortical area as well as its local intracortical processing than the spiking activity (11, 12).

Our goal was to establish an experimental model that would allow us to test the influence of preexisting synaptic activity on the increases in CBF evoked by activation of another defined neuronal network. This was felt to be important, because neuronal operations are determined by the balance between synaptic excitation and inhibition as well as the electroresponsive properties of the targeted nerve cells (13, 14). The idea of context manipulation originates from a computational study that examined the putative effects of synaptic inhibition on the relationship between neuronal activity and local CBF (15). The model predicted that synaptic inhibition would lower the evoked increases in CBF under conditions of driven excitation and that neuronal inhibition would raise CBF in a region with either low local excitatory recurrence or a region that was not otherwise driven by excitation (16). These hypotheses were tested in the experiments described below in which we stimulated the cerebellar climbing fibers (CF; excitatory) and parallel fibers (PF; net inhibitory) alone and in combination.

Methods

Experiments were performed in 10 male Wistar rats (250–350 g, Charles River Breeding Laboratories). All studies were in full compliance with the guidelines of the European community for the care and use of laboratory animals. Anesthesia was induced by halothane (Fluotec 3 Vaporizer, Cyprane Limited, Keighley, U.K.; 3.5% induction, 1.5% surgery, and 0.7% maintenance) in 30% O₂/70% N₂O. The corneal reflex and response to toe or tail pinch monitored the level of anesthesia. The trachea was cannulated for mechanical ventilation, and small catheters were placed into the right femoral artery and vein, which were perfused continuously with physiological saline. Continuous monitoring of arterial blood pressure and hourly blood samples of arterial pH, pO₂, and pCO₂ ensured maintenance of basic physiological parameters. The head was fixed in a stereotaxic frame. We used an open cranial window preparation, as described (17). The brain was superfused continuously with artificial cerebrospinal fluid at 37°C, aerated with 95% O₂/5% CO₂ (composition: 123.00 mM NaCl/2.8 mM KCl/22.00 mM NaHCO₃/1.45 mM CaCl₂/1.00 mM NaHPO₄/0.876 mM MgCl₂/3.00 mM glucose). Trepanations exposed the vermis, and the dura was removed down to the cranial part of the spinal cord to access the caudal medulla oblongata for electrical stimulation of the inferior olive. The experimental setup is depicted in Fig. 1.

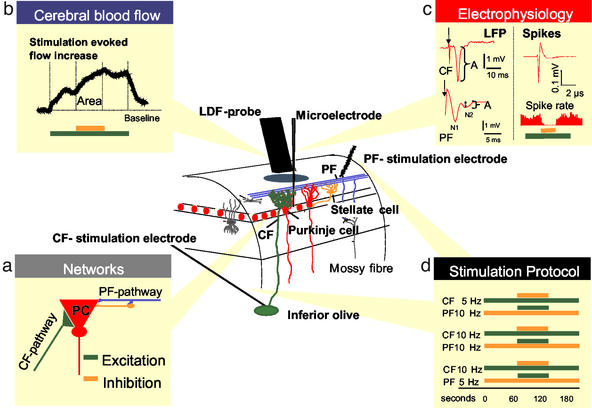
Figure 1.

Recording of spikes, LFPs, and blood flow in the cerebellar cortex. At the center is a schematic, three-dimensional drawing of the experimental set-up, including neurons of interest and placement of LDF probe and stimulating and recording electrodes. Color coding has been used to depict circuits and cell types: granule cell axons (PF) are blue, the Purkinje cell bodies and dendrites are red, stellate cells are yellow, Golgi and basket cells are dark gray, and CF are green. Bipolar stimulation at the cerebellar surface activates the superficial PF that modulate Purkinje cell activity via interaction with Purkinje cells and stellate cells. A monopolar electrode placed stereotaxically in the caudal part of the inferior olive stimulated CF that give a monosynaptic excitatory input to Purkinje cells. Field potentials and single-unit spike activity were recorded by a glass microelectrode. CBF was recorded by LDF by using a probe that was located 0.3–0.5 mm above the pial surface. (a) Functional connectivity of the two afferent pathways to the Purkinje cell (PC), representing excitatory (CF) and net inhibitory (PF) synaptic input. CFs terminate on proximal dendrites of Purkinje cells. The net effect of CF stimulation is synaptic excitation and production of complex spikes in PC. The PFs terminate in the distal dendrites of the Purkinje cells and on the inhibitory interneurons. The random activity in these fibers, produced by the mossy fiber input to the cerebellar granule cells, drives the spiking activity of Purkinje cells under control conditions. The net effect of synchronized electrical stimulation of PF on the cerebellar surface is abolition of Purkinje cell-spiking activity due to synaptic inhibition. In all of the following graphs, CBF changes evoked by CF stimulation are depicted in green and those evoked by PF are orange. (b) Original LDF recording of an evoked CBF increase (colored bars indicate stimulation period) compared with baseline (dotted line). Area marks the increase due to combined stimulation of CF (green) and PF (orange). (c) Typical examples of LFPs evoked by CF and PF stimulation. Arrowheads mark stimulus onset. Baseline and peak values were used to calculate the LFP amplitude (A). In the PF recording, N1 indicates the presynaptic action potential in the PF and N2 indicates the postsynaptic potential produced by the Purkinje cells. (c Right) A typical example of an extracellular recording of Purkinje cell spontaneous simple spike, as well as of spike rate during combined stimulation (colored bars). (d) Protocols of all stimulation combinations and frequencies; CF stimulation is excitation (green bar) and PF stimulation is net inhibition (orange bar).

Electrophysiological Recordings.

We used single-barreled glass microelectrodes, filled with 2 M saline (impedance, 2–3 MΩ; tip, 2 μm). Single-unit activity (spikes) and local extracellular synaptic field potentials (LFPs) of Purkinje cells were recorded with a single electrode at a depth of 300–600 μm in the cerebellar cortex of vermis segments 5 and 6. An Ag/AgCl ground electrode was placed in the neck muscle. The preamplified (×10) signal was A/D-converted, amplified, filtered (spikes, 300- to 2,400-Hz bandwidth; LFP, 1- to 1,000-Hz bandwidth), and digitally sampled by using 1401plus hardware (Cambridge Electronic Design, Cambridge, U.K.) connected to a PC running SPIKE 2.3 software (Cambridge Electronic Design). Digital sampling rates were 20 kHz for spikes and 5 kHz for LFPs.

Inferior Olive Stimulation.

A coated bipolar stainless-steel electrode (SNEX 200, 0.25-mm contact separation, RMI, Woodland Hills, CA) was stereotaxically lowered into the caudal part of the inferior olive as described (11). Positioning was optimized by means of the maximal response of LFP in the cerebellar hemisphere to continuous low-frequency stimulation (0.25 Hz). Pulses of 200-μs constant current with an intensity of 150 μA (ISO-flex, A.M.P.I., Jerusalem) were used at frequencies of 5 and 10 Hz.

PF Stimulation.

The same type of electrode as used for inferior olive stimulation was placed carefully on the surface of the cerebellar cortex close to the recording electrode and laser Doppler flowmetry (LDF) probe. Pulses of 200-μs constant current with an intensity of 150 μA (ISO-flex, A.M.P.I.) were used at frequencies of 5 and 10 Hz.

Stimulation Protocol.

In all experiments, the total duration of stimulation was 180 s. Under control conditions, the ongoing stimulation was applied alone for 180 s. For combined stimulation, the superimposed stimulus was applied during the middle 60 s of the ongoing stimulation (Fig. 1d). For all combinations of stimulations, the second superimposed stimulus was displaced from the first stimulus by 50 ms.

Laser Doppler Measurements.

An optic probe (410, Perimed, Stockholm; 780-nm wavelength, 250-μm fiber separation) was used for LDF (Periflux 4001 Master, Perimed) of CBF. The probe was placed on the cortical surface of a region devoid of large vessels (>100 μm) as close as possible to the microelectrode. The signal was A/D converted and recorded with the 1401plus interface and SPIKE 2.3 by using a 200-Hz digital-sampling rate.

Data Analysis and Statistics.

Values are expressed as mean ± SEM, with levels of significance determined by Wilcoxon-matched pairs test between groups. Changes were considered statistically significant at P < 0.05. Shape and amplitude identified Purkinje cell spikes before data acquisition. Automatic on- and off-line spike sorting was used to remove noise contributions to the calculated event rate (SPIKE 2.3). The LFPs were averaged, and amplitudes were calculated as the difference between peak and baseline (mean of the 15 ms before stimulation onset). The mean amplitude was calculated for each frequency. We estimated the coupling between synaptic activity and CBF by comparing the increases in CBF (area under curve) and the total evoked electrical, expressed as the summed field potential [ΣLFP = LFP amplitude (mV) × stimulation frequency (Hz)] (11). Finally, we assessed the temporal coupling between synaptic activity and CBF by comparing the maximal CBF rise for a given time period with the evoked synaptic activity for the same time period, calculated as the running summation of the LFP amplitudes (runΣLFP, ref. 18). First, a summation period was defined starting at 10 s. Second, the maximal LFP amplitudes were summated for the defined time period (runΣLFP). Third, the runΣLFP value was plotted against the maximal CBF value for the same time period. The best fit was determined by linear correlation analysis. The analysis was carried out for several summation periods by using increments of 10 s as described (18).

Results

Our measurements showed frequency-dependent increases in local CBF in response to stimulation of PF or CF as described (11, 19). We used stimulation frequencies at 5 and 10 Hz in both systems to study the combined stimulation to ensure a reasonable dynamic range of CBF values (compare gray traces in Fig. 2).

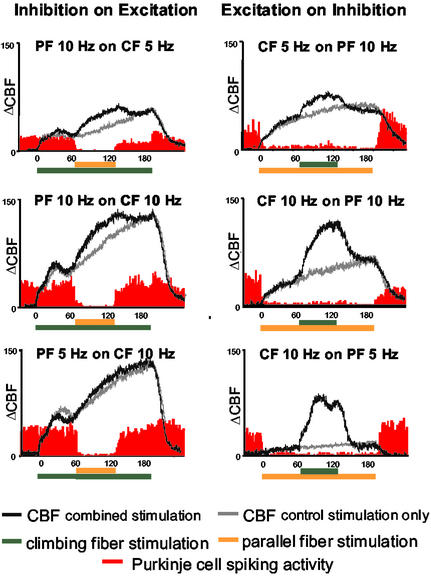
Figure 2.

Effect of interaction of combined PF and CF stimulation on CBF and Purkinje cell-spiking activity. Average of original recordings of Purkinje cell-spiking activity and CBF for each stimulation protocol is shown. Colored horizontal bars indicate stimulation periods. In each plot, the gray trace indicates CBF for control conditions in which the PF (Left) or CF (Right) was stimulated alone for 180 s. The black trace indicates CBF for the combined stimulation. PF stimulation inhibited spiking activity when applied alone and in combination with excitation (CF) and independently of the sequence of the stimulation protocols. In contrast to Purkinje cell spiking, CBF increased further in response to combined combination.

First, we examined the hypothesis that net synaptic inhibition applied on top of a state of excitatory synaptic activity resulted in a decrease in the ongoing rise in CBF (15). Synaptic excitation was achieved by stimulation of the purely excitatory CF pathway at either 5 or 10 Hz for 180 s. The net inhibitory PF input was superimposed during the middle 60-s period (at either 5 or 10 Hz). As a control, we studied the effect of excitation superimposed on a state of net inhibition by reversing the stimulus protocol. Our recordings showed that for all stimulation combinations, the superimposed stimulation raised CBF to a higher level compared with separate stimulation of the two pathways (Fig. 2). Furthermore, the magnitude of the additional CBF rise induced by combined stimulation was frequency-dependent (Fig. 2). Thus, our hypothesis was falsified: synaptic inhibition superimposed on a state of excitation did not attenuate the ongoing rise in CBF evoked by the strong excitatory CF input. The increase in CBF under conditions of combined stimulation was, across the six protocols, 17.4 ± 2.8% smaller than the algebraic sum of increases for separate stimulation of either pathway. This finding was independent of whether excitation was superimposed on inhibition or vice versa. The result indicated that the CBF response was dependent on the context in which the stimulus was applied, albeit in a different way than expected from the modeling study (15). We then turned to analyze the electrophysiological recordings in relation to the CBF findings.

We verified the stimulation-induced changes in neuronal activity by recording Purkinje cell single-unit activity (spikes) and synaptic activity (LFP). CF stimulation produces a powerful excitation of Purkinje cells that triggers prolonged bursts of high-frequency potentials, the so-called complex spike. CF stimulation also activates the inhibitory Golgi cells, which inhibit the input from the mossy fibers (20). Therefore, during CF stimulation, the spontaneous spiking activity from Purkinje cells was inhibited, and the overall number of spikes remained constant as indicated in the six graphs in Fig. 2. In contrast, PF stimulation strongly attenuated Purkinje cell-spiking activity. In Fig. 2 Left, PF stimulation was applied during the middle 60 s of the stimulation period. During this period, Purkinje cell-spiking activity was abolished, whereas Fig. 2 Right shows the abolition of spikes during the entire 180 s of PF stimulation as described (11). The present recordings show that the complex spikes evoked by CF stimulation were blocked by PF stimulation as well, independent of whether CF stimulation was ongoing, or superimposed on a block of ongoing PF stimulation. The dissociation between the spike generation in Purkinje cells and the increases in CBF was independent of the stimulation frequency.

We then examined the possibility that the CBF responses were explained by excitatory postsynaptic activity by correlating LFP and CBF amplitudes. CF stimulation generates a large, unitary LFP that reflects the postsynaptic activity of Purkinje cells (Fig. 1c), whereas presynaptic structures make negligible contributions to the extracellular ion fluxes in this pathway (11, 21). In contrast, PF stimulation generates a LFP that is composed of a large presynaptic and a small postsynaptic component (see Fig. 1). For subsequent analysis, we used only the postsynaptic component (Fig. 1c, N2), which reflects the excitation of Purkinje cells by PF stimulation. We are aware of the limitations in estimating postsynaptic activity by LFP because excitation of interneurons and the resulting inhibition gives rise to none or very small changes of LFP because of the functional anatomy of the interneurons. With these caveats in mind, we tested the hypothesis that the increases in CBF evoked by double-network stimulation were triggered by excitatory synaptic activity. To this end, we compared the LFP amplitude for the separate network stimulations (CF or PF) with that for the combined stimulation. This was possible because stimulation of each network in the combination protocol was separated by 50 ms, which gave a clear separation of the LFPs in the recordings.

The results are shown in Figs. 3 and 4. The amplitudes of the postsynaptic LFPs for each of the two pathways were smaller during combined stimulation as compared with their respective control values during separate stimulation (Fig. 3b). Thus, the LFP amplitude evoked by CF stimulation was smaller when PF was stimulated at the same time. Likewise, the excitatory postsynaptic LFP evoked by PF stimulation was smaller when CF stimulation was applied at the same time. This suggested a relative neuronal refractoriness that was related to the interaction of the two excitatory synaptic inputs on the Purkinje cells. This was observed for all frequency combinations applied, no matter which stimulus came first (Table 1). However, during the combined stimulation period, the contribution to LFPs from both networks gave a larger total sum in LFP amplitudes (ΣLFPs) (Fig. 3c) as compared with the ΣLFPs during the middle 60 s of the separate stimulated networks. This could explain the further increase in CBF during combined stimulations as in response to single network stimulations.

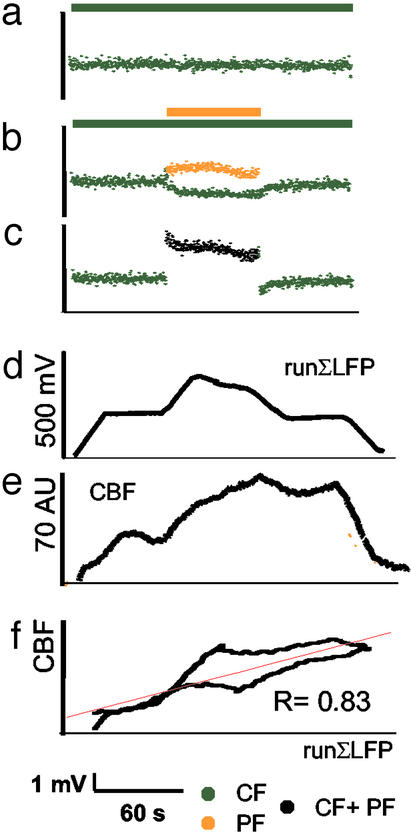
Figure 3.

Temporal coupling between increases in synaptic activity and in CBF under conditions of combined stimulation. The figure shows the averaged data for animals that were exposed to CF stimulation at 5 Hz for 180 s, with PF stimulation at 10 Hz superimposed during the middle 60 s. (a) Mean amplitudes of individual LFPs evoked by CF stimulation at 5 Hz alone over 180 s. (b) The LFP amplitude for CF stimulation decreased (green) when the mixed excitatory–inhibitory stimulus (PF) was superimposed. PF stimulation evoked postsynaptic LFPs from Purkinje cells that are shown in orange. (c) The algebraic sum of LFP amplitudes during combined stimulation of PF and CF increased. This indicated the overall increase in synaptic activity during stimulus combination (black). (d) Electrophysiological data were transformed to CBF signals by plotting a runΣLFP for a time window of 20 s vs. time. The waveform of the runΣLFP data was comparable to the CBF trace depicted in e. (f) Correlation of runΣLFP (data from d) vs. the evoked CBF increase (data from e) for the combined stimulation (R = correlation coefficient; P < 0.001). The lower part of the graph indicates the coupling between runΣLFP and CBF during stimulation, and the upper graph shows the coupling during return to baseline of the CBF response, i.e., after stop of stimulation. The red line indicates the result of the linear regression analysis.

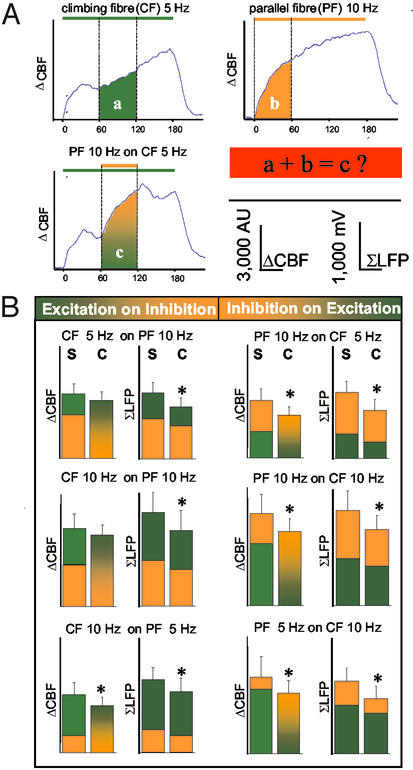
Figure 4.

Effect of interaction of two neuronal circuits on the evoked neuronal activity and CBF. (A) Examples of traces that were used to calculate whether the rise in CBF that was produced by combined stimulation was the same as the algebraic sum of CBF increments evoked by stimulation of either pathway alone. The illustration is based on averaged traces from all animals in which PF stimulation at 10 Hz was superimposed on CF stimulation at 5 Hz. The experiments tested the hypothesis that the algebraic sum of CBF increases evoked by stimulation of CF or PF alone (a and b) was the same as for combined stimulation (c). (B) The mean value of the algebraic sum of CBF for stimulation of the two pathways separately (S) compared with the mean increase in CBF recorded during combined stimulation (C). The graphs show that S was larger than C for all frequency combinations. The summed synaptic activity as indicated by ΣLFP was calculated for the same time periods as CBF and is shown for comparison. The decline in ΣLFP and CBF was similar, suggesting that the difference between the calculated and the observed rises in CBF was explained by changes in postsynaptic activity. All values are mean ± SEM; *, P < 0.05.

Table 1.

Normalized amplitudes of LFPs during combined stimulation

	With 5 Hz PF	With 10 Hz PF
CF, 5 Hz	—	0.67  ± 0.03
CF, 10 Hz	0.82  ± 0.06	0.81  ± 0.08

	With 5 Hz CF	With 10 Hz CF
PF, 5 Hz	—	0.69  ± 0.04
PF, 10 Hz	0.83  ± 0.06	0.82  ± 0.12

ΣLFP amplitudes for CF or PF during combined stimulation expressed relative to their respective control values during separate stimulation. The table shows that the ΣLFP amplitudes were smaller for combined stimulation as compared with separate stimulations. Mean ± SEM; P < 0.05, Wilcoxon matched pairs test. 

We examined the possibility that the rise in CBF during combined stimulation was coupled to alterations in excitatory synaptic activity in two ways. First, we tested the hypothesis that a time integral of synaptic activity explained the accompanying rise in CBF as described (18). Fig. 3 d–f shows that the LFP amplitudes could be transformed into a CBF response by using a running summation period of 20 s. The lower graph in Fig. 3f represents the coupling relation during stimulation, and the upper graph indicates the relation after stimulation is stopped. The red curve represents the result of the linear regression analysis. The results indicated that the time variations of LFP amplitudes correlated with the CBF responses during combined stimulation (Fig. 3f, Table 2). This confirmed the hypothesis that the increase in CBF was coupled to synaptic activity under conditions of combined stimulations.

Table 2.

Preserved temporal coupling of synaptic activity and CBF during combined stimulation

Frequencies applied	Correlation of CBF responses and runΣLFP evoked by stimulation of
	CF alone	CF with PF on top	PF alone	PF with CF on top
5 Hz CF/10 Hz PF	0.78	0.83	0.92	0.95
10 Hz CF/10 Hz PF	0.77	0.84	0.88	0.95
10 Hz CF/5 Hz PF	0.8	0.83	0.92	0.9

Correlation coefficient R (P < 0.05) of the linear correlation analysis of the time courses of CBF vs. the running integration of LFP amplitudes by using a time window of 20 s (runΣLFP) for all types of separate and combined stimulation (see Fig. 3f). 

We then compared the total increase in CBF (area under curve) and the ΣLFP evoked by stimulation of either network separately and during combined stimulation. Fig. 4A shows how we calculated the theoretical CBF value for combined stimulation. In this example, PF stimulation at 10 Hz was superimposed on CF stimulation at 5 Hz. The theoretical CBF value for combined stimulation was the algebraic sum of the rise in CBF observed for CF stimulation during the middle 60 s (a) and the rise during the first 60 s for PF stimulation (b). This then was compared with the middle 60 s during combined stimulation (c). Fig. 4B shows this comparison for all combinations of stimulations. The left column in each data pair is the algebraic sum of CBF or LFP amplitudes for separate stimulation of CF and PF, whereas the right column is the observed rise in response to the combined stimulation. The LFP amplitudes for combined stimulation matched the total increase in CBF for all combinations of stimulations, and both were smaller than the algebraic sum of responses evoked by separate stimulation of the two systems (Fig. 4). The overall reduction in ΣLFP for all combinations of stimulations was 22.5 ± 1.6%, which corresponded to the reduction in CBF of 17.4 ± 2.8%. This suggested that a relative neuronal refractoriness explained the magnitude of the CBF response under conditions of dual-network stimulation and that synaptic activity and CBF responses were coupled under these conditions.

Discussion

This study examined the context sensitivity of the activity-dependent increases in synaptic activity and CBF by stimulation of two cerebellar networks that both project to the same cell, the Purkinje cell. The results showed that stimulation of a strong monosynaptic excitatory network (CF) triggered a rise in CBF and an increase in synaptic activity that increased further in response to simultaneous stimulation of the net inhibitory PF input. Our results relate to a computational study that modeled the putative effects of synaptic inhibition on cortical activation in relation to factors of importance for the relationship between neuronal activity and local CBF (15).

That study identified three factors, which influenced the way inhibition controlled imaging results: local connectivity, context, and inhibitory connection. Thus, different task conditions produced different local responses to inhibition, depending on the current state of the local circuit. According to this model, neuronal inhibition would raise CBF in a region with either low local excitatory recurrence or a region that otherwise was not driven by excitation. Conversely, with high recurrence or driven excitation, inhibition would lower the evoked rises in CBF (15). We tested the latter hypothesis in experiments, which involved stimulation of the CF (excitatory) and PF (net inhibitory) alone and in combination. Our results showed that combined stimulation of the two networks was accompanied by net inhibition of neuronal activity (zero spikes) superimposed on a state of strong excitation (large ΣLFP) that resulted in an additional increase in CBF above the maximum achieved by the excitatory stimulus alone. Stimulation of the CF on top of a state of net inhibition evoked by PF stimulation triggered an additional increase in CBF. Thus, our hypothesis was falsified; i.e., stimulation of a net inhibitory network does not decrease the CBF signal when superimposed on a state of strong excitation, most likely because of the excitation of the inhibitory interneurons. The CBF response was independent of the order of stimulation, i.e., whether we stimulated the mixed disynaptic PF or the purely excitatory CF first. However, the increases in CBF evoked by combined stimulation of the two networks were smaller than the algebraic sum of CBF increases evoked by separate stimulations.

This might be explained by attenuation of the evoked synaptic activity for all combinations of stimulations, because the LFP amplitudes evoked by combined stimulations were smaller than for separate stimulation of each pathway. This probably relates to response adaptation because interstimulus intervals of 50 ms do not allow for complete recovery between stimuli. Thus, each stimulus results in changes in postsynaptic activity that is influenced by the preceding activity. This property of Purkinje cells is explained by opening of specific channels in dendrites that are voltage-sensitive (14, 22, 23). The dendrites of Purkinje cells contain both voltage-sensitive calcium channels and calcium- and voltage-sensitive potassium channels that are activated by depolarization and that hyperpolarize the cells for up to several seconds (23, 24). The frequency-sensitive reduction in LFP amplitudes during combined stimulation indicates that these intrinsic membrane properties of the Purkinje cell have a major influence on the outcome of stimulation. Thus, the amplitude of the neuronal response evoked by synaptic activity was context-sensitive. Synaptic activity coupled to CBF influences the amplitude of the vascular signals. Similar channels exist on neuronal dendrites, e.g., in the hippocampus and the neocortex (14). Therefore, the results we report here from the cerebellar cortex probably also apply to other brain regions.

Several previous studies have examined the refractoriness of neuronal or vascular systems in relation to closely timed stimuli (25–27). In one study, the somatosensory-evoked potentials were suppressed at the same time as the BOLD signal, suggesting that neuronal refractoriness explained the attenuation of the BOLD signal (26). However, because of sampling problems with the electrical response, it was not possible to make a quantitative assessment of the functional MRI signal in relation to neuronal activity. In another two studies, one that used intrinsic optical imaging and one that used LDF, it was suggested that the refractoriness of the hemodynamic signals was based on vascular mechanisms as the cortical-evoked potentials were preserved (25, 27).

We considered the possibility that mechanisms related to the vascular mediators contributed to the smaller CBF response produced by combined stimulation as compared with the algebraic sum of increases in CBF produced by separate stimulation of the two networks. Nitric oxide (NO) is the main modulator of CBF in both networks. In addition, potassium contributes to the increase in CBF caused by PF stimulation, whereas adenosine contributes to the CBF increases that accompany CF stimulation (19, 28–31). Limitation of the CBF response may be related to saturation of one or more steps of the NO–cGMP-signaling pathway because NO is produced by stimulation of both pathways, but further studies are needed to address this issue. However, considering that the reductions in LFP and CBF amplitudes were similar and that the vascular signals were coupled to synaptic activity, it appears more likely that the vascular responses were limited by neuronal refractoriness.

In conclusion, effective synaptic inhibition superimposed on a state of strong excitation caused a further increase in CBF and excitatory synaptic activity, probably because of excitation of inhibitory interneurons. Nevertheless, the CBF and LFP responses were smaller than expected from theoretical calculations based on data obtained from separate stimulation of the two networks. This attenuation of CBF and synaptic responses was related to the complex interplay of the known electroresponsive properties of the Purkinje cells and their synaptic interactions. We postulate that these intrinsic properties control the degree to which CBF is increased by synaptic excitation under conditions wherein CBF is coupled to increases in synaptic activity.

Abbreviations

CBF

cerebral blood flow

CF

climbing fibers

LFP

local field potentials

PF

parallel fibers

LDF

laser Doppler flowmetry

ΣLFP

summed LFP

runΣLFP

running summation of the LFP amplitudes

BOLD

blood oxygen level-dependent