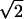Emergency response to an anthrax attack

Abstract

We developed a mathematical model to compare various emergency responses in the event of an airborne anthrax attack. The system consists of an atmospheric dispersion model, an age-dependent dose–response model, a disease progression model, and a set of spatially distributed two-stage queueing systems consisting of antibiotic distribution and hospital care. Our results underscore the need for the extremely aggressive and timely use of oral antibiotics by all asymptomatics in the exposure region, distributed either preattack or by nonprofessionals postattack, and the creation of surge capacity for supportive hospital care via expanded training of nonemergency care workers at the local level and the use of federal and military resources and nationwide medical volunteers. The use of prioritization (based on disease stage and/or age) at both queues, and the development and deployment of modestly rapid and sensitive biosensors, while helpful, produce only second-order improvements.

Despite the fatal delivery of Bacillus anthracis, the bacterium that causes anthrax, via the United States mail in 2001 (1) and the dire warnings about an airborne anthrax attack (2–4), detailed guidelines for postexposure prophylaxis in the aftermath of such an attack, specifying who receives treatment and how these people are prioritized, do not appear to be in place (ref. 5, page 2247). To investigate these issues, we formulated a mathematical model to compare several response strategies to a mass-casualty airborne anthrax attack in a large city.

The model (Fig. 1) incorporates a Gaussian plume (6), which is used to compute the number of spores inhaled by a person who is at any given location in the vicinity of an instantaneous point release of anthrax. Although the Gaussian plume model may be too simplistic to monitor and predict the spatiotemporal anthrax concentrations after an actual attack, the remaining “downstream” portion of our model can be used in conjunction with a more sophisticated atmospheric model that captures wind changes and other atmospheric complexities ignored here (7). Indeed, the atmospheric model affects the logistics only via the initial conditions, and hence the insights from our analysis are likely to be robust. Also, although the impact of a release depends on a variety of factors including the time of day of the release and the stability conditions (6), and the form (liquid or dry) of the agent and the method of dissemination (8), the cumulative level of uncertainty in these factors is dwarfed by the uncertainty in the size of the release (see Fig. 4).

Figure 1.

Graphical depiction of the simulated system, which incorporates an atmospheric dispersion model, a dose–response model, a disease progression model, and an intervention model, which is described by a two-stage queueing system in each service zone. Asymptomatics enter the antibiotics queue according to a geographic ring strategy (dashed line). People in the two queues are prioritized according to the five policies in Table 1.

Figure 4.

The impact of biosensors, which are characterized by their time delay (t_b = 6 h) to obtain results, detection limit (l_b), and geographical density (d_b). The detection delay τ equals the biosensor delay t_b if the maximum spore count at any biosensor location is greater than the detection limit l_b (i.e., the attack is detected by biosensors), and τ equals 2 days otherwise (i.e., the attack is detected via early symptomatic cases). We assume preattack distribution of antibiotics (i.e., no time is spent in the antibiotics queue), and prodromals are given priority in the hospital queue. All other parameters are set to their base case values. (a) With the geographical density fixed at 1/(9 km²), we find the number of deaths as a function of release size for three values of the detection limit. (b) With the detection limit fixed at 10⁴ spores, the number of deaths is plotted as a function of release size for three values of the geographical density. In both a and b, the number of deaths is discontinuous in the release size, following the upper death vs. release size curve to the left of the vertical line (there is a vertical line corresponding to each value of the varied parameter), and following the lower curve to the right of the vertical line.

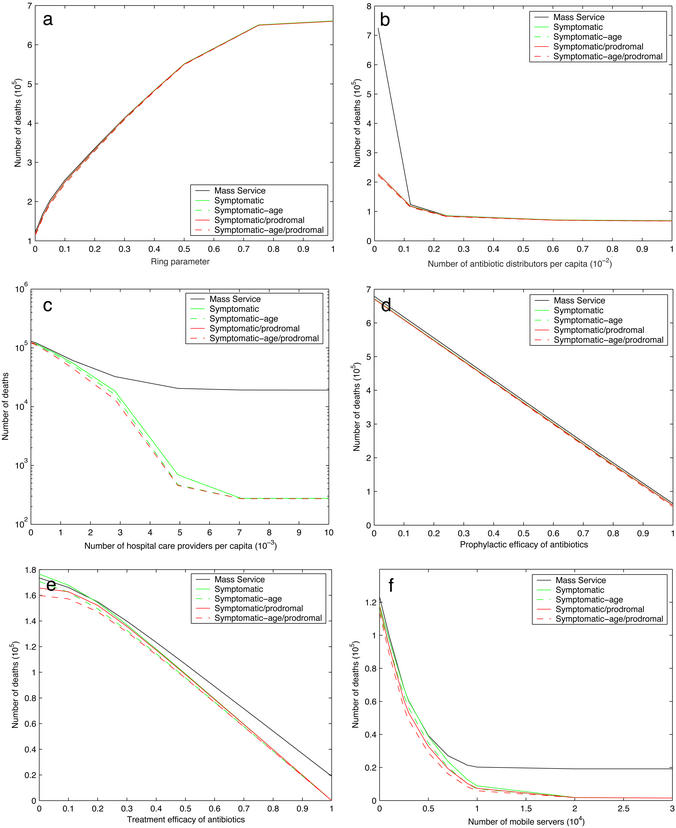
An age-dependent dose–response model, together with a population density and an age distribution, generates the fraction of people at each location of each age who are infected. Absent intervention, each infected person progresses through three log-normally distributed disease stages: incubation, prodromal, and fulminant (1). Intervention begins τ = 48 h after the attack. The region ≈200 km downwind (the first 30 km downwind is an urban area of 10.8 million people, and further downwind is a rural area occupied by 0.7 million people) and within ≈20 km crosswind of the source release is divided into service zones, each containing a two-stage queueing system that distributes oral antibiotics and provides hospital care within the zone. These servers are from local hospitals and neighborhood emergency health centers (hld.sbccom.army.mil/downloads/bwirp/nehc_green_book.pdf). At queue i = {A, H} (A = antibiotics, H = hospital), there are n_i servers per km² and the mean service time is μ. In addition, m_H mobile hospital care providers, representing federal and military personnel and nationwide medical volunteers, arrive τ_m = 18 h after the attack is detected and serve overflow hospital patients. Combination antibiotics prevent a fraction e₁ of people in the incubation stage from developing symptoms and prevent a fraction e₂ of prodromals from progressing to the fulminant stage. The remaining fraction of prodromals have their prodromal clock reset (according to another log-normal distribution) when they receive antibiotics. Everyone who enters the fulminant stage eventually dies, but those completing their hospital care while still prodromal survive. A time-varying geographic ring dictates which asymptomatics (either uninfected or incubating) enter the antibiotics queue. The ring computes the fraction of people at each location who have developed disease symptoms, a quantity we refer to as observed anthrax burden, and places people at a given location into the antibiotics queue if the observed burden at this location exceeds a specified threshold p. Hence, as the attack plays out and more people exhibit symptoms, the ring enlarges and more people are placed in queue. People who develop symptoms immediately enter the antibiotics queue if their location is not already in the ring. In addition, people enter the hospital queue as soon as they have incurred symptoms and received antibiotics, which can occur in either order. We consider five priority policies (described in Table 1) that differ by how people waiting in the two queues are prioritized for service, based on observable disease (i.e., symptomatic vs. asymptomatic) and age. The mathematical model is a system of integro-partial differential equations (see Supporting Text, which is published as supporting information on the PNAS web site, www.pnas.org).

Table 1.

Description of the five priority policies

Priority policy	Priority at antibiotics queue	Priority at hospital queue
Mass service	None	None
Symptomatic	Symptomatics	None
Symptomatic age	High, symptomatics	None
	Medium, asymptomatics over 55
	Low, asymptomatics under 55
Symptomatic/ prodromal	Symptomatics	Prodromals
Symptomatic age/ prodromal	High, symptomatics	Prodromals
	Medium, asymptomatics over 55
	Low, asymptomatics under 55

At the antibiotics queue, e.g., the symptomatic policy serves asymptomatics only if there are no symptomatics waiting for service. The third and fourth policies each build on the symptomatic policy in a different way, and the last policy combines these two policies. 

For the base-case values of the model parameters (Table 2), 1.49 million people of 11.5 million (13.1%) are infected in a long thin region (Fig. 2b) downwind of the point of release of 10¹⁵ spores (≈1 kg; ref. 9). At the time intervention begins, 12,700 people are prodromal and 17 are in the fulminant stage. Under the mass service policy in the base case, 123,400, or 8.3% of those infected, die. Relative to the mass service policy, the four other priority policies in Table 1 reduce the total number of deaths by 4.3%, 7.1%, 4.9%, and 7.7%, respectively; i.e., prioritizing symptomatics provides a 4.3% reduction in deaths, prioritizing by age generates a 2.8% reduction, and prioritizing prodromals offers a 0.6% improvement. Note that our model overestimates the benefits of prodromal priority at the hospital queue because care providers will not always be able to observe whose lives can, and cannot, be saved.

Table 2.

Parameter values for the model in the base case

Parameter	Description	Value	Ref.
Q	Amount released	1015 spores	Supporting Text
u	Wind speed	5 m/s	9
h	Release height	100 m	Supporting Text
b	Breathing rate	0.03 m3/min	9
α	Probit intercept	−9.733	Supporting Text
β	Probit dose slope	1.025	Supporting Text
γ	Probit age slope	−0.016 year−1	Supporting Text
δ	Probit age quadratic	0.0006 year−2	Supporting Text
X	Region limit downwind	201 km	This paper
Y	Region limit crosswind	18 km	This paper
θu	Urban population density (x ≤ 30 km)	104 people/km2	3
θr	Rural population density [x ∈ (30, 201) km]	102 people/km2	This paper
	Urban zone size	9 km2	Supporting Text
	Rural zone size	81 km2	Supporting Text
m1	Median incubation	10.95 days	10
d1	Dispersal factor of incubation	2.04	10
e1	Prophylactic efficacy during incubation	0.9	Supporting Text
m2	Median of prodromal phase	2.35 days	1, 10
d2	Dispersal factor of prodromal phase		Supporting Text
m3	Median of fulminant phase	1.41 days	1, 10
d3	Dispersal factor of fulminant stage		Supporting Text
e2	Prob. of infinite postantibiotic prodromal	0.4	Supporting Text
m2̃	Median of finite postantibiotic prodromal	2 days	10
d2̃	Disp. factor of finite postantibiotic prodromal		Supporting Text
	Fatality rate if febrile	1.0	1, 11
τ	Detection delay	2 days	10
nA(x, y)	Density of antibiotic servers	1.21 × 10−3θ(x, y)	Supporting Text
μA	Service rate for antibiotics	(7 min)−1	Supporting Text
nH(x, y)	Density of hospital servers	1.41 × 10−4θ(x, y)	Supporting Text
μH	Service rate in hospital	(6 h)−1	Supporting Text
mH	Number of mobile hospital servers	0	This paper
τm	Delay for mobile hospital servers	18 h	Supporting Text
p	Ring parameter	0	This paper
tb	Biosensor time delay	6 h	This paper
lb	Biosensor detection limit	104 spores	This paper
db	Biosensor density	(9 km2)−1	This paper

Figure 2.

(a) The age-dependent dose–response model for four ages, based on Eq. 2 of Supporting Text. (b) Age-aggregated spatial probability of infection, showing four contours of constant prevalence.

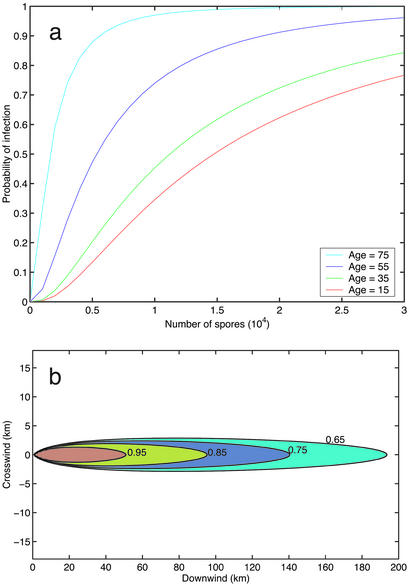
A sensitivity analysis of the number of deaths under the five priority policies for six key parameters was performed (Fig. 3). A less aggressive prophylactic strategy (i.e., higher value of the ring parameter p) is extremely costly (Fig. 3a): the death count doubles if p is increased from 0 to 0.07 under all five priority policies, and ≈660,000 people (44% of those infected) perish if only symptomatics receive antibiotics (p = 1). Moreover, our model underestimates the increase in deaths due to positive p values in Fig. 3a because we ignore the self-reporting delay of symptomatics; this delay averaged 3.5 days in the 2001 attack (1) but would likely be smaller in a subsequent large-scale attack. The death count is sensitive to the number of antibiotic distributors per capita, and the number of deaths can be nearly halved by eliminating queueing (Fig. 3b), which can be achieved by a 7.5-fold increase in the distribution capacity or by preattack distribution. The hospital queue is the system bottleneck (Fig. 3c). If care capacity is increased 75-fold, no one waits for service in the hospital queue, and further capacity increases yield no improvements. At this ideal capacity level, the number of deaths is <300 for all but the mass service policy. In the practically relevant ranges, the number of deaths is approximately linearly decreasing in the antibiotic efficacy (Fig. 3 d and e), both as prophylaxis (due primarily to patient adherence) and as treatment in the absence of hospital care (which is a medical unknown). The impact of prophylactic adherence is large: the death toll is >50% higher if e₁ is reduced from 0.9 to 0.8. Finally, under the symptomatic age/prodromal policy, deploying 2,800 mobile servers cuts the death count in half and 8,500 servers reduces it to one-tenth of the base case (Fig. 3f). Despite the 18-h delay, adding a fixed number of mobile servers has much more impact than adding the same number of local servers because the former are typically busy while the latter may be idle in less congested service zones.

Figure 3.

Sensitivity analysis for various model parameters. For all five policies in Table 1, the number of deaths versus the ring parameter (p) (a), the number of antibiotic distributors per capita [n_A(x,y)/θ(x,y)] (b), the number of hospital care providers per capita [n_H(x,y)/θ(x,y)] (c), the prophylactic efficacy (e₁) (d), the treatment efficacy (e₂) (e), and the number of mobile servers (m_H) (f).

Fig. 4 shows the impact of deploying biosensors with various characteristics (the biosensor parameter values are hypothetical because these data are classified), assuming preattack antibiotic distribution and prodromal priority at the hospital queue. The number of deaths is insensitive to the time delay to obtain biosensor results if this delay is <1 day (data not shown). Fig. 4 shows that a higher biosensor detection limit can be partially compensated for by deploying a higher geographical density of biosensors. The increase in death count by detecting the attack via early symptomatics rather than biosensors is modest when the release size is <10¹⁴ spores (or 100 g); larger releases cause a significant increase in deaths because of hospital congestion. Consequently, little can be gained in this scenario (e.g., preattack antibiotic distribution) by improving the biosensors beyond the base case values in Table 2. Finally, the upper curve in Fig. 4a provides a sensitivity analysis of the number of deaths versus the size of the release, which is the most uncertain quantity in our model. Even with preattack antibiotic distribution, ≈20,000 people would perish if only 10¹⁴ spores (100 g) were released. This curve is concave when plotted on a linear scale, and increasing the release size by 3 logs over the base case only doubles the death toll.

Because deterrence and counterproliferation are not highly effective at combating biological warfare, security from such an attack rests primarily on a strong logistical response (12, 13). Secretary of State Colin L. Powell recently presented evidence at the United Nations Security Council (14) that Iraq has produced vast quantities of anthrax, incorporated perfected drying techniques into mobile biological weapons production facilities, tested the jet spraying of 2,000 liters of simulated anthrax, authorized the use of poison gas if the United States attacks it, and is housing the base of an Al Qaeda terrorist cell. These arguments suggest that the likelihood of an attack on the scale of our base-case assumptions has increased to a nonnegligible level.

Consequently, as with the case of smallpox (13, 15) (www.whitehouse.gov/news/releases/2002/12/20021213-7.html), a concomitant increase in preparation to contain the consequences of such an attack is now urgently required. More specifically, our analysis has a number of policy implications, many stemming from the observation that aggressive hospital care for symptomatics is the bottleneck operation in this multistage service process (16). An aggressive prophylactic strategy (Fig. 3a) is crucial because it eases the bottleneck by preventing incubating people from progressing to symptoms. Many people declined or discontinued antibiotic prophylaxis during the 2001 outbreak (17, 18), and an effective education program is required to maximize adherence in a subsequent attack. Preattack distribution of antibiotics, to be taken only if an attack occurs, would eliminate the delay in the antibiotics queue and would significantly reduce the number of fatalities (Fig. 3b). If this approach is deemed too risky (Cipro, the brand name for ciprofloxacin, has unpleasant side effects, and the costs and risks of preattack distribution need to be thoroughly investigated; the U.S. government has enough Cipro to treat several million people for the recommended 60 days, http://usinfo.state.gov/topical/global/hiv/01102415.htm) then it is imperative, due to the shortage of emergency hospital workers, that nonmedical professionals and volunteers administer antibiotics (J. M. Hauer, Congressional testimony, Senate Health Education, Labor, and Pensions Committee, March 25, 1999). Increasing the number of hospital care providers is the most obvious remedy for easing the bottleneck, which could be achieved by expanded training for inhalational anthrax to nonemergency health-care workers (e.g., other doctors and nurses, respiratory therapists, emergency medical technicians with advanced life support training). Preattack training and organization of federal and military resources, the m_H mobile servers in our model, harnessed from, e.g., the Department of Defense, Veterans Administration hospitals, the Public Health Service's Disaster Medical Assistance Teams, the National Guard, the National Disaster Medical System, and the American Red Cross (J. M. Hauer, Congressional testimony, Senate Health Education, Labor, and Pensions Committee, March 25, 1999), can also significantly lower the death count from an attack (Fig. 3f); special emphasis should be given to the federal resources that are local [e.g., the National Guard (19)], which would reduce the delay τ_M in our model and further decrease the number of fatalities (data not shown). The number of mobile servers can also be increased via a government-sponsored program that encourages pulmonary specialists to travel to afflicted regions to treat patients. Perhaps such a program could be incorporated into the Medical Reserve Corps, which was recently established to enable health professionals to volunteer in their communities in the event of a large-scale emergency. Preattack vaccination of first responders is needed to prevent a depletion of intervention personnel. Also, secondary bottlenecks must be avoided: antibiotics and ventilators need to be stockpiled or rapidly obtained, and supplementary modes of transportation must be secured to transport symptomatics to hospitals. As is done in many service operations, prioritizing people in queue is a relatively easy way to achieve further service improvements, in this case fatality reductions (≈10,000 lives saved in the base case). Although the symptomatic-age policy at the antibiotics queue should not impose a logistical challenge, the prodromal policy at the hospital queue may require training from military doctors. Our base case optimistically assumes that the detection delay is only 48 h, thereby assuming that the first symptomatic cases (10) are successfully diagnosed and mobilization is rapid. Although a longer delay is extremely costly (in our base case, the death count doubles if the detection delay increases from 2 to 4.8 days), hypothetical rapid and accurate biosensors without preattack antibiotic distribution and ample hospital care resources would provide a false sense of security: even if the detection delay was reduced to 6 h, ≈70,000 deaths would be incurred in our base case. Although the results in Fig. 4 are based on a simplistic atmospheric model, they do suggest that improving biosensor technology beyond the base case values in Table 2 offers less reduction in the death count than getting people through both queues as quickly as possible.

Although many of these proposals raise legal, ethical, and institutional issues, their cumulative impact would be enormous in the face of a large-scale attack. In addition, given (i) the relative ease of obtaining anthrax, (ii) the irreducible uncertainty in the model parameters (e.g., the release size, the efficacy of antibiotics in the febrile stage, and the possibility of a dose-dependent incubation period), and hence the potentially huge death toll, (iii) the possibility of panic, flight, communications breakdown, economic disruption, and general societal dysfunction in the aftermath of an attack, (iv) the possibility of attacks in multiple cities, and (v) the difficulty and cost of mounting an effective emergency response strategy, serious consideration should be given to preattack mass vaccination should the probability of an attack loom sufficiently large. Because the necessary supply of anthrax vaccine will not be available for at least several years [although the current vaccine is safe and reliable (5), it requires a series of shots over 18 months and annual boosters to reach and maintain effectiveness, and its only producer, BioPort, has a 2-year contract to produce 10 million doses for the U.S. military, www.wral.com/wtc/1216247/detail.html], planning for an effective emergency response must continue in earnest.