A Mathematical Investigation of the Multiple Pathways to Recurrent Prostate Cancer: Comparison with Experimental Data

Abstract

Considerable research is aimed at determining the mechanisms by which hormone-refractory prostate cancer develops. In an effort to assist in the understanding of recurrent prostate cancer and the cellular processes that mediate this disease, a mathematical model is presented that describes both the pretreatment growth and the posttherapy relapse of human prostate cancer xenografts. Our goal is to evaluate the interplay between the multiple mechanisms that have been postulated as causes of androgen-independent relapse. Simulations of the model show that molecular events that render the androgen receptor irrelevant to disease progression, such as upregulation of BCL2, can result in relapse after androgen deprivation therapy. However, decreased apoptosis of androgen-independent cells alone overestimates the effects of hormone therapy when compared to experimental data. When decreased apoptosis is combined with continual androgen receptor activation, the posttherapy growth dynamics are in excellent correlation with experimental observations of the growth of LuCaP xenografts. Furthermore, the mathematical model predicts that upregulation of the androgen receptor, together with its increased activation, is alone sufficient to result in the androgen-independent growth of LNCaP xenografts. Recent experimental studies that suggest that the posttherapy increase in and continual activation of the androgen receptor are common and crucial features of recurrent prostate cancer provide validation of the model predictions. This approach provides a framework for using mathematical techniques to study novel therapeutic strategies aimed at controlling this disease.

Introduction

For American men over the age of 40, prostate cancer is now the most commonly diagnosed cancer and the second leading cause of cancer-related deaths [1]. Prognosis is generally favorable for most early-detected cases of localized prostate cancer. However, in some patients, the disease is very aggressive and even the initial diagnosis shows signs of invasion and metastasis [2]. For this advanced stage of disease, the cornerstone of treatment is androgen deprivation therapy (ADT), a type of hormone therapy in which the body is deprived of androgens through surgical or chemical castration [3–6]. ADT ceases androgen production from its primary source, the testes; however, this does not ensure its elimination from the plasma and body tissues. A small amount is produced by a secondary source, the adrenal glands, and this fount may not be affected by surgical or chemical castration [4]. Although most patients have a positive initial response to ADT, this is usually temporary. Unfortunately, the prognosis is still unfavorable due to the acquisition of an androgen-independent (AI) phenotype that is resistant to secondary endocrine therapy and to chemotherapy [6,7]. At the present time, there is no effective therapeutic option for or clear understanding of the causes of hormone-refractory prostate cancer.

The postulated mechanisms to explain AI relapse include amplification or mutation of the androgen receptor gene (AR), ligand-independent activation of the androgen receptor and alternate signaling pathways, which bypass the growth-promoting functions of the androgen receptor [4,8,9]. Many alterations in the AR have been detected in prostate cancers and a subset of these effect the ligand specificity of the receptor, permitting its activation by nonandrogens or even antiandrogens [10]. This gain of function of the androgen receptor can result in hormone-resistant prostate cancer through the acquisition of AI mechanisms for activation of the androgen receptor [11]. Most patients do not have AR mutations or amplifications, yet they retain active androgen receptor signaling after therapy. Ligand-independent routes to receptor activation could potentially result from increased protein kinase signaling, mediated by oncogenes [12]. Another possible cause of hormone resistance is that the growth-regulatory effects of the androgen receptor can be overridden by alternative, androgen receptor-independent signaling pathways such as the overexpression of the antiapoptotic protein BCL2 [12,13].

In an effort to understand the biologic characteristics of hormone-refractory prostate cancer, several experimental model systems have been derived. Currently, however, only a few models exist that exhibit the features of human prostate cancer growth [6]. In 1996, Ellis et al. [14] characterized a novel, androgen-sensitive, human prostate cancer xenograft, LuCaP 23. The LuCaP 23 xenografts were developed from human prostatic cancer metastases harvested at autopsy and propagated in athymic mice. These cells secrete large amounts of prostate-specific antigen (PSA) and exhibit many of the characteristics of clinical prostatic carcinoma, including the resumption of growth after ADT. Subsequent studies found that LuCaP 23.1 is composed of at least two tumor cell populations representing two different phenotypes: one is neuron-specific enolase (NSE) positive and the other is NSE negative [13]. Furthermore, the NSEpositive tumors, which were recovered after AI relapse in castrated hosts, also expressed BCL2, a gene product known to inhibit apoptosis. More recently, Chen et al. [12] found that hormone-refractory LuCaP tumors had more androgen receptor protein than their parental hormone-sensitive counterparts. This suggests that multiple mechanism for the acquisition of AI prostate cancer may be at work.

In this paper we present the first experimentally driven mathematical model designed to investigate interplay between the possible mechanisms of AI relapse. Comparing the model to the experimental data of LuCaP 23 xenografts shows that increased BCL2 expression, which inhibits apoptosis in AI cells, can result in AI relapse but in a way that is incompatible with the experimental data. However, combining decreased apoptosis with continued proliferation of a subset of androgen-dependent (AD) cells results in tumor relapse, which is consistent with experimental observations. These results suggest that the continual posttherapy activation of the androgen receptor is a crucial component of recurrent prostate cancer associated with the LuCaP xenografts. Furthermore, blocking the upregulation of the androgen receptor and thereby reducing the proliferation of AD cells could lead to significantly longer remissions.

We also compare the mathematical model to experimental data presented in Ref. [12] for the growth of LNCaP tumors in castrated mice. In this case, the model agrees with the experimental evidence that increased androgen receptor activation alone is sufficient to result in hormonerefractory tumor growth.

Methods

The goal of this study is to test the leading hypotheses for AI relapse through the development and simulation of a mathematical model that describes prostate tumor growth before and after hormone therapy. The tumor is viewed as a densely packed, radially symmetric sphere of radius R(t). Cell movement is produced by the local volume changes that accompany cell proliferation and death. The spheroid expands or shrinks at a rate that depends on the balance between cell growth and division and cell death within the tumor volume, the former and latter being meditated by the presence of androgen, a(r, t).

Tumor Growth Model

Prostatic cancer cells, like the normal prostatic cells from which they arise, are sensitive to androgen stimulation of their growth. The presence of androgen stimulates the daily proliferation of these AD cells while inhibiting their daily percentage of apoptotic death [7,15]. Therefore, before treatment continuous net growth occurs. In contrast, after ADT, the proliferation rate of AD cells is significantly reduced and the rate of cellular suicide is increased [7,15,16]. This results in a decline in the number of AD cells within the tumor and an initial positive response. However, in many prostate micrometastases there is also a heterogeneous presence of AI cancer cells whose proliferation rate exceeds their apoptotic death rate even after total androgen blockage is performed [7]. In the LuCaP 23 experiments, AI cells were undetectable before therapy [14]. After ADT, AI cells, which are characterized as being NSE-positive and containing large quantities of BCL2, were harvested [13].

Based on these findings, we first consider a polyclonal tumor consisting of a heterogeneous mix of two cells types (AD and AI, with AI cells being below detectable levels initially) as the mechanism by which AI relapse can occur. The governing equations for the tumor cell populations are derived by applying the principle of conservation of mass to each phenotype. For solid tumor growth, it is widely assumed that cell movement has two components: 1) net collective motion due to the velocity generated by cell growth and death [17–20] and 2) random motility [18–22]. Based on these assumptions, statements of balance may be written as follows for AD cells, p, and AI cells, q.

$$\begin{array}{c}\frac{\partial p}{\partial t}+\nabla \cdot \left(\text{u}p\right)=Dp\Delta p+\alpha p\left(\text{a}\right)p-\delta p\left(\text{a}\right)p,\\ \begin{array}{ccccccccc}\text{Time rate}& & \text{Collective}& & \text{Random}& & \text{Androgen-}& & \text{Androgen-}\\ \text{of change}& +& \text{cellular}& =& \text{cellular}& +& \text{mediated}& -& \text{mediated}\\ \text{of AD cells}& & \text{motion}& & \text{motion}& & \text{proliferation}& & \text{apoptosis}\end{array}\end{array}$$ (1)

$$\begin{array}{c}\frac{\partial q}{\partial t}+\nabla \cdot \left(\text{u}q\right)=D_q\Delta q+{\alpha }_q\left(\text{a}\right)q-{\delta }_q\left(\text{a}\right)q,\\ \begin{array}{ccccccccc}\text{Time rate}& & \text{Collective}& & \text{Random}& & \text{Androgen-}& & \text{Androgen-}\\ \text{of change}& +& \text{cellular}& =& \text{cellular}& +& \text{mediated}& -& \text{mediated}\\ \text{of AI cells}& & \text{motion}& & \text{motion}& & \text{proliferation}& & \text{apoptosis}\end{array}\end{array}$$ (2)

In Equations (1) and (2) D_p and D_q are the assumed constant random motility coefficients of the two types of tumor cells and α_p(a), α_q(a), δ_p(a), and δ_q(a), are their respective proliferation and programmed death rates. These cell proliferation and apoptotic rates are crucially dependent on the local androgen concentration, a(r, t), and their specific characteristics will be discussed in detail in the hormonal effects subsection to follow.

To assess the tumor's response to ADT it will be important to follow the evolution of the tumor volume (= 4/3πR³, for radial symmetry) or, equivalently, the tumor radius R(t). We do this by noting that under radial symmetry, the tumor radius expands at a rate that is equal to the radial component of the velocity there, i.e.,

$$\begin{array}{ccc}\begin{array}{c}\frac{dR}{dt}\\ \text{Time rate of change}\\ \text{of the tumor radius}\end{array}& \begin{array}{c}=\\ \text{=}\\ \end{array}& \begin{array}{c}u(R(t),t),\\ \text{Tumor velocity at}\\ \text{the tumor boundary}\end{array}\end{array}$$ (3)

An equation for the tumor velocity is obtained by adding Equations (1) and (2) with the additional constraint that there are no voids within the tumor so that p + q = 1. Implied by this model formulation is that we begin with a tumor of given initial cell density, p₀, q₀; radius, R₀; and androgen concentration, a₀. By symmetry, at the center of the tumor (r = 0) there is no flux of androgen and the local velocity is zero. Finally, for the tumor cell populations, we impose no flux of p and q at the tumor center and on its outer boundary.

Androgen Levels

The androgen levels within the tumor are assumed constant until the time of treatment. ADT results in the partial blockage of androgen production and the tumor levels will rapidly decrease to a new, significantly lower, steady state.

Hormonal Effects

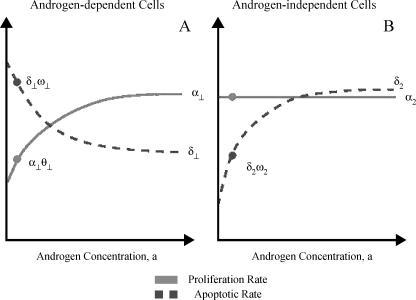
The exponential decline of androgen after ADT causes an increase in the apoptotic death rate of AD cells and a decrease in their proliferation [7,16]. A further consequence of therapy is a decrease in the apoptotic rate of AI cells with no significant difference in their proliferation rate when compared to untreated tumor cells [7]. The effect of androgen on proliferative and apoptotic activity is thus modeled by giving the growth and death rates α_p(a), α_q(a), δ_p(a), and δ_q(a) these experimentally determined characteristics. Figure 1 illustrates how cell kinetics varies with androgen availability.

Figure 1.

The effect of androgen concentration on the proliferation and apoptotic rates of AD cells (A) and AI cells (B). The circles indicate posttherapy androgen concentrations and the respective proliferation and death rates.

The function α_p(a) is chosen so that when androgen is in excess, AD cells proliferate at constant rate, α₁. After ADT, the androgen levels drop quickly and cells proliferate at a fraction of their pretreatment value, α₁θ₁, where θ₁ represents the growth rate in the absence of androgen relative to its value when androgen is abundant. In keeping with experimental observations [7], the function α_q(a) is chosen so that androgen concentration has no effect on the proliferation rate of the AI cells; in other words α_q(a) = α2 ≡ constant.

The functions δ_q(a) and δ_q(a) also suggest that when the androgen supply is plentiful, the cells die at rates δ₁ and δ₂, respectively. When androgen levels fall, the death rate of the AD cells increases to the higher rate δ₁ω₁. However, in lowandrogen environments, increased BCL2 renders the AI cells less susceptible to apoptosis and their death rate decreases to δ₂ω₂. The parameters ω₁ and ω₂ represent the respective death rates in the absence of androgen relative to their values when androgen is abundant. Based on experimental evidence [7,13], we assume that ω_q < 1 and ω_p > 1. Because AD cells are dominant when androgen is abundant [7,14], we will assume α₁ ≈ α₂, δ₁ < δ₂, and α2 < δ₂. This last inequality assures that AI cells are below detectable levels before therapy is initiated (see Figure 1).

Where possible, we make use of published data for the treatment of athymic mice that have been implanted with human prostate cancer xenograft LuCaP 23.1. For those parameters for which no experimental data are available, the goal is to quantify their influence on the model behavior. Table 1 lists each parameter, its baseline value, and source.

Table 1.

List of Baseline Parameter Values Used in Simulations and Their Sources.

Parameter	Value	Reference
α1	0.4621 d-1	[7]*
α2	0.4621 d-1	[7]†
δ1	0.3812 d-1	Best fit to data of Ellis et al. [14]
δ2	0.4765 d-1	[7]‡
θ1	0.8
ω1	1.18–1.35	Best fit
ω2	0.25–1.0	Best fit
P0	0.995	[8]§
Dp	10-10 cm2 s-1	[24]
Dq	10-10 cm2 s-1	[24]

^*Berges et al. [7] report that malignant prostatic cells from five different patients had an average cell cycle time of 48 ± 5 hours. Proliferation rate varies with cell line; we therefore base this parameter on cells dividing once every 36 hours.

^†Berges et al. [7] noted no significant change in the proliferation rate of AI cells when compared with metastatic cancer cells in untreated hosts.

^‡Berges et al. [7] noted a two-fold increase in the percentage of AI cells dying per day when compared to metastatic cancer cells in untreated hosts. We modified this to a 25% increase in the apoptotic rate, which is sufficient result in the exponential decline of any initial population of AI cells.

^§Based on the observation that AI cells were not detectable before ADT [14].

Results

Numerical Simulations

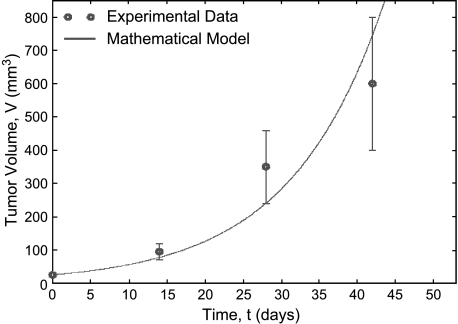
Numerical simulations of Equations (1)–(3) are performed to investigate the tumor's response to ADT for various parameter values. The fit of the mathematical model to the experimental data [14] for intact male mice bearing LuCaP 23.1 xenografts is shown in Figure 2. The proliferation rate, α₁ = 0.4621 per day, is based on the cells dividing once every 36 hours; therefore, the best fit of the model to this data allows for the estimation of the apoptotic rate, δ₁ = 0.3812 per day. Together, these parameters result in a tumor-doubling time of 8.6 days.

Figure 2.

Best fit of mathematical model of tumor volume versus time to the experimental data of [14]. Given the proliferation rate listed in Table 1, this simulation was used to estimate the apoptotic rate of the AD cells, δ_p.

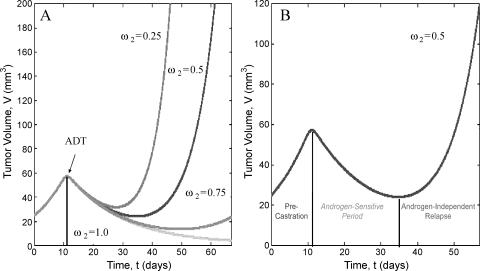
The range of behaviors the model can exhibit once ADT has been initiated is depicted in Figure 3A. All parameters are taken from Table 1 with ω₁ = 1.35 and ω₂ varying between 0.25 and 1.0. In these simulations, polyclonality and decreased apoptosis of AI cells are the only operative mechanisms for tumor relapse. In other words, the increased activation of the androgen receptor (through amplification other pathways) is not considered here as evidenced by the negative net growth rate of the AD cells. The model predicts that for certain parameter values, ADT can result in control of the tumor or in AI relapse. Notice that when ω₂, which represents the amount by which the apoptotic rate is reduced in the absence of androgen, is equal to unity (corresponding to no decreased apoptosis of AI cells) the tumor regresses. As ω₂ increases, corresponding to an increase in BCL2 expression and decreased apoptosis, the model predicts that the tumor response to therapy ranges from prolonged remission (ω₂ = 0.75) to rapid relapse (ω₂ = 0.25). Furthermore, the androgen-sensitive period is always characterized by a marked decrease in tumor volume and both the rate of posttherapy tumor growth and the time of relapse increase and ω₂ decreases.

Figure 3.

Plot of tumor volume versus time before and after ADT as predicted by the mathematical model. In (A), the relative death rate of AI cells in the absence of androgen (ω₂) is varied from 0.25 to 1.0. Tumor growth dynamics range from rapid relapse to prolonged remission or complete regression. (B) Highlights the case when ω₂ = 0.5 and illustrates the exponential tumor growth before treatment, the transient androgen-sensitive period immediately after ADT, and the eventual AI relapse.

Figure 3B highlights the phases of tumor growth before and after ADT with ω₂ = 0.5. From this simulation, it is evident that the model captures the exponential pretreatment tumor growth, the transient androgen-sensitive period immediately after treatment, and the return to exponential growth in the absence of androgen.

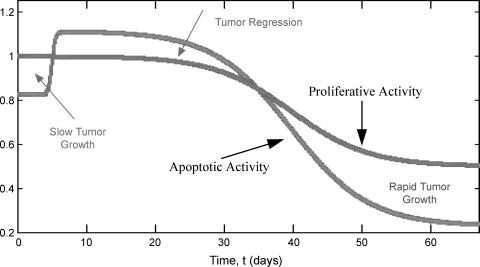
Further information regarding tumor growth and the mechanism for relapse can be gleaned from Figure 4 where the temporal variations in the proliferative activity and apoptotic activity are plotted. These quantities are defined as the total cellular proliferation (or death) within the tumor:

Figure 4.

Plot of the tumor's proliferative and apoptotic activity versus time.

$$\begin{array}{c}\text{Proliferative activity}={\alpha }_p(a)p+{\alpha }_q(a)q\\ \text{Apoptotic activity}={\delta }_p(a)p+{\delta }_a(a)q\end{array}$$ (4)

From Figure 4, it is clear that there are specific times for which proliferative activity exceeds apoptotic activity, resulting in net growth. During the androgen-sensitive period, the apoptotic activity surpasses the proliferative activity resulting in tumor regression. The model also predicts that AI relapse is associated with a decrease in apoptotic activity without an increase in proliferation. This result is in agreement with experimental observations, which found that whereas the BUdR index remained at 50% of the pretherapy value for days 28 to 112, there was a progressive decrease in the apoptotic index [16].

Comparison with Experimental Data

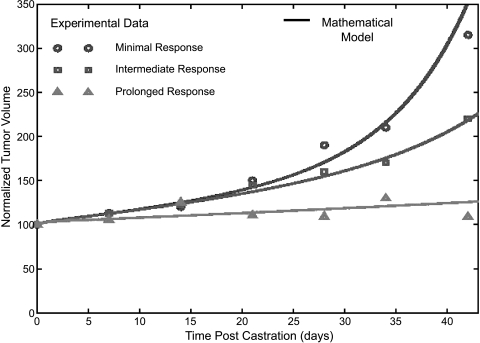
LuCaP Xenografts Figure 5 compares the mathematical model to experimental data [10] that exhibits three types of responses to therapy. For the minimal and intermediate responses, the best fit parameters are associated with a 15% decrease net proliferation of AD cells (or equivalently, an 18% increase in the apoptotic rate) and a 40% and 60% decrease in the apoptotic rate of the AI cells (ω₂ = 0.6, 0.4, respectively). The best fit for the prolonged response corresponds to a 20% increase apoptotic rate of the AD cells with no decrease in the apoptotic rate of the AI cells.

Figure 5.

Best fit of the mathematical model to the experimental data of Ellis et al. [14] for normalized tumor volume versus time post-ADT.

There is an interesting conclusion that can be drawn based on the parameters used in Figure 5 to fit the experimental data. First, note that in all cases the net growth rate of the AD cells is substantially lower than the precastration value; however, it is still positive. In fact, it is impossible to fit the data when ADT results in complete clearance of the AD cells. The implication of this result is that some amount of continual proliferation of the AD cells, even in the absence androgen, occurs. This is consistent with some mechanism of continual AR activation (whether by AR amplification or by other pathways), and is required to match the experimental data of Ellis et al. [14].

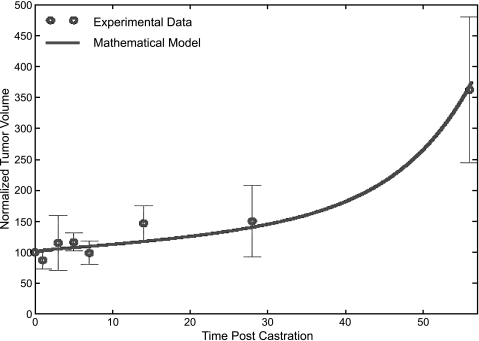
A comparison of the mathematical model and the experimental data of Bladou et al. [16] is given in Figure 6. These data show that ADT induced a significant decrease in the tumor growth rate for the first 7 days postcastration and a progressive increase thereafter. In Figure 5, ω₂ = 1.19 and ω₂ = 0.6, which again suggests the continual proliferation of AD cells even when androgen levels are low.

Figure 6.

Best fit of the mathematical model to the experimental data of Bladou et al. [16] for normalized tumor volume versus time post-ADT.

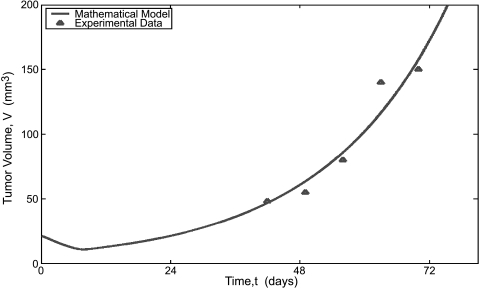
LNCaP Xenografts Figure 6 compares the mathematical model to experimental data of Chen et al. [12] for the growth of LNCaP cells in castrated mice. For these simulations, we have removed the assumption that the tumor is comprised of cells that are BCL2-positive. Therefore, the only mechanism for hormone-refractory tumor growth is upregulation and increased activation of the androgen receptor. The mathematical model predictions are very close to the experimental data and highlight the fact that upregulation of the androgen receptor is sufficient to cause AI tumor growth.

Discussion

The question of whether AI growth of prostate cancer is due to adaptation of AD cells (by amplification of the androgen receptor or some other mechanism) or to clonal selection of AI cells is yet unanswered. In an effort to assist in the understanding of hormone-refractory prostate cancer and mechanisms that possibly mediate this disease, we propose a mathematical model that describes both the pretreatment growth and the eventual post-ADT relapse of human prostate cancer xenografts (LuCaP 23 and LNCaP). Simulations of the model with polyclonality and decreased apoptosis of the AI cells predict that for certain parameter values, ADT can result in prolonged remission of the tumor or in AI relapse. In agreement with experimental observations, the relapse is associated with decrease in apoptotic activity without an increase in proliferation. The mathematical model predicts that this mechanism alone overestimates the tumor reduction during the androgen-sensitive period and is incapable of matching the experimental data for tumor volume as a function of time post-ADT. This overestimation suggests that factors that allow for the survival of some fraction of AD cells may also be operative and highlights the importance of eliminating the continual proliferation of AD cells after therapy.

Another potentially crucial factor associated with hormone- refractory cancer is increased androgen-receptor activation [4,9,12–15,23], which could allow for the reduced but continual proliferation of AD cells even when androgen levels are suboptimal. In fact, Chen et al. [12] recently found that an increase in androgen receptor mRNA was the only change that could be consistently associated with the development of hormone resistance across seven human prostate cancer xenografts (LuCaP and LNCap included). When parameters of the model are changed to allow for effects of upregulation and increased receptor activation in combination with decreased apoptosis, simulations show that the two mechanisms together agree with the LuCaP experimental data. These results imply that both increased BCL2 expression in AI cells and increased androgen receptor activation in AD cells may contribute to the recurrent growth of LuCaP 23 xenografts.

When the mathematical model is compared with the experimental data for hormone-insensitive LuCaP xenografts, there is no need to include mechanisms that bypass the functional importance of the androgen receptor. The model prediction agrees with experimental observations that upregulation and increased receptor activation is sufficient to result in AI tumor growth.

The model presented here is a preliminary study of possible causes of the continued growth of prostate cancer after ADT. The possibility of adaptation of AD cells is considered by changing the parameters of this model to describe the continual proliferation of AD cells in the androgen-depleted conditions occur posttherapy. A future investigation will modify and extend this model to describe the specific adaptation of AD cells by particular pathways, including gain of function of the androgen receptor [10], which result in increased receptor activation in response to low androgen levels. Such an investigation will assist in determining which mechanisms of receptor activation, alone and in combination, lead to relapse that is consistent with experimental data. The mathematical model described in this paper and the extensions alluded to above provide a quantitative method for studying the possible causes of AI prostate cancer growth and can be used to test novel therapeutic strategies targeted at hormone- refractory prostate cancer.

Figure 7.

Comparison of the mathematical model to the experimental data of Chen et al. [12] for tumor volume versus time in castrasted mice implanted with LNCaP tumor xenogarfts. In thse experiments tumor size was measured weakly and scored positive when size reached 40mm³.

Abbreviations

AD

androgen-dependent

ADT

androgen deprivation therapy

AI

androgen-independent

AR

androgen receptor

NSE

neuron-specific enolase