Interspecific and intraspecific competition as causes of direct and delayed density dependence in a fluctuating vole population

Abstract

A 3- to 5-year cycle of vole abundances is a characteristic phenomenon in the ecology of northern regions, and their explanation stands as a central theoretical challenge in population ecology. Although many species of voles usually coexist and are in severe competition for food and breeding space, the role of interspecific competition in vole cycles has never been evaluated statistically. After studying community effects on the population dynamics of the gray-sided vole (Clethrionomys rufocanus) in the subarctic birch forest at Kilpisjärvi, Finland, we report statistical results showing that both interspecific and intraspecific effects are important in the direct year-to-year density dependence. However, interspecific effects are not detectable in the 2-year delayed density dependence that is crucial for generating the characteristic cycles. Furthermore, we show that most of the competition takes place during the winter. The results are evaluated against two models of community dynamics. One assumes that the delayed effects are caused by an interaction with a specialist predator, and the other assumes that they are caused by overgrazing food plants. These statistical results show that vole cycles may be generated by a species-specific trophic interaction. The results also suggest that the gray-sided vole may be the focal species in the birch-forest community, as field voles may be in the taiga and as lemmings may be on the tundra.

Ever since the 3- to 5-year vole cycles were first described by Elton (1), their mechanism has been hotly debated (2). The most popular current hypothesis is that the cycles are caused by an interaction with specialist predators (3–5), but overgrazing (6) and various intrinsic factors (7, 8) have also been suggested. The dynamics of cyclic voles usually are described well by simple second-order autoregressive models (9, 10, 47). In these models, density dependence is distributed about equally between a direct effect acting within 1 year and a 2-year delayed effect. Current research aimed at understanding the vole cycle has focused on developing models that can explain this pattern of density dependence or other associated aspects of the second-order autoregressive dynamics (10–12, 47). Almost all of this work has focused on predation by weasels as the mechanism generating the delayed density dependence. This focus is not surprising, because predator–prey interaction is a simple and ecologically plausible mechanism that generates cyclic dynamics, which tend to show up as second-order autoregressive dynamics in time-series analyses (13).

So far, statistical studies of density dependence in voles have focused on a single species or treated the entire community as if it were a single species. Rarely has interspecific competition been included in the theory of population cycles, perhaps because the ecological importance of competition is secondary to that of predation (14), particularly for herbivores (15). However, field experiments indicate that interspecific competition is widespread and cannot, in general, be ignored (16–18). For voles, there is rich empirical literature that indicates strong interspecific and intraspecific competition for food and breeding space (19–25).

The fact that competition by itself is unlikely to produce population cycles also may have lead to the belief that it is irrelevant to their study. This belief is mistaken for several reasons. Although interspecific competition may not be sufficient for cyclic behavior, it may be integral in explaining the particular anatomy of the cycle. Hanski and Henttonen (26) showed that the inclusion of interspecific competition into a predator–prey model may help to explain several qualitative features of vole cycles. Furthermore, as vole predators usually do not specialize on a single species, they may generate strong apparent (27, 28) competition among voles. This apparent competition may show up as delayed interspecific density dependence, which may therefore shed light on the interaction with the predator. Competition for food may have similar effects. Finally, by separating interspecific and intraspecific effects, existing hypotheses for the cycles can be challenged to explain interspecific as well as intraspecific density dependence. In particular, we may ask whether vole cycles are single-species or community-level phenomena (29, 30).

In this paper, we focus on the strongly cyclic dynamics of the gray-sided vole (Clethrionomys rufocanus) in the subarctic birch forest at Kilpisjärvi, Finland. Covering almost 50 years of time-series data, this site provides the most extensive standardized data on a fluctuating rodent community in the world. We test a set of hypotheses about the role of other species in generating direct and delayed density dependence in the gray-sided vole. We evaluate the results by incorporating them into simple mathematical models, representing two major hypotheses for the causal mechanism behind vole cycles.

Statistical Hypotheses.

Consider the following hypotheses about the sources of density dependence in the gray-sided vole.

Hypothesis 1.

Regulation depends only on the intraspecific density (in both direct and delayed effects).

Hypothesis 2.

Regulation depends on the density of the whole vole community (in both direct and delayed effects).

Hypothesis 3.

Regulation depends on both interspecific and intraspecific density, but this dependence may function in different ways. Three different subhypotheses may be specified.

Hypothesis 3a.

Direct density regulation is intraspecific, whereas delayed regulation depends on the whole community.

Hypothesis 3b.

Direct density regulation depends on the whole community, whereas delayed regulation is intraspecific.

Hypothesis 3c.

Both direct and delayed regulation depend on both interspecific and intraspecific density but to quantitatively different degrees.

For the purpose of testing these hypotheses, we formulate a statistical model for the population dynamics of the gray-sided vole. Let X_cr(t) represent the abundance (on the log scale) of the gray-sided vole in year t, and let X_v(t) represent the log abundance of all arvicoline rodents. We define the density of other voles (i.e., excluding the gray-sided vole) as X_ov(t) = X_v(t) − X_cr(t). We use the following linear model for the yearly rate of population growth in the gray-sided vole:

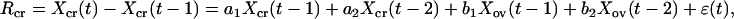1

where ɛ denotes temporally uncorrelated and normally distributed stochastic noise with zero mean (inspection of residuals supports this assumption in our forthcoming analyses); all densities are measured as deviations from their means. The parameter a₁ measures the direct (yearly) intraspecific density dependence in the population, and b₁ measures the interspecific density dependence. The parameters a₂ and b₂ measure interspecific and intraspecific 2-year delayed density dependence, respectively.

In terms of this model, the above hypotheses may be formulated as follows: hypothesis 1 corresponds to setting all b parameters to zero. Hypothesis 2 corresponds to a₁ = b₁ and a₂ = b₂. Hypothesis 3a corresponds to b₁ = 0 and a₂ = b₂. Hypothesis 3b corresponds to a₁ = b₁ and b₂ = 0. Finally, hypothesis 3c corresponds to no restrictions on the parameters.

MATERIALS AND METHODS

Study Site and Data Collection.

The Kilpisjärvi region (69° 03′ N; 20° 48′ E) is situated in the north-western Finnish Lapland. In addition to the gray-sided vole, the permanent rodent community in this area consists of the root vole (Microtus oeconomus), the field vole (Microtus agrestis), the red vole (Clethrionomys rutilus), and the lemming (Lemmus lemmus). The primary time-series data starting in 1949 come from lines of snap traps running through the birch forest from low altitude up to the tree line. Details can be found in ref. 31. The spring trapping is done immediately after the snow melt in June, and the fall trapping is done in mid-September. Reported results are based on the fall data, unless otherwise indicated. We also fitted the hypotheses to the spring data and, because there may have been a change in dynamics in the nineties, to time series truncated in 1989. The results of these analyses are not shown, as they are very similar to those reported.

The trap lines go through a mosaic of drier and more luxuriant forest, but peatlands are not well represented (32). The composition of the rodent community in productive grassy peatlands is different, dominated by the root vole (refs. 33 and 34; unpublished results). Possibly because of competitive exclusion, the gray-sided vole is much less common in these grassy areas (35). It is possible that voles in adjacent habitats may affect our study site through the migration of the voles themselves or their predators. Therefore, we included as explanatory variables the vole density from three closely adjacent study sites (obtained by snap trapping in midsummer). Site A is a highly luxuriant and productive peatland area, where regularly only the root vole is present. Site B is a somewhat less productive peatland area, where the root vole is the most common species, and site C is in the alpine zone where root voles are slightly more common than field voles and gray-sided voles. These sites may be compared with our primary study site, designated D, where gray-sided voles are usually most abundant and sometimes constitute more than 80% of the catch. However, the gray-sided vole seems to be less common in the nineties. Red voles are generally very rare but show increased presence in the birch forest in the nineties. As the red vole is smaller and socially subdominant to the other species (26), their increased presence is more likely to be a consequence rather than a cause of the reduced density of gray-sided voles. Lemmings are irregularly present in high density at all sites. Further details on the sites A–C can be found in refs. 33–35. All data used in this study are available from the authors.

Statistical Methods.

Before analysis all densities were log(1 + x)-transformed. This step was done to make the data conform to the assumptions of the linear Gaussian model. All parameters were estimated by maximum likelihood by using proc model (SAS, Institute, Cary, NC). We evaluate the hypotheses by Akaike’s information criterion [AIC = −2(log likelihood + number of parameters)]. For models with an equal number of parameters, this criterion is simply a comparison of the support (36) of the hypotheses. We also report R², the amount of variation explained by the model.

We also fitted a bivariate model with the summer and winter growth rates as dependent variables and with spring and fall densities as explanatory variables (47). As the incorporation of both seasonal variables and two “species” (the gray-sided vole and the other rodents in the community) variables produce a very large number of possible parameters, we present only a statistically optimal model chosen by AIC. This model was found by starting with variables included in the best fitted bivariate models for the series of the total community and for the gray-sided vole separately (47) and then choosing the best submodel that could be obtained by eliminating parameters from this full model.

Vole densities from the surrounding areas were evaluated as additional explanatory variables in the model for the optimal hypothesis 3b. We tested total vole density from each site, as well as the effect of the separate species averaged over the three sites. In estimating parameters, we used all available data back to 1949.

We did not attempt to use other species in the birch forest as dependent variables, because each individual species is too irregular or rare in site D to be suited for a time-series analysis. Likewise, the gray-sided vole is too rare or irregular at sites A–C to be used as a dependent variable.

RESULTS

Test of Statistical Hypotheses.

The time series of vole abundances from Kilpisjärvi are shown in Fig. 1, and the fits of the hypotheses are presented in Table 1. Note first that hypothesis 1 has poor fit compared with all other hypotheses. Hypothesis 2 has somewhat higher likelihood, but also this hypothesis is too simple. Both hypotheses 1 and 2 can be rejected firmly when compared with the best choice among hypotheses 3a, 3b, and 3c. Considering the full model in Table 1, we see that the direct response to the density of other voles is almost identical to the direct response to conspecifics. It is therefore optimal to combine these into a joint response to total vole density. However, in the delay effect, there is only a weak response to other species. The best choice is thus hypothesis 3b. This hypothesis is well supported; the likelihood ratio between hypothesis 3b and hypothesis 2 is 9.12, meaning that hypothesis 3b is 9.12 times as likely to have produced the data as is hypothesis 2.

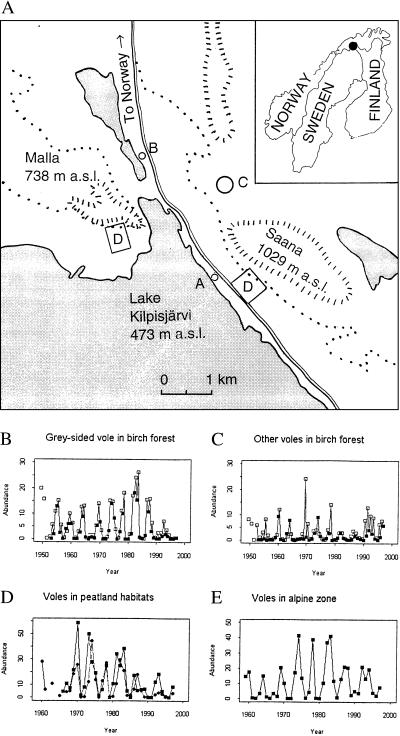
Figure 1.

Rodent dynamics at Kilpisjärvi. (A) Map of the study site. The trap lines at our main study sites in the subalpine birch forest are at the two locations marked D. Additional data from two productive peatland sites marked A and B and from an alpine site marked C were used. m a.s.l., meters above sea level. (B–E) Time series of rodent-trapping indices (voles per 100 trap nights). The abundance of gray-sided voles (B) and the abundance of other voles (C) are indicated for the sites marked D. Filled squares are spring densities, and open squares are fall densities. The gray-sided vole has been less abundant since about 1989. This reduced presence is associated with increased presence of the subordinate red vole, which previously had not been very common, and with the absence of clear peaks in total abundance. Before 1989, instances of low relative density of the gray-sided vole usually were associated with lemming outbreaks. The more pronounced lemming peaks in this series occur in 1960, 1969–1970, and 1978. (D) Summer abundance of voles in the two peatland sites. Squares refer to site A, and circles refer to site B. (E) Summer abundance of voles in the alpine region (site C).

Table 1.

Density dependence in the gray-sided vole

Hypothesis	Parameter restrictions	Model parameters (SE)				AIC	R2, %
1	b1 = b2 = 0	−0.66Xcr(t − 1)	−0.67Xcr(t − 2)			112.09	45.0
		(0.11)	(0.11)
2	a1 = b1 and a2 = b2	−0.68Xv(t − 1)	−0.64Xv(t − 2)			110.07	47.3
		(0.10)	(0.10)
3a	b1 = 0 and a2 = b2	−0.69Xcr(t − 1)	−0.65Xv(t − 2)			110.86	46.4
		(0.11)	(0.11)
3b	a1 = b1 and b2 = 0	−0.69Xv(t − 1)	−0.71Xcr(t − 2)			105.64	51.9
		(0.10)	(0.10)
3c	b2 = 0	−0.69Xcr(t − 1)	−0.71Xcr(t − 2)	−0.67Xov(t − 1)		107.64	51.9
		(0.10)	(0.11)	(0.26)
Full model	None	−0.69Xcr(t − 1)	−0.70Xcr(t − 2)	−0.64Xov(t − 1)	−0.08Xov(t − 2)	109.57	52.0
		(0.10)	(0.11)	(0.29)	(0.33)

Based on Eq. 1 in the main text, hypotheses 1–3 are fitted to the time-series data shown in Fig. 1b and c. X_cr is the log density of gray-sided vole; X_v is the log density of all voles together; and X_ov = X_v − X_cr is a measure of the density of other voles (this measurement is not identical to the log-transformed density of other voles and was chosen to preserve additivity on a log scale). The full model has no restrictions on the parameters. The model presented for hypothesis 3c is the best choice among models that include some b parameters different from the corresponding a parameters. The best model (i.e., the one with the lowest AIC) corresponds to hypothesis 3b, which says that direct regulation depends on the total vole density, whereas delayed regulation depends only on gray-sided vole density. Standard errors (SE) of regression parameters are given in parentheses. Except b₂ in the full model, all estimated parameters are significantly different from zero at P < 0.01 (t test). 

Seasonal Effects.

We have previously shown that a majority of density dependence in the gray-sided vole is generated during the winter (47). The results presented in Table 2 clarify this conclusion by showing that it is statistically optimal to attribute the entire effect of other species to the winter season. As only the fall density of other species appears in this model, the mechanism of interspecific density dependence actually is located within the winter season and is not caused by a delayed effect from the previous spring. The intraspecific density dependence is more complex and involves direct and delayed effects on both winter and summer growth.

Table 2.

Season-specific density dependence in the gray-sided vole

Seasonal R	Model parameters (SE)			R2, %
Winter R = Scr(t) − Fcr(t − 1) =	−0.60Fcr(t − 1)	−0.56Scr(t − 2)	−0.76Fov(t − 1)	62.3
	(0.09)	(0.10)	(0.21)
Summer R = Fcr(t) − Scr(t) =	−0.29Fcr(t − 1)	−0.26Fcr(t − 2)		78.5
	(0.07)	(0.07)

Let F_cr(t) and S_cr(t) denote the fall and spring densities of gray-sided voles in year t, and let F_ov(t) and S_ov(t) be the fall and spring densities of other voles. Joint estimates of density effects on the population growth during winter and during summer are given. Only effects included in the statistically optimal model are shown. The estimated residual variance of the winter and summer are 0.35 and 0.22, respectively, and their covariance is −0.08. The R² column gives the amount of variation explained by the model in spring and fall densities, respectively. Elimination of the F_ov(t − 1) effect leads to a model worse by 9.08 AIC units. Hence, the fit is much better than in a model without any effects of other voles. However, inclusion of an S_ov(t − 2) effect on the winter growth (the second-best model) is worse by only 0.88 AIC units. SE values are given in parentheses. 

Effects of Voles in Other Habitats.

Results shown in Table 3 indicate that vole densities in the three adjacent sites have low impact on the gray-sided vole in the birch forest. Although some direct density effects cannot be excluded, there is little evidence of delayed effects from these habitats.

Table 3.

Effects of vole density in adjacent habitats

Source	Model parameters (SE)				R2, %
Site A	−0.63Xv(t − 1)	−0.69Xcr(t − 2)	−0.13Ya(t − 1)	0.00Ya(t − 2)	53.1
	(0.11)	(0.13)	(0.12)	(0.13)
Site B	−0.64Xv(t − 1)	−0.59Xcr(t − 2)	−0.14Yb(t − 1)	−0.11Yb(t − 2)	54.0
	(0.14)	(0.15)	(0.14)	(0.16)
Site C	−0.50Xv(t − 1)	−0.61Xcr(t − 2)	−0.27Yc(t − 1)	0.03Yc(t − 2)	55.2
	(0.17)	(0.15)	(0.14)	(0.13)
Total L. lemmus	−0.60Xv(t − 1)	−0.66Xcr(t − 2)	−0.15Yll(t − 1)	0.04Yll(t − 2)	56.4
	(0.11)	(0.11)	(0.07)	(0.07)
Total M. oeconomus	−0.62Xv(t − 1)	−0.66Xcr(t − 2)	−0.05Ymo(t − 1)	0.00Ymo(t − 2)	52.8
	(0.14)	(0.15)	(0.06)	(0.07)
Total M. agrestis	−0.56Xv(t − 1)	−0.72Xcr(t − 2)	−0.26Yma(t − 1)	0.00Yma(t − 2)	57.8
	(0.11)	(0.11)	(0.10)	(0.10)
Total C. rufocanus	−0.62Xv(t − 1)	−0.64Xcr(t − 2)	−0.11Ycr(t − 1)	−0.01Ycr(t − 2)	53.1
	(0.13)	(0.16)	(0.10)	(0.11)

Direct and delayed effects, Y(t − 1) and Y(t − 2), of total vole density in three adjacent study areas are added as explanatory variables in the optimal model corresponding to hypothesis 3b. Site A is a highly productive peatland area totally dominated by the root vole; site B is a less productive peatland area; and site C is an alpine area. Additionally, the separate effects of lemmings, root voles, filed voles, and gray-sided voles averaged over the three sites are shown (startnig in 1959). Addition of a 2-year delayed effect can never improve the AIC, but a direct effect of total lemmings (ΔAIC = 2.28; P = 0.04), total field voles (ΔAIC = 4.22; P = 0.02), or site C (ΔAIC = 1.28; P = 0.07) may be included. All available data back to 1949 are used in this analysis. Restricting the range of years to only those where all variables are represented did not alter the results very much. An exception is site B, where a second-year delayed effect of −0.40 will be included by AIC if only data after 1967 are used. SE values are given in parentheses. 

Causal Interpretations of the Statistical Results.

Our statistical results by themselves do not specify the causal mechanisms behind the density regulation. Density-dependent effects may be caused by direct competition within or between species, but because of the short generation time of voles, the 2-year delayed effect is likely to go through a more slowly responding extrinsic third variable. The most obvious possibilities are specialist predators and food plants. To provide causal interpretations of our results, we relate the statistical density dependence to two models of community dynamics. One model assumes that the third variable is a specialist predator of voles, and the other assumes that the third variable is food plants.

Predation.

The main predators of voles in Kilpisjärvi are the least weasel (Mustela nivalis) and the stoat (Mustela erminea). The least weasel is an extremely specialized hunter of voles, and its effect may be particularly severe during the winter when it is a specialized predator under the snow. Let N_cr(t) be the density of gray-sided voles at time t, and let P(t) be the density of specialist predators at time t. Then,

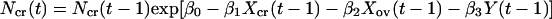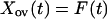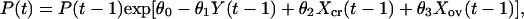2

where Y(t) = ln[P(t)], and all parameters are assumed to be nonnegative. We need not make any assumptions about the dynamics of the other voles. Hence, F(t) is an arbitrary function. The model includes intraspecific competition in the gray-sided vole (β₁), direct interspecific competition from other voles (β₂), and apparent competition (27, 28) caused by an effect of other voles on the predator (θ₃) and by an effect of predators on the gray-sided vole (β₃). The predator is self-regulated (θ₁) and dependent on the gray-sided vole (θ₂).

We now express Eqs. 2 in the same form as Eq. 1 by eliminating the predator, for which there are no data. This elimination proceeds by log transformation and then solving the first equation in Eq. 2 for Y(t − 1). Then, we use the resulting equation to eliminate Y(t) and Y(t − 1) in the last equation in Eq. 2. The result is

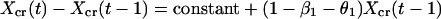3

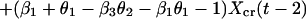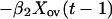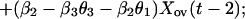which is in the same form as Eq. 1. Comparing parameters with Eq. 1 then gives

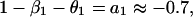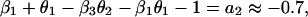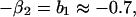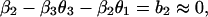4

where we have used approximate values for the estimated parameters. By manipulating these equations, we can derive some qualitative propositions about the community. (i) The gray-sided vole suffers strong interspecific competition from other voles, but it is probably weaker than the intraspecific effect (β₁ ≥ β₂ = 0.7). (ii) There is a strong predator–prey interaction between the predator and the gray-sided vole (β₃θ₂ ≥ 0.7). (iii) The predator is better at using the gray-sided vole than other voles (θ₂ − θ₃ ≥ 0.45/β₃). (iv-a) If we assume that there is strong self-regulation in the predator (θ₁ → 1), we may conclude that other voles do not affect population growth in the predator and that direct interspecific and intraspecific competition are of similar strength (θ₃ → 0 and β₁ → β₂). (iv-b) If, on the other hand, self-regulation in the predator is weak (θ₁ → 0), we may conclude that other voles cause apparent competition by influencing the predator, but that intraspecific competition is much stronger than direct interspecific competition (θ₃β₃ → 0.7 and β₁ − β₂ → 1).

In view of the predation hypothesis, these results are surprising. Although it is conceivable that lemmings are less profitable prey for weasels (37), Clethrionomys voles generally are thought to be less suitable than Microtus; Clethrionomys voles are smaller and more nimble, and they generally exhibit lower density because of their larger and nonoverlapping territories (26, 38), although the territory sizes and population densities of gray-sided voles in the subalpine birch forest are comparable to those of Microtus in their prime habitat (31, 39). In any event, the absence of delayed effects from Microtus is puzzling, because predators should be able to migrate from habitats where Microtus is abundant. We can speculate about two possible explanations of the paradox raised by the predation hypothesis. The first is that the larger and more generalist stoat, which generally exhibits more stable population sizes, keeps the vole-specialist least weasel out of areas with high Microtus density (40). Trapping and radio tracking of stoats show that the home ranges of females center closely around root vole meadows, but the larger male territories may extend into the birch forest (H.H., unpublished observation). The second possibility is that prime Microtus habitats are rare on a large spatial scale (32), making predators specialize on the gray-sided vole as the generally more abundant species. Indeed, further analyses of root voles in sites A–C indicate that gray-sided voles in the birch forest may have delayed effects on the root vole in other habitats (unpublished results). Such an effect must almost certainly be mediated by specialist predators.

Overgrazing.

Under the plant–vole model we may assume that the predominant interacting plant species is the bilberry (Vaccinium myrtillus). The annual new shoots of this species provide the majority of winter food for the gray-sided vole (32). If we let P be interpreted as the density of bilberry shoots, the model is formally similar to the predator–prey model above, except that the signs before the parameters β₃, θ₂, and θ₃ are reversed. As these three parameters always appear as products with each other in Eq. 4, the propositions about the community are mathematically the same. However, the interpretation of the parameters in this model is different; note in particular that the direct competitive effects are not related to food competition, as food is now a variable in the model, but they may be assumed to measure interference competition related to territorial behavior.

This model makes five propositions about the community. (i) There is strong interference competition from other species, but it is not as strong as interference competition within the gray-sided vole species (β₁ ≥ β₂ = 0.7). (ii) There is a strong interaction between the gray-sided vole and the plants (β₃θ₂ ≥ 0.7). (iii) The effect of other voles on the plants is less intense, indicating that there is some niche separation in terms of food (θ₂ − θ₃ ≥ 0.45/β₃). The strength of self-regulation in the plants is unknown. (iv-a) If we assume strong self-regulation in the plants (θ₁ → 1), we may infer that other voles do not affect the plants but do provide interference competition that is as strong as the intraspecific competition (θ₃ → 0 and β₁ → β₂). (iv-b) If we assume weak self-regulation in the plants(θ₁ → 0), we may infer that other voles affect the plants and provide apparent competition for the gray-sided vole but that other sources of interspecific competition are much weaker than the intraspecific competition (θ₃β₃ → 0.7 and β₁ − β₂ → 1).

These qualitative statements are in agreement with vole biology. The diet of the gray-sided vole does not completely overlap the diets of Microtus and the lemming; Microtus primarily feeds on monocot rhizomes during winter, and the lemming feeds on monocots and mosses (41–44). There is reason to expect territorial interference competition from these species (26) and within the gray-sided vole (45). The effect of plants may be more severe during the winter when the voles are more specialized. The overgrazing hypothesis is also consistent with the absence of an effect from Microtus in nearby habitats. Thus, these data are consistent with overgrazing as the cause of population cycles in the gray-sided vole.

CONCLUSIONS

Although our results point to strong competitive effects from other vole species on the gray-sided vole, it is important to realize that these competitive effects cannot cause multiannual fluctuations, because they are not delayed in time. Thus, the population cycles of the gray-sided vole in the birch forest are not generated as a result of interaction with other vole species. Rather, the mechanism must be caused by intrinsic factors or, more likely, to specialized trophic interactions, such as overgrazing of Vaccinium or preferential predation on gray-sided voles by least weasels. Our results suggest that the gray-sided vole may be the focal rodent species in the widespread Fennoscandian birch forest, as are field voles in the taiga (29) and lemmings in the tundra (46).

ABBREVIATION

AIC

Akaike’s information criterion