Monitoring molecular dynamics using coherent electrons from high harmonic generation

Abstract

We report a previously undescribed spectroscopic probe that makes use of electrons rescattered during the process of high-order harmonic generation. We excite coherent vibrations in SF₆ using impulsive stimulated Raman scattering with a short laser pulse. A second, more intense laser pulse generates high-order harmonics of the fundamental laser, at wavelengths of ≈20–50 nm. The high-order harmonic yield is observed to oscillate, at frequencies corresponding to all of the Raman-active modes of SF₆, with an asymmetric mode most visible. The data also show evidence of relaxation dynamics after impulsive excitation of the molecule. Theoretical modeling indicates that the high harmonic yield should be modulated by both Raman and infrared-active vibrational modes. Our results indicate that high harmonic generation is a very sensitive probe of vibrational dynamics and may yield more information simultaneously than conventional ultrafast spectroscopic techniques. Because the de Broglie wavelength of the recolliding electron is on the order of interatomic distances, i.e., ≈1.5 Å, small changes in the shape of the molecule lead to large changes in the high harmonic yield. This work therefore demonstrates a previously undescribed spectroscopic technique for probing ultrafast internal dynamics in molecules and, in particular, on the chemically important ground-state potential surface.

The use of ultrafast light pulses to visualize chemical dynamics has advanced our fundamental understanding of chemical and biochemical processes, by providing a means of monitoring the motion of atoms within a molecule in real time (1, 2). This new field of femtochemistry has enabled the study of important processes such as the dynamics of molecular wave packets and the biochemical basis of vision (3), as well as proton transfer across membranes.

Progress in this area of research has been driven by the development of new ultrashort-pulse light sources, as well as the development of new experimental techniques. Recent work has made use of sources of ultrafast extreme-UV (EUV) (4), x-ray (5, 6), and electron pulses (7, 8) as probes of ultrafast molecular and materials dynamics. These new probes can directly provide atomic-scale spatial resolution (e.g., electron and x-ray diffraction) or site-specific local order (e.g., photoelectron spectroscopy), providing the potential to directly observe chemical reactions in atomic-level detail as they occur. These new tools promise to provide a powerful new window into the microscopic world, particularly as the temporal resolution and energy range of these sources continues to improve.

One recent area of research motivated by these goals is the generation of ultrashort EUV light pulses through the process of high-order harmonic generation (HHG) (9). HHG pushes traditional nonlinear optics to an extreme, by coherently combining many laser photons together to generate coherent beams that span from the UV to the kiloelectronvolt (1 eV = 1.602 × 10⁻¹⁹ J) region of the spectrum. The pulses from HHG are femtosecond to attosecond in duration (10–12). Thus, in the wavelength region where these beams are bright (<100 eV), they have been used to monitor a variety of processes in chemical and materials science and for applications such as holographic imaging (13).

A number of recent experiments have used the process of HHG itself to probe molecular structure (14–17). In HHG, an atom or molecule is first field-ionized by an intense femtosecond laser. The ionized electron then propagates in the optical field and can recollide with its parent ion after a fraction of an optical cycle of the driving field (18, 19). In this picture, the energy of the high harmonic emission can be related to the energy of the recolliding electron and therefore to its de Broglie wavelength (20, 21). For electron energies of 20–100 eV, corresponding to the EUV region of the electromagnetic spectrum where HHG emission is relatively strong, the de Broglie wavelength is in the range of ≈1–3 Å. This value corresponds well to the distances between atoms in a molecule. Recent experimental and theoretical studies have exploited this relationship to show that high harmonic emission from a molecule is sensitive to the structure and orientation of a molecule (14–16, 22). These studies make use of the fact that the orientational distribution of gas-phase molecules can be readily manipulated by impulsively exciting rotational wave packets by using an ultrashort pulse (23–25). This ensemble of aligned molecules can then be used as the medium for generating high harmonics. The symmetry, shape, and orientation of the molecular orbital relative to the polarization of the driving laser field, and therefore to the propagation direction of the recolliding electron, determine the probabilities of ionization and recombination and thus high harmonic emission. Therefore, by monitoring the high harmonic yield as a function of this relative orientation, one can map out a static molecular orbital. Recent studies have shown promise that both simple two-center interference models (15, 17, 22) and tomographic reconstruction methodologies (16) can be used in the case of a diatomic or linear triatomic molecule. In the latter work, the tomographic reconstruction technique succeeded in retrieving the structure of the highest-occupied molecular orbital of N₂. Other very recent work has inferred the rearrangement of atoms within a molecule during the HHG process, by comparing spectra of isotope-substituted (CH₄, CD₄) molecules (26). This experiment is similar in character to past work where x-ray ionization could initiate molecular dynamics that could be monitored through core-hole spectroscopy (27, 28). However, these techniques are limited in that initiation and measurement of the dynamics are necessarily coupled.

In this work, we present previously undescribed and unexpected data that show that HHG is strongly modulated by small changes in the configuration of atoms within a molecule and, as a result, is extremely sensitive to vibrational dynamics. In our experiment, we first excite vibrations in an SF₆ molecule using impulsive stimulated Raman scattering (ISRS) (29–32). We then observe oscillations in the intensity of the EUV high-order harmonic emission generated from the vibrationally excited SF₆. SF₆ was chosen as a spherically symmetric molecule that has been studied using ISRS (31). A simple Fourier transform of the oscillations shows that all the Raman-active modes of SF₆ can be detected, with an asymmetric mode most visible. In the case of conventional stimulated Raman scattering, only the strong symmetric breathing mode has been observed. Based on our experimental data, we determine that the HHG process is sensitive to the relative position of atoms within the molecule with milliangstrom sensitivity. Furthermore, we expand on our experimental findings by doing simple simulations of HHG in molecules. These simulations confirm that HHG is an exceedingly sensitive probe of molecular configuration and that in general we might expect it to be sensitive to any molecular dynamics, for example, to all vibrational modes including both Raman- and non-Raman-active modes. In addition, our data show that the observed oscillations vary in amplitude with observed harmonic order and that different vibrational modes exhibit different behavior. Our data show evidence of relaxation dynamics and sensitivity to reorientation of the vibrationally excited molecules.

These observations collectively demonstrate that monitoring HHG from vibrationally excited molecules yields useful data on intramolecular dynamics that can be directly interpreted independent of complex models or tomographic deconvolution techniques. In particular, this work adds previously undescribed capabilities that are not addressed by any other spectroscopic approach because of the potential sensitivity to all vibrational modes in a molecule [both infrared (IR)- and Raman-active], the ultrafast duration of the probe, and because all vibrational modes are observed simultaneously and coherently. In the future, this approach could be applied to complex and important phenomena such as dissociation dynamics, vibrational mode coupling, fast configuration changes, and nuclear and electron dynamics during structural changes in molecules, including highly excited states and dissociating molecules. Moreover, by monitoring the change in the HHG modulation signal as a function of harmonic order (i.e., recolliding electron wavelength), it also may be possible to extend this technique to monitor dynamic molecular structure. As a result, this technique could become a broadly applicable probe of chemical dynamics, combining the ultrahigh time-resolution of conventional optical pump–probe experiments, with the potential for obtaining structural information complementary to techniques such as femtosecond electron diffraction (7) or proposed experiments using ultrashort-pulse x-rays (33) as a probe of molecular dynamics.

Results

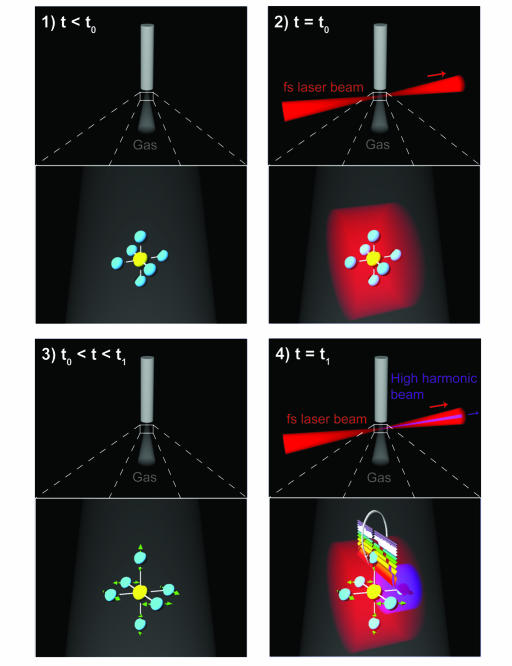
This experiment uses a Ti:sapphire ultrafast laser system producing pulses of energy of 3 mJ and 25-fs pulse duration at a repetition rate of 1 kHz and at a center wavelength of 790 nm (34, 35). The pulse is split into pump and probe pulses, with the pump pulse focused onto an SF₆ gas jet at an incident intensity of ≈5 × 10¹³ W·cm⁻². This pulse excites a vibrational wave packet in the SF₆ through ISRS (31). The probe pulse is used to generate high-order harmonics from the excited molecules and is focused collinearly into the gas at an intensity of ≈3 × 10¹⁴ W·cm⁻². This pulse is polarized parallel to the pump, with a variable pump–probe time delay. The intensity of harmonic orders 19–47 generated by the probe pulse are then recorded by using a soft-x-ray spectrometer and CCD camera, while the pump–probe time delay is varied. A schematic of the experiment is shown in Fig. 1.

Fig. 1.

Schematic of experiment. At time 0 (t₀), the femtosecond laser excites the Raman-active vibrations in SF₆ by ISRS. The vibrational wave packet then evolves in time, until times t = t₁ when a probe femtosecond laser pulse generates high-order harmonics from the vibrationally excited molecule.

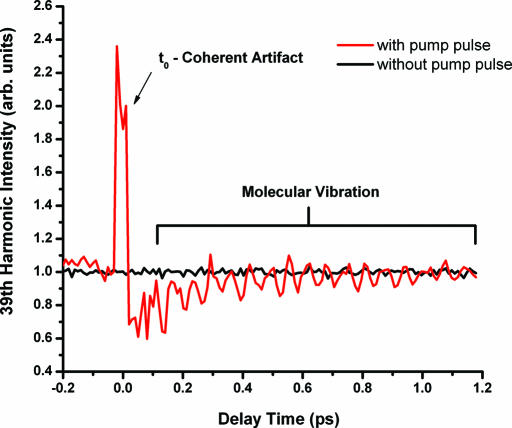
Fig. 2 shows the intensity of the 39th harmonic generated in SF₆ as a function of pump–probe time delay. The red curve shows the 39th harmonic emission from the vibrating molecules, and the black curve shows the high harmonic signal when the pump pulse is blocked (to determine the baseline noise level). When the pump and probe pulses are overlapped, a coherent artifact appears due to the superposition of the two pulses. At positive delay times, the harmonic intensity is periodically modulated with 17 oscillation periods recorded. The amplitude of the oscillations decays as the delay time is increased. At very small delay times, the baseline decreases, recovering within ≈300 fs, although the magnitude of this decrease varies between data sets.

Fig. 2.

The intensity of the 39th harmonic generated from vibrationally excited SF₆ as a function of time delay between the pump pulse and the EUV-generating probe pulse. The red curve shows the high harmonic emission with the pump pulse present. The black curve shows the emission without the pump pulse present.

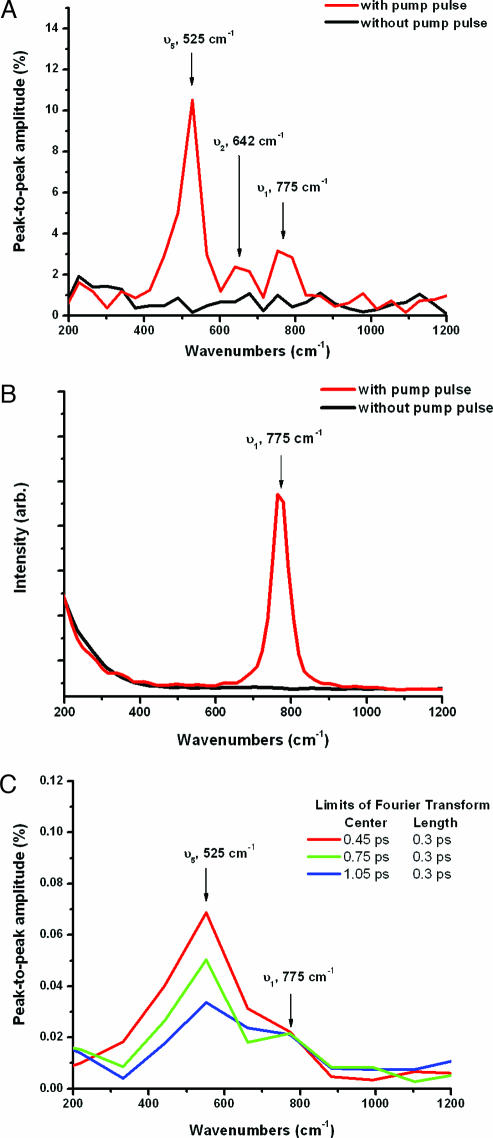
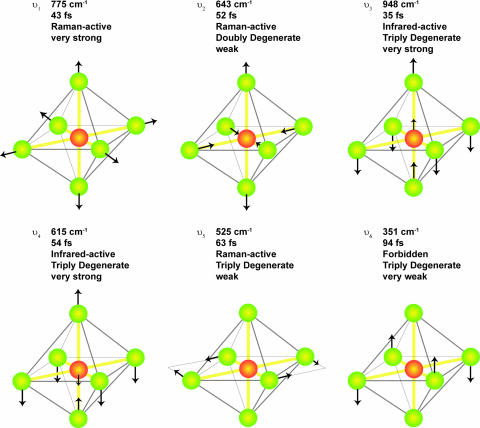
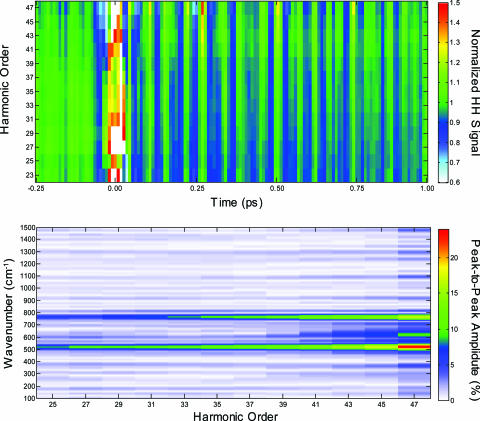
To deduce which vibrational modes are detected, Fig. 3A shows a discrete Fourier transform of the data shown in Fig. 2, for a time interval between 0.3 and 1.2 ps. The red curve shows the Fourier transform of the modulated high harmonic signal after the pump pulse excites the vibrations, whereas the black curve corresponds to the Fourier transform of the unmodulated high harmonic background (without the pump pulse present). The vertical axis corresponds to the peak-to-peak percent amplitude modulation of the high harmonic signal. Three peaks are visible at 775, 643, and 525 cm⁻¹, corresponding to oscillation periods of 43, 52, and 63 fs, respectively. The Fourier spectrum was normalized such that the spectral amplitude is the percentage modulation of the high harmonic signal in the time domain. These peaks can be assigned to the three Raman-active vibrational modes of SF₆: ν₁, ν₂, and ν₅ (36, 37). A representation of the normal vibrational modes of SF₆ is shown in Fig. 4. The mode ν₁ is totally symmetric and strongly Raman-active, whereas ν₂ and ν₅ are asymmetric and doubly and triply degenerate, respectively. These asymmetric modes are weakly Raman active. This molecule also has two IR-active modes and one forbidden mode, which are not excited by our impulsive Raman pump pulse and therefore cannot be observed in this experiment.

Fig. 3.

Comparison of vibrational frequencies. (A) Discrete Fourier transform of the 39th harmonic emission from Fig. 1, showing the three Raman-active modes of SF₆ that are excited by our ISRS pump pulse. (B) Stimulated anti-Stokes Raman scattering of a 400-fs probe pulse centered at 400 nm from SF₆, after excitation by the same ISRS pump pulse used to excite vibrations in Fig. 1. (C) Discrete Fourier transform of the harmonic emission data from Fig. 1 for 0.3-ps time intervals centered at different times after the pump pulse (0.45, 0.75, and 1.05 ps).

Fig. 4.

Normal modes of vibrations for SF₆. The wavenumber, period, degeneracy, and activity of each mode is shown (36). SF₆ has three Raman-active modes, two IR-active modes, and one forbidden mode (which are not excited in our experiment).

It is interesting to note that the spectrum in Fig. 3A demonstrates that HHG is sensitive to all three Raman-active vibrational modes in SF₆, regardless of their symmetry or degeneracy. Fig. 3B, in contrast, shows data where visible laser light is used as a probe of the ultrafast vibrational excitation. Here, only the strongly Raman-active symmetric breathing mode, ν₁, is observed. This experiment was done by using the same pump pulse to excite the molecules, in the same experimental configuration, with the exception that the experimental chamber was backfilled with SF₆ rather than using the gas jet (to increase the signal level). The excitation level of individual vibrational modes of the molecules should thus be identical to the HHG experiment. However, instead of using HHG to probe the molecular vibrations, this experiment used conventional impulsive stimulated Stokes and anti-Stokes Raman scattering, using a probe pulse of ≈400-fs duration at a 400-nm central wavelength. The molecular vibrations modulate the index of refraction of the gas and produce sidebands in the detected spectrum of the probe pulse. The data of Fig. 3B show the anti-Stokes light scattered to higher energies. Only the strongly Raman-active ν₁ mode is observed. This result is consistent with extensive earlier measurements by Bartels, Weinacht, and coworkers (31) and by Korn and coworkers (30, 38), who also observed only the ν₁ mode using visible or IR probe pulses.

The fact that conventional ISRS is insensitive to the asymmetric vibrational modes can be explained by the different probabilities for excitation and detection of each vibrational mode. The spontaneous Raman peaks reported in ref. 37 are in the ratio ν₁:ν₂:ν₅ of 20:1:1. The spontaneous Raman intensities are proportional to the square of the differential polarizability δα/δq_i, where q_i is the generalized coordinate of vibrational mode i and α is the polarizability of the molecule. In ISRS, the excitation of the mode by the short IR pump pulse will be proportional to the square of the differential polarizability, whereas the scattered Raman sideband intensity will be proportional to the fourth power of the differential polarizability. Therefore, although the asymmetric modes can be excited, as seen in Fig. 3A, they are less easily detected by IR or visible Raman scattering because the peaks would be ≈400 times smaller than the peak corresponding to the symmetric mode. This signal level is below the noise level in the data shown in Fig. 3B.

For each of the three observed vibrational modes, Fig. 5Upper shows the modulation of the high harmonic signal as a function of harmonic order for orders 19–47, which corresponds to photon energies between 30 and 72 eV. Fig. 5 Lower plots the Fourier transform of the data from Upper and shows the amplitude of the three Raman-active modes as a function of harmonic order. The amplitude of all modes increases with harmonic order, with the signal of the asymmetric mode ν₂ only observed above the noise level for harmonic orders >37.

Fig. 5.

High harmonic signal for all observed harmonic orders. (Upper) Harmonic orders 23–47 are shown as a function of time delay. The high harmonic signal has been normalized by the signal without the pump pulse present. (Lower) Amplitude of the high harmonic modulation by the excited Raman-active modes as a function of harmonic order. The amplitude of all modes significantly increases with harmonic order. The modulation of the high harmonic signal due to the ν₂ mode is above the noise level only for harmonic orders >37.

Discussion

There are three very interesting aspects to the data presented in Figs. 2–5. First, it is clear that the modulation in the high harmonic signal is more sensitive to more vibrational modes in SF₆ than are either spontaneous Raman (37) or ISRS (31, 38). Fig. 4 lists both the Raman- and IR-active vibrational modes of SF₆, with approximate graphical representations of the motion of the atoms in these modes. In our experiment, we neither excite nor observe the IR-active modes because of the impulsive Raman excitation scheme. In spontaneous Raman scattering from vibrating molecules, all three Raman-active modes can be seen, but the symmetric mode produces a much stronger signal (×20) than the asymmetric modes as discussed above. This observation is common in many molecules. Moreover, in all experiments that employ coherent stimulated Raman scattering to probe dynamics in SF₆ (31, 38) (as well as the data in Fig. 3B), only the symmetric mode ν₁ is observed. In fact, the lower-frequency asymmetric modes might be excited at levels close to that of the symmetric mode. This assumption is because our excitation pulse duration is more impulsive for the longer-period asymmetric vibrations, where the ratio of the vibrational oscillation period to the laser pulse duration will determine the strength of the impulse excitation (39).

The fact that we can observe all of the excited weak and strong Raman modes that are excited in our experiment suggests that using the modulation of high harmonic emission as a probe of vibrational dynamics in molecules might in general be sensitive to more (if not all) vibrational modes in a molecule (both IR- and Raman-excited). This finding contrasts with other detection techniques where only a subset of modes can be easily probed. Moreover, another significant advantage of our harmonic detection scheme is that a much smaller number of molecules is needed to observe the vibrational signal. Comparing the relative molecular densities in the two cases studied here (10¹⁸ molecules per cm³ over a fraction of a millimeter for the gas jet harmonic generation experiments, compared with 2 × 10¹⁹ molecules per cm³ in the backfilled chamber that extends the interaction lengths to several centimeters), we estimate that HHG requires a factor of 10³ lower density-length product than a comparable stimulated Raman scattering experiment.

The second very interesting aspect of our experiment is that high harmonic emission is sensitive to small amplitude motions of the nuclei. In our experiment, we observed modulations of up to ≈10% in high harmonic yield. We estimate that this effect results from an oscillation amplitude of ≈2% in the internuclear distance. This estimate is based on calculating the time evolution of the expectation value of the S–F internuclear distance for the symmetric breathing mode ν₁ during and after the pump laser pulse. In the calculation, the time-dependent Schrödinger equation of the molecule in the laser field is numerically solved by using the potential energy curve of the S–F bond reported in ref. 40. After the laser pulse, the relative populations of the states composing the vibrational wave packet are p(v = 0) = 0.85 and p(v = 1) = 0.14. Higher excited states are not significantly populated in this experiment.

To explore the sensitivity of high harmonic emission to different vibrational modes in a molecule, we considered theoretically high harmonic emission from diatomic and linear triatomic molecules. Exact modeling of SF₆ is very challenging because a 3D, fully quantum model would be required to reproduce the experimental data. However, a fully quantum 1D model allows us to study the magnitude of the modulation of the high harmonic emission due to the motion of the nuclei. In our simulations, we numerically solve the time-dependent Schrödinger equation for H₂⁺ and H₃²⁺, where the molecule is aligned along the polarization axis of the laser field. We model the interaction between the molecule and the laser field without the use of Born–Oppenheimer approximation but rather by using a semiclassical approximation where we describe the electron motion quantum-mechanically, whereas the motion of the nuclei is described classically. We first calculate the ground state of the molecule using a procedure that iteratively seeks the equilibrium position of all positive and negative charges involved. We assume that for our laser pulse intensity and wavelength, the nuclear motion is slow enough that the electrons can adiabatically follow the motion. Thus, the simultaneous self-consistent solution of the Schrödinger and Newtonian equations at each time step yields the instantaneous electron wavefunction. This method allows us to calculate the dipole acceleration of the electrons and (after a Fourier transform) the spectrum of the scattered radiation, i.e., the high harmonic spectrum as function of the bond length and degree of ionization as the molecule vibrates.

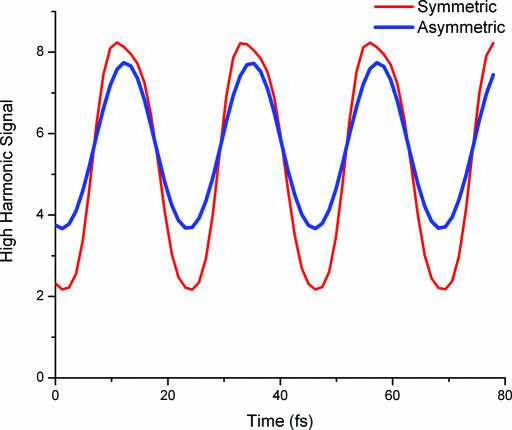
Our simulations indicate that for both the diatomic and triatomic cases, an ≈1% change in bond length results in an ≈10% modulation of the high harmonic signal, which is consistent with our estimate of the level of Raman excitation in our experiment. Moreover, calculations for a 1D triatomic molecule show that the high harmonic signal is modulated by approximately equal amounts for the two allowed vibrational modes in the molecule, only one of which would be Raman-active. The results of these simulations are shown in Fig. 6. This result also indicates that HHG should be sensitive to both Raman- and IR-active vibrational modes and, in general, to any type of molecular motion. Given the multiphoton nature of HHG, as well as the microscopic physics where a high-energy electron with a short de Broglie wavelength recollides and recombines with the molecule, it is very reasonable to expect that the process will not be governed by the same selection rules as more conventional Raman processes that determine which modes can be detected. Further experiments and simulations will be needed to accurately deduce the vibrational amplitudes of the various modes from our data, because Fig. 5 shows that the relative amplitude of the modes change as a function of harmonic order. However, dynamical changes in these modes can be observed independent of the sensitivity of the harmonic generation process to each mode.

Fig. 6.

Fully quantum numerical simulations for a 1D triatomic molecule showing the high harmonic signal as a function of delay after the vibrations are initiated. The symmetric and antisymmetric vibrational modes of the molecule modulate the high harmonic signal by approximately equal amounts, although only one mode would be Raman-active. This result indicates that HHG should be sensitive to both Raman- and IR-active vibrational modes and, in general, to any type of molecular motion.

It is interesting to note that because the noise level in our experiment is 0.5–1%, which from our calculations corresponds to an ≈0.1% modulation in bond length, the sensitivity in this experiment should be ≈2 mÅ. Such small-amplitude motions are on the order of a fraction of the de Broglie wavelength of the recolliding electron, or 0.15 nm at a photon energy of 70 eV. Our numerical calculations suggest that whereas small-amplitude motions of molecules are detectable, large-amplitude motions should modulate the high harmonic signal even more strongly. High harmonic emission may thus be useful for studying floppy molecules (41) or molecular dissociation (42). We note that when describing HHG in a three-step model (21), both the ionization rate (43) and the recombination probability will be affected by the vibrational excitation of the molecule. However, our present experiment is not able to quantitatively separate the contributions of these two processes.

Finally, another interesting aspect in our experiment is that we observe relaxation dynamics within the molecule because the amplitude of the modulation of the high harmonic signal in Fig. 2 decays for increased delay times. Fig. 3C shows the Fourier transform of the data of Fig. 2 for early and late time intervals after excitation by the pump pulse. Just after excitation, the peak corresponding to the asymmetric mode ν₅ is approximately twice as strong as the peak corresponding to the symmetric mode ν₁. However, at larger time delays of ≈1 ps, the magnitude of the asymmetric mode peak decays to the same level as that due to the symmetric mode. In contrast, no decay is observed in the case of the symmetric mode. (Because of the low spectral resolution, the other asymmetric mode ν₂ cannot be identified.) This observation of rapid decay of the ν₅ asymmetric mode can be interpreted as rotational dephasing of the excited molecular ensemble. In the impulsive Raman excitation process, the asymmetric modes will be excited in the direction of the polarization of the pump pulse. Subsequently, the molecules rotate randomly. Thus, when the probe pulse arrives, a smaller fraction of molecules will have the ν₅ mode vibrating along the polarization axis of the probe pulse. The modulation of the observed high harmonic emission signal will thus be reduced. This argument does not apply to the spherically symmetric mode ν₁, which is consistent with the observation of a constant amplitude for that mode, as shown in Fig. 3C.

An interesting question to discuss is the mechanism for the modulation of the harmonic emission in a vibrating molecule. Both the ionization step and the recombination step are expected to be sensitive to the instantaneous shape of the molecule and therefore to influence the magnitude of the EUV emission. We can make some general statements from analyzing our data. First, all observed harmonic orders are modulated similarly to the 39th harmonic shown in Fig. 2, and this modulation is in phase for all orders, as seen in Fig. 5 Upper. Because a modulation in the ionization rate would affect all orders, this observation may suggest that the ionization step contributes to modulating the HHG signal. On the other hand, Fig. 5 Lower displays the integrated strength of each Fourier peak corresponding to the amplitude of each vibrational mode as a function of harmonic order. The variation of modulation strength with harmonic order can likely be attributed to the recombination of the electron with the parent molecule, with the higher harmonics (corresponding to shorter wavelengths of the recolliding electrons) more sensitive to small displacements of the atoms in the molecule. Because our vibrational amplitudes are low (few percent of the bond length), we do not expect a quantum interference effect due to a change of bond length. This interference can suppress some harmonic orders, whereas others are enhanced at the same time, as has been observed by Kanai et al. (22) and Vozzi et al. (17). Thus, both the ionization and recombination steps contribute to modulating the high harmonic signal. However, the analysis of these modulations to extract the vibrational dynamics and dephasing in the molecule is independent of the relative contribution of ionization and recombination dynamics to the observed signal. Also, by monitoring the modulations of higher harmonic orders, the variation of the modulations might be used to extract dynamic structural information. Finally, because the timing of the electron recollision process varies with the electron energy, variations in harmonic signal as a function of harmonic order also potentially provide information on suboptical-cycle, attosecond time-scale dynamics that can compliment the pump–probe data (44). In the future, important questions such as the applicability to large molecules, the experimental verification of sensitivity to IR-active modes, as well as the ultimate time resolution of the technique, need to be studied.

Conclusion

In summary, this work demonstrates the potential for a new kind of vibrational spectroscopy, based on high-order x-ray Raman scattering, that has unique advantages. First, the high harmonic emission as a probe of internal dynamics in a molecule is more sensitive to more vibrational modes in a molecule than is the case for ultrafast visible spectroscopies and should not be limited by “dark states” present in other vibrational spectroscopies. Furthermore, these data provide useful information on dynamics even without extensive analysis of the recollision physics and phase-matching issues. This technique should thus be generally useful for observing dynamics in polyatomic molecules and could be used to investigate energy redistribution among all vibrational modes in molecules (both IR- and Raman-active), as well as monitoring coherences between vibrational modes. Second, this technique is useful for observing chemically important ground-state dynamics in molecules, and because the vibrations observed herein are small-amplitude motion, the utility of this technique to monitor (generally much larger) conformational changes in molecules is very likely. Third, HHG is a coherent ultrafast process that occurs on a subcycle timescale. Thus, it may be possible to monitor ultrafast electronic redistribution within the molecule. For example, nonadiabatic processes are ubiquitous in polyatomic molecules, where nuclear and electronic motions are coupled. Because HHG is sensitive to nuclear motion and to the symmetry of the electronic state, it shows promise as an in situ probe of femtosecond and even attosecond (11, 12, 45–47) nuclear and electron dynamics in molecules. Finally, by combining this technique with molecular alignment techniques, structural information about the molecule can be retrieved as a function of time as both vibrational and rotational wave packets evolve or as molecules are highly excited and dissociate.

Methods

A two-stage Ti:sapphire amplifier system producing 3-mJ pulses with a duration of 25 fs, at a repetition rate of 1 kHz, and at a center wavelength of 790 nm was used to generate the pump pulse and the EUV probe pulse for this experiment. The pump pulse was focused onto a continuous SF₆ gas jet at an incident intensity of ≈5 × 10¹³ W·cm⁻² and with a spot size of 35 μm (1/e² diameter). This pump pulse excited a vibrational wave packet in the SF₆ through ISRS. The probe pulse was used to generate high-order harmonics from the excited molecules. This pulse was focused collinearly with the pump pulse into the gas, at an intensity of ≈3 × 10¹⁴ W·cm⁻² and with a spot size of 25 μm (1/e² diameter). This pulse was polarized parallel to the pump and had a variable time delay. Both beams were focused into the gas jet at a distance of 300 μm from the nozzle. The nozzle of the gas jet consisted of a 5-mm section of capillary tube of 150-μm inner diameter. The stagnation pressure was 2 × 10³ torr, and the gas expanded supersonically into a chamber maintained at a pressure of 10⁻³ torr. We estimate the density of SF₆ to be ≈10¹⁸ molecules per cm³ in the region of the laser focus. The EUV radiation generated by high harmonic upconversion was separated from the fundamental laser light by passing it through two aluminum filters of 200-nm thickness, placed before and after the glancing-incidence EUV spectrometer. The intensity of harmonic orders 19–47 generated by the probe pulse was then recorded by using a soft-x-ray spectrometer (Hettrick Scientific, Richmond, CA) and x-ray CCD camera (Andor Technology, Belfast, North Ireland), whereas the pump–probe time delay was varied.

Abbreviations

EUV

extreme-UV

HHG

high-order harmonic generation

ISRS

impulsive stimulated Raman scattering.